Как найти время, скорость и расстояние

Расстояние

Мы постоянно ходим пешком и ездим на транспорте из одной точки в другую. Давайте узнаем, как можно посчитать это пройденное расстояние.

Расстояние — это длина от одного пункта до другого.

• Например: расстояние от дома до школы 3 км, от Москвы до Петербурга 705 км.

Расстояние обозначается латинской буквой s.

Единицы расстояния чаще всего выражаются в метрах (м), километрах (км).

Демоурок по математике

Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.

Скорость

Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.

Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.

Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.

Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.

Показатели скорости чаще всего выражаются в м/сек или км/час.

Скорость сближения — это расстояние, на которое сблизились два объекта за единицу времени. Чтобы найти скорость сближения двух объектов, которые движутся навстречу друг другу, надо сложить скорости этих объектов.

Скорость удаления — расстояние, на которое отдалились друг от друга два объекта за единицу времени.

Чтобы найти скорость удаления объектов, которые движутся в противоположных направлениях, нужно сложить скорости этих объектов.

Чтобы найти скорость удаления при движении с отставанием или скорость сближения при движении вдогонку, нужно из большей скорости вычесть меньшую.

Онлайн-курсы по математике для детей — отличный способ разобраться в сложных темах под руководством внимательного преподавателя.

Время

Время — самое дорогое, что у нас есть. Но кроме философии, у времени есть важная роль и в математике.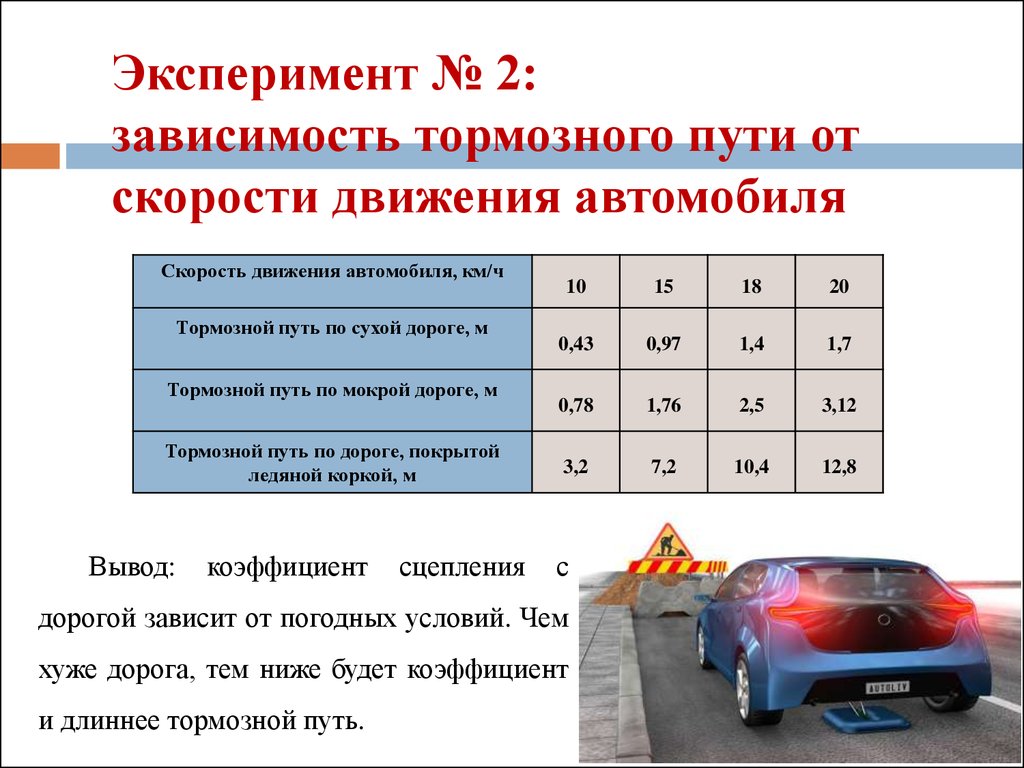

Время — это продолжительность каких-то действий, событий.

• Например: от метро до дома — 10 минут, от дома до дачи — 2 часа.

Время движения обозначается латинской буквой t.

Чаще всего вам будут встречаться такие единицы времени, как секунды, минуты и часы.

Эта формула пригодится, если нужно узнать, за какое время тело преодолеет то или иное расстояние.

Взаимосвязь скорости, времени, расстояния

Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.

Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.

Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес-браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?

Как рассуждаем:

Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров в минуту на 15 минут, мы определим расстояние от дома до магазина:

v = 50 м/мин

t = 15 мин

s = v × t = 50 × 15 = 750 (м)

Ответ: мы прошли 750 метров.

Если известно время и расстояние, то можно найти скорость: v = s : t.

Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние между двором и площадкой — 100 метров. Первый школьник добежал за 25 секунд, второй за 50 секунд. Кто добежал быстрее?

Как рассуждаем:

Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников — это расстояние, которое они пробегают за 1 секунду.

Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:

100 : 25 = 4

Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).

В нашей задаче расстояние дано в метрах, а время в секундах. Значит, будем измерять скорость в метрах в секунду (м/с).

100 м : 25 с = 4 м/с

Так мы узнали, что скорость движения первого школьника 4 метра в секунду.

Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:

100 : 50 = 2

Значит, скорость движения второго школьника составляет 2 метра в секунду.

Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.

4 (м/с) > 2 (м/с)

Скорость первого школьника больше. Значит, он добежал до спортивной площадки быстрее.

Ответ: первый школьник добежал быстрее.

Если известны скорость и расстояние, то можно найти время: t = s : v.

Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?

Как рассуждаем:

Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?

Чтобы ответить на этот вопрос, нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое дойдем до стадиона:

s = 500 м

v = 100 м/мин

t = s : v = 500 : 100 = 5 (мин)

Ответ: от школы до стадиона мы дойдем за 5 минут.

Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.

2.5. Расчёт скорости движения автомобиля

Для
всех ступеней коробки передач и
дополнительной коробки рассчиты­ваются
значения
скорости движения автомобиля в зависимости
от частоты вращения коленчатого вала
двигателя (по согласованию с руководителем
рас­чёт может производиться только
для высшей ступени дополнительной
короб­ки).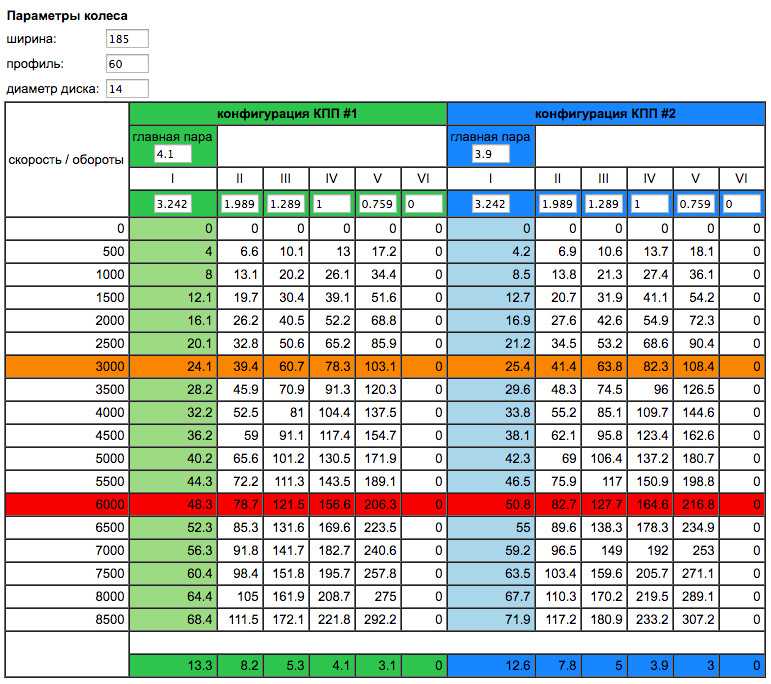

Расчёт
ведётся по формуле

где
v
—
скорость автомобиля, км/ч;

n
—
частота вращения коленчатого вала
дви­гателя, об/мин;

r_К
—
радиус качения, м;

и₀
—
передаточное число главной переда­чи;

и_к
—
передаточное число рассчитываемой
ступени коробки передач;

и_д
—
пе­редаточное число рассчитываемой
ступени дополнительной (раздаточной)
ко­робки.

Значения
частоты вращения коленчатого вала
берутся теми же, что и при построении
внешней скоростной характеристики.

Рассчитанные
значения v_t
заносятся
в столбец 4 табл. 2.1. Графики зави­симости
скорости движения автомобиля от частоты
вращения коленчатого вала двигателя
представляют собой серию лучей, выходящих
под разными углами из начала координат
рисунок 2. 2.

Рис.
2.2 Зависимости скорости движения
автомобиля от частоты вращения коленчатого
вала по передачам.

Тяговая
характеристика представляет собой
зависимость силы тяги авто­мобиля от
скорости движения по передачам. Значения
силы тяги Р_Т
рассчиты­ваются
в отдельных точках по формуле

(2.26)

где
М_К
—
крутящий момент двигателя, Нм;

η_Т
—
КПД трансмиссии.

Результаты
расчёта Р_Т
заносятся
в столбец 7 табл. 2.1, и по ним строятся
графики зависимости Р_Т
=f(V)
по
передачам.

Тяговый
баланс автомобиля описывается уравнением
тягового или силово­го баланса

Р_Т
=
Рд
+
Рв
+
Ри
,
(2. 27)

где
Р_Т
—
сила тяги автомобиля, Н;

Р_д
—
суммарная сила сопротивления дороги,
Н;

Р_в
—
сила сопротивления воздушной среды, Н;

Р_и
—
сила инерции автомоби­ля, Н.

Величина
Р_д
определяется
по выражению

Р_д
= G_aψ, (2.28)

где
G_a
— полный
вес автомобиля, Н; ψ
— суммарный
коэффициент сопротивления дороги.

Суммарный
коэффициент сопротивления дороги
является величиной, за­висящей от
скорости автомобиля. Однако учёт этой
зависимости сильно ос­ложняет
выполнение тягового расчёта и в то же
время не даёт важного для практики
уточнения. Поэтому при выполнении
тягового расчёта рекомендуется принять
значение ψ
постоянным,
равным тому значению, которое было
рассчи­тано для максимальной скорости
движения автомобиля при определении
мощ­ности двигателя, необходимой для
движения на режиме максимальной
скоро­сти, т. е. принять везде ψ=ψ_v.

При
каком-то одном выбранном значении ψ
величина
Р_д
остаётся
постоян­ной для всех расчётных точек
на всех передачах. Поэтому значение Р_д
подсчитывается
один раз и в таблицу не заносится. На
графике тяговой характеристи­ки
зависимость P_Т=f(v)
представляется
в виде прямой, параллельной оси абс­цисс.

Рис.
2.3 Тяговая характеристика автомобиля.

Сила
сопротивления воздушной среды Р_в
составляет
величину

(2.29)

где
с_х
— коэффициент
продольной аэродинамической силы;

р_в
— плотность
воздуха, кг/м³
;

к_в
— коэффициент
обтекаемости, кг/м³;

F
— лобовая
площадь авто­мобиля, м ;

v_в
— скорость
воздушного потока относительно
автомобиля, км/ч.

При
расчёте можно задать ρ_в=1,225
кг/м . Скорость воздушного потока обычно
принимается равной скорости движения
автомобиля.

Значения
Р_в
рассчитываются
для всех точек и заносятся в столбец 5
табл. 2.1. График зависимости Р_в
от
скорости представляет собой параболу,
проходящую через начало координат.

Для
удобства дальнейшего анализа этот
график смещают вверх на ве­личину,
равную Р_д
(в
принятом для сил масштабе). Фактически
при таком построении этот график выражает
зависимость (P_в+P_d)=f(v).

Сила
инерции автомобиля Р_и
после
расчёта Р_д
и
Р_в
может
быть определена как замыкающее слагаемое
силового баланса

(2. 30)

На
графике значение Р_и
определяется
отрезком прямой, проведённой для нужного
значения скорости параллельно оси
ординат, между точками пересечения этой
прямой графиков P_Т=f[v)
и
(P_д+P_в)=f(v).
Если
заданная скорость может быть обеспечена
на нескольких передачах, то каждой из
этих передач будет соответствовать
своё значение силы инерции. Рассчи­танные
значения Р_и
следует
занести в столбец 6 табл. 2.1.

Значение
Р_Т
заносится в столбец 7 табл. 2.1. Тяговая
характеристика автомобиля представлена
на рис. 2.3.

Время, скорость и расстояние | How Fast Per Second Chart

При столкновении транспортных средств, когда стороны оспаривают ответственность, они обычно оспаривают время, скорость и расстояние транспортных средств. Таким образом, вы должны быть в состоянии рассчитать, какое расстояние транспортное средство проедет за секунду при любой заданной скорости.

Как подчеркнет любой учебник по реконструкции после аварии, люди обычно переоценивают время, необходимое для того, чтобы развернуться автомобильная авария. В одном исследовании участники, просмотревшие 30-секундное событие, оценили его среднюю продолжительность в 150 секунд, что на 500 % больше, чем на самом деле.

Вы также можете понять это, просто попросив кого-нибудь оценить, сколько футов автомобиль проезжает за одну секунду, двигаясь со скоростью 65 миль в час. Спектр ответов смехотворен, и это то, что адвокаты получают от свидетелей фактов.

Обычно это работает на пользу жертве, особенно в отношении скорости. Почему? Поскольку длиннее a визуальная оценка занимает , медленнее транспортное средство должно было двигаться.

Вот пример креста:

В: Когда вы видели истца, как далеко он находился от вашего автомобиля?
О: Не уверен. Рулетки у меня не было.

В: Так что вы понятия не имеете. Вы даже не можете предложить оценку?
A: Может быть, 40 ярдов.

Вопрос: Сорок ярдов? Может быть 50?
A: Наверное да.

В: Может быть 60?
О: Не знаю. Опять же, у меня не было рулетки.

В: Сколько времени прошло до удара после того, как вы увидели автомобиль?
О: Может быть, секунду.

Q: Затем вы должны закончить и подчеркнуть, как подсудимый противоречит сам себе; суд принял судебное решение о том, как далеко транспортные средства могут проехать с течением времени при заданных скоростях. Вы согласитесь, что при скорости 30 миль в час автомобиль движется со скоростью 2 мили в минуту.
А: Да.

В: А в миле 1760 ярдов? (Здесь свидетель использует ярды. Если в футах, то в миле 5280 футов?)
А: Да.

В: Значит, при скорости 30 миль в час автомобиль движется со скоростью менее 15 ярдов в секунду?
А: Я полагаю.

В: Значит, до удара оставалось четыре секунды?
A: Независимо от того, каков ответ на этот последний вопрос, вы подчеркнули, что история подсудимого крайне непоследовательна, что существенно снижает доверие к подсудимому.

Конечно, вы хотите найти возможность исключить аргумент истца о превышении скорости, потому что это не было причинно связано с аварией, или потому что показания непрофессионального свидетеля недостаточны для подтверждения вывода о содействующей небрежности из-за превышения скорости. Утверждайте, что Майерс против Брайта, но будьте готовы к аргументу, что мнение Специального апелляционного суда Мэриленда в деле Ромеро против Бренеса имеет решающее значение.

Эта диаграмма является хорошей шпаргалкой для расчета времени, скорости, расстояния и скорости движения транспортного средства в секунду.

• 1 миля в час = 1,4667 фута в секунду
• 10 миль в час = 14,7 фута в секунду
• 20 миль в час = 29,3 фута в секунду
• 25 миль в час = 36,7 фута в секунду
• 3008 миль в секунду час = 44,0 фута в секунду
• 35 миль в час = 51,3 фута в секунду
• 40 миль в час = 58,7 фута в секунду
• 45 миль в час = 66,0 футов в секунду
• 50 миль в час = 73,3 фута в секунду
• 55 миль в час = 80,7 футов в секунду
• 60 миль в час = 88,0 футов в секунду
• 65 миль в час = 95,3 фута в секунду

Как рассчитать скорость и расстояние в случае автомобильной аварии?

Формула скорости и расстояния для автомобиля такая же, как и для любого другого объекта: расстояние ÷ время. Итак, если вы хотите рассчитать скорость автомобиля при шестидесяти милях в час, математика будет (60 х 5280) ÷ (60 х 60) = 88 футов в секунду. Итак, эта формула работает для любого вопроса «как далеко вы путешествуете?» вопросы.

Можете ли вы рассчитать скорость автомобиля по следам заноса?

Вы можете приблизительно рассчитать скорость автомобиля или грузовика, если сможете измерить маркер заноса. Формула S² = Es² + 30fd. S — скорость автомобиля, Es — конечная скорость, f — коэффициент аэродинамического сопротивления, а d — длина заноса.

Формула достаточно проста. Применение — другое дело. Расчет конечной скорости, если транспортное средство не останавливается, является сложной задачей, как и оценка коэффициента сопротивления.

Как долго останутся следы шин на дороге после автомобильной аварии?

Как долго следы шин остаются на дороге после автомобильной аварии, зависит от множества переменных. Эти переменные включают в себя шины, вес автомобиля, износ асфальта или бетона, тип тормозной системы, погоду и так далее. Следы шин могут дать вам оценку скорости, чтобы вы могли ответить на вопрос «Как далеко вы проедете со скоростью X миль в час за Y секунд?» вопросы.

Если вы являетесь адвокатом по автомобильным авариям и хотите сохранить вещественные доказательства с места аварии, вы хотите получить эти доказательства как можно раньше.

Сколько времени требуется водителю, чтобы среагировать и нажать на тормоз?

Среднестатистическому водителю требуется от 2,3 до 2,5 секунд, чтобы затормозить в экстренной ситуации. Есть данные, свидетельствующие о том, что среднее время до торможения составляет менее 2,5 секунд, если водитель воспринимает критическую внезапную чрезвычайную ситуацию. Молодые водители обычно быстрее ломаются, чем водители старшего возраста.

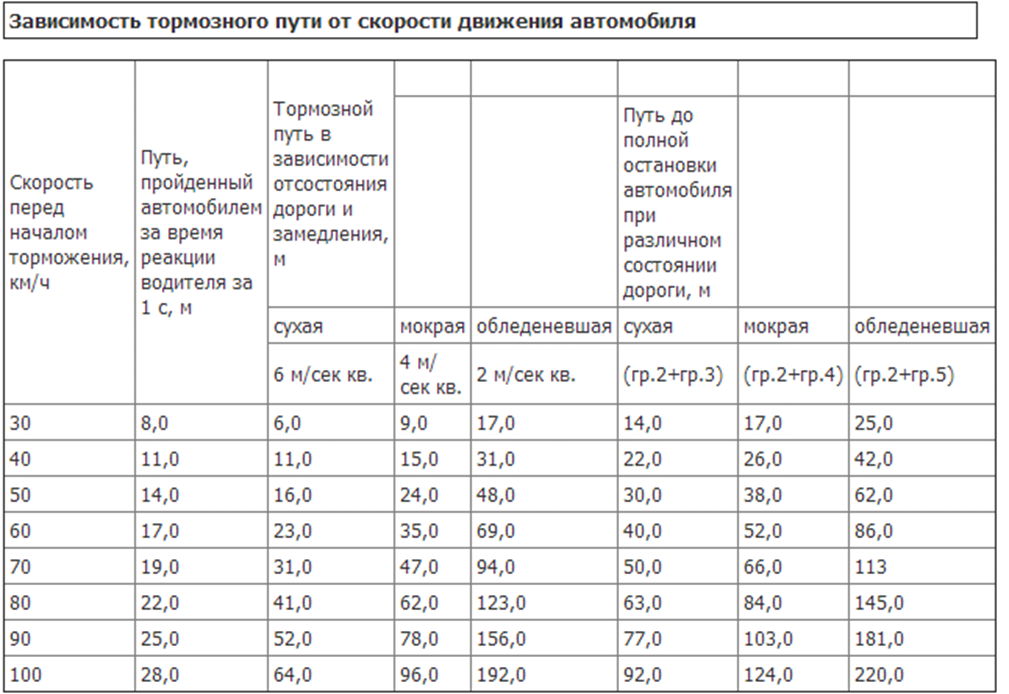
Как скорость влияет на тормозной путь?

Тормозной путь увеличивается в четыре раза при удвоении скорости.

Дополнительная информация

• Вот хорошее время, калькулятор скорости и расстояния
• Хороший пост о том, как рассчитать скорость в момент ДТП
• Перекрестный допрос эксперта Истца по предвзятости
• Образцы перекрестных допросов и других допросов свидетелей в деле о телесных повреждениях
• Инструкция присяжных Мэриленда по скорости
• Подготовка к суду: дополнительные образцы
• Обзор судебных процессов по автомобильным авариям в Мэриленде (чем занимаются наши юристы по ДТП)

Как рассчитать скорость колеса и автомобиля по частоте вращения двигателя – x-engineer.

org

Скорость автомобиля и колеса можно рассчитать как функцию частоты вращения двигателя, если известны параметры и состояние трансмиссии. В этом уроке мы собираемся рассчитать скорость автомобиля и колеса для заданного:

• оборотов двигателя
• передаточное число (включенной передачи)
• передаточное число главной передачи (на дифференциале)
• (свободное статическое) колесо радиус

Кроме того, мы предполагаем, что в сцеплении или гидротрансформаторе нет проскальзывания, поскольку двигатель механически связан с колесами.

Этот метод может быть применен к любой архитектуре трансмиссии (переднеприводной или заднеприводной), но для более легкого понимания компонентов мы будем использовать трансмиссию с полным приводом (RWD).

Изображение: Схема продольной передачи автомобиля – расчет скорости

где:
ω _e [рад/с] – частота вращения двигателя
ω _g [рад/с] – частота вращения выходного вала коробки передач
ω _d [рад/с] – частота вращения коронное колесо дифференциала
ω _wr [рад/с] – частота вращения правого колеса
ω _wl [рад/с] – частота вращения левого колеса
v _{wl wl /с]} – линейная скорость левого колеса
v _wr [м/с] – линейная скорость правого колеса
i _x [-] – передаточное число включенной передачи
i ₀ [-] – передаточное число дифференциала
r _w [м] – статический радиус колеса

Для простоты расчета предположим, что автомобиль движется прямолинейно, а также что оба колеса имеют одинаковый радиус.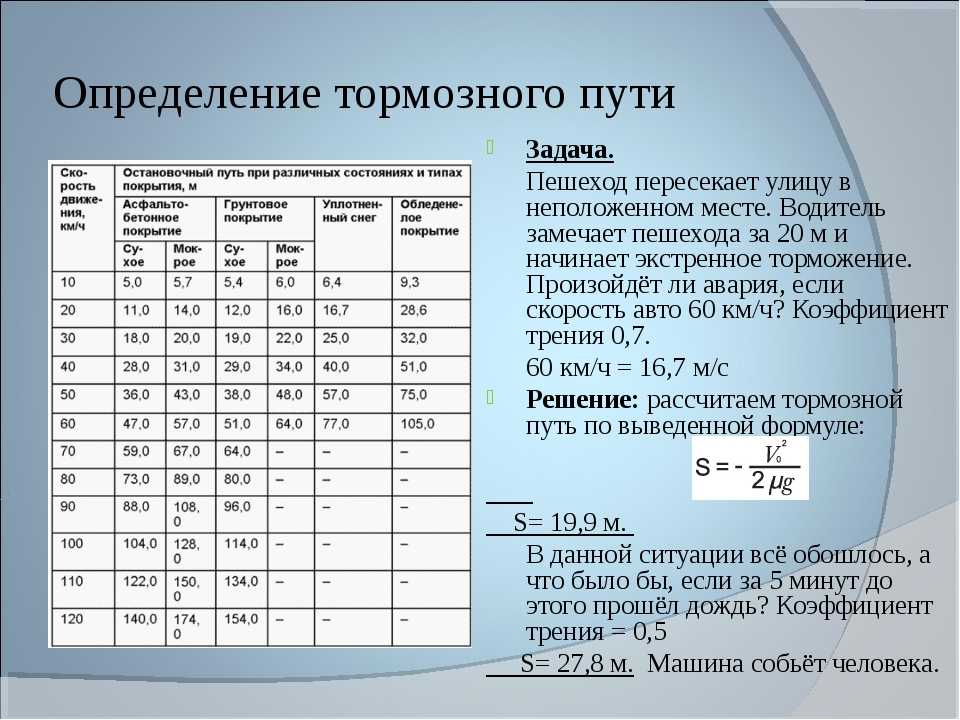 Это означает, что:

\[\omega_{wr}=\omega_{wl}=\omega_{w} \tag{1}\]

где ω _w [рад/с] — скорость вращения общего колеса.

Поскольку транспортное средство и колесо движутся вместе в линейном направлении, скорость транспортного средства (линейная) равна линейной скорости колеса. Так что, если мы посчитаем линейную скорость колеса, мы также получим скорость автомобиля.

\[v_{wr}=v_{wl}=v_{w}=v_{v} \tag{2}\]

Где v _w [м/с] — линейная скорость общего колеса и v _v [м/с] — скорость автомобиля.

Так как коробка передач связана с двигателем через сцепление (на МКПП) или гидротрансформатор (на АКПП), мы считаем, что проскальзывание ни в муфте (полностью замкнутой), ни в гидротрансформаторе абсолютно отсутствует ( блокировочная муфта замкнута). В этом случае скорость сцепления ω _c [рад/с] равна частоте вращения двигателя ω _e [рад/с] .

\[\omega_{c} = \omega_{e} \tag{3}\]

Изображение: Схема продольной передачи автомобиля – расчет скорости

В отличие от расчета крутящего момента колеса, передаточное число будет уменьшать скорость вращения колеса. Скорость выходного вала коробки передач равна скорости сцепления, деленной на передаточное число:

\[\omega_{g} = \frac{\omega_{c}}{i_{x}} \tag{4}\ ]

Скорость вращения венца дифференциала также уменьшается, будучи равной частоте вращения выходного вала редуктора, деленной на передаточное число дифференциала:

\[\omega_{d} = \frac{\omega_{g}}{i_{ 0}} \tag{5}\]

Скорости левого и правого колеса равны с дифференциальной скоростью:

\[\omega_{wr}=\omega_{wl}=\omega_{d} \tag{6}\]

Объединение всех приведенных выше уравнений дает формулу для зависимости скорости вращения колеса от частоты вращения двигателя:

\[ \omega_{w} = \frac{\omega_{e}}{i_{x} \cdot i_{0}} \tag{7}\]

Для частоты вращения двигателя преобразование из об/мин в рад/ s выполняется следующим образом:

\[\omega_{e} = \frac{N_{e} \cdot \pi}{30} \tag{8}\]

Где N _e — частота вращения двигателя в [об/мин] .

Если нам нужна скорость колеса N _w in [об/мин] , из [рад/с] , нам нужно применить обратное преобразование:

\[N_{w} = \frac{ \omega_{w} \cdot 30}{\pi} \tag{9}\]

Кроме того, линейная скорость колеса рассчитывается как функция скорости вращения и радиуса как:

\[v_{w} = \omega_{ w} \cdot r_{w} \tag{10}\]

Объединение уравнений (7), (8) и (10) дает выражение функции скорости автомобиля и колеса от частоты вращения двигателя и коробки передач и передаточных чисел дифференциала :

\[v_{v} \text{ [м/с]} = v_{w} \text{ [м/с]} = \frac{N_{e} \cdot \pi \cdot r_{w}} {30 \cdot i_{x} \cdot i_{0}} \tag{11}\]

Если мы хотим получить скорость в [км/ч] , формула будет выглядеть так:

\[\bbox[# FFFF9D]{V_{v} \text{ [км/ч]} = V_{w} \text{ [км/ч]} = \frac{3.6 \cdot N_{e} \cdot \pi \cdot r_{w}}{30 \cdot i_{x} \cdot i_{0}}} \tag{12}\]

Пример 1 .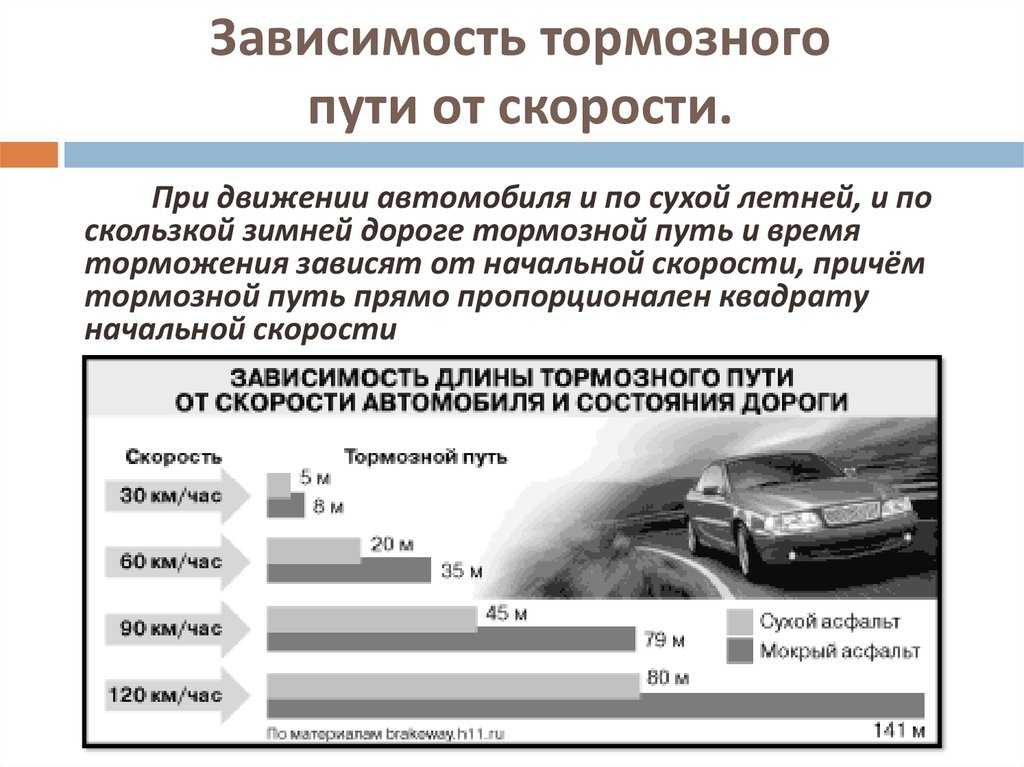 Рассчитайте скорость автомобиля в [км/ч] для автомобиля со следующими параметрами:

• Скорость двигателя, N _E = 2300 об / мин
• Короба передачи (1 ^ST ) передаточное взаимодействие, I _x = 4.171
• Final Ratio, 189 = 4.171
• .
• Маркировка размеров шин 225/55R17

Шаг 1 . Рассчитайте (свободный статический) радиус колеса по маркировке размера шины. Способ расчета радиуса колеса описан в статье Как рассчитать радиус колеса. Расчетный радиус колеса равен r _w = 0,33965 м .

Шаг 2 . Рассчитайте крутящий момент колеса, используя уравнение (12).

\[V_{v} = \frac{3,6 \cdot 2300 \cdot \pi \cdot 0,33965}{30 \cdot 4,171 \cdot 3,460} = 20,4068 \text{ км/ч} \]

Можно применить тот же метод для электромобиля скорость двигателя заменяется скоростью двигателя.