КРУТЯЩИЙ МОМЕНТ РЕДУКТОРА: Статьи
Как рассчитать передаточное число и крутящий момент?
Шестерни являются важным компонентом машин, робототехники, транспортных средств, аэрокосмической продукции и так далее. Самое простое применение шестеренок — это понижающий редуктор.
Редуктор — это устройство, которое преобразует входную скорость и крутящий момент. Под преобразованием мы подразумеваем усиление момента или сокращение частоты вращения. Уровень трансформации определяется передаточным числом. Передаточное число получается за счет зацепления двух и более прямозубых или косозубых шестерен.
Редуктор обычно используется как устройство для усиления крутящего момента. Например, вам нужно привести в действие гидравлический насос, которому требуется большой крутящий момент. Ваш источник энергии электродвигатель. Между мотором и насосом устанавливаем понижающий редуктор.
Как рассчитать передаточное число?
Если вам необходимо увеличить крутящий момент двигателя в 3 раза, вам понадобится редуктор с передаточным числом — 3. Чтобы рассчитать передаточное число двух зацепленных шестерен, нам необходимо знать:
Чтобы рассчитать передаточное число двух зацепленных шестерен, нам необходимо знать:
- число зубьев входных и выходных шестерен
- диаметр основания или радиус входных и выходных шестерен
В таблице ниже приведены физические значения, которые мы собираемся использовать в наших расчетах. Со знаком вопроса (?) переменные, которые нам нужно вычислить.
| Переменная | Описание | Данные | Единица измерения |
| zIN | количество зубьев входной шестерни | 16 | — |
| zOUT | количество зубьев ведомой шестерни | 24 | — |
| rIN | базовый радиус входной шестерни | 80 | мм |
| rOUT | базовый радиус ведомой шестерни | 120 | мм |
| i | передаточное число | ? | — |
| TqIN | входной крутящий момент | 250 | Нм |
| TqOUT | выходной крутящий момент | ? | Нм |
| ωIN | входная (вращательная) скорость | 1500 | об / мин |
| ωOUT | выходная (вращательная) скорость | ? | об / мин |
| Ft | контактная (касательная) сила | (нет потребности) | N |
| vt | контактная (касательная) скорость | (нет потребности) | РС |
Под входными данными мы понимаем источник энергии, в нашем случае это может быть электродвигатель.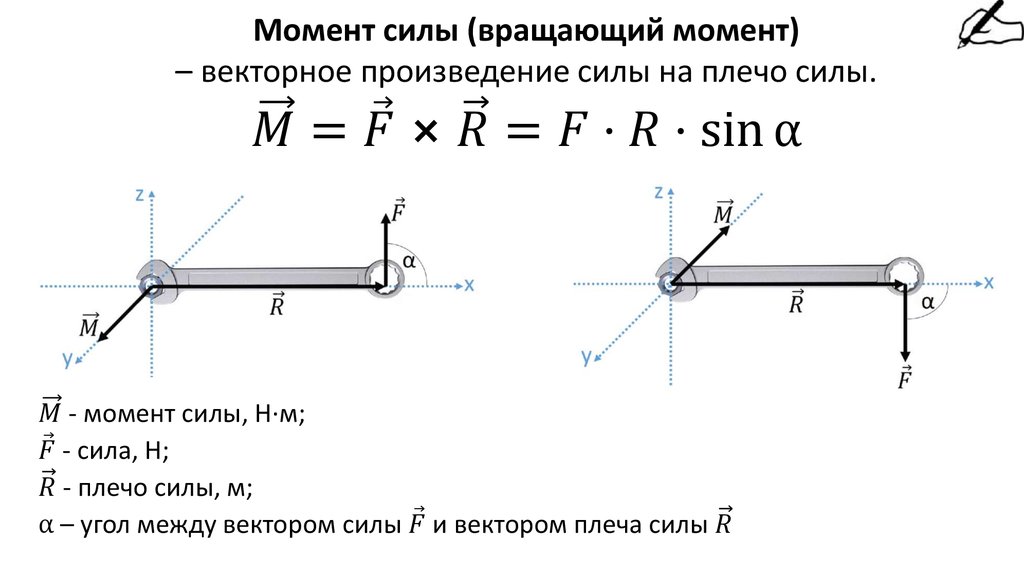
Передаточное число i можно рассчитать двумя способами:
- как отношение числа зубьев ведомой шестерни к числу зубьев ведущей шестерни
i=zOUT/zIN
- как отношение базового радиуса выходной шестерни к базовому радиусу входной шестерни
i=rOUT/rIN
Базовый радиус измеряется от центра вращения шестерни до точки контакта зубьев. Тот же результат достигается при использовании внешнего радиуса, который проходит от центра шестерни до вершины зубьев.
Заменяя математические выражения на фактическое количество зубьев и радиус, получаем передаточное число i :
i=zOUT/zIN=rOUT/rIN=24/16=120/80=1
Соотношение между выходным крутящим моментом и входным крутящим моментом следующее:
TqOUT=i⋅TqIN
Зубчатый редуктор будет увеличивать входной крутящий момент во столько раз, сколько передаточное число:
TqOUT=1.5⋅250=375 Nm
Соотношение между выходной скоростью и входной скоростью следующее:
ωOUT=ωIN/i
Зубчатый редуктор снизит входную скорость в несколько раз, равное передаточному отношению:
ωOUT=1500/1.
 5=1000 rpm
5=1000 rpm
Теперь мы собираемся продемонстрировать, почему значение выходного крутящего момента — это входной крутящий момент, умноженный на передаточное число.
В точке контакта между зубьями шестерен возникает касательная сила. Эта касательная сила может быть вычислена функцией входной шестерни и функцией выходной шестерни.
Мы знаем, что крутящий момент — это произведение прилагаемой силы на длину плеча рычага. В нашем случае сила — это тангенциальная сила между зубьями, а рычаг — это радиус шестерни.
Tqin=rIN⋅Ft
Отсюда извлекаем тангенциальную силу:
Ft=TqIN/rIN
Такое же усилие действует на ведомую шестерню:
Ft=TqOUT/rOUT
Соединяя два математических выражения тангенциальной силы, мы получаем:
TqOUT/rOUT = TqIN/rIN
TqOUT = (rOUT/rIN)⋅TqIN
TqOUT = i⋅TqIN
Теперь давайте продемонстрируем влияние передаточного числа на выходную скорость. Мы используем то же изображение, что и выше, но с обозначениями скорости вместо сил.
Схема скоростей зубчатой передачи
Тангенциальная скорость в точке контакта двух шестерен одинакова. В качестве тангенциальной силы мы можем записать функцию тангенциальной скорости входной шестерни и выходной шестерни:
Мы знаем, что тангенциальная скорость — это произведение радиуса на скорость вращения.
vt=ωIN⋅rIN
Такая же скорость применяется на выходной шестерне:
vt=ωOUT⋅rOUT
Соединяя два математических выражения тангенциальной скорости, мы получаем:
ωOUT⋅rOUT = ωIN⋅rIN
ωOUT = (rIN/rOUT) ⋅ωIN
ωOUT = ωIN/i
В конце этой статьи вы должны знать, как рассчитать функцию передаточного числа шестерен, а также влияние передаточного числа на крутящий момент и скорость.
Выбор мотор-редуктора по крутящему моменту
Зубчатые передачи внутри редуктора обеспечивают механическое преобразование, которое увеличивает крутящий момент от входного вала к выходному. Это механическое преобразование называется передаточным числом редуктора и является значением, используемым для определения увеличения крутящего момента от входа к выходу. Например, передаточное число редуктора 30: 1 означает, что выходная сторона примерно в 30 раз сильнее, чем входная. Таким образом, если мотор-редуктор должен создавать крутящий момент при полной нагрузке 30 Нм на своем выходном валу, то входной крутящий момент должен составлять 1,0 Нм. (В этом простом примере не учитываются внутренние потери зубчатой передачи, измеряемые ее общим КПД.) Если известно требование к входному крутящему моменту, легко рассчитать требуемую потребляемую мощность двигателя на основе его входной скорости. Это как раз тот момент, когда многие люди хотят сосредоточиться на входной мощности двигателя. Расчеты конструкторы должны начать с определения, какой именно крутящий момент требуется на выходном валу редуктора, а затем работать в обратном направлении, чтобы определить требуемую входную мощность двигателя.
Например, передаточное число редуктора 30: 1 означает, что выходная сторона примерно в 30 раз сильнее, чем входная. Таким образом, если мотор-редуктор должен создавать крутящий момент при полной нагрузке 30 Нм на своем выходном валу, то входной крутящий момент должен составлять 1,0 Нм. (В этом простом примере не учитываются внутренние потери зубчатой передачи, измеряемые ее общим КПД.) Если известно требование к входному крутящему моменту, легко рассчитать требуемую потребляемую мощность двигателя на основе его входной скорости. Это как раз тот момент, когда многие люди хотят сосредоточиться на входной мощности двигателя. Расчеты конструкторы должны начать с определения, какой именно крутящий момент требуется на выходном валу редуктора, а затем работать в обратном направлении, чтобы определить требуемую входную мощность двигателя.
Чтобы повысить энергоэффективность, тщательно подумайте о типе двигателя и КПД редуктора.
В некоторых случаях можно значительно повысить эффективность мотор-редуктора, заменив двигатель переменного тока с постоянным разделенным конденсатором на двигатель постоянного тока с постоянным магнитом. Они могут иметь больший потенциал максимальной эффективности, но их эффективность может быть намного ниже в фактической рабочей точке нагрузки устройства. Также имейте в виду, что мотор-редукторы с трехфазным приводом намного эффективнее однофазного эквивалента (например, 64% против 53%) и более надежны из-за своей упрощенной конструкции. Однако, когда трехфазное питание недоступно, требуется частотно-регулируемый привод для преобразования однофазного входа в трехфазный выход для мотор-редуктора. Современные частотно-регулируемые приводы экономичны и быстро окупаются, если учесть их встроенные функции, такие как плавный пуск для уменьшения механических ударов и увеличения срока службы оборудования.
Они могут иметь больший потенциал максимальной эффективности, но их эффективность может быть намного ниже в фактической рабочей точке нагрузки устройства. Также имейте в виду, что мотор-редукторы с трехфазным приводом намного эффективнее однофазного эквивалента (например, 64% против 53%) и более надежны из-за своей упрощенной конструкции. Однако, когда трехфазное питание недоступно, требуется частотно-регулируемый привод для преобразования однофазного входа в трехфазный выход для мотор-редуктора. Современные частотно-регулируемые приводы экономичны и быстро окупаются, если учесть их встроенные функции, такие как плавный пуск для уменьшения механических ударов и увеличения срока службы оборудования.
РИС. 3. Насадные мотор-редукторы
Расчет крутящего момента мотор-редуктора.
Основой расчёта крутящего момента редуктора является следующая формула:
Mc2 = Mr2 * Sf
где Mr2 – показатель, требуемый для мотор-редуктора, а Sf –коэффициент, зависящий от особенностей эксплуатации. Итоговое значение крутящего момента редуктора не может превышать номинального Mn2.
Итоговое значение крутящего момента редуктора не может превышать номинального Mn2.
Параметр Mn2, как и некоторые другие, например, Рn – мощность, М2max – параметр пиковой нагрузки, КПД, срок наработки на отказ и т.п. обозначены в паспорте изделия.
Таким образом выбор редуктора на основании значения крутящего момента носит всегда индивидуальный характер и представляет собой не всегда простую задачу.
Правильный расчет и подбор мотор-редуктора.
При выборе двигателя с редуктором важно знать, соответствуют ли расчетные характеристики выходной мощности, а также учитываются ли КПД редуктора.
Чтобы увеличить общую эффективность мотор-редуктора. Избегайте снижения эффективности двигателя из-за перегрева. Хотя червячные редукторы являются хорошим решением для ограниченного пространства, их КПД составляет всего 50%; напротив, прямозубые и косозубые шестерни, используемые в редукторах с параллельными валами, обычно имеют КПД около 98%. В ограниченных пространствах рассмотрите вариант мотор-редуктора со смещенным параллельным валом, в котором прямозубые цилиндрические и косозубые шестерни с более высоким КПД расположены вертикально, а выходной вал образует компактную U- или S-образную конфигурацию относительно приводного двигателя.
В ограниченных пространствах рассмотрите вариант мотор-редуктора со смещенным параллельным валом, в котором прямозубые цилиндрические и косозубые шестерни с более высоким КПД расположены вертикально, а выходной вал образует компактную U- или S-образную конфигурацию относительно приводного двигателя.
Максимальный крутящий момент редуктора — зачем он нужен.
Любой механический редуктор снижает обороты, передаваемые на его первичный вал, в определённое количество раз. Данная величина называется передаточным число. Однако, помимо передаточного числа, каждый редуктор имеет такую характеристику, как крутящий момент на выходном валу.
Крутящий момент редуктора – что это означает?
Существует общепризнанная единица измерения крутящего момента – Ньютоно – метры. То есть, если к выходному валу редуктора присоединить какую-либо штангу длиной один метр, то привод должен сохранять работоспособность при нагрузке на конце этой штанги равной 1 Ньютону. Нетрудно догадаться, что, чем ближе к оси выходного вала прикладывается нагрузка, тем больший крутящий момент может выдержать редуктор. Для простоты расчётов можно перевести силу Ньютона в усилие, создаваемое килограммом. Усилие 1 килограмма равен 9,81 Ньютона.
Для простоты расчётов можно перевести силу Ньютона в усилие, создаваемое килограммом. Усилие 1 килограмма равен 9,81 Ньютона.
Давайте рассмотрим на примере цилиндрического двухступенчатого редуктора РМ-650. Возьмём самое распространённое передаточное число – 31,5, обороты на входном валу – 1500 в минуту, режим работы – 100% нагрузка. Конструктивно в этом редукторе заложен максимально допустимый крутящий момент при указанных условиях равный 5116 Н.м. Что это означает? Это говорит о том, что при радиусе, допустим, барабана в 1 метр, одетого на выходной вал, редуктор РМ-650 будет выдерживать нагрузку в 5116 Ньютонов или поднимать груз в 520 кг. Соответственно, если радиус барабана будет 0,5 метра, то нагрузка допускается 10232 Н.м. или 1040 кг. Нетрудно догадаться, что создаваемый в механизме крутящий момент определяется произведением силы на длину рычага.
Для чего нужен допустимый крутящий момент редуктора?
В любом механизме или оборудовании редуктор служит промежуточным звеном между двигателем и исполнительным узлом. Для чего и зачем он нужен? Электродвигатель, имея какие-либо обороты и мощность, лишь косвенно отражает способность привода выдержать нагрузку, создаваемую механизмом. На практике редко двигатель передаёт напрямую вращение к конечному узлу или устройству, поскольку при работе куда важнее создаваемая тяга, которая создаётся за счёт передаточного числа редуктора. Определяется всё это определяется на стадии выбора габарита редуктора.
Для чего и зачем он нужен? Электродвигатель, имея какие-либо обороты и мощность, лишь косвенно отражает способность привода выдержать нагрузку, создаваемую механизмом. На практике редко двигатель передаёт напрямую вращение к конечному узлу или устройству, поскольку при работе куда важнее создаваемая тяга, которая создаётся за счёт передаточного числа редуктора. Определяется всё это определяется на стадии выбора габарита редуктора.
Чем определяется допустимый крутящий момент редукторов?
Начнём с того, что в червячных и цилиндрических редукторах допустимый крутящий момент определяется совершенно разными факторами. Рассмотрим по порядку:
- в цилиндрических редукторах одного и того же типоразмера зуб нарезается одного модуля при всех передаточных числах, а момент создаётся за счёт разности диаметров работающих в паре шестерен. В данном случае радиус шестерни является рычагом для увеличения тяги.
- в червячных редукторах всё обстоит наоборот. Радиус червячного колеса и червяка практически неизменны, а момент создаётся за счёт изменения количества зубьев на колесе.
 Если рассмотреть для примера червячный одноступенчатый редуктор Ч-80. При любых входных оборотах, максимальный момент редуктор выдерживает при передаточном числе 31,5. Почему? Объяснение простое – при малых передаточных числах червяк многозаходный, а червячное колесо имеет больше 31 зуба, при больших передаточных – червяк однозаходный, но колесо всё равно имеет больше 31 зуба. То есть максимальная толщина зуба червячного колеса наблюдается при передаточном числе 31,5. Толще зуб – больше допускаемая нагрузка.
Если рассмотреть для примера червячный одноступенчатый редуктор Ч-80. При любых входных оборотах, максимальный момент редуктор выдерживает при передаточном числе 31,5. Почему? Объяснение простое – при малых передаточных числах червяк многозаходный, а червячное колесо имеет больше 31 зуба, при больших передаточных – червяк однозаходный, но колесо всё равно имеет больше 31 зуба. То есть максимальная толщина зуба червячного колеса наблюдается при передаточном числе 31,5. Толще зуб – больше допускаемая нагрузка.
Дополнительно отметим, что у червячных редукторов больше потери на трение, что снижает их КПД по сравнению с цилиндрическими редукторами. В каталоге возможно сравнить характеристики различных редукторов.
Знать о крутящем моменте зубчатой передачи
ТОП
- org/ListItem»>
Знание передач
Первый шаг конструкции механизма с использованием шестерен
Знать о крутящем моменте зубчатой передачи
>
>
>
1. Функции редуктора
Вот список функций зубчатых передач для конструкций механизмов. (Таблица 3-1)
Таблица 3-1 Функции редуктора
| Характерные функции шестерен | Объяснение |
| Изменить направление вращения вала | (уже объяснил) |
| Преобразование вращательного движения в линейное движение | (уже объяснил) |
| Изменение направления вращения (по часовой стрелке/против часовой стрелки) | (уже объяснил) |
| Изменение количества оборотов (ускорение вверх/вниз) | (уже объяснил) |
| Изменение силы вращения (увеличение/уменьшение крутящего момента) | См. эту главу эту главу |
Вы можете увеличить или уменьшить крутящий момент шестерни (крутящую силу), изменив число оборотов.
2. Определение крутящего момента (крутящего момента)
Крутящий момент представляет собой вращающую силу, когда нагрузка F (Н) приложена на расстоянии L (мм) от центра вращения. Крутящий момент Т выражается следующей формулой в Н·мм (Ньютон-миллиметр). (Рисунок 3-1)
Рисунок 3-1 Момент затяжки
Крутящий момент T становится больше по мере того, как L (расстояние от центра вращения) становится больше, даже если нагрузка F мала. С другой стороны, крутящий момент T становится больше по мере увеличения нагрузки F, даже если L (расстояние от центра вращения) короткое.
Другими словами, крутящий момент T — это коэффициент, определяемый L (расстояние от центра вращения) и нагрузкой F.
3. Как определить передачу крутящего момента (без учета КПД машины)
Крутящий момент передачи изменяется по мере увеличения или уменьшения скорости. Как правило, при снижении скорости небольшой крутящий момент на входной стороне передается как больший крутящий момент на выходной стороне. Расчет крутящего момента зависит от количества зубьев. Позвольте мне объяснить с помощью диаграммы с использованием диаметров делительной окружности.
Как правило, при снижении скорости небольшой крутящий момент на входной стороне передается как больший крутящий момент на выходной стороне. Расчет крутящего момента зависит от количества зубьев. Позвольте мне объяснить с помощью диаграммы с использованием диаметров делительной окружности.
Крутящий момент рассчитывается следующим образом:
- Получите нагрузку F точки зацепления (на радиусе делительной окружности шестерни A) от входного крутящего момента.
- Получите крутящий момент выходной стороны от нагрузки F точки зацепления зубьев (радиус делительной окружности шестерни B).
Состояние
Номинальный крутящий момент двигателя: TA=600 Н·мм (0,6 Н·м)
Диаметр делительной окружности шестерни A φ20
Диаметр делительной окружности шестерни B φ40
Расчет передачи крутящего момента
Нагрузка в точке зацепления шестерни A: F=TA/LA=60(Н)
Крутящий момент на выходной стороне: TB=F×LB=60(Н)×20(мм)=1200(Н·мм )
Рисунок 3-2 Схема расчета передачи крутящего момента шестерни
Как видно из рисунка 3-2, при уменьшении скорости выходного вала относительно входного вала на 1/2 выходной крутящий момент увеличивается в 2 раза.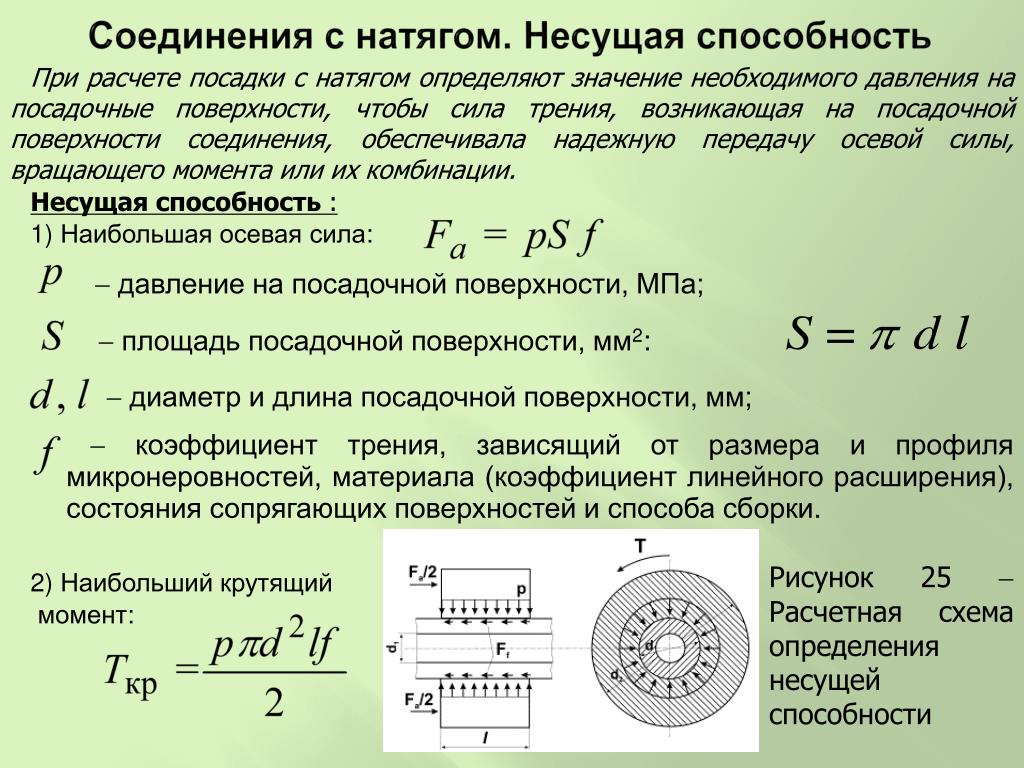
4. Учет эффективности машины
Как показано в предыдущей главе, количество оборотов шестерни можно рассчитать по количеству зубьев.
Однако вы не можете рассчитать крутящий момент передачи просто так, как показано выше, по следующим причинам:
- При зацеплении зубьев выделяется тепло, и энергия теряется.
- Звук молотка издается зацеплением зубов, и энергия теряется.
Следовательно, крутящий момент (крутящая сила) уменьшается на столько, на сколько теряется энергия, как указано выше.
Отношение сил на входе и выходе зубчатых колес называется «КПД машины», и его приблизительное значение известно в зависимости от типа зубчатого колеса. (Таблица 3-2)
Таблица 3-2 КПД редуктора по типу
| Связь двух валов | Название шестерни | КПД машины η (%) |
|---|---|---|
| параллельный вал | цилиндрическое прямозубое колесо | 98,0 — 99,5 * КПД косозубого колеса меньше, чем прямозубого, так как зубья наклонены и усилие создается в направлении тяги. 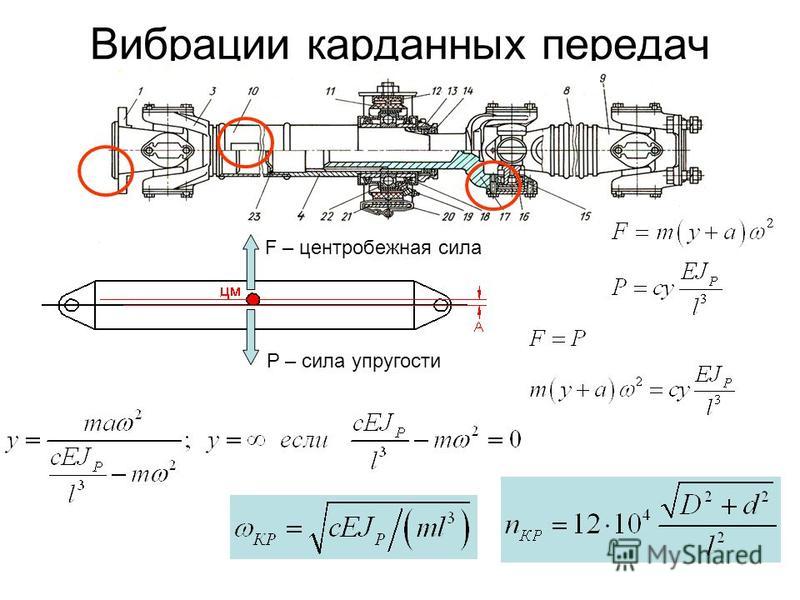 |
| косозубая шестерня | ||
| двойная косозубая шестерня | ||
| внутренняя шестерня | ||
| стойка | ||
| винтовая стойка | ||
| пересекающийся вал | прямая коническая шестерня | 98,0 — 99,0 |
| спирально-коническая шестерня | ||
| перекошенный вал | червячный редуктор | 30,0 — 90,0 |
| винтовая передача | 70,0 — 95,0 |
Примечание) Указанный выше КПД представляет собой КПД зубчатых передач без учета потерь в подшипниках или перемешивания смазки.
Показанный выше коэффициент полезного действия шестерни представляет собой значение, когда шестерни установлены правильно. При неправильной установке, например отклонении в точке пересечения конических шестерен, эффективность снизится.
«Никогда не забывайте об эффективности машины при расчете крутящего момента!»
5.
 Расчет крутящего момента трансмиссии (включая КПД машины)
Расчет крутящего момента трансмиссии (включая КПД машины)
Теперь давайте посмотрим на формулу расчета крутящего момента, включая КПД машины η. (Рисунок 3-3)
Когда входной крутящий момент шестерни А равен TA, а КПД машины равен η, крутящий момент TB, который передается на шестерню B, увеличивается по мере увеличения эффективности η.
ТБ=η(ZB/ZA)× ТА
Когда входной крутящий момент шестерни B равен TB, крутящий момент TA, который передается на шестерню A, уменьшается по мере падения эффективности η.
TA=η(ZA/ZB)× ТБ
Рисунок 3-3 Формула расчета крутящего момента трансмиссии
Упражнение для передачи крутящего момента (1)
Рассчитайте крутящий момент, передаваемый на ведомую шестерню (B). Предположим, что тип шестерни — прямозубая.
Символ на Рисунке 3-4 представляет ведущую шестерню.
[Условие]
Количество зубьев: ZA=20, ZB=40
Крутящий момент ведущей шестерни A: TA=600 (Н·мм)
Эффективность машины η: Установите на 0,99, так как используются прямозубые шестерни.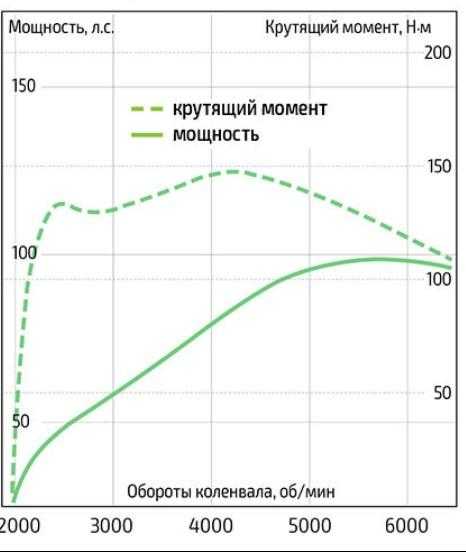
[Ответ]
Крутящий момент, передаваемый на шестерню B
TB=η(ZB/ZA)×TA
= 0,99(40/20)×600=1188(Н·мм)
Рисунок 3-4 Упражнение для передачи крутящего момента (1)
Упражнение для передачи крутящего момента (2)
Рассчитайте крутящий момент, передаваемый на червячное колесо B. (Рисунок 3-5)
[Условие]
Количество зубьев: ZA=1, ZB=30
Крутящий момент червяка A: TA=600 (Н·мм)
КПД машины η: Установите на 0,3, поскольку используются червячные передачи.
[Ответ]
Крутящий момент, передаваемый на червячное колесо B
TB=η(ZB/ZA)×TA=0,3(30/1)×600
= 5400(Н·мм)
Рисунок 3-5 Упражнение для передачи крутящего момента (2)
Упражнение для передачи крутящего момента (3)
Рассчитайте крутящий момент, передаваемый на ведомую шестерню (С). Предположим, что тип шестерни — косозубая шестерня.
Символ на Рисунке 3-6 представляет ведущую шестерню.
[Условие]
Количество зубьев: ZA=20, ZB=30, ZC=20
Крутящий момент ведущей шестерни А: TA=500 (Н·мм)
КПД машины η: Установите на 0,98, так как используются косозубые шестерни.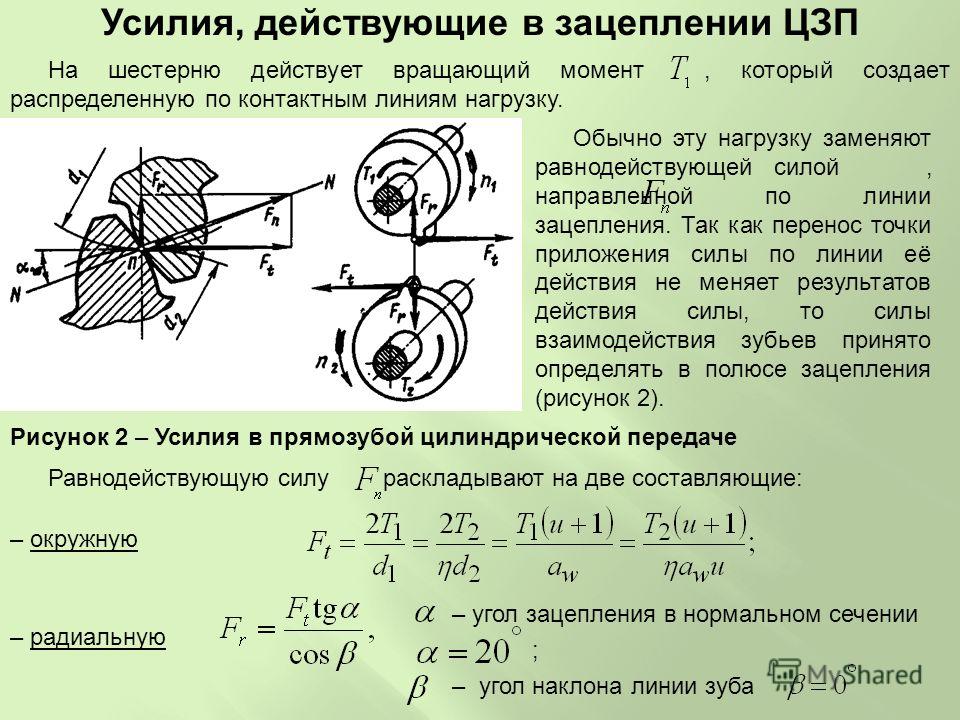
[Ответ]
Крутящий момент, передаваемый на шестерню B
TB=η(ZB/ZA)×TA
=0,98(30/20)×500=735(Н·мм)
Крутящий момент, передаваемый на шестерню C
TC=η(ZB/ ZC)×NB
=0,98(20/30)×735=480,2(Н·мм)
Рисунок 3-6 Упражнение для передачи крутящего момента (3)
«Как и количество оборотов, количество зубьев первой и последней шестерен определяет крутящий момент одноступенчатой шестерни, но крутящий момент уменьшается, поскольку на КПД машины влияет количество промежуточных шестерен!»
Упражнение для передачи крутящего момента (4)
Рассчитайте крутящий момент, передаваемый на ведомую шестерню (D). Предположим, что тип шестерни — косозубая шестерня.
Символ на Рисунке 3-7 представляет ведущую шестерню.
[Условие]
Количество зубьев: ZA=20, ZB=40, ZC=20, ZD=30
Крутящий момент ведущей шестерни A: TA=400 (Н·мм)
Эффективность машины η: Установите на 0,98, так как используются косозубые шестерни. .
.
[Ответ]
Крутящий момент, передаваемый на шестерню B
TB=η(ZB/ZA)×TA
=0,98(40/20)×400=784(Н·мм)
Крутящий момент, передаваемый на шестерню C
TC=TB=784(Н·мм)… как на тот же вал
Крутящий момент, передаваемый на шестерню D
TD=η(ZD/ZC)×TC
=0,98(30/20)×784=1152,5(Н·мм)
Рисунок 3-7 Упражнение для передачи крутящего момента (4)
Приступая к проектированию механизма с использованием зубчатых передач, важно помнить об эффективности машины. Механизм, спроектированный без учета КПД машины, может не соответствовать спецификациям из-за нехватки крутящего момента.
Мы обсуждали, что КПД машины влияет на крутящий момент передачи в зависимости от типа шестерни и количества зацеплений.
Далее мы объясним параметры, которые определяют форму зубчатых колес при проектировании зубчатых колес.
(Продолжение следует…)
*Иллюстрация: КАОСУН
ОТКАЗ ОТ ОТВЕТСТВЕННОСТИ
Цель написания этой статьи состояла в том, чтобы обучить читателей элементарному уровню зубчатой техники.
Мы надеемся, что фактическое проектирование и производство зубчатых передач и машин, использующих шестерни, осуществляется с достаточными техническими и специальными соображениями под полную ответственность пользователя.
Мы отказываемся от какой-либо ответственности и не будем компенсировать любой прямой или косвенный ущерб, причиненный механизмами, разработанными пользователями, прочитавшими эту статью.
Ссылки по теме :
Знайте о параметрах, определяющих форму зубчатых колес
Зубчатая передача: расчет передаточного числа, крутящего момента и скорости
Зубчатая передача состоит из двух или более шестерен, соединенных последовательно. Он используется для увеличения или уменьшения скорости или крутящего момента выходного вала. Термин передаточное число используется для расчета скорости и крутящего момента выходной шестерни, когда крутящий момент прикладывается к входной шестерне.
Цилиндрическая шестерня в движении
Например, коробка передач — это тип зубчатой передачи, который используется для увеличения крутящего момента двигателя и снижения скорости колес автомобиля. Увеличение крутящего момента зависит от того, на какой передаче вы едете на своем автомобиле. В этой статье мы обсудим, как рассчитать передаточное число, скорость и крутящий момент для различных зубчатых передач.
Увеличение крутящего момента зависит от того, на какой передаче вы едете на своем автомобиле. В этой статье мы обсудим, как рассчитать передаточное число, скорость и крутящий момент для различных зубчатых передач.
Чтобы понять передаточное отношение, мы предлагаем вам сначала прочитать эту статью о терминологии передач (различные термины, используемые в передачах) и различных типах передач.
Содержание
- Закон передачи
- передаточный численность
- передаточные передачи и скорость
- Переход и крутящий момент
- Типы передач и их расчет
Закон передачи
Закон Gearing Установки. между сопряженными шестернями всегда остается постоянной. Для достижения условия постоянной угловой скорости общие нормаль в точке контакта сопряженных зубьев шестерни всегда проходят через точку тангажа. Где Точка шага — это точка контакта между окружностями шага сопрягаемой шестерни.
Если угловая скорость сопрягаемой шестерни постоянна, мы можем заключить следующее соотношение:
Где ω1 и ω2: Угловая скорость в радианах/с для ведущей и ведомой шестерен соответственно.
n1 и n2 = скорость передачи в об/мин для ведущей и ведомой шестерен соответственно.
d1 и d2 = диаметр ведущей и ведомой шестерен соответственно.
T1 и T2 = количество зубьев на ведущей и ведомой шестернях соответственно.
Передаточное число
Передаточное отношение — это отношение числа зубьев ведомой и ведущей шестерен. Он используется для расчета скорости и крутящего момента выходного вала, когда входной и выходной валы соединены зубчатой передачей.
Входная шестерня, к которой прикладывается крутящий момент, известна как привод . В то время как выходная шестерня известна как ведомая шестерня . А шестерни, используемые между ведущей и ведомой шестернями, известны как промежуточные шестерни .
Передаточное отношение и скорость
Передача мощности через зубчатую передачу влияет на скорость вращения выходного вала.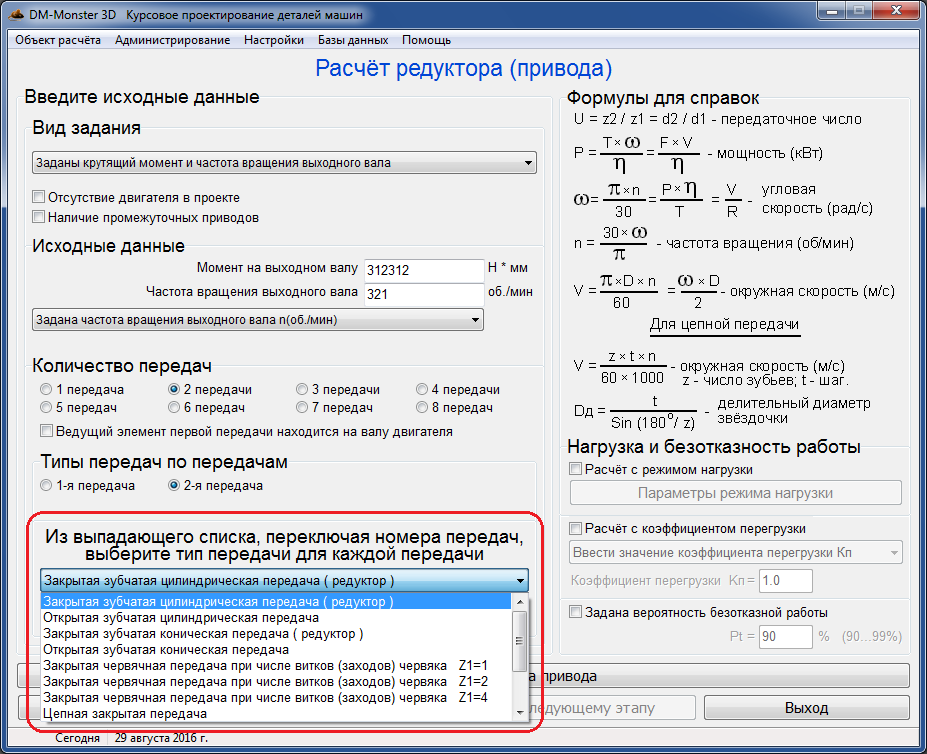
Следовательно:
Скорость вторичного вала = скорость входного вала / передаточное число
Передаточное отношение
Как показано выше, если число шестерен на выходном валу больше, чем шестерен на входном валу. Эта компоновка также известна как редуктор . При таком расположении выходной вал будет иметь более низкую скорость по сравнению с входным валом.
Цилиндрическое зубчатое колесо для увеличения скорости
Принимая во внимание, что когда мы реверсируем расположение. Другими словами, если количество шестерен на вторичном валу меньше, чем шестерен на входном валу. Скорость выходного вала будет иметь большую скорость по сравнению с входным валом.
Передаточное число и крутящий момент
Согласно закону зубчатых передач. В зубчатой передаче отношение выходного крутящего момента к входному крутящему моменту также постоянно и равно передаточному числу. Следовательно, если входной крутящий момент известен. Выходной крутящий момент можно рассчитать, умножив входной крутящий момент на передаточное число.
Типы зубчатых передач и их расчет
Зубчатая передача состоит из ряда шестерен для передачи мощности с одного вала на другой. Например, мощность от двигателя передается на колеса через коробку передач. Вот четыре различных типа зубчатой передачи.
- Простая зубчатая передача
- Составная зубчатая передача
- Реверсивная зубчатая передача
- Планетарная зубчатая передача
1) Расчет передаточного числа для простой зубчатой передачи
Простая зубчатая передача может быть двухступенчатой или многоступенчатой.
1.1) Двухступенчатая передача
Двухступенчатая передача — это тип простой зубчатой передачи. Он состоит из двух соединенных шестерен. Например, как показано ниже в двухступенчатом поезде. Gear-1 является ведущей, а Gear-2 — ведомой. Когда ведущая шестерня вращается по часовой стрелке, ведомая шестерня будет вращаться против часовой стрелки.
Вопрос: Рассчитайте скорость и крутящий момент выходного вала для простой зубчатой передачи. Где количество зубьев на ведущей и ведомой шестернях 40 и 20 соответственно. Шестерня привода вращается со скоростью 100 об/мин и крутящим моментом 10 Нм.
Где количество зубьев на ведущей и ведомой шестернях 40 и 20 соответственно. Шестерня привода вращается со скоростью 100 об/мин и крутящим моментом 10 Нм.
Количество зубьев ведущей шестерни (T1) = 40
Количество зубьев ведомой шестерни (T2) = 20
Скорость ведущей шестерни (n1) = 100 об/мин
Двухступенчатая передача
Расчет передаточного числа
GR = T2 / T1 = 20/40 = 0,5
Расчет скорости выходного вала
Скорость выходного вала/GR0 = 1,0,0,018
= 200 об/мин
Расчет крутящего момента выходного вала/шестерни
Крутящий момент, создаваемый ведомой шестерней = GR × Крутящий момент, создаваемый водителем
= 0,5 × 10 = 5 Н·м передача движения с одного вала на другой. Результирующее передаточное число может быть рассчитано путем умножения отдельных передаточных чисел.
Вопрос: Рассчитайте передаточное число для многоступенчатых поездов. Где количество зубьев на ведущей, промежуточной и ведомой шестернях составляет 40, 20 и 10 соответственно.
Где количество зубьев на ведущей, промежуточной и ведомой шестернях составляет 40, 20 и 10 соответственно.
Многозубчатая передача
Заданное количество зубьев
T1 = 40, T2 = 20, T2 = 10 между Gear-1 и Gear-2 (водитель и натяжитель).
GR(1-2) = 20/40 = 0,5
Шаг 2: Рассчитайте GR между шестерней-2 и шестерней-3 (промежуточная и ведомая шестерни).
GR(2-3) = 10/20 = 0,5
Шаг 3: Умножая передаточное число от 1 до 2 и от 2 до 3. Мы получим результирующий GR между ведущей и ведомой шестернями.
Результирующая многоступенчатая передача GR = 0,5 × 0,5 = 0,25
На основании приведенного выше расчетного передаточного числа мы можем рассчитать скорость и крутящий момент на выходной передаче.
2) Расчет передаточного числа для составной зубчатой передачи
Составные шестерни состоят из более чем одной шестерни на одной оси. Поэтому шестерни на одном валу вращаются с одинаковой скоростью и крутящим моментом.
Вопрос: Рассчитайте передаточное число составной зубчатой передачи. Где количество зубьев на ведущей и ведомой шестернях 40 и 10 соответственно с одной составной шестерней. Составная шестерня имеет одну шестерню, соединенную с ведущей шестерней с 30 зубьями, и другую шестерню, соединенную с ведомой шестерней с 20 зубьями.
Составная зубчатая передача
Заданное количество зубьев
T1 = 40, T2 = 30, T3 = 20, T4 = 10
Расчет передаточного числа для составной шестерни
-3 находятся на одном валу.
Шаг-1: Рассчитать передаточное отношение между Шестерня-1 и Шестерня-2
GR(1-2) = 30/40 = 0,75 4.
ГР(3-4) = 10/20 = 0,5
Шаг 3: Умножить GR(1-2) и GR(3-4)
Результирующая составная шестерня GR = 0,375
3) Перевернутая зубчатая передача.
Реверсивная зубчатая передача
Реверсивная зубчатая передача представляет собой тип составной зубчатой передачи, в которой входной и выходной валы находятся на одной оси.

 Если рассмотреть для примера червячный одноступенчатый редуктор Ч-80. При любых входных оборотах, максимальный момент редуктор выдерживает при передаточном числе 31,5. Почему? Объяснение простое – при малых передаточных числах червяк многозаходный, а червячное колесо имеет больше 31 зуба, при больших передаточных – червяк однозаходный, но колесо всё равно имеет больше 31 зуба. То есть максимальная толщина зуба червячного колеса наблюдается при передаточном числе 31,5. Толще зуб – больше допускаемая нагрузка.
Если рассмотреть для примера червячный одноступенчатый редуктор Ч-80. При любых входных оборотах, максимальный момент редуктор выдерживает при передаточном числе 31,5. Почему? Объяснение простое – при малых передаточных числах червяк многозаходный, а червячное колесо имеет больше 31 зуба, при больших передаточных – червяк однозаходный, но колесо всё равно имеет больше 31 зуба. То есть максимальная толщина зуба червячного колеса наблюдается при передаточном числе 31,5. Толще зуб – больше допускаемая нагрузка.