Расчет воздушного винта. Шаг- Диаметр
Чтобы обеспечить поступательное движение модели самолета, необходимо приложить к ней силу тяги. Ее создает воздушный винт, приводимый во вращение авиамодельным двигателем. Лопасти винта, вращаясь, отбрасывают поток воздуха назад — в сторону, противоположную направлению полета. Чем больше масса и скорость воздушного потока, отбрасываемого винтом, тем больше сила тяги винта.
Воздушные винты имеют различные геометрические характеристики. Важнейшими из них являются диаметр и шаг винта.
Диаметр винта DB — это диаметр окружности, описываемой при вращении концами лопастей.
Теоретический шаг винта Н — это расстояние, проходимое элементом лопасти в направлении полета за 1 оборот винта, движущегося поступательно с определенной скоростью; при этом предполагается, что винт вращается в неподатливой (твердой) среде (см.рис).
Но так как винт вращается в воздухе, частицы которого проскальзывают на поверхности винта, та за 1 оборот он проходит меньшее расстояние. Фактически пройденное расстояние называется действительным шагом или поступью винта, а разница между теоретическим (расчетным) шагом и действительным — скольжением. Действительный шаг винта можно вычислить по формуле H=v/n,
где v — скорость модели, м/с;
n— частота вращения, с-1.
Для сравнения различных винтов введено понятие относительного шага: h=H/DB у кордовых пилотажных моделей относительный шаг воздушных винтов равен (0,4—0,6) DB. Для получения полной мощности двигателя модели нужно правильно подобрать размеры винта — диаметр, шаг, ширину лопасти.
Рассмотрим упрощенный способ расчета воздушного винта для кордовой тренировочной модели с двигателем МАРЗ-2,5: скорость полета 80 км/ч (22 м/с), частота вращения винта 10 000 об/мин (166 с-1).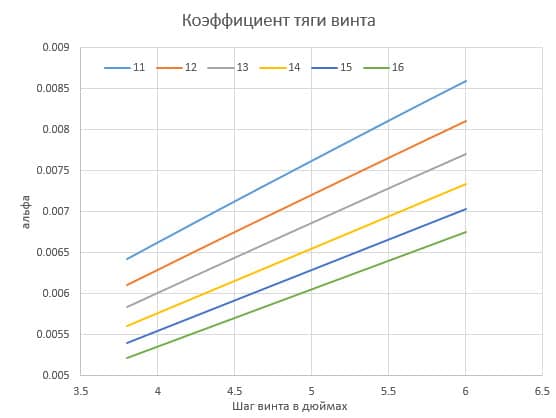
За 1 оборот винт пройдет расстояние Н = v/n= (22/166) м = 0,13 м, т. е. шаг винта Н — 130 мм.
Более детально ознакомиться со способами расчета воздушного винта можно в замечательной книге Жидкова Станислава «Секреты высоких скоростей кордовых моделей самолетов» начиная с 113 страницы
Если вам нужны простые советы и рекомендации по выбору воздушного винта для своей модели, смотрите тут.
Рис. 1. Геометрические характеристики воздушного винта
Основные геометрические характеристики винта — его диаметр D и шаг — Н.
Если предположить, что винт вращается в плотной неупругой среде и вокруг оси винта описать цилиндр произвольного радиуса — r, то сечение лопасти, лежащее на поверхности этого цилиндра будет двигаться по винтовой линии (рис. 1) с углом подъема (углом установки) —ϕ.
В развертке винтовая линия изобразится диагональю — ОВ, а сторона АВ характеризует перемещение сечения лопасти за один оборот, то есть шаг винта Н. Его можно выразить формулой:
Зная угол установки каждого сечения лопасти и радиус — r, можно найти соответствующий шаг. Если все сечения лопасти винта имеют одинаковую величину Н, то такие винты называются винтами постоянного шага; у винтов переменного шага в различных сечениях лопасти значения Н различны. Изменение шага по длине лопасти зависит от конструкции и формы винта. Обычно шаг винта к концу лопасти уменьшают.
Относительный шаг — это отношение шага к диаметру
Поскольку лопасть винта движется в упругой среде — воздухе, то за один оборот винт проходит расстояние меньше теоретического шага, именуемое поступью винта — На (рис.
1).
Разность между шагом винта и его поступью называется скольжением — S = H—На (рис. 1). Скольжение обычно дается в процентах. Для таймерных моделей с компрессионными силовыми установками оно составляет 20—40% от Н.
Из сказанного следует, что лопасть фактически движется по линии ОС, а это значит, что она имеет угол атаки α=ϕ-ß. Из рис. 1 хорошо видно, что угол атаки тем больше, чем больше скольжение S.
В расчетах часто пользуются понятием относительной поступи винта, определяемой как отношение поступи На к диаметру D.
Легко показать, что
где ns — число оборотов пинта в секунду,
D — диаметр винта,
V — скорость полета модели.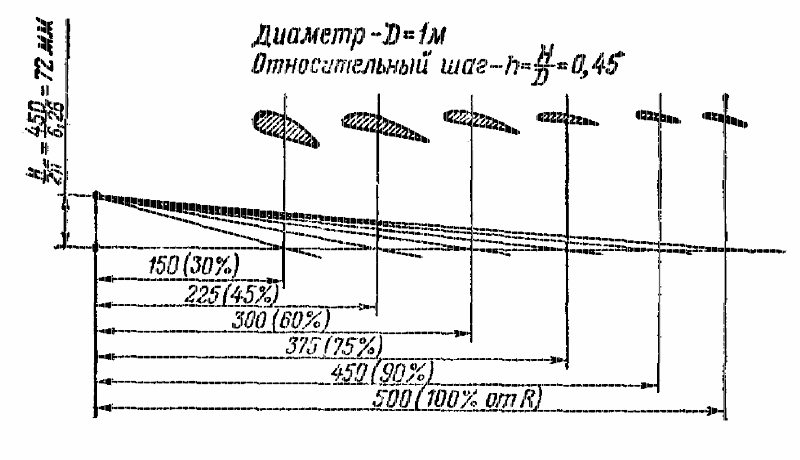
Тяга, развиваемая винтом, подсчитывается по формуле: P=αρD4ns2 кг, где α— коэффициент тяги винта, который зависит от формы лопасти, h и λ; ρ — плотность воздуха.
А вот формула для мощности, необходимой для вращения винта:
где ß— коэффициент мощности винта, зависящий от тех же параметров, что и α. Коэффициентом полезного действия винта называется отношение полезной мощности, равной Р*V, к мощности, необходимой для его вращения.
Из соотношения — получим выражение для определения коэффициента полезного действия:
Основные параметры, характеризующие работу винта, узнаем опытным путем. Проверяя винт при различных значениях λ, можно вычислить коэффициенты α и ß. Их наносят на диаграмму, называемую характеристикой винта.
Исследования производятся для винтов, имеющих одинаковую форму лопастей, диаметр и профили сечений, но разный относительный шаг. Получаются характеристики серии винтов, сходных по своим формам, но имеющих различные шаги. Характеристику строят в виде группы кривых ß по λ при различных h (рис. 2).
Рис. 2. Диаграмма-характеристика серии воздушных винтов.
Зная (мощность двигателя и соответствующее ей число оборотов, а также задавшись скоростью полета модели, можно найти необходимый шаг и диаметр винта.
Пусть N = 0,25 л. с. при ns = 167 об/сек ( 10000 об/мин), а V = 11 м/сек (около 40 (км/час). Имеется в виду таймерная модель с серийным компрессионным двигателем, скорость которой на траектории редко превышает 10—12 м/сек при диаметре винта 220—240 мм. Из формулы для определения мощности двигателя находим величину потребного ß и λ;
Если ρ=1,8, а D=0,24 м, то подставляя данные в формулы, найдем λ и ß.
На рис. 3, откладывая по осям координат значения ß и λ, находим точку А и читаем относительный шаг h и к. п. д.—η.
Рис. 3. Вычерчивание шаблонов винта.
В нашем примере h=0,6, а η = 0,54. Тогда шаг винта будет Н = h * D = 0,6* 0,24 = 0,144 м. Для винта вычерчивают шаблоны: сначала лопасть «вид сверху», на котором размечают пять сечений (рис. 3). Таким образом узнаем верхний шаблон. Параллельно оси лопасти проводят прямую АВ, перпендикулярно к ней откладывают отрезок
После этого сечения лопасти переносят на линию АВ, полученные точки соединяют с вершиной О. Эти линии дают нам углы установки сечений. Затем ширину лопасти в первом сечении (на рис.
4—12 мм) переносят на горизонтальную прямую. Из точки С восстанавливают перпендикуляр и в пересечении с наклонной линией получают точку С’. Отрезок СС’ и есть высота бокового шаблона в сечении № 1. Дальнейшее построение видно из рисунка. Полученные точки соединяют плавной линией и получают боковой шаблон лопасти.
Значительное влияние на работу винта оказывает форма лопасти в поперечном сечении (профиль). Наибольшего значения тяга достигает при расположении максимальной толщины профиля на 30% от передней кромки.
На характеристику винта влияет и форма лопасти в плане. От взаимного расположения оси продольной жесткости лопасти и точки приложения полной аэродинамической силы образуется момент, который скручивает лопасть, увеличивая или уменьшая шаг.
На рис. 4 показаны шаблоны нескольких различных винтов.
Ю.Соколов мастер спорта СССР Москва
Журнал Крылья Родины.
Кордовые модели F2B | Control line stunt | Aerobatics
Помогите посчитать силу тяги винта
Undertaken сказал(а):
двигатель Agromotor 160 Fкрутящий момент (Нм) = 10,8/2500 http://master-tehno.ru/moto-dvigateli/dvigateli-agromotor/dvigatel-agromotor-160…винт помогите взять какой-нибудь диаметром около 0,7м
Нажмите, чтобы раскрыть…
Тяга будет около 12 кг. Но не все так просто… С обычным двухлопастным винтом диаметром 70 см на таких оборотах не снять такую мощность с двигателя. Дело в том, что лопасти винта подобны крылу самолета и эффективно работают только в узком диапазоне углов атаки. При превышении происходит срыв потока. Даже при 4 лопастном винте, шаг винта получается слишком большим. Озвученный выше вариант где-то с 16 лопастями, видимо, наиболее близок в реальности.
По моим замерам, для тяги в диапазоне 25-45 кг, наиболее точный расчет тяги дает программа PropSelector, которую можно скачать здесь: http://www.
hoppenbrouwer-home.nl/ikarus/software/propselector.htm. В ней нужно указать диаметр винта, скорость полета (для зависания 0 км/час) и обороты винта, а потом подбирать шаг, чтобы потребляемая винтом мощность стала равна мощности, выдаваемой двигателем. Точность расчета будет в пределах 2-3 кг (проверено на десятке сделанных винтов диаметром от 80 см до 135 см и мощности от 5 л.с. до 15 л.с.), что является неплохим результатом, учитывая простоту программки.
Для начала, нужно выяснить мощность двигателя. В характеристиках првиеденного двигателя указан момент M=10.8 Н*м на оборотах n=2500 об/мин. Отсюда можем найти мощность на этих оборотах по формуле: P=M*2*3.14*n/60=2826 Вт = 2.826 кВт. Или 2.826*1.36=3.843 л.с..
Уже сейчас можно сказать, что с такой мощности можно снять около 11-15 кг, так как известно, что с типичными по размеру винтами на мощностях до 10 л.с., с каждой лошадиной силы снимается примерно 3-4 кг тяги. Проблема возникает, во-первых, с тем, что этим цифрам на сайте (10.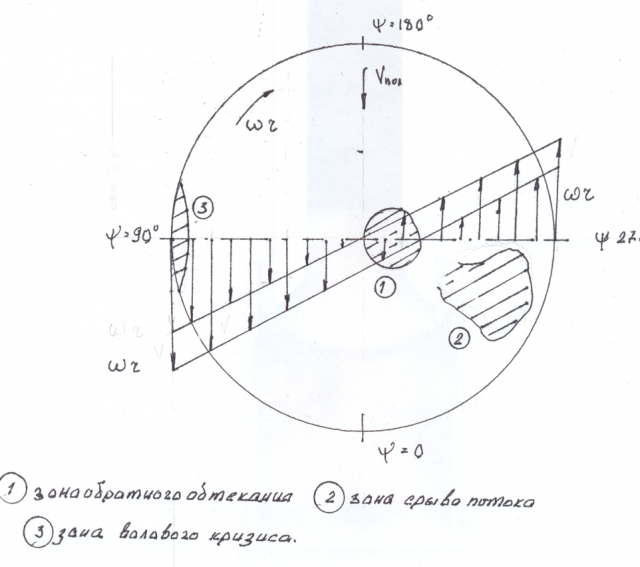
8 Нм/2500) верить нельзя, потому что все эти маркировки китайских клонов хонд пошли с тех времен, когда сама хонда писала на своих двигателях такие мощности (5.5 л.с. для GX160, 6.5 л.с. для GX200, 13 л.с. для GX390 и т.д.), но со сноской мелким шрифтом, что эта мощность получена в лабораторных условия со снятым глушителем и модицицированным двигателем. А так как в реальности никто эти двигатели после покупки в магазине, естественно, не эксплуатирует со снятым глушителем и подобранными топливными жиклерами большего диаметра, чем стоит штатный, то реальная мощность всех этих двигателей оказалась значительно меньше. Так, по моим замерам, 15-сильный движок на 3600 об/мин выдает только 11 л.с., а 6.5 л.с. в реальности имеет только 5.5 л.с.
Позже хонда отказалась от этой порочной практики завышения мощности своих двигателей и стала маркировать просто как модель, допустим, GX200. Но китайские клоны продолжают указывать на двигателе прежнюю завышенную мощность.
Так вот, если мы введем в PropSelector диаметр 0.
7 м и обороты 2500 об/мин и попытаемся подобрать шаг, чтобы мощность стала 3.843 л.с.. (которую на самом деле этот движок на этих оборотах не разовьет по описанным выше причинам, реальная будет немного меньше). То окажется, что в программе поле тяги подсветится красным. Это означает, что лопасти работают в режиме срыва, слишком большой угол атаки на лопастях (больше 15-18 градусов). Надо либо увеличить количество лопастей, либо увеличить обороты с помощью повышающего редуктора, либо изменить диаметр винта.
Могу сказать, что вот этот двигатель с заявленной мощность 7 л.с. в реальности с винтом диаметром 95 см и шагом 25-30 см без форсировки выдает статическую тягу 24-26 кг на оборотах около 3700 об/мин. А если снять ограничитель оборотов и раскрутить до 4800-5000 об/мин, то примерно 28 кг. Если же на 5000 об/мин поставить редуктор под винт диаметром 125 см, то тяга получается около 35 кг.
Undertaken сказал(а):
правильно ли я понимаю физический смысл цифры, это значит что при таких оборотах такой мотор зависьнет в воздухе при общем весе конструкции 12кг?
Нажмите, чтобы раскрыть.
..
..Да. Если речь о статической тяге.
Undertaken сказал(а):
в итоге я хочу посчитать примерную стоимость изготовления большого квадрокоптера
Нажмите, чтобы раскрыть…
Эти двигатели нельзя поворачивать винтом вниз. У них вал должен быть горизонтальным, так как там в картере плещется масло. И при наклоне оно попадет в цилиндр, что приведет к гидроудару и разрушению двигателя. Поэтому там внутри стоит датчик масла, которые при наклоне двигателя более 30 градусов или около того, экстренно глушит двигатель. На самом деле при снятом датчике масла, на холостых оборотах они кратковременно переживают падение набок =), но эксплуатировать так нельзя. Да и не получится, так как на них стоят поплавковые карбюраторы, которые работают только в вертикальном положении.
Undertaken сказал(а):
Соответственно я хочу узнать, какой двигатель для этого подойдет, а точнее какие 4 двигателя взять.
Нажмите, чтобы раскрыть…
Ну, вероятно потребуются двухтактные двигатели с мембранными карбюраторами. Их можно вращать в любую сторону. Такие карбюраторы стоят, например, на бензопилах и большинстве парамоторных двигателей. Если двухтактный двигатель с поплавковым карбюратором (бывают и такие), то сам двигатель можно повернуть боком, чтобы винт был внизу, но для карбюратора придется делать переходник, чтобы он оставался вертикальным.
Еще бывают четырехтактные двигатели с вертикальным валом, ищите в разделах про судна на воздушной подушке (СВП), там они часто используются для наддува. Но мощность их обычно еще меньше, чем у движков с горизонтальным валом, а вес такой же. То есть они с трудом могут поднять собственный вес, а на бензин, конструкцию и полезную нагрузку почти ничего не остается.
P.S. в мощность бензиновых авиамодельных двигателей верить тоже нельзя, там где пишут 50 сс и мощность 5 л.с., в реальности имеют около 2-3 л.
с. А оппозиты 100сс мощностью 10-11 л.с., в реальности имеют примерно 6-7 л.с.. Правда их можно раскрутить свыше штатных оборотов и хоть как-то компенсировать эту «недостачу», но ресурс и надежность станут совсем сомнительными…
Силовые винты Расчетное уравнение и калькулятор
Силовые винты Расчетные уравнения и калькулятор
Предварительный просмотр: Калькулятор расчета крутящего момента силовых винтов
В условиях статического равновесия винт вращается с постоянной скоростью в ответ на входной крутящий момент T, показанный на приведенной выше диаграмме свободного тела. Кроме того, на силовой винт действуют сила нагрузки F, нормальная сила N и сила трения скольжения F f . тивное движение. Сила трения противодействует относительному движению. Следовательно, направление силы трения F f будет реверсировать, когда винт перемещается в направлении нагрузки, а не против нее. Крутящие моменты, необходимые для подъема груза T R (т.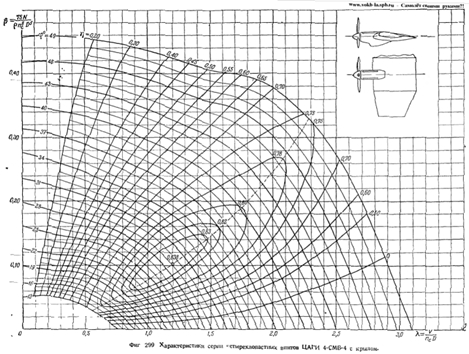
е. перемещения винта в направлении, противоположном грузу) и для опускания груза T L , составляют:
Где:
включает влияние угла боковой поверхности α, поскольку он проецируется нормально к резьбе и как функцию угла подъема. Для однозаходной резьбы Acme общего назначения α составляет 14,5 градусов, а β составляет приблизительно 0,9.68 с отклонением менее 1% для диаметров от 1/4 дюйма до 5 дюймов и шага резьбы от 2 до 16 витков на дюйм. Для квадратной резьбы β = 1.
Во многих случаях нагрузка скользит относительно втулки, что требует дополнительного входного крутящего момента 2
Шариковые и упорные конические роликоподшипники могут использоваться для уменьшения крутящего момента в буртике.
Начальный крутящий момент получается путем подстановки статических коэффициентов трения в приведенные выше уравнения. Поскольку коэффициент трения скольжения примерно на 25 процентов меньше статического коэффициента, рабочий крутящий момент несколько меньше начального крутящего момента.
Для получения точных значений коэффициентов трения конкретные данные должны быть получены из опубликованной технической литературы и проверены экспериментально.
Силовые винты могут быть самостопорящимися при высоком коэффициенте трения или малом шаге, так что π µ t d m > L или, что то же самое, µ f > tan λ. Если это условие не выполняется, винт будет самоопускаться или перекручиваться, если не будет приложен противодействующий крутящий момент.
Мера эффективности шнека η может быть сформулирована для сравнения выхода работы W o с затратами работы W i :
, где T — общий крутящий момент винта и муфты. Точно так же для одного оборота или 2π радиан и винтового перемещения L,
η = F L / ( 2 π T )
Производители винтов часто указывают выходную скорость перемещения V, дюйм/мин, как функцию требуемого крутящего момента двигателя T в фунт-силах · дюйм, работающего при n об/мин, для подъема номинальной емкость F, фунт-сила.
Таким образом, фактический КПД для этих данных составляет
η = F V / ( 2 π n T )
КПД силового винта с квадратной резьбой по отношению к углу подъема X, как показано в таблице ниже, получается из
η = (1 — µ тангенс λ) / (1 + µ cos λ)
Эффективность винта η в зависимости от угла подъема резьбы λ.
Обратите внимание на важность правильной смазки. Например, для λ = 10 градусов и µ = 0,05 η составляет более 75 процентов. Однако по мере того, как смазка со временем загрязняется грязью и пылью или химически разрушается, коэффициент трения может увеличиться до µ = 0,30, что приводит к эффективности η = 35 процентов, что удваивает требования к крутящему моменту, мощности и электроэнергии.
Где:
F = Прикладываемая осевая сила, фунт-сила
d м = средний диаметр, дюймы
d = наружный диаметр, дюймы
µ f = Коэффициент трения резьбы
L = Шаг резьбы
β = параметр геометрии резьбы
p = шаг резьбы, дюймы
n s = Количество запусков резьбы
α = Угол боковой поверхности резьбы, градусы
α n = Нормированный угол боковой поверхности резьбы, градусы
λ = угол опережения, град
V = дюйм/мин
Ссылки:
Стандартный справочник по проектированию машин, второе издание, Shigley & Mischke
Технический расчет/метод выбора | Шарико-винтовые пары
| Имя файла | Страница каталога | Размер файла | Размер несжатого файла |
|---|---|---|---|
Линейные направляющие · Программное обеспечение для технических расчетов шарико-винтовых пар, версия 2.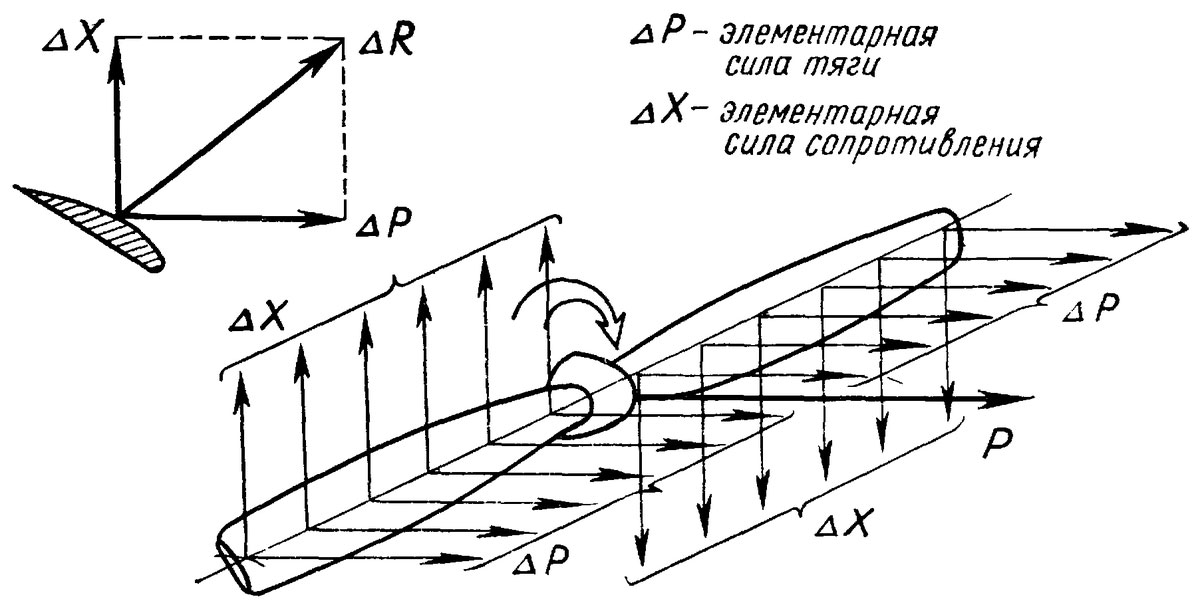 0 | — | 6,79 МБ | 6,85 МБ |
Пример выбора
Шаг (L) Выбор
Требуемый шаг рассчитывается на основе макс. скорость и
Требование максимальной скорости.
Требуется провод длиной 20 мм или более.
Выбор гайки
(1) Расчет осевой нагрузки
Применяется расчет осевой нагрузки P.1897, 6-2.
- ・Фаза постоянной скорости: осевая нагрузка (Pb) = µWg = 0,02 x 50 x 9,8 ≈ 10 (Н)
- ・Фаза ускорения: ускорение (α) = (Vmax/t) x 10-3 = 6,67 (м/с2)
Осевая нагрузка (Па) = Wα + µWg = 50 x 6,67 — 0,02 x 50 x 9,3 ≈ 343 (Н) - ・Фаза торможения: осевая нагрузка (Pc) = Wα — µWg = 50 x 6,67 — 0,02 x 50 x 9,8 ≈ 324 (Н)
(2) Количество профилей за 1 цикл
График модели рабочего цикла приводится ниже.
| Профиль движения | Ускорение | Низкая скорость | Замедление | Общее время |
|---|---|---|---|---|
| Время | 0,60 | 0,84 | 0,60 | 2,04 |
(3) Сводка по осевым нагрузкам, скорости вращения, времени движения по каждому профилю.
| Профиль движения | Ускорение | Низкая скорость | Замедление |
|---|---|---|---|
| Осевое направление | 343Н | 10Н | 324Н |
| Скорость вращения | 1500мин -1 | 3000мин -1 | 1500мин -1 |
| Коэффициент времени | 29,4% | 41,2% | 29,4% |
(4) Расчет средней осевой нагрузки
Расчет по формуле на стр. 1897, 6-3.
(5) Расчет средней скорости вращения
(6) Расчет требуемой базовой динамической грузоподъемности
(1) Расчет фактического срока службы в часах (Lho)
Фактический срок службы в часах, который представляет собой время отдыха, вычитаемое из желаемого срока службы (2,04 секунды за 4,01 цикла), может быть рассчитан следующим образом.
(2) Расчет требуемой базовой динамической грузоподъемности
Чтобы удовлетворить фактическому сроку службы, необходимая базовая номинальная динамическая грузоподъемность рассчитывается по формуле на стр.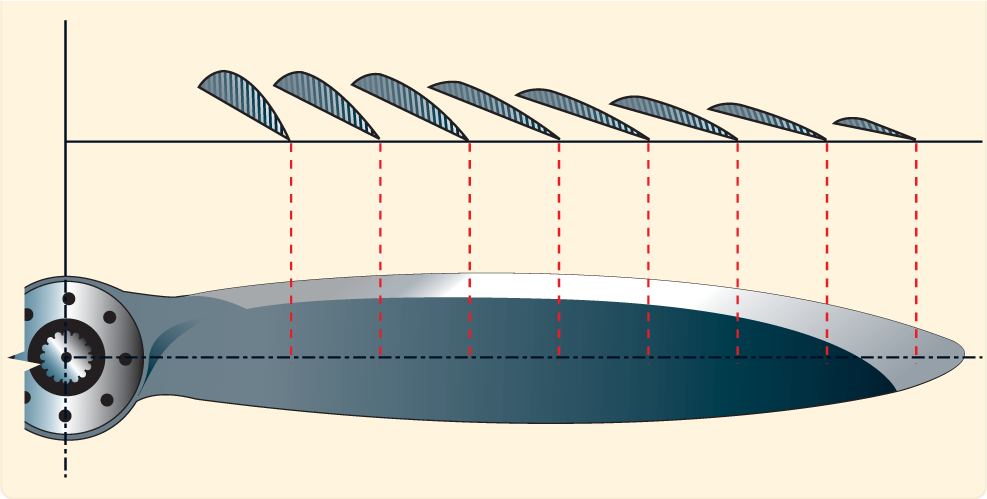
1897, 6-1.
(7) Промежуточный выбор шарико-винтовой передачи
BSS1520 временно выбран в качестве шарико-винтовой пары, удовлетворяющей требованиям базовой динамической грузоподъемности 3700 Н.
Подтверждение точности
(1) Оценка класса точности и осевого зазора
На основании списка «Точность хода шарико-винтовой передачи» на стр. 1893, 2.,
винт класса точности C5 с фактической средней погрешностью хода ±0,040/ 800~1000 мм соответствует требуемой точности ±0,1/720 мм, поэтому подходит BSS1520.
Дополнительно на основании перечня «Осевые зазоры ШВП» на стр.1893, 3.,
можно подтвердить, что BSS1520 с осевым зазором 0,005 или меньше может удовлетворить требование повторяемости ±0,01 мм.
Выбор шарико-винтовой передачи
(1) Выбор общей длины вала винта
Длина шарико-винтовой передачи (L) = макс. Ход + длина гайки + дополнительный запас + длина конца вала (оба конца),
- Макс. Ход: 720 мм
- Длина гайки: 62 мм
- Дополнительное поле: шаг x 1,5 = 60 мм
- Концы вала: 72
Длина шарико-винтовой передачи (L) = 720 + 62 + 60 + 72 = 914 мм
* Дополнительный запас предназначен для предотвращения перебега и обычно в 1,5–2 раза превышает шаг винта.