МОЩНОСТНАЯ ХАРАКТЕРИСТИКА | это… Что такое МОЩНОСТНАЯ ХАРАКТЕРИСТИКА?

топологического пространства — функция, сопоставляющая этому пространству бесконечное кардинальное число и принимающая одинаковые значения на гомеоморфных пространствах. М. х. наз. также кардинальными инвариантами. Областью определения М. х. может служить класс всех тополо-гич. пространств или нек-рый его подкласс. Следующие М. х. были выделены уже на первом этапе развития общей топологии. Пусть X- произвольное топологич. пространство. Его мощность есть мощность множества всех его точек — тривиальный инвариант. Вес — минимум мощностей всевозможных баз пространства X. Плотность — минимум мощностей всюду плотных в Xмножеств. Число Суслина — наименьший бесконечный кардинал т такой, что мощность всякого семейства попарно не пересекающихся непустых открытых множеств в X не превосходит .ЧислоЛинделёфа — наименьший бесконечный кардинал такой, что из всякого-открытого покрытия пространства Xможно выделить подпокрытие мощности . Эти простые понятия сразу доказали свою важность, войдя решающим образом в формулировки фундаментальных теорем и проблем. Примеры: регулярное пространство счетного веса метризуемо (теорема Урысона — Тихонова, 1925), бикомпакт метризуем в том и только в том случае, если вес его счетен; для пространства X любой бикомпактной группы число Суслина счетно; число Линделёфа счетно (т. е. равно ) для всякого пространства X счетного веса. Проблема Суслина: верно ли, что всякий связный упорядоченный бикомпакт X такой, что гомеоморфен обычному отрезку [0, 1], сводится к вопросу о соотношении между двумя М. х.: плотностью и числом Суслина. Для положительного решения проблемы Суслина достаточно-в указанных выше предположениях установить, что- . Вопрос о сравнении М. х. между собой — решение к-рого, как видно из приведенного примера, может иметь ключевое значение для окончательного заключения о строении пространства — занимает центральное место в теории М. х. Причина этому находится в самой природе понятия М. 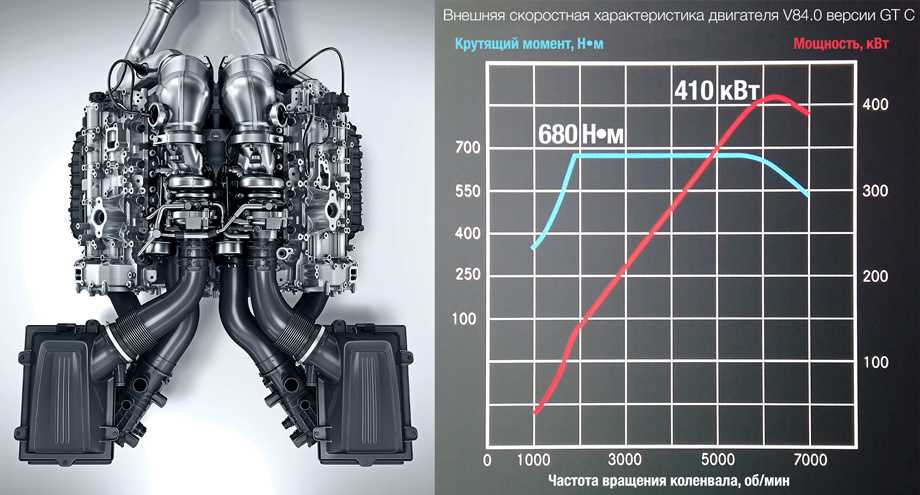х.: значениями М. х. являются кардинальные числа, совокупность к-рых вполне упорядочена по величине. Следовательно, любые две М. х.можно пытаться сравнить по величине. Возникает серия взаимосвязанных вопросов. Верно ли, что для любого для каких , когда и т. д.

С кардинальными числами можно производить вычисления: перемножать их, складывать, возводить в степень. Соответственно, можно производить вычисления и с кардинальными инвариантами — перемножать и складывать их как функции и т. д. Это открывает новые возможности для сравнения М. х.- с помощью вычислений. Всегда

— т. е. число Суслина не превосходит плотности, плотность не превосходит веса и число Линделёфа не препосходит веса. Но плотность и число Линделёфа в этом смысле не сравнимы: существуют пространства X, Y, Z, для к-рых

Неожиданной на первый взгляд представляется несравнимость мощности и веса: существуют нормальные счетные -пространства несчетного веса. Но всегда и . Для всякого -пространства X, (пишут ехр вместо ). Для всякого хаусдорфова пространства Всегда . .

В задачу сравнения могут быть естественно вовлечены не два, а большее число М. х. На этом пути получаются особенно тонкие, красивые и часто неожиданные результаты, поражающие своей общностью: для каждого хаусдорфова пространства где — наименьший бесконечный кардинал такой, что в каждой точке пространства имеется база мощности (см. [1], [2]). Исследования в теории М. х. стимулировала проблема оценки мощности бикомпакта с первой аксиомой счетности, остававшаяся нерешенной с 1923 по 1969. Оказалось: для каждого хаусдорфова пространства (теорема Архангельского, см. [2], [4]).

Вычисления М. х. возникают во всех разделах общей топологии в силу теоретико-множественной природы последней. Поэтому и применения теория М. х. находит практически во всех областях общей топологии и при любых подходах к исследованию пространств.

В частности, при изучении пространств методом покрытий на первый план выступают число Линделёфа, плотность и число Суслина. При исследовании и классификации пространств методом непрерывных отображений (в частности, при построении теории диадич. бикомпактов и теории абсолютов) возникли и сыграли ключевую роль новые М. х.: спрэд и -вес. Спрэд пространства Xесть точная верхняя грань мощностей дискретных подпространств пространства X, а -вес этого пространства — минимум мощностей всевозможных семейств (наз. -базами) непустых открытых в Xмножеств таких, что для каждого непустого открытого в Xмножества Uнайдется такое, что . При исследовании пространств методом обратных спектров важную роль играют число Суслина, характер, вес. Но имеется подход к общей топологии, при к-ром М. х. выступают и как главное средство исследования строения пространств, и как основной язык, на к-ром выражаются свойства пространств из тех или иных классов и, наконец, как средство классификации и выделения новых естественных классов топологич. пространств. В основе и здесь лежит задача сравнения M, х. Основной вопрос ставится следующим образом. Дан класс тоиологич. пространств, к-рым ограничивается область определения М. х. Как выглядят основные соотношения между кардинальными инвариантами в этих условиях? Развивая теорию М. х. для класса , мы как бы получаем «кардинальный портрет» класса . Сравнение кардинальных портретов каких-либо классов дает возможность судить

о соотношениях между этими классами, а также доставляет эффективные средства доказательства для конкретных пространств принадлежности их тому или иному классу.

Этот подход демонстрируется на примере класса метризуемых пространств. Характерной чертой здесь является совпадение для этого класса ряда основных М. х.: число Суслина равно плотности, весу и числу Линделёфа. Этот факт часто применяется, напр, чтобы доказать, что нек-рое пространство неметризуемо, достаточно показать, что на нем различаются хотя бы два из названных выше инвариантов.

Если в классе метризуемых пространств теория М. х. отличается главным образом упрощениями, то в классе бикомпактов она совершенно и нетривиальным образом меняет свой вид. Ответственны за это фундаментальные положения этой теории — совпадение для бикомпактов характера и псевдохарактера, веса и сетевого веса. При этом псевдохарактером пространства Xв точке хназ. наименьшее число открытых множеств, дающих эту точку в пересечении, а характером пространства Xв точке хназ. минимум мощностей баз пространства в этой точке. Сетевым весом наз. минимум мощностей семейств множеств в X, удовлетворяющих условию: если и где Uоткрыто в X, то найдется , для к-рого (такие семейства наз. сетями в X). Для всякого бикомпакта Xверно следующее: 1) для всех 2)

Поэтому при непрерывном отображении на бикомпакт вес не может возрастать, и если бикомпакт Xпредставлен в виде объединения двух своих подпространств и , то вес не превосходит максимума весов и (аддиционная теорема для веса). По той же причине вес бикомпакта всегда не превосходит его мощности — в частности, всякий счетный бикомпакт метризуем. Ни одно из перечисленных выше положений теории М. х. в классе бикомпактов не распространяется на класс всех вполне регулярных пространств. Важным специфич. результатом является следующий: если — бикомпакт,- кардинал,и для всех , то (теорема Чеха — Поспишила). Почти все критерии метризуемости бикомпактов также являются теоремами о М. х. Так, метризуемость бикомпакта Xравносильна любому из следующих условий: а) б) в) диагональ в является множеством типа ; г) Xобладает точечно-счетной базой.

В исследовании строения бикомпактов важная роль принадлежит тесноте. Теснотой (см. [2], [4]) пространства X наз. наименьший кардинал такой, что если то найдется , для к-рого Теснота не возрастает при возведении бикомпакта в любую конечную степень (в классе вполне регулярных пространств это — не так).

Если теснота бикомпакта не превосходит , то для каждой точки найдется семейство непустых открытых в Xмножеств такое, что и каждая окрестность точки содержит элемент семейства Поэтому л-вес каждого сепарабельного бикомпакта счетной тесноты равен Спрэд бикомпакта мажорирует его тесноту.

Особыми свойствами диадич. бикомпактов также в большой степени управляют теоремы о М. х. Так, для всякого диадич. бикомпакта его вес совпадает со спрэ-дом и с теснотой. К числу диадич. бикомпактов относятся пространства любых бикомпактных групп, так что, в частности, каждая бикомпактная группа счетной тесноты метризуема.

Для теории диадич. бикомпактов и других разделов теории М. х. важное значение имеет вопрос о поведении последних при операции умножения. Существенную роль играют здесь следующие две теоремы, первая из к-рых влечет вторую. Если F- семейство пространства такое, что для каждого и то плотность произведения всех пространств из Fне превосходит (см. [1]— [4]). Если X — произведение какого-нибудь множества пространств, плотность каждого из к-рых не превосходит , то . В последнем утверждении нет никаких ограничений на число сомножителей. В частности, получается, что число Суслина любого тихоновского куба (произведения произвольного множества отрезков) счетно. Таким образом, условие не несет в себе ограничения на мощность пространства.

Многие просто формулируемые вопросы о поведении М. х. при операции умножения оказываются весьма деликатными. Например, верно ли, что всегда оказывается связанным с гипотезой Суслина и континуум-гипотезой?

Напротив, поведение М. х. при переходе от пространства Xк его образу Y при непрерывном отображении подчиняется в основном простым общим правилам.

Напр., всегда Если f факторно, то . То обстоятельство, что основу теории М. х. составляет система простых универсальных правил этого рода, ‘также можно рассматривать как одну из причин, обеспечивающих широкую применимость этой теории.

Значительная информация о строении пространств получается при рассмотрении вопроса: как ведут себя М. х. при переходе к подпространству. Те М. х. , для к-рых из всегда следует, что наз. монотонными. К ним относятся: вес, сетевой вес, теснота, характер, спрэд. Немонотонны число Суслина, плотность, число Линделёфа. Возникают следующие вопросы: каковы те пространства X, для к-рых для всех ; каковы те , для к-рых для всех ; как отражается на топологии пространства X требование:для всех . Ответ на первый вопрос прост: сформулированное условие означает, что спрэд Xне превосходит . Но двумя последующими требованиями выделяются новые классы пространств. Исследование их оказалось зависящим от специальных гипотез теории множеств — в частности, от аксиомы Мартина.

Своеобразный характер приобретает теория М. х. на пространствах топология, групп. Так, критерий метризуемости сводится здесь просто к требованию счет-ностн характера. На языке М. х. формулируются важные свойства линейных топологич. пространств, в частности пространств непрерывных действительных функций на пространстве X. Сюда относятся теоремы о бикомпактах Эберлейна (каждый бикомпакт Эберлейна является пространством Фреше — Урысона, вес бикомпакта Эберлейна равен его числу Суслина), теорема: если X- бикомпакт, то теснота пространства С(X)в топологии поточечной сходимости счетна.

Между рядом М. х. пространств Xи С(X)имеет место соответствие типа двойственности.

Лит.:[1] JuhaszI., Cardinal functions in topology, Amst., 1971; [2] Архангельский А. В., Пономарев В. И., Основы общей топологии в задачах и упражнениях, М., 1974; [3] Engelking R., General topology, Warsz., 1977; [4] Архангельский А. В., «Успехи матем. наук», 1978, т. 33, в. 6, с. 29-84; [5] Еngelking R., General topology, Warsz., 1977.

А. В. Архангельский.

Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.

Мощностные характеристики атс.

Ne=Nтр+Nk

Nk=Nl-Nтр=Nl*hтр

Nk=Nf+Nw+/-Na+/-Nj+Nnp+Nб

Nf
– мощность затрачиваемая на преодоление
сил сопротивления качения.

Na-
мощность затрачиваемая на преодоление
подъема

Nw
– мощность, затрачиваемая на преодоление
сил лобового сопротивления.

Nj
– мощность затрачиваемая на преодоление
сил инерции.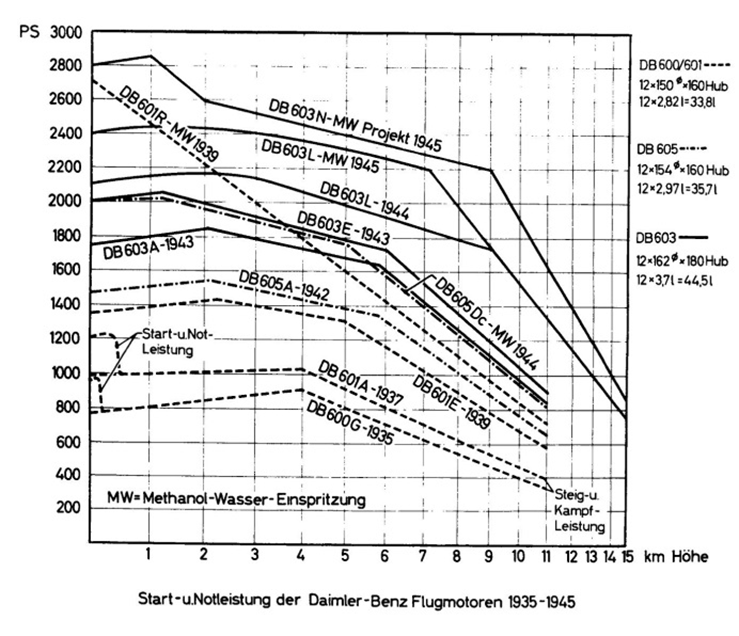 3

Лекция №8

Диаграмма
мощностного баланса.

Nрез
– расходуется на груз или пассажиров,
на преодоление подъема, на разгон.

При проектировании
необходимо обеспечивать больший запас
эффективной мощности(Nрез)
за счет увеличения мощности двигателя,
снижения сил сопротивления качения и
аэродинамического сопротивления.

Влияние
бесступенчатой трансмиссии на
тягово-скоростные свойства АТС.

Рассмотрим
гидравлические трансмиссии:

1. Гидродинамические
   трансмиссии.

2. Гидростатические
   трансмиссии (гидрообъемные)

Гидродинамические
трансмиссии.

Гидромуфта,
гидротрансформатор, комбинированная(ГТ
+ мех. трансмиссия)

Гидромуфта.

Насосное колесо
разгоняет частички масла, которые далее,
попадая на турбинное колесо, преобразуют
его энергию поступательного движения
во вращательную энергию турбинного
колеса.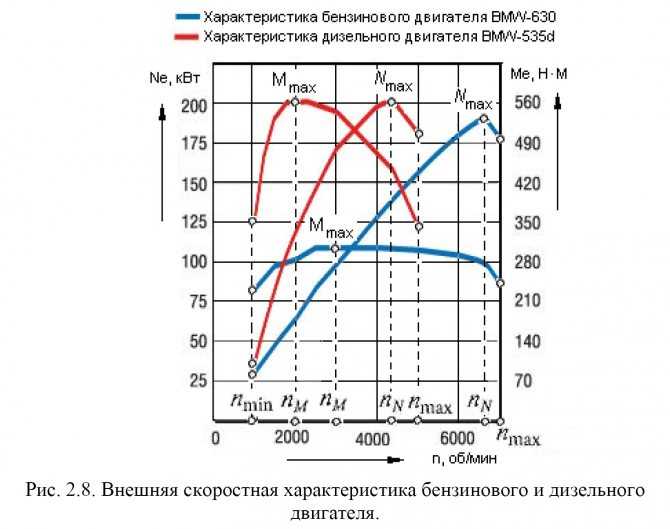

Используемое
масло: декстрон

Характеристики
работы:

Wн~Wт

Мт<=Mн

КПД:
hгм=Nпол/Nподв=Mн*Wн/Mт*Wт~0.97-0.98
при нормальной нагрузке.

При перегрузке
КПД равно 0.

Плюсы данной
конструкции: простота, плавная передача
момента, возможность срезания пиковых
нагрузок.

Минусы: Mт<=Мн,
узкий диапазон регулирования момента,
низкий КПД перегрузок

Гидротрансформатор.

Н — насосное колесо

Т – турбинное
колесо

Р – реакторное
колесо

ОМ – обгонная
муфта

Мт=Мн+Мр =>
Мт>=Мн

Hгт=
Nпол/Nподв=Mт*Wт/Mн*Wн=
Кт*iгт

Кт=(Мн+Мр)/Мн*Wн
– коэффициент трансформации

~2..2.5 для легковых

~3..3.5 для грузовых

Iгт
= Wт/Wн,
i=1/U
– передаточное отношение.

Плюсы данной
конструкции: возможность организовать
бесступенчатую трансмиссию при помощи
регулирования момента на реакторном
колесе; можно получать Мт>Мн на
достаточно широком диапазоне регулирования;
возможность срезания пиковых нагрузок,
благодаря чему увеличивается ресурс
работы двигателя; можно автоматизировать
работу трансмиссии; улучшение плавности
хода; облегчение управления.

Минусы: невысокий
КПД; сложность изготовления и высокая
цена.

Комбинированная
передача

hгмп=hгтр*hмех

Гидростатическая
трансмиссия.

ГМ – гидромотор
для каждого ведущего колеса.(Устанавливаеться
на экскаваторах)

Плюсы конструкции:
простота конструкции и управления

Минусы: вечные
утечки рабочей жидкости, низкий КПД,
влияние скоростного режима.

Электромеханические
передачи используются на 4-х палубных
кораблях.

Динамичность
АТС.

Отвечает за
приспособленность АТС к дорожным
условиям.

D-
динамический фактор

D=(Рк-Рw)/G

Pk
– касательная сила тяги на колесе

Pw
– сила аэродинамического сопротивления

G
– вес автомобиля

Определяет разгонные
характеристики АТС, чем он больше тем
лучше тягово-скоростные свойства,
ускорение, преодоление подъемов,
проходимость, буксировка прицепа.

~0.3..0.45 – для легковых

~0.6..0.8 – для
автомобилей повышенной проходимости

Dφ –
динамический
фактор по сцеплению

Условие движения
автомобиля в динамике:

Dφ ≥ D ≥ ψ

Ψ –
сопротивление
дороги

λi=
mi
/ m
– коэффициент нагрузки на ведущие
колеса; чать массы

приходиться на
ведущие колеса

Dφ
у автомобилей повышенной проходимости
выше

D=
Pk
– Pw
/ G=
1/mg((Me*Иtp*ηtp/rk)-Kw*F*v^2)
– коэффициент динамичности для
установившегося движения по ровной
дороге

Уравнение движения:

Pk
= Pw
+ Pf
— (+) Pj
— (+) Pα

Pk
—
Pw
=
Pf
— (+) Pj
— (+) Pα

D
= Pf
— (+) Pj
— (+) Pα
/ G
= f
cosα
– (+) sinα
– (+) j/g
δвр
– коэффициент динамичности для общего
случая движении

Диаграмма
динамической характеристики при полной
нагрузке

На этой диаграмме
видна величина подъема α
может преодолевать автомобиль двигаясь
на данной передаче без изменения скорости

Динамический
паспорт автомобиля

Строиться для
оценки тягово-динамических свойств
автомобиля при изменении нагрузки на
автомобиль

Этапы построения
динамического паспорта автомобиля:

1. строиться
   динамическая характеристика автомобиля
   с полной нагрузкой

2. строится монограмма
   нагрузок

3. строиться графики
   контроля буксирования по коэфециенту
   сцепления колеса с дорогой

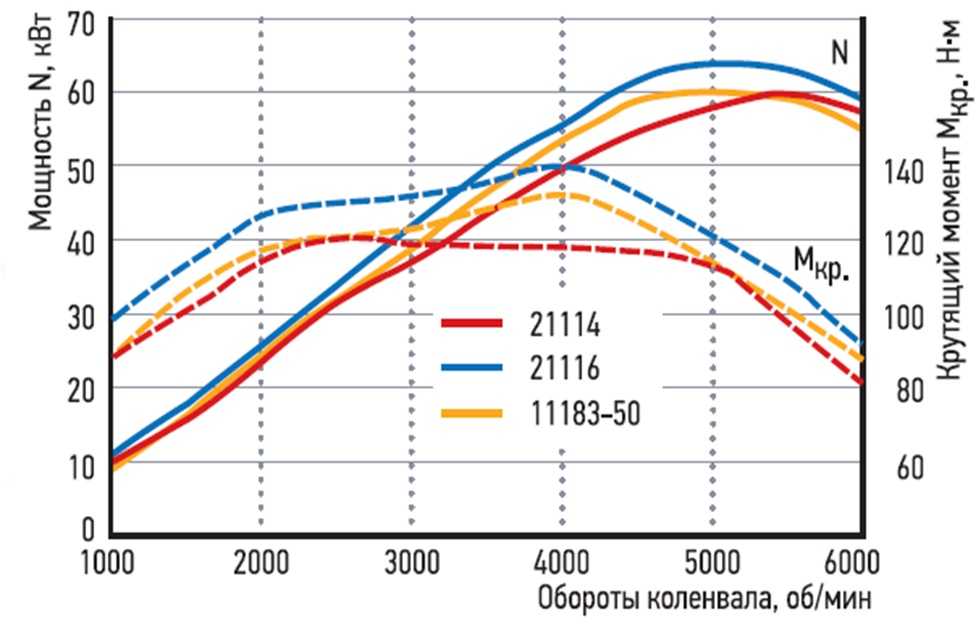
Da
– коэффициент динамичности для полной
загрузки автомобиля

Do
– коэффициент динамичности снаряженного
автомобиля

Do
Da

0. 35

0.3

0.25

0.35
0.2

0.15

0.10

0.05

0.05

25% 50% 75% Oa

v

Ga
– масса полностью загруженного
автомобиля;

Go –
масса
снаряженного автомобиля

Масштаб на Do
получается меньше

Dφ0 =
Go1/Go*φx
—> φx=
0,1 …0,8

Dφa =
Ga2/Ga*φx

Go2
– масса приходящаяся на ведущую ось
снаряженного автомобиля

Ga2
— масса приходящаяса на ведущую ось
загружаемого автомобиля

φx
– коэффициент продольного сцепления
с дорогой

Динамический
паспорт автомобиля связывает 4 параметра:

1. скорость

2. загруска АТС

3. коэффициент
   сопротивления дороге

4. сцепление колес
   с дорогой

7.

1A Определение характеристик держав

7.1A — Определение характеристик сверхдержав

Сверхдержавы, развивающиеся и региональные державы могут быть определены с использованием контрастных характеристик (экономических, политических, военных, культурных, демографических и доступа к природным ресурсам.)

Основные определения

• Сверхдержава — это страна, способная проецировать свое господствующее положение и влияние в любой точке мира.
  • США
• Развивающиеся сверхдержавы — это страны, играющие большую роль в одной из характеристик сверхдержав и обладающие растущим влиянием.
  • Китай, Бразилия, Индия, Россия
• Региональные державы могут проецировать господствующую власть и влияние на другие страны континента или региона.
  • Великобритания, Германия, Франция в Европе
  • Саудовская Аравия и Иран на Ближнем Востоке
  • Южная Африка и Нигерия в Африке

​

Характеристики сверхспособностей

Есть 6 характеристик сверхспособностей! (экономическая, политическая, военная, культурная, демографическая, природные ресурсы), используемые для определения типа власти в стране.

1)  Экономический

• Большой ВВП, высокая доля международной торговли, валюта используется в качестве резервной валюты.
• Большой ВВП создает влияние как потенциальный рынок и как дом для ТНК, создающих ПИИ.
• Поддерживает остальные 5 характеристик
• США имеют самый большой в мире совокупный ВВП — $18,5 трлн

2) 

Политическая

• Способность влиять на политику других стран посредством доминирования в переговорах. (Как на двусторонней основе, так и через международные организации.)
• Многие международные организации не имеют одинакового веса членов.
  • Право голоса может определяться экономическим вкладом, исторической ролью в основании организации (ООН), численностью населения и т. д.
• Часто за счет преобладания других характеристик.
  • большая экономика дает ей власть в торговых переговорах, военная мощь может сделать страны угрозой — давая им политическую власть

3)

Военная

• Военная мощь с глобальным охватом означает, что их можно использовать для достижения геополитических целей
• Глобальное влияние через голубые воды (океанские выходы) военно-морского флота и беспилотных летательных аппаратов, ракет и спутниковых технологий
• Показатели мощи: размер армии, расходы на оборону, ядерное оружие, межконтинентальные баллистические ракеты (МБР), размер военно-морского флота, крупный экспортер оружия, присутствие в международных военных организациях или руководство ими.
• Зависит от демографической мощи: количество военнослужащих, которые могут быть развернуты
• Зависит от экономической мощи: бюджет определяет инвестиции в военные технологии, увеличивающие мощь
• Россия обладает самыми активными ядерными боеголовками (1790)
  • США на втором месте с 1750

4)

Культура

• Возможность влиять на убеждения, ценности, идеологию и образ жизни в других странах.​
• Достигается за счет: 
  • господства средств массовой информации (кино, радио, телевидение, интернет, образование)
  • ТНК или мигрантов, представляющих культурные продукты (еда, одежда, музыка, религия)
  • навязывание точки зрения в международных соглашениях
• Показатели: глобальное распространение музыки, моды, еды, языка, религии
• В США самый высокий процент из 20 крупнейших ТНК мира — 27%.

5)

Демографический

• Большое население -> большая диаспора и работники ТНК
• Способствует экономической мощи за счет большого рынка и эффекта масштаба (так больше прибыли).
• Значит армия может быть больше.
• Китай имеет самое большое население — 1382 миллиона

6)

Ресурсы

• Контроль доступа к физическим ресурсам: энергия, полезные ископаемые
• Обеспечивает ресурсы для экономического роста
• Позволяет экспортировать их по высокой цене -> экономическая мощь
  • напр. ОПЕК и нефть
• Могут быть расположены внутри страны или могут быть получены через надежные страны-источники через транспортные пути.
• Необходим для военной мощи

Экстра

• «Сверхдержава» — это слово, обозначающее одну, доминирующую в глобальном масштабе сверхдержаву.
  • 1850-1910: Великобритания была сверхдержавой
  • 1990-2010: США были сверхдержавой

Характеристики блока питания Часто задаваемые вопросы | Electronic Design

Как характеристики источника питания влияют на электронную систему?

Характеристики источника питания влияют на производительность и конструкцию электронной системы.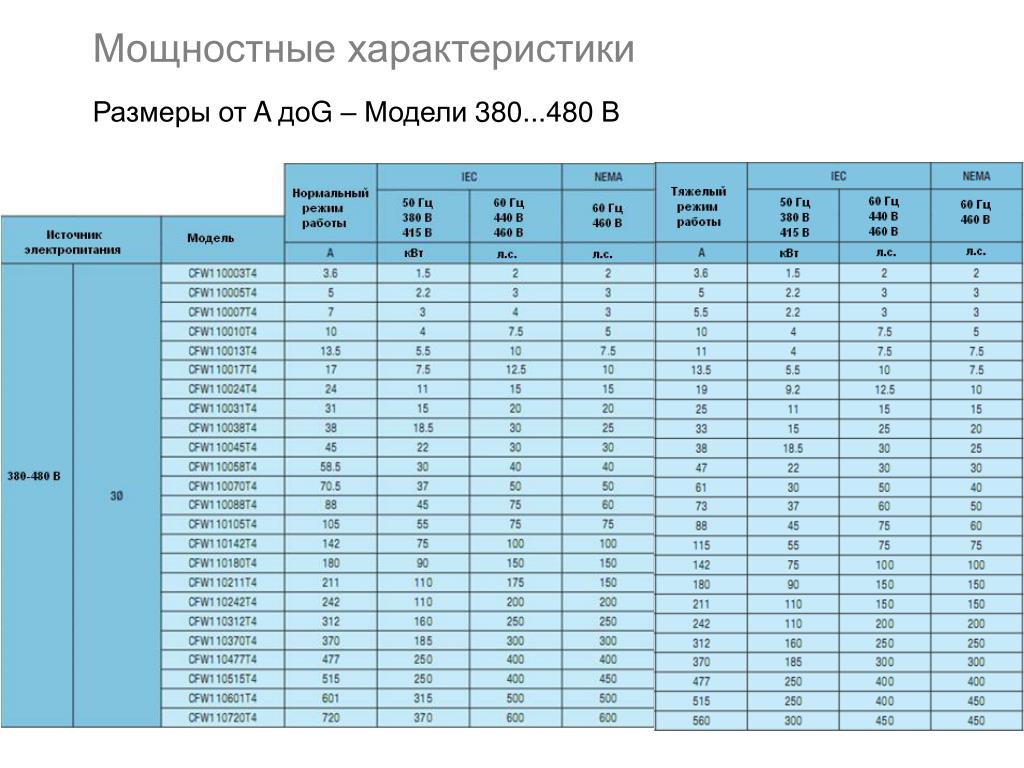 Среди важных характеристик источника питания — КПД в указанном диапазоне температур. Кроме того, имеются важные функции, защищающие источник питания и его нагрузку от повреждений, такие как перегрузка по выходному току, перегрев, пусковой ток и выходное перенапряжение. Кроме того, существуют рабочие параметры источника питания, такие как дрейф, динамический отклик, регулировка линии и регулировка нагрузки, которые могут повлиять на работу системы.

Похожие статьи

• Основы управления питанием: основы блока питания
• Основы управления питанием: характеристики блока питания
• Почему важно построить график отклика силового каскада на слабый сигнал?
• Назад к основам: ИС регулятора напряжения, часть 1
• Сбои в электроснабжении в большинстве случаев можно предотвратить
• Монолитные регуляторы переходят на более высокие напряжения

Как эффективность блока питания влияет на производительность электронной системы?

Рис.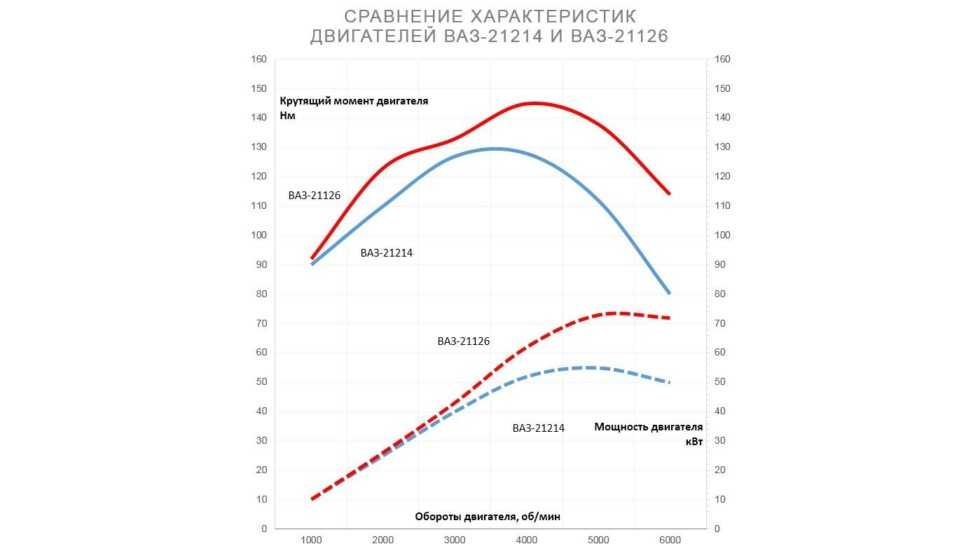 1. Типовой график эффективности источника питания

Эффективность источника питания определяет тепловые и электрические потери в системе, а также требуемую степень охлаждения. Кроме того, это влияет на физические размеры корпуса как источника питания, так и конечной системы. Кроме того, это влияет на рабочие температуры компонентов системы и, как следствие, на надежность системы. Эти факторы влияют на определение общей стоимости системы, как оборудования, так и поддержки на местах. Спецификации источников питания обычно содержат график зависимости КПД от выходного тока, как показано на рис. 9.0169 Рис. 1 . Этот график показывает, что КПД зависит от приложенного напряжения источника питания, а также от выходного тока нагрузки.

Эффективность, надежность и рабочая температура взаимосвязаны. Паспорта блоков питания обычно включают конкретные требования к воздушному потоку и радиатору. Например, рабочая температура окружающей среды влияет на выходной ток нагрузки, с которым блок питания может надежно работать.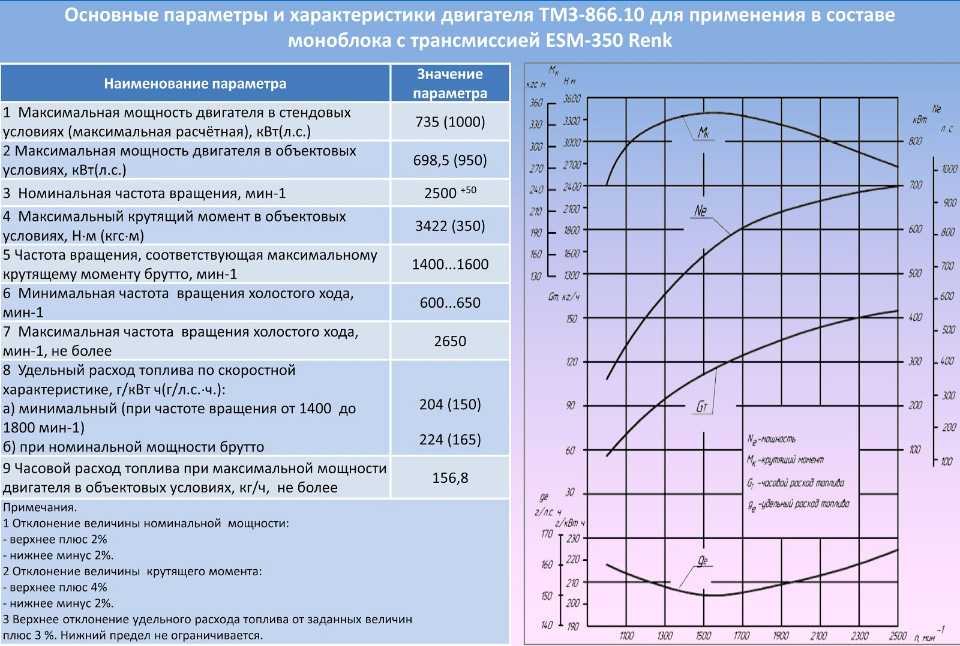 Кривые снижения мощности источника питания ( Рис. 2 ) указывают его надежный рабочий ток в зависимости от температуры. На рис. 2 показано, какой ток может безопасно работать с источником питания, если он работает с естественной конвекцией или 200 LFM и 400 LFM.

Рис. 2. Типичные кривые снижения номинальных характеристик источника питания

Существует несколько других характеристик, влияющих на работу источника питания. Среди них те, которые используются для защиты источника питания, в том числе:

Перегрузка по току: Режим отказа, вызванный выходным током нагрузки, превышающим указанный. Он ограничен максимальным током источника питания и контролируется внутренними схемами защиты. В некоторых случаях это также может привести к повреждению блока питания. Короткие замыкания между выходом источника питания и землей могут создавать токи в системе, которые ограничиваются только максимальным током и внутренним сопротивлением источника питания.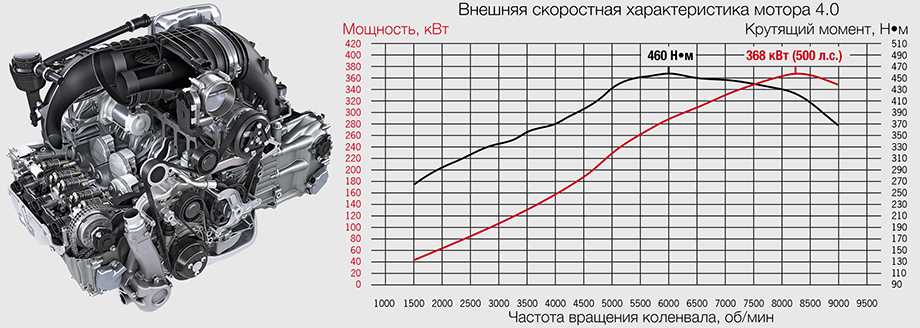 Без ограничения, этот большой ток может вызвать перегрев и повредить источник питания, а также нагрузку и ее межсоединения (дорожки на печатной плате, кабели). Поэтому большинство источников питания должны иметь ограничение тока (защиту от перегрузки по току), которое активируется, если выходной ток превышает заданный максимум.

Перегрев: Необходимо предотвращать превышение указанного предела температуры источника питания, иначе это может привести к отказу источника питания. Чрезмерная рабочая температура может привести к повреждению источника питания и подключенных к нему цепей. Поэтому во многих источниках питания используется датчик температуры и связанные схемы для отключения источника питания, если его рабочая температура превышает определенное значение. В частности, полупроводники, используемые в источнике питания, уязвимы к температурам, выходящим за указанные пределы. Многие расходные материалы имеют защиту от перегрева, которая отключает подачу, если температура превышает указанный предел.

Перенапряжение: Этот режим отказа возникает, если выходное напряжение превышает указанное значение постоянного тока, что может привести к чрезмерному постоянному напряжению, повреждающему цепи нагрузки. Как правило, нагрузки электронных систем могут выдерживать перенапряжение до 20 % без каких-либо необратимых повреждений. Если это соображение, выберите источник питания, который сводит к минимуму этот риск. Многие источники снабжены защитой от перенапряжения, которая отключает источник питания, если выходное напряжение превышает заданное значение. Другим подходом является использование ломового стабилитрона, который проводит достаточный ток при пороге перенапряжения, чтобы активировать ограничение тока источника питания и отключить его.

Плавный пуск : Ограничение пускового тока может потребоваться при первом включении питания или при горячей замене новых плат. Как правило, это достигается с помощью схемы плавного пуска, которая замедляет начальный рост тока, а затем обеспечивает нормальную работу. Если его не лечить, пусковой ток может генерировать высокий пиковый зарядный ток, который влияет на выходное напряжение источника питания. Если это важное соображение, выберите источник с этой функцией.

Блокировка минимального напряжения : Известный как UVLO, он включает питание, когда оно достигает достаточно высокого входного напряжения, и отключает питание, если входное напряжение падает ниже определенного значения. Эта функция используется для источников питания, работающих как от сети, так и от аккумуляторов. При питании от батареи UVLO отключает источник питания (а также систему), если батарея разряжается настолько, что входное напряжение питания падает слишком низко, чтобы обеспечить надежную работу.

Коррекция коэффициента мощности (PFC): Применимо только к источникам питания переменного/постоянного тока . Соотношение между напряжением сети переменного тока и током называется коэффициентом мощности. Для чисто резистивной нагрузки на линии электропередачи напряжение и ток совпадают по фазе, а коэффициент мощности равен 1,0. Однако, когда источник питания переменного/постоянного тока подключается к линии электропередачи, разность фаз напряжение-ток увеличивается, а коэффициент мощности уменьшается, поскольку процесс выпрямления и фильтрации входного переменного тока нарушает соотношение между напряжением и током в линии электропередачи. Когда это происходит, это снижает эффективность источника питания и генерирует гармоники, которые могут вызвать проблемы для других систем, подключенных к той же линии электропередач. Схемы коррекции коэффициента мощности (PFC) изменяют соотношение между напряжением и током в сети, приближая их к фазе. Это улучшает коэффициент мощности, уменьшает гармоники и повышает эффективность источника питания. Если важны гармоники в сети, выберите источник питания с PFC с коэффициентом мощности 0,9.или выше.

Электромагнитная совместимость (ЭМС):  В производимых источниках питания должны применяться методы проектирования, обеспечивающие электромагнитную совместимость (ЭМС) за счет сведения к минимуму электромагнитных помех (ЭМП).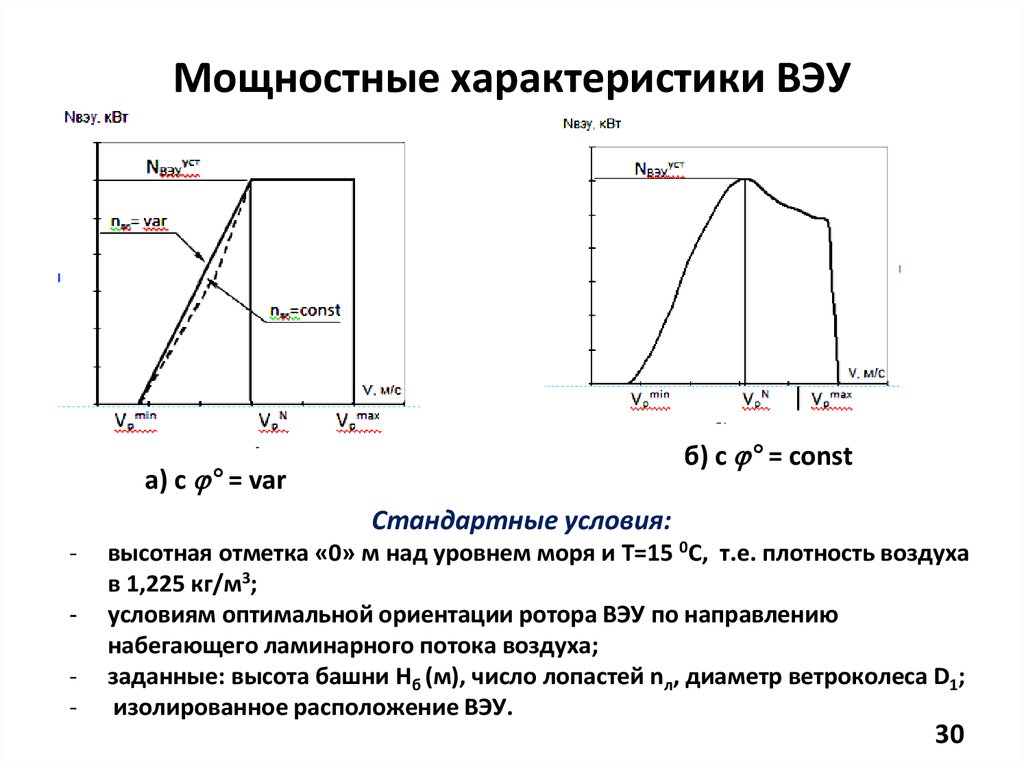 В импульсных источниках питания постоянное напряжение преобразуется в прерываемую или импульсную форму волны. Это приводит к тому, что источник питания генерирует узкополосный шум (ЭМП) на основной частоте переключения и связанных с ней гармониках. Чтобы уменьшить шум, производители должны свести к минимуму излучаемые или кондуктивные помехи.

Производители блоков питания могут свести к минимуму излучение электромагнитных помех, поместив блок питания в металлический корпус или покрыв его корпус металлическим материалом. Производителям также необходимо обратить внимание на внутреннюю компоновку источника питания и проводку, которая входит и выходит из источника питания, что может создавать электрические помехи.

Большая часть кондуктивных помех в линии электропередач возникает из-за основного переключающего транзистора или выходных выпрямителей. С помощью коррекции коэффициента мощности и надлежащей конструкции трансформатора, подключения радиатора и конструкции фильтра производитель источника питания может уменьшить кондуктивные помехи, чтобы источник мог получить одобрение регулирующего органа по электромагнитным помехам без чрезмерных затрат на фильтрацию. Всегда проверяйте, соответствует ли производитель блока питания требованиям нормативных стандартов EMI.

Нормативные стандарты

Стандарты пытаются стандартизировать характеристики ЭМС продукта в отношении электромагнитных помех. Должны соблюдаться нормативные стандарты, поскольку международные и национальные стандарты требуются для секции управления питанием конечного оборудования. Эти стандарты варьируются от одной страны к другой, поэтому производитель подсистемы питания и производитель конечной системы должны придерживаться этих стандартов там, где система будет продаваться. Инженеры-проектировщики должны понимать эти стандарты, даже если они не проводят сертификацию стандартов. Понимание этих нормативных стандартов обычно создает проблемы для разработчиков подсистем управления питанием, потому что:

·     Многие стандарты технически сложны, и для их расшифровки требуется эксперт.

·     Часто стандарты написаны в форме, которую трудно интерпретировать непосвященным, потому что обычно есть исключения и исключения, которые неясны.

·     В работе могут участвовать несколько различных агентств, поэтому некоторые из них могут относиться к одной стране или группе стран, а не к другим.

·     Стандартные требования различаются и иногда противоречат друг другу в разных юрисдикциях.

·     Стандарты постоянно развиваются, периодически вводятся новые, поэтому за ними сложно угнаться.

Какие агентства по стандартизации встречаются на уровне продуктов и систем?

1.  ANSI : Американский национальный институт стандартов осуществляет надзор за созданием, обнародованием и применением норм и руководств, непосредственно влияющих на бизнес, включая распределение энергии.

2.  Директивы ЕС (Европейского сообщества). Компании, ответственные за продукт, предназначенный для использования в Европейском сообществе, должны разработать и изготовить его в соответствии с требованиями соответствующих директив.

3.  EN (Европейская норма):  Стандартные директивы для Европейского сообщества.

4. IEC (Международная электротехническая комиссия): Разрабатывает стандарты для электрических и электронных систем.

5.  UL (Лаборатория андеррайтеров):  Сертификаты безопасности для электрических и электронных продуктов в США. Разрешение UL также можно получить через CSA.

6.  CSA (Канадская ассоциация стандартов):  Для использования электрического или электронного изделия в Канаде требуется разрешение на безопасность. Разрешение CSA также можно получить через UL.

7.  Telcordia : Стандарты телекоммуникационного оборудования в США.

8.  ETSI (Европейский институт стандартов в области телекоммуникаций) : Стандарты для телекоммуникационного оборудования.

Необходимые стандарты безопасности для источников питания содержат требования по предотвращению травм или повреждений из-за таких опасностей, как: поражение электрическим током, энергия, огонь, механическое воздействие, тепло, радиация и химические вещества.