КПД теплового двигателя | 8 класс
Содержание
В данном разделе вы уже познакомились с устройством и принципом работы двух видов теплового двигателя: двигателя внутреннего сгорания и паровой турбины. Используя эти механизмы, мы совершаем какую-то работу. Очевидно, что работа будет совершаться за счет энергии, которая выделяется при сгорании топлива. Но большая часть этой энергии теряется в окружающей среде. То есть эта часть энергии не используется полезно.
Следовательно, и работу таких механизмов тогда нужно рассчитывать специальным образом. Для этого в физике разделяют работу на полную и полезную, вводят понятие коэффициента полезного действия (КПД) механизма. На данном уроке мы познакомимся с этими величинами и рассмотрим решение задач с использованием КПД.
Полезная работа теплового двигателя
Для того чтобы судить о полезной работе теплового двигателя, обратимся еще раз к его устройству. Если рассматривать его принцип работы, то устройство любого теплового двигателя можно представить в виде простой схемы (рисунок 1).
Рисунок 1. Устройство теплового двигателя
Тепловой двигатель состоит из нагревателя, рабочего тела и холодильника.
Рабочим телом является газ или пар. Например, в паровой турбине — это пар, в газовой — газ, в двигателе внутреннего сгорания — смесь паров бензина и воздуха.
Этот газ получает некоторое количество теплоты $Q_1$ от нагревателя. Под нагревателем подразумевается не какое-то специальное механическое устройство, как можно подумать. Нагреватель в схеме теплового двигателя — это горящее топливо.
Газ нагревается и расширяется. Так он совершает работу $A_п$, используя свою внутреннюю энергию.
Но важно понимать, что часть этой внутренней энергии $Q_2$ не совершает какую-то полезную для нас работу. Она передается вместе с отработанным паром или выхлопными газами атмосфере — холодильнику.
В качестве холодильника может использоваться резервуар с водой. Отработавший пар будет в таком случае приносить дополнительную пользу — нагревать воду для ее дальнейшего использования. Но этот процесс уже требует отдельного рассмотрения.
Но этот процесс уже требует отдельного рассмотрения.
{"questions":[{"content":"Из каких частей состоит тепловой двигатель?[[choice-1]]","widgets":{"choice-1":{"type":"choice","options":["холодильник","нагреватель","рабочее тело","поршень","цилиндр","отработанный газ"],"answer":[0,1,2]}}}]}Итак, нас интересует именно та часть энергии топлива, выделяемая при его сгорании, которая превращается в полезную работу. От величины этой части энергии зависит экономичность двигателя.
Для этой характеристики мы вводим новое понятие — коэффициент полезного действия (КПД) теплового двигателя.
КПД теплового двигателя
Коэффициент полезного действия (КПД) теплового двигателя — это отношение совершенной полезной работы двигателя к энергии, полученной от нагревателя.
КПД теплового двигателя также как и КПД простейших механизмов, изученных вами в прошлом курсе, обозначается греческой буквой “эта” — $\eta$ и выражается в процентах.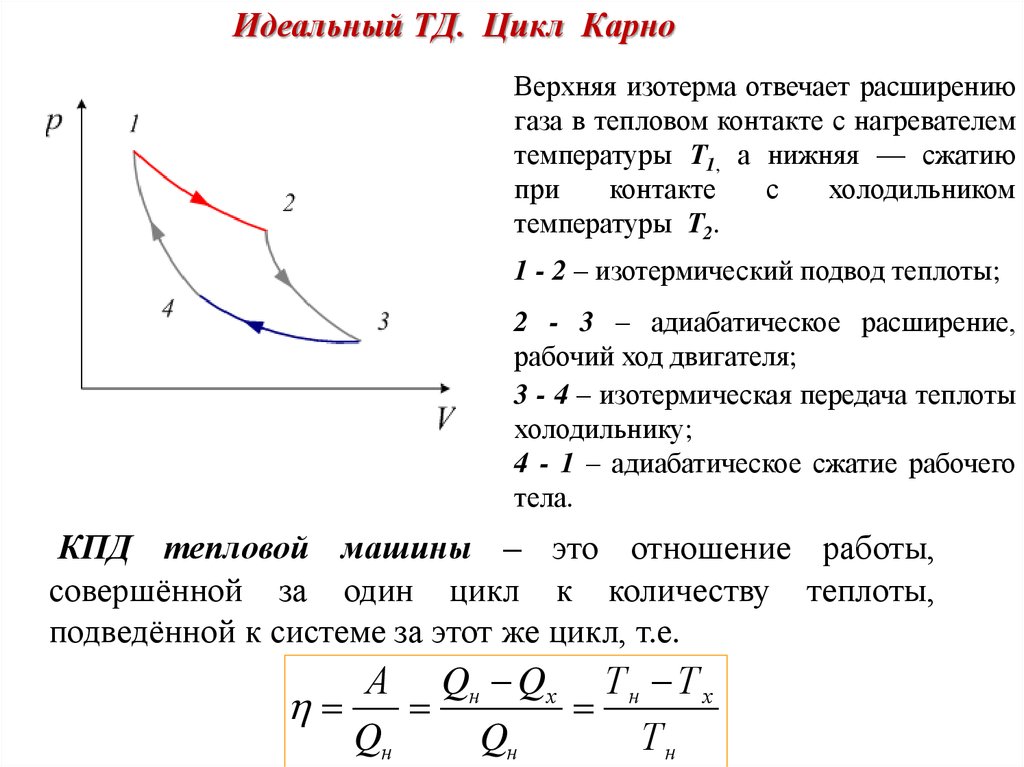
Формула для расчета КПД теплового двигателя имеет следующий вид:
$\eta = \frac{A_п}{Q_1}$,
или
$\eta = \frac{Q_1 — Q_2}{Q_1} \cdot 100 \%$,
где $A_п$ — полезная работа,
$Q_1$ — количество теплоты, полученное от нагревателя,
$Q_2$ — количество теплоты, отданное холодильнику,
$Q_1 — Q_2 = A_п$ — количество теплоты, которое пошло на совершение работы.
Например, при сгорании топлива выделяется определенное количество энергии. Одна пятая этой энергии пошла на совершение полезной работы. Это означает, что КПД двигателя равен $\frac{1}{5}$ или $20 \%$.
{"questions":[{"content":"Одна четвертая часть энергии, которая выделилась при сгорании топлива, пошла на совершение работы. Чему равен КПД этой тепловой машины?[[choice-1]]","widgets":{"choice-1":{"type":"choice","options":["$\\frac{1}{4}$","$25 \\%$","$\\frac{1}{4} \\%$","$40 \\%$"],"explanations":["","Чтобы преобразовать дробь в проценты, нужно разделить числить на знаменатель и умножить на 100 %. ","",""],"answer":[0,1]}}}]}
","",""],"answer":[0,1]}}}]}Средние значения КПД различных тепловых двигателей
В таблице 1 представлены средние значения КПД некоторых двигателей.
| Двигатель | КПД, % |
| Паровой двигатель | 8 |
| Двигатель внутреннего сгорания | 18 — 40 |
| Газовая турбина | 25 — 30 |
| Паровая турбина | 40 |
| Дизельный двигатель | 40 — 44 |
| Реактивный двигатель на жидком топливе | 47 |
Таблица 1. КПД различных двигателей
Обратите внимание, что КПД всегда меньше единицы — меньше $100 \%$. Это означает, что холодильник всегда получает некоторое количество теплоты от нагревателя.
Одной из важнейших технических задач при проектировании двигателей является повышение значения КПД.
{"questions":[{"content":"Может ли численное значение КПД быть больше единицы или 100%?[[choice-1]]","widgets":{"choice-1":{"type":"choice","options":["Может","Не может"],"explanations":["","Часть энергии от нагревателя ВСЕГДА будет поступать на холодильник, что приводит к потере энергии. 7 \space Дж} = 0.25$.
7 \space Дж} = 0.25$.Или в процентах: $\eta = 25 \%$.
Ответ: $\eta = 25 \%$.
Задачи на нахождение КПД тепловых машин с использованием графиков
На этой странице вы узнаете
- В чем прелесть фазовых переходов?
- Что лучше выбрать: Mercedes или BMW?
Люди научились летать в космос, покорять недра Земли и погружаться в глубины океана. Эти и другие достижения возможны благодаря способности извлекать максимум пользы из имеющихся ресурсов. Сегодня мы разберем задачи, которые заставят тепловые процессы играть на нашей стороне.
Тепловые машины и их КПД
Рекомендация: перед тем как приступить к выполнению задач неплохо было бы повторить тему «Уравнение состояния идеального газа» . Но ключевую теорию, на которой основано решение задач, сейчас разберем вместе.
| В чем прелесть фазовых переходов? Вспомним, что фазовые переходы — это переход из одного агрегатного состояния в другое. |
Мы не почувствуем, как испарится капелька у нас на руке, потому что это требует мало тепла от нашего тела. Но мы можем наблюдать, как горят дрова в мангале, когда мы жарим шашлык, потому что выделяется огромное количество теплоты. Стоит задаться вопросом: и что? Много энергии — хорошо, но что с ней делать?
Человечество придумало такие устройства, которые могут переработать тепловую энергию в механическую.
Тепловые двигатели, или тепловые машины, — устройства, способные преобразовывать внутреннюю энергию в механическую.
Их устройство довольно просто: они на входе получают какую-то энергию (в основном — энергию сгорания топлива), а затем часть этой теплоты расходуется на совершение работы механизмом. Например, в машинах часть энергии от сгоревшего бензина идет на движение автомобиля. Схематично можно изобразить так:
Рабочее тело — то, что совершает работу — принимает от нагревателя количество теплоты Q1, из которой A уходит на работу механизма. Остаток теплоты Q2 рабочее тело отдает холодильнику, по сути — это потеря энергии.
Остаток теплоты Q2 рабочее тело отдает холодильнику, по сути — это потеря энергии.
Физика не была бы такой заманчивой, если б все в ней было идеально. Как и в любом процессе или преобразовании, здесь возможны потери, зачастую очень большие. Поэтому “индикатором качества” машины является КПД, с которым мы уже сталкивались в механике:
Коэффициент полезного действия (КПД) тепловой машины — это отношение полезной работы двигателя к энергии, полученной от нагревателя.
| \(\eta = \frac{A}{Q_1}\) , где \(\eta\) — КПД, |
Мы должны понимать, что КПД на практике никогда не получится больше 1, поскольку всегда будут тепловые потери.
Полезную работу можно расписать как Q1 — Q2 (по закону сохранения энергии). Тогда формула примет вид:
\(\eta = \frac{Q_1 — Q_2}{Q_1} = 1 — \frac{Q_2}{Q_1}\)
Цикл Карно
Мы знаем, что потери — это плохо, поэтому должны предотвращать их. Как это сделать? Нам ничего делать не нужно, за нас уже сделал Сади Карно, французский физик, разработавший цикл, в котором машины достигают наивысшего КПД. Этот цикл носит его имя и состоит из двух изотерм и двух адиабат.
Как это сделать? Нам ничего делать не нужно, за нас уже сделал Сади Карно, французский физик, разработавший цикл, в котором машины достигают наивысшего КПД. Этот цикл носит его имя и состоит из двух изотерм и двух адиабат.
1-2 изотермическое расширение
2-3 адиабатическое расширение
3-4 изотермическое скажите
4-1 адиабатическое сжатие
- Температура верхней изотермы 1-2 — температура нагревателя;
- Температура нижней 3-4 — температура холодильника.
Цикл Карно — цикл идеальной тепловой машины, которая достигает наивысшего КПД.
Формулу, по которой можно рассчитать ее КПД выражается через температуры:
| \(\eta = \frac{T_1 — T_2}{T_1} = 1 — \frac{T_2}{T_1}\), где T1 — температура нагревателя, |
| Что лучше выбрать: Mercedes или BMW? Не то круто, что красиво, а то, что по Карно работает! Поэтому присматривайте такой автомобиль, у которого высокий КПД. |
Приступим к задачам
Задание 27.1. Одноатомный газ совершает циклический процесс, как показано на рисунке. На участке 1–2 газ совершает работу A12 = 1520 Дж. Участок 3–1 представляет собой адиабатный процесс. Количество теплоты, отданное газом за цикл холодильнику, равно |Qхол| = 4780 Дж. Найдите работу газа |A13| на адиабате, если количество вещества постоянно.
Решение:
- Первое, с чего лучше начинать задачи по термодинамике — исследование процессов.
1-2: продолжение прямой проходит через начало координат, поэтому график функционально можно записать, как p = aV, где a — какое-то число, константа. Графиком является не изотерма, поскольку график изотермы в координатах p-V — гипербола. Из уравнения Менделеева-Клапейрона следует: \(\frac{pV}{T} = const\). Отсюда можно сделать вывод, что возрастает температура, так как растут давление и объем. Температура и объем растут, значит, увеличивается и внутренняя энергия и объем соответственно.
Температура и объем растут, значит, увеличивается и внутренняя энергия и объем соответственно.
2-3: процесс изохорный, поскольку объем постоянен, следовательно, работа газом не совершается. Рассмотрим закон Шарля: \(\frac{p}{T} = const\). Давление в этом процессе растет, тогда растет и температура, поскольку дробь не должна менять свое значение. Делаем вывод, что внутренняя энергия тоже увеличивается.
3-1: адиабата по условию, то есть количество теплоты в этом переходе равно нулю из определения адиабатного процесса. Работа газа отрицательна, так как газ уменьшает объем.
Оформим все данные в таблицу.
Определим знаки Q, используя первый закон термодинамики: Q = ΔU + A.
Из этих данных сразу видно, что количество теплоты, отданное холодильнику — это количество теплоты в процессе 2-3.
- Первый закон термодинамики для процесса 1-2 запишется в виде:
Q12 = ΔU12 + A12.
Работа A12 — площадь фигуры под графиком процесса, то есть площадь трапеции:
\(A_{12} = \frac{p_0 + 2p_0}{2} * V0 =\frac{3p_0V_0}{2}\).
Запишем изменение внутренней энергии для этого процесса через давление и объем. Мы выводили эту формулу в статье «Первое начало термодинамики»:
\(\Delta U_{12} = \frac{3}{2}(2p_0 * 2V_0 — p_0V_0) = \frac{9p_0V_0}{2}\).
Заметим, что это в 3 раза больше работы газа на этом участке:
\(\Delta U_{12} = 3A_{12} \rightarrow Q_{12} = 4A_{12}\).
- Работа цикла — площадь фигуры, которую замыкает график,тогда . A = A12 — |A31|. С другой стороны, работа цикла вычисляется как разность между энергиями нагревателя и холодильника: A = Q12 — |Q31|.
Сравним эти формулы:
Q12 -|Q31| = A12 — |A31|,
подставим выражения из предыдущего пункта:
4A12 — |Q31| = A12 — |A31| \(\rightarrow\) |A31| = -3A12 + |Q31| = -31520 + 4780 = 220 Дж.
Задание 27.2. Найти КПД цикла для идеального одноатомного газа.
Решение:
- КПД цикла определим по формуле: \(\eta = \frac{A}{Q}\), где Q — количество теплоты от нагревателя, а А — работа газа за цикл. Найдем А как площадь замкнутой фигуры: A = (2p1 — p1)(3V1 — V1) = 2p1V1.
- Найдем процесс, который соответствует получению тепла от нагревателя. Воспользуемся теми же приемами, что и в прошлой задаче:
1-2: давление растет, объем не меняется. По закону Шарля \(\frac{p}{T} = const\) температура тоже растет. Работа газа равна 0 при изохорном процессе, а изменение внутренней энергии положительное.
2-3: давление не меняется, растет объем, а значит, работа газа положительна. По закону Гей-Люссака \(\frac{V}{T} = const\) температура тоже растет, растет и внутренняя энергия.
3-4: давление уменьшается, следовательно, и температура уменьшается. При этом процесс изохорный и работа газа равна 0.
При этом процесс изохорный и работа газа равна 0.
4-1: давление не меняется, объем и температура уменьшаются — работа газа отрицательна и внутренняя энергия уменьшается.
Оформим данные в таблицу:
Отметим, что необходимое Q = Q12 + Q23.
- Запишем первый закон термодинамики для процессов 1-2 и 2-3:
\(Q_{12} = U_{12} + A_{12} = \Delta U_{12} = \frac{3}{2}(2p_1V_1 -p_1V_1) = \frac{3}{2}p_1V_1\).
\(Q_{23} = \Delta U_{23} + A_{23}\), работу газа найдем как площадь под графиком: A23 = 2p1(3V1 — V1) = 4p1V1.
\(\Delta U_{12} = \frac{3}{2}(2p_1 * 3V_1 — 2p_1V_1) = 6p_1V_1\).
\(Q_{23} = \Delta U_{23} + A_{23} = 10p_1V_1\).
- Мы готовы считать КПД: \(\eta = \frac{A}{Q} = \frac{A}{Q_{12} + Q_{23}} = \frac{2p_1V_1}{\frac{3}{2}p_1V_1 + 10p_1V_1} = \frac{4}{23} \approx 0,17\).
Фактчек
- Тепловые двигатели — устройства, способные преобразовывать внутреннюю энергию в механическую.

- Тепловая машина принимает тепло от нагревателя, отдает холодильнику, а рабочим телом совершает работу.
- Коэффициент полезного действия (КПД) тепловой машины — это отношение полезной работы двигателя к энергии, полученной от нагревателя.
\(\eta = \frac{A}{Q_1} = \frac{Q_1 — Q_2}{Q_1} = 1 — \frac{Q_2}{Q_1}\) - Цикл Карно — цикл с максимально возможным КПД: \(\eta = \frac{T_1 — T_2}{T_1} = 1 — \frac{T_2}{T_1}\)
- Не забываем, что работа считается, как площадь фигуры под графиком.
Проверь себя
Задание 1.
1 моль идеального газа переходит из состояния 1 в состояние 2, а потом — в состояние 3 так, как это показано графике. Начальная температура газа равна T0 = 350 К. Определите работу газа при переходе из состояния 2 в состояние 3, если k = 3, а n = 2.
- 5672
- 4731
- 5817
- 6393
Задание 2.
1 моль идеального одноатомного газа совершает цикл, который изображен на pV-диаграмме и состоит из двух адиабат, изохоры, изобары. Модуль отношения изменения температуры газа при изобарном процессе ΔT12 к изменению его температуры ΔT34 при изохорном процессе равен 1,5. Определите КПД цикла.
Модуль отношения изменения температуры газа при изобарном процессе ΔT12 к изменению его температуры ΔT34 при изохорном процессе равен 1,5. Определите КПД цикла.
- 0,6
- 0,5
- 0,8
- 1
Ответы: 1 — 3 Дж; 2 — 1.
Тепловой двигатель – Эффективность – Определение, классификация, формула и диаграмма PV
Транспортные средства широко используются для перемещения из одного места в другое. В настоящее время каждая семья может иметь хотя бы двухколесный транспорт. Вы только представьте, как движутся машины? Какая энергия используется в нем? Какой процесс произошел? Тепловая машина — единственный ответ на все эти вопросы.
Что такое тепловая машина?
Тепловая машина – это устройство, используемое для преобразования тепловой энергии в механическую работу, полезную для людей. Для проведения процедуры используется простой аппарат. Тепловая машина имеет несколько преимуществ наряду с некоторыми ограничениями.
Тепловая машина имеет несколько преимуществ наряду с некоторыми ограничениями.
Классификация тепловых двигателей
У нас есть пять различных типов тепловых двигателей. Среди пяти известных и широко используемых тепловых двигателей есть два типа. Характеристика произошла на основе принципа, который используется для преобразования тепловой энергии в механическую работу. Итак, типы тепловых двигателей следующие:
Двигатель Стирлинга.
Какова функция теплового двигателя?
Основной функцией любой тепловой машины является преобразование доступной тепловой энергии в полезную механическую работу. Он проходит различные процедуры, чтобы преобразовать то же самое.
Определение эффективности тепловой машины
Как правило, мы знаем, что эффективность — это способность. Однако здесь эффективность тепловой машины представляет собой отношение разницы между горячим источником и стоком к температуре горячего источника. Его также можно назвать тепловым КПД тепловой машины. Максимальный КПД тепловой машины возможен при наибольшей разнице между горячим и холодным резервуарами. Эффективность не имеет единиц.
Его также можно назвать тепловым КПД тепловой машины. Максимальный КПД тепловой машины возможен при наибольшей разнице между горячим и холодным резервуарами. Эффективность не имеет единиц.
Тепловой КПД может варьироваться от одной тепловой машины к другой тепловой машине. Чтобы лучше понять это, давайте возьмем надежные тепловые двигатели и их КПД. КПД различных тепловых двигателей таков:
Эффективность сохранения тепловой энергии океана составляет всего 3%.
Автомобильные бензиновые двигатели имеют КПД почти 25%.
Точно так же угольные электростанции имеют КПД 49%.
Эффективность газовой турбины с комбинированным циклом составляет около 60%.
КПД тепловой машины Формула
Поскольку КПД тепловой машины представляет собой долю тепла и полученной полезной работы, ее можно выразить с помощью формулы и символа. Формула эффективности тепловой энергии равна,
η = \[\frac{W}{Q_{H}}\]
Где,
η = тепловой КПД.
Вт = Получена полезная работа.
Q H = Заданное количество тепловой энергии.
Это известно как формула теплового двигателя.
Согласно второму закону термодинамики невозможно получить 100-процентный тепловой КПД. Он всегда колеблется между 30% и 60% тепловой эффективности из-за изменений окружающей среды и других факторов. Мы также можем считать выполненную работу разностью между первоначально поглощенным количеством теплоты и выделенным теплом. Это может быть выражено как
(η) = \[\frac{\left [ Q_{1} -Q_{2}\right ]}{Q_{1}}\]
Концепция теплового двигателя была впервые введена и открыта французским физиком Карно в 1824 году. Двигатель Карно — идеальная тепловая машина. Поскольку это самый эффективный тепловой двигатель, его КПД составляет \[\frac{\left [T_{1}-T_{2} \right]}{T_{1}}\]. Его можно измерить для каждого цикла Карно.
Из формулы и диаграммы мы можем понять, что КПД идеальной тепловой машины также зависит от разницы между горячим и холодным резервуарами.
Диаграмма PV
Это диаграмма давление-объем, которая помогает изучать и анализировать эффективность тепловой машины. Он действует как инструмент визуализации для тепловой машины. Поскольку мы знаем, что рабочим веществом будет любой газ, диаграмма PV объясняет визуальные эффекты тепловой машины с учетом закона идеального газа. Несмотря на то, что температура может постоянно меняться, диаграмма PV помогает объяснить три элемента состояния переменных. Он также использует первый закон термодинамики для объяснения изменений тепловых двигателей.
(изображение будет загружено в ближайшее время)
(изображение будет загружено в ближайшее время)
Если мы посмотрим на рисунок, мы сможем понять, что это диаграмма PV одного циклического процесса тепловой машины. Он появился как замкнутый цикл. Площадь внутри цикла представляет объем работы, которую мы проделали в процессе, и объем полезной работы, которую мы получили. Диаграмма давление-объем является полезным и выгодным инструментом визуализации для изучения и анализа тепловой машины.
Диаграмма давление-объем является полезным и выгодным инструментом визуализации для изучения и анализа тепловой машины.
Вывод
Следовательно, тепловой двигатель представляет собой систему преобразования тепловой энергии в механическую работу. КПД тепловой машины – это отношение разницы между горячим источником и стоком к температуре горячего источника. КПД тепловой машины зависит от разницы между горячим резервуаром и холодным резервуаром. Мы привели формулу для определения КПД тепловой машины. Кроме того, мы не можем получить 100% КПД ни одной тепловой машины.
4.3: Тепловые двигатели - LibreTexts по физике
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4366
- OpenStax
- OpenStax
Цели обучения
К концу этого раздела вы сможете:
- Описать функцию и компоненты тепловой машины
- Объясните КПД двигателя
- Рассчитать КПД двигателя для заданного цикла идеального газа
Тепловая машина — это устройство, используемое для извлечения тепла из источника и последующего преобразования его в механическую работу, которая используется во всех видах приложений. Например, паровой двигатель поезда старого образца может производить работу, необходимую для движения поезда. В связи с конструкцией и применением тепловых двигателей возникает несколько вопросов. Например, каков максимальный процент извлеченной теплоты, который можно использовать для совершения работы? Оказывается, это вопрос, на который можно ответить только с помощью второго закона термодинамики.
Например, паровой двигатель поезда старого образца может производить работу, необходимую для движения поезда. В связи с конструкцией и применением тепловых двигателей возникает несколько вопросов. Например, каков максимальный процент извлеченной теплоты, который можно использовать для совершения работы? Оказывается, это вопрос, на который можно ответить только с помощью второго закона термодинамики.
Второй закон термодинамики можно формально сформулировать несколькими способами. Одно представленное до сих пор утверждение касается направления спонтанного теплового потока, известного как утверждение Клаузиуса. Несколько других утверждений основаны на тепловых двигателях. Всякий раз, когда мы рассматриваем тепловые двигатели и связанные с ними устройства, такие как холодильники и тепловые насосы, мы не используем нормальные знаки для теплоты и работы . Для удобства мы предполагаем, что символы \(Q_h, \, Q_c\) и W представляют только количества переданной теплоты и выполненной работы, независимо от того, кто является отдающим или получающим. Входит ли тепло в систему или выходит из нее, и работа, совершаемая системой или системой, указывается соответствующими знаками перед символами и направлением стрелок на диаграммах.
Входит ли тепло в систему или выходит из нее, и работа, совершаемая системой или системой, указывается соответствующими знаками перед символами и направлением стрелок на диаграммах.
Рисунок \(\PageIndex{1}\): схематическое изображение тепловой машины. Энергия перетекает из горячего резервуара в холодный резервуар при совершении работы.
Получается, что для создания тепловой машины нам нужно более одного источника/поглотителя тепла. Мы вернемся к этому позже в этой главе, когда будем сравнивать различные формулировки второго закона термодинамики. На данный момент мы предполагаем, что тепловой двигатель построен между источником тепла (высокотемпературным резервуаром или горячим резервуаром) и поглотителем тепла (низкотемпературным резервуаром или холодным резервуаром), схематично представленным на рисунке \(\PageIndex{1} \). Двигатель поглощает тепло \(Q_h\) от источника тепла ( горячий резервуар ) с температурой по Кельвину \(T_h\), использует часть этой энергии для производства полезной работы Вт , а затем сбрасывает оставшуюся энергию в виде тепла \(Q_c\) в теплоотвод ( холодный резервуар ) температуры Кельвина \(T_c\). Силовые установки и двигатели внутреннего сгорания являются примерами тепловых двигателей. Электростанции используют пар, произведенный при высокой температуре, для привода электрогенераторов, при этом отводя тепло в атмосферу или близлежащий водоем в роли поглотителя тепла. В двигатель внутреннего сгорания , горячая газовоздушная смесь используется для толкания поршня, и тепло отводится в окружающую атмосферу аналогичным образом.
Силовые установки и двигатели внутреннего сгорания являются примерами тепловых двигателей. Электростанции используют пар, произведенный при высокой температуре, для привода электрогенераторов, при этом отводя тепло в атмосферу или близлежащий водоем в роли поглотителя тепла. В двигатель внутреннего сгорания , горячая газовоздушная смесь используется для толкания поршня, и тепло отводится в окружающую атмосферу аналогичным образом.
Рисунок \(\PageIndex{2}\): Тепло, выделяемое атомной электростанцией, направляется в градирни, где выбрасывается в атмосферу.
Настоящие тепловые двигатели имеют множество различных конструкций. Примеры включают двигатели внутреннего сгорания, такие как те, которые используются в большинстве автомобилей сегодня, и двигатели внешнего сгорания, такие как паровые двигатели, используемые в старых поездах с паровыми двигателями. На рисунке \(\PageIndex{2}\) показана фотография работающей атомной электростанции. Атмосфера вокруг реакторов действует как резервуар холода, а тепло, выделяемое в результате ядерной реакции, обеспечивает тепло от горячего резервуара.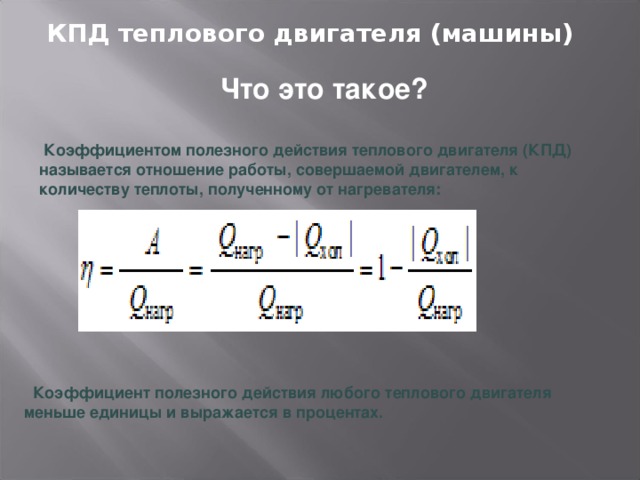
Тепловые двигатели работают, перемещая рабочее вещество через цикл. В паровой электростанции рабочим веществом является вода, которая сначала находится в жидком состоянии, затем испаряется, затем используется для привода турбины и, наконец, снова конденсируется в жидкое состояние. Как и все рабочие вещества в циклических процессах, когда вода возвращается в исходное состояние, она повторяет ту же последовательность.
На данный момент мы предполагаем, что циклы тепловых двигателей обратимы, поэтому потери энергии на трение или другие необратимые эффекты отсутствуют. Предположим, что механизм на рисунке \(\PageIndex{1}\) проходит один полный цикл и что \(Q_h\), \(Q_c\) и Вт представляют количество теплоты и работу, выполненную за этот цикл. Поскольку начальное и конечное состояния системы одинаковы, \(\Delta E_{int} = 0\) для цикла. Таким образом, из первого закона термодинамики имеем
\[\begin{align} W &= Q - \Delta E_{int} \\[4pt] &= (Q_h - Q_c) - 0, \label{eq1} \end{align} \]
так что
\[W = Q_h - Q_c. \label{eq2} \]
\label{eq2} \]
Наиболее важной характеристикой тепловой машины является ее КПД ( e ) , что просто «то, что мы получаем», деленное на «то, что мы вкладываем» в течение каждого цикла, как определено
\[e = \dfrac{W_{выход}}{Q_{вход}}. \метка{eq3}\]
Если тепловой двигатель работает между двумя тепловыми резервуарами, мы получаем \(W\) и добавляем \(Q_h\), поэтому КПД двигателя равен
.
\[\begin{align} e &= \dfrac{W}{Q_h} \\[4pt] &= 1 - \dfrac{Q_c}{Q_h}. \label{eq4} \end{align} \]
Здесь мы использовали уравнение \ref{eq2} на последнем шаге этого выражения для эффективности.
Пример \(\PageIndex{1}\): Газонокосилка
Газонокосилка имеет КПД \(25\%\) и среднюю мощность 3,00 кВт. Что такое
- средняя работа и
- минимальный выброс тепла в воздух газонокосилкой за одну минуту использования?
Стратегия
Из средней мощности, т. е. скорости производства работы, мы можем вычислить работу, выполненную за заданное истекшее время. Затем, исходя из приведенной эффективности, мы можем вычислить минимальный расход тепла \(Q_c = Q_h(1 - e)\) с \(Q_h = Q_c + W\). 93 \times 60 \times 1.00 \, J \\[4pt] &= 180 \, kJ.\end{align} \]
е. скорости производства работы, мы можем вычислить работу, выполненную за заданное истекшее время. Затем, исходя из приведенной эффективности, мы можем вычислить минимальный расход тепла \(Q_c = Q_h(1 - e)\) с \(Q_h = Q_c + W\). 93 \times 60 \times 1.00 \, J \\[4pt] &= 180 \, kJ.\end{align} \]
Пояснение
По мере повышения эффективности минимальное тепловыделение падает. Это помогает нашей окружающей среде и атмосфере, поскольку не выбрасывается столько отработанного тепла.
Эта страница под названием 4.3: Тепловые двигатели распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.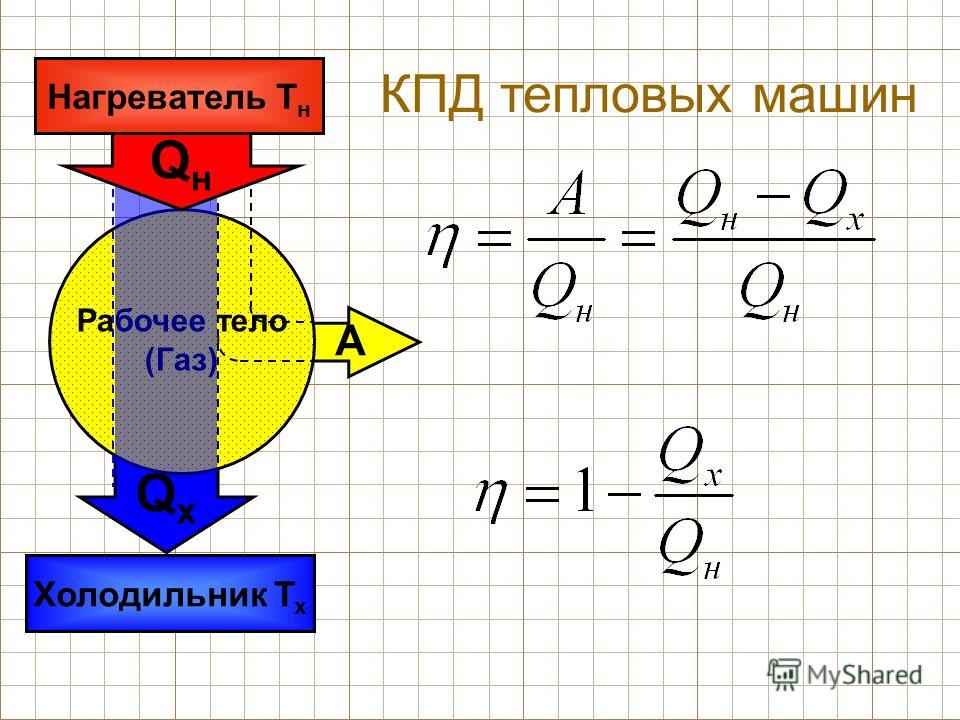

 ","",""],"answer":[0,1]}}}]}
","",""],"answer":[0,1]}}}]} 7 \space Дж} = 0.25$.
7 \space Дж} = 0.25$. Они могут выделять большое количество теплоты.
Они могут выделять большое количество теплоты.
