Резонанс напряжений и резонанс токов
схемотехника расчеты переменный ток
В физике резонансом называется явление, при котором в колебательном контуре частота свободных колебаний совпадает с частотой вынужденных колебаний. В электричестве аналогом колебательного контура служит цепь, состоящая из сопротивления, ёмкости и индуктивности. В зависимости от того как они соединены различают резонанс напряжений и резонанс токов.
Резонанс напряжений
Резонанс напряжений возникает в последовательной RLC-цепи.
Условием возникновения резонанса является равенство частоты источника питания резонансной частоте w=wр, а следовательно и индуктивного и емкостного сопротивлений xL=xC. Так как они противоположны по знаку, то в результате реактивное сопротивление будет равно нулю. Напряжения на катушке UL и на конденсаторе UC будет противоположны по фазе и компенсировать друг друга. Полное сопротивление цепи при этом будет равно активному сопротивлению R, что в свою очередь вызывает увеличение тока в цепи, а следовательно и напряжение на элементах.
Полное сопротивление цепи при этом будет равно активному сопротивлению R, что в свою очередь вызывает увеличение тока в цепи, а следовательно и напряжение на элементах.
При резонансе напряжения UC и UL могут быть намного больше, чем напряжение источника, что опасно для цепи.
С увеличением частоты сопротивление катушки увеличивается, а конденсатора уменьшается. В момент времени, когда частота источника будет равна резонансной, они будут равны, а полное сопротивление цепи Z будет наименьшим. Следовательно, ток в цепи будет максимальным.
Из условия равенства индуктивного и емкостного сопротивлений найдем резонансную частоту
Исходя из записанного уравнения, можно сделать вывод, что резонанса в колебательном контуре можно добиться изменением частоты тока источника (частота вынужденных колебаний) или изменением параметров катушки L и конденсатора C.
Следует знать, что в последовательной RLC-цепи, обмен энергией между катушкой и конденсатором осуществляется через источник питания.
Резонанс токов
Резонанс токов возникает в цепи с параллельно соединёнными катушкой резистором и конденсатором.
Условием возникновения резонанса токов является равенство частоты источника резонансной частоте w=wр, следовательно проводимости BL=BC. То есть при резонансе токов, ёмкостная и индуктивная проводимости равны.
Для наглядности графика, на время отвлечёмся от проводимости и перейдём к сопротивлению. При увеличении частоты полное сопротивление цепи растёт, а ток уменьшается. В момент, когда частота равна резонансной, сопротивление Z максимально, следовательно, ток в цепи принимает наименьшее значение и равен активной составляющей.
Выразим резонансную частоту
Как видно из выражения, резонансная частота определяется, как и в случае с резонансом напряжений.
Явление резонанса может носить как положительный, так и отрицательный характер. Например, любой радиоприемник имеет в своей основе колебательный контур, который с помощью изменения индуктивности или емкости настраивают на нужную радиоволну. С другой стороны, явление резонанса может привести к скачкам напряжения или тока в цепи, что в свою очередь приводит к аварии.
§56. Резонанс напряжений и резонанс токов
Явление резонанса.
Электрическая цепь, содержащая индуктивность и емкость, может служить колебательным контуром, где возникает процесс колебаний электрической энергии, переходящей из индуктивности в емкость и обратно. В идеальном колебательном контуре эти колебания будут незатухающими.
При подсоединении колебательного контура к источнику переменного тока угловая частота источника ω может оказаться равной угловой частоте ω0, с которой происходят колебания электрической энергии в контуре. В этом случае имеет место явление резонанса, т. е. совпадения частоты свободных колебаний ω0, возникающих в какой-либо физической системе, с частотой вынужденных колебаний ω, сообщаемых этой системе внешними силами.
В этом случае имеет место явление резонанса, т. е. совпадения частоты свободных колебаний ω0, возникающих в какой-либо физической системе, с частотой вынужденных колебаний ω, сообщаемых этой системе внешними силами.
Резонанс в электрической цепи можно получить тремя способами: изменяя угловую частоту ω источника переменного тока, индуктивность L или емкость С. Различают резонанс при последовательном соединении L и С — резонанс напряжений и при параллельном их соединении — резонанс токов. Угловая частота ω0, при которой наступает резонанс, называется резонансной, или собственной частотой колебаний резонансного контура.
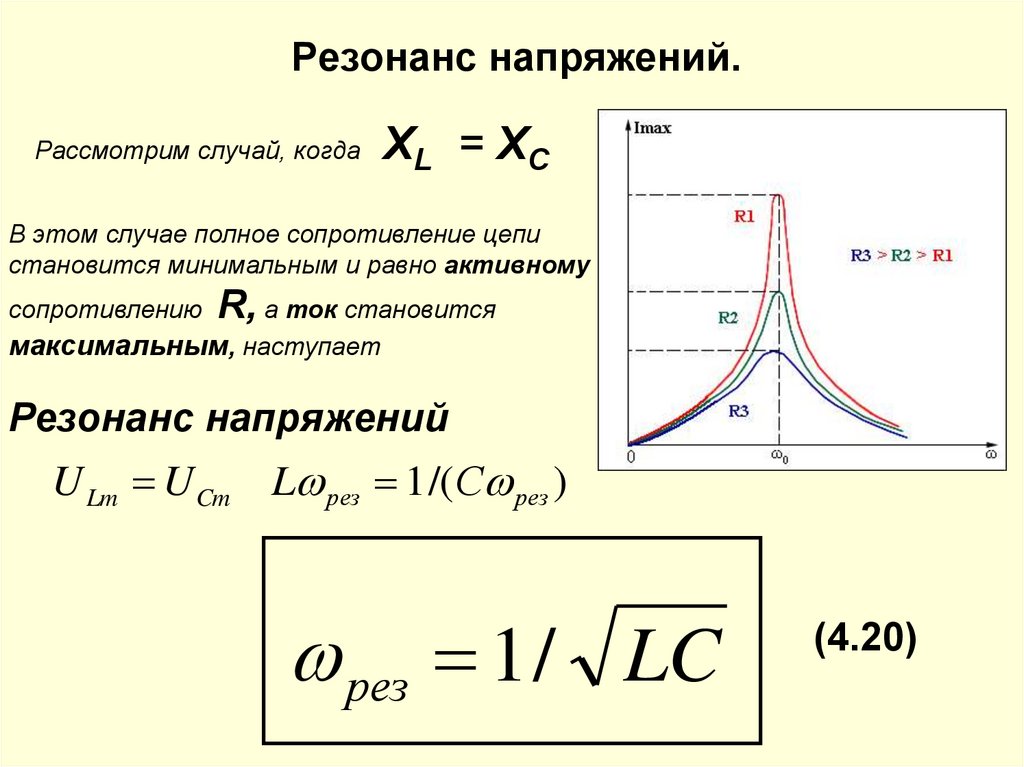
Резонанс напряжений.
При резонансе напряжений (рис. 196, а) индуктивное сопротивление XL равно емкостному Хси полное сопротивление Z становится равным активному сопротивлению R:
Z = √( R2 + [ω0L — 1/(ω0C)]2 ) = R
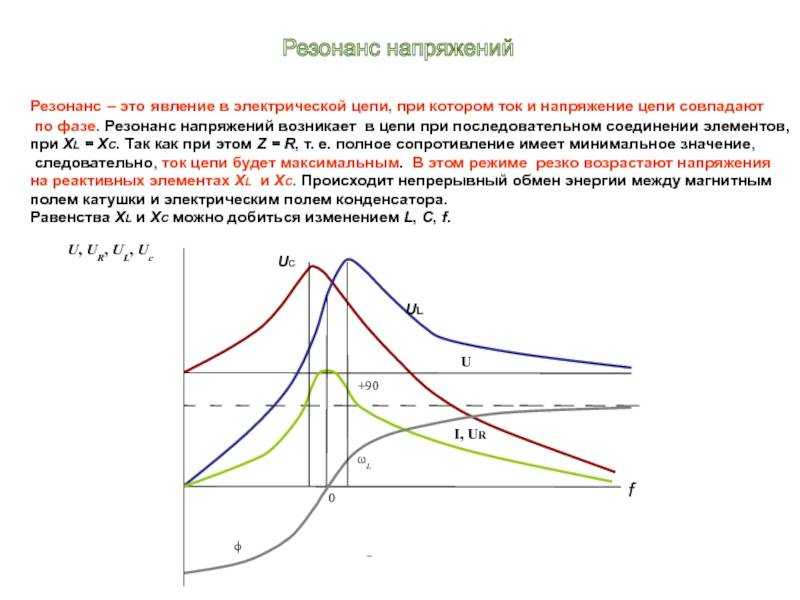
В этом случае напряжения на индуктивности UL и емкости Uc равны и находятся в противофазе (рис.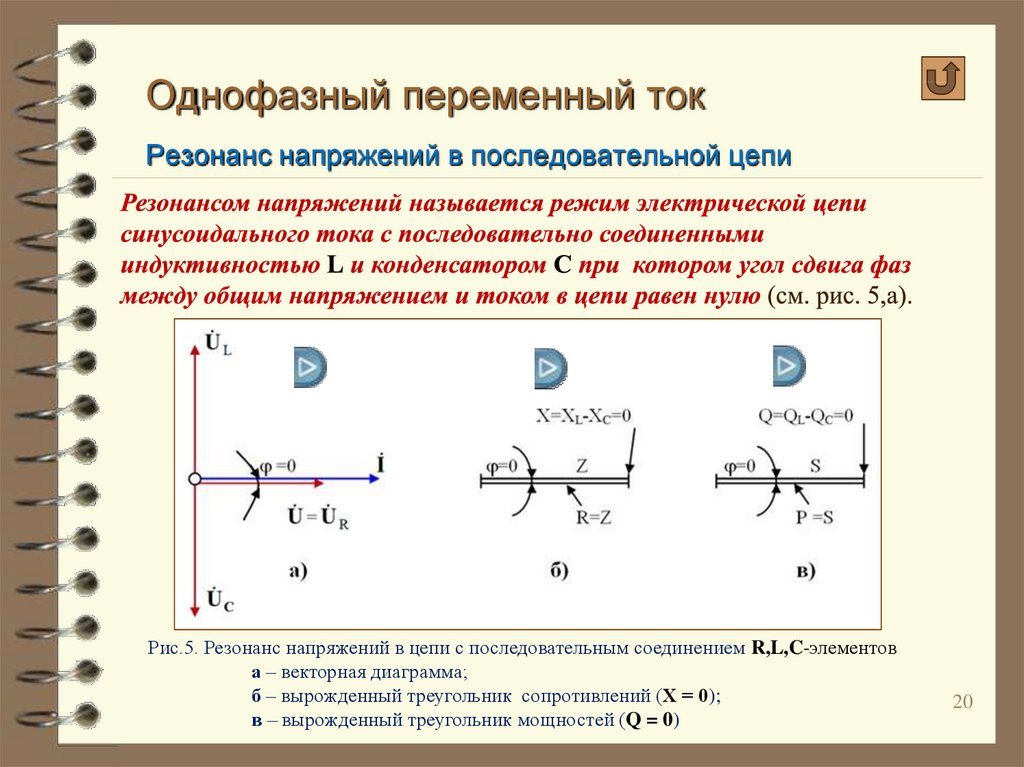 196,б), поэтому при сложении они компенсируют друг друга. Если активное сопротивление цепи R невелико, ток в цепи резко возрастает, так как реактивное сопротивление цепи X = XL—Xс становится равным нулю. При этом ток I совпадает по фазе с напряжением U и I=U/R. Резкое возрастание тока в цепи при резонансе напряжений вызывает такое же возрастание напряжений UL и Uc, причем их значения могут во много раз превышать напряжение U источника, питающего цепь.
196,б), поэтому при сложении они компенсируют друг друга. Если активное сопротивление цепи R невелико, ток в цепи резко возрастает, так как реактивное сопротивление цепи X = XL—Xс становится равным нулю. При этом ток I совпадает по фазе с напряжением U и I=U/R. Резкое возрастание тока в цепи при резонансе напряжений вызывает такое же возрастание напряжений UL и Uc, причем их значения могут во много раз превышать напряжение U источника, питающего цепь.
Угловая частота ω0, при которой имеют место условия резонанса, определяется из равенства ωoL = 1/(ω0С).
Рис. 196. Схема (а) и векторная диаграмма (б) электрической цепи, содержащей R, L и С, при резонансе напряжений
Отсюда имеем:
ωo = 1/√(LC) (74)
Если плавно изменять угловую частоту ω источника, то полное сопротивление Z сначала начинает уменьшаться, достигает наименьшего значения при резонансе напряжений (при ωo), а затем увеличивается (рис. 197, а). В соответствии с этим ток I в цепи сначала возрастает, достигает наибольшего значения при резонансе, а затем уменьшается.
197, а). В соответствии с этим ток I в цепи сначала возрастает, достигает наибольшего значения при резонансе, а затем уменьшается.
Рис. 197. Зависимость тока I и полного сопротивления Z от ω для последовательной (а) и параллельной (б) цепей переменного тока
Резонанс токов.
Резонанс токов может возникнуть при параллельном соединении индуктивности и емкости (рис. 198, а). В идеальном случае, когда в параллельных ветвях отсутствует активное сопротивление (R1=R2 = 0), условием резонанса токов является равенство реактивных сопротивлений ветвей, содержащих индуктивность и емкость, т. е. ωoL = 1/(ωoC).
Рис. 198. Электрическая схема (а) и векторные диаграммы (б и в) при резонансе токов
Так как в рассматриваемом случае активная проводимость G = 0, ток в неразветвленной части цепи при резонансе I=U √(G2+(BL-BC)2)= 0. Значения токов в ветвях I1 и I2 будут равны (рис. 198,б), но токи будут сдвинуты по фазе на 180° (ток IL в индуктивности отстает по фазе от напряжения U на 90°, а ток в емкости I с опережает напряжение U на 90°).
198,б), но токи будут сдвинуты по фазе на 180° (ток IL в индуктивности отстает по фазе от напряжения U на 90°, а ток в емкости I с опережает напряжение U на 90°).
Следовательно, такой резонансный контур представляет собой для тока I бесконечно большое сопротивление и электрическая энергия в контур от источника не поступает. В то же время внутри контура протекают токи IL и Iс, т. е. имеет место процесс непрерывного обмена энергией внутри контура. Эта энергия переходит из индуктивности в емкость и обратно.
Как следует из формулы (74), изменяя значения емкости С или индуктивности L, можно изменять частоту колебаний ω0 электрической энергии и тока в контуре, т. е. осуществлять настройку контура на требуемую частоту.
Если бы в ветвях, в которых включены индуктивность и емкость, не было активного сопротивления, этот процесс колебания энергии продолжался бы бесконечно долго, т. е. в контуре возникли бы незатухающие колебания энергии и токов IL и Iс.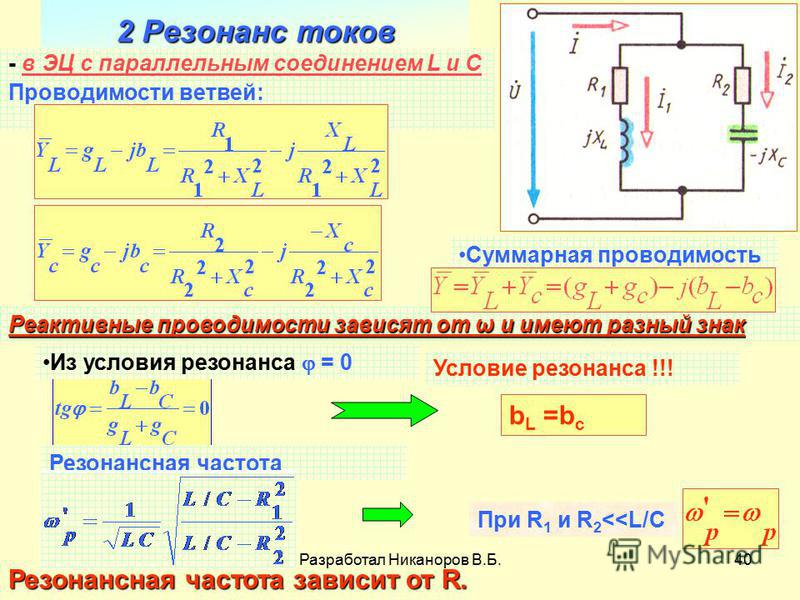
Однако реальные катушки индуктивности и конденсаторы всегда поглощают электрическую энергию (из-за наличия в катушках активного сопротивления проводов и возникновения в конденсаторах токов смещения, нагревающих диэлектрик), поэтому в реальный контур при резонансе токов поступает от источника некоторая электрическая энергия и по неразветвленной части цепи протекает некоторый ток I.
Условием резонанса в реальном резонансном контуре, содержащем активные сопротивления R1 и R2, будет равенство реактивных проводимостей BL = BC ветвей, в которые включены индуктивность и емкость.
Из рис. 198, в следует, что ток I в неразветвленной части цепи совпадает по фазе с напряжением U, так как реактивные токи 1L и Iс равны, но противоположны по фазе, вследствие чего их векторная сумма равна нулю.
Если в рассматриваемой параллельной цепи изменять частоту ωо источника переменного тока, то полное сопротивление цепи начинает увеличиваться, достигает наибольшего значения при резонансе, а затем уменьшается (см.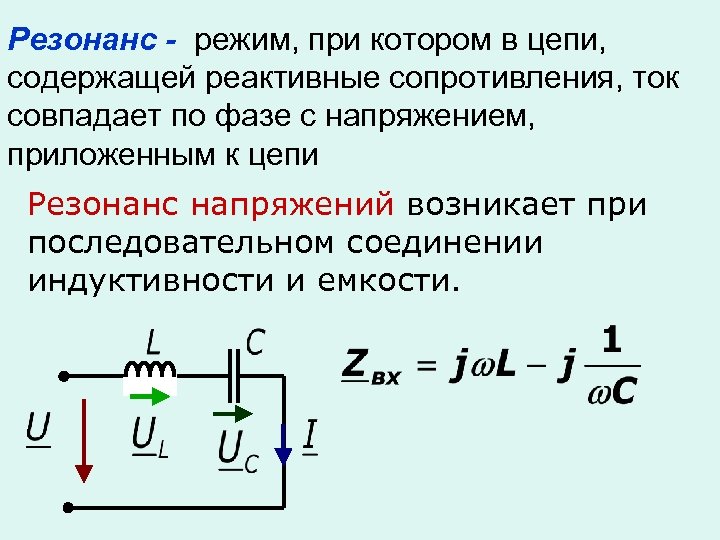 рис. 197,б). В соответствии с этим ток I начинает уменьшаться, достигает наименьшего значения Imin = Ia при резонансе, а затем увеличивается.
рис. 197,б). В соответствии с этим ток I начинает уменьшаться, достигает наименьшего значения Imin = Ia при резонансе, а затем увеличивается.
В реальных колебательных контурах, содержащих активное сопротивление, каждое колебание тока сопровождается потерями энергии. В результате сообщенная контуру энергия довольно быстро расходуется и колебания тока постепенно затухают. Для получения незатухающих колебаний необходимо все время пополнять потери энергии в активном сопротивлении, т. е. такой контур должен быть подключен к источнику переменного тока соответствующей частоты ω0.
Явления резонанса напряжения и тока и колебательный контур получили весьма широкое применение в радиотехнике и высокочастотных установках. При помощи колебательных контуров мы получаем токи высокой частоты в различных радиоустройствах и высокочастотных генераторах.
Колебательный контур — важнейший элемент любого радиоприемника. Он обеспечивает его избирательность, т. е. способность выделять из радиосигналов с различной длиной волны (т. е. с различной частотой), посланных различными радиостанциями, сигналы определенной радиостанции.
е. способность выделять из радиосигналов с различной длиной волны (т. е. с различной частотой), посланных различными радиостанциями, сигналы определенной радиостанции.
резонансных RLC-цепей
резонансных RLC-цепей
Резонанс в цепях переменного тока подразумевает особую частоту, определяемую значениями сопротивления, емкости и индуктивности. Для последовательного резонанса условие резонанса прямолинейно и характеризуется минимальным импедансом и нулевой фазой. Параллельный резонанс, более распространенный в электронной практике, требует более тщательного определения.  | Индекс Цепи переменного тока | |||||||||||||||||||||||||||||||||||
|

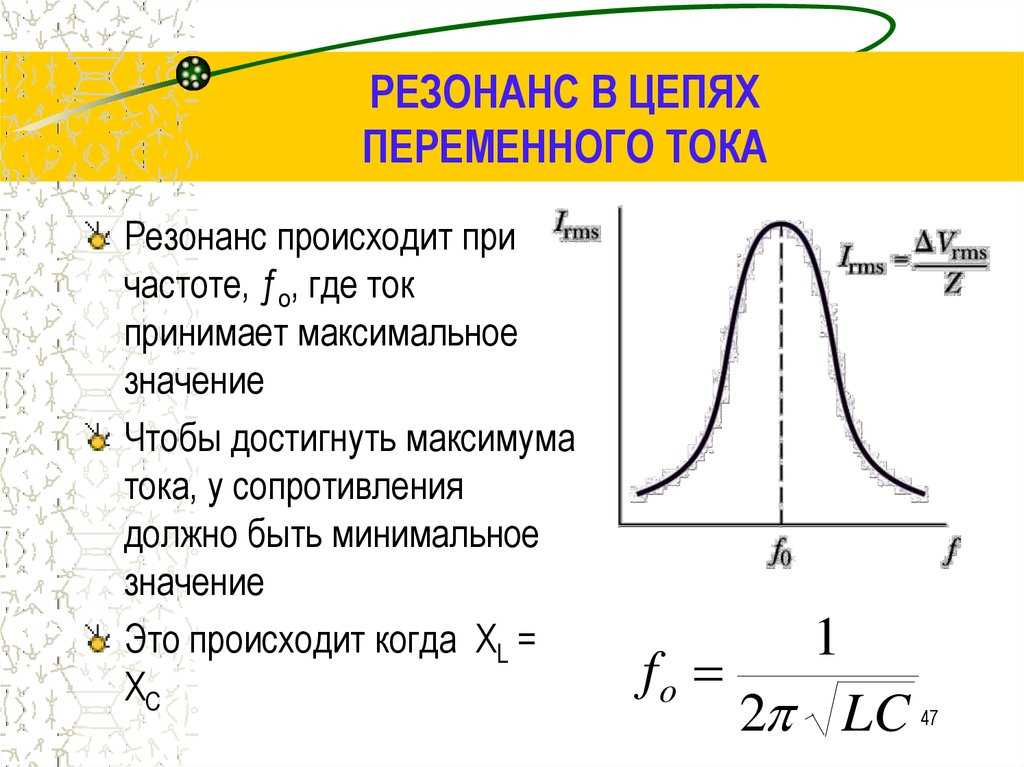 Если отклик схемы имеет более узкий пик вокруг выбранной частоты, мы говорим, что схема имеет более высокую «избирательность». «Коэффициент качества» Q, как описано ниже, является мерой этой избирательности, и мы говорим о схеме, имеющей «высокую добротность», если она более узко избирательна.
Если отклик схемы имеет более узкий пик вокруг выбранной частоты, мы говорим, что схема имеет более высокую «избирательность». «Коэффициент качества» Q, как описано ниже, является мерой этой избирательности, и мы говорим о схеме, имеющей «высокую добротность», если она более узко избирательна.



 0262 принято .
0262 принято .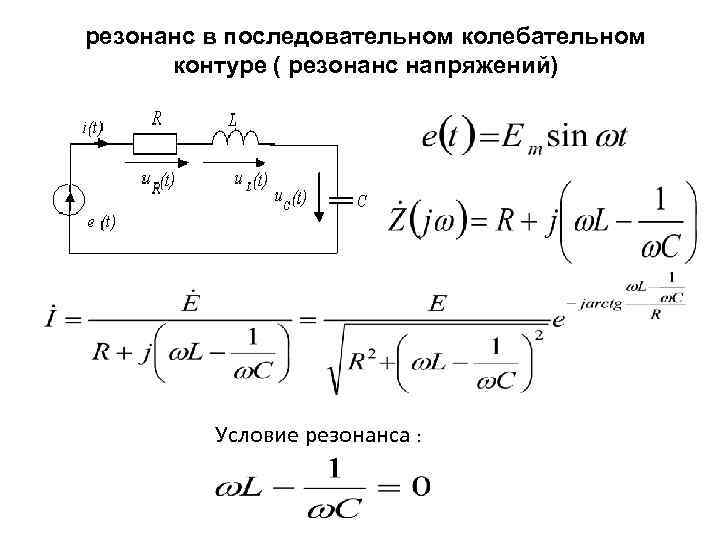
 Единственное, что отделяет вас от пункта назначения, это бессовестный металлоискатель, который требует, чтобы вы прошли сквозь него, не заставив его бип !
Единственное, что отделяет вас от пункта назначения, это бессовестный металлоискатель, который требует, чтобы вы прошли сквозь него, не заставив его бип !