Сборник задач абитуриенту. ОСНОВЫ ТЕРМОДИНАМИКИ. Циклы. Тепловые машины. Тема 14-7

ОСНОВЫ ТЕРМОДИНАМИКИ. Циклы. Тепловые машины. Тема 14-7

14.101. В идеальной тепловой машине за счет каждого килоджоуля энергии, получаемой от нагревателя, совершается работа A = 300 Дж. Определите КПД машины и температуру T₁ нагревателя, если температура холодильника T₂ = 280 К.

Ответ

14.102. Совершая замкнутый цикл, газ получил от нагревателя 420 Дж теплоты. Какую работу совершил газ, если КПД цикла 10 %?

Ответ

14.103. В ходе цикла Карно рабочее вещество получает от нагревателя количество теплоты – 300 кДж. Температуры нагревателя и холодильника равны соответственно T₁ = 450 K и T₂ = 280 K. Определите работу A, совершаемую рабочим веществом за цикл.

Ответ

14.104. Тепловая машина совершает работу 200 Дж, при этом холодильнику передается 300 Дж энергии. Определите КПД (в процентах) тепловой машины.

Ответ

14.105. КПД тепловой машины 50 %. Какую работу совершает машина за один цикл, если холодильнику при этом передается 700 Дж теплоты?

Ответ

14.106. двигатель внутреннего сгорания имеет КПД $\eta$ = 28 % при температуре горения топлива t₁ = 927 °C и при температуре отходящих газов t₂ = 447 °C. На какую величину $\Delta \eta$ КПД идеальной тепловой машины, работающей при тех же температурах нагревателя и холодильника, превышает КПД данного двигателя?

Ответ

14.107. КПД идеальной тепловой машины, работающей по циклу Карно, равен 25 %. Какова температура (в °С) нагревателя, если температура холодильника 27 °С?

Ответ

14.108. Идеальная тепловая машина передает холодильнику 80 % теплоты, полученной от нагревателя. Найдите температуру (в Кельвинах) нагревателя, если температура холодильника 248 К.

Ответ

14.109. КПД идеальной тепловой машины, работающей по циклу Карно, равен 80 %. Во сколько раз абсолютная температура нагревателя больше абсолютной температуры холодильника?

Ответ

14.110. Идеальный газ работает по циклу Карно. Абсолютная температура нагревателя 400 К, холодильника 300 К. Во сколько раз увеличится КПД цикла, если абсолютную температуру нагревателя повысить на 200 К?

Ответ

14.111. Идеальный газ совершает цикл Карно. Абсолютная температура нагревателя в 4 раза больше абсолютной температуры холодильника. Определите долю (в процентах) теплоты, отдаваемой холодильнику.

Ответ

14.112. Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу 100 Дж. Температура нагревателя 100 °С, температура холодильника 0 °С. Найдите количество тепла, отдаваемое за один цикл холодильнику.

Ответ

14.113. Рабочее тело тепловой машины, работающей по идеальному циклу Карно, в каждом цикле получает от нагревателя ΔQ = 8,4 кДж и k = 80 % из них передает холодильнику. Определите КПД η цикла и работу A, совершаемую машиной в каждом цикле.

Ответ

14.114. В каком случае КПД цикла Карно возрастет больше: при увеличении температуры нагревателя на ΔT или при уменьшении температуры холодильника на такую же величину?

Ответ

Во втором случае

14.115. Водород совершает цикл Карно. Найдите КПД цикла, если при адиабатном расширении: а) объем газа увеличивается в n = 2 раза; б) давление увеличивается в n = 2 раза.

Ответ

14.116. Найдите КПД η цикла, состоящего из двух изохор и двух адиабат, если в пределах цикла объем идеального газа изменяется в n = 10 раз. Рабочим веществом является азот.

Ответ

14.117. Один моль идеального газа находится в цилиндре под поршнем при температуре T₁. Газ при постоянном давлении нагревают до температуры T₂, затем при постоянном объеме нагревают до температуры T₃. Далее газ охлаждают при постоянном давлении, и его объем падает при этом до первоначального значения. Затем газ при постоянном объеме возвращают в начальное состояние. Какую работу совершил газ за цикл?

Ответ

A = νR(T₃ − T₂)(T₂ − T₁)/ T₂

14.118. На подъем груза весом 1000 кН на высоту 6 м пошло 80 % всей механической работы, полученной в результате работы идеальной тепловой машины, у которой разность температур нагревателя и холодильника равна 125 К, а отношение количества теплоты, полученной от нагревателя, к его абсолютной температуре равно 300 Дж/К. Сколько циклов было совершено за время подъема груза?

Ответ

14.119. Идеальный одноатомный газ совершает замкнутый цикл, состоящий из двух изохорных и двух изобарных процессов. При изохорном нагревании давление увеличивается в 2 раза, а при изобарном нагревании объем увеличивается на 70 %. Найдите КПД (в процентах) цикла.

Ответ

14.120. Идеальный одноатомный газ совершает циклический процесс, состоящий из изохорного нагревания, при котором давление газа возрастает на 40 %, затем изобарного расширения и, наконец, возвращения в исходное состояние в процессе, в котором давление изменяется прямо пропорционально объему. Найдите КПД (в процентах) цикла.

Ответ

14.121. Идеальная холодильная машина, работающая по обратному циклу Карно, используется для замораживания воды при 0 °С. Теплота отдается окружающему воздуху, температура которого 27 °С. Сколько минут потребуется для превращения в лед 420 г воды, если холодильная машина потребляет от сети мощность 25 Вт? Удельная теплота плавления льда 330 кДж/кг.

Ответ

Тепловые машины.

1. Идеальная тепловая машина работает по циклу Карно с температурой нагревателя 580 К и температурой холодильника  и совершает за один цикл работу 3 кДж. Количество теплоты, полученное за один цикл рабочим телом от нагревателя, равно

1) 2 кДж                             2) 3 кДж                                    3) 6 кДж                                         4) 9 кДж

Известно, что  ,  – сразу переходим к шкале температур Кельвина. Зная температуры нагревателя и холодильника, можем найти КПД машины:

КПД машины еще можно записать иначе:  , откуда искомое количество теплоты:  , или 6 кДж

Ответ: 3.

2. КПД тепловой машины 30%. За 10 с рабочему телу машины поступает от нагревателя 3 кДж теплоты. Средняя полезная мощность машины равна

1) 9 Вт                             2) 30 Вт                                    3) 90 Вт                                         4) 300 Вт

Средняя полезная мощность машины – это скорость выполнения работы, или работа, произведенная в единицу времени. Время у нас есть – 10 секунд, осталось найти производимую работу. Зная КПД, это сделать несложно:

,   Дж.

Найдем теперь среднюю мощность:  Вт

Ответ: 3.

3.Температура холодильника тепловой машины 400 К, температура нагревателя на 200 К больше, чем у холодильника. Максимально возможный КПД машины равен

1) 1/5                            2) 1/3                                    3) 1/2                                        4) 3/5

Определим температуру нагревателя:  .

Максимальным КПД машины будет, если она работает по циклу Карно. Тогда ее наибольший КПД: 

Ответ: 2.

4. Идеальная тепловая машина работает по циклу Карно, совершая за один цикл работу 2 кДж. Количество теплоты 2 кДж рабочее тело двигателя отдает за один цикл холодильнику, температура которого

. Температура нагревателя равна

1)                            2)                                    3)                                        4) 

Известно, что  Дж,  Дж. Переходим к шкале Кельвина: . Если машина идеальная и потерь тепла не происходит, то тепло, взятое от нагревателя, пойдет на выполнение работы и частично будет передано холодильнику:  Дж. Тогда КПД машины , а теперь можем записать КПД через температуры нагревателя и холодильника:

, откуда и найдем температуру нагревателя:  ,  К, и не забудем, что ответ нам предложено дать в градусах Цельсия:  

Ответ: 1.

5. Иде­аль­ная теп­ло­вая ма­ши­на с тем­пе­ра­ту­рой хо­ло­диль­ни­ка 300 К и тем­пе­ра­ту­рой на­гре­ва­те­ля 400 К за один цикл своей ра­бо­ты по­лу­ча­ет от на­гре­ва­те­ля ко­ли­че­ство теп­ло­ты 10 Дж. За счёт со­вер­ша­е­мой ма­ши­ной ра­бо­ты груз мас­сой 10 кг под­ни­ма­ет­ся вверх с по­верх­но­сти земли. На какую вы­со­ту над землёй под­ни­мет­ся этот груз через 100 цик­лов ра­бо­ты ма­ши­ны?

1) 7,5 м
2) 10 м
3) 0,1 м
4) 2,5 м

Работа, которую совершает машина, пойдет на подъем груза. То есть нужно определить работу, совершаемую за цикл, и затем узнать, какая работа совершена за 100 циклов. Тело поднимается вверх, значит, его потенциальная энергия увеличивается. Вся работа, таким образом, пойдет на увеличение этой потенциальной энергии, и мы узнаем, на какую высоту подняли тело. Делаем!

Сначала работа за цикл.  Известно, что Дж,   К,  К. КПД машины (она идеальная):  , КПД через работу:  , а работа за один цикл тогда   Дж. Понятно, что за 100 циклов  будет совершена в 100 раз большая работа: 250 Дж.

Теперь пора вспомнить формулу потенциальной энергии: , и, наконец, находим высоту:  м.

Ответ: 4.

6. Иде­аль­ная теп­ло­вая ма­ши­на имеет тем­пе­ра­ту­ру хо­ло­диль­ни­ка 300 К и на­гре­ва­те­ля 800 К. Ко­ли­че­ство теп­ло­ты, по­сту­па­ю­щее за один цикл ра­бо­ты ма­ши­ны от на­гре­ва­те­ля к ра­бо­че­му телу, уве­ли­чи­ли на 160 Дж. Опре­де­ли­те, как и на сколь­ко из­ме­ни­лось ко­ли­че­ство теп­ло­ты, ко­то­рое отдаёт ра­бо­чее тело хо­ло­диль­ни­ку, если из­вест­но, что КПД теп­ло­вой ма­ши­ны остал­ся не­из­мен­ным?

1) уве­ли­чи­лось на 30 Дж
2) уве­ли­чи­лось на 60 Дж
3) умень­ши­лось на 60 Дж
4) умень­ши­лось на 160 Дж

Найдем КПД машины:  . КПД машины можно записать . Тогда  , .

Теперь изменим количество теплоты  на 160 Дж: . Тогда  . Итак, количество теплоты, отдаваемое холодильнику, вырастет на 60 Дж.

Ответ: 2.

 7. На гра­фи­ке при­ве­де­на за­ви­си­мость КПД иде­аль­ной теп­ло­вой ма­ши­ны  от тем­пе­ра­ту­ры    ее хо­ло­диль­ни­ка. Чему равна тем­пе­ра­ту­ра на­гре­ва­те­ля этой теп­ло­вой ма­ши­ны?

2) 700 К
3) 1000 К
4) 1200 К

Возьмем на графике какую-нибудь точку, которой будут соответствовать целые значения КПД и температуры холодильника, например:

И по этим данным определим температуру нагревателя:  ,

,

K.

Ответ: 3.

Урок 25. тепловые двигатели. кпд тепловых двигателей — Физика — 10 класс

Физика, 10 класс

Урок 25. Тепловые двигатели. КПД тепловых двигателей

Перечень вопросов, рассматриваемых на уроке:

1) Понятие теплового двигателя;

2)Устройство и принцип действия теплового двигателя;

3)КПД теплового двигателя;

4) Цикл Карно.

Глоссарий по теме

Тепловой двигатель – устройство, в котором внутренняя энергия топлива превращается в механическую.

КПД (коэффициент полезного действия) – это отношение полезной работы, совершенной данным двигателем, к количеству теплоты, полученному от нагревателя.

Двигатель внутреннего сгорания – двигатель, в котором топливо сгорает непосредственно в рабочей камере (внутри) двигателя.

Реактивный двигатель – двигатель, создающий необходимую для движения силу тяги посредством преобразования внутренней энергии топлива в кинетическую энергию реактивной струи рабочего тела.

Цикл Карно – это идеальный круговой процесс, состоящий из двух адиабатных и двух изотермических процессов.

Нагреватель – устройство, от которого рабочее тело получает энергию, часть которой идет на совершение работы.

Холодильник – тело, поглощающее часть энергии рабочего тела (окружающая среда или специальные устройства для охлаждения и конденсации отработанного пара, т.е. конденсаторы).

Рабочее тело — тело, которое расширяясь, совершает работу (им является газ или пар)

Основная и дополнительная литература по теме урока:

1. Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 269 – 273.

2. Рымкевич А.П. Сборник задач по физике. 10-11 класс. -М.: Дрофа,2014. – С. 87 – 88.

Открытые электронные ресурсы по теме урока

http://kvant.mccme.ru/1973/12/teplovye_mashiny.htm

Теоретический материал для самостоятельного изучения

Сказки и мифы разных народов свидетельствуют о том, что люди всегда мечтали быстро перемещаться из одного места в другое или быстро совершать ту или иную работу. Для достижения этой цели нужны были устройства, которые могли бы совершать работу или перемещаться в пространстве. Наблюдая за окружающим миром, изобретатели пришли к выводу, что для облегчения труда и быстрого передвижения нужно использовать энергию других тел, к примеру, воды, ветра и т.д. Можно ли использовать внутреннюю энергию пороха или другого вида топлива для своих целей? Если мы возьмём пробирку, нальём туда воду, закроем её пробкой и будем нагревать. При нагревании вода закипит, и образовавшие пары воды вытолкнут пробку. Пар расширяясь совершает работу. На этом примере мы видим, что внутренняя энергия топлива превратилась в механическую энергию движущейся пробки. При замене пробки поршнем способным перемещаться внутри трубки, а саму трубку цилиндром, то мы получим простейший тепловой двигатель.

Тепловой двигатель – тепловым двигателем называется устройство, в котором внутренняя энергия топлива превращается в механическую.

Вспомним строение простейшего двигателя внутреннего сгорания. Двигатель внутреннего сгорания состоит из цилиндра, внутри которого перемещается поршень. Поршень с помощью шатуна соединяется с коленчатым валом. В верхней части каждого цилиндра имеются два клапана. Один из клапанов называют впускным, а другой – выпускным. Для обеспечения плавности хода поршня на коленчатом вале укреплен тяжелый маховик.

Рабочий цикл ДВС состоит из четырех тактов: впуск, сжатие, рабочий ход, выпуск.

Во время первого такта открывается впускной клапан, а выпускной клапан остается закрытым. Движущийся вниз поршень засасывает в цилиндр горючую смесь.

Во втором такте оба клапана закрыты. Движущийся вверх поршень сжимает горючую смесь, которая при сжатии нагревается.

В третьем такте, когда поршень оказывается в верхнем положении, смесь поджигается электрической искрой свечи. Воспламенившаяся смесь образует раскаленные газы, давление которых составляет 3 -6 МПа, а температура достигает 1600 -2200 градусов. Сила давления толкает поршень вниз, движение которого передается коленчатому валу с маховиком. Получив сильный толчок маховик будет дальше вращаться по инерции, обеспечивая движение поршня и при последующих тактах. Во время этого такта оба клапана остаются закрытыми.

В четвертом такте открывается выпускной клапан и отработанные газы движущимся поршнем выталкиваются через глушитель (на рисунке не показан) в атмосферу.

Любой тепловой двигатель включает в себя три основных элемента: нагреватель, рабочее тело, холодильник.

Для определения эффективности работы теплового двигателя вводят понятие КПД.

Коэффициентом полезного действия называют отношение полезной работы, совершенной данным двигателем, к количеству теплоты, полученному от нагревателя.

Q₁ – количество теплоты полученное от нагревания

Q₂ – количество теплоты, отданное холодильнику

– работа, совершаемая двигателем за цикл.

Этот КПД является реальным, т.е. как раз эту формулу и используют для характеристики реальных тепловых двигателей.

Зная мощность N и время работы t двигателя работу, совершаемую за цикл можно найти по формуле

Передача неиспользуемой части энергии холодильнику.

В XIX веке в результате работ по теплотехнике французский инженер Сади Карно предложил другой способ определения КПД (через термодинамическую температуру).

Главное значение этой формулы состоит в том, что любая реальная тепловая машина, работающая с нагревателем, имеющим температуру Т₁, и холодильником с температурой Т₂, не может иметь КПД, превышающий КПД идеальной тепловой машины. Сади Карно, выясняя при каком замкнутом процессе тепловой двигатель будет иметь максимальный КПД, предложил использовать цикл, состоящий из 2 адиабатных и двух изотермических процессов

Цикл Карно — самый эффективный цикл, имеющий максимальный КПД.

Не существует теплового двигателя, у которого КПД = 100% или 1.

Формула дает теоретический предел для максимального значения КПД тепловых двигателей. Она показывает, что тепловой двигатель тем эффективнее, чем выше температура нагревателя и ниже температура холодильника. Лишь при температуре холодильника, равной абсолютному нулю, η = 1.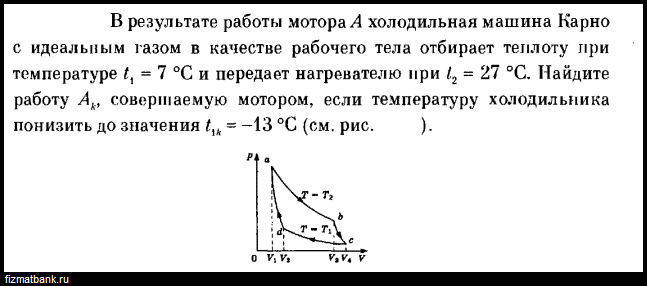

Но температура холодильника практически не может быть ниже температуры окружающего воздуха. Повышать температуру нагревателя можно. Однако любой материал (твердое тело) обладает ограниченной теплостойкостью, или жаропрочностью. При нагревании он постепенно утрачивает свои упругие свойства, а при достаточно высокой температуре плавится.

Сейчас основные усилия инженеров направлены на повышение КПД двигателей за счет уменьшения трения их частей, потерь топлива вследствие его неполного сгорания и т. д. Реальные возможности для повышения КПД здесь все еще остаются большими.

Повышение КПД тепловых двигателей и приближение его к максимально возможному — важнейшая техническая задача.

Тепловые двигатели – паровые турбины, устанавливают также на всех АЭС для получения пара высокой температуры. На всех основных видах современного транспорта преимущественно используются тепловые двигатели: на автомобильном – поршневые двигатели внутреннего сгорания; на водном – двигатели внутреннего сгорания и паровые турбины; на железнодорожном – тепловозы с дизельными установками; в авиационном – поршневые, турбореактивные и реактивные двигатели.

Сравним эксплуатационные характеристики тепловых двигателей.

КПД:

Паровой двигатель – 8%.

Паровая турбина – 40%.

Газовая турбина – 25-30%.

Двигатель внутреннего сгорания – 18-24%.

Дизельный двигатель – 40– 44%.

Реактивный двигатель – 25%.

Широкое использование тепловых двигателей не проходит бесследно для окружающей среды: постепенно уменьшается количество кислорода и увеличивается количество углекислого газа в атмосфере, воздух загрязняется вредными для здоровья человека химическими соединениями. Возникает угроза изменения климата. Поэтому нахождение путей уменьшения загрязнения окружающей среды является сегодня одной из наиболее актуальных научно-технических проблем.

Примеры и разбор решения заданий

1. Какую среднюю мощность развивает двигатель автомобиля, если при скорости 180 км/ч расход бензина составляет 15 л на 100 км пути, а КПД двигателя 25%?

Дано: v=180км/ч = 50 м/с, V = 15 л = 0,015 м³, s = 100 км = 10⁵ м, ɳ = 25% = 0,25, ρ = 700 кг/м³, q = 46 × 10⁶ Дж/кг.

Найти: N.

Решение:

Запишем формулу для расчёта КПД теплового двигателя:

Работу двигателя, можно найти, зная время работы и среднюю мощность двигателя:

Количество теплоты, выделяющееся при сгорании бензина, находим по формуле:

Учитывая всё это, мы можем записать:

Время работы двигателя можно найти по формуле:

Из формулы КПД выразим среднюю мощность:

.

Подставим числовые значения величин:

После вычислений получаем, что N=60375 Вт.

Ответ: N=60375 Вт.

2. Тепловая машина имеет КПД 25 %. Средняя мощность передачи теплоты холодильнику составляет 4 кВт. Какое количество теплоты рабочее тело получает от нагревателя за 20 с?

Дано: ɳ = 25%, N = 4000 Вт, t = 20 с.

Найти: Q₁.

Решение

  =

– это количество теплоты, отданное холодильнику

Молекулярная физика и термодинамика

Для работы любой тепловой машины по замкнутому циклу необходима внешняя среда, которую условно можно представить себе как два тела — нагреватель, находящийся при температуре Т_mах, и холодильник, находящийся при температуре T_min(T_min < Т_mах). Предполагается, что при контакте с нашей системой температуры нагревателя и холодильника не меняются. При контакте с нагревателем система получает тепло, при контакте с холодильником — отдает его.

В термодинамике существует теорема Карно (рис. 5.2):

Рис. 5.2. Леонар Сади Карно (французский физик и военный инженер)

Реализация максимально возможного КПД достигается в так называемом цикле Карно, когда идеальный газ проходит замкнутый цикл, составленный из двух адиабат и двух изотерм (рис. 5.3).

Рис. 5.3. Цикл Карно (обходится по часовой стрелке) — комбинация двух изотерм 1—2, 3—4 и двух адиабат 2—3 и 4—1; теплообмен со средой осуществляется на изотермических участках цикла: на участке 1—2 газ получает теплоту Q₁, а на участке 3—4 отдает теплоту Q₂

Убедимся, что показанный замкнутый процесс действительно имеет КПД, соответствующий формуле (5. 5). Температура системы равна T₁ в точках 1, 2 и T₂ в точках 3, 4. Значения остальных термодинамических параметров (р, V) будут иметь в качестве индекса номер соответствующей точки на диаграмме. Нам надо вычислить количества полученной Q₁, и отданной Q₂теплоты, найти совершенную газом работу А_Ц = Q₁ – Q₂ и определить КПД цикла. Сразу заметим, что на участках 2-3 и 4-1 система не обменивается теплом с внешней средой. Следовательно, теплоту Q_{1газ получает на участке 1-2, а теплоту Q2отдает на участке 3-4. Рассмотрим подробнее различные участки цикла.}

См. анимацию «Цикл Карно»

Изотерма 1—2. На этом участке газ находится в контакте с нагревателем и происходит изотермическое расширение от объема V₁ до объема V₂. Температура Т₁ не меняется, следовательно, не изменяется внутренняя энергия, а вся полученная теплота расходуется на совершение газом работы:

Величину работы газа при изотермическом процессе мы уже вычисляли ранее, так что с учетом формулы (2.13) находим

Адиабата 2—3. Здесь система отсоединяется от нагревателя и не обменивается теплом с внешней средой: Q₂₃ = 0. Газ продолжает расширяться, но уже адиабатно. Работа совершается за счет внутренней энергии газа, и его температура падает до значения Т₂. На этом участке цикла нам нужна информация, доставляемая уравнением адиабаты:

Изотерма 3—4. Система подключается к холодильнику, и газ начинает сжиматься. Внутренняя энергия остается неизменной, над газом совершается работа (А₃₄ < 0), а выделяющееся

тепло

передается холодильнику. Имеем аналогично (5.6)

Адиабата 4—1. Система отключена от внешней среды и продолжает сжиматься изотермически, что приводит к повышению ее температуры до Т₁. В конечном итоге система возвращается в первоначальное состояние. Поскольку точки 4 и 1 лежат на адиабате, получаем связь объемов и температур, аналогичную (5.7):

Из уравнений (5.7) и (5.9) находим отношения объемов

откуда следует, что

Поэтому отдаваемую холодильнику теплоту Q₂(см. уравнение (5.8)) можно записать как

Используя выражение (5.6) для теплоты, полученной системой, находим совершенную в ходе цикла работу

Из проведенного анализа следует также, что максимальная температура в цикле равна Т_mах = Т₁, а минимальная — Т_min = Т₂. Если разделить (5.12) на (5.6), то немедленно получим выражение (5.5) для КПД цикла Карно, из которого выпадают все параметры, кроме температур холодильника и нагревателя.

Пример 1. Котел тепловой станции работает при температуре около t₁ = 550 °С. Отработанное тепло отводится к реке при температуре около t₂ = 20 °С.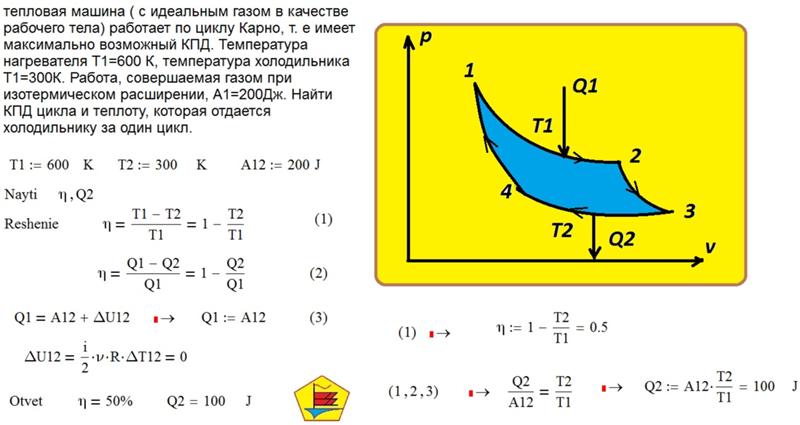 Найдем максимально возможный КПД этой станции (рис. 5.4).

Рис. 5.4. Схема работы тепловой машины Карно

Поскольку в формуле для КПД цикла Карно используются абсолютные температуры, надо перейти от шкалы Цельсия к шкале Кельвина: Т₁ = 550 + 273 = 823 К, Т₂ = 20 + 273 = 293 К. Теперь находим КПД тепловой станции:

Конечно, реальный КПД станции заметно ниже.

Если цикл Карно осуществить в обратном направлении, то есть против часовой стрелки на рис. 5.2, то для определения эффективности холодильной установки надо использовать формулы (5.3), (5.4) и выражения (5.6), (5.11). Получаем тогда

Печально, но чем ниже температура внешней среды Т₁, тем меньше мы нуждаемся в холодильнике, и тем эффективнее он работает.

Рис. 5.5. Схема работы холодильной установки

Приведем численный пример. Если кондиционер поддерживает в комнате температуру t₂ = 20 °С, а температура наружного воздуха равна t₁ = 30 °С, то для холодильного коэффициента имеем

а для КПД холодильника

Конечно, на самом деле температура тепловыделяющего элемента больше наружной температуры на 20–30 градусов, так что разность температур может достигать 30–40 градусов, что приводит к значениям

Напомним, что речь идет об идеальных установках, работающих по циклу Карно. Реальный типичный кондиционер потребляет мощность 750 Вт, перекачивая за час около 5 МДж тепловой энергии. Это значит, что за секунду кондиционер совершает работу А = 750 Дж и отнимает у воздуха в комнате теплоту

Отсюда находим

Мы видим, что реальный кондиционер гораздо менее эффективен, нежели идеальный холодильник Карно.

Пример 2. Пусть в домашнем холодильнике поддерживается температура t₂ = –3 °С (Т₂ = 270 К), а температура в кухне равна t₁ = 27 °С (T₁ = 300 К). Пусть далее мотор холодильника потребляет мощность N = 200 Вт. Предполагая, что холодильник работает по циклу Карно и что тепловыделяющий элемент имеет температуру окружающего воздуха, определим мощность потока тепловой энергии, перекачиваемой из камеры холодильника в кухню.

За время t мотор совершит работу

КПД холодильника равен

откуда находим количество теплоты, поступающее в кухню в единицу времени:

Обратите внимание, что холодильник работает как весьма эффективный обогреватель помещения. Надо только оплачивать потребляемую мотором мощность 200 Вт, а в кухню поступит в 10 раз большая энергия, 90 % которой перекачивается из камеры холодильника (90 % — КПД холодильника в этом примере). Любопытно, что если бы вместо холодильника был включен обогреватель той же мощности, то он нагревал бы помещение в 10 раз слабее.

Наши численные оценки можно рассматривать как пример теплового загрязнения окружающей среды, свойственного технической цивилизации.

Дополнительная информация

http://eqworld.ipmnet.ru/ru/library/physics/thermodynamics.htm — Я. де Бур Введение в молекулярную физику и термодинамику, Изд. ИЛ, 1962 г. — стр. 202–205,  ч. 2, гл. 2,  § 10: описан процесс ожижения газа Клода — Гейландта.

Тема 8. Второе начало термодинамики. Энтропия

⇐ ПредыдущаяСтр 12 из 28Следующая ⇒

Второй закон (начало) термодинамики – отдача тепловой машины ограничена значениями температуры нагревателя (Т_н) и холодильника (Т_х), т. е. теплота может создавать работу только при разности температур, при этом максимально возможный коэффициент полезного действия (КПД) тепловой машины равен:

.

Тепловая машина, имеющая такой КПД, называется идеальной, она работает по циклу Карно – это круговой процесс, который состоит из двух изотерм и двух адиабат. Все реальные тепловые машины имеют меньший КПД:

.

Работа тепловой машины равна разности тепла полученного от нагревателя и отданного холодильнику: .

Энтропия– это приведенное тепло:S=Q/T. Энтропия – это функция состояния системы, т.е. ее изменение определяется разностью значений энтропий в конечном и начальном состоянии и не зависит от пути перехода системы из начального в конечное состояние: . Следовательно, в любом круговом процессе изменение энтропии равно нулю.

Работа теплового двигателя определяется и изменением энтропии рабочего тела:

, .

Последнее слагаемое в уравнении определяет тепло, рассеиваемое в пространстве, т. е. поглощаемое холодильником.

Изменение энтропии равно нулю в обратимых (замкнутых) процессахи при адиабатном процессе, когда тепло не поступает в систему. Если тепло поступает в систему — ее энтропия возрастает, если тепло забирается у системы, ее энтропия уменьшается.

Второй закон термодинамики с использованием понятия энтропии: в самопроизвольных процессах, происходящих в замкнутой системе, энтропия не убывает: .

Изменение энтропии системы при переходе из состояния 1 в состояние 2 можно рассчитать по формуле:

.

Например, как изменяется энтропия газа при совершении цикла Карно (на рисунке представлен цикл Карно в координатах (P,V) и (T,S)): (1-2) — изотермическое расширение (работа расширения газа совершается засчет тепла, поступающего в систему) – энтропия возрастает; (2-3) – адиабатное расширение тепло (не поступает) – энтропия не изменяется;(3-4) – изотермическое охлаждение (газ сжимается и отдает свое тепло) – энтропия уменьшается;(4-1) – адиабатное сжатие — энтропия не изменяется; (1-2-3-4-1) – замкнутый цикл – энтропия не изменяется.

Третий закон термодинамики: энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения температуры к нулю Кельвина: .

Пример 8.1. КПД цикла Карно равен 60%. Если температура нагревателя 400К, то температура холодильника равна:

ð300 ð240 R160 ð200

Решение: Запишем выражение для КПД идеальной тепловой машины в процентах: . Выведем формулу для расчета температуры холодильника: , .

Рассчитаем: .

Пример 8.2. Идеальная тепловая машина работает по циклу Карно. При этом 80% количества теплоты, получаемого от нагревателя, передается холодильнику. Количество теплоты, получаемое от нагревателя, равно 75 кДж. Работа, совершаемая машиной за один цикл, равна … £ 94 R 15 £ 30 £ 60

Решение: работа тепловой машины равна: .

Известно, что , .

Рассчитаем работу машины:

Пример 8. 3. Идеальная тепловая машина работает по циклу Карно. За один цикл тепловой работы энтропия рабочего тела …

£уменьшится £ возрастет R не изменится

Решение: для полного цикла Карно и для других обратимых процессов изменение энтропии равно нулю.

Пример 8.4. Идеальная тепловая машина работает по циклу Карно. В процессе изотермического расширения 1-2 энтропия рабочего тела…

R возрастет £ не изменится £ уменьшится

Решение: тепло поступает в систему — ее энтропия возрастает.

Пример 8.5.Идеальная тепловая машина работает по циклу Карно. Если температуру холодильника уменьшить, то КПД цикла…

£ уменьшится £ не изменится R увеличится

Решение: при уменьшении температуры холодильника, возрастает разность температур холодильника и нагревателя, следовательно, КПД машины увеличится.

Пример 8.6. При изотермическом расширении идеального газа:

£ выделяется теплота, увеличивается энтропия

£ выделяется теплота, уменьшается энтропия

R поглощается теплота, увеличивается энтропия

£ поглощается теплота, уменьшается энтропия

Решение: изотермический процесс – это процесс, при котором температура газа не изменяется, т.е. его внутренняя энергия не расходуется на процесс расширения. Расширение происходит за счет поступающего извне тепла, т.е. энтропия возрастает.

Иначе можно воспользоваться формулой изменения энтропии и получить тот же ответ: .

; ;

Пример 8.7.В процессе диффузии энтропия изолированной термодинамической системы:

£ уменьшается R увеличивается £ не изменяется

Решение: диффузия – это процесс перемещения молекул примеси в результате хаотических столкновений с другими молекулами. В результате объём пространства занятого молекулами примеси возрастает – и возрастает их энтропия.

Пример 8.8. Процесс, изображенный на рисунке в координатах (Т,S), где S – энтропия, является…

£ изотермическое расширение

R адиабатическое сжатие

£ изохорное нагревание

£ изобарное расширение

Решение: энтропия не изменяется – это адиабатный процесс. Температура возрастает – это возможно при адиабатном сжатии газа.

Пример 8.9. На рисунке представлен цикл тепловой машины в координатах (T,S). Укажите нагреватели и холодильники с соответствующими температурами.

£ Нагреватели — T3,T5; Холодильники — T1,T2,T4

£ Нагреватели — T3,T4,T5; Холодильники — T1,T2

R Нагреватели — T4,T5; Холодильники — T1,T2,T3

£ Нагреватели — T2,T4,T5; Холодильники — T1,T3

Решение: Т₅ – энтропия возрастает ( , температура не изменяется( , – тепло поступает в систему – это нагреватель;

Т₄ – ( ,( – нагреватель;

Т3 – ( , ( – холодильник;

Т2 – ( , ( – холодильник;

Т1 – ( , ( – холодильник.

©2015 arhivinfo.ru Все права принадлежат авторам размещенных материалов.

Циклы. Тепловые машины

1.9.
У тепловой машины, работающей по прямому
циклу Карно, температура нагревателя
в 1,5 раза больше температуры холодильника.
За один цикл машина производит работу
60 кДж. Вычислить работу, затрачиваемую
за цикл на изотермическое сжатие рабочего
вещества.

2.9.
Идеальная тепловая машина, работающая
по циклу Карно, получает за каждый цикл
от нагревателя 2 кДж теплоты. Температура
нагревателя 400 К, температура
холодильника 300 К. Найти количество
теплоты, отдаваемого холодильнику за
один цикл.

3.9.
Идеальная холодильная машина, работающая
по обратному циклу Карно, совершает за
один цикл работу, равную 30 кДж. При
этом она берёт теплоту от тела с
температурой минус 10 °С и передаёт
теплоту телу с температурой 17 °С. Найти
количество теплоты, отнятого от холодного
тела за один цикл.

4.9.
Тепловая машина работает по циклу Карно.
Температуры нагревателя и холодильника
соответственно 550 и 330 К. Рабочим телом
служит воздух массой 16 кг. Известно, что
давление воздуха в конце изотермического
расширения равно давлению в начале
адиабатического сжатия и цикл протекает
54 с. Определить тепловую мощность,
подводимую к машине.

5.9.
Идеальная холодильная машина работает
как тепловой насос по обратному циклу
Карно. При этом она берёт теплоту от
воды с температурой 3°С и передаёт её
воздуху с температурой 27°С. Найти
коэффициент 
— отношение теплоты, переданной за
некоторый промежуток времени воздуху
к работе машины за это же время.

6.9.
КПД паровой машины составляет 50 % от
КПД. тепловой машины, работающей по
циклу Карно между теми же температурами.
Температура пара, поступающего из котла
в паровую машину, 260 С,
температура конденсатора 90 С.
Определить мощность паровой машины,
если она потребляет за 10 часов 10 ГДж
энергии.

7.9.
Двухатомный идеальный газ совершает
цикл Карно, при этом на каждый киломоль
этого газа при адиабатическом сжатии
затрачивается работа 3 МДж. Температура
нагревателя равна 460 К. Определить КПД
цикла. Ответ дать в процентах.

8.9.
Цикл состоит из двух изотерм (Т₁
= 778 К, Т₂
= 356 К) и двух изобар (р₁/р₂
= 8). Определить КПД цикла, если рабочим
веществом служит идеальный газ, число
степеней свободы молекул которого равно
5. Ответ дать в процентах.

9.9. Совершая
замкнутый цикл, газ получил от нагревателя
420 Дж теплоты.
Какую работу совершил газ, если КПД
цикла 10 %?

10.9. Тепловая
машина совершает работу 200 Дж, при этом
холодильнику передается
300 Дж энергии. Определить КПД (в процентах)
тепловой машины.

11.9.
КПД тепловой машины 50 %. Какую работу
совершает машина за один цикл,
если холодильнику при этом передается
700 Дж теплоты?

12.9.
КПД идеальной тепловой машины, работающей
по циклу Карно, равен
25 %. Какова температура (в °С) нагревателя,
если температура холодильника
27 °С?

13.9.
Идеальная тепловая машина передает
холодильнику 80 % теплоты, полученной от
нагревателя. Найти температуру
нагревателя, если температура
холодильника 248 К.

14.9.
КПД идеальной тепловой машины, работающей
по циклу Карно, равен
80 %. Во сколько раз абсолютная температура
нагревателя больше абсолютной
температуры холодильника?

15.9.
Идеальный газ работает по циклу Карно.
Абсолютная температура нагревателя
400 К, холодильника 300 К. Во сколько раз
увеличится КПД цикла, если абсолютную
температуру нагревателя повысить на
200 К?

16.9.
Идеальная тепловая машина, работающая
по циклу Карно, совершает за один
цикл работу 100 Дж. Температура нагревателя
100 °С, температура холодильника
0 °С. Найти количество тепла, отдаваемое
за один цикл холодильнику.

17.9.
На подъем груза весом 1000 кН на высоту 6
м пошло 80 % всей механической работы,
полученной в результате работы идеальной
тепловой машины, у которой
разность температур нагревателя и
холодильника равна 125 К, а отношение
количества теплоты, полученной от
нагревателя, к его абсолютной температуре
равно 300 Дж/К.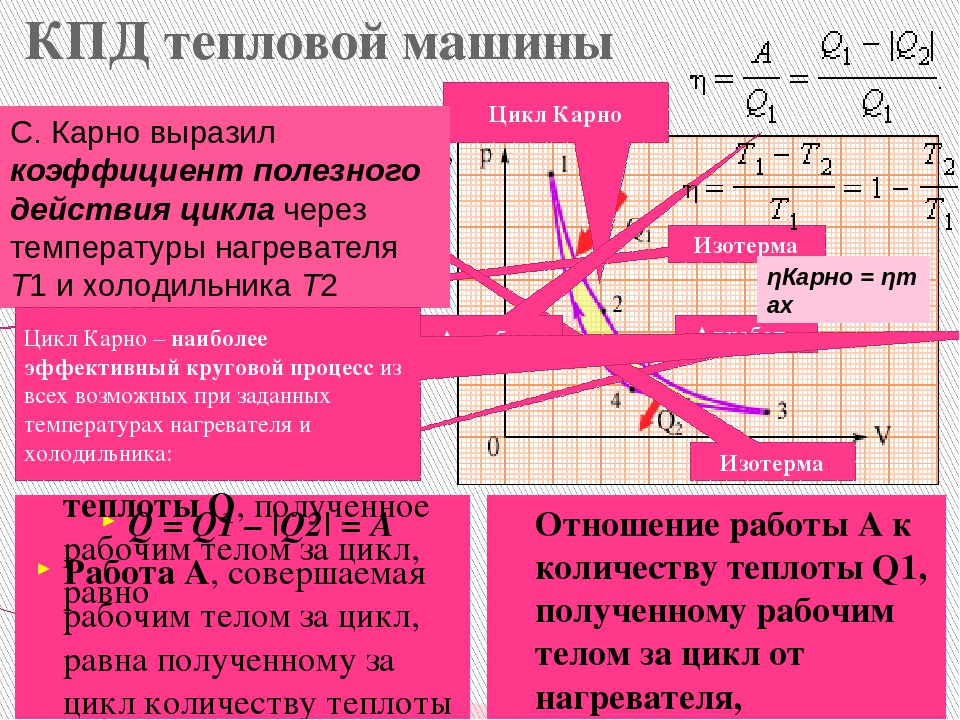 Сколько циклов было
совершено за время подъема груза?

18.9.
Идеальный одноатомный газ совершает
замкнутый цикл, состоящий из
двух изохорных и двух изобарных процессов.
При изохорном нагревании давление
увеличивается в 2 раза, а при изобарном
нагревании объем увеличивается на
70 %. Найти КПД (в процентах) цикла.

19.9.
Идеальный одноатомный газ совершает
циклический процесс, состоящий
из изохорного нагревания, при котором
давление газа возрастает на 40 %, затем
изобарного расширения и, наконец,
возвращения в исходное состояние в
процессе,
в котором давление изменяется прямо
пропорционально объему. Найти
КПД (в процентах) цикла.

20.9.
Идеальная холодильная машина, работающая
по обратному циклу Карно,
используется для замораживания воды
при 0 °С. Теплота отдается окружающему
воздуху, температура которого 27 °С.
Сколько минут потребуется для превращения
в лед 420 г воды, если холодильная машина
потребляет от сети мощность
25 Вт? Удельная теплота плавления льда
3,25·10⁵
Дж/кг.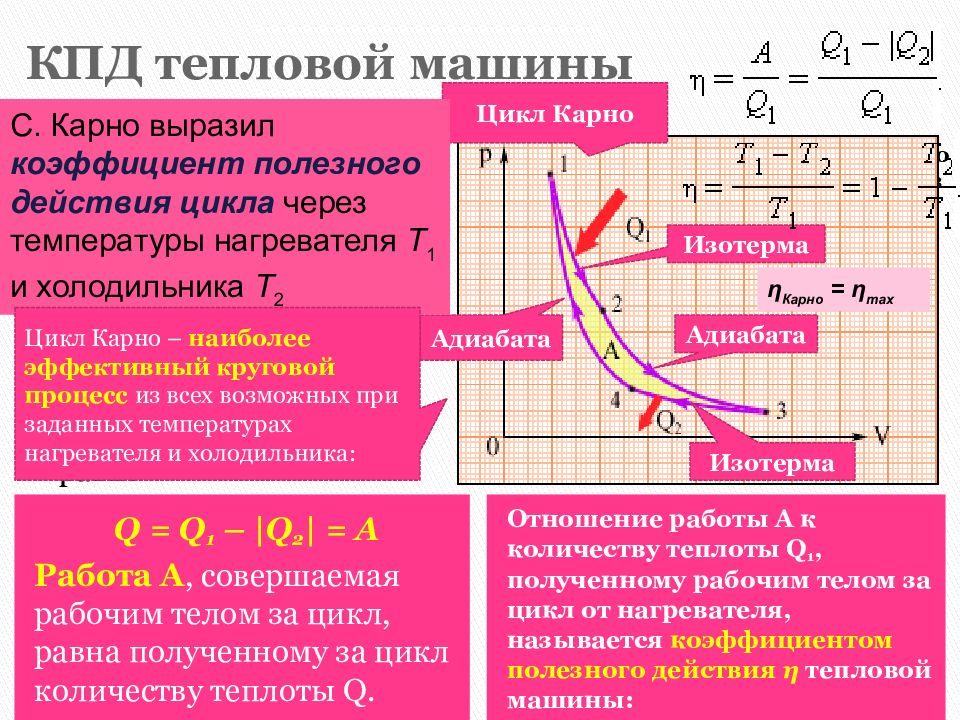

КПД тепловой машины — Энциклопедия по машиностроению XXL

Каков максимальный КПД тепловой машины, работающей между температурами 400 и 18 °С.  [c.30]

Французский инженер Сади Карно (1796—1832) в 1824 г. установил чрезвычайно важную для практики зависимость КПД тепловой машины от температуры Г, нагревателя и температуры Тч холодильника независимо от конструкции и выбора рабочего тела максимальное значение КПД тепловой машины определяется выражением  [c.104]

Выражение для максимального значения КПД тепловой машины показывает, что для повышения коэффициента полезного действия тепловых машин  [c.104]

Следовательно, основной путь повышения КПД тепловых машин — это повышение температуры нагревателя.  [c.104]

Определите максимальный КПД тепловой машины, если температура нагревателя равна 227 °С, а температура холодильника — 27 С.  [c.122]

Максимальный КПД тепловой машины определяется выражением  [c.123]

Вычислите максимальное значение КПД тепловой машины с температурой нагревателя 427 С и температурой холодильника 27 °С.  [c.126]

КПД тепловой машины 103 Кристаллическая решетка 90 Кристаллические тела 88 Критическая масса 330  [c.361]

Открытие второго начала связано с анализом работы тепловых машин, чем и определяется его исходная формулировка. Впервые работа тепловых машин была теоретически рассмотрена в 1824 г. Сади Карно, который в своем исследовании Размышления о движущей силе огня и о машинах, способных развивать эти силы , доказал, что КПД тепловых машин, работающих по предложенному им циклу (циклу Карно), не зависит от природы вещества, совершающего этот цикл. Позднее Клаузиус и В. Томсон, по-новому обосновывая эту теорему Кар но, почти одновременно положили основание тому, что теперь входит в содержание второго начала.  [c.40]

Теорема Карно указывает путь повышения КПД тепловых машин. Она сыграла руководящую роль в развитии основ теплотехники. Хотя 1НИ одна применяемая в технике тепловая машина не работает по циклу Карно, значение этого цикла состоит в том, что oiH имеет наибольший КПД по сравнению с циклами, работающими в тех же температурных пределах, и является мерой КПД всех других циклов ( ).  [c.69]

К нагревателю (обратный К. ц.). Анализируя К. ц., можно доказать Карно теорему о макс. кпд тепловых машин, Г[ T. —T jTl, это доказательство используют для формулировки второго начала термодинамики.  [c.243]

По определению КПД тепловой машины, работающей по произвольному циклу, равен  [c.73]

Эффективный КПД тепловой машины, представляющий отношение ее полезной работы к количеству подведенной с топливом теплоты, равен  [c.258]

Именно это обстоятельство в сочетании со вторым законом термодинамики позволяет утверждать, что (16) представляет собой максимально возможный КПД тепловой машины.  [c.25]

Постепенно, путем улучшения организации и взаимодействия элементов системы, их совершенствования и специализации удается увеличить У. В некоторых случаях этот процесс может проходить также частично и за счет познания принципиальных ограничений в (1), т.е. с ростом научного значения / d в (1) приближается к / (как, например, исследования Карно приблизили нас к пределу КПД тепловой машины).  [c.275]

Используя в качестве рабочего тела неразбавленные продукты сгорания (с максимальной эксергией), ДВС имеют самый высокий из всех тепловых машин КПД. Однако инерционные силы, связанные с возвратно-поступательным движением поршня, возрастают с увеличением как размеров цилиндра, так и частоты вращения вала, что затрудняет создание ДВС большой мощности. Большим их недостатком являются и высокие требования к качеству потребляемого топлива (жидкого или газа),  [c. 59]

Рабочий цикл тепловой машины и ее КПД. В результате совершения рабочего цикла газ возвращается в начальное состояние, его внутренняя энергия принимает первоначальное значение. Следовательно, за цикл изменение внутренней энергии рабочего тела равно нулю  [c.103]

Любая реальная тепловая машина может иметь КПД, не превышающий это максимальное значение  [c.104]

Температура пара, применяемого в современных паротурбинных установках, не превышает 580 С (температура нагревателя Г, = 853 К), а температура пара на выходе из турбины обычно не ниже 30 °С (температура холодильника Гг = 303 К) поэтому максимальное значение КПД паротурбинной установки как тепловой машины равно  [c.108]

Тепловая машина за цикл совершает работу 500 Дж и получает от нагревателя количество теплоты 1500 Дж. Вычислите КПД машины.  [c.126]

Тепловая машина с КПД 25% получает от нагревателя 800 Дж. Какую полезную работу она совершает  [c.126]

Тепловая машина получает за цикл от нагревателя 800 Дж и отдает холодильнику 600 Дж. Вычислите КПД машины.  [c.126]

Это положение непосредственно вытекает из сопоставления выражения КПД обратимых тепловых машин с математическим выражением принципа исключения вечного двигателя второго рода (т [c.54]

КПД термогенераторов пока составляет в лучшем случае 8 %. При температурах порядка 1000—1100 К можно ожидать, что КПД составит 15 %. Если учесть, что наиболее совершенные тепловые электростанции имеют КПД 40—50 %, то станет ясным, что термоэлементы из твердых полупроводников не могут быть использованы в большой энергетике . Однако по мере упрощения технологии, уменьшения размеров термобатарей и их стоимости будет расти использование термоэлектрических генераторов в малой энергетике и в устройствах утилизации тепловых отходов высокотемпературных тепловых машин.  [c.580]

Как известно, термический КПД любого цикла тепловой машины определяется выражением (1.121). Удельное количество теплоты  [c.63]

Сади Карно предложил цикл тепловой машины, который имеет максимальный термический КПД при заданной разнице температур между  [c.47]

Как известно, термический КПД любого цикла тепловой машины определяется выражением (58). Если — текущая температура процессов, в которых отводится теплота, а Г, — текущая температура процессов, в которых подводится теплота, то  [c.306]

За прошедшие 60 лет отмечены следующие существенные отклонения от прогноза Н. А. Умова началась и быстро проходит эпоха нефти и природного газа, наступила и еще долго продлится эра атомной энергии (рис. 1.1), передвинулся на отметку примерно 40% предел повышения КПД тепловых двигателей (рис. 1.2) при этом поршневые паровые машины окончательно вытеснены турбинами и двигателями внутреннего сгорания. Однако постоянно возобновляющиеся энергоресурсы (ветер, приливы и отливы, волны, солнечное излучение, тепло недр Земли), как и прежде практически почти не используются.  [c.11]

Какой должна быть температура нагревателя, для того чтобы стало возможным достинсение максимального значения КПД тепловой машины 80% при температуре холодильника 300 К  [c.126]

В первом сочинении по термодинамике, онубликованном С. Карно в 1824 г., была поставлена и решена проблема возможного повышения коэффициента полезного действия тепловых двигателей. Относительно КПД тепловых машин Карно установил две теоремы, которые ровместно эквивалентны второму началу термодинамики. Докажем эти теоремы, исходя из второго начала.  [c.66]

Если в рассматриваемой системе хотя бы один прсщесс в реализуемых циклах является необратимым, то энтропия такой системы будет величиваться. Для обоснования этого утверждения следует показать, что КПД тепловой машины, работающей между источниками теплоты с температурами Т, и по необратимому циклу, меньше КПД тепловой машины, работающей между теми же источниками теплоты, но по об-I атимому циклу (т) р ). Выражение (58) свидетельствует о том, что в этом случае должно выполняться условие  [c.56]

У тепловых машин фактор энергопотребления отодвигает на заднцй план стоимость машины, а иногда и расходы на труд. Есть машины, у которых расход энергии незначителен вследствие высокого КПД (электрогенераторы, редукторы и т. п.). Если к тому же невелик и расход на оплату труда, то стоимость машины приобретает доминирующее зна-ченйе.  [c.15]

Анализ особенностей тепловых процессов, выполненный Р. Клаузиусом, был далеко не очевиден, но логически безупречен. Обратив внимание на то, что формулировка второго закона термодинамики носит качественный характер, он задался целью найти его математическую форму. Он считал необходимым связать второй закон с некоторой характерной физической величиной, аналогично тому, как первый закон оказался связанным с существова1шем энергии, явился законом ее сохранения и превращения. Максимальный КПД идеальной тепловой машины, как впервые показал С. Карно, определяется соотношением  [c.81]

Термический КПД цнкла Карно при изогермич . ских источниках имеет макси.мальное значение в заданном интервале температур по сравнению с другими циклами и, следовательно, является эталоном, с которым сравнивают циклы существующих тепловых машин. Реальный тепловой двигатель тем совершеннее, чем ближе значение его КПД к КПД цикла Карно в том же интервале температур.  [c.49]

Анализ соотношений (1.78) и (1.79) показывает, что термический КПД теплового двигателя и коэффициент холодопроизводи-тельности зависят только от соотношения абсолютных температур. Чем больше различие в абсолютных температурах, тем выше эффективность работы тепловой машины. Из выражения (1.78) следует также, что термический КПД двигателя, работающего по циклу Карно, всегда меньше единицы. Он обращается в единицу только в двух практически недостижимых случаях при Т, = и = 0. При равенстве Т, = КПД двигателя обращается в нуль. Это значит, что для работы теплового двигателя необходимо наличие разности температур Т, и Т . В тепловых двигателях в качестве наивысшей температуры Т цикла обычно понимается температура сгорания рабочей смеси, а в качестве низшей температуры — температура окружающей среды.  [c.46]

КПД всякого необратимого теплового двигателя и холодопро-изводительность необратимой холодильной машины, осуществляющих процессы при заданных температурах (Т, > Т ), всегда меньше соответственно КПД и холодопроизводительности обратимой тепловой машины (т1 [c.54]

Исследование термодинамических циклов тепловых машин является основной задачей технической термодинамики. Однако провести подробное исследование цикла, установить его основные характеристики (работу, КПД) при изменении отдельных параметров на реальной установке можно лишь в ограниченных пределах. Поэтому при исследовании циклов энергетических установок вместо натурных испытаний целесообразно использовать различные модели. Модели бывают разные в зависимости от модели различают предметное, физичеекое, аналоговое и математическое моделирование.  [c.238]

Сравним формулы (1.290) и (1.124) они идентичны. Следовательно, формз -ла (1.290) определяет термический КПД некоторого эквивалентного цикла Карно, равный термическому КПД исследуемого цикла. Таким образом, любой цикл тепловой машины может быть заменен эквивалентным циклом Карно с температурами и Tj p. При наличии лГ-диаграммы среднепланиметрическая температура может быть определена планиметрированием площад й треугольников (рис. 1.33, а). Средняя тем-  [c.64]

Для пояснения этого важного выводя рассмотрим пзолировапиую систему, в которой имеются три источника теплоты с темнературам1Г Т, > Т > Т.2 (рис. 17). Эти источники теплоты можно использовать для получения работы в тепловых машинах-двигателях, работающих по циклам Карно. Допустим, что одна машина работает но циклу Карно с источниками теплоты, имеющи.ми температуры Tj и и совершает работу /ц с КПД никла Л( = I — T Ti. Другая машина работает ио циклу Карио с источниками теплоты, имеющими температуры Т и T a, и совершает работу /ц с КПД цикла г , = 1 — TJT. Одновременно с работой машин теплота от источника с температурой Т > Т  [c.58]

Универсальная тепловая машина стирлинг . Была запатентована Р. Стирлингом в 1816 г., но оценена должным образом только в последние десятилетия. Эта машина простым переводом управляющего устройства может быть переключена на работу ДВшС, холодильной машины и теплового насоса. Ее показатели как ДВшС выше показателей всех других ДВшС, а в ряде случаев и ДВС (табл. 7.1). Поскольку стирлинг нуждается в охлаждении, его показатели повышаются в условиях применения па морских аппаратах. Теоретический цикл стирлинга — регенеративный цикл Карно. Максимальная температура цикла 600—700° С, максимальное давление 100—200 бар, i- ,k = 70%, г) = 35—45%, КПД регенератора — 95—98%.  [c.143]

Работа Карно, не содержавшая ни одной математической зависимости, прошла незамеченной. И только через 10 лет, после выхода в свет мемуара О движущей силе теплоты члена Парижской и члена-корреспонден-та Петербургской академий наук Бенуа Клапейрона К1799—1864), она стала чуть ли не сенсацией. Клапейрон перевел сочинение Карно на математический язык, вскрыв великое содержание этого труда. Он первым стал применять графический метод исследования работы тепловых машин, вычисляя величину работы как площадь под кривой процесса в системе координат давление— удельный объем. Однако и Клапейрон не сумел вывести формулу КПД Карно в современном виде.  [c.116]

Эти достоинства эксергии сделали ее чрезвычайно модной в последние годы. Однако не все отдают себе отчет в том, что эксергетический метод расчета позволяет учесть потери лишь из-за необратимости процессов, в чем не всегда есть необходимость. Так, совершенно разные по конфигурации и эффективности теоретические, обратимые циклы тепловых машин и идеальный цикл Карно имеют одинаковый эксергетический КПД, равный 100%. При использовании же тепла для технологических нужд (выпарки, плавки металла и т. д.) запас работоспособности тепл01Н0сителя — эксергия не имеет прямого значения.  [c.161]

Идеальный тепловой двигатель Карно: пересмотр второго закона термодинамики

Цели обучения

К концу этого раздела вы сможете:

• Определите цикл Карно.
• Рассчитайте максимальный теоретический КПД ядерного реактора.
• Объясните, как диссипативные процессы влияют на идеальный двигатель Карно.

Рис. 1. Пьющая птица (источник: Arabesk.nl, Wikimedia Commons)

Новинка, известная как пьющая птица (см. Рис. 1), является примером двигателя Карно.Он содержит хлористый метилен (смешанный с красителем) в брюшной полости, который кипит при очень низкой температуре — около 100 ° F. Чтобы работать, нужно намочить голову птицы. Когда вода испаряется, жидкость движется вверх в голову, отчего птица становится тяжелой и снова погружается в воду. Это охлаждает хлористый метилен в голове, и он перемещается обратно в брюшную полость, в результате чего дно птицы становится тяжелым и опрокидывается. За исключением очень небольшого расхода энергии — первоначального увлажнения головы — птица становится своего рода вечным двигателем.

Мы знаем из второго закона термодинамики, что тепловой двигатель не может быть на 100% эффективным, так как всегда должна быть некоторая теплопередача Q _c в окружающую среду, которую часто называют отходящим теплом. Насколько эффективна тогда тепловая машина? На этот вопрос теоретически ответил в 1824 году молодой французский инженер Сади Карно (1796–1832 гг.) В своем исследовании появившейся в то время технологии тепловых двигателей, имеющих решающее значение для промышленной революции. Он разработал теоретический цикл, который теперь называется циклом Карно , который является наиболее эффективным из возможных циклических процессов.Второй закон термодинамики можно переформулировать в терминах цикла Карно, и поэтому Карно фактически открыл этот фундаментальный закон. Любой тепловой двигатель, использующий цикл Карно, называется двигателем Карно .

Что критически важно для цикла Карно — и, по сути, определяет его, — так это то, что используются только обратимые процессы. Необратимые процессы связаны с диссипативными факторами, такими как трение и турбулентность. Это увеличивает теплоотдачу Q _c в окружающую среду и снижает КПД двигателя.Очевидно, что обратимые процессы лучше.

Двигатель Карно

С точки зрения обратимых процессов, второй закон термодинамики имеет третью форму:

Двигатель Карно, работающий между двумя заданными температурами, имеет максимально возможный КПД по сравнению с любым тепловым двигателем, работающим между этими двумя температурами. Кроме того, все двигатели, в которых используются только обратимые процессы, имеют одинаковую максимальную эффективность при работе между одинаковыми заданными температурами.

На рисунке 2 показана диаграмма PV для цикла Карно. Цикл включает два изотермических и два адиабатических процесса. Напомним, что и изотермические, и адиабатические процессы в принципе обратимы.

Карно также определил эффективность идеального теплового двигателя, то есть двигателя Карно. Всегда верно, что эффективность циклического теплового двигателя определяется как:

[латекс] \ displaystyle {Eff} = \ frac {Q _ {\ text {h}} — Q _ {\ text {c}}} {Q _ {\ text {h}}} = 1- \ frac {Q _ {\ текст {c}}} {Q _ {\ text {h}}} \\ [/ latex]

Карно обнаружил, что для идеального теплового двигателя соотношение [латекс] \ frac {Q _ {\ text {c}}} {Q _ {\ text {h}}} \\ [/ latex] равно отношению абсолютные температуры тепловых резервуаров.То есть [латекс] \ frac {Q _ {\ text {c}}} {Q _ {\ text {h}}} = \ frac {T _ {\ text {c}}} {T _ {\ text {h}} } \\ [/ latex] для двигателя Карно, так что максимальная или эффективность Карно Eff _C определяется как

[латекс] \ displaystyle {Eff} _ {\ text {C}} = 1- \ frac {T _ {\ text {c}}} {T _ {\ text {h}}} \\ [/ latex]

, где T _h и T _c указаны в градусах Кельвина (или по любой другой шкале абсолютных температур). Никакая настоящая тепловая машина не может работать так хорошо, как КПД Карно — фактический КПД около 0.7 из этого максимума обычно — лучшее, что может быть достигнуто. Но идеальный двигатель Карно, как и пьяная птица наверху, хотя и является увлекательной новинкой, имеет нулевую мощность. Это делает его нереалистичным для любых приложений.

Интересный результат Карно подразумевает, что 100% эффективность будет возможна только в том случае, если T _c = 0 K, то есть, только если холодный резервуар находится на абсолютном нуле, что практически и теоретически невозможно. Но физический смысл таков: единственный способ задействовать всю теплопередачу в работе — это удалить из всю тепловую энергию , а для этого требуется холодный резервуар с абсолютным нулем.

Также очевидно, что наибольшая эффективность достигается, когда соотношение [латекс] \ frac {T _ {\ text {c}}} {T _ {\ text {h}}} \\ [/ latex] как можно меньше . Так же, как обсуждалось для цикла Отто в предыдущем разделе, это означает, что эффективность максимальна для максимально возможной температуры горячего резервуара и минимально возможной температуры холодного резервуара. (Эта установка увеличивает площадь внутри замкнутого контура на диаграмме PV ; также кажется разумным, что чем больше разница температур, тем легче направить теплопередачу на работу.Фактические температуры резервуара теплового двигателя обычно связаны с типом источника тепла и температурой окружающей среды, в которой происходит передача тепла. Рассмотрим следующий пример.

Рис. 2. PV Диаграмма для цикла Карно, использующего только обратимые изотермические и адиабатические процессы. Теплоотдача Q _h происходит в рабочее тело во время изотермического пути AB, который происходит при постоянной температуре T _h .Теплообмен Q _c происходит из рабочего тела во время изотермического пути CD, который происходит при постоянной температуре T _c . Выход сети W равен площади внутри пути ABCDA. Также показана схема двигателя Карно, работающего между горячим и холодным резервуарами при температурах T _h и T _c . Любой тепловой двигатель, использующий обратимые процессы и работающий между этими двумя температурами, будет иметь такой же максимальный КПД, что и двигатель Карно.

Пример 1. Максимальный теоретический КПД ядерного реактора

Ядерный энергетический реактор имеет воду под давлением 300ºC. (Более высокие температуры теоретически возможны, но практически невозможны из-за ограничений, связанных с материалами, используемыми в реакторе.) Передача тепла от этой воды — сложный процесс (см. Рисунок 3). Пар, вырабатываемый в парогенераторе, используется для привода турбогенераторов. В конце концов пар конденсируется в воду при 27ºC, а затем снова нагревается, чтобы запустить цикл заново.Рассчитайте максимальный теоретический КПД теплового двигателя, работающего между этими двумя температурами.

Рис. 3. Принципиальная схема ядерного реактора с водой под давлением и паровых турбин, которые преобразуют работу в электрическую энергию. Теплообмен используется для генерации пара, отчасти для предотвращения радиоактивного загрязнения генераторов. Используются две турбины, поскольку это дешевле, чем использование одного генератора, вырабатывающего такое же количество электроэнергии. Перед возвратом в теплообменник пар конденсируется в жидкость, чтобы поддерживать низкое давление пара на выходе и способствовать прохождению пара через турбины (эквивалентно использованию холодного резервуара с более низкой температурой).Значительная энергия, связанная с конденсацией, должна рассеиваться в окружающей среде; в этом примере используется градирня, поэтому прямая передача тепла в водную среду отсутствует. (Обратите внимание, что вода, поступающая в градирню, не контактирует с паром, протекающим по турбинам.)

Стратегия

Поскольку температуры указаны для горячего и холодного резервуаров этой тепловой машины, [латекс] {Eff} _ {\ text {C}} = 1- \ frac {T _ {\ text {c}}} {T _ {\ text {h}}} \\ [/ latex] можно использовать для расчета эффективности Карно (максимальной теоретической).Эти температуры необходимо сначала перевести в градусы Кельвина.

Решение

Температуры горячего и холодного резервуаров равны 300 ° C и 27,0 ° C соответственно. Таким образом, в градусах Кельвина T _h = 573 K и T _c = 300 K, так что максимальная эффективность составляет [латекс] \ displaystyle {Eff} _ {\ text {C}} = 1- \ frac {T _ {\ text {c}}} {T _ {\ text {h}}} \\ [/ latex].

Таким образом,

[латекс] \ begin {array} {lll} {Eff} _ {\ text {C}} & = & 1- \ frac {300 \ text {K}} {573 \ text {K}} \\\ text { } & = & 0.476 \ text {или} 47.6 \% \ end {array} \\ [/ latex]

Обсуждение

Фактический КПД типичной атомной электростанции составляет около 35%, что немного лучше, чем в 0,7 раза больше максимально возможного значения, что является данью превосходной инженерной мысли. Электростанции, работающие на угле, нефти и природном газе, имеют более высокий фактический КПД (около 42%), потому что их котлы могут достигать более высоких температур и давлений. Температура холодного резервуара на любой из этих электростанций ограничена местными условиями.На рисунке 4 показан (а) внешний вид атомной электростанции и (б) внешний вид угольной электростанции. Оба имеют градирни, в которые вода из конденсатора попадает в градирню рядом с верхом и разбрызгивается вниз, охлаждаясь за счет испарения.

Рис. 4. (a) Атомная электростанция (предоставлено BlatantWorld.com) и (b) угольная электростанция. Оба имеют градирни, в которых вода испаряется в окружающую среду, что составляет Q _c . Ядерный реактор, поставляющий Q _h , размещен внутри куполообразных корпусов защитной оболочки.(Источник: Роберт и Михаэла Викол, publicphoto.org)

Поскольку все реальные процессы необратимы, фактическая эффективность теплового двигателя никогда не может быть такой же высокой, как у двигателя Карно, как показано на рисунке 5a. Даже при наличии самого лучшего теплового двигателя всегда есть процессы рассеяния в периферийном оборудовании, таком как электрические трансформаторы или автомобильные трансмиссии. Это еще больше снижает общий КПД за счет преобразования части выходной мощности двигателя обратно в теплообмен, как показано на рисунке 5b.

Рис. 5. Настоящие тепловые двигатели менее эффективны, чем двигатели Карно. (а) Настоящие двигатели используют необратимые процессы, уменьшающие теплопередачу к работе. Сплошные линии представляют реальный процесс; пунктирные линии — это то, что двигатель Карно будет делать между теми же двумя резервуарами. (б) Трение и другие диссипативные процессы в выходных механизмах теплового двигателя преобразуют часть его работы в теплоотдачу в окружающую среду.

Сводка раздела

• Цикл Карно — это теоретический цикл, который является наиболее эффективным из возможных циклических процессов.Любой двигатель, использующий цикл Карно, который использует только обратимые процессы (адиабатические и изотермические), известен как двигатель Карно.
• Любой двигатель, использующий цикл Карно, обладает максимальной теоретической эффективностью.
• Хотя двигатели Карно являются идеальными двигателями, на самом деле ни один двигатель не достигает теоретической максимальной эффективности Карно, поскольку диссипативные процессы, такие как трение, играют роль. Циклы Карно без потери тепла возможны при абсолютном нуле, но в природе такого никогда не наблюдалось.

Концептуальные вопросы

1. Подумайте о пьющей птице в начале этого раздела (рис. 1). Хотя птица обладает максимально возможной теоретической эффективностью, если со временем предоставить ее самой себе, она перестанет «пить». Какие диссипативные процессы могут привести к прекращению движения птицы?
2. Можно ли в тепловых двигателях использовать улучшенные технические средства и материалы для уменьшения передачи тепла в окружающую среду? Могут ли они полностью исключить передачу тепла в окружающую среду?
3. Меняет ли второй закон термодинамики принцип сохранения энергии?

Задачи и упражнения

1.Определенный бензиновый двигатель имеет КПД 30,0%. Какой была бы температура горячего резервуара для двигателя Карно с таким КПД, если бы он работал с температурой холодного резервуара 200ºC?

2. Ядерный реактор с газовым охлаждением работает при горячей и холодной пластовых температурах от 700 ° C до 27,0 ° C. а) Каков максимальный КПД теплового двигателя, работающего между этими температурами? (b) Найдите отношение этого КПД к КПД Карно стандартного ядерного реактора (найденного в Примере 1).

3. (a) Какова температура горячего резервуара двигателя Карно с КПД 42,0% и температурой холодного резервуара 27,0 ° C? (b) Какой должна быть температура горячего резервуара для реального теплового двигателя, который достигает 0,700 от максимального КПД, но все еще имеет КПД 42,0% (и холодный резервуар при 27,0 ° C)? (c) Подразумевает ли ваш ответ практические ограничения эффективности бензиновых двигателей автомобилей?

4. Паровозы имеют КПД 17,0% и работают с температурой горячего пара 425ºC.а) Какой была бы температура холодного резервуара, если бы это был двигатель Карно? (б) Какой была бы максимальная эффективность этой паровой машины, если бы температура в ее холодном резервуаре составляла 150 ° C?

5. В практических паровых машинах используется пар с температурой 450 ° C, который позже выпускается при 270 ° C. а) Каков максимальный КПД такой тепловой машины? (b) Поскольку пар с 270ºC все еще достаточно горячий, вторая паровая машина иногда работает на выхлопе первой. Каков максимальный КПД второго двигателя, если его выхлоп имеет температуру 150ºC? (c) Каков общий КПД двух двигателей? (d) Показать, что это такой же КПД, как у одного двигателя Карно, работающего при температуре от 450 до 150 ° C.

6. Угольная электростанция имеет КПД 38%. Температура пара, выходящего из котла, составляет [латекс] \ text {550} \ text {\ textordmasculine} \ text {C} [/ latex]. Какой процент от максимальной эффективности достигает эта станция? (Предположим, что температура окружающей среды [латекс] \ text {20} \ text {\ textordmasculine} \ text {C} [/ latex].)

7. Готовы ли вы финансово поддержать изобретателя, который продает устройство, которое, по ее утверждениям, имеет теплопередачу 25 кДж при 600 К, теплопередачу в окружающую среду при 300 К и работает 12 кДж? Поясните свой ответ.

8. Необоснованные результаты (a) Предположим, вы хотите создать паровой двигатель, который передает тепло в окружающую среду при 270ºC и имеет КПД Карно 0,800. Какой температуры горячего пара нужно использовать? б) Что неразумного в температуре? (c) Какая посылка необоснованна?

9. Необоснованные результаты Рассчитайте температуру холодного резервуара парового двигателя, который использует горячий пар при 450ºC и имеет КПД Карно 0,700. б) Что неразумного в температуре? (c) Какая посылка необоснованна?

Глоссарий

Цикл Карно: циклический процесс, в котором используются только обратимые процессы, адиабатические и изотермические процессы

Двигатель Карно: тепловой двигатель, использующий цикл Карно

КПД Карно: максимальный теоретический КПД для тепловой машины

Избранные решения проблем и упражнения

1.403ºC

3. (а) 244ºC; (б) 477 ° С; (c) Да, поскольку автомобильные двигатели не могут быть слишком горячими без перегрева, их эффективность ограничена.

5. (a) [латекс] {\ mathit {\ text {Eff}}} _ {\ text {1}} = 1- \ frac {{T} _ {\ text {c, 1}}} {{ T} _ {\ text {h, 1}}} = 1- \ frac {\ text {543 K}} {\ text {723 K}} = 0 \ text {.} \ Text {249} \ text {или } \ text {24} \ text {.} 9 \% \\ [/ latex]

(b) [латекс] {\ mathit {\ text {Eff}}} _ {2} = 1- \ frac {\ text {423 K}} {\ text {543 K}} = 0 \ text {.} \ text {221} \ text {или} \ text {22} \ text {.} 1 \% \\ [/ latex]

(c) [латекс] {\ mathit {\ text {Eff}}} _ {1} = 1- \ frac {{T} _ {\ text {c, 1}}} {{T} _ {\ text {h, 1}}} \ Rightarrow {T} _ {\ text {c, 1}} = {T} _ {\ text {h, 1}} \ left (1, -, {\ mathit {\ text { eff}}} _ {1} \ right) \ text {аналогично} {T} _ {\ text {c, 2}} = {T} _ {\ text {h, 2}} \ left (1- { \ mathit {\ text {Eff}}} _ {2} \ right) \\ [/ latex]

с использованием T _{h, 2} = T _{c, 1} в приведенном выше уравнении дает

[латекс] \ begin {array} {l} {T} _ {\ text {c, 2}} = {T} _ {\ text {h, 1}} \ left (1- {Eff} _ {1 } \ right) \ left (1- {Eff} _ {2} \ right) \ Equiv {T} _ {\ text {h, 1}} \ left (1- {Eff} _ {\ text {total}} \ right) \\\ поэтому \ left (1- {Eff} _ {\ text {total}} \ right) = \ left (1 — {\ mathit {\ text {Eff}}} _ {1} \ right) \ left (1- {Eff} _ {2} \ right) \\ {Eff} _ {\ text {total}} = 1- \ left (1-0.249 \ right) \ left (1-0,221 \ right) = 41,5 \% \ end {array} \\ [/ latex]

(d) [латекс] {\ text {Eff}} _ {\ text {total}} = 1- \ frac {\ text {423 K}} {\ text {723 K}} = 0 \ text {.} \ text {415} \ text {или} \ text {41} \ text {.} 5 \\% \\ [/ latex]

7. Передача тепла в холодный резервуар составляет [латекс] {Q} _ {\ text {c}} = {Q} _ {\ text {h}} — W = \ text {25} \ text {кДж} — \ text {12} \ text {kJ} = \ text {13} \ text {kJ} \\ [/ latex], поэтому эффективность равна [latex] \ mathit {Eff} = 1- \ frac {{Q} _ {\ text {c}}} {{Q} _ {\ text {h}}} = 1- \ frac {\ text {13} \ text {кДж}} {\ text {25} \ text {кДж} } = 0 \ текст {.} \ text {48} \\ [/ latex]. Эффективность Карно составляет [латекс] {\ mathit {\ text {Eff}}} _ {\ text {C}} = 1- \ frac {{T} _ {\ text {c}}} {{T} _ { \ text {h}}} = 1- \ frac {\ text {300} \ text {K}} {\ text {600} \ text {K}} = 0 \ text {.} \ text {50} \\ [/латекс]. Фактический КПД составляет 96% от КПД Карно, что намного выше, чем лучший из когда-либо достигнутых, составляющий около 70%, поэтому ее схема, скорее всего, будет мошеннической.

9. (a) -56,3ºC (b) Температура слишком низкая для мощности паровой машины (местная среда). Это ниже точки замерзания воды.(c) Предполагаемая эффективность слишком высока.

4.5 Цикл Карно — Университетская физика, том 2

Цели обучения

• Опишите цикл Карно с ролями всех четырех задействованных процессов
• Краткое описание принципа Карно и его значения
• Продемонстрировать эквивалентность принципа Карно и второго начала термодинамики

В начале 1820-х годов Сади Карно (1786–1832), французский инженер, заинтересовался повышением эффективности практических тепловых двигателей.В 1824 году его исследования привели его к предложению гипотетического рабочего цикла с максимально возможной эффективностью между одними и теми же двумя резервуарами, известного теперь как цикл Карно. Двигатель, работающий в этом цикле, называется двигателем Карно. Цикл Карно имеет особое значение по ряду причин. На практике этот цикл представляет собой обратимую модель паровой электростанции и холодильника или теплового насоса. Тем не менее, это также очень важно с теоретической точки зрения, поскольку играет важную роль в разработке другого важного положения второго закона термодинамики.Наконец, поскольку в его работе задействованы только два резервуара, его можно использовать вместе со вторым законом термодинамики для определения шкалы абсолютной температуры, которая действительно не зависит от какого-либо вещества, используемого для измерения температуры.

При идеальном газе в качестве рабочего вещества этапы цикла Карно, представленные на рис. 4.11, следующие.

1. Изотермическое расширение. Газ находится в тепловом контакте с тепловым резервуаром с температурой Th.Чт. Газ поглощает тепло QhQh из теплового резервуара и ему позволяют изотермически расширяться, выполняя работу W1.W1. Поскольку внутренняя энергия EintEint идеального газа является функцией только температуры, изменение внутренней энергии равно нулю, то есть ΔEint = 0ΔEint = 0 во время этого изотермического расширения. Используя первый закон термодинамики, ΔEint = Q − W, ΔEint = Q − W, мы находим, что тепло, поглощаемое газом, равно
   Qh = W1 = nRThlnVNVM.Qh = W1 = nRThlnVNVM.

   Рис. 4.11. Четыре процесса цикла Карно. Предполагается, что рабочим веществом является идеальный газ, термодинамический путь которого MNOP представлен на рисунке 4.12.

   Рис. 4.12. Общая работа, выполняемая газом в цикле Карно, показана в виде площади, ограниченной контуром MNOPM .

2. Адиабатическое расширение . Газ термически изолирован и ему позволено расширяться, выполняя работу W2.W2. Поскольку это расширение является адиабатическим, температура газа падает — в данном случае с ThtoTc.ThtoTc. Из pVγ = constant pVγ = constant и уравнения состояния идеального газа pV = nRTpV = nRT имеем
   TVγ − 1 = постоянная, TVγ − 1 = постоянная,
   чтобы
   ThVNγ − 1 = TcVOγ − 1.ThVNγ − 1 = TcVOγ − 1.
3. Изотермическое сжатие . Газ помещается в тепловой контакт с холодным резервуаром при температуре TcTc и изотермически сжимается. Во время этого процесса работа W3W3 выполняется с газом, и он отдает тепло QcQc холодному резервуару. Рассуждения, использованные в шаге 1, теперь дают
   Qc = nRTclnVOVP, Qc = nRTclnVOVP,
   где QcQc — тепло, отдаваемое газом в холодный резервуар.
4. Адиабатическое сжатие . Газ термически изолирован и возвращается в исходное состояние путем сжатия.При этом работа W4W4 производится на газе. Поскольку сжатие является адиабатическим, температура газа повышается — в данном конкретном случае от TctoThTctoTh. Обоснование шага 2 теперь дает
   TcVPγ − 1 = ThVMγ − 1, TcVPγ − 1 = ThVMγ − 1.
   Полная работа, выполняемая газом в цикле Карно, определяется выражением
   W = W1 + W2 − W3 − W4. W = W1 + W2 − W3 − W4.

Эта работа равна площади, ограниченной петлей, показанной на диаграмме pV на рис. 4.12. Поскольку начальное и конечное состояния системы одинаковы, изменение внутренней энергии газа в цикле должно быть нулевым, то есть ΔEint = 0ΔEint = 0.Тогда первый закон термодинамики дает

W = Q − ΔEint = (Qh − Qc) −0, W = Q − ΔEint = (Qh − Qc) −0,

и

Чтобы определить КПД этого двигателя, сначала разделим QcbyQh: QcbyQh:

QcQh = TcThlnVO / VPlnVN / VM.QcQh = TcThlnVO / VPlnVN / VM.

Когда адиабатическая постоянная из шага 2 делится на таковую из шага 4, мы находим

Подставляя это в уравнение для Qc / Qh, Qc / Qh, получаем

Наконец, с помощью уравнения 4.2 мы находим, что эффективность этого идеального газового двигателя Карно определяется как

е = 1 − TcTh.е = 1 − TcTh.

4,5

Двигатель не обязательно должен соответствовать циклу двигателя Карно. Однако все двигатели имеют один и тот же эффект net , а именно поглощение тепла из горячего резервуара, выполнение работы и отвод тепла в холодный резервуар. Это заставляет нас задаться вопросом: имеют ли все обратимые циклы, действующие между одними и теми же двумя резервуарами, одинаковую эффективность? Ответ на этот вопрос исходит из второго закона термодинамики, обсуждавшегося ранее: Все реверсивные двигательные циклы производят точно такой же КПД .Кроме того, как и следовало ожидать, все настоящие двигатели, работающие между двумя резервуарами, менее эффективны, чем реверсивные двигатели, работающие между теми же двумя резервуарами. Это тоже следствие второго закона термодинамики, показанного ранее.

Цикл холодильника Карно на идеальном газе представлен диаграммой pV на рис. 4.13. Это двигатель Карно, работающий в обратном направлении. Холодильник отводит тепло QcQc из холодного резервуара при TcTc, когда идеальный газ расширяется изотермически.Затем газ сжимается адиабатически до тех пор, пока его температура не достигнет Th, Th, после чего изотермическое сжатие газа приводит к тому, что тепло QhQh отводится в высокотемпературный резервуар с Th.Th. Наконец, цикл завершается адиабатическим расширением газа, в результате чего его температура падает до Tc.Tc.

Рис. 4.13. Работа, проделанная с газом в одном цикле холодильника Карно, показана в виде площади, ограниченной петлей MPONM .

Работа, проделанная на идеальном газе, равна площади, ограниченной траекторией на диаграмме pV .По первому закону эта работа отнесена к

.

Анализ, аналогичный анализу, проведенному для двигателя Карно, дает

В сочетании с уравнением 4.3 это дает

KR = TcTh-TcKR = TcTh-Tc

4,6

для КПД идеального газового холодильника Карно. Аналогичным образом мы можем вычислить коэффициент полезного действия теплового насоса Карно как

KP = QhQh − Qc = ThTh−Tc.KP = QhQh − Qc = ThTh − Tc.

4,7

Мы только что нашли уравнения, представляющие КПД двигателя Карно и КПД холодильника Карно или теплового насоса Карно, при условии, что в обоих устройствах в качестве рабочего вещества используется идеальный газ.Однако эти уравнения являются более общими, чем следует из их вывода. Вскоре мы покажем, что оба они действительны, независимо от того, какое рабочее вещество используется.

Карно обобщил свое исследование двигателя Карно и цикла Карно в то, что теперь известно как принцип Карно:

Принцип Карно

Ни один двигатель, работающий между двумя резервуарами при постоянной температуре, не может иметь большей эффективности, чем реверсивный двигатель.

Этот принцип можно рассматривать как еще одно утверждение второго закона термодинамики и можно показать, что он эквивалентен утверждению Кельвина и утверждению Клаузиуса.

Пример 4.2

Двигатель Карно

Двигатель Карно имеет КПД 0,60, а температура его холодного резервуара составляет 300 К. а) Какова температура горячего резервуара? (b) Если двигатель выполняет 300 Дж работы за цикл, сколько тепла удаляется из высокотемпературного резервуара за цикл? (c) Сколько тепла отводится в низкотемпературный резервуар за цикл?

Стратегия

По температурной зависимости теплового КПД двигателя Карно мы можем определить температуру горячего резервуара.Затем, исходя из определения эффективности, мы можем найти тепло, отводимое при задании работы, выполняемой двигателем. Наконец, экономия энергии приведет к тому, сколько тепла должно быть сброшено в холодный резервуар.

Решение

1. Из e = 1 − Tc / The = 1 − Tc / Th имеем
   0.60 = 1−300KTh, 0.60 = 1−300KTh,
   чтобы температура горячего резервуара была
   Th = 300K1-0,60 = 750K. Th = 300K1-0,60 = 750K.
2. По определению, КПД двигателя равен e = W / Qe = W / Q, так что тепло, отводимое из высокотемпературного резервуара за цикл, равно
   Qh = We = 300J0.60 = 500 Дж. Qh = We = 300 Дж. 0,60 = 500 Дж.
3. Из первого закона тепло, выделяемое двигателем в низкотемпературный резервуар за цикл, равно
   Qc = Qh − W = 500 Дж − 300 Дж = 200 Дж. Qc = Qh − W = 500 Дж − 300 Дж = 200 Дж.

Значение

Двигатель Карно имеет максимально возможную эффективность преобразования тепла в работу между двумя резервуарами, но это не обязательно означает, что он на 100% эффективен на 100%. По мере увеличения разницы температур горячего и холодного резервуаров эффективность двигателя Карно увеличивается.

Пример 4.3

Тепловой насос Карно

Представьте, что тепловой насос Carnot работает при температуре наружного воздуха от 0 ° C0 ° C до внутренней температуры от 20,0 ° C20,0 ° C. Какие работы нужны, если во внутреннюю часть дома доставляется тепло 30,0 кДж?

Стратегия

Поскольку предполагается, что тепловой насос является насосом Карно, его коэффициент полезного действия определяется выражением KP = Qh / W = Th / (Th-Tc) .KP = Qh / W = Th / (Th-Tc). Таким образом, мы можем найти работу Вт, от отдаваемого тепла Qh.Qh.

Решение

Необходимая работа получена от
W = Qh / KP = Qh (Th-Tc) / Th = 30кДж × (293K-273K) / 293K = 2кДж.W = Qh / KP = Qh (Th-Tc) / Th = 30кДж × (293K-273K) / 293K = 2кДж.

Значение

Отметим, что эта работа зависит не только от тепла, подаваемого в дом, но и от температуры снаружи и внутри. Зависимость от температуры на улице делает их нецелесообразными для использования в областях, где температура на улице намного ниже комнатной.

С точки зрения затрат на электроэнергию тепловой насос является очень экономичным средством обогрева зданий (рис. 4.14). Сравните этот метод с прямым преобразованием электрической энергии в тепло с помощью резистивных нагревательных элементов.В этом случае одна единица электроэнергии дает не более одной единицы тепла. К сожалению, у тепловых насосов есть проблемы, которые ограничивают их полезность. Они довольно дороги в приобретении по сравнению с резистивными нагревательными элементами, и, как показывает коэффициент полезного действия теплового насоса Carnot, они становятся менее эффективными при снижении наружной температуры. Фактически, ниже –10–10 ° C выделяемое ими тепло меньше энергии, используемой для их работы.

Рис. 4.14. Фотография теплового насоса (большая коробка), расположенного вне дома.Этот тепловой насос расположен в районе с теплым климатом, например на юге США, поскольку он был бы слишком неэффективным в северной части Соединенных Штатов. (кредит: модификация работы Питера Стивенса)

Проверьте свое понимание 4.3

Двигатель Карно работает между резервуарами при температуре от 400 ° C до 400 ° C и от 30 ° C до 30 ° C. а) Каков КПД двигателя? (b) Если двигатель выполняет 5,0 Дж работы за цикл, сколько тепла за цикл он поглощает из высокотемпературного резервуара? (c) Сколько тепла за цикл отводится в резервуар с холодной температурой? (d) Какие температуры в холодном резервуаре дадут минимальную и максимальную эффективность?

Проверьте свое понимание 4.4

Холодильник Carnot работает между двумя тепловыми резервуарами, температура которых составляет 0 ° C0 ° C и 25 ° C25 ° C. а) Каков коэффициент полезного действия холодильника? (b) Если с рабочим телом за цикл выполняется 200 Дж работы, сколько тепла за цикл отбирается из холодного резервуара? (c) Сколько тепла за цикл сбрасывается в горячий резервуар?

Калькулятор КПД Карно

Если вас интересует термодинамика, вам обязательно стоит попробовать этот калькулятор КПД Карно.Это удобный инструмент, который поможет вам определить тепловой КПД двигателя, работающего по циклу Карно. Продолжайте читать, чтобы узнать, что такое цикл Карно, как решить уравнение эффективности Карно и почему вам не следует использовать этот тип двигателя в своем автомобиле.

Что такое тепловой двигатель Карно?

Тепловая машина Карно работает по циклу Карно, наиболее эффективному процессу теплового двигателя, разрешенному законами термодинамики. В этом цикле двигатель выполняет четыре последовательных процесса, а затем возвращается в исходное состояние.

Сам двигатель состоит из двух неподвижных тел и рабочего тела (жидкость паровое тело). Два неподвижных тела имеют постоянную температуру; первая, называемая «печь», имеет высокую температуру Th , а вторая, называемую «холодильником», — низкотемпературную Tc .

Четыре фазы цикла Карно:

1. Изотермическое расширение при Th . Рабочее вещество расширяется при постоянной температуре Th , выполняя работу с окружающей средой.

2. Адиабатическое расширение . Рабочее вещество расширяется дальше, воздействуя на окружающую среду, но теряет часть своей внутренней энергии. Потеря энергии означает охлаждение до температуры Tc .

3. Изотермическое сжатие при Tc . Окружающие выполняют работу над рабочим телом, сжимая его при постоянной температуре Tc . Поскольку давление ниже, чем на шаге 1, объем работы меньше, чем работа, произведенная тогда.

4. Адиабатическое сжатие . Окружающая среда продолжает работать над рабочим веществом, сжимая его еще больше. Сжатие приводит к повышению температуры до Th . В конце шага 4 рабочее вещество находится точно в том же положении, что и до шага 1.

Уравнение эффективности Карно

Двигатель Карно — самый эффективный тепловой двигатель, который можно построить. Чтобы найти его КПД η , необходимо применить следующее уравнение:

η = (Th - Tc) / Th * 100%

И Th , и Tc являются абсолютными температурами (выраженными в Кельвинах).

Например, вы можете попытаться вычислить КПД Карно двигателя, работающего между двумя телами: одно при температуре 25 ° C, а другое при 135 ° C. Чтобы найти результат, вам необходимо выполнить следующие действия:

1. Используйте преобразователь температуры для перевода 25 ° C в градусы Кельвина. Вы также можете произвести расчеты вручную; в данном случае Tc = 25 + 273,15 = 298,15 К .

2. Повторите шаг 1 для температуры горячего резервуара. В данном случае Th = 135 + 273.15 = 408,15 К .

3. Введите эти значения в уравнение эффективности Карно:

η = (Th - Tc) / Th * 100%

η = (408,15 - 298,15) / 408,15 * 100%

η = 110 / 408,15 * 100%

η = 26,95%

4. КПД Карно равен 26,95%. Обязательно проверьте правильность результата с помощью этого калькулятора теплового КПД!

Можно ли построить двигатель Карно?

Двигатель Карно представляет собой идеализированный вариант теплового двигателя.Тем не менее теоретически можно было бы построить двигатель по модели двух резервуаров с постоянными температурами и рабочим телом.

Причина, по которой двигатель не имеет практического применения, заключается в продолжительности каждого процесса. Изотермические процессы идут ужасно медленно; Прежде чем действительно произойдет теплопередача, потребуется огромное количество времени. Как заключил Шредер, «не утруждайте себя установкой двигателя Карно в свой автомобиль. Это увеличит расход топлива, но пешеходы будут обгонять вас по шоссе.»

4.5 Цикл Карно — Университетская физика, том 2

Цели обучения

• Опишите цикл Карно с ролями всех четырех задействованных процессов
• Краткое описание принципа Карно и его значения
• Продемонстрируйте эквивалентность принципа Карно и второго начала термодинамики

В начале 1820-х годов Сади Карно (1786–1832), французский инженер, заинтересовался повышением эффективности практических тепловых двигателей.В 1824 году его исследования привели его к предложению гипотетического рабочего цикла с максимально возможной эффективностью между одними и теми же двумя резервуарами, известного теперь как цикл Карно . Двигатель, работающий в этом цикле, называется двигателем Карно . Цикл Карно имеет особое значение по ряду причин. На практике этот цикл представляет собой обратимую модель паровой электростанции и холодильника или теплового насоса. Тем не менее, это также очень важно с теоретической точки зрения, поскольку играет важную роль в разработке другого важного положения второго закона термодинамики.Наконец, поскольку в его работе задействованы только два резервуара, его можно использовать вместе со вторым законом термодинамики для определения шкалы абсолютной температуры, которая действительно не зависит от какого-либо вещества, используемого для измерения температуры.

При идеальном газе в качестве рабочего вещества этапы цикла Карно, представленные на рис. 4.11, следующие.

1. Изотермическое расширение. Газ находится в тепловом контакте с тепловым резервуаром при температуре [латекс] {T} _ {\ text {h}}.[/ latex] Газ поглощает тепло [латекс] {Q} _ {\ text {h}} [/ latex] из теплового резервуара и имеет возможность изотермически расширяться, выполняя работу [латекс] {W} _ {1}. [/ latex] Поскольку внутренняя энергия [latex] {E} _ {\ text {int}} [/ latex] идеального газа является функцией только температуры, изменение внутренней энергии равно нулю, то есть [латекс] \ text {Δ} {E} _ {\ text {int}} = 0 [/ latex] во время этого изотермического расширения. Используя первый закон термодинамики, [латекс] \ text {Δ} {E} _ {\ text {int}} = Q-W, [/ latex], мы находим, что количество тепла, поглощаемого газом, равно

   [латекс] {Q} _ {\ text {h}} = {W} _ {1} = nR {T} _ {\ text {h}} \ phantom {\ rule {0.2em} {0ex}} \ text {ln} \ frac {{V} _ {N}} {{V} _ {M}}. [/ Latex]

   Рисунок 4.11 Четыре процесса цикла Карно. Предполагается, что рабочим веществом является идеальный газ, термодинамический путь которого MNOP представлен на рисунке 4.12.

   Рис. 4.12 Общая работа, выполняемая газом в цикле Карно, показана в виде площади, заключенной в контур MNOPM.

2. Адиабатическое расширение . Газ термически изолирован и ему позволено расширяться, выполняя работу [латекс] {W} _ {2}.{\ gamma -1}. [/ latex]

3. Изотермическое сжатие . Газ помещается в тепловой контакт с холодным резервуаром при температуре [латекс] {T} _ {\ text {c}} [/ latex] и изотермически сжимается. Во время этого процесса работа [латекс] {W} _ {3} [/ latex] выполняется с газом, и он отдает тепло [латекс] {Q} _ {\ text {c}} [/ latex] холоду. резервуар. Рассуждения, использованные на шаге 1, теперь дают

   [латекс] {Q} _ {\ text {c}} = nR {T} _ {\ text {c}} \ phantom {\ rule {0.2em} {0ex}} \ text {ln} \ frac {{ V} _ {O}} {{V} _ {P}}, [/ latex]

   где [латекс] {Q} _ {\ text {c}} [/ latex] — это тепло, отдаваемое газом в холодный резервуар.{\ gamma -1}. [/ latex]

   Общая работа, выполняемая газом в цикле Карно, определяется как

   .

   [латекс] W = {W} _ {1} + {W} _ {2} — {W} _ {3} — {W} _ {4}. [/ Latex]

Эта работа равна площади, ограниченной петлей, показанной на диаграмме pV на рис. 4.12. Поскольку начальное и конечное состояния системы одинаковы, изменение внутренней энергии газа в цикле должно быть нулевым, то есть [latex] \ text {Δ} {E} _ {\ text {int} } = 0 [/ латекс]. Тогда первый закон термодинамики дает

[латекс] W = Q- \ text {Δ} {E} _ {\ text {int}} = \ left ({Q} _ {\ text {h}} — {Q} _ {\ text {c} } \ right) -0, [/ latex]

и

[латекс] W = {Q} _ {\ text {h}} — {Q} _ {\ text {c}}.[/ латекс]

Чтобы определить эффективность этого движка, сначала разделим [latex] {Q} _ {\ text {c}} \ phantom {\ rule {0.2em} {0ex}} \ text {by} \ phantom {\ rule { 0.2em} {0ex}} {Q} _ {\ text {h}}: [/ latex]

[латекс] \ frac {{Q} _ {\ text {c}}} {{Q} _ {\ text {h}}} = \ frac {{T} _ {\ text {c}}} {{ T} _ {\ text {h}}} \ phantom {\ rule {0.2em} {0ex}} \ frac {\ text {ln} {V} _ {O} \ text {/} {V} _ {P }} {\ text {ln} {V} _ {N} \ text {/} {V} _ {M}}. [/ latex]

Когда адиабатическая постоянная из шага 2 делится на таковую из шага 4, мы находим

[латекс] \ frac {{V} _ {O}} {{V} _ {P}} = \ frac {{V} _ {N}} {{V} _ {M}}.[/ латекс]

Подставляя это в уравнение для [latex] {Q} _ {\ text {c}} \ text {/} {Q} _ {\ text {h}}, [/ latex], получаем

[латекс] \ frac {{Q} _ {\ text {c}}} {{Q} _ {\ text {h}}} = \ frac {{T} _ {\ text {c}}} {{ T} _ {\ text {h}}}. [/ Latex]

Наконец, с помощью уравнения 4.2 мы находим, что эффективность этого идеального газового двигателя Карно определяется как

[латекс] e = 1- \ frac {{T} _ {\ text {c}}} {{T} _ {\ text {h}}}. [/ Latex]

Двигатель не обязательно должен соответствовать циклу двигателя Карно.Однако все двигатели имеют одинаковый эффект net , а именно поглощение тепла из горячего резервуара, выполнение работы и отвод тепла в холодный резервуар. Это заставляет нас задаться вопросом: имеют ли все обратимые циклы, действующие между одними и теми же двумя резервуарами, одинаковую эффективность? Ответ на этот вопрос исходит из второго закона термодинамики, обсуждавшегося ранее: Все реверсивные двигательные циклы производят точно такой же КПД . Кроме того, как и следовало ожидать, все настоящие двигатели, работающие между двумя резервуарами, менее эффективны, чем реверсивные двигатели, работающие между теми же двумя резервуарами.Это тоже следствие второго закона термодинамики, показанного ранее.

Цикл холодильника Карно на идеальном газе представлен диаграммой pV на рис. 4.13. Это двигатель Карно, работающий в обратном направлении. Холодильник извлекает тепло [латекс] {Q} _ {\ text {c}} [/ latex] из холодного резервуара в [latex] {T} _ {\ text {c}} [/ latex], когда идеальный газ расширяется изотермически. Затем газ сжимается адиабатически до тех пор, пока его температура не достигнет [латекса] {T} _ {\ text {h}}, [/ latex], после чего изотермическое сжатие газа приводит к выделению тепла [латекс] {Q} _ {\ text {h}} [/ latex] сбрасывается в высокотемпературный резервуар в [latex] {T} _ {\ text {h}}.[/ latex] Наконец, цикл завершается адиабатическим расширением газа, в результате чего его температура падает до [latex] {T} _ {\ text {c}}. [/ latex]

Рис. 4.13 Работа, проделанная с газом в одном цикле холодильника Карно, показана в виде площади, ограниченной контуром MPONM.

Работа, проделанная на идеальном газе, равна площади, ограниченной траекторией на диаграмме pV . По первому закону эта работа отнесена к

.

[латекс] W = {Q} _ {\ text {h}} — {Q} _ {\ text {c}}.[/ латекс]

Анализ, аналогичный анализу, проведенному для двигателя Карно, дает

[латекс] \ frac {{Q} _ {\ text {c}}} {{T} _ {\ text {c}}} = \ frac {{Q} _ {\ text {h}}} {{ T} _ {\ text {h}}}. [/ Latex]

В сочетании с уравнением 4.3 это дает

[латекс] {K} _ {\ text {R}} = \ frac {{T} _ {\ text {c}}} {{T} _ {\ text {h}} — {T} _ {\ текст {c}}} [/ latex]

для КПД идеального газового холодильника Карно. Аналогичным образом мы можем вычислить коэффициент полезного действия теплового насоса Карно как

[латекс] {K} _ {\ text {P}} = \ frac {{Q} _ {\ text {h}}} {{Q} _ {\ text {h}} — {Q} _ {\ текст {c}}} = \ frac {{T} _ {\ text {h}}} {{T} _ {\ text {h}} — {T} _ {\ text {c}}}.[/ латекс]

Мы только что нашли уравнения, представляющие КПД двигателя Карно и КПД холодильника Карно или теплового насоса Карно, при условии, что в обоих устройствах в качестве рабочего вещества используется идеальный газ. Однако эти уравнения являются более общими, чем следует из их вывода. Вскоре мы покажем, что оба они действительны, независимо от того, какое рабочее вещество используется.

Карно обобщил свое исследование двигателя Карно и цикла Карно в то, что теперь известно как принцип Карно :

Принцип Карно

Ни один двигатель, работающий между двумя резервуарами при постоянной температуре, не может иметь большей эффективности, чем реверсивный двигатель.

Этот принцип можно рассматривать как еще одно утверждение второго закона термодинамики и можно показать, что он эквивалентен утверждению Кельвина и утверждению Клаузиуса.

Пример

Двигатель Карно

Двигатель Карно имеет КПД 0,60, а температура его холодного резервуара составляет 300 К. а) Какова температура горячего резервуара? (b) Если двигатель выполняет 300 Дж работы за цикл, сколько тепла удаляется из высокотемпературного резервуара за цикл? (c) Сколько тепла отводится в низкотемпературный резервуар за цикл?

Стратегия

Из температурной зависимости теплового КПД двигателя Карно можно найти температуру горячего резервуара.Затем, исходя из определения эффективности, мы можем найти тепло, отводимое при задании работы, выполняемой двигателем. Наконец, экономия энергии приведет к тому, сколько тепла должно быть сброшено в холодный резервуар.

Решение

1. Из [latex] e = 1- {T} _ {\ text {c}} \ text {/} {T} _ {\ text {h}} [/ latex] получаем

[латекс] 0.60 = 1- \ frac {300 \ phantom {\ rule {0.2em} {0ex}} \ text {K}} {{T} _ {\ text {h}}}, [/ latex]

, чтобы температура горячего резервуара была

[латекс] {T} _ {\ text {h}} = \ frac {300 \ phantom {\ rule {0.2em} {0ex}} \ text {K}} {1-0.60} = 750 \ phantom {\ rule {0.2em} {0ex}} \ text {K}. [/ Latex]

• По определению, КПД двигателя [латекс] e = W \ text {/} Q [/ latex], так что тепло, отводимое от высокотемпературного резервуара за цикл, составляет

[латекс] {Q} _ {\ text {h}} = \ frac {W} {e} = \ frac {300 \ phantom {\ rule {0.2em} {0ex}} \ text {J}} { 0.60} = 500 \ phantom {\ rule {0.2em} {0ex}} \ text {J}. [/ Latex]

• Из первого закона тепло, отдаваемое двигателем в низкотемпературный резервуар за цикл, равно

[латекс] {Q} _ {\ text {c}} = {Q} _ {\ text {h}} — W = 500 \ phantom {\ rule {0.2em} {0ex}} \ text {J} -300 \ phantom {\ rule {0.2em} {0ex}} \ text {J} = 200 \ phantom {\ rule {0.2em} {0ex}} \ text {J }. [/ latex]

Значение

Двигатель Карно имеет максимально возможную эффективность преобразования тепла в работу между двумя резервуарами, но это не обязательно означает, что он эффективен [latex] 100 \ text {%} [/ latex]. По мере увеличения разницы температур горячего и холодного резервуаров эффективность двигателя Карно увеличивается.

Пример

A Тепловой насос Carnot

Представьте, что тепловой насос Карно работает при наружной температуре [латекс] 0 \ phantom {\ rule {0.2em} {0ex}} \ text {° C} [/ latex] и внутренняя температура [латекс] 20,0 \ phantom {\ rule {0.2em} {0ex}} \ text {° C} [/ latex]. Какие работы нужны, если во внутреннюю часть дома доставляется тепло 30,0 кДж?

Стратегия

Поскольку предполагается, что тепловой насос является насосом Карно, его коэффициент полезного действия определяется как [латекс] {K} _ {\ text {P}} = {Q} _ {\ text {h}} \ text {/} W = {T} _ {\ text {h}} \ text {/} \ left ({T} _ {\ text {h}} — {T} _ {\ text {c}} \ right). [/ латекс] Таким образом, мы можем найти работу W из подводимого тепла [латекс] {Q} _ {\ text {h}}.[/ латекс]

Решение

Необходимая работа получена от

[латекс] W = {Q} _ {\ text {h}} \ text {/} {K} _ {\ text {P}} = {Q} _ {\ text {h}} \ left ({T } _ {\ text {h}} — {T} _ {\ text {c}} \ right) \ text {/} {T} _ {\ text {h}} = 30 \ phantom {\ rule {0.2em } {0ex}} \ text {kJ} \ phantom {\ rule {0.2em} {0ex}} × \ phantom {\ rule {0.2em} {0ex}} \ left (293 \ phantom {\ rule {0.2em} {0ex}} \ text {K} -273 \ phantom {\ rule {0.2em} {0ex}} \ text {K} \ right) \ text {/} 293 \ phantom {\ rule {0.2em} {0ex} } \ text {K} = 2 \ phantom {\ rule {0.2em} {0ex}} \ text {kJ}. [/ latex]

Значение

Отметим, что эта работа зависит не только от тепла, подаваемого в дом, но и от температуры снаружи и внутри.Зависимость от температуры на улице делает их нецелесообразными для использования в областях, где температура на улице намного ниже комнатной.

С точки зрения затрат на электроэнергию тепловой насос является очень экономичным средством обогрева зданий (рис. 4.14). Сравните этот метод с прямым преобразованием электрической энергии в тепло с помощью резистивных нагревательных элементов. В этом случае одна единица электроэнергии дает не более одной единицы тепла. К сожалению, у тепловых насосов есть проблемы, которые ограничивают их полезность.Они довольно дороги в приобретении по сравнению с резистивными нагревательными элементами, и, как показывает коэффициент полезного действия теплового насоса Carnot, они становятся менее эффективными при снижении наружной температуры. Фактически, ниже [латекс] –10 \ phantom {\ rule {0.2em} {0ex}} \ text {° C} [/ latex] выделяемое ими тепло меньше энергии, используемой для их работы.

Рис. 4.14 Фотография теплового насоса (большая коробка), расположенного вне дома. Этот тепловой насос расположен в районе с теплым климатом, например на юге США, поскольку он был бы слишком неэффективным в северной части Соединенных Штатов.(кредит: модификация работы Питера Стивенса)

Проверьте свое понимание

Двигатель Карно работает между резервуарами в [latex] 400 \ phantom {\ rule {0.2em} {0ex}} \ text {° C} [/ latex] и [latex] 30 \ phantom {\ rule {0.2em} { 0ex}} \ text {° C} [/ латекс]. а) Каков КПД двигателя? (b) Если двигатель выполняет 5,0 Дж работы за цикл, сколько тепла за цикл он поглощает из высокотемпературного резервуара? (c) Сколько тепла за цикл отводится в резервуар с холодной температурой? (d) Какие температуры в холодном резервуаре дадут минимальную и максимальную эффективность?

Показать решение

а.[латекс] e = 1- {T} _ {\ text {c}} \ text {/} {T} _ {\ text {h}} = 0,55 [/ latex]; б. [латекс] {Q} _ {\ text {h}} = eW = 9.1 \ phantom {\ rule {0.2em} {0ex}} \ text {J} [/ latex]; c. [латекс] {Q} _ {\ text {c}} = {Q} _ {\ text {h}} — W = 4.1 \ phantom {\ rule {0.2em} {0ex}} \ text {J} [/ латекс]; d. [латекс] -273 \ phantom {\ rule {0.2em} {0ex}} \ text {°} \ text {C} [/ latex] и [latex] 400 \ phantom {\ rule {0.2em} {0ex}} \ text {°} \ text {C} [/ latex]

Проверьте свое понимание

Холодильник Карно работает между двумя тепловыми резервуарами, температура которых составляет [латекс] 0 \ phantom {\ rule {0.2em} {0ex}} \ text {°} \ text {C} [/ latex] и [latex] 25 \ phantom {\ rule {0.2em} {0ex}} \ text {°} \ text {C} [/ латекс]. а) Каков коэффициент полезного действия холодильника? (b) Если с рабочим телом за цикл выполняется 200 Дж работы, сколько тепла за цикл отбирается из холодного резервуара? (c) Сколько тепла за цикл сбрасывается в горячий резервуар?

Показать решение

а. [латекс] {K} _ {\ text {R}} = {T} _ {\ text {c}} \ text {/} \ left ({T} _ {\ text {h}} — {T} _ {\ text {c}} \ right) = 10,9 [/ латекс]; б.[латекс] {Q} _ {\ text {c}} = {K} _ {\ text {R}} W = 2,18 \ phantom {\ rule {0.2em} {0ex}} \ text {kJ} [/ latex ]; c. [латекс] {Q} _ {\ text {h}} = {Q} _ {\ text {c}} + W = 2.38 \ phantom {\ rule {0.2em} {0ex}} \ text {кДж} [/ латекс]

Сводка

• Цикл Карно является наиболее эффективным двигателем для обратимого цикла, разработанного между двумя резервуарами.
• Принцип Карно — это еще один способ сформулировать второй закон термодинамики.

Концептуальные вопросы

Следует ли повышать или понижать температуру горячего резервуара для повышения эффективности двигателя Карно? А как насчет холодного резервуара?

Показать решение

Чтобы повысить эффективность, температура горячего резервуара должна быть повышена, а холодного резервуара должна быть максимально понижена.Это можно увидеть в уравнении 4.3.

Как можно спроектировать двигатель Карно с эффективностью [latex] 100 \ text {%} [/ latex]?

Какие типы процессов происходят в цикле Карно?

Показать решение

адиабатические и изотермические процессы

Проблемы

Температура холодного и горячего резервуаров, между которыми работает холодильник Карно, составляет [латекс] -73 \ phantom {\ rule {0.2em} {0ex}} \ text {°} \ text {C} [/ latex] и [ латекс] 270 \ phantom {\ rule {0.2em} {0ex}} \ text {° C} [/ latex] соответственно. Каков его коэффициент полезного действия?

Показать решение

Предположим, холодильник Карно работает между [latex] {T} _ {\ text {c}} \ phantom {\ rule {0.2em} {0ex}} \ text {и} \ phantom {\ rule {0.2em} {0ex }} {T} _ {\ text {h}}. [/ Latex] Вычислите объем работы, необходимый для извлечения 1,0 Дж тепла из холодного резервуара, если (a) [latex] {T} _ {\ text {c }} = 7 \ phantom {\ rule {0.2em} {0ex}} \ text {°} \ text {C} [/ latex], [latex] {T} _ {\ text {h}} = 27 \ phantom {\ rule {0.2em} {0ex}} \ text {°} \ text {C} [/ latex]; (б) [латекс] {T} _ {\ text {c}} = — 73 \ phantom {\ rule {0.2em} {0ex}} \ text {°} \ text {C} [/ latex], [latex] {T} _ {\ text {h}} = 27 \ phantom {\ rule {0.2em} {0ex}} \ text {°} \ text {C;} [/ latex] (c) [латекс] {T} _ {\ text {c}} = — 173 \ phantom {\ rule {0.2em} {0ex}} \ text {°} \ text {C} [/ latex], [latex] {T} _ {\ text {h}} = 27 \ phantom {\ rule {0.2em} {0ex}} \ text {°} \ text { C} [/ латекс]; и (d) [латекс] {T} _ {\ text {c}} = — 273 \ phantom {\ rule {0.2em} {0ex}} \ text {°} \ text {C} [/ latex], [ латекс] {T} _ {\ text {h}} = 27 \ phantom {\ rule {0.2em} {0ex}} \ text {°} \ text {C} [/ latex].

Двигатель Карно работает между резервуарами при 600 и 300 К.Если двигатель потребляет 100 Дж за цикл в горячем резервуаре, какова его рабочая мощность за цикл?

Показать решение

Двигатель мощностью 500 Вт управляет холодильником Карно между [латексом] -5 \ phantom {\ rule {0.2em} {0ex}} \ text {°} \ text {C} [/ latex] и [latex] 30 \ phantom {\ rule {0.2em} {0ex}} \ text {° C} [/ latex]. а) Какое количество тепла в секунду отбирается изнутри холодильника? б) Сколько тепла отводится наружному воздуху за секунду?

Нарисуйте цикл Карно на диаграмме температура-объем.

Показать решение

Тепловой насос Карно работает между [латексом] 0 \ phantom {\ rule {0.2em} {0ex}} \ text {° C} [/ latex] и [латексом] 20 \ phantom {\ rule {0.2em} {0ex }} \ text {° C} [/ латекс]. Сколько тепла отводится внутрь дома на каждые 1,0 Дж работы насоса?

Двигатель, работающий между резервуарами тепла в [латексе] 20 \ phantom {\ rule {0.2em} {0ex}} \ text {°} \ text {C} [/ latex] и [latex] 200 \ phantom {\ rule { 0.2em} {0ex}} \ text {°} \ text {C} [/ latex] извлекает 1000 Дж за цикл из горячего резервуара.а) Какую максимально возможную работу двигатель может выполнять за цикл? (б) Для этой максимальной работы, сколько тепла отводится в холодный резервуар за цикл?

Показать решение

Предположим, что двигатель Карно может работать между двумя резервуарами как тепловой двигатель или как холодильник. Как коэффициент полезного действия холодильника связан с эффективностью теплового двигателя?

Двигатель Карно используется для измерения температуры теплового резервуара.Двигатель работает между тепловым резервуаром и резервуаром, состоящим из воды в ее тройной точке. (a) Если 400 Дж за цикл удаляются из резервуара тепла, а 200 Дж за цикл откладываются в резервуаре тройной точки, какова температура резервуара тепла? (b) Если 400 Дж за цикл удаляются из резервуара тройной точки, а 200 Дж за цикл откладываются в резервуаре тепла, какова температура резервуара тепла?

Показать решение

Какова минимальная работа холодильника, если он должен извлекать 50 Дж за цикл изнутри морозильной камеры при [латексе] -10 \ phantom {\ rule {0.2em} {0ex}} \ text {° C} [/ latex] и отводит тепло в воздух [латекс] 25 \ phantom {\ rule {0.2em} {0ex}} \ text {° C} [/ latex] ?

Глоссарий

Цикл Карно

Цикл

, состоящий из двух изотерм при температурах двух резервуаров и двух адиабатических процессов, соединяющих изотермы

Двигатель Карно

Тепловой двигатель Карно, холодильник или тепловой насос, работающий по циклу Карно

Принцип Карно

Принцип, регулирующий эффективность или производительность теплового устройства, работающего по циклу Карно: любое обратимое тепловое устройство, работающее между двумя резервуарами, должно иметь одинаковый КПД или коэффициент производительности, больший, чем у необратимого теплового устройства, работающего между теми же двумя резервуарами

Лицензии и авторство

Цикл Карно. Автор : OpenStax College. Расположен по адресу : https://openstax.org/books/university-physics-volume-2/pages/4-5-the-carnot-cycle. Лицензия : CC BY: Attribution . Условия лицензии : Загрузите бесплатно с https://openstax.org/books/university-physics-volume-2/pages/1-introduction

3. Двигатель Карно работает в диапазоне температур 500

Расшифрованный текст изображения: 3. Двигатель Карно работает в диапазоне температур от 500 K до 300 K.Двигатель развивает мощность 2400 Вт, которая используется для привода холодильника Карно, работающего в диапазоне температур от 500 K до 200 K. (a) (5 баллов) Показать, что двигатель отводит 3600 Дж тепла в холодный резервуар в секунду? (b) (5 баллов) Сколько тепла холодильник отдает горячему резервуару в секунду? (c) (5 баллов) Каково изменение энтропии горячего резервуара в секунду? Обратите внимание, что двигатель и холодильник используют один и тот же горячий резервуар.
Термодинамика (16% (a) Используйте диаграмму P-V, чтобы проиллюстрировать цикл Карно.Четко укажите тип процесса и чистую работу, выполняемую газом в каждом цикле. Что особенного в цикле Карно? (6%) (b) Тепловой двигатель Карно забирает 774 Дж тепла из высокотемпературного резервуара и отводит 458 Дж в низкотемпературный резервуар. (I) Рассчитайте работу, выполняемую двигателем Карно. (296) (ii) Рассчитайте КПД двигателя по Карно. (2%) (iii) Предположим, что низкотемпературный резервуар имеет температуру 20 ° C. Рассчитайте температуру высокотемпературного резервуара.(396) (iv) Производитель заявляет, что он создал тепловой двигатель, который отбирает 1000 Дж тепла из того же высокотемпературного резервуара, рассчитанного в (iii), и отводит 900 Дж тепла в низкотемпературный резервуар с температурой 20 ° C. Его заявление нарушает второй закон термодинамики? Поясните свой ответ. (3%)
Z. (1870, Tnermodynamics (a) Напишите уравнение для первого закона термодинамики. Четко определите все символы, которые вы используете в уравнении. (2%) (b) Два моля одноатомного идеального газа изначально находятся в состоянии A и имеют объем 0.05 м3 и температуре 25 ° C. Газ расширяется при постоянном давлении po до конечного объема 0,1 м3. 0,05 0,1 (i) Рассчитайте значение давления po- (3%) (ii) Рассчитайте работу, совершаемую газом, когда газ расширяется из состояния A в состояние B. (296) (iii) Рассчитайте тепло, поглощаемое газом в описанном выше процессе. (4%) (c) Предположим, что одноатомный идеальный газ расширяется из того же начального состояния в такое же конечное состояние по другому пути ACB, как показано на рисунке ниже 1.1 po PoT A 0.05 0,1 (i) Рассчитайте работу, совершаемую газом, когда газ расширяется по пути ACB. (296) (ii) Рассчитайте тепло, поглощаемое газом, когда газ расширяется по пути ACB (2%) (iii) Студент утверждает следующее для идеального газа, расширяющегося двумя разными путями: «Если начальное и конечное состояния газ одинаковы для двух путей, поглощаемое тепло всегда одно и то же «. Прав ли ученик? Дайте адекватное объяснение в поддержку своего ответа. (3%)

Предыдущий вопрос Следующий вопрос

Эффективность Карно — Энергетическое образование

Рисунок 1: Горячий источник обеспечивает энергию, необходимую для выполнения работы в термодинамическом процессе.Эффективность Карно зависит только от температуры горячего источника и холодной раковины. ^[1]

КПД Карно описывает максимальный тепловой КПД, которого может достичь тепловой двигатель в соответствии со вторым законом термодинамики. Этот закон был выведен Сади Карно в 1824 году. Карно размышлял над идеей максимальной эффективности в тепловом двигателе, задаваясь вопросом, может ли эффективность теплового двигателя приближаться к 100%, или существует верхний предел, который нельзя превышать? ^[2] Оказалось, что существует максимальное значение, и Карно разработал идеальный двигатель, который теоретически мог бы обеспечить такую ​​эффективность, известный как двигатель Карно.Максимальная эффективность, известная как эффективность Карно [math] \ eta_ {max} [/ math], зависит только от температур горячего источника и холодного стока [math] T_H [/ math] и [math] T_L [ / math], как показано на рисунке 1, и задается уравнением ниже ^[3]

(1)

[математика] \ eta_ {max} = 1- \ frac {T_L} {T_H} [/ math]

Второй закон требует, чтобы отходящее тепло производилось в термодинамическом процессе, в котором работа выполняется источником тепла. Такой процесс описывается уравнением

(2)

[математика] Q_H = Q_L + W [/ математика]

С тепловым КПД

(3)

[математика] \ eta = \ frac {W} {Q_H} [/ математика]

Где:

• [math] Q_H [/ math] — тепло, подаваемое в систему от топлива
• [math] Q_L [/ math] — тепло, отдаваемое системой в поглотитель холода, известное как отработанное тепло.
• [math] W [/ math] — полезная работа, выполняемая системой.

Следовательно, КПД Карно дает максимально достижимый объем работы от любого теплового двигателя.Из уравнения 1 видно, что эффективность может быть увеличена путем увеличения [math] T_H [/ math] или уменьшения [math] T_L [/ math]. Поэтому в идеале было бы желательно сделать температуру холодного радиатора равной абсолютному нулю, но, как известно, это невозможно. На самом деле холодный сток — это окружающая среда Земли. Это означает, что холодная раковина имеет температуру около 280-300 Кельвинов, а горячие источники — от горящего топлива с температурой около 1100 Кельвинов (хотя исследования всегда пытаются поднять эту температуру выше).Эти температуры дают значение эффективности Карно [math] \ eta_ {max} \ приблизительно 70 \% [/ math] или около того. ^[4]

Двигатель Карно

Двигатель Карно — это идеализированный двигатель, использующий процессы с обратимыми механическими и тепловыми взаимодействиями. Это означает, что двигатель может совершать свои движения и возвращаться в исходное состояние без увеличения энтропии (без потерь энергии). Чтобы двигатель мог вернуться в исходное состояние без увеличения энтропии , двигатель должен находиться в тепловом равновесии на протяжении всего цикла.Условия существования такого двигателя: ^[2]

• Механические взаимодействия : энергия не теряется в виде трения, следовательно, во время этих механических процессов ([math] Q = 0 [/ math]), известных как адиабатический процесс, теплопередача отсутствует.

• Тепловые взаимодействия : передача тепла бесконечно медленная (известная как квазистатическая ). Это означает, что разница температур между системой и теплом на входе / выходе почти одинакова, что приводит к передаче тепла в течение бесконечного количества времени.Эти обмены должны выполняться, поддерживая постоянную внутреннюю температуру системы, что называется изотермическим процессом.

Двигатель, который обладает только этими свойствами, известен как двигатель Карно, который является «полностью реверсивным двигателем» и демонстрирует максимальный тепловой КПД ([math] \ eta_ {max} [/ math]) и, если он работает как холодильник, коэффициент полезного действия ([math] K_ {max} [/ math]). Хотя такой двигатель мог бы максимизировать эффективность, с точки зрения эффективности он ужасно непрактичен, поскольку его идеализированные процессы требуют очень много времени для выполнения значительного объема работы.По словам Шредера, «не беспокойтесь об установке двигателя Карно в свой автомобиль; хотя это увеличит расход топлива, вас будут обгонять пешеходы». ^[5]

Чтобы узнать больше о двигателе Карно, посетите NASA или Hyperphysics.

Список литературы

1. ↑ Wikimedia Commons [Online], Доступно: http://upload.wikimedia.org/wikipedia/en/a/a2/Heat_engine.png
2. ↑ ^{2,0 2,1} Р. Д. Найт, «Пределы эффективности» в книге «Физика для ученых и инженеров: стратегический подход», 3-е изд.Сан-Франциско, США: Pearson Addison-Wesley, 2008, глава 19, раздел 5, стр. 540-542.
3. ↑ Hyperphysics, Цикл Карно [Online], Доступно: http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/carnot.html
4. ↑ Из Министерства энергетики США https://www.energy.gov/fe/how-gas-turbine-power-plants-work, по состоянию на 21 июля 2020 г.
5. ↑ McMaster Physics and Astronomy, Цикл Карно [Online], Доступно: http://www.physics.mcmaster.ca/~morozov/3K03/Lecture9.pdf

КПД Карно — обзор

4.5 Транспортировка

Автомобильные двигатели имеют КПД Карно около 60%, но на практике КПД составляет около 25%. Пока двигатель внутреннего сгорания (Отто) продолжает использоваться, значительное повышение эффективности маловероятно, но все же возможна значительная дополнительная экономия. Альтернативы включают электромобили и автомобили на топливных элементах. Транспортный сектор важен, потому что на транспорт приходится 27% общего потребления энергии в Соединенных Штатах.Большая часть энергии, используемой для транспортировки, основана на нефти. Это означает, что страны-импортеры зависят от добросовестности стран-экспортеров и от их постоянной готовности поставлять нефть по относительно низким ценам. В то время как Соединенные Штаты платят одни из самых высоких цен за нефть, как потому, что отечественная нефть дороже, чем импортная нефть, так и потому, что средняя стоимость транспортировки велика, цена бензина на заправке является одной из самых низких в мире. В основном это связано с различиями в налоговых структурах между странами.

В Европе автомобили обычно меньше, чем в Соединенных Штатах, из-за более высоких цен на энергоносители, которые потребители платят за бензин и дизельное топливо (из-за высоких местных налогов). В меньших по размеру автомобилях для производства требуется меньше материалов, а из-за меньшего веса они дешевле в эксплуатации. Многие водители в Соединенных Штатах не хотят покупать маленькие автомобили, потому что они обеспокоены безопасностью (это, по-видимому, частично ответственно за бум продаж внедорожников или внедорожников).По иронии судьбы, хотя люди во внедорожниках с меньшей вероятностью погибнут или получат травмы при прямом лобовом, заднем или боковом столкновении, общий уровень смертности среди внедорожников выше, чем в автомобилях меньшего размера, из-за большого количества смертельных случаев в авариях с опрокидыванием. относительно высокая вероятность возникновения.

Американские автомобили намного легче, чем в 1970-х годах, что является прямым результатом первого энергетического кризиса. Обычный пригородный автомобиль имеет пробег около 30 миль / галлон. Понятно, что вес большинства автомобилей можно было бы еще уменьшить.Уравновешивающая тенденция — продавать все больше и больше внедорожников и пикапов. Эти автомобили весят больше обычных автомобилей и, как следствие, имеют меньший пробег. К 2000 году менее половины всех транспортных средств, приобретенных для личного пользования в Соединенных Штатах, были обычными автомобилями. Большой внедорожник может иметь пробег всего 17 миль / галлон, а маленький пикап — 25 миль / галлон. Причина увеличения пробега у автомобилей законодательная — Конгресс принял стандарты корпоративной средней экономии топлива (CAFE) после первого энергетического кризиса, чтобы заставить производителей увеличить пробег, и это сработало.Рост количества внедорожников и пикапов порадовал производителей, поскольку на эти автомобили не распространялись стандарты CAFE. Кроме того, низкие средние цены на энергоносители в конце 1990-х годов убаюкивали водителей, ожидая, что дешевая импортная нефть останется доступной. Политическое давление в пользу повышения стандартов CAFE ослабло, и пробег автомобилей остался на прежнем уровне. В результате в среднем автопарке американских автомобилей пробег уменьшился. Самый низкий средний пробег автопарка был достигнут примерно в 1989 году. Уменьшился пробег даже импортных автомобилей.Исходя из истории, только законодательный мандат будет успешным в увеличении пробега при отсутствии внешних угроз, таких как гигантский скачок мировых цен на нефть.

До 1970-х годов большинство американских автомобилей были заднеприводными; теперь большинство из них — передний привод, что более энергоэффективно. Большинство современных автомобильных двигателей являются более эффективными двигателями с верхним расположением распредвала. Однако гораздо больше энергии можно было бы сэкономить, продолжая искать способы уменьшения лобового сопротивления и устанавливая усовершенствованные автоматические трансмиссии с электронным управлением.Другие меры, некоторые из которых были введены частично, включают улучшенные системы впрыска топлива, улучшенные шины, улучшенные смазочные материалы и снижение трения двигателя. Все эти меры являются хорошими мерами по сохранению, поскольку они бесплатны или дешевы (низкая стоимость означает короткую окупаемость).

Стремление Калифорнии к автомобилям, не загрязняющим окружающую среду, привело к установлению квот на автомобили с низким уровнем выбросов. Было предложено много идей для автомобилей, которые работают на электричестве или энергии, накопленной в высокотехнологичных маховиках на основе эпоксидной смолы.Большие надежды Калифорнии на так называемые автомобили с нулевым уровнем выбросов были явно неоправданными, и было разработано или произведено лишь несколько электромобилей. Были трудности с конструкцией аккумуляторов (обычные свинцово-кислотные автомобильные аккумуляторы довольно много весят). Никель-металлогидридные батареи — очевидная предпочтительная технология для электромобилей. Кроме того, автомобили с батарейным питанием плохо работают при низких температурах окружающей среды, поэтому эти автомобили не распространены за пределами юго-запада.Еще одним ударом по автомобилям с батарейным питанием является отсутствие зарядной инфраструктуры. И такие транспортные средства на самом деле не имеют выбросов ноль , потому что газ, нефть или уголь нужно сжигать, чтобы произвести электричество, используемое для подзарядки аккумуляторов.

Поиски в Калифорнии увеличили перспективы для автомобилей с низким уровнем выбросов, которые являются гибридными (комбинированные бензиновые двигатели и электрические системы, которые работают вместе). Гибридные функции, обеспечивающие экономию топлива, включают автоматическое отключение двигателя при остановках и рекуперативное торможение (преобразование работы, выполняемой при торможении, в энергию, запасенную в батарее).В гибридах бензиновый двигатель работает только с максимальной эффективностью или близкой к ней, а избыток энергии заряжает батареи. Поскольку топливо обычное, а электрическая система перезаряжается при использовании, нет необходимости в специальной инфраструктуре, как в случае с чистой электричеством. Honda представила первый коммерческий гибрид Insight, за которым быстро последовала Toyota с Prius. Honda начала продавать гибридные модели Civic.

Топливные элементы, представляющие собой устройства, сочетающие топливо (в идеале водород) с кислородом из воздуха без горения, как ожидается, в ближайшем будущем будут снабжать автомобили энергией.Если бы водород производился электролизом с использованием солнечной энергии, такой автомобиль действительно имел бы нулевые выбросы (за пределами воды, полученной из соединения водорода и кислорода). Топливные элементы использовались в прошлом для транспортировки, но обычно жидкометаллические топливные элементы в автобусах из-за относительно высокой температуры эксплуатации (от 300 до 1200 ° C). Разработка низкотемпературных топливных элементов с протонообменной мембраной привела производителей автомобилей к инженерным разработкам. Обычно они на 50% эффективнее преобразовывают топливо в энергию, что примерно в два раза эффективнее двигателей Отто.(Очень маленькие топливные элементы используются в качестве альтернативы аккумуляторным блокам в некоторых электронных устройствах.)

Вариант топливных элементов страдает от отсутствия инфраструктуры для подачи водорода в транспортные средства и проблемы с транспортировкой достаточного количества водорода. Водород — это разбавленный газ, и он имеет гораздо меньшее количество энергии на единицу объема, чем жидкое топливо.