Изменение физических величин в процессах, часть 1. 1.Температуру холодильника идеальной тепловой машины уменьшили, оставив температуру нагревателя прежней
1.Температуру холодильника идеальной тепловой машины уменьшили, оставив температуру нагревателя прежней. Количество теплоты, полученное газом от нагревателя за цикл, не изменилось. Как изменились при этом КПД тепловой машины, количество теплоты, отданное газом за цикл холодильнику, и работа газа за цикл?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась;
2) уменьшилась;
3) не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| КПД тепловой машины | Количество теплоты, отданное газом
холодильнику за цикл работы | Работа газа за цикл |
2. Температуру холодильника идеальной тепловой машины увеличили, оставив температуру нагревателя прежней. Количество теплоты, полученное газом от нагревателя за цикл, не изменилось. Как изменились при этом КПД тепловой машины, количество теплоты, отданное газом за цикл холодильнику, и работа газа за цикл?
Температуру холодильника идеальной тепловой машины увеличили, оставив температуру нагревателя прежней. Количество теплоты, полученное газом от нагревателя за цикл, не изменилось. Как изменились при этом КПД тепловой машины, количество теплоты, отданное газом за цикл холодильнику, и работа газа за цикл?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась;
2) уменьшилась;
3) не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| КПД тепловой машины | Количество теплоты, отданное газом
холодильнику за цикл работы | Работа газа за цикл |
3.В закрытом сосуде находится идеальный газ. Как при охлаждении сосуда с газом изменятся величины: давление газа, его плотность и внутренняя энергия?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась;
2) уменьшилась;
3) не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Давление газа | Плотность газа | Внутренняя энергия газа |
4.В сосуде под поршнем находится идеальный газ. Если при нагревании газа его давление остается постоянным, то как изменятся величины: объем газа, его плотность и внутренняя энергия?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась;
2) уменьшилась;
3) не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Объем газа | Плотность газа | Внутренняя энергия газа |
5. Идеальный одноатомный газ переходит из состояния 1 в состояние 2 (см. диаграмму).
Идеальный одноатомный газ переходит из состояния 1 в состояние 2 (см. диаграмму).
Масса газа не меняется. Как меняются в ходе указанного на диаграмме процесса давление газа, его объем и внутренняя энергия?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается;
2) уменьшается;
3) не меняется.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Давление | Объем | Внутренняя энергия |
6.Идеальный одноатомный газ переходит из состояния 1 в состояние 2 (см. диаграмму).
Масса газа не меняется. Как меняются в ходе указанного на диаграмме процесса давление газа, его объем и внутренняя энергия?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается;
2) уменьшается;
3) не меняется.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Давление | Объем | Внутренняя энергия |
7.Установите соответствие между процессами в идеальном газе и формулами, которыми они описываются (N — число частиц, p — давление, V — объем, T — абсолютная температура, Q — количество теплоты).
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
8.В сосуде неизменного объема находится идеальный газ. Если часть газа выпустить из сосуда при постоянной температуре, то как изменятся величины: давление газа, его плотность и количество вещества в сосуде?
Для каждой величины определите соответствующий характер ее изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины.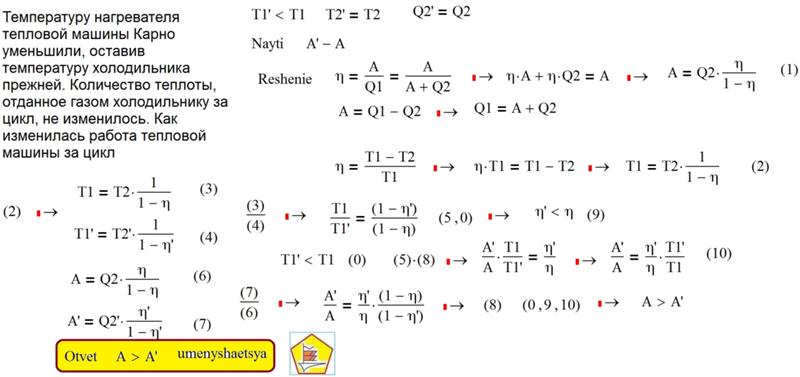 Цифры в ответе могут повторяться.
Цифры в ответе могут повторяться.
| Давление газа | Плотность газа | Количество вещества |
9.В сосуде неизменного объема находится идеальный газ. Часть газа выпускали из сосуда так, что давление оставалось неизменным. Как изменились при этом температура газа, оставшегося в сосуде, его плотность и количество вещества?
Для каждой величины определите соответствующий характер ее изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Температура газа | Плотность газа | Количество вещества |
10.В сосуде под поршнем находится 3 моля гелия. Что произойдет с давлением газа на стенки сосуда, температурой и объемом газа при его изотермическом расширении?
Что произойдет с давлением газа на стенки сосуда, температурой и объемом газа при его изотермическом расширении?
К каждому элементу первого столбца подберите соответствующий элемент из второго и внесите в строку ответов выбранные цифры под соответствующими буквами.
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ИЗМЕНЕНИЕ ВЕЛИЧИНЫ | |
| А) Давление газа
Б) Температура газа В) Объем газа | 1) Увеличивается
2) Уменьшается 3) Не изменится |
11.Используя первый закон термодинамики, установите соответствие между особенностями теплового процесса в идеальном газе и его названием.
К каждому элементу первого столбца подберите соответствующий элемент из второго и внесите в строку ответов выбранные цифры под соответствующими буквами.
| ОСОБЕННОСТИ ТЕПЛОВОГО ПРОЦЕССА | НАЗВАНИЕ ТЕПЛОВОГО ПРОЦЕССА | |
| А) Все передаваемое газу количество теплоты идет на совершение газом работы
Б) Изменение внутренней энергии газа равно количеству переданной теплоты, при этом газ не совершает работы | 1) Изохорный
2) Изотермический 3) Изобарный 4) Адиабатный |
12. Одноатомный идеальный газ неизменной массы совершает положительную работу в изотермическом процессе. Как изменяются в этом процессе объем, давление и внутренняя энергия газа? К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под со-ответствующими буквами.
Одноатомный идеальный газ неизменной массы совершает положительную работу в изотермическом процессе. Как изменяются в этом процессе объем, давление и внутренняя энергия газа? К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под со-ответствующими буквами.
Для каждой величины определите соответствующий характер изменения:
1) увеличивается;
2) уменьшается;
3) не изменяется.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Объём газа | Давление газа | Внутренняя энергия газа |
13.В закрытом сосуде находятся водяной пар и некоторое количество воды. Как изменятся при изотермическом уменьшении объема сосуда следующие три величины: давление в сосуде, масса воды, масса пара?
Для каждой величины определите соответствующий характер изменения:
1) увеличится;
2) уменьшится;
3) не изменится.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Давление в сосуде | Масса воды | Масса пара |
Пояснение. Ключом к пониманию этого задания является определение понятия насыщенного водяного пара. По определению это такой пар, который находится в динамическом равновесии с жидкостью. При изотермическом уменьшении объема сосуда с водяным паром динамическое равновесие сохранится, но при этом часть водяного пара сконденсируется.
14.Установите соответствие между физическими константами и их размерностями. К каждой позиции первого столбца подберите нужную позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
| ФИЗИЧЕСКИЕ КОНСТАНТЫ | ИХ РАЗМЕРНОСТИ | |
| А) Постоянная Больцмана
Б) Универсальная газовая постоянная | 1)
2) 3) 4) |
Пояснение. Константы встречаются в формулах в различных комбинациях с другими физическими величинами. По этой причине размерность той или иной константы может быть представлена в виде различных комбинаций размерностей других физических величин. С целью проверки правильности конечного результата полезно бывает убедиться в том, что получена правильная комбинация размерностей величин. Это задание — иллюстрация на тему о пользе правила размерностей.
Константы встречаются в формулах в различных комбинациях с другими физическими величинами. По этой причине размерность той или иной константы может быть представлена в виде различных комбинаций размерностей других физических величин. С целью проверки правильности конечного результата полезно бывает убедиться в том, что получена правильная комбинация размерностей величин. Это задание — иллюстрация на тему о пользе правила размерностей.
15.Установите соответствие между физическими величинами и приборами для их измерения. К каждой позиции первого столбца подберите нужную позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ПРИБОРЫ ДЛЯ ИХ ИЗМЕРЕНИЯ | |
| А) Давление
Б) Температура | 1) Калориметр
2) Термометр 3) Манометр 4) Динамометр |
16. В сосуде, объем которого можно изменять, находится идеальный газ. Как изменятся при адиабатическом увеличении объема сосуда следующие три величины: температура газа, его давление, концентрация молекул газа?
В сосуде, объем которого можно изменять, находится идеальный газ. Как изменятся при адиабатическом увеличении объема сосуда следующие три величины: температура газа, его давление, концентрация молекул газа?
Для каждой величины определите соответствующий характер изменения:
1) увеличится;
2) уменьшится;
3) не изменится.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Температура газа | Давление газа | Концентрация молекул газа |
Пояснение. Для анализа изменений, которые возникнут в газе, необходимо воспользоваться первым началом термодинамики и формулой, которая связывает давление газа с концентрацией его молекул и температурой.
17.Установите соответствие между физическими величинами и их определениями. К каждой позиции первого столбца подберите нужную позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
К каждой позиции первого столбца подберите нужную позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ИХ ОПРЕДЕЛЕНИЯ | |
| А) Внутренняя энергия идеального газа
Б) Удельная теплота плавления вещества | 1) Величина, численно равная количеству тепла, которое необходимо для плавления одного моля вещества
2) Суммарная кинетическая энергия внутримолекулярного движения в газе 3) Суммарная кинетическая энергия «частиц» газа 4) Величина, численно равная количеству тепла, которое нужно сообщить единице массы этого вещества, взятого при температуре плавления, для его перехода из твердого состояния в жидкое |
18.По мере повышения температуры воды от до вода находилась сначала в твердом состоянии, затем происходил процесс плавления, и нагревание жидкой воды. Изменялась ли внутренняя энергия воды во время этих трех процессов и если изменялась, то как? Установите соответствие между физическими процессами, перечисленными в первом столбце, и изменениями внутренней энергии воды, перечисленными во втором столбце.
Изменялась ли внутренняя энергия воды во время этих трех процессов и если изменялась, то как? Установите соответствие между физическими процессами, перечисленными в первом столбце, и изменениями внутренней энергии воды, перечисленными во втором столбце.
| ФИЗИЧЕСКИЕ ПРОЦЕССЫ | ИХ ИЗМЕНЕНИЯ | |
| А) Нагревание льда
Б) Плавление льда В) Нагревание жидкой воды | 1) Остаётся неизменной
2) Увеличивается 3) Уменьшается |
19.По мере понижения температуры от до вода находилась сначала в жидком состоянии, затем происходил процесс ее отвердевания, и дальнейшее охлаждение твердой воды — льда. Изменялась ли внутренняя энергия воды во время этих трех процессов и если изменялась, то как? Установите соответствие между физическими процессами, перечисленными в первом столбце, и изменениями внутренней энергии воды, перечисленными во втором столбце.
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ИЗМЕНЕНИЕ ВНУТРЕННЕЙ ЭНЕРГИИ | |
| А) Охлаждение жидкой воды
Б) Отвердевание воды В) Охлаждение льда | 1) Остаётся неизменной
2) Увеличивается 3) Уменьшается |
20.Внутренняя энергия молей одноатомного идеального газа равна U. Газ занимает объем V. R — универсальная газовая постоянная. Чему равны давление и температура газа? Установите соответствие между физическими величинами и выражениями для них.
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ВЫРАЖЕНИЕ ДЛЯ НЕЁ | |
| А) Давление газа
Б) Температура газа | 1)
2) 3) 4) |
21.Установите взаимосвязь между физическим прибором и физическим явлением, лежащим в основе его работы.
| ИЗОПРОЦЕСС | ФИЗИЧЕСКОЕ ЯВЛЕНИЕ | |
| А) счетчик Гейгера
Б) жидкостный термометр | 1) Ионизация газа
2) Тепловое расширение тел 3) Упругие свойства газа 4) Поверхностное натяжение жидкости |
К каждой позиции первого столбца подберите соответствующую позицию второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
22.В тепловой машине один моль идеального одноатомного газа совершает процесс, изображенный на рисунке 1. Этот циклический процесс заменяют на другой, изображенный на рисунке 2, не изменяя ни газ, ни его количество. Как в результате изменятся следующие физические величины: передаваемое газу от нагревателя количество теплоты; совершаемая машиной механическая работа; КПД тепловой машины?
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ИХ ИЗМЕНЕНИЕ | |
| А) передаваемое газу от нагревателя количество теплоты за цикл
Б) совершаемая машиной механическая работа за цикл В) КПД тепловой машины | 1) Увеличивается
2) Уменьшается 3) Не изменится |
23. В тепловой машине один моль идеального одноатомного газа совершает процесс, изображенный на рисунке 1. Этот циклический процесс заменяют на другой, изображенный на рисунке 2, не изменяя ни газ, ни его количество. Как в результате изменятся следующие физические величины: передаваемое газу от нагревателя количество теплоты; совершаемая машиной механическая работа; КПД тепловой машины?
В тепловой машине один моль идеального одноатомного газа совершает процесс, изображенный на рисунке 1. Этот циклический процесс заменяют на другой, изображенный на рисунке 2, не изменяя ни газ, ни его количество. Как в результате изменятся следующие физические величины: передаваемое газу от нагревателя количество теплоты; совершаемая машиной механическая работа; КПД тепловой машины?
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ИХ ИЗМЕНЕНИЕ | |
| А) Передаваемое газу от нагревателя количество теплоты за цикл
Б) Совершаемая машиной механическая работа за цикл В) КПД тепловой машины | 1) Увеличивается
2) Уменьшается 3) Не изменится |
24.Идеальный одноатомный газ, находящийся в герметично закрытом сосуде с жёсткими стенками, нагревают. Как изменяются в этом процессе следующие физические величины: концентрация молекул, внутренняя энергия газа, теплоёмкость газа?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается;
2) уменьшается;
3) не изменяется.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Концентрация молекул | Внутренняя энергия газа | Теплоёмкость газа |
25. На рисунке изображён циклический процесс, совершаемый над одноатомным идеальным газом в количестве 1 моль.
Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. Запишите в таблицу выбранные цифры под соответствующими буквами.
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ФОРМУЛЫ | |
| А) Количество теплоты, поглощаемое газом в процессе изобарического расширения
Б) Изменение внутренней энергии газа в процессе изохорического охлаждения | 1)
2) 3) 4) |
26. На рисунке изображена диаграмма четырёх последовательных изменений состояния 2 моль идеального газа. Какие процессы связаны с наименьшим положительным значением работы газа и наибольшим положительным значением работы внешних сил?
На рисунке изображена диаграмма четырёх последовательных изменений состояния 2 моль идеального газа. Какие процессы связаны с наименьшим положительным значением работы газа и наибольшим положительным значением работы внешних сил?
Установите соответствие между такими процессами и номерами процессов на диаграмме. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
| ПРОЦЕССЫ | НОМЕРА ПРОЦЕССОВ | |
| А) Работа газа положительна и минимальна
Б) Работа внешних сил положительна и максимальна | 1) 1
2) 2 3) 3 4) 4 |
27. На рисунке изображена диаграмма четырёх последовательных изменений состояния 2 моль идеального газа. Какие процессы связаны с наименьшим положительным значением работы газа и наибольшим положительным значением работы внешних сил?
Установите соответствие между такими, процессами и номерами процессов на диаграмме.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
| ПРОЦЕССЫ | НОМЕРА ПРОЦЕССОВ | |
| А) Работа газа положительна и минимальна
Б) Работа внешних сил положительна и максимальна | 1) 1
2) 2 3) 3 4) 4 |
28. На рисунке изображена диаграмма четырёх последовательных изменений состояния 2 моль идеального газа. Какие процессы связаны с наименьшим положительным значением работы газа и работы внешних сил?
Установите соответствие между такими процессами и номерами процессов на диаграмме. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
| ПРОЦЕССЫ | НОМЕРА ПРОЦЕССОВ | |
| А) Работа газа положительна и минимальна
Б) Работа внешних сил положительна и минимальна | 1) 1
2) 2 3) 3 4) 4 |
29. В цилиндрическом сосуде под поршнем находится газ. Поршень может перемещаться в сосуде без трения. На дне сосуда лежит стальной шарик (см. рисунок). В сосуд закачивается ещё такое же количество газа при неизменной температуре. Как изменится в результате этого объём газа, его давление и действующая на шарик архимедова сила?
В цилиндрическом сосуде под поршнем находится газ. Поршень может перемещаться в сосуде без трения. На дне сосуда лежит стальной шарик (см. рисунок). В сосуд закачивается ещё такое же количество газа при неизменной температуре. Как изменится в результате этого объём газа, его давление и действующая на шарик архимедова сила?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Обьем газа | Давление газа | Архимедова сила |
30. В цилиндрическом сосуде под поршнем находится газ. Поршень может перемещаться в сосуде без трения. На дне сосуда лежит стальной шарик (см. рисунок). Газ охладили. Как изменится в результате этого объём газа, его давление и действующая на шарик архимедова сила?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Цифры в ответе могут повторяться.
| Обьем газа | Давление газа | Архимедова сила |
31. На рисунке изображена диаграмма четырёх последовательных изменений состояния 2 моль идеального газа. Какие процессы связаны с наибольшими положительными значениями работы газа и работы внешних сил?
Установите соответствие между такими процессами и номерами процессов на диаграмме. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
| ПРОЦЕССЫ | НОМЕРА ПРОЦЕССОВ | |
| А) Работа газа положительна и максимальна
Б) Работа внешних сил положительна и максимальна | 1) 1
2) 2 3) 3 4) 4 |
32. На рисунке показан график изменения температуры Т вещества при постоянном давлении по мере выделения им количества теплоты Q. В начальный момент времени вещество находилось в газообразном состоянии. Какие участки графика соответствуют конденсации пара и остыванию вещества в твёрдом состоянии?
На рисунке показан график изменения температуры Т вещества при постоянном давлении по мере выделения им количества теплоты Q. В начальный момент времени вещество находилось в газообразном состоянии. Какие участки графика соответствуют конденсации пара и остыванию вещества в твёрдом состоянии?
Установите соответствие между тепловыми процессами и участками графика. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
| ПРОЦЕССЫ | УЧАСТКИ ГРАФИКА | |
| А) Конденсация пара
Б) Остывание твёрдого вещества | 1) 1
2) 2 3) 3 4) 4 |
33.В цилиндре под поршнем находится твёрдое вещество. Цилиндр поместили в раскалённую печь. На рисунке показан график изменения температуры Т вещества по мере поглощения им количества теплоты Q. Какие участки графика соответствуют нагреванию вещества в газообразном состоянии и кипению жидкости?
Какие участки графика соответствуют нагреванию вещества в газообразном состоянии и кипению жидкости?
Установите соответствие между тепловыми процессами и участками графика. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные
| ПРОЦЕССЫ | УЧАСТКИ ГРАФИКА | |
| А) Нагревание вещества в газообразном состоянии
Б) Кипение жидкости | 1) 1
2) 2 3) 3 4) 4 |
34. В цилиндре под поршнем находится твёрдое вещество. Цилиндр поместили в раскалённую печь. На рисунке показан график изменения температуры Т вещества по мере поглощения им количества теплоты Q. Какие участки графика соответствуют плавлению вещества и нагреванию вещества в газообразном состоянии? Установите соответствие между тепловыми процессами и участками графика.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
| ПРОЦЕССЫ | УЧАСТКИ ГРАФИКА | |
| А) Плавление
Б) Нагревание газа | 1) 1
2) 2 3) 3 4) 4 |
35.В начальный момент в сосуде под лёгким поршнем находится только жидкий эфир. На рисунке показан график зависимости температуры t эфира от времени его нагревания и последующего охлаждения. Установите соответствие между процессами, происходящими с эфиром, и участками графика.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
| ПРОЦЕССЫ | УЧАСТКИ ГРАФИКА | |
| А) Нагревание паров эфира
Б) Конденсация эфира | 1) BC
2) CD 3) DE 4) EF |
36. В начальный момент в сосуде под лёгким поршнем находится только жидкий эфир. На рисунке показан график зависимости температуры t эфира от времени его нагревания и последующего охлаждения. Установите соответствие между процессами, происходящими с эфиром, и участками графика.
В начальный момент в сосуде под лёгким поршнем находится только жидкий эфир. На рисунке показан график зависимости температуры t эфира от времени его нагревания и последующего охлаждения. Установите соответствие между процессами, происходящими с эфиром, и участками графика.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
| ПРОЦЕССЫ | УЧАСТКИ ГРАФИКА | |
| А) Охлаждение паров эфира
Б) Кипение эфира | 1) BC
2) CD 3) DE 4) EF |
37.В начальный момент в сосуде под лёгким поршнем находится только жидкий эфир. На рисунке показан график зависимости температуры t эфира от времени его нагревания и последующего охлаждения. Установите соответствие между процессами, происходящими с эфиром, и участками графика.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
| ПРОЦЕССЫ | УЧАСТКИ ГРАФИКА | |
| А) Кипение эфира
Б) Конденсация эфира | 1) BC
2) CD 3) DE 4) EF |
38.В начальный момент в сосуде под лёгким поршнем находится только жидкий эфир. На рисунке показан график зависимости температуры t эфира от времени его нагревания и последующего охлаждения. Установите соответствие между процессами, происходящими с эфиром, и участками графика.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
| ПРОЦЕССЫ | УЧАСТКИ ГРАФИКА | |
| А) Конденсация эфира
Б) Нагревание жидкого эфира | 1) AB
2) BC 3) DE 4) EF |
39. В сосуде под поршнем находится вода и водяной пар. Объём сосуда медленно изотермически увеличивают, при этом в сосуде еще остается вода. Как изменяются при этом масса пара и его давление? Для каждой величины подберите соответствующий характер изменения:
В сосуде под поршнем находится вода и водяной пар. Объём сосуда медленно изотермически увеличивают, при этом в сосуде еще остается вода. Как изменяются при этом масса пара и его давление? Для каждой величины подберите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Масса пара | Давление пара |
40. В цилиндрическом сосуде под массивным поршнем находится газ. Поршень не закреплён и может перемещаться в сосуде без трения (см. рисунок). В сосуд закачивается ещё такое же количество газа при неизменной температуре. Как изменятся в результате этого давление газа и концентрация его молекул?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Цифры в ответе могут повторяться.
| Давление газа | Концентрация
молекул газа |
41.Один моль идеального одноатомного газа совершает адиабатическое сжатие. Как изменяются в результате такого процесса давление и температура газа?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается;
2) уменьшается;
3) не изменяется.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Давление | Температура |
42.Один моль идеального одноатомного газа совершает адиабатическое расширение. Как изменяются в результате такого процесса давление и температура газа?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается;
2) уменьшается;
3) не изменяется.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Давление | Температура |
43.Идеальная тепловая машина работает с использованием цикла Карно. Температуру холодильника машины понижают, при этом температура нагревателя и количество теплоты, которое рабочее тело получает от нагревателя за один цикл, остаются неизменными. Как изменяются в результате этого КПД тепловой машины и совершаемая машиной за один цикл работа?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается;
2) уменьшается;
3) не изменяется.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| КПД тепловой машины | Работа, совершаемая машиной
за один цикл |
44. Идеальная тепловая машина работает с использованием цикла Карно. Температуру холодильника машины повышают, при этом температура нагревателя и количество теплоты, которое рабочее тело получает от нагревателя за один цикл, остаются неизменными. Как изменяются в результате этого КПД тепловой машины и совершаемая машиной за один цикл работа?
Идеальная тепловая машина работает с использованием цикла Карно. Температуру холодильника машины повышают, при этом температура нагревателя и количество теплоты, которое рабочее тело получает от нагревателя за один цикл, остаются неизменными. Как изменяются в результате этого КПД тепловой машины и совершаемая машиной за один цикл работа?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается;
2) уменьшается;
3) не изменяется.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| КПД тепловой машины | Работа, совершаемая машиной
за один цикл |
45.Горячее вещество, первоначально находившееся в жидком состоянии, медленно охлаждали. Мощность теплоотвода постоянна. В таблице приведены результаты измерений температуры вещества с течением времени.
| Время, мин. | ||||||||
| Температура, °С |
Выберите из предложенного перечня два утверждения, которые соответствуют результатам проведённых измерений, и укажите их номера.
1) Процесс кристаллизации вещества занял более 25 мин.
2) Удельная теплоёмкость вещества в жидком и твёрдом состояниях одинакова.
3) Температура плавления вещества в данных условиях равна 232 °С.
4) Через 30 мин. после начала измерений вещество находилось только в твёрдом состоянии.
5) Через 20 мин. после начала измерений вещество находилось только в твёрдом состоянии.
46.На графиках А и Б приведены диаграммы p−T и p−V для процессов 1−2 и 3−4 (гипербола), проводимых с 1 моль гелия. На диаграммах p – давление, V – объём и T – абсолютная температура газа. Установите соответствие между графиками и утверждениями, характеризующими изображённые на графиках процессы. К каждой позиции первого столбца подберите соответствующую позицию второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
| ГРАФИКИ | УТВЕРЖДЕНИЯ | |
| А)
Б) | 1) Над газом совершают работу, при этом газ отдаёт положительное количество теплоты.
2) Газ получает положительное количество теплоты, при этом его внутренняя энергия не изменяется. 3) Над газом совершают работу, при этом его внутренняя энергия увеличивается. 4) Газ получает положительное количество теплоты, при этом его внутренняя энергия увеличивается. 
|
47.В изолированной системе тело А имеет температуру +40 °C, а тело Б — температуру +65 °C. Эти тела привели в тепловой контакт друг с другом. Через некоторое время наступило тепловое равновесие. Как в результате изменились температура тела Б и суммарная внутренняя энергия тел А и Б?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась;
2) уменьшилась;
3) не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Температура тела Б | Суммарная внутренняя энергия тел
А и Б |
48.Плотность водяного пара в воздухе при температуре T равна ρ. Плотность насыщенного водяного пара при этой температуре равна ρн. Молярная масса воды μводы = 18 г/моль, а сухого воздуха μвозд. = 29 г/моль. Установите соответствие между физическими величинами и формулами, по которым их можно определить. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
= 29 г/моль. Установите соответствие между физическими величинами и формулами, по которым их можно определить. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
| ФИЗИЧЕСКАЯ ВЕЛИЧИНА | ФОРМУЛА | |
| А) относительная влажность воздуха при температуре T
Б) парциальное давление водяного пара при температуре T | 1)
2) 3) 4) |
49.Парциальное давление водяного пара в воздухе при температуре T равно p. Давление насыщенного водяного пара при этой температуре равно pн. Молярная масса воды μводы = 18 г/моль, а сухого воздуха μвозд. = 29 г/моль. Установите соответствие между физическими величинами и формулами, по которым их можно определить. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
| ФИЗИЧЕСКАЯ ВЕЛИЧИНА | ФОРМУЛА | |
| А) относительная влажность воздуха при температуре T
Б) плотность водяного пара при температуре T | 1)
2) 3) 4) |
50.В цилиндрическом сосуде, расположенном горизонтально, находится идеальный газ. Сосуд закрыт поршнем, который может перемещаться без трения. Давление снаружи атмосферное. Сосуд с газом нагревают так, что температура газа повышается. Как изменятся в результате этого объём газа в сосуде и внутренняя энергия газа?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Цифры в ответе могут повторяться.
51.В цилиндрическом сосуде, расположенном горизонтально, находится идеальный газ. Сосуд закрыт поршнем, который может перемещаться без трения. Давление снаружи атмосферное. Газу медленно сообщают некоторое количество теплоты, в результате чего объём газа увеличивается. Как изменятся в результате этого давление газа в сосуде и его внутренняя энергия?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
52.В изолированной системе тело А имеет температуру +50 °C, а тело Б — температуру +75 °C. Эти тела привели в тепловой контакт друг с другом. Через некоторое время наступило тепловое равновесие. Как в результате изменились температура тела А и суммарная внутренняя энергия тел А и Б?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась;
2) уменьшилась;
3) не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Температура тела А | Суммарная внутренняя энергия тел
А и Б |
ID_8560 1/6 neznaika.pro — PDF Free Download
ID_6041 1/26 neznaika.pro
1 Графики функций Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов. На рисунках изображены
Подробнее
/ /11
Вариант 3580291 1. Задание 9 7729 Идеальный газ медленно переводят из состояния 1 в состояние 3. Процесс 1 2 3 представлен на графике зависимости давления газа p от его объёма V (см. рисунок). Считая,
Задание 9 7729 Идеальный газ медленно переводят из состояния 1 в состояние 3. Процесс 1 2 3 представлен на графике зависимости давления газа p от его объёма V (см. рисунок). Считая,
Подробнее
ID_9518 1/5 neznaika.pro
1 Механика. Изменение физических величин в процессах Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных
Подробнее
Физка_Диагностика_май_2012
Физка_Диагностика_май_212 Задание A1 Тело массой 2 кг движется прямолинейно. Уравнение зависимости его координаты от времени имеет вид: х = -5 + 1t — t 2. Какой из графиков соответствует зависимости проекции
Подробнее
Открытый банк заданий ЕГЭ
Воздушный шар объемом 2500 м 3 с массой оболочки 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. Какова максимальная масса груза, который может поднять шар, если воздух
Какова максимальная масса груза, который может поднять шар, если воздух
Подробнее
ID_6260 1/5 neznaika.pro
1 Кинематика Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов. Зависимость координаты
Подробнее
Учитель: Горшкова Л.А. МБОУ СОШ 44 г. Сургут
Учитель: Горшкова Л.А. МБОУ СОШ 44 г. Сургут Цель: повторение основных понятий, законов и формул ТЕРМОДИНАМИКИ в соответствии с кодификатором ЕГЭ 1. Тепловое равновесие и температура. 2. Внутренняя энергия.
Подробнее
Промежуточная аттестация 10 класс
МОУ СОШ 5 имени 63-го Угличского пехотного полка Промежуточная аттестация 10 класс Составитель: учитель физики Камкова А. Ю. 1.Вид и цель работы: промежуточная аттестация с целью выявления уровня усвоения
Ю. 1.Вид и цель работы: промежуточная аттестация с целью выявления уровня усвоения
Подробнее
2,5 2,5. a x, м/с 2 2,5
Часть 1 Ответами к заданиям 1 4 являются цифра, число или последовательность цифр. Запишите ответ в поле ответа в тексте работы, а затем перенесите в БЛАНК ОТВЕТОВ 1 справа от номера соответствующего задания,
Подробнее
ID_969 1/8 neznaika.pro
Вариант 1 Часть 1 Ответами к заданиям 1 23 являются слово, число или последовательность цифр или чисел. Запишите ответ в соответствующее поле справа. Каждый символ пишите без пробелов. Единицы измерения
Подробнее
ID_ / neznaika.pro
1 Расстояние на карте Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов. Определите по
Определите по
Подробнее
ID_5486 1/5 neznaika.pro
1 Физические явления и законы Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов. Два тела
Подробнее
Диагностическая работа по ФИЗИКЕ
Диагностическая работа по ФИЗИКЕ 0 класс. Разделы: «Механика», «МКТ и термодинамика», «Электродинамика» Инструкция по выполнению работы Для выполнения экзаменационной работы по физике отводится 40 минут.
Подробнее
ID_2095 1/5 neznaika.pro
1 Простой линейный алгоритм для формального исполнителя Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных
Подробнее
ID_5287 1/5 neznaika.
 pro
pro
1 Квантовая физика. Задание с выбором ответа Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов.
Подробнее
Демонстрационный вариант 1
Тестовые задания на экзамене по курсу «Физика. Механика. Термодинамика» Демонстрационный вариант 1 1. Материальная точка движется вдоль оси x. Закон движения точки имеет вид x ( t ) = At, где A постоянная.
Подробнее
ТЕМА.
ТЕМА Лекция 8. Работа газа в циклическом процессе. Тепловые двигатели. Цикл Карно. Матрончик Алексей Юрьевич кандидат физико-математических наук, доцент кафедры общей физики НИЯУ МИФИ, эксперт ГИА-11 по
Подробнее
Отложенные задания (81)
Отложенные задания (81) На стол поставили две одинаковые бутылки, наполненные равным количеством воды комнатной температуры. Одна из них завернута в мокрое полотенце, другая в сухое. Измерив через некоторое
Одна из них завернута в мокрое полотенце, другая в сухое. Измерив через некоторое
Подробнее
ПОДГОТОВКА К ЕГЭ по ФИЗИКЕ
Национальный исследовательский ядерный университет «МИФИ» ПОДГОТОВКА К ЕГЭ по ФИЗИКЕ Лекция 8. Внутренняя энергия газа. Первый закон термодинамики. Работа газа в циклическом процессе. Тепловые двигатели
Подробнее
ID_6115 1/5 neznaika.pro
1 Квантовая физика. Задание с выбором ответа Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов.
Подробнее
Диагностическая работа по ФИЗИКЕ
Диагностическая работа по ФИЗИКЕ класс. Разделы: «Механика», «МК и термодинамика», «Электродинамика» Инструкция по выполнению работы Для выполнения экзаменационной работы по физике отводится 4 минут. Работа
Работа
Подробнее
учебный год
Приложение к рабочей программе по физике для 10 класса Примерные оценочные и методические материалы для осуществления текущего контроля успеваемости и промежуточной аттестации учащихся 10-го класса по
Подробнее
ДИНАМИКА задания типа В Страница 1 из 6
ДИНМИК задания типа В Страница 1 из 6 1. Спутник движется вокруг Земли по круговой орбите радиусом R. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. (M
Подробнее
Примеры решения задач.
Примеры решения задач Пример 6 Один конец тонкого однородного стержня длиной жестко закреплен на поверхности однородного шара так, что центры масс стержня и шара, а также точка крепления находятся на одной
Подробнее
Решение задач на КПД цикла
Решение задач на КПД цикла КПД теплового двигателя, рабочий цикл которого задан графически, можно найти несколькими способами Перечислим формулы и факты, которые надо знать для решения задач этого раздела
Подробнее
Физика ЕГЭ 2015 Тренировочный вариант 1
Часть 1 1. Тело начинает двигаться из начала координат вдоль оси Ох, причем проекция скорости v x меняется с течением времени по закону, приведенному на графике. Через 2 с ускорение тела равно 1) 0 м/с
Тело начинает двигаться из начала координат вдоль оси Ох, причем проекция скорости v x меняется с течением времени по закону, приведенному на графике. Через 2 с ускорение тела равно 1) 0 м/с
Подробнее
Занятие 8. Термодинамика
Занятие 8. Термодинамика Вариант 4… Как изменяется внутренняя энергия идеального газа при повышении его температуры?. Увеличивается. Уменьшается. Не изменяется 4. Это не связанные величины 4… Давление
Подробнее
Задания 25 по физике (часть 1)
Задания 25 по физике (часть 1) 1. Если подвесить к легкой упругой пружине некоторый груз, то пружина, находясь в равновесии, окажется растянутой на 10 см. Чему будет равен период свободных колебаний этого
Подробнее
ID_1014 1/5 neznaika.pro
1 Простой линейный алгоритм для формального исполнителя Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных
Подробнее
Краевая диагностическая работа по ФИЗИКЕ
ФИЗИКА, класс Вариант, Октябрь 2009 Краевая диагностическая работа по ФИЗИКЕ ВАРИАНТ При выполнении заданий А А8 в бланке ответов под номером выполняемого задания поставьте знак «х» в клеточку, номер которой
Подробнее
ЦИКЛИЧЕСКИЕ ПРОЦЕССЫ. ТЕПЛОВАЯ МАШИНА
Сегодня среда, 9 июля 04 г. ЦИКЛИЧЕСКИЕ ПРОЦЕССЫ. ТЕПЛОВАЯ МАШИНА Лекция 5 Содержание лекции: *Прямой цикл. Тепловая машина *Коэффициент полезного действия тепловой машины *Цикл Карно. Теоремы Карно *Обратный
Подробнее
Демонстрационный вариант 1
Тестовые задания на экзамене по курсу «Физика. Механика. Термодинамика» Демонстрационный вариант 1 1. Материальная точка движется равномерно по окружности со скоростью v. Определите модуль изменения вектора
Подробнее
Задача 2: «Цикл Стирлинга и регенерация»
Задача : «Цикл Стирлинга и регенерация» В некоторых тепловых двигателях для повышения их коэффициента полезного действия (КПД) используют регенерацию. Так называют возвращение части количества теплоты,
Подробнее
Первое начало термодинамики для нескольких изопроцессов
|
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
|
⇐ ПредыдущаяСтр 9 из 10Следующая ⇒
Работа
Первое начало термодинамики
Тепловая машина
КПД тепловой машины КПД, количество теплоты, полученное от нагревателя и отданное холодильнику
КПД, механическая работа и количество теплоты, полученное от нагревателя
КПД, механическая работа и количество теплоты, отданное холодильнику
КПД, температуры нагревателя и холодильника
Остальные задачи
КПД замкнутого цикла
Читайте также: |
Домашнее задание по физике на тему «Принципы работы тепловых двигателей»
Пояснительная записка
Тема домашнего задания: Принципы работы тепловых двигателей.
Класс: 11
Цели задания: повторение пройденного материала, развитие самостоятельности.
Степень сложности: средний
Тип задания: индивидуальное
Рекомендуемое количество времени на выполнение: 1 час.
Инструкция к выполнению: Пройти тестирование по теме Принципы работы тепловых двигателей. Тест содержит десять тестовых заданий в формате ЕГЭ (часть А). За каждый правильный ответ выставляется по 1 баллу. 6-7 баллов «тройка», 7-8 «хорошо», 9-10 «отлично».
Способ проверки: задания размещаюся в сети интернет с использованием сервисов для проведения тестирования, проверка производится автоматически с сохранением результата, итоги подводятся в классе на следующем занятии.
Тестовые задания
1. При повышении КПД теплового двигателя стремятся его приблизить к
1) 100 % 3) 70 %
2) к КПД идеального цикла Карно 4) 50 %
2. Тепловая машина с КПД 40 % за цикл работы получает от нагревателя количество теплоты, равное 500 Дж. Какую работу машина совершает за цикл?
1) 300 Дж 3) 200 Дж
2) 180 Дж 4) 75 Дж
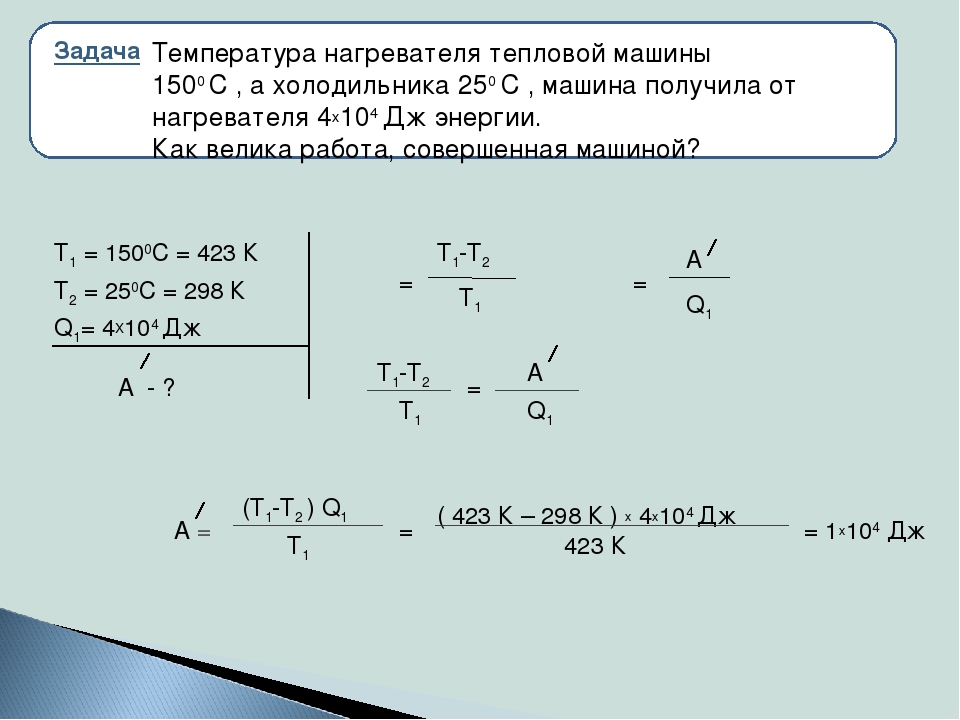
3. Температура холодильника идеальной тепловой машины Карно равна 294 К. Какой должна быть температура ее нагревателя, чтобы КПД машины был равен 40 %?
1) 1200 К 2) 800 К 3) 600 К 4) 490 К
4. Тепловая машина за цикл получает от нагревателя количество теплоты 25 Дж и совершает работу 100 Дж. Чему равен КПД тепловой машины?
1) 200 % 3) 50 %
2) 20 % 4) Такая машина невозможна
5. Температура нагревателя идеальной тепловой машины 500 К, а температура холодильника 300 К. Двигатель получил от нагревателя количество теплоты 40 кДж. Какую работу совершило рабочее тело?
1) 16,7 кДж 3) 16 кДж
2) 3 кДж 4) 97 кДж
6. Тепловая машина имеет КПД 25 %. Средняя мощность передачи энергии холодильнику в ходе ее работы составляет 3 кВт. Какое количество теплоты получает рабочее тело машины от нагревателя за 10 с?
1) 0,4 Дж 3) 400 Дж
2) 40 Дж 4) 40 кДж
7. Температуру холодильника тепловой машины, работающей по циклу Карно, увеличили, оставив температуру нагревателя прежней. Количество теплоты, полученное газом от нагревателя за цикл, не изменилось. Как изменилась при этом работа газа за цикл?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
8. За цикл, показанный на рисунке, газ получает от нагревателя количество теплоты Q=5,1 кДж. КПД цикла равен 4/17. Масса газа постоянна. На участке 1-2 газ совершает работу
1
) 1,2 Дж 3) 2,6 Дж
2) 1,8 кДж 4) 3,9 кДж
9. Тепловая машина с КПД 40% за цикл работы продолжительностью 10 с получает от нагревателя 200 Дж. Какова средняя мощность, с которой теплота передается холодильнику?
1) 8 Вт 3) 10 Вт
2) 6 Вт 4) 16 Вт
10. Идеальная тепловая машина Карно за цикл своей работы получает от нагревателя 10 кДж теплоты. Средняя мощность передачи теплоты холодильнику за цикл составляет 140 Вт, продолжительность цикла 30 с. Каков КПД тепловой машины?
1) 25 % 3) 60 %
2) 42 % 4) 90 %
Ответы:
№ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
ответ | 2 | 3 | 4 | 4 | 3 | 4 | 2 | 2 | 1 | 2 |
Список использованых источников:
Открытый банк заданий ЕГЭ по физике
http://ege.fipi.ru/os11/xmodules/qprint/index.php ?proj=BA1F39653304A5B041B656915DC36B38
Задание №12 ЕГЭ по физике 🐲 СПАДИЛО.РУ
Молекулярно-кинетическая теория
Задание №12 в ЕГЭ по физике — последнее тестовое задание на тему термодинамики.
Теория к заданию №12 ЕГЭ по физике
КПД тепловой машины
Тепловая машина, или тепловой двигатель, представляет собой устройство, используемое для совершения механической работы механизмами (мотоциклами, автомобилями и др.). В самом общем виде это происходит так: в устройство подается топливо, внутренняя энергия которого преобразуется в механическую энергию. Работа при этом совершается за счет расширения газа (рабочего тела), возникающего при повышении его температуры при сгорании топлива. Повторяющийся круговой процесс такого плана, реализуемый в тепловых машинах, называют циклом Карно. Коэффициент полезного действия (КПД) – это величина, показывающая эффективность функционирования механизма. КПД обозначают греческой буквой ɳ («эта»). Вычисляется КПД так: где Т1 – температура нагревателя, Т2 – температура холодильника. Выражение Q1–Q2называют полезной работой, т.е. Q1–Q2=Ап. Поэтому КПД можно выразить формулой: где Q – кол-во теплоты, получаемой двигателем от нагревателя. КПД выражается в процентах или в долях. Формулы, которые необходимо применять для получения результата в долях, приведены выше. Для получения КПД в процентах следует использовать уравнения:
Адиабатный процесс
Адиабатный (адиабатический) процесс связан с первым термодинамическим законом. При нем изменение теплоты в системе равно сумме изменений тепловой энергии и выполненной работы, которую выполняет газ. Он протекает без передачи газу теплоты. Не происходит и передача теплоты газом внешней среде. Адиабатический процесс графически изображается так:
Разбор типовых вариантов № 12 ЕГЭ по физике
Демонстрационный вариант 2018
Тепловая машина работает по циклу Карно. Температуру холодильника тепловой машины повысили, оставив температуру нагревателя прежней. Количество теплоты, полученное газом от нагревателя за цикл, не изменилось. Как изменились при этом КПД тепловой машины и работа газа за цикл?
Для каждой величины определите соответствующий характер изменения:
- увеличилась,
- уменьшилась,
- не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| КПД тепловой машины | Работа газа за цикл |
Алгоритм решения:
- Записываем формулу расчета КПД. Анализируем, что произойдет, если температуру нагревателя увеличить.
- Записываем формулу для КПД, выраженного через работу. Анализируем, как изменится эта величина.
- Записываем ответ.
Решение:
1. Для любого двигателя показатель КПД определяется формулой:
,
где Тн – температурный показатель нагревателя, Тх – температурный показатель холодильника. Т.к. величина Тх в формуле присутствует со знаком «–», значит, повышение значения этой величины ведет к уменьшению результата (т.е. ɳ). Вывод: увеличение температурного показателя холодильника приведет к уменьшению полезного коэффициента. Правильный вариант ответа – 2.
2. КПД выражается через работу так: ɳ=𝐴/𝑄н. Отсюда А= ηQн. Из формулы видно, что ɳ пропорционально А. Вывод: если уменьшится КПД, работа тоже уменьшится. Прав.вариант ответа – 2.
3. Заполняем таблицу:
| КПД тепловой машины | Работа газа за цикл |
| 2 | 2 |
Ответ: 22
Первый вариант задания (Демидова, №3)
На рисунках приведены графики А и Б двух процессов, 1-2 и 3-4, происходящих с 1 моль гелия. Графики построены в координатах V-T и p-V, где р — давление, V — объём, Т — абсолютная температура газа. Установите соответствие между графиками и утверждениями, характеризующими изображённые на графиках процессы. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
| ГРАФИКИ | УТВЕРЖДЕНИЯ 1) Над газом совершают работу, при этом его внутренняя энергия увеличивается. 2) Над газом совершают работу, при этом газ отдаёт положительное количество теплоты. 3) Газ получает положительное количество теплоты и совершает работу. 4) Газ получает положительное количество теплоты, при этом его внутренняя энергия увеличивается. |
Алгоритм решения:
- Рассматриваем первый график таблицы. Ищем правильное предложение в графе справа.
- Проводим анализ второго графика в левой графе таблицы. Определяем правильный ответ в графе справа.
- Записываем ответ.
Решение:
1. На графике А) температура повышается, но объем не изменяется. Это изохорный процесс, поэтому газ не совершает работы, и над газом работа не совершается. Поскольку темп-ра увеличивается (происходит нагревание), газ получает некоторое кол-во теплоты. Из 1-го з-на термодинамики (Q=∆U+A) следует, что его внутр.энергия возрастает. Анализируем утверждения: 1) Утверждение 1 неверно в своей первой части; 2) Утверждение 2 неверно полностью; 3) Утверждение 3 неверно в своей 2-й части; 4) Утверждение 4 верно.
2. Вариант Б) показывает: уменьшаются показатели объема газа и давления. Происходит сжатие газа; это означает, что над газом производится работа. Применив ур-ние Менделеева-Клапейрона (pV=νRT), делаем вывод: при снижении объема и давления должна снижаться и температура. А из этого утверждения в свою очередь следует, что снижается внутр.энергия газа. Кол-во теплоты (положительное) при этом отдается. Работа над газом в данном случае совершается. Анализируем утверждения: 1) Утверждение 1 неверно во 2-й своей части; 2) Утверждение 2 верно; 3) Утверждения 3 и 4 неверны полностью.
Ответ: 42
Второй вариант задания (Демидова, №20)
Установите соответствие между процессами в идеальном газе и формулами, которыми они описываются (N — число частиц, р — давление, V — объём, Т — абсолютная температура, Q — количество теплоты.) К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
| ПРОЦЕССЫА) изохорный процесс при N = const Б) адиабатный процесс при N = const | ФОРМУЛЫ |
Алгоритм решения:
- Анализируем, что происходит при изохорном типе процесса. Определяем, какой вариант равенств соответствует такому процессу.
- Анализируем, каким образом происходит адиабатический процесс. Устанавливаем, какое равенство соответствует данному процессу.
- Записываем ответ.
Решение:
1. Справа вариантом А) записано, что происходит изохорный процесс. Он совершается при постоянном показателе объема. В этом случае действует з-н Шарля: р/Т= const. Такое равенство стоит под 1-м номером.
2. При адиабатическом процессе Б) не происходит теплового обмена со средой, то есть выполняется равенство: Q=0. Значит, правильные предложения 1 и 4.
Ответ: 14
Решение вопросов № 1 — 10 к тесту № 2 в формате ЕГЭ «Молекулярная физика и термодинамика».
Просмотр содержимого документа
«Решение вопросов № 1 — 10 к тесту № 2 в формате ЕГЭ «Молекулярная физика и термодинамика».»
В сосуде, разделённом перегородкой на две равные части, находится влажный воздух. Температура и давление воздуха в обеих частях сосуда одинаковы. Его относительная влажность в одной половине сосуда 20%, а в другой – 80%. Какой станет влажность воздуха в сосуде, если перегородку убрать?
Дано: | Решение: |
Т1 = Т2 р1 = р2 φ1 = 20% φ2 = 80% Найти: φ’ | φ1 =* 100%, ρ1 = , φ2 =* 100%, ρ2 = , где – плотность насыщенного водяного пара при температуре Т1, ρ1 и ρ2 — плотность водяного пара в первой и второй части сосуда при температуре Т1. Масса водяного пара в первой части сосуда m1 = ρ1V, во второй части – m2 = ρ2V. Плотность водяного пара, после того как убрали перегородку ρ’ = = = = . φ’ = * 100% = * 100% = 50%. Ответ: 50%. |
Тепловая машина работает по циклу Карно. Температуру нагревателя тепловой машины увеличили, оставив температуру холодильника прежней. Количество теплоты, отданное рабочим телом холодильнику за цикл, не изменилось. Как изменились при этом КПД тепловой машины и количество теплоты, полученное газом за цикл от нагревателя?
Для каждой величины определите соответствующий характер её изменения:
1) | увеличилась |
2) | уменьшилась |
3) | не изменилась |
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
КПД тепловой машины | Количество теплоты, полученное газом |
Решение: η = 1 — , где η – КПД идеальной тепловой машины, – температура холодильника, – температура нагревателя. Из формулы следует, при увеличении Т1 и неизменном Т2, η увеличится. η = 1 – , где – количество теплоты, отданное газом холодильнику, – количество теплоты, полученное газом за цикл от нагревателя. Откуда = . Следовательно, при увеличении КПД тепловой машины, количество теплоты, полученное газом за цикл от нагревателя, также увеличится.
Ответ: 11.
С идеальным одноатомным газом, который находится в сосуде с поршнем, провели два опыта. В первом опыте газу сообщили, закрепив поршень, количество теплоты Q1, в результате чего его температура повысилась на ΔТ = 1 К. Во втором опыте, предоставив газу возможность изобарно расширяться, сообщили ему количество теплоты Q2, которое на 208 Дж больше, чем Q1. В результате температура газа повысилась, как и в первом случае, на ΔТ. Какова, по данным этих двух опытов, молярная масса газа, если его масса m = 1 кг?
Дано: | Решение: |
m = 1 кг 1. V = const, ΔТ = 1 К, Q1 2. p = const, Q2 – Q1 = 208 Дж, ΔТ = 1 К Найти: М | Первый закон термодинамики для изохорного процесса Q1 = ΔU= , где ΔU – изменение внутренней энергии газа в первом опыте. Первый закон термодинамики для изобарного процесса Q1 = ΔU + А = = , где ΔU – изменение внутренней энергии газа во втором опыте, А – работа газа при изобарном расширении и А = pΔV, pΔV = , согласно уравнению Менделеева-Клапейрона. Q2 – Q1 = , откуда М = , М ≈ 0,04 . Ответ: М ≈ 0,04 . |
Относительная влажность воздуха в закрытом сосуде с поршнем равна 50%. Какова будет относительная влажность воздуха в сосуде, если объём сосуда при неизменной температуре уменьшить в 2 раза?
Дано: | Решение: |
Т = const, V2 = , φ1 = 50% Найти: φ2 | При изотермическом процессе Т = const, согласно закону Бойля-Мариотта p1V1 = p2V2, следовательно из условия задачи p2 = 2p1. Где p1 — давление водяного пара в начальном состоянии, p2 — давление водяного пара при уменьшении объема в 2 раза. φ1 =* 100%, φ2 =* 100%, где – давление насыщенного водяного пара при температуре Т. φ2 =* 100% = 2φ1 = 100%. Ответ: 100%. |
В закрытом сосуде под поршнем находится водяной пар при температуре 100 °С под давлением 20 кПа. Каким станет давление пара, если, сохраняя его температуру неизменной, уменьшить объём пара в 4 раза?
Дано:
Решение:
Т = const,
V2 = ,
p = 20 кПа,
t = 100°С
Найти:
р2
Из условия задачи делаем вывод, что водяной пар ненасыщенный. Насыщенный водяной пар при температуре t = 100°С имеет давление p0 = 100 кПа.
При изотермическом процессе Т = const, согласно закону Бойля-Мариотта p1V1 = p2V2, следовательно из условия задачи p2 = 4p1. Где p1 — давление водяного пара в начальном состоянии, p2 — давление водяного пара при уменьшении объема в 4 раза.
p2 = 80 кПа.
Ответ: 80 кПа.
В запаянной с одного конца длинной горизонтальной стеклянной трубке постоянного сечения (см. рисунок) находится столбик воздуха длиной l1 = 30,7 см, запертый столбиком ртути. Если трубку поставить вертикально отверстием вверх, то длина воздушного столбика под ртутью будет равна l2 = 23,8 см. Какова длина ртутного столбика? Атмосферное давление 747 мм рт. ст. Температуру воздуха в трубке считать постоянной.
Дано: | Решение: |
Т = const, l1 = 30,7 см, l2 = 23,8 см, ратм = 747 мм рт.ст. Найти: l | При Т = const, согласно закону Бойля-Мариотта(Б-М) p1V1 = p2V2, где p1 — давление воздуха в горизонтальной трубке, p2 — давление воздуха в вертикальной трубке. Так как столбик ртути находится в равновесии, то p1 = ратм, p2 = ратм + ррт, ррт – давление ртутного столбика в вертикальной трубке и оно равно ррт = ρртg l. Объемы воздуха в горизонтальной трубке V1 = S l1, в вертикальной трубке V2 = S l2. Подставим значения давления и объема воздуха в закон Б-М: ратм S l1 = (ратм + ррт) S l2. ратм l1 = (ратм + ррт) l2, ратм l1 = ратмl2 + рртl2, ррт = = ратм ( – 1). ррт = 747 мм рт.ст. ( – 1) = 216,6 мм рт.ст., l = 21,7 см. Ответ: 21,7 см. |
В комнате размерами 4×5×3 м, в которой воздух имеет температуру 10 °C и относительную влажность 30%, включили увлажнитель воздуха производительностью 0,2 л/ч. Чему станет равна относительная влажность воздуха в комнате через 1,5 ч? Давление насыщенного водяного пара при температуре 10 °C равно 1,23 кПа. Комнату считать герметичным сосудом.
Дано: | Решение: |
Т = const, V = 60 м3, p0 = 1,23 кПа, t = 10°С, φ = 30% τ = 1,5 ч, = Найти: φ’ | За время τ превратилось в пар вода объемом Vτ = ∙ τ = 0,3 л. Определим массу водяного пара, поступившего в комнату m = V ρ = 0,0003 м3 ∙ 1000 = 0,3 кг. Из уравнения Менделеева-Клапейрона найдем давление, создаваемое этим паром p = = = 653, 3 Па. Определим относительную влажность, создаваемую этим паром φ1 =* 100% = ∙ 100% = 53%. Относительная влажность воздуха в комнате станет φ’= φ + φ1 = 83%. Ответ: 83%. |
При переводе одноатомного идеального газа из состояния 1 в состояние 2 концентрация молекул n пропорциональна давлению р (см. рисунок). Масса газа в процессе остаётся постоянной.
Из приведённого ниже списка выберите два правильных утверждения, характеризующих процесс 1–2, и укажите их номера.
| 1) | Средняя кинетическая энергия теплового движения молекул газа остаётся неизменной. |
| 2) | Плотность газа уменьшается. |
| 3) | Абсолютная температура газа увеличивается. |
| 4) | Происходит изотермическое сжатие газа. |
| 5) | Среднеквадратическая скорость теплового движения молекул газа увеличивается. |
Решение: так как концентрация молекул n пропорциональна давлению р, и m = const, то согласно p = nkT, температура в данном процессе неизменна.
Концентрация газа показывает число молекул газа в единице объема n = . В данном процессе концентрация газа уменьшается при неизменной массе газа (m = m0∙N), следовательно, объем газа увеличивается, а плотность газа ρ = уменьшается.
Ответ: 12 или 21.
Для плавления куска льда при температуре его плавления требуется количество теплоты, равное 3 кДж. Этот кусок льда внесли в тёплое помещение. Зависимость температуры льда от времени представлена на рисунке. Определите среднюю тепловую мощность, подводимую к куску льда в процессе плавления.
Решение: По графику определяем время плавления льда (горизонтальный участок, т.к. при плавлении температура не меняется) t = 10 мин = 600 с. Среднюю тепловую мощность Р найдем по формуле Р = , Р = = 5Вт.
Ответ: 5 Вт.
| |||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||
Решение:
Проверяем вариант № 1. Из таблицы следует, что переход газа из состояния 1 в состояние 4 протекал при постоянной температуре. Согласно закону Бойля-Мариотта p1V1 = p2V2, Следовательно, если = = , то = = 2. Этот вариант неверный.
Проверяем № 2. Переведем температуру в К. T4 = 300К, T5 = 330К, T6 = 450К, T7 = 600К. Из таблицы следует, что = const при переходе газа из состояния 5 в состояние 7, а значит V = const. Этот вариант верный.
Проверяем № 3. Внутренняя энергия идеального газа пропорциональна температуре. = = ≈1,36. Вариант неверный.
№ 4. При Т = const , pV = const. Так как при переходе от состояния 2 к состоянию 3 давление газа уменьшается, то объем газа увеличивается. Газа совершает положительную работу, поэтому получает тепло. Первый закон термодинамики для изотермического процесса Q = A. Вариант верный.
№ 5. Изохорный процесс V = const, Δ V = 0, следовательно A = 0, газ работы не совершал. Вариант неверный.
Ответ: 24 или 42.
.
МЦКО по Физике 11 класс. Официальные варианты №4001, 4002 от 25.11.2020 (задания)
Проверочная работа проводится с целью определения уровня усвоения обучающимися одиннадцатых классов предметного содержания курса по физике и выявления элементов содержания, вызывающих наибольшие затруднения. Официальная дата проведения 25 ноября 2020 года
Официальное МЦКО 4001: Скачать в PDF
Официальное МЦКО 4002: Скачать в PDF
Решать МЦКО онлайн на сайте 4001:
Решать МЦКО онлайн на сайте 4002:
Пример заданий из данной работы:
2. Сколько грузиков массой 50 г необходимо подвесить на закреплённую на штативе пружину жёсткостью 80 Н/м, чтобы она растянулась на 2,5 см?
3. Какую минимальную работу необходимо совершить, чтобы лежащую на полу небольшую коробку массой 5 кг поднять и положить на стол высотой 80 см?
4. Находчивый школьник решил взвесить рыбу на самодельных весах из лёгкой удочки (см. рисунок). В качестве гири он использовал батон хлеба
массой 0,5 кг. Какова масса рыбы?
5. Брусок толщиной 10 см и массой 1 кг плавает в воде, погрузившись ровно наполовину (см. рисунок). Из приведённого ниже списка выберите два правильных утверждения.
1) Плотность материала, из которого изготовлен брусок, равна 1 000 кг/м3.
2) Сила Архимеда, действующая на брусок, равна 20 Н.
3) Если воду заменить на керосин, то глубина погружения бруска увеличится.
4) Если на брусок положить груз массой 1,5 кг, то брусок утонет.
5) Если на брусок сверху положить ещё два таких же бруска, то глубина погружения брусков увеличится на 20 см.
В ответе запишите номера выбранных утверждений.
6. Скорость полёта искусственного спутника Земли в результате изменения его орбиты увеличилась. Как изменились при этом сила притяжения спутника к Земле и высота его орбиты? Для каждой величины определите соответствующий характер изменения: ФИЗИЧЕСКАЯ ВЕЛИЧИНА ХАРАКТЕР ИЗМЕНЕНИЯ
1) увеличилась
2) уменьшилась
3) не изменилась
A) сила притяжения спутника к Земле
Б) высота орбиты спутника
Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
8. В первом сосуде содержится гелий, а во втором – аргон. Средняя кинетическая энергия теплового движения молекул газов в сосудах одинакова. Объём первого сосуда в 4 раза больше объёма второго. Определите отношение абсолютной температуры гелия к абсолютной температуре аргона.
9. В ходе некоторого процесса одноатомному идеальному газу в количестве 0,4 моль сообщили количество теплоты, равное 1 500 Дж, при этом внутренняя энергия газа увеличилась на 900 Дж. Какую работу совершил газ?
10. В сосуде находится вода массой 500 г при температуре 100 оС и нормальном атмосферном давлении. Какое количество теплоты необходимо, чтобы эта вода полностью выкипела?
12. Температуру холодильника тепловой машины Карно повысили, оставив температуру нагревателя прежней. Количество теплоты, полученное газом от нагревателя за цикл, не изменилось. Как изменились при этом КПД тепловой машины и работа газа за цикл? Для каждой величины определите характер её изменения: ФИЗИЧЕСКАЯ ВЕЛИЧИНА ХАРАКТЕР ИЗМЕНЕНИЯ
1) увеличилась
2) уменьшилась
3) не изменилась
A) КПД тепловой машины
Б) работа газа за цикл
Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
14. Во сколько раз уменьшится модуль сил взаимодействия двух небольших металлических шариков одинакового диаметра, имеющих заряды q1 = +4 нКл и q2 = –2 нКл, если шарики привести в соприкосновение и раздвинуть на прежнее расстояние?
15. В паспорте электрического чайника указано: «1650 Вт, 220 В». Найдите силу тока в нагревательном элементе чайника при его включении в сеть с таким напряжением.
22. В калориметр с водой бросили кусочки тающего льда. В некоторый момент кусочки льда перестали таять. Первоначальная масса воды
в калориметре 330 г. Определите первоначальную температуру воды в калориметре, если масса воды в нём увеличилась на 63 г. Тепловыми
потерями можно пренебречь.
Вам будет интересно:
МЦКО по Химии 11 класс. Официальные варианты №4001, 4002 от 19.11.2020 (задания и ответы)
* Олимпиады и конкурсы
* Готовые контрольные работы
* Работы СтатГрад
* Официальные ВПР
Поделиться:
Идеальный тепловой двигатель Карно: пересмотр второго закона термодинамики
Цели обучения
К концу этого раздела вы сможете:
- Определите цикл Карно.
- Рассчитайте максимальный теоретический КПД ядерного реактора.
- Объясните, как диссипативные процессы влияют на идеальный двигатель Карно.
Рис. 1. Пьющая птица (источник: Arabesk.nl, Wikimedia Commons)
Новинка, известная как пьющая птица (см. Рис. 1), является примером двигателя Карно.Он содержит хлористый метилен (смешанный с красителем) в брюшной полости, который кипит при очень низкой температуре — около 100 ° F. Чтобы работать, нужно намочить голову птицы. Когда вода испаряется, жидкость движется вверх в голову, в результате чего птица становится тяжелой и снова погружается в воду. Это охлаждает хлористый метилен в голове, и он перемещается обратно в брюшную полость, в результате чего дно птицы становится тяжелым и опрокидывается. За исключением очень небольшого расхода энергии — первоначального увлажнения головы — птица становится своего рода вечным двигателем.
Мы знаем из второго закона термодинамики, что тепловой двигатель не может быть на 100% эффективным, поскольку всегда должен быть некоторый теплообмен Q c в окружающую среду, который часто называют отходящим теплом. Насколько эффективна тогда тепловая машина? На этот вопрос теоретически ответил в 1824 году молодой французский инженер Сади Карно (1796–1832) в своем исследовании появившейся в то время технологии тепловых двигателей, имеющих решающее значение для промышленной революции. Он разработал теоретический цикл, который теперь называется циклом Карно , который является наиболее эффективным из возможных циклических процессов.Второй закон термодинамики можно переформулировать в терминах цикла Карно, и поэтому Карно фактически открыл этот фундаментальный закон. Любой тепловой двигатель, использующий цикл Карно, называется двигателем Карно .
Что критически важно для цикла Карно — и, по сути, определяет его, — так это то, что используются только обратимые процессы. Необратимые процессы связаны с диссипативными факторами, такими как трение и турбулентность. Это увеличивает теплоотдачу Q c в окружающую среду и снижает КПД двигателя.Очевидно, что обратимые процессы лучше.
Двигатель Карно
С точки зрения обратимых процессов, второй закон термодинамики имеет третью форму:
Двигатель Карно, работающий между двумя заданными температурами, имеет максимально возможный КПД по сравнению с любым тепловым двигателем, работающим между этими двумя температурами. Кроме того, все двигатели, в которых используются только обратимые процессы, имеют одинаковую максимальную эффективность при работе между одинаковыми заданными температурами.
На рисунке 2 показана диаграмма PV для цикла Карно. Цикл включает два изотермических и два адиабатических процесса. Напомним, что и изотермические, и адиабатические процессы в принципе обратимы.
Карно также определил эффективность идеального теплового двигателя, то есть двигателя Карно. Всегда верно, что эффективность циклического теплового двигателя определяется как:
[латекс] \ displaystyle {Eff} = \ frac {Q _ {\ text {h}} — Q _ {\ text {c}}} {Q _ {\ text {h}}} = 1- \ frac {Q _ {\ текст {c}}} {Q _ {\ text {h}}} \\ [/ latex]
Карно обнаружил, что для идеального теплового двигателя соотношение [латекс] \ frac {Q _ {\ text {c}}} {Q _ {\ text {h}}} \\ [/ latex] равно отношению абсолютные температуры тепловых резервуаров.То есть [латекс] \ frac {Q _ {\ text {c}}} {Q _ {\ text {h}}} = \ frac {T _ {\ text {c}}} {T _ {\ text {h}} } \\ [/ latex] для двигателя Карно, так что максимальная или эффективность Карно Eff C определяется как
[латекс] \ displaystyle {Eff} _ {\ text {C}} = 1- \ frac {T _ {\ text {c}}} {T _ {\ text {h}}} \\ [/ latex]
, где T h и T c указаны в градусах Кельвина (или по любой другой шкале абсолютных температур). Никакая настоящая тепловая машина не может работать так хорошо, как КПД Карно — фактический КПД около 0.7 из этого максимума обычно — лучшее, что может быть достигнуто. Но идеальный двигатель Карно, как и пьяная птица наверху, хотя и является увлекательной новинкой, имеет нулевую мощность. Это делает его нереалистичным для любых приложений.
Интересный результат Карно подразумевает, что 100% эффективность будет возможна только в том случае, если T c = 0 K, то есть, только если холодный резервуар находится на абсолютном нуле, что практически и теоретически невозможно. Но физический смысл таков: единственный способ задействовать всю теплопередачу в работе — это удалить из всю тепловую энергию , а для этого требуется холодный резервуар с абсолютным нулем.
Также очевидно, что наибольшая эффективность достигается, когда соотношение [латекс] \ frac {T _ {\ text {c}}} {T _ {\ text {h}}} \\ [/ latex] как можно меньше . Так же, как обсуждалось для цикла Отто в предыдущем разделе, это означает, что эффективность максимальна для максимально возможной температуры горячего резервуара и минимально возможной температуры холодного резервуара. (Эта установка увеличивает площадь внутри замкнутого контура на диаграмме PV ; также кажется разумным, что чем больше разница температур, тем легче направить теплопередачу на работу.Фактические температуры резервуара теплового двигателя обычно связаны с типом источника тепла и температурой окружающей среды, в которой происходит передача тепла. Рассмотрим следующий пример.
Рис. 2. PV Диаграмма для цикла Карно, использующего только обратимые изотермические и адиабатические процессы. Теплоотдача Q h происходит в рабочее тело во время изотермического пути AB, который происходит при постоянной температуре T h .Теплообмен Q c происходит из рабочего тела во время изотермического пути CD, который имеет место при постоянной температуре T c . Выход сети W равен площади внутри пути ABCDA. Также показана схема двигателя Карно, работающего между горячим и холодным резервуарами при температурах T h и T c . Любой тепловой двигатель, использующий обратимые процессы и работающий между этими двумя температурами, будет иметь такой же максимальный КПД, что и двигатель Карно.
Пример 1. Максимальный теоретический КПД ядерного реактора
Ядерный энергетический реактор имеет воду под давлением 300ºC. (Более высокие температуры теоретически возможны, но практически невозможны из-за ограничений, связанных с материалами, используемыми в реакторе.) Передача тепла от этой воды — сложный процесс (см. Рисунок 3). Пар, вырабатываемый в парогенераторе, используется для привода турбогенераторов. В конце концов пар конденсируется в воду при 27ºC, а затем снова нагревается, чтобы запустить цикл заново.Рассчитайте максимальный теоретический КПД теплового двигателя, работающего между этими двумя температурами.
Рис. 3. Принципиальная схема ядерного реактора с водой под давлением и паровых турбин, которые преобразуют работу в электрическую энергию. Теплообмен используется для генерации пара, отчасти для предотвращения радиоактивного загрязнения генераторов. Используются две турбины, поскольку это дешевле, чем использование одного генератора, вырабатывающего такое же количество электроэнергии. Перед возвратом в теплообменник пар конденсируется в жидкость, чтобы поддерживать низкое давление пара на выходе и способствовать прохождению пара через турбины (эквивалентно использованию холодного резервуара с более низкой температурой).Значительная энергия, связанная с конденсацией, должна рассеиваться в окружающей среде; в этом примере используется градирня, поэтому прямая передача тепла в водную среду отсутствует. (Обратите внимание, что вода, поступающая в градирню, не контактирует с паром, протекающим по турбинам.)
Стратегия
Поскольку температуры указаны для горячего и холодного резервуаров этой тепловой машины, [латекс] {Eff} _ {\ text {C}} = 1- \ frac {T _ {\ text {c}}} {T _ {\ text {h}}} \\ [/ latex] можно использовать для расчета эффективности Карно (максимальной теоретической).Эти температуры необходимо сначала перевести в градусы Кельвина.
Решение
Температуры горячего и холодного резервуаров равны 300 ° C и 27,0 ° C соответственно. Таким образом, в градусах Кельвина T h = 573 K и T c = 300 K, так что максимальная эффективность составляет [латекс] \ displaystyle {Eff} _ {\ text {C}} = 1- \ frac {T _ {\ text {c}}} {T _ {\ text {h}}} \\ [/ latex].
Таким образом,
[латекс] \ begin {array} {lll} {Eff} _ {\ text {C}} & = & 1- \ frac {300 \ text {K}} {573 \ text {K}} \\\ text { } & = & 0.476 \ text {или} 47.6 \% \ end {array} \\ [/ latex]
Обсуждение
Фактический КПД типичной атомной электростанции составляет около 35%, что немного лучше, чем в 0,7 раза больше максимально возможного значения, что является данью превосходной инженерной мысли. Электростанции, работающие на угле, нефти и природном газе, имеют более высокий фактический КПД (около 42%), потому что их котлы могут достигать более высоких температур и давлений. Температура холодного резервуара на любой из этих электростанций ограничена местными условиями.На рисунке 4 показан (а) внешний вид атомной электростанции и (б) внешний вид угольной электростанции. Оба имеют градирни, в которые вода из конденсатора попадает в градирню рядом с верхом и разбрызгивается вниз, охлаждаясь за счет испарения.
Рис. 4. (a) Атомная электростанция (предоставлено BlatantWorld.com) и (b) угольная электростанция. Оба имеют градирни, в которых вода испаряется в окружающую среду, что составляет Q c . Ядерный реактор, поставляющий Q h , размещен внутри куполообразных корпусов защитной оболочки.(Источник: Роберт и Михаэла Виколь, publicphoto.org)
Поскольку все реальные процессы необратимы, реальный КПД теплового двигателя никогда не может быть таким большим, как КПД двигателя Карно, как показано на рисунке 5a. Даже при наличии самого лучшего теплового двигателя всегда есть процессы рассеяния в периферийном оборудовании, таком как электрические трансформаторы или автомобильные трансмиссии. Это еще больше снижает общий КПД за счет преобразования части выходной мощности двигателя обратно в теплообмен, как показано на рисунке 5b.
Рис. 5. Настоящие тепловые двигатели менее эффективны, чем двигатели Карно. (а) Настоящие двигатели используют необратимые процессы, уменьшающие теплопередачу к работе. Сплошные линии представляют реальный процесс; пунктирные линии — это то, что двигатель Карно будет делать между теми же двумя резервуарами. (б) Трение и другие диссипативные процессы в выходных механизмах теплового двигателя преобразуют часть его работы в теплоотдачу в окружающую среду.
Сводка раздела
- Цикл Карно — это теоретический цикл, который является наиболее эффективным из возможных циклических процессов.Любой двигатель, использующий цикл Карно, который использует только обратимые процессы (адиабатический и изотермический), известен как двигатель Карно.
- Любой двигатель, использующий цикл Карно, обладает максимальной теоретической эффективностью.
- Хотя двигатели Карно являются идеальными двигателями, в действительности ни один двигатель не достигает теоретической максимальной эффективности Карно, так как диссипативные процессы, такие как трение, играют роль. Циклы Карно без потери тепла возможны при абсолютном нуле, но в природе такого никогда не наблюдалось.
Концептуальные вопросы
- Подумайте о пьющей птице в начале этого раздела (рис. 1). Хотя птица обладает максимально возможной теоретической эффективностью, если со временем предоставить ее самой себе, она перестанет «пить». Какие диссипативные процессы могут привести к прекращению движения птицы?
- Можно ли в тепловых двигателях использовать улучшенные технические средства и материалы для уменьшения передачи тепла в окружающую среду? Могут ли они полностью исключить передачу тепла в окружающую среду?
- Меняет ли второй закон термодинамики принцип сохранения энергии?
Задачи и упражнения
1.Определенный бензиновый двигатель имеет КПД 30,0%. Какой была бы температура горячего резервуара для двигателя Карно с таким КПД, если бы он работал с температурой холодного резервуара 200 ° C?
2. Ядерный реактор с газовым охлаждением работает при горячей и холодной пластовых температурах от 700 ° C до 27,0 ° C. а) Каков максимальный КПД теплового двигателя, работающего между этими температурами? (b) Найдите отношение этого КПД к КПД Карно стандартного ядерного реактора (найденного в Примере 1).
3. (a) Какова температура горячего резервуара двигателя Карно с КПД 42,0% и температурой холодного резервуара 27,0 ° C? (b) Какой должна быть температура горячего резервуара для реального теплового двигателя, который достигает 0,700 максимального КПД, но все еще имеет КПД 42,0% (и холодный резервуар при 27,0 ° C)? (c) Подразумевает ли ваш ответ практические ограничения эффективности бензиновых двигателей автомобилей?
4. Паровозы имеют КПД 17,0% и работают с температурой горячего пара 425ºC.а) Какой была бы температура холодного резервуара, если бы это был двигатель Карно? (б) Какой была бы максимальная эффективность этой паровой машины, если бы температура в ее холодном резервуаре составляла 150 ° C?
5. В практических паровых машинах используется пар с температурой 450ºC, который позже выпускается при 270ºC. а) Каков максимальный КПД такого теплового двигателя? (b) Поскольку пар с 270ºC все еще достаточно горячий, вторая паровая машина иногда работает на выхлопе первой. Каков максимальный КПД второго двигателя, если его выхлоп имеет температуру 150ºC? (c) Каков общий КПД двух двигателей? (d) Покажите, что это такой же КПД, как у одиночного двигателя Карно, работающего при температуре от 450 ° C до 150 ° C.
6. Угольная электростанция имеет КПД 38%. Температура пара, выходящего из котла, составляет [латекс] \ text {550} \ text {\ textordmasculine} \ text {C} [/ latex]. Какой процент от максимальной эффективности достигает эта станция? (Предположим, что температура окружающей среды [латекс] \ text {20} \ text {\ textordmasculine} \ text {C} [/ latex].)
7. Готовы ли вы финансово поддержать изобретателя, который продает устройство, которое, по ее утверждению, имеет теплоотдачу 25 кДж при 600 К, теплоотдачу в окружающую среду при 300 К и работает 12 кДж? Поясните свой ответ.
8. Необоснованные результаты (a) Предположим, вы хотите создать паровой двигатель, который передает тепло в окружающую среду при 270ºC и имеет КПД Карно 0,800. Какой температуры горячего пара нужно использовать? б) Что неразумного в температуре? (c) Какая посылка необоснованна?
9. Необоснованные результаты Рассчитайте температуру холодного резервуара парового двигателя, который использует горячий пар при 450ºC и имеет КПД Карно 0,700. б) Что неразумного в температуре? (c) Какая посылка необоснованна?
Глоссарий
Цикл Карно: циклический процесс, в котором используются только обратимые процессы, адиабатические и изотермические процессы
Двигатель Карно: тепловой двигатель, использующий цикл Карно
КПД Карно: максимальный теоретический КПД для тепловой машины
Избранные решения проблем и упражнения
1.403ºC
3. (а) 244 ° С; (б) 477 ° С; (c) Да, поскольку автомобильные двигатели не могут быть слишком горячими без перегрева, их эффективность ограничена.
5. (a) [латекс] {\ mathit {\ text {Eff}}} _ {\ text {1}} = 1- \ frac {{T} _ {\ text {c, 1}}} {{ T} _ {\ text {h, 1}}} = 1- \ frac {\ text {543 K}} {\ text {723 K}} = 0 \ text {.} \ Text {249} \ text {или } \ text {24} \ text {.} 9 \% \\ [/ latex]
(b) [латекс] {\ mathit {\ text {Eff}}} _ {2} = 1- \ frac {\ text {423 K}} {\ text {543 K}} = 0 \ text {.} \ text {221} \ text {или} \ text {22} \ text {.} 1 \% \\ [/ latex]
(c) [латекс] {\ mathit {\ text {Eff}}} _ {1} = 1- \ frac {{T} _ {\ text {c, 1}}} {{T} _ {\ text {h, 1}}} \ Rightarrow {T} _ {\ text {c, 1}} = {T} _ {\ text {h, 1}} \ left (1, -, {\ mathit {\ text { eff}}} _ {1} \ right) \ text {аналогично} {T} _ {\ text {c, 2}} = {T} _ {\ text {h, 2}} \ left (1- { \ mathit {\ text {Eff}}} _ {2} \ right) \\ [/ latex]
с использованием T h, 2 = T c, 1 в приведенном выше уравнении дает
[латекс] \ begin {array} {l} {T} _ {\ text {c, 2}} = {T} _ {\ text {h, 1}} \ left (1- {Eff} _ {1 } \ right) \ left (1- {Eff} _ {2} \ right) \ Equiv {T} _ {\ text {h, 1}} \ left (1- {Eff} _ {\ text {total}} \ right) \\\ поэтому \ left (1- {Eff} _ {\ text {total}} \ right) = \ left (1 — {\ mathit {\ text {Eff}}} _ {1} \ right) \ left (1- {Eff} _ {2} \ right) \\ {Eff} _ {\ text {total}} = 1- \ left (1-0.249 \ right) \ left (1-0,221 \ right) = 41,5 \% \ end {array} \\ [/ latex]
(d) [латекс] {\ text {Eff}} _ {\ text {total}} = 1- \ frac {\ text {423 K}} {\ text {723 K}} = 0 \ text {.} \ text {415} \ text {или} \ text {41} \ text {.} 5 \\% \\ [/ latex]
7. Передача тепла в холодный резервуар составляет [латекс] {Q} _ {\ text {c}} = {Q} _ {\ text {h}} — W = \ text {25} \ text {кДж} — \ text {12} \ text {kJ} = \ text {13} \ text {kJ} \\ [/ latex], поэтому эффективность равна [latex] \ mathit {Eff} = 1- \ frac {{Q} _ {\ text {c}}} {{Q} _ {\ text {h}}} = 1- \ frac {\ text {13} \ text {кДж}} {\ text {25} \ text {кДж} } = 0 \ текст {.} \ text {48} \\ [/ latex]. Эффективность Карно равна [латекс] {\ mathit {\ text {Eff}}} _ {\ text {C}} = 1- \ frac {{T} _ {\ text {c}}} {{T} _ { \ text {h}}} = 1- \ frac {\ text {300} \ text {K}} {\ text {600} \ text {K}} = 0 \ text {.} \ text {50} \\ [/латекс]. Фактический КПД составляет 96% от КПД Карно, что намного выше, чем лучший из когда-либо достигнутых, составляющий около 70%, поэтому ее схема, скорее всего, будет мошеннической.
9. (a) -56,3ºC (b) Температура слишком низкая для мощности паровой машины (местная среда). Это ниже точки замерзания воды.(c) Предполагаемая эффективность слишком высока.
Boddeker’s PHY132 Lecture
Ch 19 Тепловые двигатели, | ||||||||||||||||||||||
Тепловые двигатели и 2 nd | ||||||||||||||||||||||
А | А А Автомобильная промышленность и т. Д. | |||||||||||||||||||||
А рабочее тело поглощает энергию за счет ТЕПЛА от высокого работу делает двигатель энергия вытесняется теплом в резервуар с более низкой температурой | ||||||||||||||||||||||
Предположим, что тепловая машина подключена к двум резервуарам энергии, л ф Каков КПД этого двигателя? | Тепло, необходимое для плавления 15,0 г Hg Q Q = 0,015 (1,18×104) Q c = 177 Дж | Энергия, поглощенная 1.00 г алюминия Q Q = 0,001 (3,97×105) Q ч = 397 Дж | объем работы W двигатель = Q h Вт двигатель = 397-177 Вт двигатель = 220 Дж | |||||||||||||||||||
eff = W двигатель эфф = 220/397 эфф = 55.4% | Теоретический (Карно) эфф макс = 1 T C / T H эфф макс = 1 (273,15-38,9) / эфф макс = 74,9% | |||||||||||||||||||||
Демо: http: //www.stirlingenergy.ru / break_news.htm | ||||||||||||||||||||||
Тепловые насосы и | ||||||||||||||||||||||
А | ||||||||||||||||||||||
Для режима отопления COP (обогреватель) = Q ч | Для режима охлаждения COP (рефрижератор) = Q c Хорошие холодильники имеют КПД, КС, | |||||||||||||||||||||
Клаузиус выписка Энергия НЕ передается самопроизвольно за счет тепла | ||||||||||||||||||||||
Пример Холодильник имеет коэффициент полезного действия, равный Найдите (а) работа, необходимая в каждом цикле и (б) энергия, направленная к горячему | а. COP (рефрижератор) = Q c 5,00 = Работа = 24,0 Джоуля г. Q ч = Q c + Q ч = 120 + 24 Q ч = | |||||||||||||||||||||
Реверсивный и | ||||||||||||||||||||||
А по тому же пути на фотоэлектрической диаграмме.Также каждые точки на этом пути — состояние равновесия. | An Все | |||||||||||||||||||||
Некоторые Если А | Почти как (Почему | |||||||||||||||||||||
Карно | ||||||||||||||||||||||
Теорема Карно Нет реальной тепловой машины, работающей между | ||||||||||||||||||||||
Какой коэффициент полезного действия у холодильника COP рефриг = T C / ∆T COP рефриг = (273,15 + -3) / 30 COP рефрижератор = 9 | ||||||||||||||||||||||
Пример Тепловой двигатель, работающий при температуре от 200 ° C до 80,0 ° C, достигает 20,0% 10,0 кДж работы? | Карно двигатель eff c = ∆T / эфф с = (200-80) / эфф c = 25,3% | Если эффективность 20%, мы получаем только 25,3% * 20% = 5,06% эфф = 5,06% Q ч = 197 кДж | ||||||||||||||||||||
Бензин и Дизель | ||||||||||||||||||||||
Впускной Сжатие Горение B C Мощность Выхлоп Выхлоп Если тогда Отто e Или e | Химический ПЭ в Положительная работа на газе PE по Q h Газ адиабатически расширяется P внезапно падает В падает от В 1 до В 2 γ = C P / C V где V 1 / V 2 степень сжатия | |||||||||||||||||||||
Пример Бензиновый двигатель имеет степень сжатия 6.00 и использует (а) Каков КПД двигателя, если он работает в (b) Что если? Если фактический КПД составляет 15,0%, какой | eff otto = 1 (В 2 eff otto = 1 (1/6) 1.4 — эфф отто = 51,2% потерь = eff otto потерь = 51,2% — 15% потерь = 36,2% | |||||||||||||||||||||
Энтропия | ||||||||||||||||||||||
Энтропия Энтропия | ||||||||||||||||||||||
Микрогосударство: Macrostate: описание с использованием состояния | Далеко Таким образом | |||||||||||||||||||||
dS = dQ r / T ∆S ∆S ∆S Для Таким образом, ∆S = 0 Теперь рассмотрим не-Карно ср Так (интеграл по замкнутому контуру, вы увидите это намного больше в электрическом |
Квазистатический, обратимый Начальный: T i и V i ; dQ r = dE внутр — dW dQ r = dE int — (-PdV) dQ r = nC v dT + nRT (dV / V) (разделить на T) dQ r / T = nC v dT / T ∆S ∆S ∆S = nC v ln (T f / T i ) | |||||||||||||||||||||
Пример Ванночка для льда содержит 500 г жидкой воды при 0 ° C.Рассчитать | Для процесса замораживания, изменение энтропии, ∆S = ∆Q / T ∆S ∆S ∆S = -610 Дж / К | |||||||||||||||||||||
Изменения энтропии в | ||||||||||||||||||||||
полная энтропия изолированной системы, которая претерпевает изменение, НЕ МОЖЕТ уменьшиться В В | ||||||||||||||||||||||
Энтропия в свободном состоянии (нет dS = dQ r / T ∆S ∆S ∆S | Изменение энтропии T f = (м 1 c 1 T c dS = dQ c / T ∆S | |||||||||||||||||||||
Температура на поверхности Солнца приблизительно равна | ∆S система = ∆ (Q / ∆S система = ∆ (1000/290 ∆S система = 3,27 Дж / К | |||||||||||||||||||||
Энтропия под микроскопом | ||||||||||||||||||||||
Пусть Пусть А | ||||||||||||||||||||||
Как Ансайт Как | Ответ: В и Вт 1 Вт 1 Вт 1 = 8 | |||||||||||||||||||||
Что Это означает, что если добавляется другая частица размером V M , то Так W = (w 1 ) (w 2 ) Добавить W = (w 1 ) (w 2 ) (w 3 ), где w 1 Или W = w 1 3 Так Вт и Вт и | А Вт f набор Вт f / Вт и Вт f ln (W f / к B к B к B ln (W f ) к B ln (W f ) ср S f — S i = n (R) ln (V f / V i ) Таким образом, S f Или ΔS = k B ln (Работа) | |||||||||||||||||||||
Если вы подбрасываете два кубика, какое общее количество способов | 2 3 4 5 6 7 8 9 10 11 12 1,1 1,2 1,3 1,4 1,5 1,6 2,1 2,2 2,3 2,4 2,5 2,6 3,1 3,2 3,3 3,4 3,5 3,6 4,1 4,2 4,3 4,4 4,5 4,6 5,1 5,2 5,3 5,4 5,5 5,6 6,1 6,2 6,3 6,4 6,5 6,6 1 2 3 4 5 6 5 4 3 2 1 | |||||||||||||||||||||
Как видите, только одна комбинация даст вам 12; (6,6) И 7 может быть | ||||||||||||||||||||||
13.8: Цикл Карно, эффективность и энтропия
В начале 19 века паровые двигатели стали играть все более важную роль в промышленности и на транспорте. Однако систематический набор теорий преобразования тепловой энергии в движущую силу паровыми двигателями еще не был разработан. Николя Леонар Сади Карно (1796-1832), французский военный инженер, опубликовал в 1824 году размышлений о движущей силе огня . В книге предложена обобщенная теория тепловых двигателей, а также идеализированная модель термодинамической системы для тепловой двигатель, который теперь известен как цикл Карно.Карно разработал основы второго закона термодинамики, и его часто называют «отцом термодинамики».
Цикл Карно
Цикл Карно состоит из следующих четырех процессов:
- Обратимый процесс изотермического расширения газа. В этом процессе идеальный газ в системе поглощает \ (q_ {in} \) количество тепла от источника тепла при высокой температуре \ (T_ {high} \), расширяется и воздействует на окружающую среду.
- Обратимый процесс адиабатического расширения газа.В этом процессе система теплоизолирована. Газ продолжает расширяться и воздействовать на окружающую среду, в результате чего система охлаждается до более низкой температуры, \ (T_ {low} \).
- Обратимый изотермический процесс сжатия газа. В этом процессе окружающая среда работает с газом при \ (T_ {low} \) и вызывает потерю тепла \ (q_ {out} \).
- Обратимый процесс адиабатического сжатия газа. В этом процессе система теплоизолирована. Окружающая среда продолжает работать с газом, в результате чего температура снова поднимается до \ (T_ {high} \).
Рисунок \ (\ PageIndex {1} \): Идеальная газопоршневая модель цикла Карно.
Схема P-V
P-V-диаграмма цикла Карно показана на рисунке \ (\ PageIndex {2} \). В изотермических процессах I и III ∆U = 0, поскольку ∆T = 0. В адиабатических процессах II и IV q = 0. Работа, тепло, ∆U и ∆H каждого процесса в цикле Карно сведены в Таблицу \ (\ PageIndex {1} \).
Рисунок \ (\ PageIndex {2} \): диаграмма P-V цикла Карно.
| Процесс | w | д | ΔU | ΔH |
|---|---|---|---|---|
| I | \ (- nRT_ {high} \ ln \ left (\ dfrac {V_ {2}} {V_ {1}} \ right) \) | \ (nRT_ {high} \ ln \ left (\ dfrac {V_ {2}} {V_ {1}} \ right) \) | 0 | 0 |
| II | \ (n \ bar {C_ {v}} (T_ {low} -T_ {high}) \) | 0 | \ (n \ bar {C_ {v}} (T_ {low} -T_ {high}) \) | \ (n \ bar {C_ {p}} (T_ {low} -T_ {high}) \) |
| III | \ (- nRT_ {low} \ ln \ left (\ dfrac {V_ {4}} {V_ {3}} \ right) \) | \ (nRT_ {low} \ ln \ left (\ dfrac {V_ {4}} {V_ {3}} \ right) \) | 0 | 0 |
| IV | \ (n \ bar {C_ {v}} (T_ {high} -T_ {low}) \) | 0 | \ (n \ bar {C_ {v}} (T_ {hight} -T_ {low}) \) | \ (n \ bar {C_ {p}} (T_ {high} -T_ {low}) \) |
| Полный цикл | \ (- nRT_ {high} \ ln \ left (\ dfrac {V_ {2}} {V_ {1}} \ right) -nRT_ {low} \ ln \ left (\ dfrac {V_ {4}} {V_ {3}} \ right) \) | \ (nRT_ {high} \ ln \ left (\ dfrac {V_ {2}} {V_ {1}} \ right) + nRT_ {low} \ ln \ left (\ dfrac {V_ {4}} {V_ { 3}} \ справа) \) | 0 | 0 |
Диаграмма T-S
Диаграмма T-S цикла Карно показана на рисунке \ (\ PageIndex {3} \).В изотермических процессах I и III ∆T = 0. В адиабатических процессах II и IV ∆S = 0, поскольку dq = 0. ∆T и ∆S каждого процесса в цикле Карно показаны в таблице \ (\ PageIndex {2} \).
Рисунок \ (\ PageIndex {3} \): T-S диаграмма цикла Карно.
| Процесс | ΔT | ΔS |
|---|---|---|
| I | 0 | \ (- nR \ ln \ left (\ dfrac {V_ {2}} {V_ {1}} \ right) \) |
| II | \ (T_ {низкий} -T_ {высокий} \) | 0 |
| III | 0 | \ (- nR \ ln \ left (\ dfrac {V_ {4}} {V_ {3}} \ right) \) |
| IV | \ (T_ {высокий} -T_ {low} \) | 0 |
| Полный цикл | 0 | 0 |
КПД
Цикл Карно — наиболее эффективный из возможных двигателей, основанный на предположении об отсутствии побочных затратных процессов, таких как трение, и предположении об отсутствии теплопроводности между различными частями двигателя при разных температурах. {C_ {V} / R} = \ dfrac {V_ {4}} {V_ {1}} \]
А так как T 1 = T 2 и T 3 = T 4 ,
\ [\ dfrac {V_ {3}} {V_ {4}} = \ dfrac {V_ {2}} {V_ {1}} \]
Следовательно,
\ [\ text {efficiency} = \ dfrac {nRT_ {high} \ ln \ left (\ dfrac {V_ {2}} {V_ {1}} \ right) -nRT_ {low} \ ln \ left (\ dfrac {V_ {2}} {V_ {1}} \ right)} {nRT_ {high} \ ln \ left (\ dfrac {V_ {2}} {V_ {1}} \ right)} \]
\ [\ boxed {\ text {efficiency} = \ dfrac {T_ {high} -T_ {low}} {T_ {high}}} \]
Сводка
Цикл Карно имеет максимально возможный КПД двигателя (хотя другие циклы имеют такой же КПД), основанный на предположении об отсутствии побочных затратных процессов, таких как трение, и предположении об отсутствии теплопроводности между различными частями двигателя. при разных температурах.
Проблемы
- Теперь вы работаете с двигателем Карно с КПД 40%, который отводит тепло в радиатор с температурой 298 К. Если вы хотите повысить КПД двигателя до 65%, до какой температуры вам нужно будет поднять резервуар тепла. ?
- Двигатель Карно поглощал 1,0 кДж тепла при 300 К и израсходовал 400 Дж тепла в конце цикла. Какая температура в конце цикла?
- Комнатный обогреватель, работающий по циклу Карно, нагревает дом со скоростью 30 кДж / с, чтобы поддерживать температуру в помещении на уровне 72 ºF.Какая мощность работает у обогревателя, если температура наружного воздуха 30 ºF?
Список литературы
- Goldstein, M. J. Chem. Educ. , 1980 , 57, 114-116
- Bader, M. J. Chem. Educ. , 1973 , 50 , 834
- W. F. Luder. J. Chem. Educ. , 1944 , 21 , 600-601
- Salter, C. J. Chem. Educ. , 2000 , 77, 1027-1030
Авторы и авторство
11.8. Тепловые двигатели и холодильники
На рисунке XI.8 схематично показан путь состояния рабочего тела в обобщенном тепловом двигателе. В верхней части цикла (непрерывная кривая) рабочее тело расширяется, и машина выполняет работу. Работа, выполненная на двигателя, составляет фунтов стерлингов фунтов стерлингов или площадь под этой частью кривой. В нижней части цикла (штриховая кривая) происходит сжатие рабочего тела; работа ведется по нем.Эта работа — область под пунктирной частью цикла. чистая работа, выполненная на двигатель во время цикла — это работа, выполненная на двигатель при расширении минус работа, выполненная на во время компрессионной части цикла, и это область замыкает циклом.
Во время одной части любого цикла теплового двигателя тепло подается на двигатель, а во время других частей тепло теряется из его.Как описано в Разделе 11.1, КПД η тепловой машины определяется как
\ [\ eta = \ frac {\ textbf {net} ~ \ text {внешняя работа сделана} ~ \ textbf {by} ~ \ text {двигатель во время цикла}} {\ text {подача тепла} ~ \ textbf { to} ~ \ textbf {двигатель во время цикла.}} \]
Обратите внимание, что слово «net» не появляется в знаменателе. КПД также может быть вычислено из
\ [\ eta = \ frac {Q _ {\ text {in}} — Q _ {\ text {out}}} {Q _ {\ text {in}}}, \]
, хотя я подчеркиваю, что это не определение .
В двигателе Карно , который является наиболее эффективным из возможных двигателей для данной температуры источника и поглотителя, КПД составляет
\ [\ eta = \ frac {T_ {2} -T_ {1}} {T_ {2}}, \]
, где T 2 и T 1 — соответственно температуры горячего источника и холодного стока.
Если рабочее вещество проходит цикл в плоскости PV в направлении против часовой стрелки , то устройство представляет собой холодильник .
В этом случае площадь, ограниченная циклом, равна чистой работе, которая выполняется на рабочем веществе. Если холодильник работает по обратному циклу Карно , рабочее вещество забирает (независимо от того, что оно пытается охладить), количество тепла Q 1 при изотермическом расширении от d до c (см. Рисунок XI.1, но с перевернутыми стрелками) и отводит a (большее) количество тепла Q 2 при изотермическом сжатии от b до a .Это количество Q 2 выталкивается в комнату — поэтому при включении холодильника в комнате становится теплее. (Что — вы никогда не замечали?) Холодильный эффект равен Q 1 , поскольку это количество тепла, забираемого холодильником от охлаждаемого тела.
Коэффициент полезного действия холодильника определяется как
.
\ [\ frac {\ text {охлаждающий эффект}} {\ text {net work done} ~ \ textbf {on} ~ \ text {двигатель во время цикла.}} \]
Согласно первому закону термодинамики знаменатель выражения равен Q 2 — Q 1 , а для обратимого цикла Карно энтропия in равна энтропии out, так что Q 2 / Q 1 = T 2 / T 1 . Следовательно, коэффициент полезного действия холодильного цикла Карно можно рассчитать из
.
\ [\ frac {T_ {1}} {T_ {2} -T_ {1}}.\]
Это, конечно, может быть намного больше 1, но ни один холодильник, работающий между одним и тем же источником и температурой стока, не может иметь коэффициент полезного действия выше, чем у реверсивного холодильника Карно.
Конечно, в настоящем холодильнике («холодильнике») рабочим веществом не является идеальный газ, и при этом не следует цикл Карно — слишком много практических трудностей на пути к достижению этой идеальной мечты. Как уже упоминалось в другом месте этого курса, я не практичный человек и не подхожу для описания реальных, практичных машин.Фундаментальные принципы, описанные в этом разделе, конечно, все еще применимы в реальном мире! В реальном холодильнике рабочее вещество (хладагент , ) представляет собой летучую жидкость, которая испаряется в одной части работы и конденсируется в жидкость в другой части. В промышленных холодильниках хладагентом может быть аммиак, но он считается слишком опасным для домашнего использования. Некоторое время в моде был фреон, который представлял собой смесь хлорфторуглеродов, таких как CCl 2 F 2 , но известно, что выходящие за пределы хлорфторуглеродов в течение некоторого времени вызывают разложение озона (O 3 ) в атмосферу, тем самым разрушая нашу защиту от ультрафиолетового излучения Солнца.Хлорфторуглероды в значительной степени заменены гидрофторуглеродами, такими как C 2 H 2 F 4 , которые считаются менее разрушительными для озонового слоя. Точная формула или смесь, несомненно, является коммерческой тайной.
Жидкость нагнетается вокруг системы труб с помощью насоса, который называется , компрессор . Незадолго до того, как жидкость попадет в морозильную камеру, она находится в жидкой форме, перемещаясь по довольно узким трубам. Затем он подается через сопло в систему более широких труб (испаритель , ), окружающую морозильную камеру, и там он испаряется, забирая тепло от продуктов и воздуха в морозильной камере.Вентилятор также может распределять охлажденный воздух по остальной части холодильника. После выхода из морозильной камеры пар возвращается в компрессор, где он, естественно, сжимается (поэтому насос называется компрессором). Это производит тепло, которое рассеивается в комнате, когда жидкость проталкивается через ряд труб и лопаток, известных как конденсатор, в задней части холодильника, где жидкость снова конденсируется в жидкую форму. Затем цикл начинается заново.
Может оказаться полезным следующее описание тепловых двигателей и холодильников Карно.(Но просто помните, что, хотя циклы Карно являются наиболее эффективными двигателями и холодильниками для заданных температур источника и поглотителя, практическая реализация реального двигателя или холодильника может не совпадать с этим теоретическим идеалом.)
Обозначение :
T 2 = более высокая температура
T 1 = более низкая температура
Q 2 = тепло, полученное или потерянное при T 2
Q 1 = тепло, полученное или потерянное при T 1
\ (\ Delta S = 0 \ qquad \ frac {Q_ {1}} {T_ {1}} = \ frac {Q_ {2}} {T_ {2}} \)
Тепловой двигатель :
\ (\ Delta U = 0 \ quad \ text {Сетевая работа выполнена} ~ \ textbf {by} ~ \ text {engine} = Q_ {2} -Q_ {1}.\)
\ (\ text {Эффективность} \ eta = \ frac {Q_ {in} -Q _ {\ text {out}}} {Q _ {\ text {in}}} = \ frac {Q_ {2} -Q_ {1 }} {Q_ {2}} = \ frac {T_ {2} -T_ {1}} {T_ {2}} \)
Холодильник :
\ (\ Delta U = 0 \ qquad \ text {Сетевая работа выполнена} ~ \ textbf {on} ~ \ text {Холодильник} = Q_ {2} -Q_ {1} \)
\ (\ text {Коэффициент полезного действия} P = \ frac {Q _ {\ text {in}}} {Q _ {\ text {oxt}} — Q _ {\ text {in}}} = \ frac {Q_ {1 }} {Q_ {2} -Q_ {1}} = \ frac {T_ {1}} {T_ {2} -T_ {1}} \)
Тепловой насос :
Принцип действия теплового насоса такой же, как и у холодильника, за исключением того, что его назначение иное.Цель холодильника — отвод тепла от чего-либо (например, еды) и, таким образом, охлаждение. То, что отводимое таким образом тепло поступает в комнату, чтобы сделать ее теплее (по крайней мере, в принципе), является случайным. Важным является то, сколько тепла извлекается из пищи, и поэтому целесообразно определить коэффициент полезного действия холодильника как холодильный эффект (т.е. Q 1 ), разделенный на выполненную чистую работу. на холодильнике, за цикл.Но с тепловым насосом цель — обогреть комнату , отбирая тепло извне. То, что снаружи может стать прохладнее (по крайней мере, в принципе), случайно. Таким образом, для теплового насоса подходящим определением коэффициента производительности является тепловой эффект (т.е. Q 2 ), деленный на чистую работу, выполненную в холодильнике за цикл.
\ (\ Delta U = 0 \ qquad \ text {Сетевая работа выполнена} ~ \ textbf {on} ~ \ text {тепловой насос} = Q_ {2} -Q_ {1} \)
\ (\ text {Коэффициент производительности} ~ P = \ frac {Q _ {\ mathrm {out}}} {Q _ {\ mathrm {out}} — Q _ {\ mathrm {in}}} = \ frac {Q_ { 2}} {Q_ {2} -Q_ {1}} = \ frac {T_ {2}} {T_ {2} -T_ {1}} \)
Из этого уравнения видно, что чем теплее снаружи ( T 1 ), тем выше коэффициент полезного действия.Поэтому вы можете задаться вопросом, практично ли использовать тепловой насос для обогрева здания в холодном климате, например зимой в Квебеке. А если нет, можно ли изобрести двигатель, который одновременно является холодильником и тепловым насосом; Другими словами, он извлекает тепло из пищи (то есть охлаждает) и передает это тепло (плюс немного больше из-за работы, которая выполняется на холодильнике / тепловом насосе) в комнату, чтобы эффективно нагреть комнату. . Ответ на этот вопрос содержится в статье в Victoria Times-Colonist от 11 июня 2006 г., которую я воспроизвожу с разрешения ниже.
Кондиционер
Назначение холодильника («холодильник») — перекачивать некоторое количество тепла Q 1 из пищи (или того, что нужно хранить в прохладном состоянии). Величина Q 1 — это «охлаждающий эффект». Во время работы холодильника в комнату отводится несколько большее количество тепла, хотя это не должно приводить к очень заметному повышению температуры в помещении, отчасти потому, что комната имеет большую теплоемкость. Отчасти потому, что большая часть этого тепла будет теряться через окна.Коэффициент полезного действия холодильника — это охлаждающий эффект за цикл, Q 1 , деленный на чистую работу, выполненную холодильником за цикл, и для цикла Карно его можно рассчитать из T 1 / ( T 2 — T 1 ).
Назначение теплового насоса состоит в том, чтобы перекачивать немного тепла Q 1 извне и (исходя из работы, проделанной с насосом) перекачивать большее количество Q 2 тепла в комнату — достаточно большой, чтобы заметно обогреть комнату, если предположить, что вы не держите все окна настежь открытыми.Следовательно, коэффициент полезного действия должен быть определен как Q 2 , деленный на чистую работу, выполненную на холодильнике за цикл. Для цикла Карно он может быть рассчитан из T 2 / ( T 2 — T 1 ).
Есть и третья возможность, а именно кондиционер. Он будет включать осушитель воздуха, но в нашем контексте мы рассматриваем его как устройство, предназначенное для перекачивания тепла из комнаты наружу, а не извне в комнату.Если это удастся, в комнате станет прохладнее, чем на улице. Таким образом, кондиционер больше похож на холодильник в том смысле, что коэффициент полезного действия — это тепло Q 1 , отбираемое за цикл из комнаты, разделенное на чистую работу, выполненную на машине за цикл. Для цикла Карно он может быть рассчитан из T 1 / ( T 2 — T 1 ).
\ (\ Delta U = 0 \ qquad \ text {Сетевая работа выполнена} ~ \ textbf {on} ~ \ text {кондиционер} = Q_ {2} -Q_ {1} \).
\ (\ text {Коэффициент полезного действия} P = \ frac {Q _ {\ text {in}}} {Q _ {\ text {out}} — Q _ {\ text {in}}} = \ frac {Q_ {1 }} {Q_ {2} -Q_ {1}} = \ frac {T_ {1}} {T_ {2} -T_ {1}} \).
Те, кто читал до сих пор, будут иметь представление о том, что есть вещи, называемые тепловыми двигателями , холодильниками , тепловыми насосами и кондиционерами , которые представлены циклами Карно или аналогичными циклами со стрелками, направленными в разные стороны, несколько уравнений с разными нижними индексами и слегка отличающиеся определения эффективности или коэффициента полезного действия.С тех пор, как я подготовил эти заметки, я обнаружил, что в реальном мире действительно существуют реальные твердые машины, называемые тепловыми двигателями, холодильниками, тепловыми насосами и кондиционерами . Я обнаружил две очень милые маленькие брошюры, описывающие настоящие тепловые насосы и настоящие кондиционеры, и то, как вы можете установить их для обогрева или охлаждения вашего дома. Они называются «Отопление и охлаждение с тепловым насосом» и «Кондиционер в вашем доме» , каждая примерно по 50 страниц. Мои копии датированы 1996 годом, исправлены в 2004 году, хотя, смею предположить, вы сможете получить более свежие.Их можно бесплатно получить в Energy Publications, Office of Energy Efficiency, Natural Resources Canada, c / o S.J.D.S., 1779 Pink Road, Gatineau, Province of Québec, Canada J9J 3N7. Я нашел их очаровательными.
Страница не найдена | MIT
Перейти к содержанию ↓
- Образование
- Исследовать
- Инновации
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О Массачусетском технологическом институте
- Подробнее ↓
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О Массачусетском технологическом институте
Меню ↓
Поиск
Меню
Ой, похоже, мы не смогли найти то, что вы искали!
Попробуйте поискать что-нибудь еще!
Что вы ищете?
Увидеть больше результатов
Предложения или отзывы?
11.9 Обратимый идеал
11.9 Обратимый идеал
|
11.9 Обратимый идеал
Утверждения предыдущего раздела, описывающие второй закон, таковы:
явно здравый смысл: да, еще нужно включить холодильник, и
нет, вы не можете пропустить периодические остановки на заправке.Что за
сюрприз!
Более того, они кажутся бесполезными. Например, говорят
что для работы нашего холодильника требуется электричество, но они этого не говорят
сколько. Это может быть мегаватт, это может быть нановатт.
Введите человеческую изобретательность. С некоторой смекалкой два простых
утверждения второго закона могут быть значительно усилены, позволяя
на их основе будет построено все здание.
Первое понимание состоит в том, что если мы ограничены безжалостной природой,
стрела времени, то стоит изучить устройства, которые почти игнорируют
эта стрелка. Если вы снимаете устройство в кино, и оно выглядит почти
точно правильно при движении назад устройство называется (почти
точно) «обратимый». Примером может служить механизм, который тщательно
разработан, чтобы двигаться практически без трения. Если привести в движение,
движение замедлится лишь незначительно во время короткометражного фильма.Когда этот фильм прокручивается в обратном направлении, на первый взгляд кажется, что
совершенно нормально. Если вы посмотрите более внимательно, вы увидите небольшой
проблема: в обратном фильме устройство немного разгоняется,
вместо того, чтобы тормозить из-за трения как надо. Но это
почти правильно: потребуется лишь очень небольшое количество дополнительных
энергии для ускорения фактического движения устройства в обратном направлении, как это происходит в
перевернутый фильм.
Знаки доллара могут появиться перед вашими глазами после прочтения последнего
предложение: это предполагает, что почти обратимые устройства могут потребовать очень
мало энергии для бега.В контексте второго закона это предполагает, что
возможно, стоит изучить холодильные устройства и двигатели, которые
практически обратимы.
Второе важное открытие — смотреть туда, где есть свет. Почему нет
изучить, скажем, холодильный аппарат, который достаточно прост, чтобы
быть проанализированы подробно? Как минимум, это даст стандарт
с которыми можно сравнивать другие холодильные устройства. И так это
будет сделано.
Теоретически простое холодильное устройство называется холодильным устройством «цикла Карно» или тепловым насосом Карно. А
Схема представлена на рисунке 11.11. Вещество,
хладагент циркулирует через четыре устройства с целью
переноса тепла из холодильника на кухню.В обсуждаемом устройстве хладагент будет приниматься
идеальный газ с постоянной удельной теплоемкостью, например, гелий. Ты бы
не очень хочу использовать идеальный газ в качестве хладагента в реальном
холодильник, но цель здесь не в том, чтобы сделать практичный
холодильник, который можно продать с прибылью. Цель здесь —
создать устройство, которое может быть точно проанализировано, и идеальный газ
описывается простыми математическими формулами, обсуждаемыми в основах физики
классы.
Рассмотрим детали устройства. Хладагент попадает в холодильник.
при температуре ниже, чем внутри холодильника. Затем он движется
через длинную систему трубопроводов, позволяющую теплу выходить из холодильника
в более холодный хладагент внутри труб. Эта система трубопроводов
называется теплообменником. Возникает первая проблема обратимости: тепло
поток определенно необратим. Тепловой поток, если смотреть назад,
течь от холодного к более горячему, и это неправильно.Единственное, что
можно сделать, чтобы свести к минимуму эту проблему, насколько это возможно,
минимизировать перепады температур. Хладагент можно отправлять в
чуть холоднее, чем внутри холодильника. Конечно,
если разница температур небольшая, поверхность, через которую
тепловые потоки в хладагент должны быть очень большими, чтобы
приличное количество тепла прочь. Один непрактичный аспект циклов Карно
в том, что они огромны; эта система трубопроводов не может быть маленькой.Будь то как
возможно, теоретический результат состоит в том, что теплообмен в
Холодильник можно представить как (почти) изотермический.
После выхода из холодильника хладагент
сжатый, чтобы повысить его температуру до немного выше, чем у
кухня. Для этого требуется проделать объем работы, указывая на то, что
потребность в электричестве для работы холодильника. Чтобы избежать необратимых
теплопроводность в процессе сжатия, компрессор
термически тщательно изолирован, чтобы исключить любой теплообмен с его
окружение.Кроме того, компрессор очень тщательно спроектирован так, чтобы его можно было
почти без трения. В нем установлены дорогие подшипники, которые работают почти с
нет трения. Кроме того, сам хладагент имеет «вязкость»; он испытывает внутреннее трение, если есть
значительные градиенты его скорости. Это сделало бы работу
требуется, чтобы сжать его больше идеального, и чтобы
минимизировать этот эффект, градиенты скорости можно минимизировать, используя
много хладагента.Это также сводит к минимуму любые
внутренняя теплопроводность в хладагенте, которая может возникнуть.
Вязкость также является проблемой для теплообменников, поскольку
перепады давления вызывают увеличение скорости. С большим количеством
хладагента, перепады давления в теплообменниках также
сведены к минимуму.
Теперь хладагент направляется в теплообменник, открытый на кухню.
воздуха. Так как поступает немного горячее, чем в кухню, тепло будет поступать
из хладагента на кухню.Опять же температура
разница должна быть небольшой, чтобы процесс был почти обратимым.
Наконец, хладагент расширяется, что снижает его
температура ниже, чем в холодильнике. Расширение происходит
внутри тщательно спроектированной турбины, потому что это вещество
объем работы при реверсивном расширении, а турбина
фиксирует эту работу. Он используется для запуска качественного генератора и
восстановить часть электроэнергии, необходимой для работы компрессора.Затем хладагент снова поступает в холодильник, и цикл повторяется.
Если этот холодильник Карно проанализировать теоретически,
{D.59}, получается очень простой результат. Соотношение
тепло, сбрасываемое устройством на кухню, в
тепло, отводимое от холодильника, точно такое же, как
отношение температуры на кухне к температуре
холодильник:
| (11.14) |
Это очень полезный результат, потому что сеть
который должен попасть в устройство, в силу сохранения энергии
разница между и. Можно определить «коэффициент полезного действия», который представляет собой отношение
отвод тепла от холодильника до необходимой мощности
ввод:
| (11,15) |
На самом деле некоторая необратимость в реальной жизни неизбежна, и
правда требуемых работ будет больше.Приведенная выше формула дает необходимое
работать, если все действительно идеально.
Это же устройство можно использовать зимой для обогрева внутренней части
твой дом. Помните, что тепло было сброшено на кухню.
Итак, просто зачеркните кухня
при высокой температуре
сторону на рисунке 11.11 и напишите дом.
И зачеркните «холодильник» и напишите
снаружи.
Устройство отводит тепло снаружи и
сбрасывает его в ваш дом.Это то же самое устройство, но оно используется
для другой цели. Это причина того, что это не
больше называется холодильным циклом
, но «тепловым
насос.» Для теплового насоса интересующей величиной является
количество тепла, сбрасываемого на высокотемпературной стороне, в ваш
жилой дом. Таким образом, альтернативный коэффициент полезного действия теперь определяется как
| (11.16) |
Приведенная выше формула идеальна.Реальная производительность будет меньше, поэтому
требуемых работ будет больше.
Интересно отметить, что если вы возьмете количество
электричество и слить его в простой резистивный нагреватель, он добавляет
ровно столько тепла в ваш дом. Если вы сбросите то же самое
количество электричества в тепловом насосе Carnot, который использует его для перекачки
тепла снаружи, количество тепла, добавленного к вашему дому, будет
намного больше, чем. Например, если это 300 К
(27 C) внутри и 275 K (2 C) снаружи,
количество добавляемого тепла составляет 300/25 = 12 Вт, что в двенадцать раз больше, чем вы
достал от резистивного ТЭНа!
Если вы запустите цикл охлаждения Карно в обратном порядке, как на рисунке
11.12, все стрелки меняются местами, и он превращается в
тепловой двигатель.
Теперь устройство сильно нагревается.
стороны температуры и выдает чистый объем работы. Высота
температурная сторона — это место, где вы сжигаете топливо. Низкий
температура может быть охлаждающей воды из местной реки.В
В заявлении Кельвина-Планка говорится, что устройство не будет работать, если не
тепла от сгорания сбрасывается до более низкой температуры. В
автомобильный двигатель, выхлоп и радиатор — это те, которые забирают большую часть
тепло прочь. Поскольку устройство практически обратимо, цифры для
передаваемое тепло и чистая работа не сильно отличаются от
необратная версия. Но теперь цель состоит в том, чтобы создать работу, поэтому
«Тепловой КПД» теплового двигателя определяется как
| (11.17) |
К сожалению, это всегда меньше единицы. И приблизиться к
что двигатель должен работать горячим; температура, при которой топливо
пригорел должен быть очень горячим.
(Обратите внимание, что небольшие поправки к строго обратному охлаждению
процесс нужен; в частности, для процесса теплового двигателя, чтобы
работы, теперь вещество должно быть немного холоднее, чем на
сторона с высокой температурой и немного горячее, чем на
сторона низких температур.Тепло не может течь от холодного к более горячему.
Но поскольку это небольшие изменения, математика почти не изменилась.
В частности, численные значения для и
почти не изменится, хотя сейчас жар идет в обратном направлении.)
Последний вопрос, который необходимо решить: нельзя ли использовать другие устройства?
лучше, чем у Карно.Например, обычное тепло не могло
насос более эффективен, чем реверсивная версия Карно, при нагревании
жилой дом? Ну, разложите их по разным окнам и посмотрите. (Карно
потребуется большое окно.) Предположим, что оба устройства имеют размер
производят такой же тепловой поток в дом. Если подумать, так как
машина Карно реверсивная, запустите ее в обратном направлении; это можно сделать
без изменения его номеров для тепловых потоков и сети
заметно, и это покажет различия между
устройств.
Идея показана на рисунке 11.13. Обратите внимание, что чистое тепло
поток в дом теперь равен нулю, подтверждая, что запуск Карно в
реверс действительно показывает различия между устройствами. Чистое тепло
обменяется с наружным воздухом, и есть чистая работа. Введите
Кельвин-Планк. Согласно Кельвину-Планку, тепло не может быть просто
взяты из наружного воздуха и превращены в полезную сетку. В
чистая работа, извлекаемая из воздуха, должна быть отрицательной.Итак
работа, необходимая для обычного теплового насоса, должна быть больше, чем
что восстановлено перевернутым Карно, избыток в конечном итоге
тепло в наружном воздухе. Итак, обычный тепловой насос требует больше работы.
чем у Карно, работающего нормально. Поэтому никакое устройство не может быть больше
эффективнее, чем у Карно. В лучшем случае общий
устройство тоже обратимо. В этом случае ни одно устройство не может выиграть,
потому что обычное устройство можно заставить работать в обратном направлении вместо
Карно один.Вот тот случай, когда оба устройства так идеально
построено так, что любая работа, выполняемая в универсальном устройстве, почти
100% восстановлено перевернутой машиной Карно, с незначительным
количество работы превращается в тепло за счет трения или других
необратимость и попадание в наружный воздух.
Вывод такой:
Все обратимые устройства, передающие тепло при заданной высокой температуре
и низкая температура, (и нигде
else,) имеют такую же эффективность.У необратимых устройств меньше.
Чтобы убедиться, что это верно и для холодильных циклов, просто отметим, что
из-за сохранения энергии. Отсюда следует, что, рассматриваемый как холодильный
цикл, не только обычный тепловой насос, указанный выше, требует больше работы, он
также отводит меньше тепла с холодной стороны. Чтобы увидеть, что это относится к
тепловые двигатели тоже, просто поместите обычный тепловой двигатель рядом с перевернутым
Карно один производит такую же мощность.Тогда чистая работа равна нулю, и
тепловой поток стандартного устройства лучше быть больше
чем цикл Карно, потому что в противном случае чистое тепло текло бы
от холода к горячему, что противоречит утверждению Клаузиуса. Тепловой поток
это мера количества сожженного топлива, поэтому
необратимое универсальное устройство потребляет больше топлива.
Практические устройства могут обмениваться теплом при более чем двух температурах, и
можно сравнить с набором циклов Карно, делающих то же самое.Это тогда
увидел, что это плохие новости; для максимальной теоретической эффективности нагрева
двигатель, вы предпочитаете теплообмен на максимально возможной
температуры и самой низкой доступной температуры, а для тепловых насосов
и холодильники, при самой низкой доступной высокой температуре и
самая высокая доступная низкая температура. Но реальная жизнь и теория
конечно не то же самое.
Поскольку эффективность цикла Карно однозначно связана с
соотношение температур между горячей и холодной сторонами, возможно
определить температурную шкалу с помощью цикла Карно.Единственный
нужно выбрать одну эталонную температуру для сравнения
с, как вода в своей тройной точке. Фактически это было предложено
Кельвин как концептуальное определение, чтобы противопоставить его более раннему
определения, основанные на термометрах, содержащих ртуть или аналогичный
жидкость, объемное расширение которой считывается. Хотя такое вещество, как
ртуть увеличивается в объеме очень линейно с (Кельвином)
температура, она не расширяется точно линейно вместе с ней.Так
незначительные колебания температуры будут происходить в зависимости от того, какое вещество
произвольно выбран для эталонного термометра. С другой
стороны, второй закон требует, чтобы все вещества, используемые в Carnot
цикл даст ту же температуру Карно без отклонений
разрешено. Можно отметить, что определение температуры, используемое в
эта глава полностью соответствует главе Кельвина, потому что
Все вещества
включают идеальные газы.
Тепловые насосы и холодильники — Физика колледжа, главы 1-17
Сводка
- Опишите использование тепловых двигателей в тепловых насосах и холодильниках.
- Продемонстрируйте, как тепловой насос работает для обогрева внутреннего пространства.
- Объясните разницу между тепловыми насосами и холодильниками.
- Рассчитайте коэффициент полезного действия теплового насоса.
Рисунок 1. Практически в каждом доме есть холодильник.Большинство людей не осознают, что они тоже делят свои дома с тепловым насосом. (кредит: Id1337x, Wikimedia Commons)
Тепловые насосы, кондиционеры и холодильники используют передачу тепла от холода к горячему. Это тепловые двигатели, работающие задом наперед. Мы говорим «в обратном направлении», а не в обратном направлении, потому что, за исключением двигателей Карно, все тепловые двигатели, хотя они и могут работать в обратном направлении, не могут быть полностью реверсированы. Передача тепла происходит из холодного резервуара [латекс] \ boldsymbol {Q _ {\ textbf {c}}} [/ latex] в горячий. Для этого требуется ввод работы [латекс] \ boldsymbol {W}, [/ latex], который также преобразуется в теплопередачу.Таким образом, теплопередача к горячему резервуару составляет [латекс] \ boldsymbol {Q _ {\ textbf {h}} = Q _ {\ textbf {c}} + W}. [/ Latex] (Обратите внимание, что [latex] \ boldsymbol {Q_ {\ textbf {h}}}, \: \ boldsymbol {Q _ {\ textbf {c}}}, [/ latex] и [latex] \ boldsymbol {W} [/ latex] положительные, их направления указаны на схемах а не знаком.) Тепловой насос предназначен для передачи тепла [латекс] \ boldsymbol {Q _ {\ textbf {h}}} [/ latex] в теплую среду, например, в доме зимой. Кондиционеры и холодильники предназначены для передачи тепла [латекс] \ boldsymbol {Q _ {\ textbf {c}}} [/ latex] из прохладной окружающей среды, например, для охлаждения комнаты или хранения продуктов при более низких температурах, чем в среда.(Фактически, тепловой насос может использоваться как для обогрева, так и для охлаждения помещения. По сути, это кондиционер и нагревательный элемент в одном устройстве. В этом разделе мы сосредоточимся на его режиме обогрева.)
Рис. 2. Тепловые насосы, кондиционеры и холодильники — это тепловые машины, работающие в обратном направлении. Показанный здесь основан на (реверсивном) двигателе Карно. (а) Принципиальная схема, показывающая передачу тепла из холодного резервуара в теплый резервуар с помощью теплового насоса. Направления W , Q h и Q c противоположны направлениям в тепловом двигателе.(b) Диаграмма PV для цикла Карно, аналогичная показанной на рисунке 3, но в обратном порядке по пути ADCBA. Площадь внутри цикла отрицательная, что означает, что имеется сетевой ввод. Имеется передача тепла Q c в систему из холодного резервуара по пути DC и передача тепла Q h из системы в горячий резервуар по пути BA.
Большим преимуществом использования теплового насоса для поддержания тепла в доме, а не просто сжигания топлива является то, что тепловой насос подает [латекс] \ boldsymbol {Q _ {\ textbf {h}} = Q _ {\ textbf {c}} + W}.[/ latex] Теплоотдача происходит от наружного воздуха, даже при температуре ниже нуля, во внутреннее пространство. Вы платите только за [латекс] \ boldsymbol {W}, [/ latex] и получаете дополнительную теплоотдачу [латекса] \ boldsymbol {Q _ {\ textbf {c}}} [/ latex] снаружи бесплатно ; во многих случаях в отапливаемое пространство передается как минимум вдвое больше энергии, чем используется для работы теплового насоса. Когда вы сжигаете топливо, чтобы согреться, вы платите за все. Недостатком является то, что затраты на работу (требуемые вторым законом термодинамики) иногда дороже, чем просто сжигание топлива, особенно если работа выполняется за счет электроэнергии.
Основные компоненты теплового насоса в режиме нагрева показаны на рисунке 3. Используется рабочая жидкость, например хладагент, не содержащий CFC. В наружных змеевиках (испарителе) теплопередача [латекс] \ boldsymbol {Q _ {\ textbf {c}}} [/ latex] происходит от холодного наружного воздуха к рабочему телу, превращая его в газ.
Рис. 3. Простой тепловой насос состоит из четырех основных компонентов: (1) конденсатор, (2) расширительный клапан, (3) испаритель и (4) компрессор. В режиме нагрева теплопередача Q c происходит к рабочему телу в испарителе (3) из более холодного наружного воздуха, превращая его в газ.Компрессор с электрическим приводом (4) увеличивает температуру и давление газа и нагнетает его в змеевики конденсатора (1) внутри отапливаемого пространства. Поскольку температура газа выше, чем температура в комнате, передача тепла от газа к комнате происходит, когда газ конденсируется в жидкость. Затем рабочая жидкость охлаждается, поскольку она течет обратно через расширительный клапан (2) к змеевикам испарителя наружного блока.
Компрессор с электрическим приводом (рабочая нагрузка [латекс] \ boldsymbol {W} [/ latex]) повышает температуру и давление газа и нагнетает его в змеевики конденсатора, которые находятся внутри отапливаемого пространства.Поскольку температура газа выше, чем температура внутри комнаты, происходит передача тепла в комнату, и газ конденсируется в жидкость. Затем жидкость течет обратно через редукционный клапан к змеевикам испарителя наружного блока, охлаждаясь за счет расширения. (В цикле охлаждения змеевики испарителя и конденсатора меняются ролями, и направление потока жидкости меняется на противоположное.)
Качество теплового насоса оценивается по тому, сколько тепла [латекс] \ boldsymbol {Q _ {\ textbf {h}}} [/ latex] происходит в теплое пространство, по сравнению с тем, сколько работы [латекс] \ boldsymbol { W} [/ latex] не требуется.Исходя из соотношения того, что вы получаете к затраченным средствам, мы определяем коэффициент полезного действия теплового насоса ([latex] \ boldsymbol {\ textbf {COP} _ {\ textbf {hp}}} [/ latex ]) быть
[латекс] \ boldsymbol {\ textbf {COP} _ {\ textbf {hp}} =} [/ latex] [латекс] \ boldsymbol {\ frac {Q _ {\ textbf {h}}} {W}}. [ / латекс]
Поскольку эффективность теплового двигателя равна [латекс] \ boldsymbol {Eff = W / Q _ {\ textbf {h}}}, [/ latex], мы видим, что [латекс] \ boldsymbol {\ textbf {COP} _ {\ textbf {hp}} = 1 / Eff}, [/ latex] важный и интересный факт.Во-первых, поскольку эффективность любого теплового двигателя меньше 1, это означает, что [latex] \ textbf {COP} _ {\ textbf {hp}} [/ latex] всегда больше 1, то есть тепловой насос всегда имеет больше теплопередачи [латекс] \ boldsymbol {Q _ {\ textbf {h}}} [/ latex], чем вложено в него усилий. Во-вторых, это означает, что тепловые насосы лучше всего работают при небольших перепадах температур. Эффективность идеального, или двигателя Карно, равна [latex] \ boldsymbol {Eff _ {\ textbf {C}} = 1- (T _ {\ textbf {c}} / T _ {\ textbf {h}})}; [ / latex] таким образом, чем меньше разница температур, тем меньше эффективность и больше [латекс] \ boldsymbol {\ textbf {COP} _ {\ textbf {hp}}} [/ latex] (потому что [latex] \ boldsymbol {\ textbf {COP} _ {\ textbf {hp}} = 1 / Eff} [/ latex]).Другими словами, тепловые насосы не работают так хорошо в очень холодном климате, как в более умеренном.
Трение и другие необратимые процессы снижают эффективность теплового двигателя, но они приносят пользу работе теплового насоса. не . в тепловой насос.
Рис. 4. Когда реальный тепловой двигатель работает в обратном направлении, часть предполагаемых затрат работы ( W ) идет на теплопередачу до того, как он попадет в тепловой двигатель, тем самым снижая его коэффициент полезного действия COP л.с. .На этом рисунке W ‘ представляет собой часть W , которая идет в тепловой насос, в то время как остаток W теряется в виде тепла трения ( Q f ) в холодный резервуар. Если бы весь W пошел в тепловой насос, то Q h было бы больше. В лучшем тепловом насосе используются адиабатические и изотермические процессы, поскольку теоретически не было бы диссипативных процессов, снижающих передачу тепла к горячему резервуару.
Пример 1: Лучший
COP л.с. теплового насоса для домашнего использования
Тепловой насос, используемый для обогрева дома, должен использовать цикл, который производит рабочую жидкость при температурах выше, чем типичная температура в помещении, чтобы могла происходить передача тепла внутрь. Точно так же он должен производить рабочую жидкость при температурах ниже, чем температура наружного воздуха, чтобы передача тепла происходила извне. Поэтому его горячая и холодная резервуарные температуры не могут быть слишком близкими, что ограничивает его [латекс] \ boldsymbol {COP _ {\ textbf {hp}}}.{\ circ} \ textbf {C}}? [/ latex]
Стратегия
Перевернутый двигатель Карно будет работать с максимальной производительностью в качестве теплового насоса. Как отмечалось выше, [latex] \ boldsymbol {COP _ {\ textbf {hp}} = 1 / Eff}, [/ latex], поэтому нам нужно сначала вычислить эффективность Карно, чтобы решить эту проблему.
Решение
Эффективность Карно по абсолютной температуре определяется по формуле :
.
[латекс] \ boldsymbol {Eff _ {\ textbf {C}} = 1 -} [/ latex] [latex] \ boldsymbol {\ frac {T _ {\ textbf {c}}} {T _ {\ textbf {h}} }}.[/ латекс]
Температура в градусах Кельвина составляет [латекс] \ boldsymbol {T _ {\ textbf {h}} = 318 \ textbf {K}} [/ latex] и [latex] \ boldsymbol {T _ {\ textbf {c}} = 258 \ textbf {K}}, [/ latex] так что
[латекс] \ boldsymbol {Eff _ {\ textbf {C}} = 1 -} [/ latex] [latex] \ boldsymbol {\ frac {258 \ textbf {K}} {318 \ textbf {K}}} [/ латекс] [латекс] \ boldsymbol {= 0,1887}. [/ латекс]
Таким образом, из обсуждения выше,
[латекс] \ boldsymbol {COP _ {\ textbf {hp}} =} [/ latex] [latex] \ boldsymbol {\ frac {1} {Eff}} [/ latex] [latex] \ boldsymbol {=} [/ латекс] [латекс] \ boldsymbol {\ frac {1} {0.1887}} [/ latex] [latex] \ boldsymbol {= 5.30}, [/ latex]
или
[латекс] \ boldsymbol {COP _ {\ textbf {hp}} =} [/ latex] [латекс] \ boldsymbol {\ frac {Q _ {\ textbf {h}}} {W}} [/ латекс] [латекс] \ boldsymbol {= 5.30}, [/ латекс]
, так что
[латекс] \ boldsymbol {Q _ {\ textbf {h}} = 5.30 \ textbf {W}}. [/ Latex]
Обсуждение
Это означает, что теплопередача тепловым насосом в 5,30 раз больше, чем вложенная в него работа. Это будет стоить в 5,30 раза больше для той же теплопередачи от электрического комнатного обогревателя, чем для теплопередачи, производимой этим тепловым насосом.Это не нарушение сохранения энергии. Холодный окружающий воздух обеспечивает 4,3 Дж на 1 Дж работы от электрической розетки.
Рис. 5. Теплоотдача снаружи внутрь, а также работа, выполняемая для запуска насоса, происходит в тепловом насосе из приведенного выше примера. Обратите внимание, что холодная температура, создаваемая тепловым насосом, ниже, чем температура наружного воздуха, поэтому происходит передача тепла рабочей жидкости. Компрессор насоса создает температуру выше температуры в помещении для передачи тепла в дом.
Настоящие тепловые насосы работают не так хорошо, как идеальный в предыдущем примере; их значения [латекс] \ boldsymbol {COP _ {\ textbf {hp}}} [/ latex] варьируются от 2 до 4. Этот диапазон означает, что теплопередача [латекс] \ boldsymbol {Q _ {\ textbf {h}} } [/ latex] от тепловых насосов в 2-4 раза больше, чем работа [latex] \ boldsymbol {W} [/ latex], вложенная в них. Однако их экономическая осуществимость все еще ограничена, поскольку [латекс] \ boldsymbol {W} [/ latex] обычно поставляется за счет электроэнергии, которая стоит больше на джоуль, чем передача тепла за счет сжигания топлива, такого как природный газ.Кроме того, первоначальная стоимость теплового насоса выше, чем у многих печей, поэтому тепловой насос должен работать дольше, чтобы окупить его стоимость. Тепловые насосы, скорее всего, будут экономически лучше там, где зимние температуры мягкие, электричество относительно дешево, а другие виды топлива относительно дороги. Кроме того, поскольку они могут охлаждать и обогревать помещение, они имеют преимущества там, где также желательно охлаждение в летние месяцы. Таким образом, одни из лучших мест для тепловых насосов — теплый летний климат с прохладной зимой.На рисунке 6 показан тепловой насос, называемый в некоторых странах « обратным циклом» или «охладителем сплит-системы » .
Рисунок 6. В жаркую погоду теплопередача происходит от воздуха внутри помещения к воздуху снаружи, охлаждая помещение. В прохладную погоду происходит передача тепла от воздуха снаружи к воздуху внутри, нагревая комнату. Это переключение достигается за счет изменения направления потока рабочей жидкости на противоположное.
Кондиционеры и холодильники предназначены для охлаждения чего-либо в теплой среде.Как и в случае с тепловыми насосами, для передачи тепла от холода к горячему требуется дополнительная работа, а это дорого. О качестве кондиционеров и холодильников судят по тому, сколько тепла [латекс] \ boldsymbol {Q _ {\ textbf {c}}} [/ latex] происходит из холодной среды, по сравнению с тем, сколько работы [латекс] \ boldsymbol { W} [/ latex] не требуется. То, что считается преимуществом теплового насоса, в холодильнике считается отходящим теплом. Таким образом, мы определяем коэффициент полезного действия [латекс] \ boldsymbol {(COP _ {\ textbf {ref}})} [/ latex] кондиционера или холодильника как
.
[латекс] \ boldsymbol {COP _ {\ textbf {ref}} =} [/ latex] [латекс] \ boldsymbol {\ frac {Q _ {\ textbf {c}}} {W}}.[/ латекс]
Еще раз отмечая, что [латекс] \ boldsymbol {Q _ {\ textbf {h}} = Q _ {\ textbf {c}} + W}, [/ latex], мы видим, что кондиционер будет иметь более низкий коэффициент полезного действия, чем тепловой насос, потому что [латекс] \ boldsymbol {COP _ {\ textbf {hp}} = Q _ {\ textbf {h}} / W} [/ latex] и [latex] \ boldsymbol {Q _ {\ textbf {h}} } [/ latex] больше, чем [latex] \ boldsymbol {Q _ {\ textbf {c}}}. [/ latex] В задачах и упражнениях этого модуля вы покажете, что
[латекс] \ boldsymbol {COP _ {\ textbf {ref}} = COP _ {\ textbf {hp}} — 1} [/ latex]
для теплового двигателя, используемого в качестве кондиционера или теплового насоса, работающего между двумя одинаковыми температурами.Настоящие кондиционеры и холодильники обычно работают замечательно, имея значения [latex] \ boldsymbol {COP _ {\ textbf {ref}}} [/ latex] в диапазоне от 2 до 6. Эти числа лучше, чем [latex] \ boldsymbol { Значения COP _ {\ textbf {hp}}} [/ latex] для упомянутых выше тепловых насосов, потому что разница температур меньше, но они меньше, чем у двигателей Карно, работающих между теми же двумя температурами.
Был разработан тип системы оценки [latex] \ boldsymbol {COP} [/ latex], которая называется «рейтинг энергоэффективности» ([latex] \ boldsymbol {EER} [/ latex]).Этот рейтинг является примером того, что единицы, не относящиеся к системе СИ, по-прежнему используются и актуальны для потребителей. Чтобы упростить жизнь потребителю, Австралия, Канада, Новая Зеландия и США используют рейтинг Energy Star из 5 звезд — чем больше звездочек, тем более энергоэффективным является устройство. [Latex] \ boldsymbol {EER \ textbf {s }} [/ latex] выражаются в смешанных единицах британских тепловых единиц (Btu) за час нагрева или охлаждения, деленных на потребляемую мощность в ваттах. Комнатные кондиционеры легко доступны с [латексом] \ boldsymbol {EER \ textbf {s}} [/ latex] в диапазоне от 6 до 12.Хотя это не то же самое, что только что описанный [latex] \ boldsymbol {COP \ textbf {s}} [/ latex], эти [latex] \ boldsymbol {EER \ textbf {s}} [/ latex] хороши для целей сравнения — чем больше [латекс] \ boldsymbol {EER}, [/ latex], тем дешевле будет эксплуатироваться кондиционер (но тем выше, вероятно, будет его покупная цена).
[латекс] \ boldsymbol {EER} [/ latex] кондиционера или холодильника можно выразить как
[латекс] \ boldsymbol {EER =} [/ latex] [латекс] \ boldsymbol {\ frac {Q _ {\ textbf {c}} / t_1} {W / t_2}}, [/ latex]
где [latex] \ boldsymbol {Q _ {\ textbf {c}}} [/ latex] — это количество теплопередачи от холодной среды в британских тепловых единицах, [latex] \ boldsymbol {t_1} [/ latex] — время в часах, [latex] \ boldsymbol {W} [/ latex] — это вводимая работа в джоулях, а [latex] \ boldsymbol {t_2} [/ latex] — время в секундах.
СТРАТЕГИИ РЕШЕНИЯ ПРОБЛЕМ ДЛЯ ТЕРМОДИНАМИКИ
- Изучите ситуацию, чтобы определить, задействовано ли тепло, работа или внутренняя энергия. Найдите любую систему, в которой основными методами передачи энергии являются тепло и работа. Тепловые двигатели, тепловые насосы, холодильники и кондиционеры являются примерами таких систем.
- Определите интересующую систему и нарисуйте помеченную диаграмму системы, показывающую поток энергии.
- Определите, что именно необходимо определить в проблеме (определите неизвестные). Письменный список полезен. Максимальная эффективность означает, что задействован двигатель Карно. Эффективность — это не то же самое, что коэффициент полезного действия.
- Составьте список того, что дано или может быть выведено из проблемы, как указано (укажите известные). Обязательно отличите теплопередачу в системе от теплопередачи из системы, а также вложенную работу от выходной мощности. Во многих ситуациях полезно определить тип процесса, например изотермический или адиабатический.
- Решите соответствующее уравнение для количества, которое необходимо определить (неизвестное).
- Подставьте известные величины вместе с их единицами измерения в соответствующее уравнение и получите численные решения с указанием единиц.
- Проверьте ответ, чтобы узнать, разумен ли он: имеет ли он смысл? Например, КПД всегда меньше 1, тогда как коэффициенты производительности больше 1.
- Артефакт второго закона термодинамики — это способность обогревать внутреннее пространство с помощью теплового насоса.Тепловые насосы сжимают холодный окружающий воздух и при этом нагревают его до комнатной температуры без нарушения принципов консервации.
- Чтобы рассчитать коэффициент полезного действия теплового насоса, используйте уравнение [латекс] \ boldsymbol {COP _ {\ textbf {hp}} = \ frac {Q _ {\ textbf {h}}} {W}}. [/ Latex]
- Холодильник — это тепловой насос; он забирает теплый окружающий воздух и расширяет его, чтобы охладить.
Концептуальные вопросы
1: Объясните, почему тепловые насосы не работают в очень холодном климате так же хорошо, как в более мягком.То же самое и с холодильниками?
2: В некоторых странах Северной Европы дома строятся без каких-либо систем отопления. Они очень хорошо изолированы и согреваются теплом тела жителей. Однако, когда жителей нет дома, в этих домах все равно тепло. Какое возможное объяснение?
3: Почему холодильники, кондиционеры и тепловые насосы работают наиболее рентабельно для циклов с небольшой разницей между [латексом] \ boldsymbol {T _ {\ textbf {h}}} [/ латексом] и [латексом] \ boldsymbol {T _ {\ textbf {c}}}? [/ latex] (Обратите внимание, что температура используемого цикла имеет решающее значение для его [латекса] \ boldsymbol {COP} [/ latex].)
4: Менеджеры продуктовых магазинов утверждают, что общее потребление энергии летом составляет минус , если в магазине поддерживается низкая температура . Приведите аргументы в поддержку или опровержение этого утверждения, учитывая, что в магазине множество холодильников и морозильников.
5: Можно ли охладить кухню, оставив дверцу холодильника открытой?
Задачи и упражнения
1: Каков коэффициент полезного действия идеального теплового насоса с теплопередачей при холодной температуре [латекс] \ boldsymbol {-25.6 \ textbf {J}} [/ latex] (один киловатт-час)? (c) Обсудите, насколько реалистична эта стоимость. Обратите внимание, что рейтинг энергоэффективности [латекс] (\ boldsymbol {EER}) [/ latex] кондиционера или холодильника определяется как количество британских тепловых единиц теплопередачи из холодной среды в час, деленное на ватт входная мощность.
10: Покажите, что коэффициенты производительности холодильников и тепловых насосов связаны соотношением [латекс] \ boldsymbol {COP _ {\ textbf {ref}} = COP _ {\ textbf {hp}} — 1}.[/ латекс]
Начните с определения [latex] \ boldsymbol {COP} [/ latex] s и отношения сохранения энергии между [латексом] \ boldsymbol {Q _ {\ textbf {h}}}, \: \ boldsymbol {Q_ { \ textbf {c}}}, [/ latex] и [latex] \ boldsymbol {W}. [/ latex]
Глоссарий
- тепловой насос
- Аппарат, передающий тепло от холода к горячему
- КПД
- для теплового насоса — это отношение теплопередачи на выходе (горячий резервуар) к произведенной работе; для холодильника или кондиционера это отношение теплоотдачи от холодного резервуара к произведенной работе
Решения
Задачи и упражнения
1:
4.7 \ textbf {J}} [/ latex]
(б) 40 центов
(c) Эта стоимость кажется вполне реальной; там говорится, что работа кондиционера в течение всего дня будет стоить 9,59 долларов (если он будет работать непрерывно).
