получил нагревателя количество теплоты
|
| ||||||
| Специальный поиск | ||||||
|
Физика
Теория вероятностей и мат. статистика
Гидравлика
Теор. механика
Прикладн. механика
Химия
Электроника
Витамины для ума
| Главная Поиск по сайту Формулы Все задачи Помощь Контакты Билеты
| |||||
получил нагревателя количество теплоты Задача 50319 Газ, являясь рабочим веществом в цикле Карно, получил от нагревателя количество теплоты Q1 = 4,36 кДж и совершил при этом работу А = 2,4 кДж. Определить температуру нагревателя, если температура холодильника Т2 = 273 К.
Задача 26403 Идеальная тепловая машина работает по циклу Карно. При этом N = 55% количества теплоты, получаемой от нагревателя, передается холодильнику. Машина получает от нагревателя при температуре t1 = 250 °С количество теплоты Q = 10 кДж. Определите КПД цикла; работу, совершаемую за один цикл, и температуру холодильника t2.
Задача 17311 Тепловая машина Карно совершает работу с двумя молями одноатомного идеального газа между тепловым резервуаром с температурой 327°С и холодильником с температурой 27°С. Отношение наибольшего объема газа к наименьшему объему в данном процессе равно восьми. Какую работу совершает машина за один цикл? Какое количество теплоты получает от нагревателя и отдает холодильнику? Чему равно изменение энтропии при изотермическом сжатии?
Задача 17905 Определить работу идеальной тепловой машины за один цикл, если она в течение цикла получает от нагревателя количество теплоты 2095 Дж.
Задача 21171 Цикл состоит из процессов, изображенных на рисунке. При этом V1 = 1 м3, V2 = 3 м3, р2 = 104 Па. Кривая 1-3 изотерма. (Т = 500 К). Найти полезную работу; количество теплоты, переданное холодильнику; количество теплоты, полученное от нагревателя; КПД цикла.
Задача 22040 Идеальная тепловая машина 80% теплоты, получаемой от нагревателя, передает холодильнику. Количество теплоты, получаемое от нагревателя за 1 цикл ΔQ = 0,625 кДж. Найти: 1) КПД цикла; 2) работу, совершаемую при полном цикле.
| ||||||
Термодинамика — Студопедия
Поделись
Цель занятия: применение теоретических знаний для решения задач.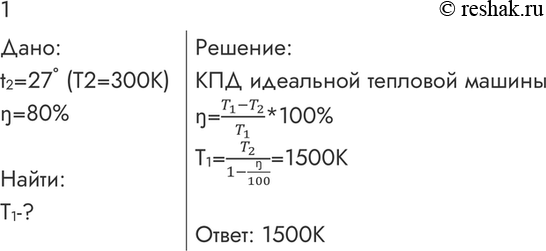
Подготовка к занятию: лекции № 32–34. Касьянов В.А. Физика-10 § 45-49.
В-1
Задание на занятие:
1. Может ли повыситься температура газа без его нагревания, т.е. без теплопередачи?
2. Рассчитать изменение внутренней энергии воздуха массой 5 кг при нагревании от 10 до 30 . Молярную массу воздуха следует принять равной 4 г/моль.
3. Найдите работу идеального газа при изобарном расширении от начального объёма 10 л до конечного 15 л, если давление газа 104 Па постоянно. Вычислите изменение внутренней энергии газа.
4. Водород массой 20 г нагревается изобарно от температуры 300 К до температуры 350 К. Какую работу совершает газ при этом нагревании? Найдите изменение его внутренней энергии в результате этого процесса.
5. С какой скоростью (в м/с) должна лететь свинцовая пуля, чтобы расплавиться при ударе о стену? Температура летящей пули 120 °С. Считать, что всё количество теплоты, выделившееся при ударе, пошло на нагревание и плавление пули. Удельная теплоемкость и удельная теплота плавления свинца равны соответственно 126 Дж/(кг•°С) и 300 кДж/кг. Температура плавления свинца равна 327 °С.
Удельная теплоемкость и удельная теплота плавления свинца равны соответственно 126 Дж/(кг•°С) и 300 кДж/кг. Температура плавления свинца равна 327 °С.
6. В идеальной тепловой машине за счёт каждого килоджоуля энергии, получаемой от нагревателя, совершается работа 400 Дж. Определите КПД машины и температуру нагревателя, если температура холодильника 300 К.
7. Какое количество теплоты было подведено к идеальному газу, если работа, совершаемая газом при изобарном расширении, составляет 3,8 кДж?
8. Газ переводится из состояния 1 в состояние 2 двумя различными способами: 1-а-2; 1-б-2.
а) В каком из этих случаев совершается большая работа? Во сколько раз отличаются работы?
б) Какому состоянию газа соответствует наименьшая температура?
В-2
Задание на занятие:
1. Почему для изобарного нагревания газа требуется большее количество теплоты, чем для изохорного на столько же Кельвин?
2. Рассчитать изменение внутренней энергии гелия массой 7 кг при нагревании от 23 до 50 .
3. Для изобарного нагревания газа, количество которого равно 830 моль, на 750 К газу сообщили количество теплоты, равное 6,5 МДж. Определите работу газа и изменение его внутренней энергии.
4. Найдите работу идеального газа при изобарном сжатии от начального объёма 40 л до конечного 15 л, если давление газа 104 Па постоянно. Вычислите изменение внутренней энергии газа.
5. С какой высоты должен упасть кусок льда, имеющий температуру -1 , чтобы при ударе о землю он полностью расплавился? Удельная теплоемкость и удельная теплота плавления льда равны соответственно 2100 Дж/(кг•°К) и 332 кДж/кг. Температура плавления льда равна 0 °С.
6. Какое количество теплоты получил азот массой 6 г при изобарном нагревании на 100К?
7. В идеальной тепловой машине за счёт каждого килоджоуля энергии, получаемой от нагревателя, совершается работа 600 Дж. Определите КПД машины и температуру нагревателя, если температура холодильника 200 К.
8. При изобарном нагревании объем гелия увеличился в 3 раза
(см. рис.). Какую работу совершил газ? Какое количество теплоты ему передано? Масса гелия 12 г, начальная температура равна -123 °C.
рис.). Какую работу совершил газ? Какое количество теплоты ему передано? Масса гелия 12 г, начальная температура равна -123 °C.
Содержание отчёта:
1. Записать наименование и цель занятия.
2. Ответить на контрольные вопросы и получить допуск к работе.
3. Выполнить задания.
Контрольные вопросы:
1. Как рассчитать значение внутренней энергии идеального газа?
2. Записать формулу работы идеального газа при изобарном нагревании?
3. Как рассчитать количество теплоты нагревания, плавления, парообразования?
4. Сформулируйте первый закон термодинамики.
5. Сформулируйте второй закон термодинамики.
6. Записать формулу для расчёта КПД тепловой машины.
ПРИЛОЖЕНИЕ
Термодинамика — наука о наиболее общих свойствах макроскопических физических систем, находящихся в состоянии термодинамического равновесия и о процессах перехода между этими состояниями.
Внутренняя энергия тела — это суммарная кинетическая энергия движения молекул тела и потенциальная энергия их взаимодействия.
· Для идеального газа :
· Для реального газа :
Количество теплоты-часть внутренней энергии, теряемой или приобретаемой телом при теплопередаче.
Нагревание (охлаждение):
Плавление (отвердевание):
Парообразование (конденсация):
Горение топлива:
Работа в термодинамике-процесс изменения внутренней энергии системы, связанный с перемещением ее частей друг относительно друга.
· Изохорный процесс (1) :
· Изобарный процесс (2) :
· Изотермический процесс (3):
Первый закон термодинамики:
Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе:
Второй закон термодинамики:
Невозможно передать тепло от холодной системе к горячей без изменений в них или в окружающих телах.
Тепловой двигатель-устройство для преобразования внутренней энергии в механическую.
КПД тепловой машины:
КПД идеальной тепловой машины:
Применение I начала термодинамики к изопроцессам:
1.
2.
3.
Практическая работа № 8.
Беспорядок и нехватка энергии – Колледж физики, главы 1-17
15 Термодинамика
Резюме
- Дайте определение энтропии и рассчитайте прирост энтропии в системе с обратимыми и необратимыми процессами.
- Объясните ожидаемую судьбу Вселенной в терминах энтропии.
- Рассчитать возрастающий беспорядок в системе.
Рисунок 1. Лед в этом напитке медленно тает. В конце концов жидкость достигнет теплового равновесия, как и предсказывает второй закон термодинамики. (кредит: Джон Салливан, PDPhoto.org)
Есть еще один способ выразить второй закон термодинамики. Эта версия относится к концепции под названием энтропия . Изучив его, мы увидим, что направления, связанные со вторым законом — например, передача тепла от горячего к холодному — связаны с естественной тенденцией систем становиться неупорядоченными и с меньшим количеством энергии, доступной для использования в качестве работы. Фактически можно показать, что энтропия системы является мерой ее беспорядка и недоступности энергии для совершения работы.
Изучив его, мы увидим, что направления, связанные со вторым законом — например, передача тепла от горячего к холодному — связаны с естественной тенденцией систем становиться неупорядоченными и с меньшим количеством энергии, доступной для использования в качестве работы. Фактически можно показать, что энтропия системы является мерой ее беспорядка и недоступности энергии для совершения работы.
УСТАНОВЛЕНИЕ СОЕДИНЕНИЙ: ЭНТРОПИЯ, ЭНЕРГИЯ И РАБОТА
Вспомните, что простое определение энергии — это способность выполнять работу. Энтропия — это мера того, сколько энергии недоступно для выполнения работы. Хотя все формы энергии взаимопреобразуемы и все они могут быть использованы для совершения работы, даже в принципе не всегда возможно преобразовать всю доступную энергию в работу. Эта недоступная энергия представляет интерес для термодинамики, потому что область термодинамики возникла из усилий по преобразованию тепла в работу.
Мы можем увидеть, как определяется энтропия, вспомнив наше обсуждение двигателя Карно. Мы отметили, что для цикла Карно и, следовательно, для любых обратимых процессов \textbf{h}}}.[/latex]Перестановка терминов дает
Мы отметили, что для цикла Карно и, следовательно, для любых обратимых процессов \textbf{h}}}.[/latex]Перестановка терминов дает
[латекс]\boldsymbol{\frac{Q_{\textbf{c}}}{T_{\textbf{c}}}}[/latex] [латекс]\boldsymbol{=}[/латекс][латекс]\boldsymbol{\frac{Q_{\textbf{h}}}{T_{\textbf{h}}}}[/latex]
для любого обратимого процесс.[латекс]\boldsymbol{Q_{\textbf{c}}}[/latex] и [латекс]\boldsymbol{Q_{\textbf{h}}}[/latex]являются абсолютными значениями теплопередачи при температурах [латекс]\boldsymbol{T_{\textbf{c}}}[/latex] и [латекс]\boldsymbol{T_{\textbf{h}}},[/latex] соответственно. Это соотношение [латекс]\boldsymbol{Q/T}[/латекс] определяется как изменение энтропии [латекс]\boldsymbol{\Delta{S}}[/latex]для обратимого процесса,
[латекс]\boldsymbol{\Delta{S}=}[/latex][латекс]\boldsymbol {\left(\frac{Q}{T}\right)_{\textbf{rev}}},[/latex]
, где[latex]\boldsymbol{Q}[/latex] — теплопередача, которая положительна для теплопередачи внутрь и отрицательна для теплопередачи наружу, а[латекс]\boldsymbol{T}[/латекс]является абсолютной температурой, при которой происходит обратимый процесс. Единицей энтропии в системе СИ является джоуль на кельвин (Дж/К). Если температура изменяется во время процесса, то обычно хорошим приближением (для небольших изменений температуры) будет считать [латекс]\boldsymbol{T}[/латекс] средней температурой, избегая необходимости использования интегрального исчисления для нахождения [латекс]\boldsymbol{\Delta{S}}.[/латекс]
Единицей энтропии в системе СИ является джоуль на кельвин (Дж/К). Если температура изменяется во время процесса, то обычно хорошим приближением (для небольших изменений температуры) будет считать [латекс]\boldsymbol{T}[/латекс] средней температурой, избегая необходимости использования интегрального исчисления для нахождения [латекс]\boldsymbol{\Delta{S}}.[/латекс]
Определение [латекс]\жирныйсимвол{\Delta{S}}[/латекс] строго справедливо только для обратимых процессов, например, используемых в двигателе Карно. Однако мы можем найти[latex]\boldsymbol{\Delta{S}}[/latex]точно даже для реальных необратимых процессов. Причина в том, что энтропия[latex]\boldsymbol{S}[/latex]системы, как и внутренняя энергия[latex]\boldsymbol{U},[/latex]зависит только от состояния системы, а не от того, как она достиг такого состояния. Энтропия есть свойство состояния. Таким образом, изменение энтропии[латекс]\boldsymbol{\Delta{S}}[/латекс]системы между состоянием 1 и состоянием 2 одинаково, независимо от того, как происходит изменение. Нам просто нужно найти или представить себе обратимый процесс, который переводит нас из состояния 1 в состояние 2, и вычислить[latex]\boldsymbol{\Delta{S}}[/latex]для этого процесса. Это будет изменение энтропии для любого процесса, переходящего из состояния 1 в состояние 2 (см. рис. 2).0005 Рис. 2. Когда система переходит из состояния 1 в состояние 2, ее энтропия изменяется на одну и ту же величину Δ S независимо от того, следуют ли по гипотетическому обратимому пути или по реальному необратимому пути.
Нам просто нужно найти или представить себе обратимый процесс, который переводит нас из состояния 1 в состояние 2, и вычислить[latex]\boldsymbol{\Delta{S}}[/latex]для этого процесса. Это будет изменение энтропии для любого процесса, переходящего из состояния 1 в состояние 2 (см. рис. 2).0005 Рис. 2. Когда система переходит из состояния 1 в состояние 2, ее энтропия изменяется на одну и ту же величину Δ S независимо от того, следуют ли по гипотетическому обратимому пути или по реальному необратимому пути.
Теперь посмотрим на изменение энтропии двигателя Карно и его тепловых резервуаров за один полный цикл. Горячий резервуар имеет потерю энтропии[латекс]\boldsymbol{\Delta{S}_{\textbf{h}}=-Q_{\textbf{h}}/T_{\textbf{h}}},[/ латекс], потому что из него происходит передача тепла (помните, что когда тепло передается наружу, тогда [латекс]\boldsymbol{Q}[/латекс] имеет отрицательный знак). Холодный резервуар имеет прирост энтропии[латекс]\boldsymbol{\Delta{S}_{\textbf{c}}=Q_{\textbf{c}}/T_{\textbf{c}}},[/latex ]потому что в нем происходит теплопередача. (Мы предполагаем, что резервуары достаточно велики, чтобы их температура была постоянной.) Таким образом, общее изменение энтропии равно
(Мы предполагаем, что резервуары достаточно велики, чтобы их температура была постоянной.) Таким образом, общее изменение энтропии равно
[латекс] \boldsymbol{\Delta{S}_{\textbf{tot}}=\Delta{S}_{\textbf{h}}+\Delta{S}_{\textbf{c}}} .[/latex]
Таким образом, поскольку мы знаем, что [латекс]\boldsymbol{Q _{\textbf{h}}/T _{\textbf{h}}=Q _{\textbf{c}}/T _{\textbf {c}}}[/latex]для двигателя Карно,
[латекс]\boldsymbol{\Delta{S}_{\textbf{tot}}=-}[/latex][латекс]\boldsymbol{\frac {Q_{\textbf{h}}}{T_{\textbf{h}}}}[/latex][latex]\boldsymbol{+}[/latex][latex]\boldsymbol{\frac{Q_{\textbf {c}}}{T_{\textbf{c}}}}[/latex][latex]\boldsymbol{=0}.[/latex]
Этот общий результат означает, что полное изменение энтропии системы в любом обратимом процессе равно нулю.
Энтропия различных частей системы может изменяться, но общее изменение равно нулю. Кроме того, система не влияет на энтропию своего окружения, так как между ними не происходит теплообмена. Таким образом, обратимый процесс не меняет ни полной энтропии системы, ни энтропии ее окружения. {\circ}\textbf{C})},[ /latex] при условии, что ни в одном из резервуаров нет изменения температуры. (См. рис. 3.)
{\circ}\textbf{C})},[ /latex] при условии, что ни в одном из резервуаров нет изменения температуры. (См. рис. 3.)
Стратегия
Как рассчитать изменение энтропии для необратимого процесса, если [латекс]\boldsymbol{\Delta{S}_{\textbf{tot}}=\Delta{S}_{\textbf{ h}}+\Delta{S}_{\textbf{c}}}[/latex]действителен только для обратимых процессов? Помните, что общее изменение энтропии горячего и холодного резервуаров будет одинаковым независимо от того, идет ли речь об обратимом или необратимом процессе передачи тепла от горячего к холодному. Итак, мы можем рассчитать изменение энтропии горячего резервуара для гипотетического обратимого процесса, при котором от него происходит теплоотдача 4000 Дж; то делаем то же самое для гипотетического обратимого процесса, при котором теплопередача 4000 Дж происходит в холодный резервуар. Это приводит к тем же изменениям в горячем и холодном резервуарах, которые произошли бы, если бы теплопередача между ними происходила необратимо, и, таким образом, вызывает такие же изменения энтропии.
Решение
Теперь вычислим два изменения энтропии, используя [латекс]\boldsymbol{\Delta{S}_{\textbf{tot}}=\Delta{S}_{\textbf{h}}+ \Delta{S}_{\textbf{c}}}.[/latex]Во-первых, для теплопередачи от горячего резервуара,
[латекс]\boldsymbol{\Delta{S}_{\textbf{h} }=}[/латекс][латекс]\boldsymbol{\frac{-Q _{\textbf{h}}}{T _{\textbf{h}}}}[/latex][латекс]\boldsymbol{=}[ /латекс][латекс]\boldsymbol{\frac{-4000\textbf{J}}{600\textbf{K}}}[/latex][латекс]\boldsymbol{=-6,67\textbf{J/K}} .[/латекс]
А для холодного резервуара
[латекс]\boldsymbol{\Delta{S}_{\textbf{c}}=}[/latex][латекс]\boldsymbol{\frac{Q_{\textbf{c }}}{T _{\textbf{c}}}}[/latex][latex]\boldsymbol{=}[/latex][latex]\boldsymbol{\frac{4000\textbf{J}}{250\textbf { K}}}[/latex][latex]\boldsymbol{=16.0\textbf{ J/K}}.[/latex]
Таким образом, общее количество равно
[latex]\begin{array}{lcl} \ boldsymbol{\Delta{S}_{\textbf{tot}}} & \boldsymbol{=} & \boldsymbol{\Delta{S}_{\textbf{h}}+\Delta{S}_{\textbf{ c}}} \\ {}& \boldsymbol{=} & \boldsymbol{(-6,67 +16,0)\textbf{ J/K}} \\ {} & \boldsymbol{=} & \boldsymbol{9. 33\textbf{ Дж/К}.} \end{array}[/latex]
33\textbf{ Дж/К}.} \end{array}[/latex]
Обсуждение
Существует увеличение энтропии для системы двух тепловых резервуаров, подвергающихся этому необратимому переносу тепла. Мы увидим, что это означает потерю способности выполнять работу с переданной энергией. Энтропия увеличилась, и энергия стала недоступна для выполнения работы.
Рис. 3. (а) Теплопередача от горячего объекта к холодному является необратимым процессом, приводящим к общему увеличению энтропии. б) одно и то же конечное состояние и, следовательно, одинаковое изменение энтропии у объектов достигается, если между двумя объектами происходят обратимые процессы теплообмена, температуры которых совпадают с температурами соответствующих объектов в необратимом процессе.
Логично, что энтропия увеличивается при передаче тепла от горячего к холодному. Поскольку изменение энтропии равно[latex]\boldsymbol{Q/T},[/latex]существует большее изменение при более низких температурах. Таким образом, уменьшение энтропии горячего объекта меньше, чем увеличение энтропии холодного объекта, что приводит к общему увеличению, как и в предыдущем примере. Этот результат очень общий:
Таким образом, уменьшение энтропии горячего объекта меньше, чем увеличение энтропии холодного объекта, что приводит к общему увеличению, как и в предыдущем примере. Этот результат очень общий:
Энтропия увеличивается для любой системы, подвергающейся необратимому процессу.
Что касается энтропии, то есть только две возможности: энтропия постоянна для обратимого процесса и возрастает для необратимого процесса. Существует четвертая версия второго закона термодинамики, сформулированного в терминах энтропии :
Полная энтропия системы либо увеличивается, либо остается постоянной в любом процессе; она никогда не уменьшается.
Например, теплопередача не может происходить самопроизвольно от холодного к горячему, потому что энтропия уменьшилась бы.
Энтропия сильно отличается от энергии. Энтропия не сохраняется, а возрастает во всех реальных процессах. Обратимые процессы (например, в двигателях Карно) — это процессы, в которых происходит наибольшая передача тепла для работы, а также те, которые поддерживают постоянную энтропию. Таким образом, мы приходим к установлению связи между энтропией и наличием энергии для выполнения работы.
Таким образом, мы приходим к установлению связи между энтропией и наличием энергии для выполнения работы.
Что означает изменение энтропии и почему оно должно нас интересовать? Одна из причин заключается в том, что энтропия напрямую связана с тем, что не всякая теплопередача может быть преобразована в работу. Следующий пример дает некоторое представление о том, как увеличение энтропии приводит к уменьшению передачи тепла в работу.
Пример 2. Меньшая работа производится при данной теплопередаче, когда изменение энтропии больше
(a) Рассчитайте работу двигателя Карно, работающего при температуре от 600 К до 100 К, при передаче 4000 Дж тепла двигателю. (b) Теперь предположим, что теплопередача 4000 Дж происходит сначала из резервуара с температурой 600 К в резервуар с температурой 250 К (без совершения какой-либо работы, что приводит к увеличению энтропии, вычисленной выше), а затем передается в двигатель Карно, работающий при температуре 250 К. и 100 К. Какой объем работы производится? (См. рис. 4.)
рис. 4.)
Стратегия
В обеих частях мы должны сначала вычислить эффективность Карно, а затем объем работы.
Решение (a)
Эффективность Карно определяется как {\textbf{c}}}{T_{\textbf{h}}}}.[/latex]
Замена данных температур дает
[латекс]\boldsymbol{Eff _{\textbf{C}}=1- }[/latex][latex]\boldsymbol{\frac{100\textbf{K}}{600\textbf{K}}}[/latex][latex]\boldsymbol{=0,833}.[/latex]
Теперь объем работы можно рассчитать, используя определение КПД любой тепловой машины, данное формулой
[латекс]\boldsymbol{Eff=}[/latex][латекс]\boldsymbol{\frac{W}{Q_{ \textbf{h}}}}.[/latex]
Решение для[latex]\boldsymbol{W}[/latex]и замена известных терминов дает
[latex]\begin{array}{lcl} \boldsymbol{ W} & \boldsymbol{=} & \boldsymbol{Eff_{\textbf{C}}Q_{\textbf{h}}} \\ {} & \boldsymbol{=} & \boldsymbol{(0,833)(4000\textbf { J})=3333\textbf{ J}.} \end{массив}[/latex] 9{\prime}_{\textbf{C}}Q_{\textbf{h}}} \\ {} & \boldsymbol{=} & \boldsymbol{(0,600)(4000\textbf{J})=2400\textbf {J}. } \end{array}[/latex]
} \end{array}[/latex]
Обсуждение
Во втором процессе при той же теплоотдаче работы меньше на 933 Дж. Этот результат важен. Одна и та же теплопередача в двух совершенных двигателях производит разную работу, потому что изменение энтропии в этих двух случаях различно. Во втором случае энтропия больше, а работы меньше. Энтропия связана с ип наличие энергии для выполнения работы.
Рис. 4. (a) Двигатель Карно, работающий при температуре от 600 К до 100 К, имеет теплопередачу 4000 Дж и выполняет работу 3333 Дж. (b) 4000 Дж тепла сначала необратимо передаются в резервуар с температурой 250 К, а затем переходят в двигатель Карно. Увеличение энтропии, вызванное передачей тепла в более холодный резервуар, приводит к уменьшению выхода работы на 2400 Дж. При совершении работы происходит постоянная потеря энергии в размере 933 Дж.
Когда энтропия увеличивается, определенное количество энергии становится постоянно недоступным для выполнения работы. Энергия не теряется, но изменяется ее характер, так что часть ее никогда не может быть превращена в совершение работы, то есть в организованную силу, действующую на расстоянии. Например, в предыдущем примере работа была выполнена на 933 Дж меньше после увеличения энтропии на 9,33 Дж/К при передаче тепла 4000 Дж из резервуара с температурой 600 К в резервуар с температурой 250 К. Можно показать, что количество энергии, которое становится недоступным для работы, равно
Энергия не теряется, но изменяется ее характер, так что часть ее никогда не может быть превращена в совершение работы, то есть в организованную силу, действующую на расстоянии. Например, в предыдущем примере работа была выполнена на 933 Дж меньше после увеличения энтропии на 9,33 Дж/К при передаче тепла 4000 Дж из резервуара с температурой 600 К в резервуар с температурой 250 К. Можно показать, что количество энергии, которое становится недоступным для работы, равно
[латекс]\boldsymbol{W_{\textbf{unavail}}=\Delta{S}\cdotp{T}_0},[/latex]
, где[латекс]\boldsymbol{T_0}[/латекс] — самая низкая используемая температура. В предыдущем примере
[латекс]\boldsymbol{W_{\textbf{unavail}}=(9.33\textbf{J/K})(100\textbf{K})=933\textbf{J}}[/latex]
как нашел.
В ранней энергичной Вселенной вся материя и энергия были легко взаимозаменяемы и идентичны по своей природе. Гравитация играла жизненно важную роль в молодой Вселенной. Хотя может и казался беспорядочным, и, следовательно, внешне энтропийным, на самом деле существовала огромная потенциальная энергия, доступная для выполнения работы — вся будущая энергия во Вселенной.
По мере взросления Вселенной возникала разница температур, что создавало больше возможностей для работы. Например, звезды горячее планет, которые теплее ледяных астероидов, а те еще теплее вакуума пространства между ними.
Большинство из них остывают после своего обычно бурного рождения, когда они были обеспечены собственной энергией — ядерной энергией в случае звезд, вулканической энергией на Земле и других планетах и так далее. Однако без дополнительных затрат энергии их дни сочтены.
По мере увеличения энтропии все меньше и меньше энергии во Вселенной доступно для выполнения работы. На Земле у нас все еще есть большие запасы энергии, такие как ископаемое и ядерное топливо; масштабные перепады температур, которые может обеспечить энергия ветра; геотермальная энергия из-за разницы температур в слоях Земли; и приливной энергии из-за нашего изобилия жидкой воды. При их использовании определенная доля содержащейся в них энергии никогда не может быть преобразована в работу. В конце концов, все топливо будет исчерпано, все температуры выровняются, и тепловые двигатели не смогут функционировать или выполнять работу.
В конце концов, все топливо будет исчерпано, все температуры выровняются, и тепловые двигатели не смогут функционировать или выполнять работу.
Энтропия увеличивается в замкнутой системе, такой как Вселенная. Но в некоторых частях Вселенной, например, в Солнечной системе, это не локально замкнутая система. Энергия течет от Солнца к планетам, пополняя запасы энергии Земли. Солнце будет продолжать снабжать нас энергией еще около пяти миллиардов лет. Мы будем наслаждаться прямой солнечной энергией, а также побочными эффектами солнечной энергии, такими как энергия ветра и энергия биомассы фотосинтезирующих растений. Энергия Солнца будет поддерживать нашу воду в жидком состоянии, а гравитационное притяжение Луны будет по-прежнему обеспечивать приливную энергию. Но геотермальная энергия Земли будет медленно иссякать и не будет пополняться.
Но с точки зрения Вселенной и очень долгосрочной, очень крупномасштабной картины, энтропия Вселенной увеличивается, и поэтому доступность энергии для выполнения работы постоянно уменьшается. В конце концов, когда все звезды умерли, все формы потенциальной энергии были использованы, и все температуры уравнялись (в зависимости от массы Вселенной, либо при очень высокой температуре после всемирного сжатия, либо при очень низкой температуре непосредственно перед вся деятельность прекращается) не будет возможности выполнять работу. 9{100}}[/latex]лет.
В конце концов, когда все звезды умерли, все формы потенциальной энергии были использованы, и все температуры уравнялись (в зависимости от массы Вселенной, либо при очень высокой температуре после всемирного сжатия, либо при очень низкой температуре непосредственно перед вся деятельность прекращается) не будет возможности выполнять работу. 9{100}}[/latex]лет.
Энтропия связана не только с недоступностью энергии для выполнения работы — она также является мерой беспорядка. Это понятие было первоначально постулировано Людвигом Больцманом в 1800-х годах. Например, растопить глыбу льда — значит взять хорошо структурированную и упорядоченную систему молекул воды и превратить ее в беспорядочную жидкость, в которой молекулы не имеют фиксированных положений. (См. рис. 5.) В процессе происходит значительное увеличение энтропии, как видно из следующего примера. 9{\circ}\textbf{ C}}.[/latex]
Стратегия
Как и прежде, изменение энтропии можно рассчитать по определению [latex]\boldsymbol{\Delta{S}}[/ латекс], как только мы найдем энергию[латекс]\boldsymbol{Q}[/латекс], необходимую для таяния льда.
Решение
Изменение энтропии определяется как:
[латекс]\boldsymbol{\Delta{S}=}[/латекс][латекс]\boldsymbol{\frac{Q}{T}}. [/latex]
Здесь[latex]\boldsymbol{Q}[/latex]теплопередача, необходимая для растапливания 1,00 кг льда, равна 93\textbf{ J/K}.} \end{array}[/latex]
Обсуждение
Это значительное увеличение энтропии, сопровождающее увеличение беспорядка.
Рисунок 5. Когда лед тает, он становится более неупорядоченным и менее структурированным. Систематическое расположение молекул в кристаллической структуре заменяется более случайным и менее упорядоченным движением молекул без фиксированного положения или ориентации. Его энтропия увеличивается, потому что в него происходит передача тепла. Энтропия есть мера беспорядка. 9{\circ}\textbf{ C}}.[/latex]В результате получилось три результата: энтропия увеличилась, часть энергии стала недоступной для выполнения работы, а система стала менее упорядоченной. Давайте подумаем о каждом из этих результатов.
Давайте подумаем о каждом из этих результатов.
Во-первых, энтропия увеличилась по той же причине, что и в приведенном выше примере. Смешение двух водоемов имеет такой же эффект, как передача тепла от горячего и такой же перенос тепла к холодному. Смешивание уменьшает энтропию горячей воды, но увеличивает энтропию холодной воды на большую величину, вызывая общее увеличение энтропии.
Во-вторых, когда смешаны две массы воды, температура будет только одна — с ними нельзя запустить тепловую машину. Энергия, которая могла бы использоваться для работы тепловой машины, теперь недоступна для выполнения работы.
В-третьих, смесь менее упорядочена или, говоря другим языком, менее структурирована. Вместо того, чтобы иметь две массы при разных температурах и с разным распределением молекулярных скоростей, теперь у нас есть одна масса с одинаковой температурой.
Эти три результата — энтропия, недоступность энергии и беспорядок — не только связаны, но фактически эквивалентны.
Некоторые люди неправильно понимают второй закон термодинамики, сформулированный в терминах энтропии, говоря, что процесс эволюции жизни нарушает этот закон. Со временем сложные организмы развились из гораздо более простых предков, что представляет собой значительное уменьшение энтропии биосферы Земли. Это факт, что живые организмы в ходе эволюции стали высокоструктурированными и имеют гораздо более низкую энтропию, чем вещества, из которых они вырастают. Но всегда возможно уменьшение энтропии одной части Вселенной при условии, что общее изменение энтропии Вселенной увеличивается. В форме уравнения мы можем записать это как
[латекс]\boldsymbol{\Delta{S}_{\textbf{tot}}=\Delta{S}_{\textbf{syst}}+\Delta{S}_{\textbf{envir}}>0 }.[/латекс]
Таким образом, [latex]\boldsymbol{\Delta{S}_{\textbf{syst}}}[/latex] может быть отрицательным, пока [latex]\boldsymbol{\Delta{S}_{\textbf{envir} }}[/latex] положительна и больше по величине.
Как система может уменьшить свою энтропию? Необходима передача энергии. Если я соберу разбросанные по комнате шарики и положу их в чашку, моя работа уменьшит энтропию этой системы. Если я соберу железную руду из земли, переделаю ее в сталь и построю мост, моя работа уменьшит энтропию этой системы. Энергия, исходящая от Солнца, может уменьшить энтропию локальных систем на Земле, то есть [латекс]\жирныйсимвол{\Delta{S}_{\textbf{syst}}}[/латекс]отрицательна. Но общая энтропия остальной части Вселенной увеличивается на большую величину, то есть [латекс]\жирный символ{\Delta{S}_{\textbf{envir}}}[/латекс] положительна и больше по величине. Таким образом, [латекс]\boldsymbol{\Delta{S}_{\textbf{tot}}=\Delta{S}_{\textbf{syst}}+\Delta{S}_{\textbf{envir}}> 0},[/latex]а второй закон термодинамики равен , а не нарушено.
Если я соберу разбросанные по комнате шарики и положу их в чашку, моя работа уменьшит энтропию этой системы. Если я соберу железную руду из земли, переделаю ее в сталь и построю мост, моя работа уменьшит энтропию этой системы. Энергия, исходящая от Солнца, может уменьшить энтропию локальных систем на Земле, то есть [латекс]\жирныйсимвол{\Delta{S}_{\textbf{syst}}}[/латекс]отрицательна. Но общая энтропия остальной части Вселенной увеличивается на большую величину, то есть [латекс]\жирный символ{\Delta{S}_{\textbf{envir}}}[/латекс] положительна и больше по величине. Таким образом, [латекс]\boldsymbol{\Delta{S}_{\textbf{tot}}=\Delta{S}_{\textbf{syst}}+\Delta{S}_{\textbf{envir}}> 0},[/latex]а второй закон термодинамики равен , а не нарушено.
Каждый раз, когда растение накапливает некоторую солнечную энергию в виде химической потенциальной энергии или восходящий поток теплого воздуха поднимает парящую птицу, Землю можно рассматривать как тепловую машину, работающую между горячим резервуаром, снабжаемым Солнцем, и холодным резервуаром. обеспечивается темным космическим пространством — тепловой машиной высокой сложности, вызывающей локальное уменьшение энтропии, поскольку она использует часть теплопередачи от Солнца в дальний космос. В результате этой массивной теплопередачи происходит большое общее увеличение энтропии. Небольшая часть этой теплопередачи хранится в структурированных системах на Земле, вызывая гораздо меньшее локальное уменьшение энтропии. (См. рис. 6.)
обеспечивается темным космическим пространством — тепловой машиной высокой сложности, вызывающей локальное уменьшение энтропии, поскольку она использует часть теплопередачи от Солнца в дальний космос. В результате этой массивной теплопередачи происходит большое общее увеличение энтропии. Небольшая часть этой теплопередачи хранится в структурированных системах на Земле, вызывая гораздо меньшее локальное уменьшение энтропии. (См. рис. 6.)
Рис. 6. Энтропия Земли может уменьшиться в процессе перехвата небольшой части теплопередачи от Солнца в дальний космос. Энтропия для всего процесса значительно возрастает по мере того, как Земля становится более структурированной с живыми системами и накопленной энергией в различных формах.
ИССЛЕДОВАНИЯ PHET: ОБРАТИМЫЕ РЕАКЦИИ
Наблюдайте за протеканием реакции с течением времени. Как полная энергия влияет на скорость реакции? Варьируйте температуру, высоту барьера и потенциальную энергию. Запишите концентрации и время, чтобы извлечь коэффициенты скорости. Проведите температурно-зависимые исследования для извлечения параметров Аррениуса. Эту симуляцию лучше всего использовать под руководством учителя, поскольку она представляет собой аналогию химических реакций.
Проведите температурно-зависимые исследования для извлечения параметров Аррениуса. Эту симуляцию лучше всего использовать под руководством учителя, поскольку она представляет собой аналогию химических реакций.
Рисунок 7. Обратимые реакции
- Энтропия — это потеря энергии, доступной для выполнения работы.
- Другая форма второго начала термодинамики гласит, что полная энтропия системы либо увеличивается, либо остается постоянной; она никогда не уменьшается.
- Энтропия равна нулю в обратимом процессе; она увеличивается в необратимом процессе.
- Конечной судьбой Вселенной, скорее всего, будет термодинамическое равновесие, при котором универсальная температура постоянна и нет энергии для выполнения работы.
- Энтропия также связана с тенденцией к беспорядку в замкнутой системе.
- энтропия
- измерение беспорядка системы и ее неспособности выполнять работу в системе
- изменение энтропии
- отношение теплопередачи к температуре[латекс]\boldsymbol{Q/T}[/латекс]
- второй закон термодинамики в терминах энтропии
- полная энтропия системы либо увеличивается, либо остается постоянной; никогда не уменьшается
Температура стока двигателя Карно 27°С.
 КПД двигателя 25%.
КПД двигателя 25%.
Тогда температура источника —
Выбор набора вопросов:
Рекомендуется MCQS — 118 Вопрос
EREDRENDED PYQS (STRICTLY NCERT BASIC)
ncert на основе NCERT)
ncert на основе NCERT)
ncert). Цель) На основе MCQ
AR и MCQ других типов
Padma Shri H C Verma (Objective Exercises) Based MCQs
Past Year (2019 onward — NTA Papers) MCQs
Past Year (2016 — 2018) MCQs
Past Year (2006 — 2015) MCQ
Температура стока двигателя Карно 27° C . КПД двигателя 25%. Тогда температура источника —
(1) 227° С
(2) 327° C
(3) 127° C
(4) 27° C
Q95:
82
% From NCERT
(1)
( 2)
(3)
(4)
Подтема: Тепловой двигатель и холодильник |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс, описанный ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Пожалуйста, сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальные книги MCQ NEETprep с онлайн-решениями для аудио/видео/текста через Telegram Bot
Книги NEET MCQ для 11 й Физика, химия и биология
Температура резервуара с эффективностью работы двигателя Карно 70% это 1000 К . Температура его раковины составляет —
(1) 300 K
(2) 400 K
(3) 500 K
(4) 700 K
Q96:
K
Q96:
7888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888тели K
.
87
%от NCERT
(1)
(2)
(3)
(4)
Subtopic: Heat Engine & Olne In Engine & Olnegator |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс, описанный ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробную версию в курсе ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Пожалуйста, сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальные книги MCQ от NEETprep с онлайн-решениями для аудио/видео/текста через Telegram Bot
Книги NEET MCQ для 11 й Физика, химия и биология
В двигателе Карно, когда T 2 = 0 ° C и T 1 = 200 ° C , его эффективность составляет η 1 и когда T 1 1 и когда T 1 1 и когда T 1
08 °
°
и когда T
4 1 1 . T 2 = –200° C , его эффективность η2. Каково значение η 1 / η 2 ?
1. 0,577
0,577
2. 0,733
3. 0,638
4. Не вычисляется
Q97:
75
%от NCERT
(1)
(2)
(3)
(4). Двигатель |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс, описанный ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробную версию в курсе ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальные книги MCQ NEETprep с онлайн-решениями для аудио/видео/текста через Telegram Bot
Книги NEET MCQ для 11 th Физика, химия и биология
27° C и –123° C , is
(1) 50%
(2) 24%
(3) 0,75%
(4) 0,4%
Q98:
80
% от NCERT
(1)
(2)
- 9000
- 9999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999н.

(4)
Подтема: Тепловой двигатель и холодильник |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс, описанный ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробную версию в курсе ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Пожалуйста, сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальные книги MCQ NEETprep с онлайн-решениями для аудио/видео/текста через Telegram Bot
Книги NEET MCQ для 11 й Физика, химия и биология
Двигатель Карно работает между 00005
C
° С . КПД двигателя составит —
(1) 13
(2) 25
(3) 34
(4) 35
Q99:
89
% From NCERT
(1)
(2)
(3)
(4)
Подтема: Тепловой двигатель и холодильник |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс, описанный ниже.

NEET 2023 — Целевая партия — Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробную версию в курсе ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Пожалуйста, сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальные книги MCQ от NEETprep с онлайн-решениями для аудио/видео/текста через Telegram Bot
Книги NEET MCQ для 11 th Физика, химия и биология
Эффективность двигателя Карно на выходе 50% при температуре на выходе 50% 500 К . Чтобы повысить эффективность до 60%, сохраняя температуру на входе такой же, какова температура на выходе?
(1) 200 K
(2) 400 K
(3) 600 K
(4) 800 K
Q100:
76
% From NCERT
(1)
(2)
(3)
(4)
Subtopic: Тепловой двигатель и холодильник |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс, описанный ниже.

NEET 2023 — Целевая партия — Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробную версию в курсе ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Пожалуйста, сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальные книги MCQ от NEETprep с онлайн-решениями для аудио/видео/текста через Telegram Bot
Книги NEET MCQ для 11 й Физика, химия и биология
Идеальный тепловой двигатель, работающий при температуре T 1 и T 2 имеет КПД η, новый КПД при удвоении температуры источника и стока будет
(1) η2 5 9005 0 90 0 0 2
(3) 2 η
(4) 3 η
Q101:
88
% From NCERT
(1)
(2)
(3)
(4)
Подтема: Тепловая машина и холодильник |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс, описанный ниже.

NEET 2023 — Целевая партия — Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробную версию в курсе ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Пожалуйста, сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальных книг MCQ от NEETprep с онлайн-решениями для аудио/видео/текста через Telegram Bot
NEET MCQ Books for 11 th Physics, Chemistry & Biology
Двигатель должен работать между двумя резервуарами при температуре 727° C и 227° C . Максимально возможный КПД такого двигателя составляет —
(1) 1/2
(2) 1/4
(3) 3/4
(4) 1
Q102:
- 8 8
(1)
(2)
(3)
(4)
(1)
(2)
(3)
(4)
(1)
(2)
(3)
(4)
- 8
% От NCERT
Подтема: Тепловой двигатель и холодильник |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс, описанный ниже.

NEET 2023 — Целевая партия — Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробную версию в курсе ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Пожалуйста, сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получить NEETprep 9
NEET MCQ Books for 11 th Physics, Chemistry & Biology
Тепловая машина на идеальном газе работает в цикле Карно между 227°C и
. и 127° С . Он поглощает 6 × 10 4 кал тепла при более высокой температуре. Количество теплоты, перешедшей в работу, равно —
(1) 2,4 × 10 4 кал
(2) 6 × 10 4 cal
(3) 1.2 × 10 4 cal
(4) 4.8 × 10 4 cal
Q103:
76
% From NCERT
Подтопператор |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс, описанный ниже.

NEET 2023 — Целевая партия — Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробную версию в курсе ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Пожалуйста, сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальные книги MCQ от NEETprep с онлайн-решениями для аудио/видео/текста через Telegram Bot
Книги NEET MCQ для 11 й Физика, химия и биология
Какой из следующих процессов является обратимым?
(1) Теплопередача излучением
(2) Электрический нагрев нихромовой проволоки
(3) Теплопередача теплопроводностью
(4) Изотермическое сжатие
%От NCERT
Субтопические: типы процессов |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс, описанный ниже.

NEET 2023 — Целевая партия — Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробную версию в курсе ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Пожалуйста, сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальные книги MCQ от NEETprep с онлайн-решениями для аудио/видео/текста через Telegram Bot
Книги NEET MCQ для 11 th Физика, химия и биология
Выберите набор вопросов:
Recommended MCQs — 118 Questions
Recommended PYQs (STRICTLY NCERT Based)
NCERT Exercise Based MCQs
NCERT Exemplar (Objective) Based MCQs
AR & MCQ другого типа
Padma Shri HC Verma (Целевые упражнения) MCQ на основе
Прошлый год (2019 г.



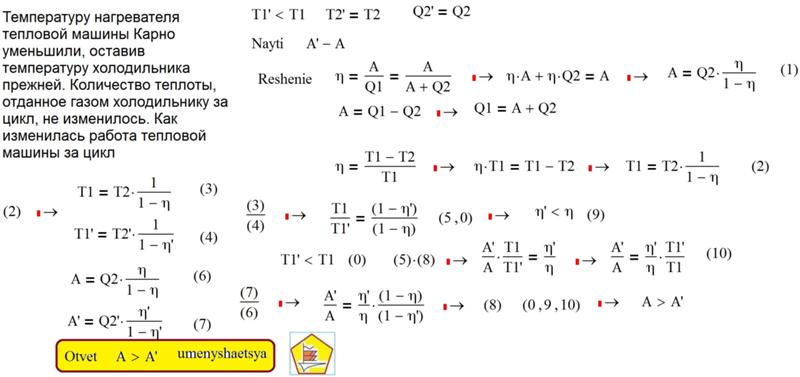
 Температура нагревателя 500 К, холодильника 300 К.
Температура нагревателя 500 К, холодильника 300 К.