§ 32. Работа газа при его расширении
Если
находящийся под поршнем в цилиндрическом
сосуде, газ расширяясь, передвигает
поршень на расстояние
,
то производит над ним работу,
гдеS
– площадь поршня.
Рисунок
32.1
Полная
работа, совершаемая газом при изменении
его объема равна:
.
(32.1)
Равновесные
процессы – это процессы, состоящие из
последовательности равновесных
состояний. Они протекают так, что
изменение термодинамических параметров
за конечный промежуток времени бесконечно
мало. Все реальные процессы неравновесные,
но в ряде случаев (достаточно медленные
процессы) неравновесностью реальных
процессов можно пренебречь.
Равновесные
процессы можно изображать графически
в координатах (р,V).
Так работа определяется площадью
заштрихованной полоски, а полная работа
– площадью под кривой между
и.
Рисунок
32.2
При
неравновесных процессах значения
параметров разных частях системы
различны и не существует (р,V)
— точек, характеризующих состояние всей
системы. Поэтому графическое изображение
неравновесного процесса невозможно.
§ 33. Теплоемкость
Теплоемкость
тела характеризует количество тепла,
необходимое для нагревания этого тела
на один градус. Однако её не удобно
использовать на практике, поскольку
для одного и того же вещества, но разной
массы теплоемкость будет разной. Поэтому
в рассмотрение вводят понятие удельной
теплоемкости.
Удельная
теплоемкость вещества с
– это величина, равная количеству
теплоты, необходимому для нагревания
1 кг
вещества на 1 К.
Единица
удельной теплоемкости – Дж/(кг К).
Молярная
теплоёмкость- величина, равная количеству теплоты,
необходимому для нагревания 1 моль
вещества на 1К.
Единица
молярной теплоемкости – Дж/(моль К).
Исходя
из определения молярной
и
удельной теплоемкостимежду ними существует связь и:.
В
общем случае, теплоемкость существенно
зависит от условий нагревания. Поэтому
различают разные теплоемкости.
Различают
теплоёмкости (удельную и молярную) при
постоянном объёме (и)
и при постоянном давлении (),
если в процессе нагревания вещества
его объем или давление поддерживаются
постоянными.
§ 34. Молярная теплоемкость при постоянном объеме
Из
первого начала термодинамики
,
с учетоми
для
одного моля газа получим:
.
Приработа
внешних сил равна нулю и сообщаемая
газу извне теплота идет только на
увеличение его внутренней энергии.
равна
изменению внутренней энергии 1 моль
газа при повышении его температуры на
1 К.
Поскольку
,
то.
§ 35. Молярная теплоемкость при постоянном давлении. Уравнение Майера
Если
газ нагревается при,
то
,
–внутренняя
энергия идеального газа не зависит ни
от p,
ни отV,
а определяется только Т.
Дифференцируя
уравнение Клапейрона-Менделеева по Т
при
,
получим уравнение Майера:
.
(35.1)
всегда
больше
на величину универсальной газовой
постоянной. Универсальная газовая
постояннаяR
численно равна работе изобарического
расширения одного моля идеального газа
при повышении его температуры на один
кельвин. Формулу (35.1) впервые в 1842 г.
получил Р. Майер и она носит название
формулы Майера.
Это
объясняется тем, что при нагревании
газа при постоянном давлении требуется
ещё дополнительное количество теплоты
на совершение работы расширения газа,
так как постоянство давления обеспечивается
увеличением объёма газа.
.
(35.2)
При
рассмотрении термодинамических процессов
важную роль играет величина, которая
называется коэффициентом Пуассона:
.
Глава 15. Работа газа в циклическом процессе. Тепловые двигатели. Цикл Карно
В программу школьного курса физики входит ряд вопросов, связанных с тепловыми двигателями. Школьник должен знать основные принципы работы теплового двигателя, понимать определение коэффициента полезного действия (КПД) циклического процесса, уметь находить эту величину в простейших случаях, знать, что такое цикл Карно и его КПД.
Тепловым двигателем (или тепловой машиной) называется процесс, в результате которого внутренняя энергия какого-то тела превращается в механическую работу. Тело, внутренняя энергия которого превращается двигателем в работу, называется нагревателем двигателя. Механическая работа в тепловых машинах совершается газом, который принято называть рабочим телом (или рабочим веществом) тепловой машины. При расширении рабочее тело и совершает полезную работу.
При расширении рабочее тело и совершает полезную работу.
Для того чтобы сделать процесс работы двигателя циклическим, необходимо еще одно тело, температура которого меньше температуры нагревателя и которое называется холодильником двигателя. Действительно, если при расширении газ совершает положительную (полезную) работу (левый рисунок; работа газа численно равна площади «залитой» фигуры), то при сжатии газа он совершает отрицательную («вредную») работу, которая должна быть по абсолютной величине меньше полезной работы. А для этого сжатие газа необходимо проводить при меньших температурах, чем расширение, и, следовательно, газ перед сжатием необходимо охладить. На среднем рисунком показан процесс сжатия газа 2-1, в котором газ совершает отрицательную работу , абсолютная величина которой показана на среднем рисунке более светлой «заливкой». Чтобы суммарная работа газа за цикл была положительна, площадь под графиком расширения должна быть больше площади под графиком сжатия. А для этого газ перед сжатием следует охладить. Кроме того, из проведенных рассуждений следует, что работа газа за цикл численно равна площади цикла на графике
Кроме того, из проведенных рассуждений следует, что работа газа за цикл численно равна площади цикла на графике
|
|
зависимости давления от объема, причем со знаком «плюс», если цикл проходится по часовой стрелке, и «минус» — если против.
Таким образом, двигатель превращает в механическую работу не всю энергию, взятую у нагревателя, а только ее часть; остальная часть этой энергии используется не для совершения работы, а передается холодильнику, т.е. фактически теряется для совершения работы. Поэтому величиной, характеризующей эффективность работы двигателя, является отношение
(15.1) |
где — работа, совершаемая газом в течение цикла, — количество теплоты, полученное газом от нагревателя за цикл. Отношение (15.1) показывает, какую часть количества теплоты, полученного у нагревателя, двигатель превращает в работу и называется коэффициентом полезного действия (КПД) двигателя.
Если в течение цикла рабочее тело двигателя отдает холодильнику количество теплоты (эта величина по своему смыслу положительна), то для работы газа справедливо соотношение . Поэтому существует ряд других форм записи формулы (15.1) для КПД двигателя
(15.2) |
Французский физик и инженер С. Карно доказал, что максимальным КПД среди всех процессов, использующих некоторое тело с температурой в качестве нагревателя, и некоторое другое тело с температурой ( ) в качестве холодильника, обладает процесс, состоящий из двух изотерм (при температурах нагревателя и холодильника ) и двух адиабат (см. рисунок).
|
|
Изотермам на графике отвечают участки графика 1-2 (при температуре нагревателя ) и 3-4 (при температуре холодильника ), адиабатам — участки графика 2-3 и 4-1. Этот процесс называется циклом Карно. КПД цикла Карно равен
(15. |
Теперь рассмотрим задачи. В задаче 15.1.1 необходимо использовать то обстоятельство, что работа газа в циклическом процессе численно равна площади цикла на графике зависимости давления от объема, причем со знаком «плюс», если цикл проходится по часовой стрелке, и «минус» — если против. Поэтому во втором цикле работа газа положительна, в третьем отрицательна. Первый цикл состоит из двух циклов, один из которых проходится по, второй — против часовой стрелки, причем, как следует из графика 1, площади этих циклов равны. Поэтому работа газа за цикл в процессе 1 равна нулю (правильный ответ — 2).
Поскольку в результате совершения циклического процесса газ возвращается в первоначальное состояние (задача 15.1.2), то изменение внутренней энергии газа в этом процессе равно нулю (ответ 2).
Применяя в задаче 15.1.3 первый закон термодинамики ко всему циклическому процессу и учитывая, что изменение внутренней энергии газа равно нулю (см. предыдущую задачу), заключаем, что (ответ 3).
предыдущую задачу), заключаем, что (ответ 3).
Поскольку работа газа численно равна площади цикла на диаграмме «давление-объем», то работа газа в процессе в задаче 15.1.4 равна (ответ 1). Аналогично в задаче 15.1.5 газ за цикл совершает работу (ответ 1).
Работа газа в любом процессе равна сумме работ на отдельных участках процесса. Поскольку процесс 2-3 в задаче 15.1.6 — изохорический, то работа газа в этом процессе равна нулю. Поэтому (ответ 3).
По определению КПД показывает, какую часть количества теплоты, полученного у нагревателя, двигатель превращает в работу (задача 15.1.7 — ответ 4).
Работа двигателя за цикл равна разности количеств теплоты, полученного от нагревателя и отданного холодильнику : . Поэтому КПД цикла есть
|
|
(задача 15.1.8 — ответ 3).
По формуле (15.3) находим КПД цикла Карно в задаче 15. 1.9
1.9
|
|
(ответ 2).
Пусть температура нагревателя первоначального цикла Карно равна , температура холодильника (задача 15.1.10). Тогда по формуле (15.3) для КПД первоначального цикла имеем
|
|
Отсюда находим . Поэтому для КПД нового цикла Карно получаем
|
|
(ответ 2).
В задаче 15.2.1 формулы (2), (3) и (4) представляют собой разные варианты записи определения КПД теплового двигателя (см. формулы (15.1) и (15.2)). Поэтому не определяет КПД двигателя только формула 1. (ответ 1).
Мощностью двигателя называется работа, совершенная двигателем в единицу времени. Поскольку работа двигателя равна разности полученного от нагревателя и отданного холодильнику количеств теплоты, имеем для мощности двигателя в задаче 15. 2.2
2.2
|
|
(ответ 3).
По формуле (15.2) имеем для КПД двигателя в задаче 15.2.3
|
|
где — количество теплоты, полученное от нагревателя, — количество теплоты, отданное холодильнику (правильный ответ — 2).
Для нахождения КПД теплового двигателя в задаче 15.2.4 удобно использовать последнюю из формул (15.2). Имеем
|
|
где — работа газа, — количество теплоты, отданное холодильнику. Поэтому правильный ответ в задаче — 3.
Пусть газ совершает за цикл работу (задача 15.2.5). Поскольку количество теплоты, полученное от нагревателя равно ( — количество теплоты, отданное холодильнику), и работа составляет 20 % от этой величины, то для работы справедливо соотношение = 0,2 ( + 100). Отсюда находим = 25 Дж (ответ 1).
Поскольку работа теплового двигателя в задаче 15.2.6 равна 100 Дж при КПД двигателя 25 %, то двигатель получает от нагревателя количество теплоты 400 Дж. Поэтому он отдает холодильнику 300 Дж теплоты в течение цикла (ответ 4).
В задаче 15.2.7 газ получает или отдает теплоту только в процессах 1-2 и 3-1 (процесс 2-3 по условию адиабатический). Поэтому данное в условии задачи количество теплоты является количеством теплоты, полученным от нагревателя в течение цикла, — количеством теплоты, отданном холодильнику. Поэтому работа газа равна (ответ 1). |
Цикл, данный в задаче 15.2.8, состоит из двух изотерм 2-3 и 4-1 и двух изохор 1-2 и 3-4. Работа газа в изохорических процессах равна нулю. Сравним работы газа в изотермических процессах. Для этого удобно построить график зависимости давления от объема в рассматриваемом процессе, поскольку работа газа есть площадь под этим графиком. |
Для сравнения работ газа на различных участках процесса в задаче 15.2.9 построим график зависимости давления от объема. Этот график представлен на рисунке. Из рисунка следует, что работы газа в процессах 1-2 и 3-4 одинаковы по модулю (этим работам отвечают площади прямоугольников, «залитых» на рисунке светлой и темной «заливкой»). Работе газа на участке 4-1 отвечает площадь под графиком 4-1, которая меньше площади под графиком 1-2. Работе газа на участке 2-3 отвечает площадь под кривой 2-3 на рисунке, которая заведомо больше площади «залитых» прямоугольников. Поэтому в процессе 2-3 газ и совершает наибольшую по абсолютной величине (среди рассматриваемых процессов) работу (ответ 2.).
Поэтому в процессе 2-3 газ и совершает наибольшую по абсолютной величине (среди рассматриваемых процессов) работу (ответ 2.).
Согласно определению коэффициент полезного действия представляет отношение работы газа за цикл к количеству теплоты , полученному от нагревателя . Как следует из данного в условии задачи 15.2.10 графика, и в процессе 1-2-4-1 и в процессе 1-2-3-1 газ получает теплоту только на участке 1-2. Поэтому количество теплоты, полученное газом от нагревателя в процессах
1-2-4-1 и 1-2-3-1 одинаково. А вот работа газа в процессе 1-2-4-1 вдвое меньше (так площадь треугольника 1-2-4 как вдвое меньше площади треугольника 1-2-4-1). Поэтому коэффициент полезного действия процесса 1-2-4-1 вдвое меньше коэффициента полезного действия процесса 1-2-3-1 (ответ 1).
Работа, совершаемая газом
Термодинамика — раздел физики Состояние газа определяется Ученые определяют работу W как продукт Вт = F * с Для газа работа есть произведение Вт = р * В Мы можем сделать W = (сила / площадь) * (площадь * длина) = сила * длина В метрической системе единицей работы является джоуль, в английской системе W = S [p] dV На графике Как упоминалось выше, существует несколько вариантов изменения состояния Обратите внимание, что не только работа, совершаемая газом, зависит от процесса, но и Деятельность: Экскурсии с гидом
Навигация ..
|
термодинамика — Работа, совершаемая газом
Ответ на вопрос ОП заключается в том, что работу, совершаемую системой, всегда можно оценить с учетом движения против внешней силы (давления). Для квазиравновесного процесса эту работу можно оценить и с учетом изменения внутреннего давления и объема газа; но вообще для неквазиравновесного, необратимого процесса работа не может быть оценена по изменению внутреннего давления и объема в газе, так как газ не находится в определенном состоянии.
Для квазиравновесного процесса эту работу можно оценить и с учетом изменения внутреннего давления и объема газа; но вообще для неквазиравновесного, необратимого процесса работа не может быть оценена по изменению внутреннего давления и объема в газе, так как газ не находится в определенном состоянии.
Ниже приводится подробная оценка работы газа, расширяющего и толкающего поршень.
Подробная оценка также отвечает на вопрос @ATHARVA в более раннем комментарии о газе, расширяющемся и перемещающем поршень. В частности, , почему вес поршня не входит в работу, совершаемую газом ? Судя по комментариям и ответам других, ответ на этот вопрос вызывает путаницу. А если на поршень действует еще и внешнее давление (например, атмосферы), и от других сил на поршень, обусловленных внешними нагрузками, приводимыми в движение поршнем, то почему они тоже не входят в работу, совершаемую газом? Ответ таков: нас интересует работа, совершаемая системой над своим окружением; для примера с поршнем это работа, совершаемая газом (системой) над поршнем (окружающей средой), но это не полная работа, выполняемая над поршнем.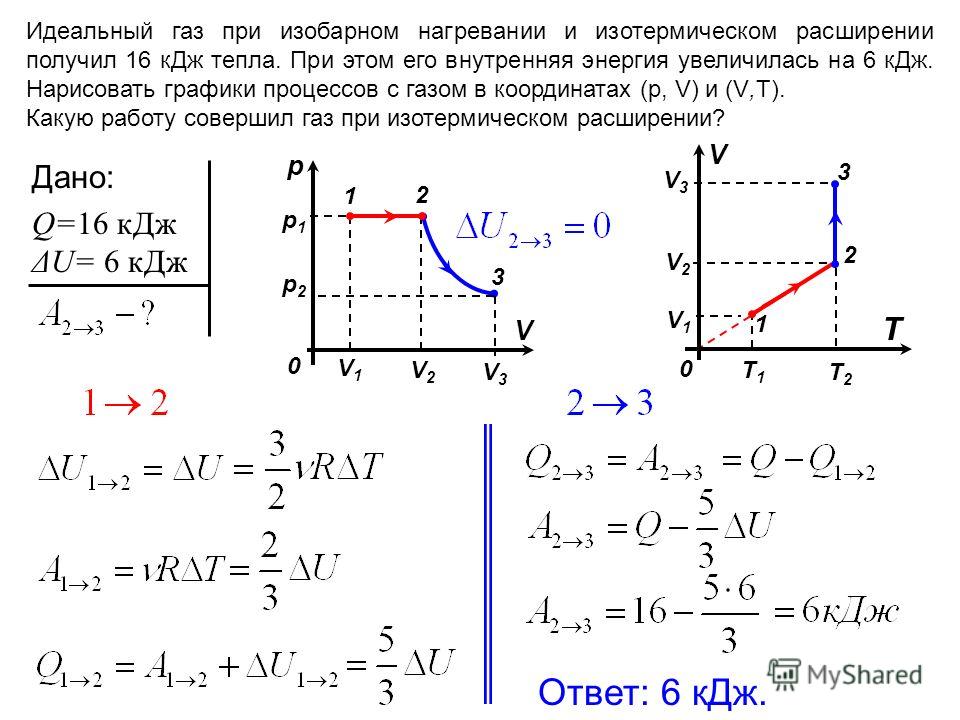
Ответы на оба эти вопроса следуют с использованием подробной оценки работы, выполняемой на поршень одной силой, от давления газа, в отличие от чистой работы, выполняемой полной силой на поршне, векторной суммы всех сил на поршень: сила от давления газа, вес поршня, внешнее атмосферное давление на поршень и другие силы на поршень из-за внешних нагрузок, приводимых в движение поршнем.
Пусть система определена как газ в сосуде, замкнутая термодинамическая система постоянной массы с подвижной границей, являющейся границей раздела газа с подвижным поршнем над газом. Поршень рассматривается как твердое тело, а внутренняя энергия твердого тела не может изменяться (например, твердое тело нельзя сжать). Нижняя часть поршня подвергается воздействию газа, а верхняя часть подвергается воздействию атмосферы. . Первоначально поршень покоится. К газу добавляется некоторое количество тепла $Q_{gas}$, чтобы поршень двигался вверх в направлении $\vec x$. Нас интересует работа $W_{gas}$, совершаемая системой, газом, над его окружением, поршнем.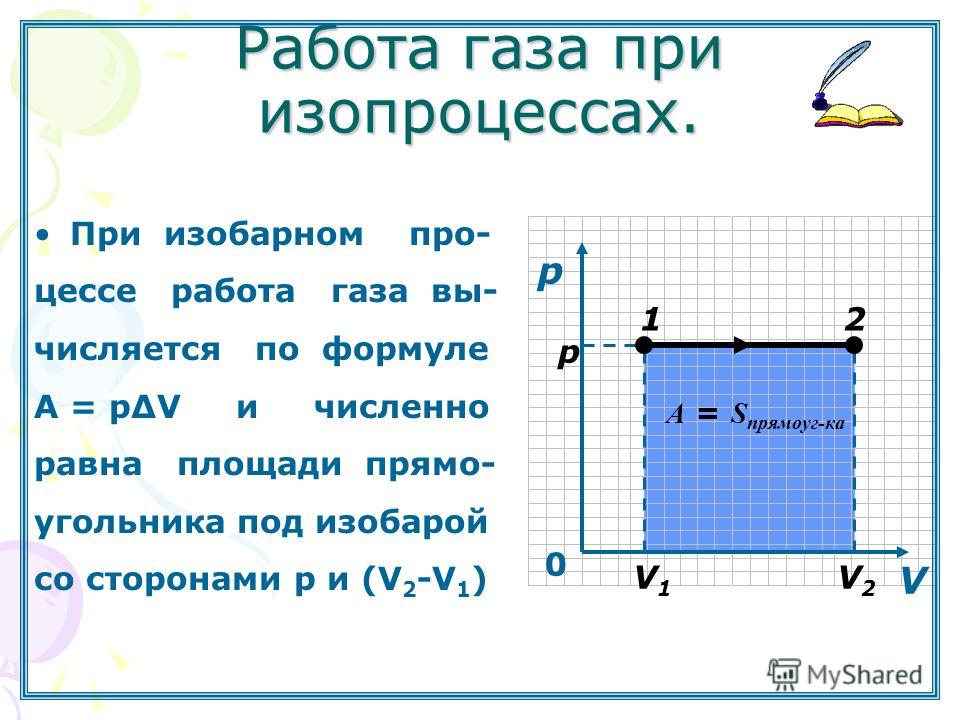 $W_{gas}$ положителен из-за движения поршня вверх. Из первого закона термодинамики,
$W_{gas}$ положителен из-за движения поршня вверх. Из первого закона термодинамики,
$Q_{газ} — W_{газ} = \Delta U$, где $\Delta U$ — изменение внутренней энергии $U$ газа.
Пусть $F_{ext}$ (здесь называемая внешней силой) будет полной силой, действующей на поршень со стороны внешней среды (газа). $F_{ext}\hat i = -(mg + P_{atm}A + F_{other})\hat i$, где $g$ — ускорение свободного падения, $P_{atm}$ — атмосферное давление, $ A$ — площадь поршня массы $m$, $F_{other}$ — сила реакции на поршень от внешних нагрузок, приводимых в движение поршнем, $\hat i$ — единичный вектор, положительный вверх. $V$ – объем газа.
В квазиравновесном (медленном) процессе поршень движется медленно и имеет нулевое ускорение; газ всегда находится в определенном термодинамическом состоянии, и состояние медленно изменяется при движении поршня. Поскольку ускорение поршня равно нулю, сумма всех сил (полная сила), действующих на поршень, равна нулю: $F_{ext} \hat i + P_{gas}A \hat i = 0$, где $P_{gas }$ — давление газа. {V_2} P_{gas}( V) dV$. Может сложиться впечатление, что $F_{ext}$ не учитывается, но поскольку 9{V_2} P_{ext}(V) dV$, так как давления $P_{gas}$ и $P_{ext}$ равны.
{V_2} P_{gas}( V) dV$. Может сложиться впечатление, что $F_{ext}$ не учитывается, но поскольку 9{V_2} P_{ext}(V) dV$, так как давления $P_{gas}$ и $P_{ext}$ равны.
Вот простая аналогия. Рассмотрим приложенную силу, медленно толкающую массу (твердое тело) вверх против силы тяжести, где приложенная сила лишь бесконечно мало превышает силу тяжести. Это квазистатический процесс в учебниках по механике. Приложенная сила и сила тяжести равны по величине, но противоположны по направлению, поэтому общая сила, действующая на массу, равна нулю. Масса имеет нулевое ускорение, поскольку результирующая сила равна нулю, полная работа над массой не совершается и кинетическая энергия массы не изменяется. Однако работа приложенной силы $W_{applied}$ не равна нулю, а является произведением приложенной силы на расстояние, на которое объект медленно движется вверх. Работа, совершаемая приложенной силой здесь, аналогична работе, совершаемой газом в обсуждении газа и поршня, а работа, совершаемая силой тяжести, аналогична работе, совершаемой внешней силой; каждая из этих сил по отдельности действует на массу, но результирующая сила (нулевая сила) не работает.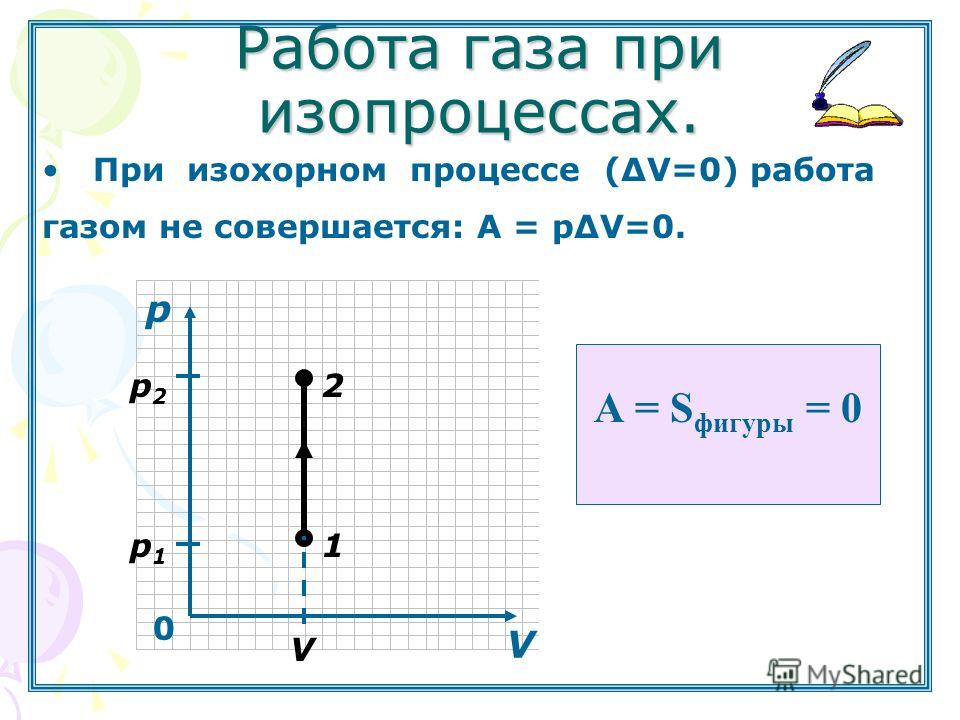

 3)
3) График зависимости давления от объема для заданного в условии процесса приведен на рисунке. Поскольку изотерме 2-3 соответствует бóльшая температура, чем изотерме 4-1, то она будет расположена выше на графике . Объем газа в процессе 2-3 увеличивается, в процессе 4-1 уменьшается. Таким образом, график процесса на графике проходится по часовой стрелке, и, следовательно, работа газа за цикл положительна (ответ 1).
График зависимости давления от объема для заданного в условии процесса приведен на рисунке. Поскольку изотерме 2-3 соответствует бóльшая температура, чем изотерме 4-1, то она будет расположена выше на графике . Объем газа в процессе 2-3 увеличивается, в процессе 4-1 уменьшается. Таким образом, график процесса на графике проходится по часовой стрелке, и, следовательно, работа газа за цикл положительна (ответ 1).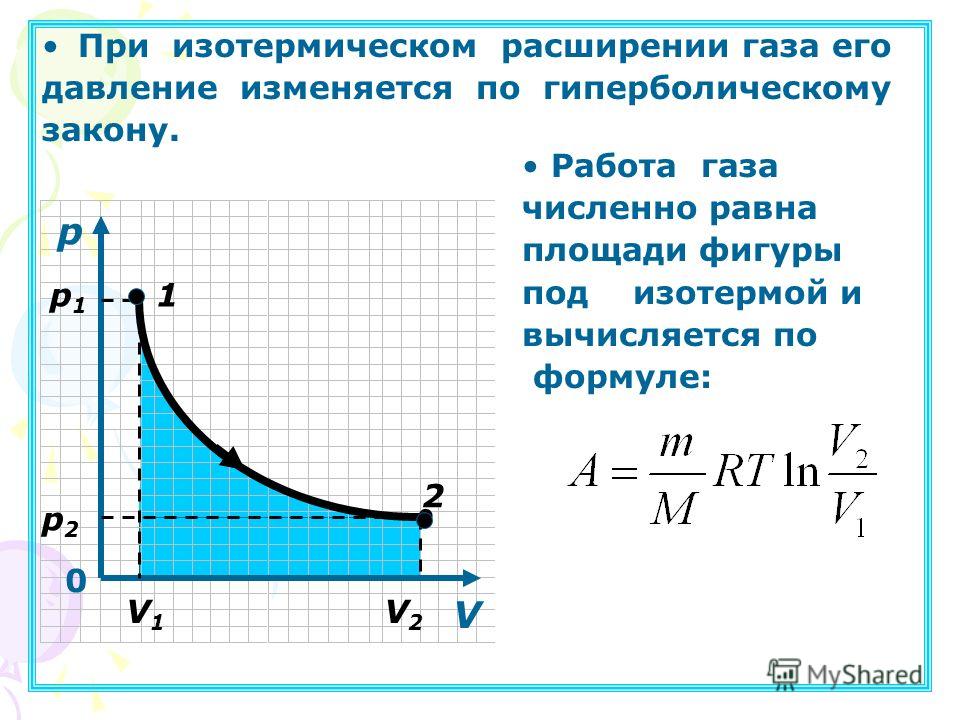 В аэродинамике мы больше всего
В аэродинамике мы больше всего Термодинамика помогает нам определить объем работы
Термодинамика помогает нам определить объем работы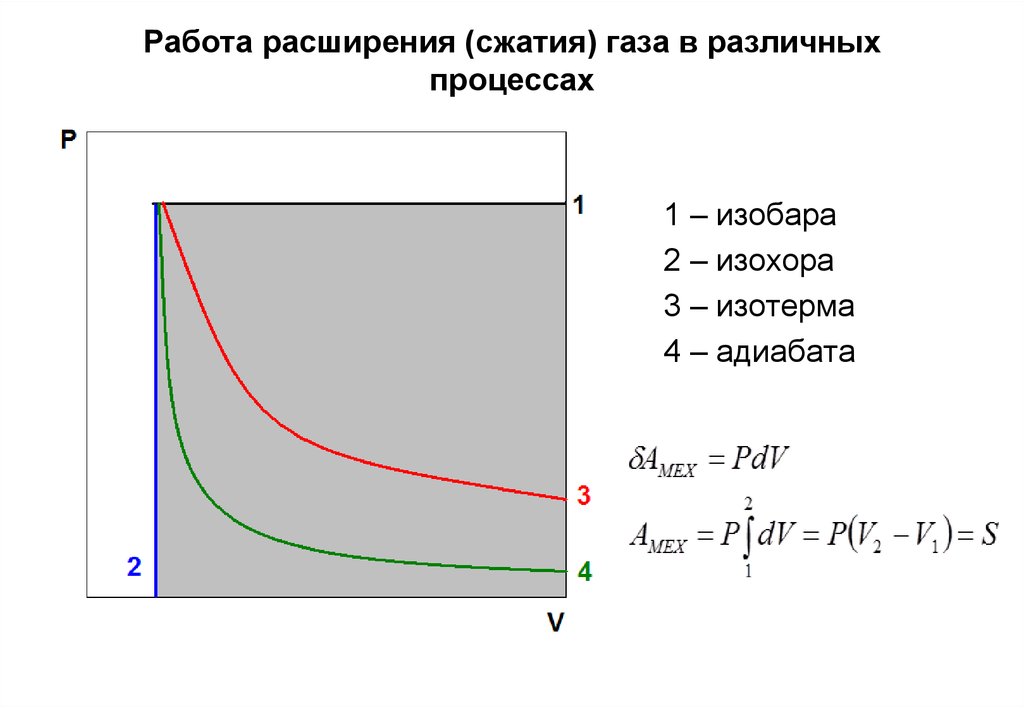
 Линия
Линия