Поршень — Физика
По́ршень — деталь цилиндрической формы, совершающая возвратно-поступательное Строение Поршень подразделяется на три части, o o o Для передачи усилия от поршня (или Поршень может быть односторонним или двухсторонним. Днище Форма днища зависит от выполняемой Функции уплотнения, выполняемые Уплотняющая часть Днище и уплотняющая часть образуют Направляющая часть Юбка поршня (тронк) является его |
Простая физика — EASY-PHYSIC
В эту статью намеренно сведены задачи про газы в сосудах, закрытых поршнями — легкими и тяжелыми. Под влиянием нагрева газы меняют свое состояние и сдвигают поршни в новое состояние равновесия. Как правило, нужно определить сдвиг поршня или отношение объемов.
Под влиянием нагрева газы меняют свое состояние и сдвигают поршни в новое состояние равновесия. Как правило, нужно определить сдвиг поршня или отношение объемов.
Задача 1.
В закрытом цилиндрическом сосуде находится газ при нормальных условиях. Сосуд расположен горизонтально и разделен подвижным поршнем в отношении . В каком отношении поршень будет делить сосуд, если его меньшую часть нагреть до , а большую охладить до ?
Понятно, что, раз поршень в равновесии, то давление одинаково с обеих сторон: .
К задаче 1
Состояние газа в левой части сосуда описывается уравнением:
Его количество пропорционально величине:
Количество газа в правой части сосуда пропорционально:
После изменения температур в левой части состояние газа таково:
А в правой:
Возьмем отношение двух последних равенств:
То есть, подставляя и , получим:
Ответ:
Задача 2.
В закрытом цилиндрическом сосуде находится газ при температуре . Внутри сосуд перегорожен легким, не проводящим тепло поршнем радиуса см на две части объемами см и см. Поршень находится в равновесии. На какое расстояние переместится поршень, если большую часть газа нагреть на 30К? Температура в другой части не меняется.
Давление изначально одинаково с обеих сторон: .
К задаче 2
Состояние газа в левой части сосуда описывается уравнением:
А в правой части:
После того как газ нагрели, его давление и объем в обеих частях сосуда должны измениться, но по-прежнему давление слева и справа равны:
Возьмем отношение двух последних равенств:
Количество газа в меньшей части сосуда пропорционально величине:
Количество газа в правой части сосуда пропорционально:
Тогда:
Так как объем равен произведению , то
Тогда
Но , поэтому в левой части имеем:
И, так как , то
Наконец,
Но нам неизвестно, поэтому вместо этой величины используем отношение :
Ответ: поршень сдвинется на 0,67 см.
Задача 3.
Сосуд с газом плотно закрыт пробкой, площадь сечения которой см. До какой температуры надо нагреть газ, чтобы пробка вылетела из сосуда, если сила трения, удерживающая пробку, Н? Начальное давление воздуха в сосуде Па, начальная температура .
Газ, находящийся в сосуде, изначально оказывает давление на пробку. Только его недостаточно для того, чтобы выдавить ее. Поэтому считаем, что избыточное давление, то есть изменение давления – как раз и выдавит пробку. Тогда
В свою очередь,
А так как процесс изохорный, то
Тогда
И
Тогда
Или
Откуда
Ответ: газ надо нагреть на , то есть до температуры .
Задача 4.
В цилиндрическом сосуде с газом находится в равновесии тяжелый поршень. Масса газа и температура под поршнем и над ним одинаковы. Отношение объема над поршнем к объему под поршнем равно 3. Каким будет это отношение, если температуру в сосуде увеличить в 2 раза?
Рассмотрим состояние газа до нагрева. Температура обеих частей одинакова, массы равны, то есть
Температура обеих частей одинакова, массы равны, то есть
При этом понятно, что давления разные в обеих частях, так как объемы не одинаковы:
К задаче 4
Следовательно, так как , то
И
Аналогично и после нагрева: так как газ нагревают в обеих частях сосуда, и масса газа в обеих частях одинакова, то можно записать, что
Искомое отношение –
А
И
Подставим давление поршня:
Перейдем к объемам:
Подставим эти соотношения:
Запишем объем после нагрева через приращение объема:
Перейдем к полному объему сосуда:
Теперь мы имеем всего две неизвестных в одном уравнении, и можем разделить все уравнение, например, на :
Где — заметим, что корень должен быть меньше 1 по модулю и при этом положительный, иначе будет потерян физический смысл.
Выбираем в связи с вышеизложенными соображениями второй корень. Тогда .
Тогда .
Найдем оба объема частей сосуда после подогрева:
Наконец, отношение объемов (Алилуйя! Мы сделали это!):
Работа
Работа
Работа
| Определение работы | Тепло и работа | Сохранение энергии | Внутренняя энергия |
| Взаимное превращение тепла и работы | Функции состояния | Калориметр | |
Определение работы
Работа может быть определена как произведение силы, используемой для перемещения
объект, умноженный на расстояние, на которое перемещается объект.
w = F x d
Представьте себе систему, состоящую из образца аммиака, запертого в поршне и цилиндре,
как показано на рисунке ниже.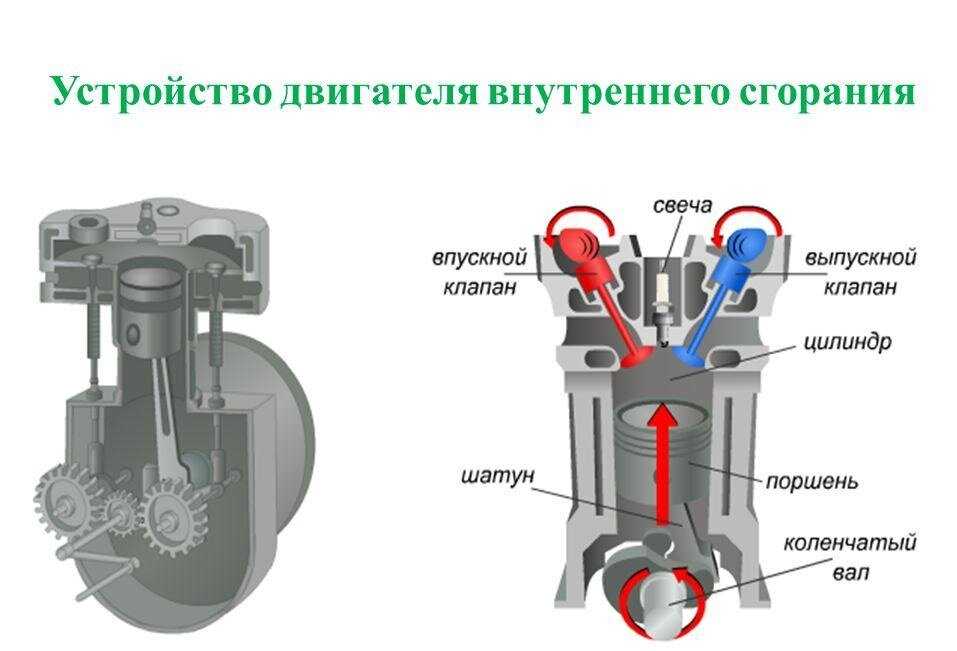 Предположим, что давление газа, давит на поршень
Предположим, что давление газа, давит на поршень
просто уравновешивает вес поршня, так что объем газа остается постоянным. В настоящее время
считать, что газ разлагается с образованием азота и водорода, увеличивая количество газа
частицы в контейнере. Если температура и давление газа остаются постоянными,
это означает, что объем газа должен увеличиться.
2 NH 3 ( г )
N 2 ( г ) + 3 Н 2 ( г )
Объем газа можно увеличить, частично вытолкнув поршень из цилиндра.
Совершаемая работа равна произведению силы, действующей на поршень, на
расстояние, на которое перемещается поршень.
ш = F x г
Давление ( P ), которое газ оказывает на поршень, равно силе (F)
с которой он давит на поршень, деленную на площадь поверхности ( A )
поршень.
Таким образом, сила, действующая на газ, равна произведению его давления на
площадь поверхности поршня.
F = P x A
Подстановка этого выражения в уравнение, определяющее работу, дает следующее
результат.
w = ( P x A ) x d
Произведение площади поршня на расстояние, на которое перемещается поршень, равно
изменение объема системы при расширении газа. Условно,
изменение объема представлено символом В .
В
= А х г
Таким образом, величина работы, совершаемой при расширении газа, равна произведению
давление газа, умноженное на изменение объема газа.
| с | = П В
Джоуль – измерение теплоты и работы
По определению, один джоуль — это работа, совершаемая при приложении силы в один ньютон для перемещения
объект один метр.
1 Дж = 1 Н·м
Поскольку работа может быть преобразована в теплоту и наоборот, система СИ использует джоуль для
измерять энергию в виде теплоты и работы.
Первый закон термодинамики: сохранение
Энергия
Первый закон термодинамики гласит, что энергия не может быть создана или
уничтожен. Система может получать или терять энергию. Но любое изменение энергии системы
должно сопровождаться эквивалентным изменением энергии его окружения, потому что
полная энергия Вселенной постоянна. Первый закон термодинамики можно описать
следующим уравнением.
E унив
= E сис
+ E доп.
= 0
(Индексы univ , sys и surr обозначают вселенную,
системы и ее окружения.)
Внутренняя энергия
Энергию системы часто называют ее внутренней энергией , потому что она
представляет собой сумму кинетической и потенциальной энергий частиц, образующих систему.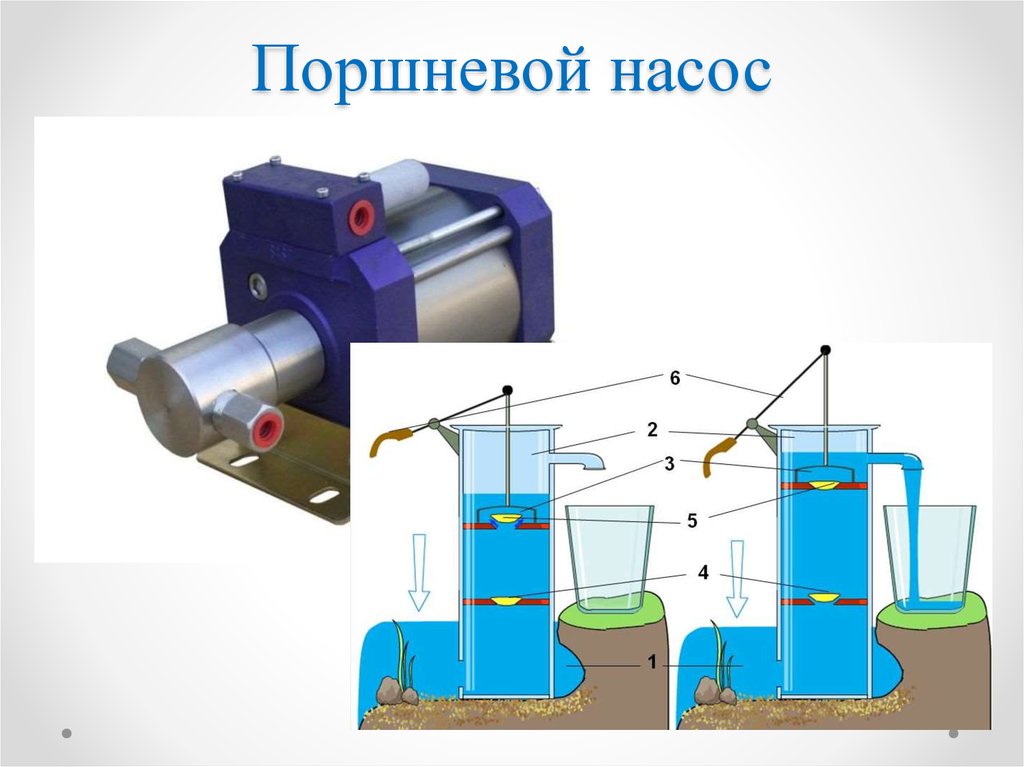
Потому что
отсутствие взаимодействия между частицами, единственный вклад во внутреннюю энергию идеального
газа есть кинетическая энергия частиц. Внутренняя энергия идеального газа равна
следовательно, прямо пропорциональна температуре газа.
(В этом уравнении R — постоянная идеального газа, а T — температура
газа в единицах Кельвина.)
Хотя трудно, если не невозможно, написать уравнение для более сложных
системы, внутренняя энергия системы по-прежнему прямо пропорциональна ее
температура. Поэтому мы можем использовать изменения температуры системы для мониторинга.
изменение его внутренней энергии.
Величина изменения внутренней энергии системы определяется как
разница между начальным и конечным значениями этой величины.
Е сис
= E окончательный — E начальный
Поскольку внутренняя энергия системы пропорциональна ее температуре, E
положительна при повышении температуры системы.
Первый закон термодинамики: взаимопревращение
тепла и работы
Энергия может передаваться между системой и ее окружением до тех пор, пока энергия
энергия, полученная одним из этих компонентов Вселенной, равна энергии, потерянной
Другой.
Е сис
= — E исп.
Энергия может передаваться между системой и ее окружением в виде либо
тепло ( q ) или рабочий ( w ).
Е сис
= ч + ш
Когда тепло поступает в систему, это может привести к повышению температуры системы или
Работа.
q = E сис
— с
Правило знаков для отношения между внутренней энергией системы и
задано теплоты , пересекающей границу между системой и ее окружением.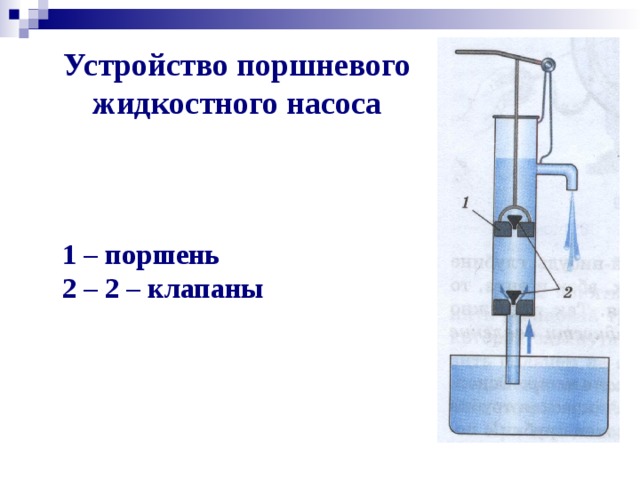
на рисунке ниже.
- Когда тепло, поступающее в систему, увеличивает температуру системы, внутренний
энергия системы увеличивается, и E
положительный. - Когда температура системы снижается из-за выхода тепла из системы, E
отрицательно.
Соглашение о знаках для связи между работой и внутренней энергией
система показана в левой части рисунка ниже.
- Когда система воздействует на окружающую среду, энергия теряется, и E
отрицательно. - Когда окружающая среда совершает работу над системой, внутренняя энергия системы становится равной
больше, поэтому E
положительный.
Соотношение между величиной работы, совершаемой системой при ее расширении, и
изменение объема системы ранее описывалось следующим уравнением.
| с | = П В
На приведенном выше рисунке показано, что можно включить соглашение о знаках для работы расширения.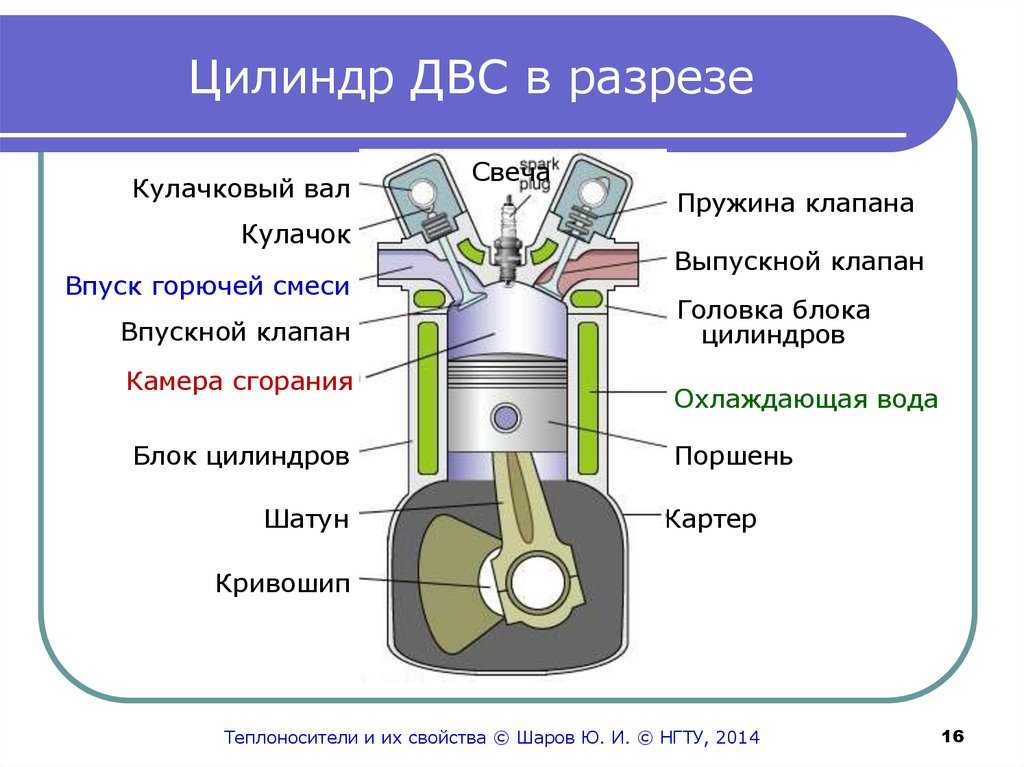
записав это уравнение следующим образом.
w = — P В
Функции состояния
Когда уравнения связывают два или более свойств, описывающих состояние
системы, они называются уравнениями состояния . Например, закон идеального газа
уравнение состояния.
PV = нРТ
Функция состояния с зависит только от состояния системы, а не от
путь, используемый для достижения этого состояния.
Температура является функцией состояния. Сколько бы раз мы ни нагревали, ни охлаждали, ни расширяли,
сжать или иным образом изменить систему, чистое изменение температуры зависит только от
на начальное и конечное состояния системы.
Т
= T окончательный — T начальный
То же самое можно сказать об объеме, давлении и количестве молей газа в
образец. Все эти величины являются функциями состояния.
Все эти величины являются функциями состояния.
Теплота и работа — это , а не функции состояния. Работа не может быть функцией государства, потому что она
пропорциональна расстоянию, на которое перемещается объект, которое зависит от пути, по которому он двигался
от начального до конечного состояния. Если работа не является функцией состояния, то теплота не может быть
государственная функция либо. Согласно первому закону термодинамики изменение
внутренняя энергия системы равна сумме переданной теплоты и работы
между системой и ее окружением.
Е сис
= ч + ш
Если Е
зависит не от пути перехода от начального состояния к конечному, а от количества
работы зависит от используемого пути, количество отдаваемой или поглощаемой теплоты должно зависеть
на пути.
Термодинамические свойства системы, являющиеся функциями состояния
обычно обозначаются заглавными буквами ( T , V , P , E и так далее
на).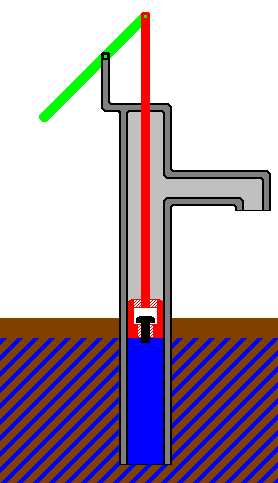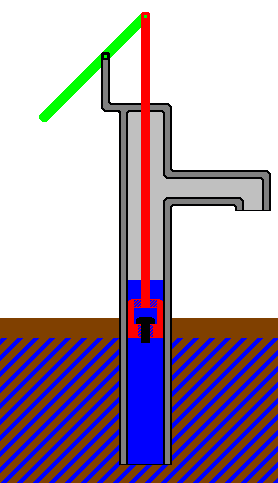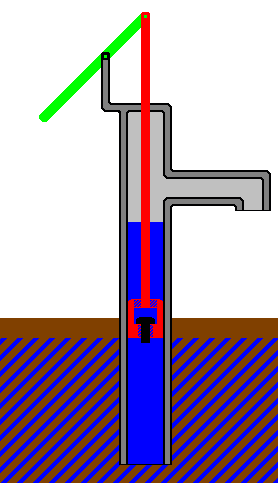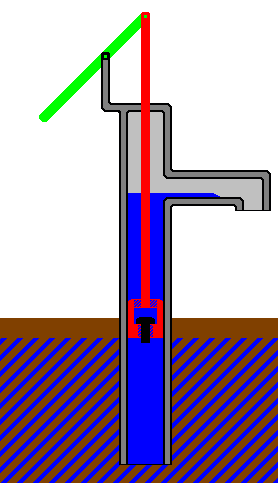 Термодинамические свойства, не являющиеся функциями состояния, часто описываются формулой
Термодинамические свойства, не являющиеся функциями состояния, часто описываются формулой
строчные буквы ( q и w ).
| Практическая задача 3: Что из следующего (а) Температура, T (б) Объем, В (с) Давление, P (d) Количество молей газа, n (e) Внутренняя энергия, E Нажмите |
Измерение тепла с помощью калориметра
Количество теплоты, выделяемой или поглощаемой в ходе химической реакции, можно измерить с помощью
калориметр, как показано на рисунке ниже.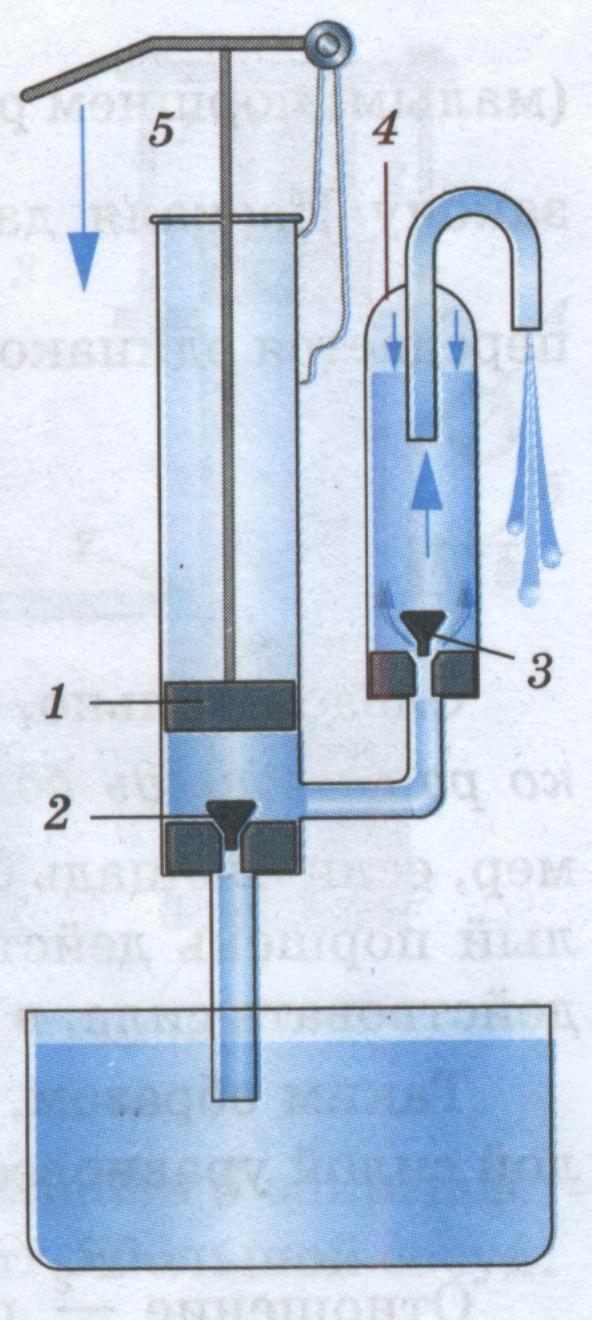
Поскольку реакция происходит в герметичном контейнере при постоянном объеме, никакая работа
расширение происходит во время реакции. Теплота, выделяемая или поглощаемая в результате реакции, равна
равно изменению внутренней энергии системы за время
реакция:
Е сис
= q V .
Количество теплоты, отдаваемое или поглощаемое водой в калориметре, может быть
рассчитывается исходя из теплоемкости воды.
| Практическая задача 4: Природный газ в CH 4 ( г ) + 2 O 2 ( г ) CO 2 ( г ) + 2 H 2 5 г Рассчитайте теплоту, выделяемую при взаимодействии 0,160 г метана с избытком кислорода в Нажмите Нажмите |
Тепло — это большое количество . Наиболее распространенный способ преобразования
Измерение теплоты в интенсивную величину заключается в вычислении теплоты реакции в
единиц килоджоулей на моль. Результатом этого расчета является величина, известная как молярный
теплота реакции . По определению, молярная теплота реакции – это теплота, выделяемая или
поглощается реакцией, выраженной в килоджоулях на моль одного из реагентов
в реакции.
Ньютоновская механика — Силы на поршне
спросил
Изменено
4 года, 2 месяца назад
Просмотрено
494 раза
$\begingroup$
Когда мы нагреваем любой контейнер с газом, снабженный поршнем, часть тепловой энергии увеличивает его внутреннюю энергию, а остальная часть совершает работу над поршнем.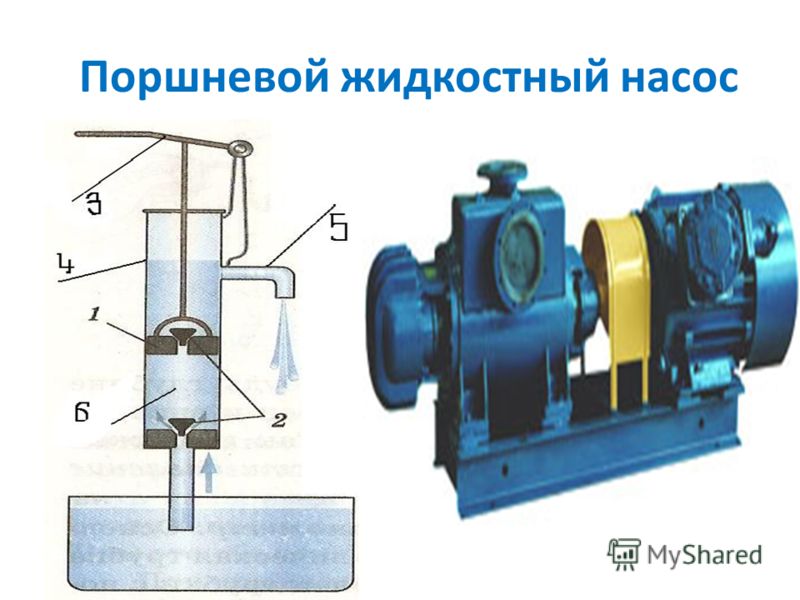
Но когда газ приводит в действие поршень, поршень приобретает скорость. Как поршень вернется в состояние покоя после набора скорости? Если присутствует внешняя атмосфера, внешнее давление воздуха будет препятствовать движению поршня, и когда внешнее давление станет равным внутреннему давлению, на поршень будет действовать результирующая сила 0. Однако у него все еще будет скорость, поэтому он переместится немного дальше, а затем начнет колебаться. Как оно успокоится? Я изучил, что поршень остановится в одной из моих книг
- ньютоновская механика
- термодинамика
- идеальный газ
- осцилляторы
$\endgroup$
$\begingroup$
Когда мы говорим о термодинамических изменениях, мы почти всегда предполагаем, что они происходят обратимо, то есть бесконечно медленно. В этом контексте мы имеем в виду, что мы увеличиваем температуру на крошечную величину, и в ответ поршень перемещается на крошечную величину с пренебрежимо малой скоростью. Мы продолжаем повторять это, пока температура не поднимется на желаемую величину. Скорость поршня остается фактически нулевой на протяжении всего процесса, поэтому скорость поршня фактически равна нулю после завершения повышения температуры.
Мы продолжаем повторять это, пока температура не поднимется на желаемую величину. Скорость поршня остается фактически нулевой на протяжении всего процесса, поэтому скорость поршня фактически равна нулю после завершения повышения температуры.
Очевидно, это идеализированный процесс, и в реальной жизни температура повышается со скоростью, превышающей ноль. Однако в реальной жизни всегда есть источники демпфирования, например. вязкость газа и трение в цилиндре, которые остановят поршень.
Хорошим примером из жизни является автомобильный двигатель. Температура в цилиндре резко повышается, когда топливо сгорает, и в результате поршень вылетает наружу. Предположим, что цилиндр бесконечно длинный, а поршень ни с чем не связан. Затем поршень будет двигаться наружу до тех пор, пока давление в цилиндре не станет меньше атмосферного, после чего он начнет замедляться, в конце концов остановится, а затем снова вернется. В отсутствие каких-либо сил трения или демпфирования поршень будет колебаться вечно.



 Благодаря этому значительно увеличивается износостойкость поршня.
Благодаря этому значительно увеличивается износостойкость поршня.