23)Цикл Карно. Расчет кпд идеальной тепловой машины, работающей по прямому обратимому циклу Карно. Теоремы Карно. Способы повышения кпд тепловых машин.

В
1824 г. С. Карно предложил и исследовал
идеальный тепловой цикл, названный в
последствии циклом
Карно. Этот цикл
состоит из двух изотерм и двух адиабат
(рис). Карно также сформулировал две
теоремы, определяющие максимальное
значение КПД теплового двигателя.

1-2
изобарное сжатие

2-3
изотермическое расширение

3-4
адиабатическое расширение

4-1
изотермическое сжатие

«Коэффициент
полезного действия тепловой машины,
работающей по циклу Карно, зависит
только от температур Т₁
и Т₂
нагревателя и холодильника, но не зависит
от устройства машины, а также от вида
используемого рабочего вещества».

«Коэффициент
полезного действия всякой тепловой
машины не может превосходить коэффициента
полезного действия идеальной машины,
работающей по циклу Карно с теми же
самыми температурами нагревателя и
холодильника».

Наибольшим
КПД при заданных температурах нагревателя
T_нагр
и холодильника T_хол
обладает тепловой двигатель, где рабочее
тело расширяется и сжимается по циклу
Карно
(рис. 2), график которого состоит из двух
изотерм (2–3 и 4–1) и двух адиабат (3–4 и
1–2).

Теорема
Карно
доказывает, что КПД такого двигателя
не зависит от используемого рабочего
тела, поэтому его можно вычислить,
используя соотношения термодинамики
для идеального газа:
Великое
прозрение Карно состоит в том, что он
показал, что ни один тепловой двигатель,
работающий при двух заданных температурах,
не может быть эффективнее идеального
двигателя Карно (это утверждение называют
теоремой
Карно). В
противном случае мы столкнулись бы с
нарушением второго
начала термодинамики,
поскольку такой двигатель отбирал бы
тепло от менее нагретого резервуара и
передавал бы его более нагретому. (На
самом деле, второе начало термодинамики
является следствием теоремы Карно. )Теорема
Карно 1)КПД
тепловой машины, работающей с данными
нагревателя и холодильником по прямому
обратному циклу карно, не зависит от
рода вещества, а определяется лишь Т_н
и Т_х.
2)КПД тепловой машины, работающей по
прямому обратному циклу будет всегда
больше КПД тепловой машины, работающей
по не обратному циклу с тем же нагревателем
и холодильником.

коэффициент.
II закон термодинамики в формулировке
Клаузиуса.

Обратный
цикл – цикл проходящий против часовой
стрелки.

Холодильный
коэффициент — безразмерная величина
(обычно больше единицы), характеризующая
эффективность работы холодильной
машины. Она равна
отношению холодопроизводительности
к количеству энергии (работе), затраченной
в единицу времени на осуществление
холодильного цикла. Определяется типом
холодильного цикла, по котором у работает
машина, совершенством её основных
элементов и для одной и той же машины
зависит от температурных условий её
работы. При заданной температуре
окружающей среды Т
на единицу полученного искусственного
холода затрачивается тем большая
энергия, чем ниже температура охлаждаемого
объекта.

Холодильная
машина — устройство,
служащее для отвода теплоты от охлаждаемого
тела при температуре более низкой, чем
температура окружающей среды. Х. м.
работают по принципу теплового
насоса
— отнимают теплоту от охлаждаемого
тела и с затратой энергии (механической,
тепловой и т.д.) передают её охлаждающей
среде, имеющей более высокую температуру,
чем охлаждаемое тело.

«Теплота
не может самопроизвольно переходить
от тела менее нагретого к телу более
нагретому».Рудольф Клаузиус.

Второе
начало термодинамики не только установило
границы преобразования тепла в работу,
но и позволило построить рациональную
шкалу температур (термодинамическая
шкала температур) и установить направление
процессов, происходящих в теплоизолированных
системах.

Х.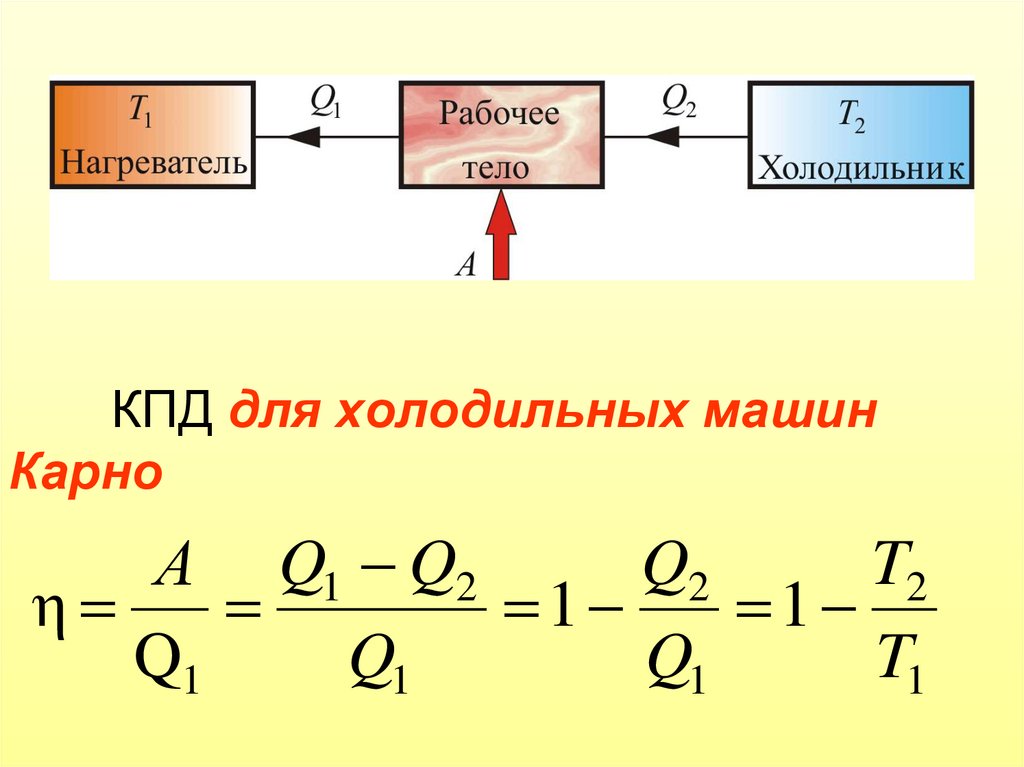 м.
– устройство, которое
работает по обратному циклу, передовая
теплоту от < нагретых к > нагретым
телам за счет А^’
внешних сил. Основные компоненты: 1)
холодильник,

2)
рабочее тело, 3)нагреватель.

25)Приведенное
количество теплоты. Приведенное
количество теплоты в обратимых и
необратимых процессах – неравенство
Клаузиуса.

Рассматривая
процессы превращения тепла в работу,
Р. Клаузиус сформулировал термодинамическое
неравенство (неравенство
Клаузиуса): «Приведенное
количество тепла, полученное системой
в ходе произвольного кругового процесса,
не может быть больше нуля».

где
Q
– количество тепла, полученное системой
при температуре Т, Q₁

количество тепла, получаемое системой
от участков окружающей среды с температурой
Т₁,
Q^₂
– количество тепла, отдаваемое системой
участкам окружающей среды при температуре
Т₂.
Неравенство Клаузиуса позволяет
установить верхний предел термического
КПД при переменных температурах
нагревателя и холодильника.

,

где
Т_{1 макс}
– максимальная температура участка
среды, от которого система получает
тепло; Т_{2 мин} –
минимальная температура участка среды,
которому система отдает тепло.

Из
выражения для обратимого цикла Карно
следует, что

или

,

т.е.
для обратимого цикла неравенство
Клаузиуса переходит в равенство. Это
означает, что приведенное количество
тепла, полученное системой в ходе
обратимого процесса, не зависит от вида
процесса, а определяется только начальным
и конечным состояниями системы. Поэтому
приведенное количество тепла, полученное
системой в ходе обратимого процесса,
служит мерой изменения функции состояния
системы, называемой энтропией.

26)
Энтропия термодинамических систем —
функция состояния.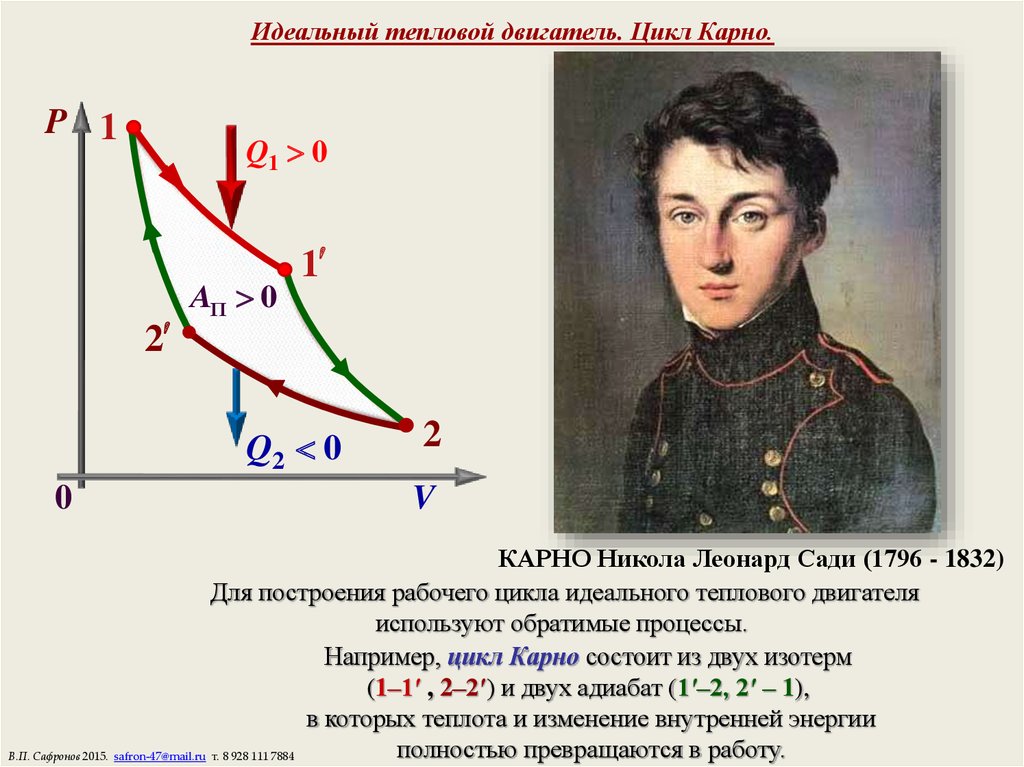 Изменение
энтропии в замкнутых системах при
обратимых и необратимых процессах.
Закон возрастания энтропии. Примеры,
подтверждающие закон возрастания
энтропии.

Энтропия
системы – функция ее
состояния, определенная с точностью до
произвольной постоянной. Приращение
энтропии равно приведенному количеству
тепла, которое нужно сообщить системе,
чтобы перевести ее из начального
состояния в конечное по любому обратимому
процессу.

,

.

Важной
особенностью энтропии является ее
возрастание в изолированных системах
(закон возрастания энтропии): «Энтропия
теплоизолированной (адиабатической)
системы не может убывать; она возрастает,
если в системе идет необратимый процесс,
и остается постоянной при обратимом
процессе в системе».

Необратимые
процессы в системе приводят к установлению
равновесного состояния. В этом состоянии
энтропия изолированной системы достигает
максимума и в дальнейшем никакие
макроскопические процессы в системе
невозможны.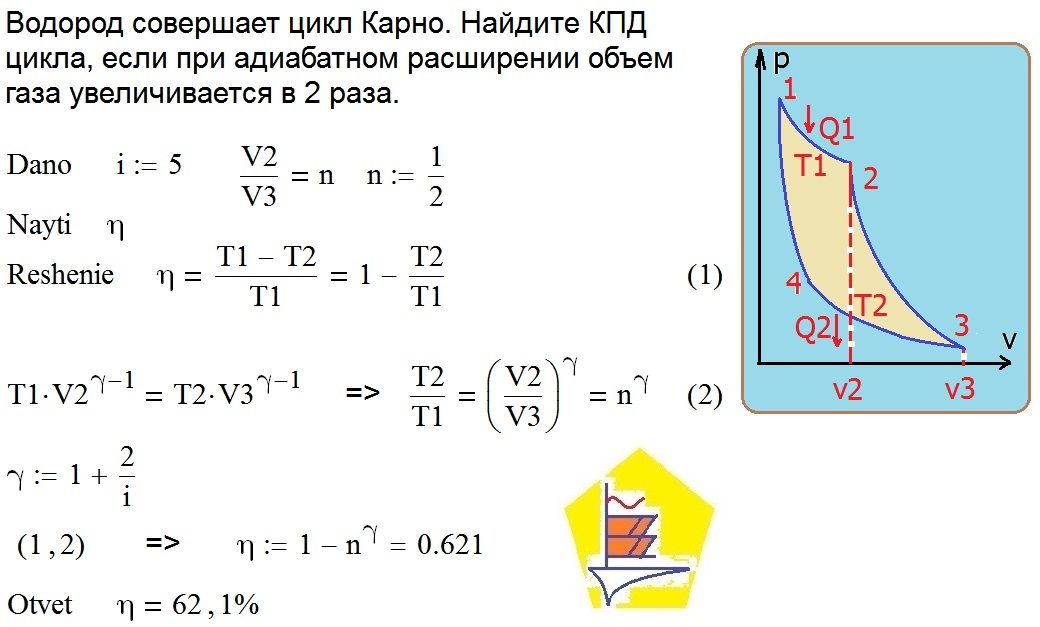

Изменение
энтропии при наличии теплообмена с
окружающей средой, может быть каким
угодно: как больше нуля, так и меньше
нуля.

Получим
выражение для приращения энтропии
идеального газа при переходе из состояния
с параметрами T₁,
V₁
в состояние с параметрами T₂,
V₂:

Из
выражения для приращения энтропии газа
следует, что энтропия является функцией
двух параметров 
температуры и объема S=S(T,V).

Введение
энтропии позволяет объединить первое
и второе начала термодинамики в виде
термодинамического неравенства

,

где
знак равенства относится к обратимым
процессам, знак неравенства 
к необратимым. Энтропия, как и внутренняя
энергия, связана с микроскопическим
строением системы и статистическим
характером теплового движения частиц
системы.

§8. Тепловые машины — ЗФТШ, МФТИ

Пусть есть тело, называемое рабочим телом, которое может совершать цикл (не обязательно равновесный), периодически вступая в тепловой контакт с двумя телами.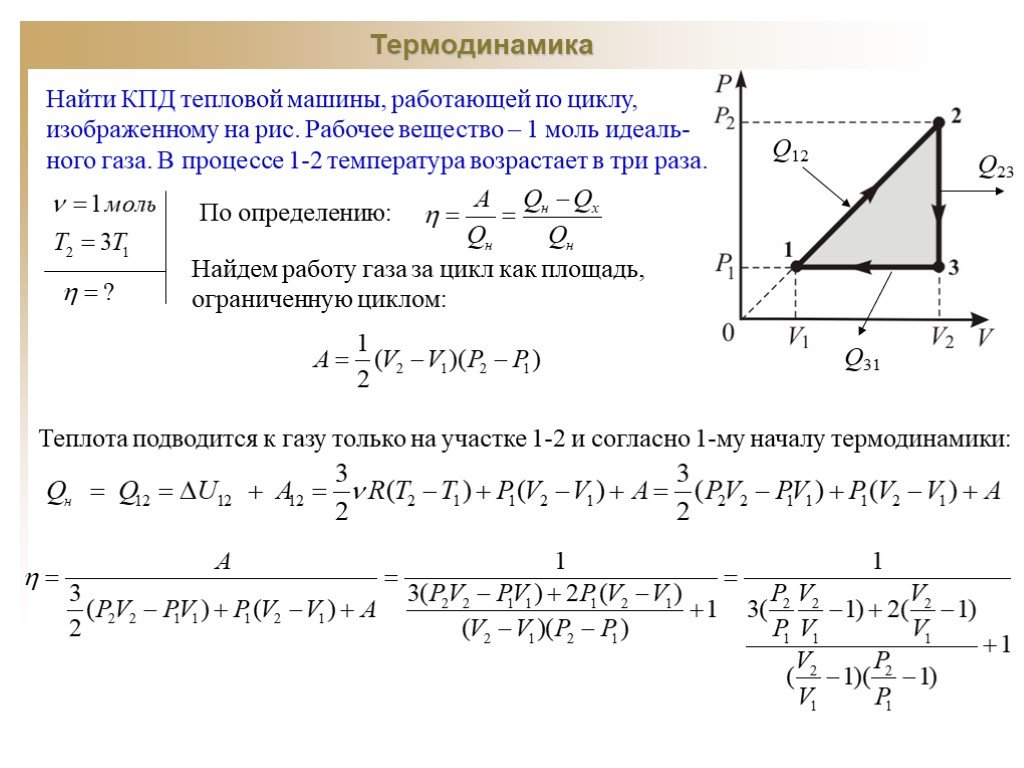 Тело с более высокой температурой назовём условно нагревателем, а с более низкой температурой – холодильником. За цикл рабочее тело совершает положительную или отрицательную работу $$ A$$. Такое устройство будем называть тепловой машиной. Тепловая машина, которая служит для получения механической работы, называется  тепловым двигателем. Тепловая машина, служащая для передачи количества теплоты от менее нагретого тела (холодильника) к более нагретому (нагревателю), используя работу окружающих тел над рабочим телом, называется тепловым насосом или холодильной установкой (холодильником). Деление на тепловые насосы и холодильные установки условное, связанное с предназначением этих тепловых машин. Тепловой насос используется для поддержания в помещении температуры, которая выше температуры окружающей среды. Холодильная установка используется для поддержания в некотором объёме  (камере)  температуры  более  низкой, чем снаружи. {-})=A.$$ Поэтому

Видим, что КПД теплового двигателя меньше единицы. Причиной этого является то, что для обеспечения периодичности в работе теплового двигателя необходимо часть тепла, взятого у нагревателя, обязательно отдать холодильнику.

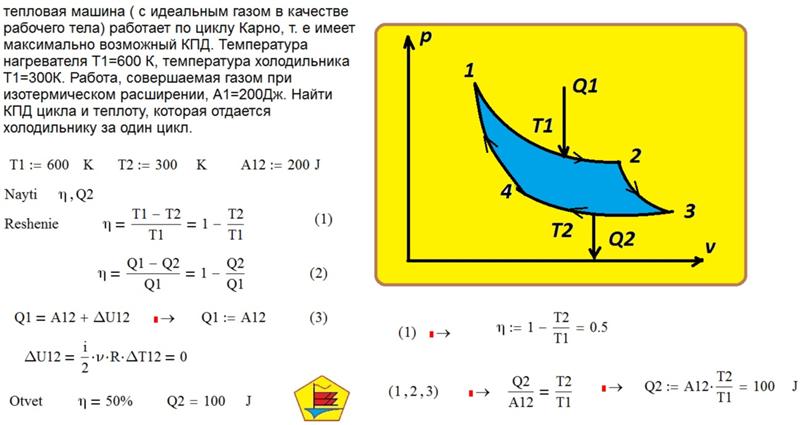
С. Карно (1796 – 1832) установил, что максимальный КПД теплового двигателя, работающего с нагревателем температуры $$ {T}_{1}$$ и холодильником температуры $$ {T}_{2}$$, независимо от рабочего тела есть 

Это достигается, если рабочее тело совершает цикл Карно, т. е. равновесный цикл, состоящий из двух адиабат и двух изотерм с температурами $$ {T}_{1}$$ и $$ {T}_{2}$$. На изотерме с $$ {T}_{1}$$ рабочее тело получает тепло от нагревателя, а на изотерме с $$ {T}_{2}$$ – отдаёт тепло холодильнику. Цикл Карно для идеального газа изображён на рис. 9:  `1-2` и `3-4` – изотермы, `2-3` и  `4-1` – адиабаты.  Тепловая  машина,  работающая   по прямому или обратному циклу Карно, называется идеальной тепловой машиной.

идеальных двигателей | Физика Фургон

Категория
Выберите категориюО фургоне физикиЭлектричество и магнитыВсе остальноеСвет и звукДвижение вещейНовая и захватывающая физикаСостояния материи и энергииКосмосПод водой и в воздухе

Подкатегория

Поиск

Задайте вопрос

Последний ответ: 22.10.2007

Вопрос:

Мы не можем сделать тепловую машину со 100% КПД, но можем ли мы сделать 9КПД 9%?
— Яджу Арья (15 лет)
Dayanand Model School, Джаландхар, Пенджаб, Индия

A:

Тепловые двигатели подчиняются законам термодинамики. Если вы проработаете математику, вы получите максимальную эффективность, зависящую от температур горячего и холодного резервуара. Мы показываем, что максимально возможная эффективность = 1- T _c /T _h , где T _c и T _h — температуры коллектора в градусах Кельвина, поэтому в принципе мы можем получить любую эффективность, какую захотим (при условии, что это меньше 100%) просто выбрав Т _h и T _c сильно отличаются.

Проблема в том, что для достижения максимальной эффективности все должно происходить очень медленно. [Причина этого в том, что в некоторых точках цикла тепло перетекает из более горячей области в более холодную из-за разницы температур. Однако максимальная эффективность достигается только тогда, когда разница температур становится небольшой, что замедляет поток тепла./ мВт] 

Адам

Вот еще одна проблема. На земле сбросное тепло будет сбрасываться где-то с температурой около Т _С = 300К. Чтобы получить КПД 99% даже при медленной работе, потребуется T _H > 30 000K. Нет материалов, способных выдержать такую ​​температуру. Майк В.

(опубликовано 22.10.2007)

Дополнение №1: Эффективность Карно

Вопрос:

Я думал по причинам, которые не могу вспомнить, что максимальный КПД любой тепловой машины только на 40% можно назвать двигателем Карно.
— Девон (26 лет)
Лансинг

А:

То 1-T _c /T _h , о котором писал Адам, является эффективностью Карно. Причины, по которым КПД двигателя не превышает 40% в большинстве типичных приложений, — это те, о которых мы упоминали. Предположим, что тепло отводится в типичную окружающую среду при T _c = 300K. Чтобы получить эффективность Карно выше 40%, необходимо, чтобы T _h было выше 500К. Это вполне возможно, но вы не можете получить намного горячее, не исчерпав подходящих материалов. Если вы затем вспомните, что реальный КПД всегда меньше, чем КПД Карно, как из-за трения, так и из-за проблемы теплового потока, о которой мы упоминали выше, редко можно найти примеры лучше, чем 40%.

Учитывая исключительную изощренность многих ваших вопросов, я удивлен, что вы не знакомы с причиной ограничения Карно. По мере того, как тепло Q уходит из горячего резервуара, его энтропия S уменьшается на Q/T _ч . (Это по определению T.) Согласно второму закону термодинамики ни один процесс не уменьшает чистое значение S. Таким образом, поток тепла к холодному резервуару должен составлять не менее (Q/T _ч )T _c . Это энергия, недоступная для выполнения работы. Таким образом, из энергии Q, извлекаемой из горячего источника, для совершения работы остается не более Q(1-T _с /Т _ч ).

Mike W.

(опубликовано 14.01.2013)

Дополнение к этому ответу

Связанные вопросы

• теплоизоляция

  14?

• медленный слив горячей воды

• теплоемкость при постоянном объеме или давлении

• сохранение молока холодным

• предотвращение теплового равновесия

• Диффузионное движение в ячейках

• Горячая и холодная вода

• Тепловая вместимость при постоянном давлении или объеме

• Ductile-Crittle Transition

по-прежнему курсив?

Вопросы и ответы по Expore в смежных категориях

• Температура и жара

Идеальная тепловая машина Карно

Что такое идеальная тепловая машина Карно?

Идеальная тепловая машина Карно — это идеальная тепловая машина, работающая по циклу Карно. Модель этого двигателя была разработана Николя Леонардом Сади Карно в 1824 году. Его работа аналогична тепловой машине и основана на втором законе термодинамики.

Второй закон термодинамики

Направление движения тепла определяется этим законом. Невозможно построить циклическую машину, которая собирает теплоту от источника, превращает всю эту теплоту в работу и не отбрасывает никакой теплоты для стока. Утверждение Кельвина-Планка относится к приведенному выше выражению второго закона.

Механический труд может быть полностью преобразован в теплоту, но обратное неверно. Теплота и труд в этом отношении неодинаковы. Теперь мы рассмотрим несколько приложений второго закона термодинамики.

Тепловой двигатель

Устройство, используемое для преобразования тепловой энергии в механическую, называется тепловым двигателем. Для преобразования теплоты в работу с помощью тепловой машины необходимо выполнение следующих условий.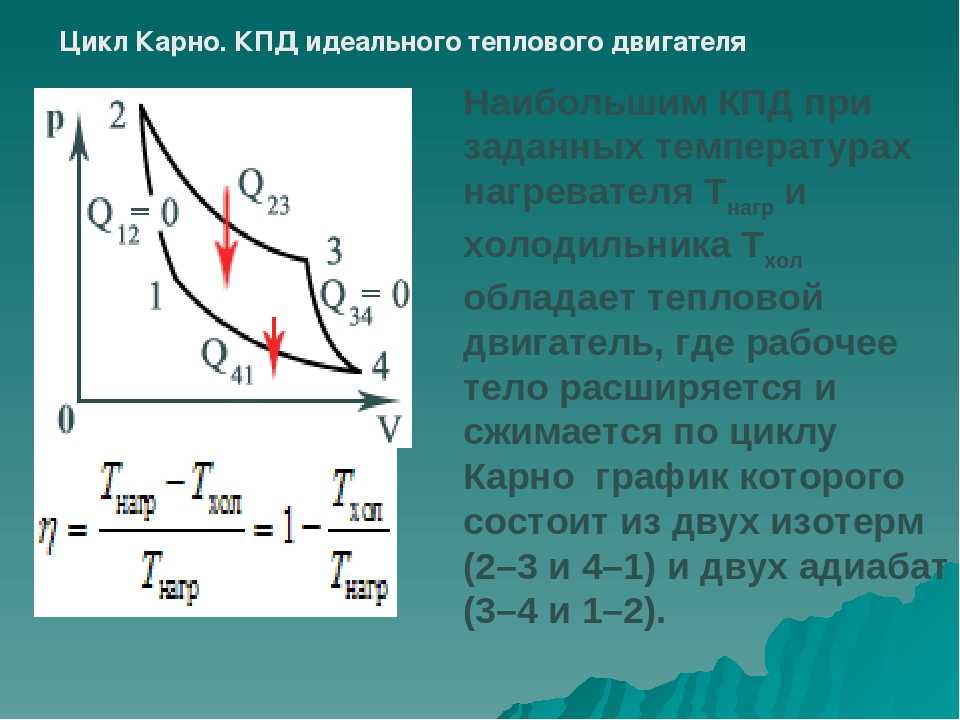 Должно быть тело с более высокой температурой «T1», из которого извлекается тепло. Его называют источником. Корпус двигателя должен содержать рабочее тело. Должно быть тело с более низкой температурой «T₂», которое может отводить тепло. Это называется раковиной.

Работа теплового двигателя

Двигатель получает количество «Q1» тепла от источника.

Часть этого тепла преобразуется в работу «Вт». Оставшееся тепло «Q» отбрасывается в сток.

Таким образом,   

Q1 = W+Q₂

или работа, совершаемая двигателем, равна

W=Q₁-Q₂

определяется как доля общего количества тепла, подводимого к двигателю, которое преобразуется в работу.

Математически,

Поскольку 𝛈=  W/Q₁

Или 𝛈= Q₁-Q2/Q₁ = 1-Q2/Q₁

Идеальная тепловая машина Карно

Цикл Карно. Модель этого двигателя была разработана Николя Леонардом Сади Карно в 1824 году. Она состоит из разных частей.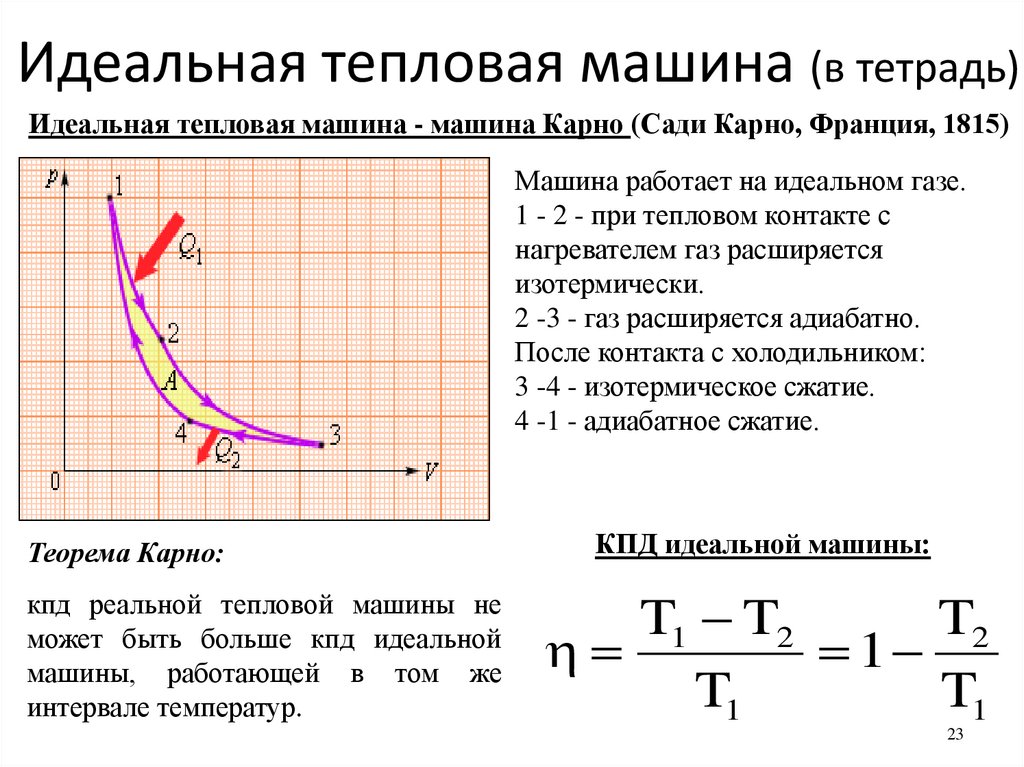

Источник: Резервуар тепловой энергии с проводящим верхом, поддерживающим постоянную температуру T1K. Источник настолько велик, что выделение из него любого количества тепла не меняет его температуры.

Корпус тепловой машины: Представляет собой бочку с идеально изолирующими стенками и токопроводящим дном. Он оснащен герметичным поршнем, способным скользить внутри ствола без трения. В бочке находится некоторое количество идеального газа.

Раковина

: Это огромное тело при более низкой температуре T₂, имеющее идеально проводящую вершину. Размер раковины настолько велик, что любое количество отводимого в нее тепла не увеличивает ее температуру.

Изолирующая подставка: Это подставка, изготовленная из идеально изолирующего материала, так что ствол, помещенный на нее, становится полностью изолированным от окружающей среды.

Работа идеальной тепловой машины Карно и ее процессы 

Когда работает машина Карно, рабочее тело двигателя подвергается другому процессу, известному как цикл Карно, и этот цикл состоит из четырех различных этапов.

1. Первый этап: — Известен как процесс изотермического расширения

В этом такте ствол помещается над источником. Поршень постепенно отталкивается назад по мере расширения газа. Падение температуры из-за расширения компенсируется подводом тепла от источника и, следовательно, температура остается постоянной. Состояние газа меняется с A(P₁, V1) на B(P₂, V2). Если W1 — работа, совершенная в этом процессе, то теплота Q₁, полученная от источника, равна

Q₁ = W1 = -nRT1 loge(V2 / V1)

2. Второй этап:- Известный как процесс адиабатического расширения

Бочка снимается с источника и размещается над изолирующей стойкой. Поршень отталкивается назад, так что газ адиабатически расширяется, что приводит к падению температуры с T1 до T₂. Состояние газа меняется с B(P₂, V₂) на C(P3, V3). Если W₂ — работа, выполненная в этом случае, то:

W₂ = nCv(T2 — T1)

3. Третий этап: — Известен как процесс изотермического сжатия

Бочка размещается над раковиной. Поршень толкается вниз, тем самым сжимая газ. Тепло, выделяемое за счет сжатия, течет к сливу, поддерживает постоянную температуру ствола. Состояние газа меняется с C(P3, V3) на D(P4, V4). Если W — работа, совершаемая в этом процессе, а Q — теплота, отводимая в сток, то:

W3 = -nRT₂ loge(V4 / V3)

4. Четвертая стадия. Известна как процесс адиабатического сжатия .

Бочка размещается над изолирующей подставкой. Поршень перемещается вниз, адиабатически сжимая газ до тех пор, пока температура газа не повысится от T₂ до T1. Состояние газа изменится с D(P4, V4) на A(P1, V1). Если W4 — работа, выполненная в этом процессе, то:

W4 = nCv(T1 – T2)

Теплота, преобразованная в работу в машине Карно – nRT₂ loge(V4 / V3) + nCv(T1 – T2)

⇒ -nR[ T1 loge(V2 / V1) + T2 loge(V4 / V3) ] 

Для BC, T1V2𝜸 – 1 = T2V3𝜸 – 1 

Для DA, T1V1𝜸 – 1 = T2V4𝜸 – 1

(V2 / V1)𝜸 – 1 = (V3 / V4)𝜸 – 1  ⇒  V2 / V1 = V3 / V4

Таким образом, чистая работа, выполненная двигателем за время один цикл равен площади, ограниченной индикаторной диаграммой цикла.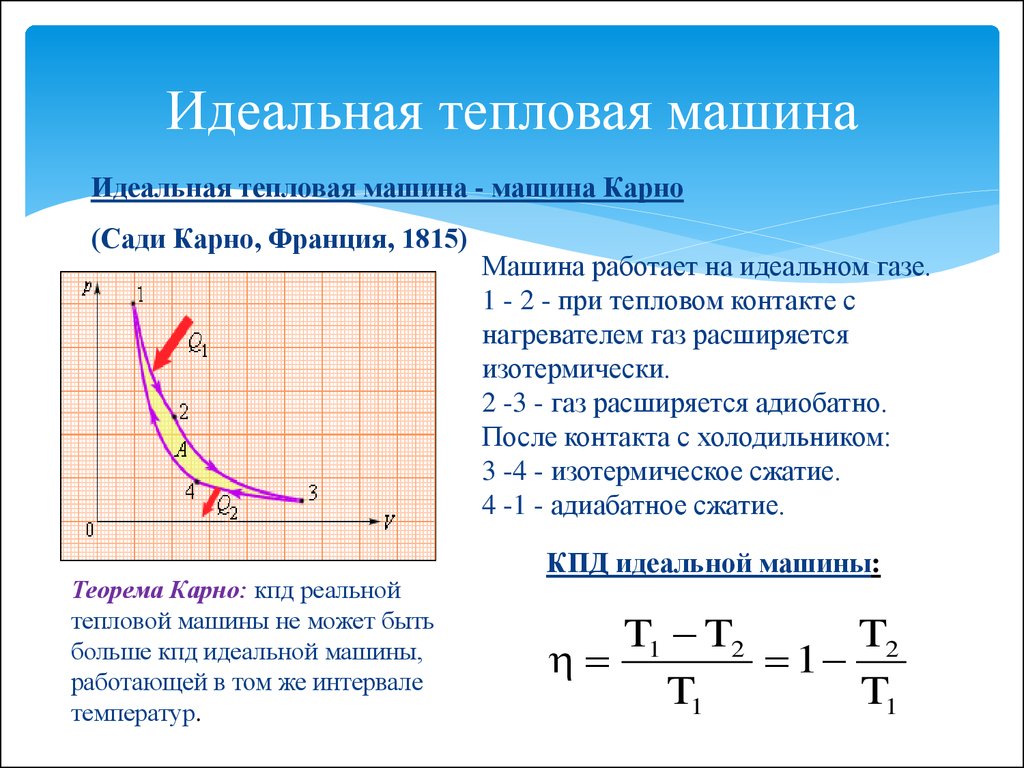 Аналитически:

Wцикл = -nR(T1 – T2) loge(V2 / V1) 

КПД идеальной тепловой машины Карно ) к общему теплу, подводимому к двигателю. Таким образом:

𝛈 = мод W/Q1 = (Q1 – Q2)/Q1

𝛈 = nR(T1 – T2) loge(V2 / V1) / nRT1 loge(V2 / V1)  = (T1 – T2) / T1

𝛈 = 1 – Q2 / Q1 = 1 – T2 / T1

Некоторые важные моменты, касающиеся идеальной тепловой машины Карно

1. Эффективность двигателя зависит от температуры, в которой он работает.
2. 𝛈 не зависит от природы рабочего вещества.
3. 𝛈 является единицей, только если T2  = 0. Поскольку абсолютный нуль недостижим, следовательно, даже идеальный двигатель не может быть на 100% эффективнее.
4. 𝛈 единица, только если Q2 = 0 Но 𝛈 = 1 никогда не бывает возможным даже для идеального двигателя. Следовательно, Q2 ≠ 0,
5. . Таким образом, невозможно извлечь теплоту из одного тела и преобразовать ее всю в работу.
6. Если T2  = T1 , то 𝛈 = 0
7. В реальных тепловых машинах много потерь на трение и т.