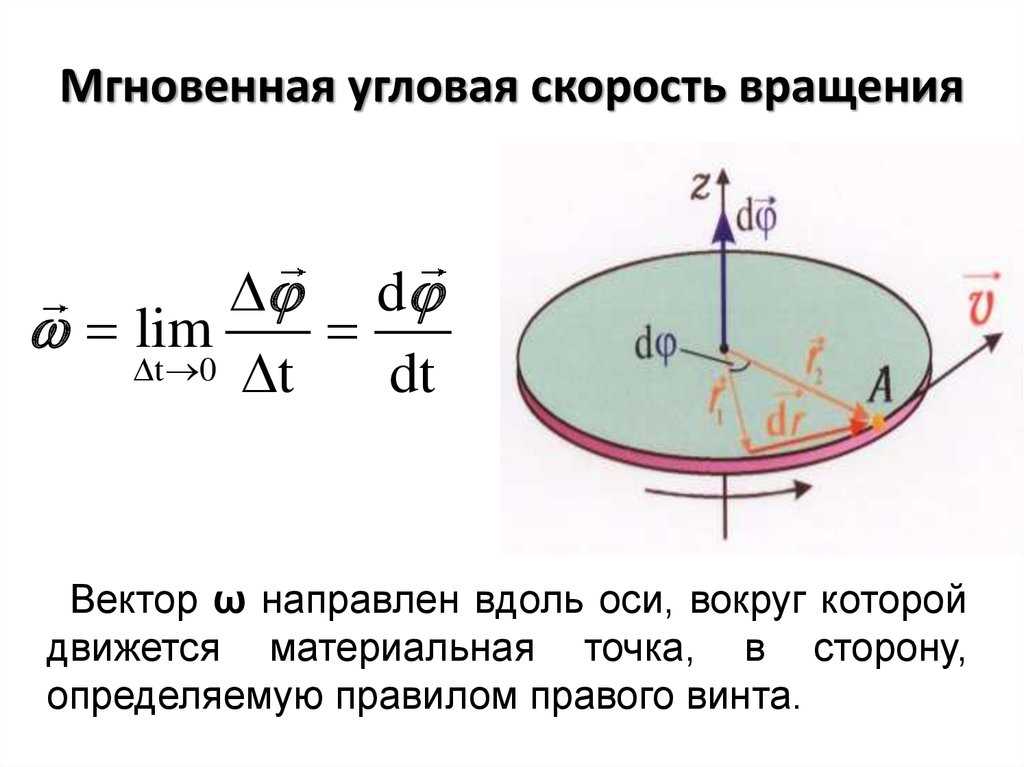
4 способа расчета угловой скорости колеса барабана
Пример решения задачи по определению угловой скорости колеса заданного радиуса и приводимого в движение приложенным моментом из состояния покоя, которое посредством невесомой нити двигает груз по шероховатой поверхности.
Задача
Однородное колесо 1 массой M и радиусом r1 приводится в движении из состояния покоя приложенным моментом mвр. Груз 2 массой m посредством невесомой нити, намотанной на колесо барабана, движется по шероховатой поверхности, коэффициент трения скольжения которой равен f (рисунок 3.6).
Рисунок 3.6
Определить угловую скорость колеса в 4 случаях:
- а) mвр=A;
- б) mвр=a∙t, где a – постоянная, t – время;
- в) mвр=b∙φ, где b – постоянная, φ – угол поворота барабана;
- г)
где c – постоянная,
– угловая скорость колеса.
Другие примеры решений >
Помощь с решением задач >
Пример решения
Механическая система состоит из двух тел: барабана 1, вращающегося вокруг оси x, и груза 2, движущегося поступательно.
Выделим все силы, действующие на систему:
P1 = M∙g – сила тяжести барабана;
R1 и R2 – составляющие реакции колеса по осям Oz и Oy;
mвр – вращающий момент;
P2 = M∙g – сила тяжести груза;
N – нормальная реакция плоскости;
Fтр = f∙N = f∙m∙g – сила трения при скольжении груза о плоскость.
Согласно теореме об изменении момента количества движения механической системы относительно оси
где
Kx – кинетический момент системы.
Кинетический момент системы определяется по формуле
где kб – кинетический момент барабана;
kгр – кинетический момент груза;
Тогда
Итак,
Окончательно получим
Решим последнее соотношение относительно угловой скорости колеса в четырех случаях, указанных в условии задачи.
Случай (а) mвр=A (A = const).
Для удобства в выражении (3.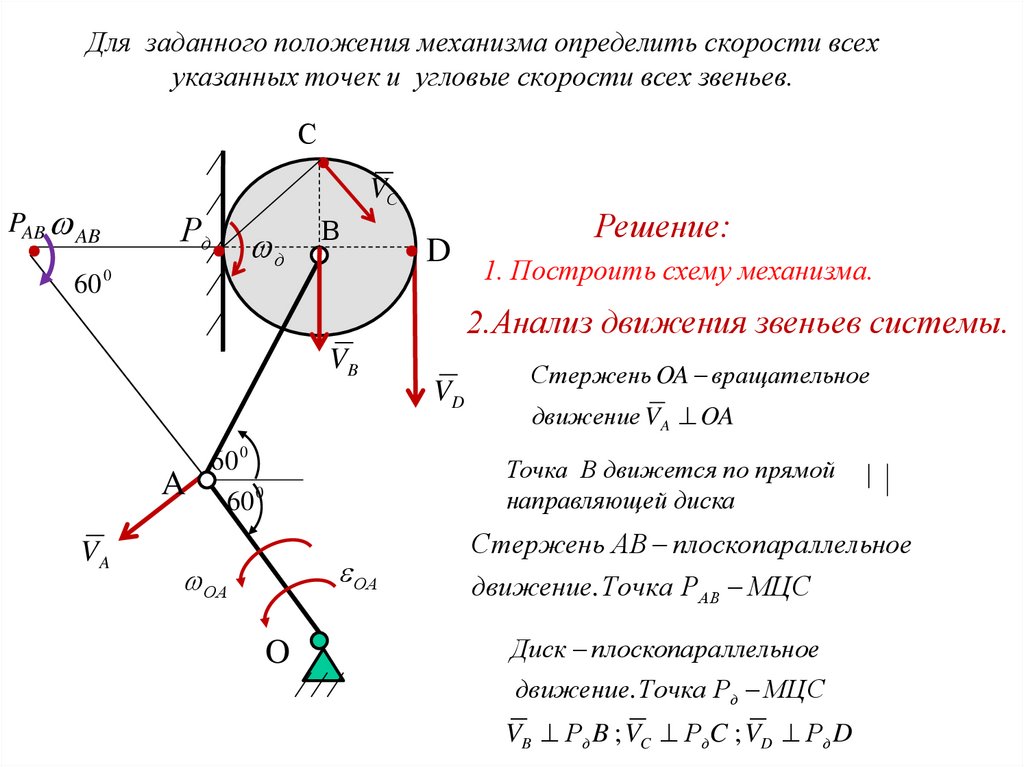 15) введем для момента инерции системы обозначение
15) введем для момента инерции системы обозначение
Тогда
Разделив переменные и проинтегрировав обе части уравнения, получим
Окончательно будем иметь
Случай (б) mвр = a∙t.
Разделив переменные и проинтегрировав обе части этого уравнения
получим
Случай (в) mвр = b∙φ.
Так как правая часть зависит от угла поворота φ и прямого разделения переменных совершить невозможно, произведем замену переменной t:
тогда
Разделим переменные и проинтегрируем полученное уравнение
откуда
Случай (г)
Разделив переменные, проинтегрируем и определим угловую скорость
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Подробнее
Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.
НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ
На нашем сайте можно бесплатно скачать:
— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку
Сохранить или поделиться с друзьями
Помощь с решением
ВЫБЕРИТЕ РАЗДЕЛ МЕХАНИКИ
- Техническая механика (техмех)
- Теоретическая механика (теормех)
- Сопротивление материалов (сопромат)
- Строительная механика (строймех)
- Теория механизмов и машин (ТММ)
- Детали машин и ОК (ДМ)
Поиск формул и решений задач
Угловая скорость
1. 54 Найти угловую скорость вращения электрона вокруг ядра
В первом приближении можно считать, что электрон в атоме водорода движется по круговой орбите с линейной скоростью v. Найти угловую скорость ω вращения электрона вокруг ядра и его нормальное ускорение аn.
1. 55 Найти для точек на ободе колеса угловую скорость
Колесо радиусом R = 10 см вращается с угловым ускорением ε = 3,14 рад/с2.
1. 60 Найти через время после начала движения угловую скорость
Колесо радиусом R = 0,1 м вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением φ=А+B+Ct2, где В = 2 рад/с и С = 1 рад/с3.
1. 41 Найти угловую скоростью суточного вращения Земли
Найти угловую скоростью ω: а) суточного вращения Земли; б) часовой стрелки на часах; в) минутной стрелки на часах; г) искусственного спутника Земли, движущегося по круговой орбите с периодом вращения Т = 88 мин.
1. 46 Найти угловое ускорение колеса
Колесо, вращаясь равноускоренно, достигло угловой скорости ω = 20 рад/с через N = 10 об после начала вращения. Найти угловое ускорение ε колеса.
469 Определить максимальную мощность необходимую для вращения…
Проволочный контур площадью \(S = 500\) см2 и сопротивлением \(R = 0,1\) Ом равномерно вращается в однородном магнитном поле (\(B = 0,5\) Тл). Ось вращения лежит в плоскости кольца и перпендикулярна линиям магнитной индукции.
422 Определить магнитный момент при вращении диска…
Диск радиусом \(R = 8\) см несет равномерно распределенный по поверхности заряд (\(\sigma = 100\) нКл/м2). Определить магнитный момент \({P_m}\), обусловленный вращением диска, относительно оси, проходящей через его центр и перпендикулярной плоскости диска.
425 Найти магнитный момент обусловленный вращением…
Тонкое кольцо радиусом \(R = 10\) см несет равномерно распределенный заряд \(Q = 80\) нКл. Кольцо вращается с угловой скоростью \(\omega = 50\) рад/с относительно оси, совпадающей с одним из диаметров кольца. Найти магнитный момент \({P_m}\), обусловленный вращением кольца.
426 Найти магнитный момент обусловленный вращением стержня. ..
..
Заряд \(Q = 0,1\) мкКл равномерно распределен по стержню длиной \(L = 50\) см. Стержень вращается с угловой скоростью \(\omega = 20\) рад/с относительно оси, перпендикулярной стержню и проходящей через его середину. Найти магнитный момент \({P_m}\), обусловленный вращением стержня.
429 Определить магнитный момент P…
По поверхности диска радиусом \(R = 15\) см равномерно распределен заряд \(Q = 0,2\) мкКл. Диск вращается с угловой скоростью \(\omega = 30\) рад/с относительно оси, перпендикулярной плоскости диска и проходящей через его центр.
152 С какой угловой скоростью будет вращаться скамья…
На скамье Жуковского стоит человек и держит в руках стержень вертикально по оси скамьи. Скамья с человеком вращается с угловой скоростью ω = 4 рад/с.
153 С какой угловой скоростью будет вращаться платформа…
Платформа в виде диска диаметром D = 3 м и массой m1 = 180 кг может вращаться вокруг вертикальной оси.
155 С какой скоростью станет вращаться скамья. ..
..
На скамье Жуковского стоит человек и держит в руке за ось велосипедное колесо, вращающееся вокруг своей оси с угловой скоростью ω = 25 рад/с. Ось колеса расположена вертикально и совпадает с осью скамьи Жуковского.
158 С какой угловой скоростью начнет вращаться скамья…
На краю неподвижной скамьи Жуковского диаметром D = 0,8 м и массой m1 = 6 кг стоит человек массой m2 = 60 кг.
159 С какой угловой скоростью начнет вращаться платформа…
Горизонтальная платформа массой M = 150 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой ν2 = 8 мин-1. Человек массой m = 70 кг стоит при этом на краю платформы.
168 Определить линейную и угловую скорости спутника…
Определить линейную и угловую скорости спутника Земли, обращающегося по круговой орбите на высоте r = 1000 км. Ускорение свободного падения g у поверхности Земли и ее радиус Rз считать известными.
107 Во сколько раз путь будет больше модуля перемещения…
Материальная точка движется по окружности с постоянной угловой скоростью ω = π/6 рад/с. Во сколько раз путь ΔS, пройденный точкой за время T = 4 с, будет больше модуля ее перемещения Δr ?
109 Каково наибольшее ускорение движения человека…
По краю равномерно вращающейся с угловой скоростью ω = 1 рад/с платформы идет человек и обходит платформу за время t = 9,9 с. Каково наибольшее ускорение а движения человека относительно Земли? Принять радиус платформы R = 2 м.
143 Определить момент инерции маховика…
На обод маховика диаметром D = 60 см намотан шнур, к концу которого привязан груз массой m = 2 кг.
Калькулятор угловой скорости
Автор Wojciech Sas, PhD
Отзыв от Bogna Szyk и Jack Bowater
Последнее обновление: 02 ноября 2022 г.
Содержание:
- Что такое угловая скорость?
- Формулы угловой скорости
- Единицы измерения угловой скорости
- Зависимость угловой скорости от угловой частоты
- Как найти угловую скорость Земли?
- Физические величины, зависящие от угловой скорости
- Сохранение углового момента
Этот калькулятор угловой скорости представляет собой простой в использовании инструмент, который дает немедленный ответ на вопрос « Как найти угловую скорость? «. В тексте вы найдете несколько формул угловой скорости , узнаете о различных единицах угловой скорости и, наконец, оцените угловую скорость Земли!
В тексте вы найдете несколько формул угловой скорости , узнаете о различных единицах угловой скорости и, наконец, оцените угловую скорость Земли!
Задумывались ли вы когда-нибудь, какова связь между угловой скоростью и угловой частотой или где применяется угловая скорость? Читайте дальше, чтобы узнать, и стать экспертом в области кругового движения.
🙋 Перейдите к нашему калькулятору кругового движения, чтобы также узнать о других важных величинах для вращающегося тела.
Что такое угловая скорость?
Угловая скорость описывает вращательное движение тел. Он измеряет, насколько быстро они движутся вокруг некоторого центра вращения. Мы можем думать о двух разных видах вращения. Первый описывает движение центра масс данного объекта вокруг определенной точки в пространстве , которую мы можем описать как начало координат. Некоторые примеры включают планеты, движущиеся вокруг Солнца, или автомобиль, съезжающий с шоссе.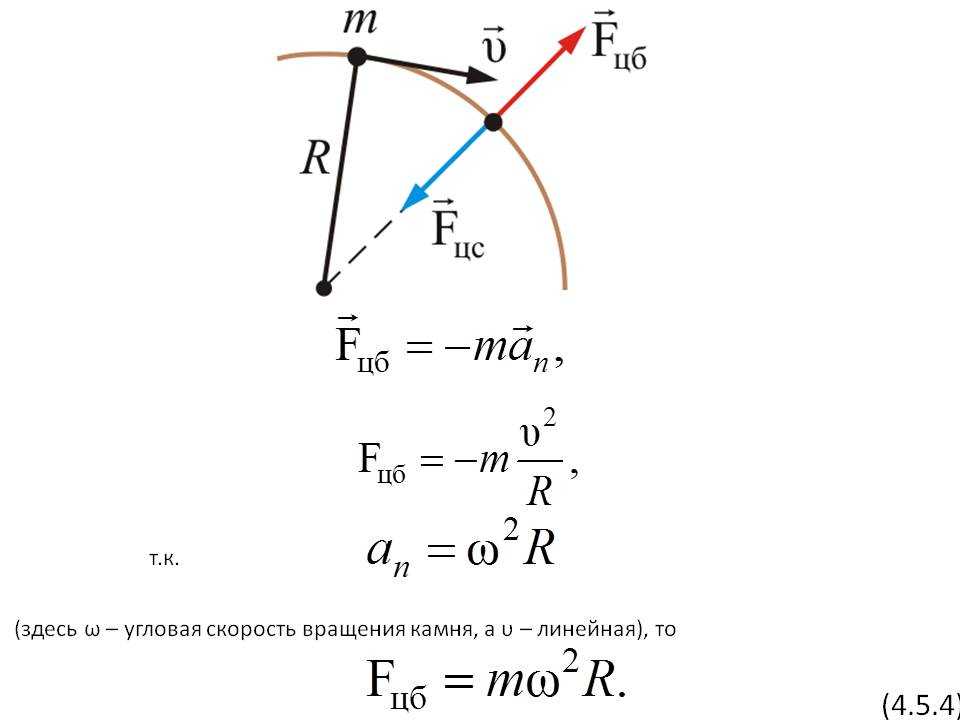
Второй рассказывает о вращении тела вокруг собственного центра масс — спине (не путать с квантовым свойством частиц, также называемым спином). Наверняка вы видели, как баскетболист крутит мяч на пальце.
В целом можно сказать, что чем быстрее движение, тем выше угловая скорость. Мы должны перейти к уравнениям угловой скорости, описанным в следующем разделе, чтобы определить некоторые конкретные значения.
Формулы угловой скорости
Этот калькулятор угловой скорости использует две разные формулы угловой скорости в зависимости от ваших входных параметров.
Первое уравнение угловой скорости аналогично уравнению для линейной скорости:
ω = (α₂ - α₁) / t = Δα / t ,
где α₁ и α₁ 9005 круг, а Δα — их разность. t – время, за которое происходит изменение угла. Как видите, для нормальной скорости есть отношение смещения положения за период, а здесь мы используем угол вместо расстояния.
Мы можем вывести вторую формулу угловой скорости из соотношения линейной скорости и радиуса, используя векторное произведение, которое равно:
v = ω × r .
Мы можем переписать это выражение, чтобы получить уравнение угловой скорости:
ω = r × v / |r|² ,
где все эти переменные являются векторами , а |r| обозначает абсолютное значение радиуса. Фактически угловая скорость представляет собой псевдовектор, направление которого перпендикулярно плоскости вращательного движения.
Единицы угловой скорости
Существует несколько единиц измерения угловой скорости, и те, которые мы используем в нашем калькуляторе угловой скорости, перечислены ниже:
рад/сили радиан в секунду - Определение исходит прямо из первой формулы угловой скорости. Он показывает, насколько велик поворот (или угол), на который тело движется за заданное время,об/минили оборотов в минуту - Единица, наиболее часто встречающаяся в практическом применении. С его помощью можно описать, как быстро вращается колесо или двигатель. Вы можете легко себе представить разницу между
С его помощью можно описать, как быстро вращается колесо или двигатель. Вы можете легко себе представить разницу между 10и100 RPM.Гцили герц - Те же единицы, которые используются для частоты, но редко используются в контексте угловой скорости. Это чем-то похоже наоб/мин, говорящее нам, сколько полных оборотов сделано за заданное время. Разница в том, что раньше основной единицей времени была минута, а здесь – секунда.
Естественно, все эти единицы угловой скорости пересчитываются между собой с использованием следующих соотношений:
1 RMP = 0,10472 рад/с = 0,01667 Гц ,
или наоборот:
,2 3 = рад /с = 60 об/мин .
Угловая скорость в зависимости от угловой частоты
Посмотрите определение угловой частоты:
ω = 2·π·f ,
, где f – частота. Как мы видим, он обозначается той же буквой.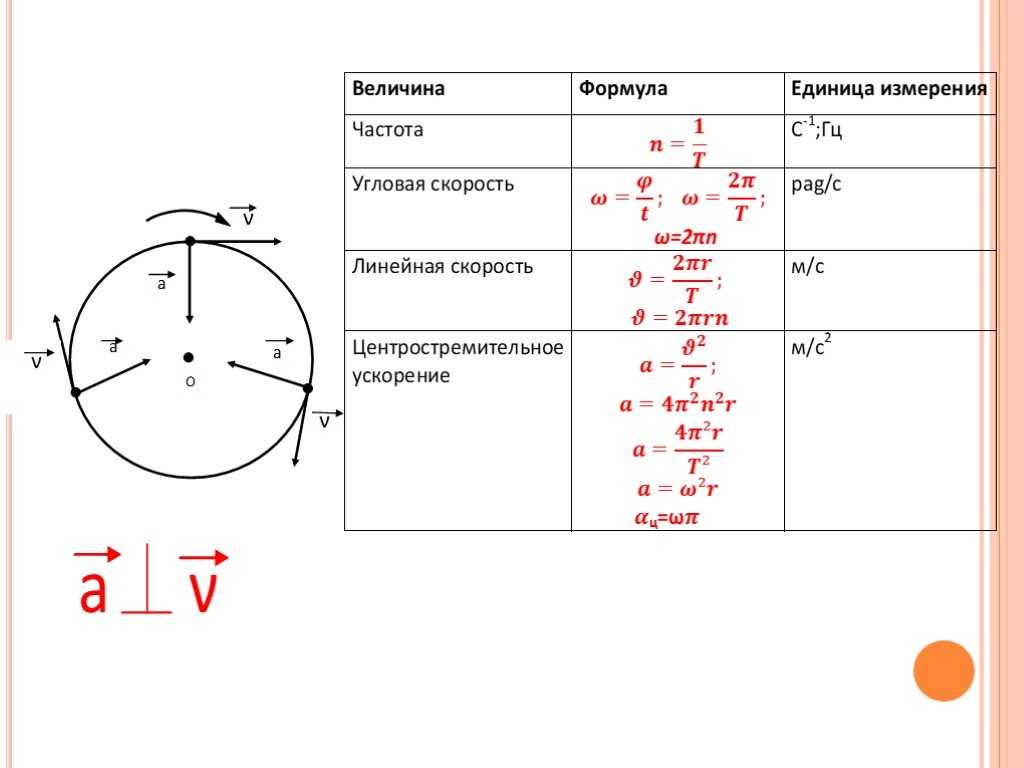 Кроме того, единицей угловой частоты является
Кроме того, единицей угловой частоты является рад/с , точно так же, как и для угловой скорости. Поэтому может возникнуть вопрос: «Чем отличается угловая скорость от угловой частоты?».
Ответ относительно прост. Связь между угловой частотой и угловой скоростью аналогична связи между скоростью и скоростью . Первое есть величина второго; другими словами, угловая частота является скаляром, тогда как угловая скорость является (псевдо)вектором.
Мы обычно используем угловую частоту, когда говорим о гармоническом движении, примером которого является простой маятник. Как вы понимаете, движение не обязательно должно быть представлено стандартным вращением, а просто движением, которое периодически повторяет свое положение. Однако угловая скорость строго связана с движением вокруг некоторой точки. Поэтому можно сказать, что угловая частота является более общей величиной, и мы можем использовать ее для описания широкого круга физических задач. Напротив, угловая скорость включает только вращательное движение.
🙋 У нас есть специальный инструмент, который объясняет, как рассчитать угловую частоту. Обязательно проверьте калькулятор угловой частоты!
Как найти угловую скорость Земли?
Как насчет того, чтобы воспользоваться нашим калькулятором угловой скорости? Оценим угловую скорость Земли! Во-первых, мы учитываем скорость вращения. Мы знаем, что Земля совершает полный оборот относительно далеких звезд примерно за 23 ч 56 мин 4 с , что составляет примерно 23,934 ч . Весь поворот составляет угол 2π рад , поэтому результирующая угловая скорость равна:
ω₁ = 2π рад / 23,934 ч = 0,2625 рад/ч = 0,00007292 рад/с /s (в экспоненциальном представлении).
Теперь, когда мы знаем угловую скорость вращения Земли, мы можем оценить ее линейную скорость на экваторе. Для этого нам нужен радиус Земли, примерно 6371 км . Нам осталось только подставить значения во вторую формулу угловой скорости:
v₁ = r₁ · ω₁ = 6 371 км · 7,292·10⁻⁵ рад/с = 0,4646 км/с = 464,6 м/с .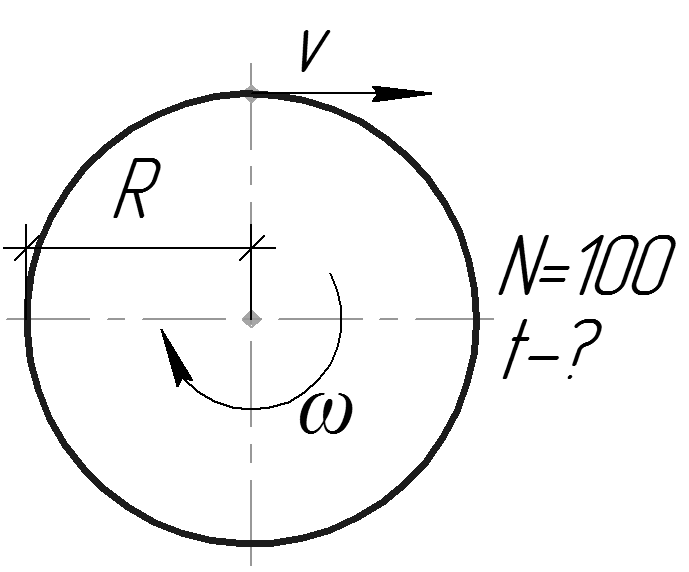
Чтобы вычислить линейную скорость относительно центра Земли, все, что вам нужно сделать, это умножить этот результат на косинус широты вашего города. Кстати, вы когда-нибудь задумывались, почему ракеты обычно стартуют с космодромов, расположенных вблизи экватора, а не с полюсов? Ну, почти 500 м/с ускорение в начале составляет значительную долю его конечной скорости. Таким образом, перемещение точки старта как можно ближе к экватору уменьшает количество топлива, необходимого для разгона ракеты.
После этого можно еще раз спросить, как найти угловую скорость Земли, но на этот раз орбитальную. Все расчеты аналогичны, но нам нужно изменить время с 23,943 ч на один год, что составляет примерно 365,25 дней. Изменение угла такое же, полный оборот.
ω₂ = 2π рад / 23,934 ч = 0,0000001991 рад/с = 1,991·10⁻⁷ рад/с ,
и линейная скорость Земли относительно Солнца (для среднего радиуса 1,496·10⁸ км ) равно:
v₂ = 1,496·10⁸ км · 1,991·10⁻⁷ рад/с = 29,785 км/с .
Мы движемся довольно быстро, не так ли?
Физические величины, зависящие от угловой скорости
Существует несколько физических величин, связанных с угловой скоростью, некоторые из которых перечислены ниже:
Угловое ускорение - Описывает, как угловая скорость изменяется со временем. Чем выше разница угловых скоростей, тем больше значение углового ускорения. Не стесняйтесь проверить, как это работает на практике, с помощью нашего калькулятора углового ускорения.Кинетическая энергия вращения - мера энергии при круговом движении. Как и в случае с кинетической энергией, зависимость (угловой) скорости является квадратичной.Центробежная сила. Ее можно почувствовать в машине, когда она поворачивается. Чем быстрее вы выполняете поворот или чем он круче, тем выше становится центробежная сила, которую мы отчетливо чувствуем.Эффект Кориолиса. Это заставляет объекты вращаться, если они находятся на вращающемся теле (например, на Земле), а не двигаться по прямой линии.
Система шкивов - Это не физическая величина, точнее говоря, это интересное устройство, которое связано с угловой скоростью. Простейшая система состоит из двух шкивов, обычно с разными окружностями или радиусами. Их соединяет пояс, поэтому их линейные скорости одинаковы , но так как они разного размера, их угловые скорости изменяются пропорционально . Зная это и имея какой-нибудь двигатель с вполне определенной скоростью вращения, мы можем с хорошей точностью задавать угловую скорость выходного элемента, просто регулируя его размер.
Сохранение углового момента
Несколько фундаментальных правил говорят нам о величинах, сохраняющихся в изолированных системах. Наиболее известны законы сохранения энергии и сохранения импульса. Вместе с ними существует также сохранение момента количества движения . Если мы рассмотрим два момента времени, мы можем записать правило как:
I₁ · ω₁ = I₂ · ω₂ ,
, где I₁ и I₂ — начальный и конечный моменты инерции масс соответственно. , величины, описывающие распределение массы относительно центра тел.
, величины, описывающие распределение массы относительно центра тел.
Мы видим, что при увеличении момента инерции угловая скорость уменьшается, и наоборот . Итак, каковы последствия этого явления? Представим, что вы фигурист. Когда вы вращаетесь, вы обладаете некоторой угловой скоростью. Если ваши руки широко раскрыты, момент инерции масс относительно велик . Затем вы приближаете руки к остальной части тела. Как следствие, ваш момент инерции уменьшается на , поэтому, поскольку общий угловой момент должен сохраняться, ваш угловая скорость увеличивается - значит крутиться будешь быстрее! Это не магия, просто физика!
Если вам не нравится кататься на коньках, можно попробовать проверить правило на обычном вращающемся стуле. Просто помните, безопасность превыше всего! Убедитесь, что есть достаточно места для проведения этого эксперимента. После этого просто начните вращаться и посмотрите, как изменится ваша угловая скорость, когда вы двигаете руками вперед и назад. Кроме того, вы можете усилить эффект, используя гантели. В результате вы можете совместить и тренировки, и развлечения в одно целое!
Кроме того, вы можете усилить эффект, используя гантели. В результате вы можете совместить и тренировки, и развлечения в одно целое!
Wojciech Sas, PhD
#1 Угловая разность
Изменение угла (Δα)
Время (t)
Угловая скорость (ω)
#2 Радиальная скорость
)
Скорость (
) Скорость (
)
Угловая скорость (ω)
Ознакомьтесь с 20 похожими калькуляторами вращательного и периодического движения 🌎
Угловое ускорениеУгловое смещениеУгловая частота… Еще 17
6.1 Угол вращения и угловая скорость
Цели обученияУгол вращенияУгловая скорость
Цели обучения
К концу этого раздела вы сможете делать следующее:
Определение длины дуги, угла поворота, радиуса кривизны и угловой скоростиРассчитать угловую скорость вращения колеса автомобиля
В кинематике мы изучали движение по прямой и ввели такие понятия, как перемещение, скорость и ускорение. Двумерная кинематика имеет дело с движением в двух измерениях. Движение снаряда - это частный случай двумерной кинематики, в котором объект проецируется в воздух, подвергаясь действию силы гравитации, и приземляется на расстоянии. В этой главе мы рассмотрим ситуации, когда объект не приземляется, а движется по кривой. Начнем изучение равномерного кругового движения с определения двух угловых величин, необходимых для описания вращательного движения.
Двумерная кинематика имеет дело с движением в двух измерениях. Движение снаряда - это частный случай двумерной кинематики, в котором объект проецируется в воздух, подвергаясь действию силы гравитации, и приземляется на расстоянии. В этой главе мы рассмотрим ситуации, когда объект не приземляется, а движется по кривой. Начнем изучение равномерного кругового движения с определения двух угловых величин, необходимых для описания вращательного движения.
Угол поворота
Когда объекты вращаются вокруг некоторой оси — например, когда компакт-диск (CD) на рис. 6.2 вращается вокруг своего центра — каждая точка объекта движется по дуге окружности. Рассмотрим линию от центра компакт-диска к его краю. Каждая яма, используемая для записи звука вдоль этой линии, проходит под одним и тем же углом за одно и то же время. Угол поворота представляет собой величину поворота и аналогичен линейному расстоянию. Определяем угол поворота
Размер ΔθΔθ 12{Δθ} {} должен быть отношением длины дуги к радиусу кривизны.
6.1 Δθ=Δср.Δθ=Δср. размер 12{Δθ= {{Δs} над {r} } } {}
Рис. 6.2 Все точки на компакт-диске движутся по дугам окружности. Ямки вдоль линии от центра к краю все перемещаются на один и тот же угол ΔθΔθ размер 12{Δθ} {} за время ΔtΔt размер 12{Δt} {}.
Рисунок 6.3 Радиус окружности поворачивается на угол ΔθΔθ величиной 12{Δθ} {}. Длина дуги ΔsΔs размером 12{Δs} {} описана на окружности.
Длина дуги ΔsΔs размер 12{Δs} {} — это расстояние, пройденное по круговому пути, как показано на рисунке 6.3. Обратите внимание, что rr размер 12{r} {} — это радиус кривизны кругового пути.
Мы знаем, что для одного полного оборота длина дуги равна длине окружности радиуса rr размера 12{r} {}. Длина окружности равна 2πr2πr размера 12{2πr} {}. Таким образом, за один полный оборот угол поворота равен
.
6.2 Δθ=2πrr=2π.Δθ=2πrr=2π. size 12{Δθ= {{2πr} over {r} } =2π"."} {}
Этот результат является основой для определения единиц, используемых для измерения углов поворота, ΔθΔθ size 12{Δθ} {} в радианах (рад), определяемый таким образом, что
6,3 2πрад = 1 оборот.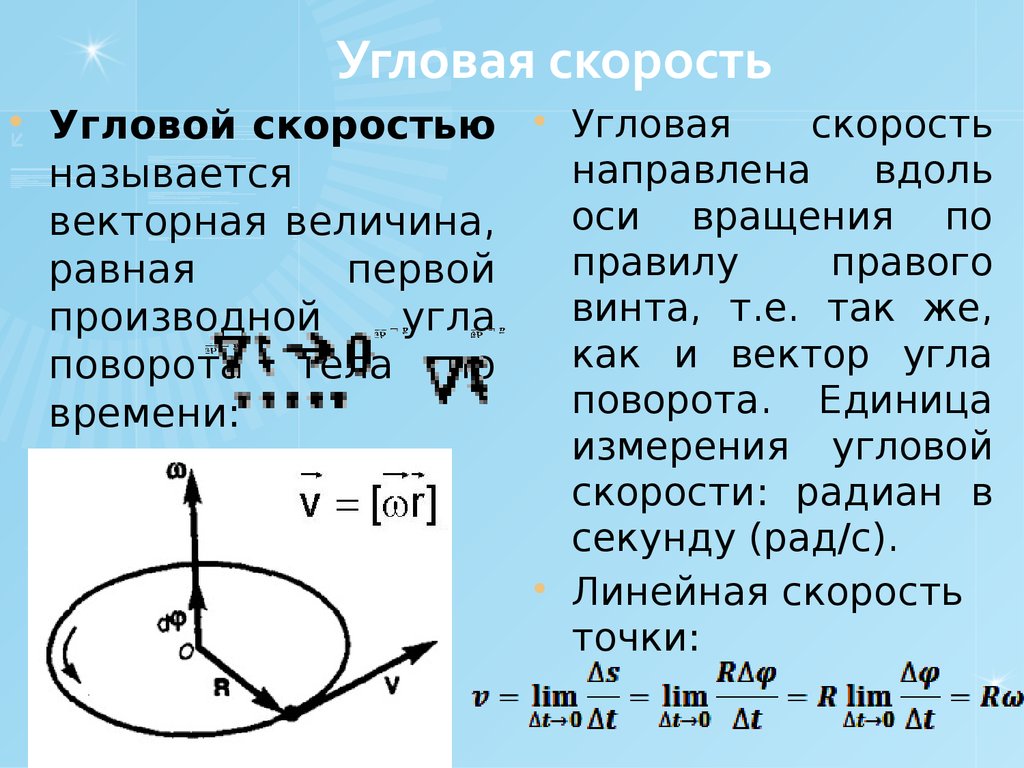 2πрад = 1 оборот. размер 12{2π" рад "=" 1 оборот."} {}
2πрад = 1 оборот. размер 12{2π" рад "=" 1 оборот."} {}
Сравнение некоторых полезных углов, выраженных как в градусах, так и в радианах, показано в таблице 6.1.
| Градусы | Измерение в радианах |
|---|---|
| 30º30º размер 12{"30"°} {} | π6π6 размер 12{ { {π} более {6} } } {} |
| 60º60º размер 12{"60"°} {} | π3π3 размер 12{ { {π} над {3} } } {} |
| 90º90º размер 12{"90"°} {} | π2π2 размер 12{ { {π} более {2} } } {} |
| 120º120º размер 12{"120"°} {} | 2π32π3 размер 12{ { {2π} над {3} } } {} |
| 135º135º размер 12{"135"°} {} | 3π43π4 размер 12{ { {3π} над {4} } } {} |
| 180º180º размер 12{"180"°} {} | ππ размер 12{π} {} |
Таблица 6. 1 Сравнение угловых единиц
1 Сравнение угловых единиц
Рисунок 6.4 Точки 1 и 2 поворачиваются на один и тот же угол (ΔθΔθ размер 12{Δθ} {}), но точка 2 перемещается по дуге большей длины ΔsΔs размер 12{ влево (Δs вправо )} {}, поскольку она находится на большем расстояние от центра вращения (r)(r) размер 12{ \( r \) } {}.
Если Δθ=2πΔθ=2π размер 12{Δθ=2π} {} рад, то компакт-диск совершил один полный оборот, и каждая точка на компакт-диске вернулась в исходное положение. Поскольку в круге или одном обороте есть 360º360º размера 12{"360"°} {}, соотношение между радианами и градусами, таким образом, равно
6,4 2πrad=360º2πrad=360º size 12{2π" rad"="360" rSup { size 8{ circ } } } {}
так что
6,5 1rad=360º2π≈7π≈57.3ºº1rad . размер 12{1" рад"= {{"360" rSup {размер 8{круг} } } более {2π} } ="57" "." 3 rSup { size 8{ circ } } "."} {}
Угловая скорость
Как быстро вращается объект? Определим угловую скорость ωω величиной 12{ω} {} как скорость изменения угла.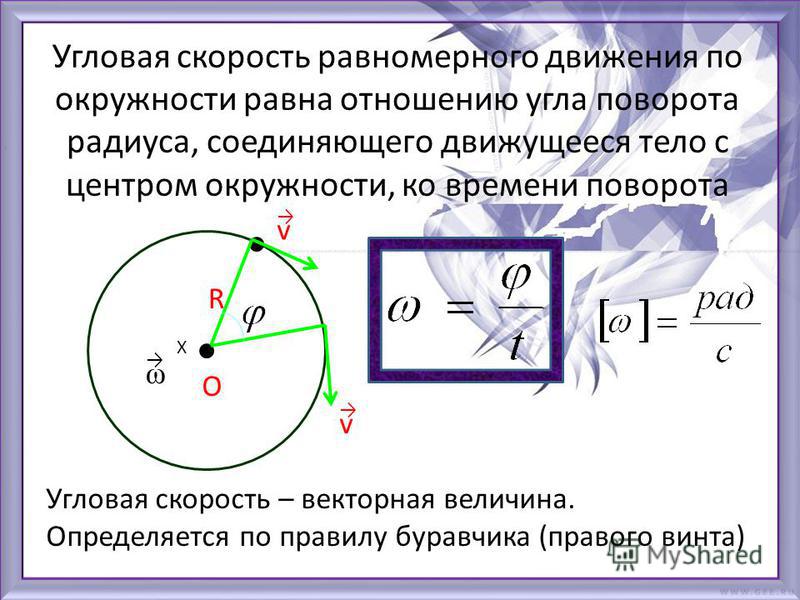 В символах это
В символах это
6,6 ω=ΔθΔt,ω=ΔθΔt, размер 12{ω= {{Δθ} над {Δt} } ","} {}
где угловой поворот ΔθΔθ размер 12{Δθ} {} происходит за время ΔtΔt размер 12{Δt} {}. Чем больше угол поворота за данный промежуток времени, тем больше угловая скорость. Единицами угловой скорости являются радианы в секунду (рад/с).
Угловая скорость ωω размера 12{ω} {} аналогична линейной скорости vv размера 12{v} {}. Чтобы получить точное соотношение между угловой и линейной скоростью, мы снова рассмотрим ямку на вращающемся компакт-диске. Эта яма перемещается по дуге длиной ΔsΔs размером 12{Δs} {} за время ΔtΔt размером 12{Δt} {}, поэтому она имеет линейную скорость
6,7 v=ΔsΔt.v=ΔsΔt. size 12{v= {{Δs} над {Δt} } "."} {}
Из Δθ=ΔsrΔθ=Δsr size 12{Δθ= {{Δs} над {r} } } {} мы видим, что Δs= rΔθΔs=rΔθ размер 12{Δs=rΔθ} {}. Подстановка этого выражения в выражение для размера vv 12{v} {} дает
6,8 v=rΔθΔt=rω.v=rΔθΔt=rω. size 12{v= {{rΔθ} над {Δt} } =rω"."} {}
Мы запишем это отношение двумя разными способами и получим два разных понимания
6,9 v=rω или ω=vr. v=rω или ω=vr. размер 12{v=rω``"или "ω= { {v} над {r} } "."} {}
v=rω или ω=vr. размер 12{v=rω``"или "ω= { {v} над {r} } "."} {}
Первое соотношение в v=rω или ω=vrv=rω или ω=vr size 12{v=rω``"или "ω= { {v} over {r} } } {} утверждает, что линейная скорость vv размер 12{v} {} пропорционален расстоянию от центра вращения, поэтому он является наибольшим для точки на ободе (наибольший размер rr 12{r} {}), как и следовало ожидать. Мы также можем назвать эту линейную скорость vv размером 12{v} {} точки на ободе тангенциальной скоростью . Второе соотношение в v=rω или ω=vrv=rω или ω=vr size 12{v=rω``" или "ω= {{v} over {r}}} {} можно проиллюстрировать, рассмотрев шину движущийся автомобиль. Обратите внимание, что скорость точки на ободе шины такая же, как скорость vv размера 12{v} {} автомобиля. (см. рис. 6.5). Таким образом, чем быстрее движется автомобиль, тем быстрее вращается шина — большой размер vv 12{v} {} означает большой размер ωω 12{ω} {}, потому что v=rωv=rω размер 12{v=rω} {}. Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью (ωω размер 12{ω} {}), будет производить большую линейную скорость (vv размер 12{v} {}) для автомобиля.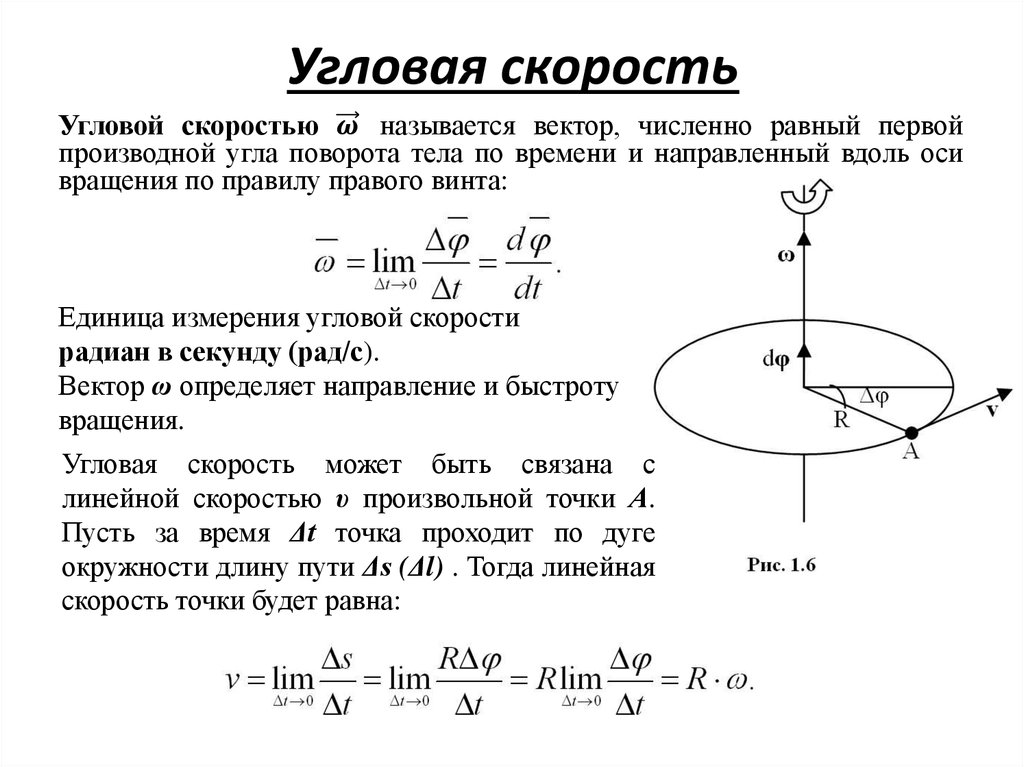
Рисунок 6.5 Автомобиль, движущийся со скоростью vv размера 12{v} {} вправо, имеет шину, вращающуюся с угловой скоростью ωω размера 12{ω} {}. Скорость протектора шины относительно оси равна vv размер 12{v}{}, такой же, как если бы автомобиль был на домкрате. Таким образом, автомобиль движется вперед с линейной скоростью v=rωv=rω размер 12{v=rω} {}, где rr размер 12{r} {} — радиус шины. Большая угловая скорость шины означает большую скорость автомобиля.
Пример 6.1 Как быстро вращается автомобильная шина?
Рассчитайте угловую скорость автомобильной шины радиусом 0,300 м, когда автомобиль движется со скоростью 15,0 м/с15,0 м/с Размер 12{"15" "." 0`"м/с"} {} (около 54 км/ч54км/ч размер 12{"54"`"км/ч"} {}) (см. рис. 6.5.
Стратегия
Поскольку линейная скорость обод шины такой же, как и скорость автомобиля, мы имеем
v=15,0 м/с. v=15,0 м/с. размер 12 {v} {}
Радиус шины принимается равным
r=0,300 м. r=0,300 м. размер 12{r} {} Зная
vv size 12{v} {} и rr size 12{r} {}, мы можем использовать второе соотношение в v=rω, ω=vrv=rω, ω=vr size 12{v=rω,``ω= { {v} над {r} } } {} для вычисления угловой скорости.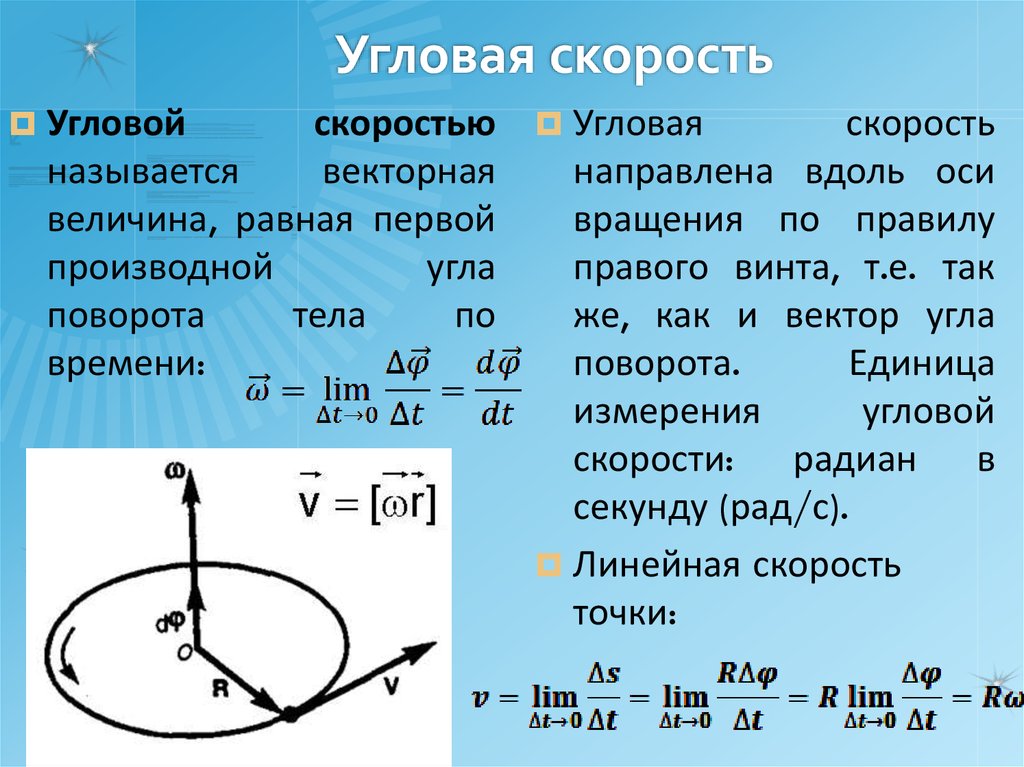
Решение
Для расчета угловой скорости воспользуемся следующим соотношением
6.10 ω=vr.ω=vr. размер 12{ω= { {v} над {r} } "."} {}
Подстановка известных,
6,11 ω=15,0м/с0,300м=50,0рад/с.ω=15,0м/с0. 300 м = 50,0 рад/с. размер 12{ω= {{"15" "." 0" м/с"} более {0 "." "300"" м"} } ="50" "." 0" рад/с."} {}
Обсуждение
Когда мы исключаем единицы измерения в приведенном выше расчете, мы получаем 50,0/с. Но угловая скорость должна иметь единицы рад/с. Поскольку радианы на самом деле безразмерны, поскольку определяются как отношение расстояния, мы можем просто вставить их в ответ для угловой скорости. Также обратите внимание, что если бы землеройная машина с колесами гораздо большего размера, скажем, радиусом 1,20 м, двигалась с той же скоростью 15,0 м/с, его колеса вращались бы медленнее. Они будут иметь угловую скорость
6,12 ω=(15,0 м/с)/(1,20 м)=12,5 рад/с. ω=(15,0 м/с)/(1,20 м)=12,5 рад/с.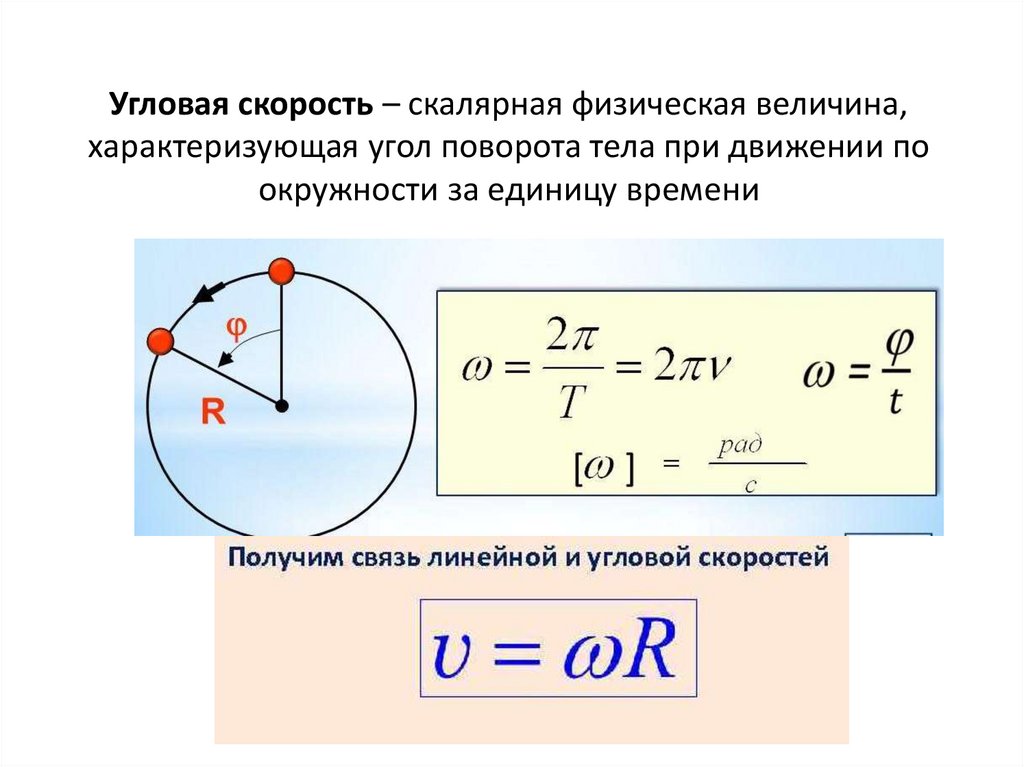 размер 12{ω= \("15" "." 0`"м/с" \) / \( 1 "." "20"`м \) ="12" "." 5`"рад/с."} {}
размер 12{ω= \("15" "." 0`"м/с" \) / \( 1 "." "20"`м \) ="12" "." 5`"рад/с."} {}
Оба ωω размера 12{ω} {} и vv размера 12{v} {} имеют направления, следовательно, они являются угловой и линейной скоростями , соответственно. Угловая скорость имеет только два направления относительно оси вращения — либо по часовой стрелке, либо против часовой стрелки. Линейная скорость касается траектории, как показано на рис. 6.6.
Эксперимент на вынос
Привяжите предмет к концу веревки и раскачайте его по горизонтальному кругу над головой (раскачивая на запястье). Поддерживайте постоянную скорость при раскачивании объекта и измеряйте угловую скорость движения. Какова примерная скорость объекта? Определите точку рядом с вашей рукой и выполните соответствующие измерения, чтобы рассчитать линейную скорость в этой точке. Определите другие круговые движения и измерьте их угловые скорости.
Рис. 6.6 Когда объект движется по кругу, в данном случае муха на краю старомодной виниловой пластинки, ее мгновенная скорость всегда касается окружности.

 С его помощью можно описать, как быстро вращается колесо или двигатель. Вы можете легко себе представить разницу между
С его помощью можно описать, как быстро вращается колесо или двигатель. Вы можете легко себе представить разницу между