Как измерить емкость и индуктивность с помощью осциллографа. » Хабстаб
Сегодня на рынке продается множество приборов, измеряющих емкость и индуктивность, только стоят они в несколько раз дороже китайского мультиметра. Тот кому каждый день необходимо производить замеры емкости или индуктивности непременно купит себе такой, а что делать если такая необходимость возникает крайне редко? В таком случае можно применить описанный ниже метод.
Известно, что если на интегрирующую RC цепочку подать прямоугольный импульс, то форма импульса изменится и будет такой как на картинке.
Время, за которое напряжение на конденсаторе достигнет 63% от подаваемого, называется тау. Формула по которой считается тау изображена на рисунке.
В таком случае говорят, что интегрирующая цепочка сгладила фронты прямоугольного импульса.
Так же известно, что если на параллельный LC контур подать прямоугольный импульс, в контуре возникнут затухающие колебания, частота, которых равна резонансной частоте контура. Резонансная частота контура находится по формуле Томсона, из которой можно выразить индуктивность.
Резонансная частота контура находится по формуле Томсона, из которой можно выразить индуктивность.
Подключается контур через конденсатор малой емкости, чем меньше тем лучше, который ограничивает ток, поступающий в контур. Давайте рассмотрим, как конденсатор малой емкости ограничивает ток.
Для того, чтобы конденсатор зарядился до номинального напряжения ему надо передать определенный заряд. Чем меньше емкость конденсатора, тем меньший заряд ему необходим, чтобы напряжение на обкладках достигло напряжения импульса. Когда мы подаем импульс, конденсатор, малой емкости, очень быстро заряжается и напряжение на обкладках конденсатора становится равно напряжению импульса. Так как напряжение конденсатора и импульса равны, нет разности потенциалов, следовательно ток не течет. При чем ток может перестать течь через конденсатор спустя некоторое время от начала импульса, а оставшуюся часть времени импульса энергия к контуру подводится не будет.
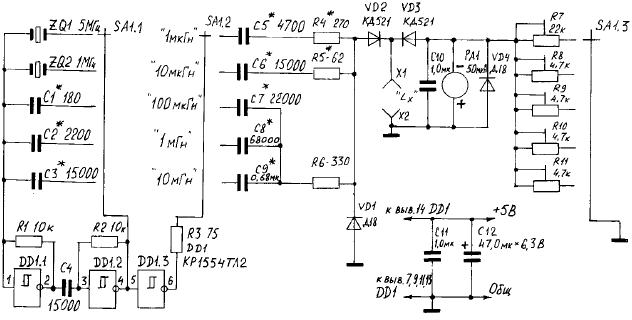
Для проведения эксперимента нам потребуется генератор импульсов прямоугольной формы с частотой 5-6KHz.
Можно собрать его по схеме на рисунке ниже или воспользоваться генератором сигналов, я делал обоими способами.
Теперь, вспомнив, как ведет себя при подаче прямоугольного импульса интегрирующая RC цепочка и параллельный LC контур, соберем простую схему изображенную на картинке.
Сначала измерим емкость конденсатора, место его подключения на схеме обозначено С?. Резистора 1K под рукой не нашлось, поэтому я использовал 100 Ohm и вместо конденсатора 10pF использовал конденсатор 22pF. В принципе номинал резистора можно выбрать любой, но не ниже 50 Ohm, иначе сильно просядет напряжение генератора.
В данном эксперименте я буду использовать генератор сигналов, выходное сопротивление которого равно 50 Ohm. Включим генератор и установим амплитуду 4V, если собирать генератор по схеме то регулировать амплитуду можно, изменяя напряжение питания.
Подключим щупы осциллографа параллельно конденсатору. На осциллографе должна появиться следующая картинка.
На осциллографе должна появиться следующая картинка.
Немного увеличим её.
Измерим время, за которое напряжение на конденсаторе достигает 63% от напряжения импульса или 2,52V.
Оно равно 14,8uS. Так как сопротивление генератора включено последовательно с нашей цепочкой его необходимо учесть, в итоге активное сопротивление равно 150 Ohm. Разделим значение тау(14,8 uS) на сопротивления(150 Om) и найдем емкость, она равна 98,7 nF . На конденсаторе написано, что емкость равна 100nF.
Теперь измерим индуктивность. На схеме место подключения катушки индуктивности обозначено L?. Подключаем катушку, включаем генератор и подключаем щуп осциллографа параллельно контуру. На осциллографе увидим такую картинку.
Увеличиваем развертку.
Видим, что период колебаний равен 260KHz.
Ёмкость щупа равна 100pF и в данном случае её необходимо учесть потому, что она составляет 10% от емкости контура. Суммарная емкость контура равна 1,1nF. Теперь подставим в форму для нахождения индуктивности, емкость конденсатора(1,1nF) и частоту колебаний(260KHz). Для таких вычислений я пользуюсь программой Coil32.
Суммарная емкость контура равна 1,1nF. Теперь подставим в форму для нахождения индуктивности, емкость конденсатора(1,1nF) и частоту колебаний(260KHz). Для таких вычислений я пользуюсь программой Coil32.
Получилось 340,6uH, судя по маркировке индуктивность равна 347uH и это отличный результат. Этот способ позволяет измерять индуктивность с погрешность до 10% .
Теперь мы знаем как измерить емкость конденсатора и индуктивность катушки, используя осциллограф.
Как измерить ёмкость и индуктивность с помощью генератора и осциллографа + online-калькулятор — radiohlam.ru
Для многих любителей электроники актуальной является задача измерения емкостей конденсаторов и индуктивностей дросселей, поскольку, в отличие от резисторов, эти компоненты нередко бывают не промаркированы (особенно SMD). Между тем, имея генератор синусоидальных колебаний и осциллограф (приборы, которые должны быть в любой радиолюбительской лаборатории), эта задача довольно просто решается.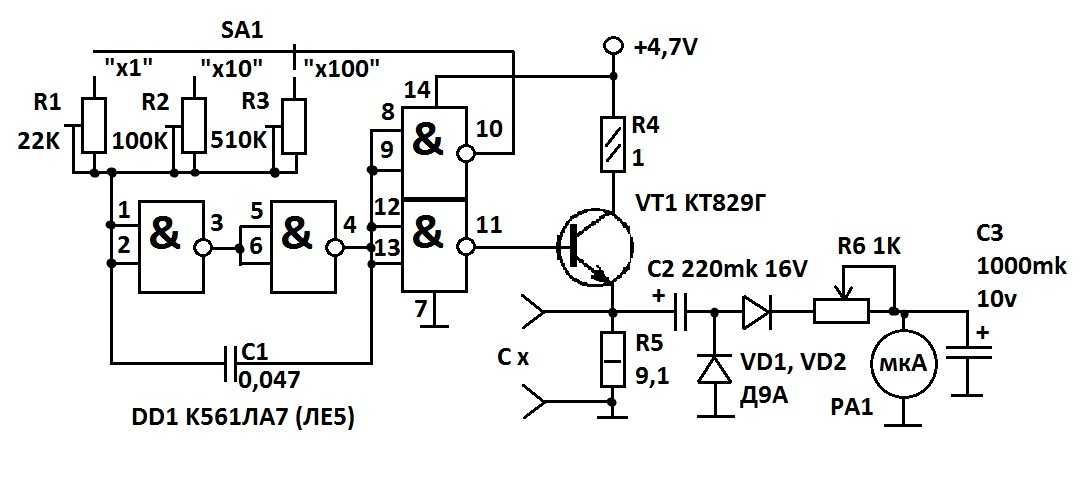 Всё, что для этого нужно — это вспомнить начальный курс электротехники.
Всё, что для этого нужно — это вспомнить начальный курс электротехники.
Рассмотрим простейшую схему — последовательно соединённые резистор и конденсатор. Пусть эта схема подключена к источнику синусоидальных колебаний. Запишем уравнения для напряжений на элементах нашей схемы в операторной форме: UR = I * R, UC = -j * I / ωC. Из этих уравнений очевидно, что амплитудные значения напряжений будут относится следующим образом: UR / UC = R * ωC (конечно, напряжения будут сдвинуты по фазе, но нас это в данном случае не волнует, нас волнуют
только амплитуды).
Думаю, что многие уже догадались к чему я клоню. Да-да, из последнего уравнения довольно просто вычисляется ёмкость:
C = UR/UC * 1/ωR или, с учетом того, что ω= 2πf, получим C = UR/UC * 1/2πfR ; (1)
Итак, алгоритм простой: подключаем последовательно с измеряемой ёмкостью резистор, подключаем к этой схеме генератор синусоидальных колебаний и осциллографом измеряем амплитуды напряжений на нашем конденсаторе и резисторе. Изменяя частоту, добиваемся, чтобы амплитуда напряжений на обоих элементах была примерно одинаковой (так измерение получится точнее). Далее, подставляя измеренные значения амплитуд в формулу (1), находим искомую ёмкость конденсатора.
Изменяя частоту, добиваемся, чтобы амплитуда напряжений на обоих элементах была примерно одинаковой (так измерение получится точнее). Далее, подставляя измеренные значения амплитуд в формулу (1), находим искомую ёмкость конденсатора.
Аналогично можно вывести формулу для подсчета индуктивности:
L = UL/UR * R/ω или, с учётом того, что ω= 2πf, получим L = UL/UR * R/2πf ; (2)
Таким образом, имея генератор синусоидальных колебаний и осциллограф, с помощью формул (1) и (2) оказывается довольно просто вычислить неизвестную ёмкость или индуктивность (благо резисторы практически всегда имеют маркировку).
Алгоритм действий следующий:
1) Собираем схему из последовательно соединённых резистора известного номинала и исследуемой ёмкости (индуктивности).
2) Подключаем эту схему к генератору синусоидальных колебаний и изменением частоты добиваемся того, чтобы амплитуды напряжений на обоих элементах схемы были примерно одинаковы.
3) По формуле (1) или (2) вычисляем номинал исследуемой ёмкости или индуктивности.
Несмотря на то, что наши элементы не идеальные, есть допуск на номинал резистора и всегда есть некоторые погрешности измерений, результат получается довольно точным (по крайней мере можно без труда идентифицировать ёмкость в стандартном ряду). Пусть у меня при измерении ёмкости получилась величина 1,036 нФ. Очевидно, что на исследуемом конденсаторе должна была быть нанесена маркировка 1 нФ.
Для того, чтобы вам легче было сориентироваться с номиналами резисторов, приведу некоторые примеры:
— для ёмкости 15 пФ в схеме с резистором 200 кОм амплитуды напряжений будут примерно равны на частоте 53 кГц;
— для ёмкости 1 нФ в схеме с резистором 10 кОм амплитуды напряжений будут примерно равны на частоте 15,9 кГц;
— для ёмкости 0,1 мкФ в схеме с резистором 680 Ом амплитуды напряжений будут примерно равны на частоте 2,34 кГц;
— для индуктивности 3 мкГн в схеме с резистором 120 Ом амплитуды напряжений будут примерно равны на частоте 6,3 МГц;
— для индуктивности 100 мкГн в схеме с резистором 120 Ом амплитуды напряжений будут примерно равны на частоте 190 кГц.
Таким образом, диапазон измеряемых емкостей и индуктивностей зависит только от диапазона частот, с которыми могут работать ваши генератор и осциллограф.
На основе этого метода можно изготовить прибор для автоматического измерения емкостей и индуктивностей.
Online-калькулятор для расчёта емкостей и индуктивностей:
(для правильности расчётов используйте в качестве десятичной точки точку, а не запятую)
1) Расчёт емкостей:
R=кОм; f=кГц;
UR=мВ;
UC=мВ;
C=
2) Расчёт индуктивностей:
R=Ом; f=МГц;
UR=мВ;
UL=мВ;
L=
Как пользоваться измерительными приборами для измерения индуктивности
Любое проводящее тело имеет определенную конечную индуктивность. Эта индуктивность является неотъемлемым свойством проводящего тела и всегда одинакова, независимо от того, находится ли этот проводник или устройство под напряжением в электрической цепи или находится на полке на складе.
Индуктивность прямого отрезка провода можно значительно увеличить, намотав его в виде спиральной катушки, после чего магнитные поля, возникающие вокруг соседних витков, объединяются для создания единого более сильного магнитного поля. Индуктивность катушки зависит от квадрата числа витков.
Индуктивность катушки также значительно увеличивается, если катушка сконструирована вокруг сердечника, состоящего из материала, обладающего высокой проницаемостью для магнитного потока. (Поток представляет собой произведение среднего значения магнитного поля на площадь, перпендикулярную к которой оно пересекается. Поток в магнитной цепи аналогичен току в электрической цепи.) 50 или 60 Гц. Индуктивные эффекты более выражены на более высоких частотах, поэтому для РЧ-индуктора обычно достаточно воздушного сердечника.
Одним из определяющих свойств катушки является то, что при снятии приложенного напряжения, прерывая ток, магнитное поле разрушается и электрическая энергия, ранее использованная для создания магнитного поля, резко возвращается в цепь. Это просто проявление того факта, что магнитное поле и движущийся друг относительно друга проводник вызывают в проводнике ток.
Это просто проявление того факта, что магнитное поле и движущийся друг относительно друга проводник вызывают в проводнике ток.
Скорость изменения тока в катушке индуктивности пропорциональна приложенному к ней напряжению, определяемому известным уравнением:
V = L dI/dt
Где L — индуктивность в генри, V — напряжение, I — ток, t — время. Подобно конденсатору и в отличие от резистора, импеданс катушки индуктивности зависит от частоты. Полное сопротивление представляет собой векторную сумму сопротивления (когда и если в цепи есть резистор или эквивалент) и индуктивного или емкостного реактивного сопротивления. В конденсаторе более высокая частота соответствует более низкому емкостному реактивному сопротивлению. В катушке индуктивности более высокая частота соответствует более высокому индуктивному реактивному сопротивлению. Катушка не противодействует потоку постоянного тока, за исключением:
• Небольшое сопротивление из-за емкости провода
• Мгновенное индуктивное сопротивление при первом включении катушки из-за работы, необходимой для создания магнитного поля. (Во время нарастания постоянный ток в основном переменный.)
(Во время нарастания постоянный ток в основном переменный.)
Уравнение для емкостного реактивного сопротивления:
X C = 1/2πfC
Где X C = емкостное реактивное сопротивление в омах; f = частота в герцах; C = емкость
Уравнение для индуктивного реактивного сопротивления:
X L = 2πfL
Где X L = реактивное сопротивление индуктивности в Омах; f = частота в герцах; L = индуктивность
Эти уравнения обладают поразительной симметрией. Один является зеркальным отражением другого, разница заключается в роли, которую играет частота. В емкостном реактивном сопротивлении f находится в знаменателе, а в индуктивном реактивном сопротивлении — в числителе. Емкостное и индуктивное сопротивление, а также общий импеданс выражаются в омах, как и в сопротивлении постоянному току, и они полностью соответствуют закону Ома, при том понимании, что эти свойства зависят от частоты.
Высококачественные мультиметры часто включают емкостной режим. Для этого измерения достаточно прощупать выводы исследуемого устройства. В интересах безопасности и точности может потребоваться разрядка устройства большой емкости, такого как электролитический конденсатор, с использованием разумного сопротивления в течение соответствующего периода времени. Шунтировать его отверткой не рекомендуется, потому что электролит может быть пробит из-за сильного тока, не говоря уже о вспышке дуги в больших устройствах. После разрядки проверьте, проверив напряжение.
Для этого измерения достаточно прощупать выводы исследуемого устройства. В интересах безопасности и точности может потребоваться разрядка устройства большой емкости, такого как электролитический конденсатор, с использованием разумного сопротивления в течение соответствующего периода времени. Шунтировать его отверткой не рекомендуется, потому что электролит может быть пробит из-за сильного тока, не говоря уже о вспышке дуги в больших устройствах. После разрядки проверьте, проверив напряжение.
Можно ожидать, что показания конденсаторов, измеренные с помощью мультиметра в емкостном режиме, будут занижены на целых 10 %. Этой точности достаточно для многих приложений, таких как пусковая цепь электродвигателя или фильтрация источника питания. Более высокая точность доступна при выполнении динамического теста. Одна из стратегий прецизионного измерения заключается в создании схемы, которая преобразует емкость в частоту, которую затем можно определить с помощью счетчика.
Для измерения индуктивности устройства, собственной индуктивности цепи или более широко распространенной распределенной индуктивности лучше всего подходит измеритель LCR. Он подвергает тестируемое устройство (соответствующим образом разряженным и изолированным от любых окружающих цепей, которые могут подать на него питание или создать нерелевантный параллельный импеданс) переменному напряжению известной частоты, обычно одно среднеквадратичное значение вольта на один килогерц. Счетчик одновременно измеряет напряжение на и ток через устройство. Из соотношения этих сумм алгебраически вычисляется импеданс.
Он подвергает тестируемое устройство (соответствующим образом разряженным и изолированным от любых окружающих цепей, которые могут подать на него питание или создать нерелевантный параллельный импеданс) переменному напряжению известной частоты, обычно одно среднеквадратичное значение вольта на один килогерц. Счетчик одновременно измеряет напряжение на и ток через устройство. Из соотношения этих сумм алгебраически вычисляется импеданс.
Впоследствии усовершенствованные счетчики измеряют фазовый угол между приложенным напряжением и результирующим током. Они используют эту информацию для отображения эквивалентной емкости, индуктивности и сопротивления рассматриваемого устройства. Измеритель работает в предположении, что емкость и индуктивность, которые он обнаруживает, существуют либо в параллельной, либо в последовательной конфигурации.
Конденсаторы имеют определенную величину непреднамеренной индуктивности и сопротивления из-за их выводов и пластин. Точно так же катушки индуктивности имеют некоторое сопротивление из-за своих выводов и определенную емкость, потому что их клеммы приравниваются к пластинам. Точно так же резисторы, а также полупроводники на высоких частотах приобретают емкостные и индуктивные свойства.
Точно так же резисторы, а также полупроводники на высоких частотах приобретают емкостные и индуктивные свойства.
Как правило, измеритель предполагает, что подразумеваемые устройства подключены последовательно, когда он выполняет измерения LR. Точно так же предполагается, что они параллельны, когда выполняются измерения CR, из-за последовательной геометрии катушки и параллельной геометрии конденсатора.
Многие LCR-метры применяют выход источника сигнала через резистор источника к неизвестному устройству Z X и резистору диапазона R r . Усилитель заставляет тот же ток, который протекает через неизвестное устройство, течь через резистор R 9.0020 r , управляя соединением неизвестного устройства и R r до 0 В. Напряжения V 1 и V 2 на неизвестном устройстве и на R r соответственно подключены к селекторному переключателю. Выход коммутатора подключен к дифференциальному усилителю. Действительные и мнимые компоненты сигналов напряжения и тока получаются путем умножения этих напряжений на прямоугольную волну, когерентную стимулу (в фазовом детекторе). Это дает выходной сигнал, пропорциональный синфазной или квадратурной составляющей напряжения. Выход поступает на аналого-цифровой преобразователь с двойным наклоном, который считывает микроконтроллер. Комплексное отношение напряжения к току равно комплексному импедансу. Другие параметры, такие как L и C, математически выводятся из скорректированного значения импеданса.
Это дает выходной сигнал, пропорциональный синфазной или квадратурной составляющей напряжения. Выход поступает на аналого-цифровой преобразователь с двойным наклоном, который считывает микроконтроллер. Комплексное отношение напряжения к току равно комплексному импедансу. Другие параметры, такие как L и C, математически выводятся из скорректированного значения импеданса.
Как портативные, так и настольные измерители LCR в более продвинутых моделях позволяют пользователю выбирать частоту подаваемого переменного напряжения. Смысл в том, что тестируемый индуктор или конденсатор будут реагировать более характерным образом в дискретной полосе частот.
Настольные измерители LCR также обычно имеют четырехпроводную (Кельвин) опцию, которая значительно повышает стабильность и точность при измерениях с низким импедансом, где контакт наконечника зонда может ухудшить показания.
Индуктивность, емкость или сопротивление можно измерить с помощью мостовой схемы. Для этого измерения переменные калиброванные элементы обнуляются на детекторе, в отличие от измерения фазового угла, как в обычном измерителе LCR.
Если измеритель LCR недоступен, существуют различные методы измерения индуктивности с помощью осциллографа. Один метод измерения индуктивности на крутизне напряжения-тока включает подключение катушки индуктивности к импульсному источнику напряжения с рабочим циклом менее 50%. С помощью токоизмерительного щупа осциллографа определите пиковый ток в амперах и время между импульсами в микросекундах. Умножьте эти суммы и разделите произведение на пиковый ток. Это величина индуктивности тестируемого устройства.
Другой метод измерения индуктивности с помощью осциллографа включает последовательное подключение резистора известного номинала к проверяемой катушке индуктивности и подачу сигнала. Частота регулируется таким образом, чтобы на обоих устройствах появлялись одинаковые напряжения.
Третий метод определения индуктивности устройства состоит в размещении катушки индуктивности параллельно известной емкости. Полученный накопительный контур затем последовательно подключается к резистору, и с помощью осциллографа определяется резонансная частота. Отсюда можно рассчитать индуктивность.
Отсюда можно рассчитать индуктивность.
Эти методы, хотя и жизнеспособны, требуют некоторой работы со схемой и обширных расчетов, в то время как измеритель LCR обеспечивает прямое считывание с достаточной точностью для большинства приложений.
Измерения емкости и индуктивности с помощью осциллографа и функционального генератора
В большинстве лабораторий имеется достаточный запас цифровых мультиметров для измерения сопротивления постоянному току, но когда
речь идет об измерении индуктивности, емкости и импеданса, это не всегда
легко найти LCR метр.
Счетчики LCR работают, подавая переменное напряжение на устройство
при тестировании и измерения результирующего тока, как по амплитуде, так и по
фазы относительно сигнала напряжения переменного тока. Емкостное сопротивление будет иметь
форма волны тока, которая опережает форму волны напряжения. Индуктивное сопротивление будет
имеют форму волны тока, которая отстает от формы волны напряжения. К счастью, если
у вас есть осциллограф и генератор функций в вашей лаборатории, вы можете использовать
аналогичный метод для проведения многочастотных измерений импеданса с хорошим
Результаты. Этот подход также может быть адаптирован для использования в качестве учебной лаборатории.
Этот подход также может быть адаптирован для использования в качестве учебной лаборатории.
упражнение.
Рис. 1.
Импеданс моделируется как
конденсатор или катушка индуктивности с эквивалентным последовательным сопротивлением.
Что такое импеданс?
Импеданс – это полное сопротивление протеканию тока в
цепь переменного тока. Он состоит из сопротивления (действительного) и реактивного сопротивления.
(мнимый) и обычно представляется в комплексной записи как Z = R + jX ,
где R — сопротивление, а X — реактивное сопротивление.
Реальные компоненты состоят из проводов, соединений,
проводников и диэлектрических материалов. Эти элементы в совокупности составляют
характеристик импеданса компонента, и этот импеданс изменяется в зависимости от
частота тестового сигнала и уровень напряжения, наличие постоянного напряжения смещения
или факторы тока и окружающей среды, такие как рабочая температура или
высота. Из этих потенциальных влияний частота тестового сигнала часто является
Из этих потенциальных влияний частота тестового сигнала часто является
наиболее значимый фактор.
В отличие от идеальных компонентов, реальные компоненты не являются чисто
индуктивная или емкостная. Все компоненты имеют последовательное сопротивление, т.
Параметр R в его импедансе. Но у них также есть несколько вкладчиков в их
реактивное сопротивление. Например, конденсатор имеет последовательную индуктивность, которая становится больше
проявляется на высоких частотах. Когда мы измеряем реальный конденсатор, ряд
индуктивность (ESL) повлияет на показания емкости, но мы не сможем
измерять его как отдельный компонент.
Методы измерения импеданса
Метод ВАХ, описанный в этом примечании по применению, является всего лишь
один из многих методов измерения импеданса. Другие включают метод моста.
и резонансный метод.
Метод ВАХ использует значение напряжения и тока между
тестируемое устройство (DUT) для расчета неизвестного импеданса, Z x . Текущий
Текущий
измеряется путем измерения падения напряжения на последовательно включенном прецизионном резисторе
с тестируемым устройством, как показано на рисунке 2. Уравнение 1 показывает, как можно использовать схему
найти Z х .
Уравнение 1:
Теоретическая точность
В этом примечании по применению мы будем использовать Tektronix AFG2021
генератор сигналов произвольной формы и осциллограф Tektronix серии MDO4000.
измерение. Полоса пропускания AFG2021 20 МГц хорошо подходит для этого.
измерение. Точность усиления по постоянному току MDO4000 составляет 2 % при настройке 1 мВ/дел.
1,5% при других настройках по вертикали. Как вы можете видеть в уравнении 1,
Точность измерения напряжения осциллографом является наиболее важным фактором в
общая точность теста.
На основании уравнения 1 теоретическая точность этого
метод измерения должен составлять около 4% при настройке MDO4000 1 мВ/дел и 3%
при других настройках.
Так как частота дискретизации осциллографа намного
выше частот стимулов, используемых в этих тестах, ошибка
вклад фазовых измерений будет пренебрежимо мал.
Рис. 3.
Тестовая установка для
оценка конденсатора, как в примере 1.
Пример испытания
В следующих двух примерах представлены конденсатор/катушка индуктивности/
Измерение ESR с помощью осциллографа и функционального генератора.
Используемое оборудование:
- AFG2021 Генератор сигналов/функций
- Осциллограф MDO4104C
- А 1 кОм
прецизионный резистор - Конденсаторы и катушки индуктивности, подлежащие испытанию
- Два пробника напряжения Tektronix TPP1000
Для этого применения большинство осциллографов и функций
генераторы дадут приемлемые результаты, так как тестовые частоты ниже
100 кГц. Однако мы воспользуемся статистикой измерений на MDO4000.
Серия в этом примере.
Рис. 4.
Осциллограммы напряжения и
измерения, проведенные в узлах A1 и A2.
Пример 1: керамический конденсатор емкостью 10 мкФ
Установите тестовую схему, как показано на рис. 3. Примечание.
3. Примечание.
что R ESR и
C связаны с тестируемым керамическим конденсатором, и что R fg представляет собой выходное сопротивление 50 Ом конденсатора.
генератор функций.
Настройте генератор функций на вывод 1,9 В
амплитуда, синусоида 100 Гц. Вы можете использовать ручку или клавиатуру AFG2021 для
установить напряжение и частоту. Отрегулируйте настройку масштаба по вертикали
осциллограф, чтобы использовать как можно больше экрана — используя как можно больше
диапазон, насколько это возможно, вы улучшите точность вашего напряжения
измерения.
С помощью осциллографа проверьте узлы A1 и A2. Рисунок 4
показывает результирующую форму волны.
Выберите режим получения среднего значения осциллографа
и установите количество средних значений равным 128. Это уменьшит влияние случайных
шум в ваших измерениях. Настройте осциллограф на измерение канала 1.
частота, фаза между каналом 2 и каналом 1, амплитуда канала 1 и
амплитуда канала 2, как показано на рис. 4. Если ваш осциллограф поддерживает
4. Если ваш осциллограф поддерживает
статистики измерений, таких как серия MDO4000, записывайте средние значения для
расчеты. В противном случае запишите самые последние значения.
Из настройки измерений мы знаем:
- Частота стимула, f = 100 Гц
- Прецизионный резистор, Rref = 1 кОм
Из измерений, сделанных на осциллографе и показанных
на рисунке 4:
- Амплитуда напряжения, измеренная на A1, В A1 = 1,929 В
- Амплитуда напряжения, измеренная на A2, В A2 = 0,310 В
- Разность фаз между напряжением, измеренным на A2, относительно A1, θ = -79,95°
Обратите внимание, что в узле A1 напряжение имеет фазовый угол 0°,
то есть он находится в фазе с выходным сигналом функционального генератора. На А2 напряжение равно
смещены вперед на фазовый угол θ.
Можно определить полное сопротивление тестируемого конденсатора
используя уравнение 1.
Полное сопротивление может быть выражено в полярной форме, где
величина определяется уравнением 2.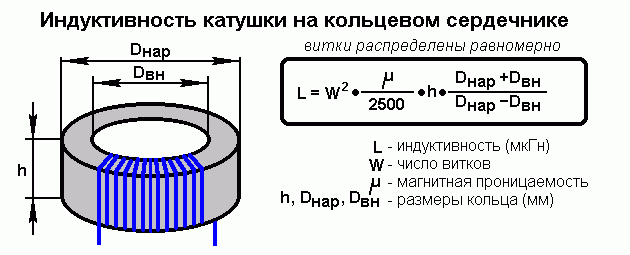
Уравнение 2:
Угол сопротивления определяется вычитанием двух
углы:
Уравнение 3:
Для теста в нашем примере мы можем использовать Уравнение 2
и Уравнение 3, чтобы найти величину и угол импеданса
проверяемый конденсатор:
Теперь мы можем преобразовать импеданс в прямоугольную форму.
найти сопротивление и емкость.
Используя приведенные выше уравнения, мы можем найти ESR и
Емкость ИУ:
Уравнения 4 и 5:
Используя уравнения 4 и 5, мы можем рассчитать ESR
и емкость испытуемого конденсатора:
|
В таблице 1 сравниваются результаты, полученные с помощью осциллографа.
и генератор функций для результатов, достигнутых с помощью недорогого ВАЦ и
традиционный LCR-метр. Измеритель LCR, использованный в этом случае, поддерживал только тест
частоты 100 Гц и 1 кГц, которые являются общими тестовыми частотами компонентов.
Вы заметите, что эти три метода достаточно хорошо коррелируют друг с другом.
Значения пассивных компонентов указаны с особым
с учетом частоты, и измерители LCR часто имеют более одной тестовой частоты для
эта причина. В таблице 1 показаны результаты с использованием осциллографа/функции
комбинация генераторов на пяти различных частотах. Вы можете увидеть эффект от
паразитная индуктивность в испытательной цепи по мере увеличения испытательной частоты –
измеренная емкость падает по мере увеличения испытательной частоты. См. раздел о
«Диапазон измерения» для получения дополнительной информации о тестовых частотах.
Для достижения наилучших результатов вам необходимо сохранить значение
прецизионного резистора (R ref )
достаточно низким, чтобы дать значительную волну напряжения в узле A2.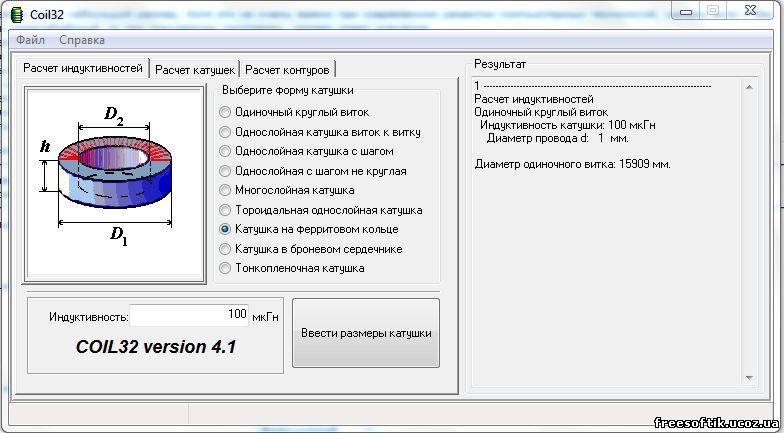 Резистор
Резистор
также должно быть больше 50 Ом или выходного импеданса функционального генератора.
будет учитываться при измерении.
Рис. 5.
Тестовая установка для
оценка индуктора, как в примере 2.
Пример 2: индуктор 10 мГн
Схема и процедура тестирования почти идентичны
те, которые использовались для проверки конденсатора в примере 1.
Используйте генератор функций для вывода 1,9 В
амплитуда синусоиды 10 кГц. Сигнал подается на эталонный резистор и
проверяемый индуктор.
С помощью осциллографа проверьте узлы A1 и A2. Рисунок 6
показывает два результирующих сигнала.
Рисунок 6. Кривые напряжения и измерения
взятых в узлах A1 и A2.
Выберите режим получения среднего значения осциллографа
и установите количество средних значений равным 128. Это уменьшит влияние случайных
шум в ваших измерениях. Настройте осциллограф на измерение канала 1.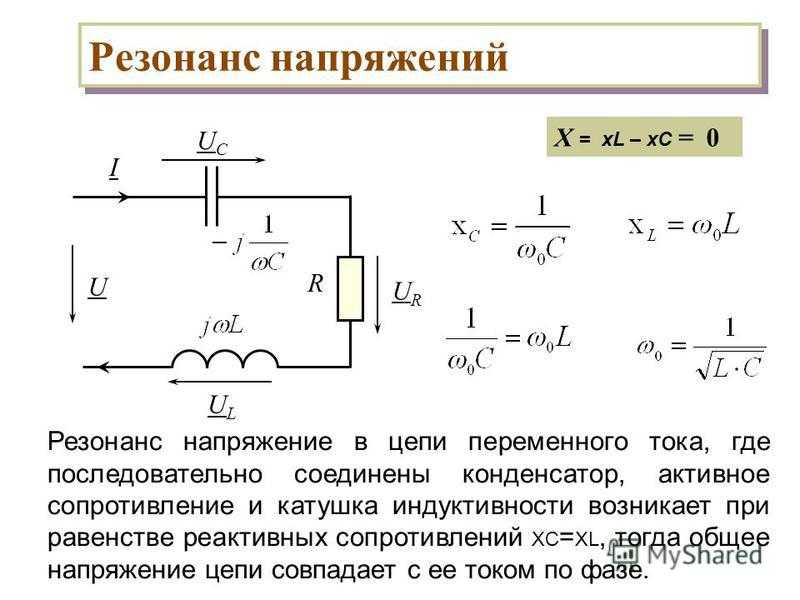
частота, фаза между каналом 2 и каналом 1, амплитуда канала 1 и
амплитуда канала 2, как показано на рис. 6. Если ваш осциллограф предлагает
статистики измерений, таких как серия MDO4000, записывайте средние значения для
расчеты. В противном случае запишите самые последние значения.
Из настройки измерений мы знаем:
- Частота стимула, f = 10 кГц
- Прецизионный резистор, R № = 1 кОм
Из измерений, сделанных на осциллографе и показанных
на рисунке 6:
измерено на A2 относительно A1, θ
= 56,03°
Обратите внимание, что в узле A1 напряжение имеет фазовый угол 0°,
то есть он находится в фазе с выходным сигналом функционального генератора. На А2 напряжение равно
смещены вперед на фазовый угол θ.
Мы можем использовать те же уравнения для расчета импеданса
ИУ, которое мы использовали для измерения конденсатора в примере 1. Импеданс может
Импеданс может
быть выражено в полярной форме, где величина и угол импеданса равны
предоставлено:
Теперь мы можем преобразовать в прямоугольную форму
импеданс найти сопротивление и индуктивность
Используя приведенные выше уравнения, мы можем найти ESR и
Индуктивность ИУ:
Уравнения 6 и 7:
Используя уравнение 6 и уравнение 7, мы можем рассчитать ESR
и индуктивность для тестируемого индуктора:
| по | через USB | по LCR | по | через USB | по LCR |
Частота | Индуктивность | Индуктивность | Индуктивность | СОЭ (Ом) | СОЭ (Ом) | СОЭ (Ом) |
10 Гц | 12 | 10,3 | Н/Д | 20,5 | 20,8 | Н/Д |
100 Гц | 10,1 | 10,4 | 10. | 20,6 | 20,9 | 20,9 |
1 кГц | 10,3 | 10,2 | 10,1 | 20,5 | 22 | 21,5 |
10 кГц | 10 | 9,8 | 9,76 | 29,8 | 31,5 | 29,4 |
Таблица 2. Сравнительная таблица примера 2.
Опять же, в таблице 2 сравниваются полученные результаты с
осциллограф и генератор функций для достижения результатов с помощью недорогого ВАЦ и
традиционный LCR-метр. Эти три метода хорошо коррелируют.
В таблице 2 также показаны результаты, полученные с помощью осциллографа/
Комбинация функциональных генераторов на четырех различных частотах. См. раздел
См. раздел
в разделе «Диапазон измерения» для получения дополнительной информации о тестовых частотах.
Еще раз, вам может понадобиться поэкспериментировать со значением R ref , чтобы получить лучшее
Результаты.
| Рисунок 7. Емкость/частота коробка. | Рисунок 8. Индуктивность/частота коробка. |
Диапазон измерения
Существуют практические ограничения на частоту стимула и
значения конденсатора или катушки индуктивности тестируемого устройства для этого метода измерения импеданса.
На рис. 7 показано окно емкости/частоты. Если емкость
значение и частота тестирования попадают в поле, тогда вы сможете
измерить это. В заштрихованной области точность измерения будет около 3%,
а вне заштрихованной области точность падает примерно до 5%. Эти неопределенности
предположим, что вы позаботились о том, чтобы использовать весь экран осциллографа,
усреднил 128 циклов сигналов и использовал среднее значение
амплитуды и фазы для выполнения вычислений.

 1
1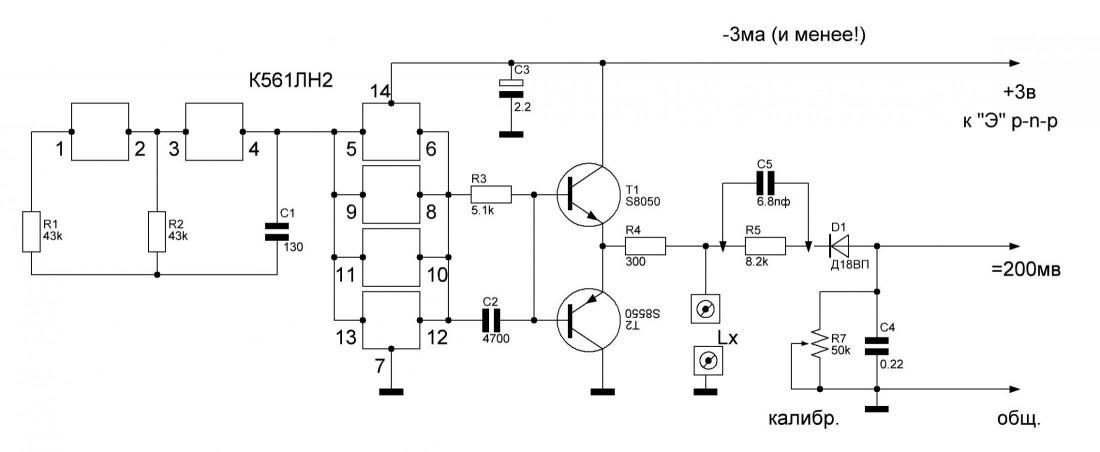 31
31