Формула полезной работы в физике

Вычисление полезной работы через КПД

Определение

Коэффициентом полезного действия (при сокращённом написании КПД) именуют безразмерную физическую величину, характеризующую отношение энергии, которую система потратила с пользой для нас, к полному количеству полученной энергии.

Измерять КПД принято в процентах. Например, КПД 35%, означает, что почти две трети энергии пошли на ненужные траты, стали рассеянным в пустую теплом, были потрачены на истирание деталей машины, образование искр и т. п.

Важно. 35% совсем не плохой КПД. У паровозов первой половины 20 века он составлял всего 10%. Лишь одна десятая образующегося при сгорании топлива тепла шла на перемещение состава, остальное рассеивалось в атмосфере. Среднеэксплуатационный КПД у современных тепловозов 20-22%. КПД машин на бензиновом ДВС равен 25%. КПД дизеля – 33%. Хорошо на этом фоне выглядит КПД электромобилей. Он у них около 90%.

В формуле нахождения полезной работы да в физике в основном КПД обозначают буквой из греческого алфавита η (эта).

Полезная работа в физике и ненужные траты энергии

Прежде чем говорить о том, как найти полезную работу в физике, следует сказать о ней самой. Дело в том что полезная работа в физике – величина очень даже субъективная. Она напрямую связана с человеческим восприятием, с тем, чего нам нужно получить от системы. Поэтому часто, когда говорят о КПД, имеют в виду различные технические устройства, а не природные объекты.

Хотя технологии постоянно развиваются избежать значительных потерь энергии всё же не удаётся. Получается, что:

Aзатр > Aполез

Aзатр – затраченная работа, Aполез – полезная работа, та что идёт на осуществление нужного нам процесса.

Как бы мы ни пытались уменьшить ненужные потери энергии, полностью от них избавиться не получиться. Непреодолимой преградой для этого является первый закон термодинамики. Из него явственно следует, что КПД любого устройства и механизма ни при каких обстоятельствах не может быть больше единицы и даже стать равным ей.

Формула

Общая формула КПД:

\[η = (Aполез/Aзатр) * 100%\].

Мощность представляет собой работу, совершённую за единицу времени. В связи с этим КПД можно посчитать как отношение входной мощности системы к выходной. Т. е.

η = Pвх/Pвых.

Как найти полезную работу в физике используя формулы для разных физических процессов

Вид формул, как найти полезную работу в физике, зависит от природы физических явлений, использующихся для преобразования затраченной энергии в нужную.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Как найти полезную работу в физике механической системы

Лучше всего это показать на конкретном примере. Допустим, нам требуется найти КПД процесса, при котором мальчик вкатывает санки весом 4 кг на горку длиной 12, высотой 2 м. Он прикладывает для этого силу, равную 15 Н.

Решение:

Напомним, что общая формула для КПД

η = (Aполез/Aзатр) * 100%

Aполез в нашем случае равна потенциальной энергии (Eп), которую нужно потратить на то, чтобы поднять санки на высоту, т. е.  Aполез = m*g*h.

Затраченная мальчиком работа равна произведению силы на перемещение, т. е. Aзатр = F*S.

Подставляем в общую формулу для КПД

η = (m*g*h*100)/(F*S)

При подстановке численных значений получаем

η = 4*9,8*2/15*12 * 100% = 78,4/180 * 100% ≃ 43,6 %

Из этого примера ясно, чему равна полезная работа в физике механической системы, выраженная через КПД.

Формула

\[Aполез = (η*F*S)/100\]

Формула полезной работы в физике термодинамической системы

Именно по ней судят об эффективности тепловых машин. Допустим, нам нужно отыскать КПД тепловой машины, рабочее тело которой берёт от нагревателя 20кДж, а холодильнику отдаёт 10кДж.

Решение:

Тепловая машина работает следующим образом: нагреватель передаёт определённое количество теплоты рабочему телу, оно из-за этого расширяется, совершая тем самым механическую работу. Однако в последнюю переходит далеко не вся часть переданной тепловой энергии. Чтобы вернуть систему в исходное состояние и начать новый цикл приходится использовать холодильник. 2)/R *t = UIt

В нашем примере она примет вид

η = Q/A *100% = Q/UIt *100%

Переводим минуты в секунды и, подставляя численные значения, получаем

η = 22176/220*1,4*120 *100% = 60%

Формула полезной работы электродинамической системы будет:

Формула

\[Aполез = (η*U*I*t)/100%\]

определение и расшифровка, полезная работа, формула КПД и применение в физике

Физика — это наука, которая изучает процессы, происходящие в природе. Наука эта очень интересная и любопытная, ведь каждому из нас хочется удовлетворить себя ментально, получив знания и понимание того, как и что в нашем мире устроено. Физика, законы которой выводились не одно столетие и не одним десятком ученных, помогает нам с этой задачей, и мы должны только радоваться и поглощать предоставленные знания.

Но в то же время физика — наука далеко непростая, как, собственно, и сама природа, но разобраться в ней было бы очень интересно. Сегодня мы будем говорить о коэффициенте полезного действия. Мы узнаем, что такое КПД и зачем он нужен. Рассмотрим все наглядно и интересно.

Содержание:

• Определение и расшифровка КПД
• Полезная работа
• Физическая формула КПД
• Применение в разных сферах физики
• Видео

Определение и расшифровка КПД

Расшифровка аббревиатуры — коэффициент полезного действия. Однако и такое толкование с первого раза может оказаться не особо понятным. Этим коэффициентом характеризуется эффективность системы или какого-либо отдельного тела, а чаще — механизма. Эффективность характеризуется отдачей или преобразованием энергии.

Этот коэффициент применим практически ко всему, что нас окружает, и даже к нам самим, причём в большей степени. Ведь совершаем мы полезную работу все время, только вот как часто и насколько это важно, уже другой вопрос, с ним и используется термин «КПД».

Важно учесть, что этот коэффициент — величина неограниченная, она, как правило, представляет собой либо математические значения, к примеру, 0 и 1, либо же, как это чаще бывает — в процентах.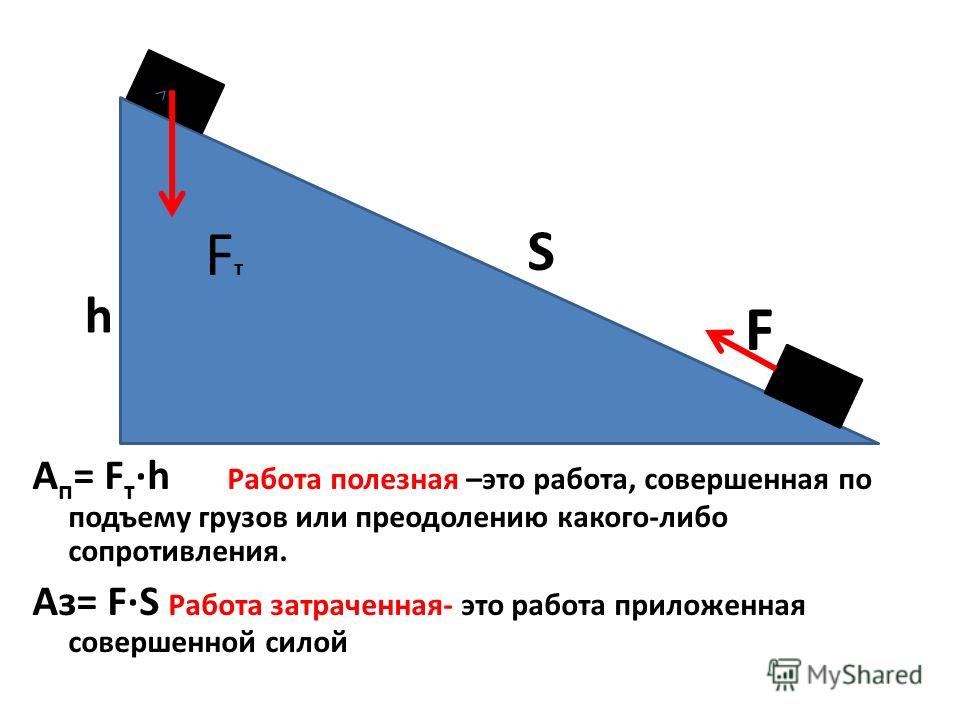

В физике этот коэффициент обозначается буквой Ƞ, или, как её привыкли называть, Эта.

Полезная работа

При использовании каких-либо механизмов или устройств мы обязательно совершаем работу. Она, как правило, всегда больше той, что необходима нам для выполнения поставленной задачи. Исходя из этих фактов различается два типа работы: это затраченная, которая обозначается большой буквой, А с маленькой з (Аз), и полезная — А с буквой п (Ап). Для примера, возьмем такой случай: у нас есть задача поднять булыжник определенной массой на определенную высоту. В этом случае работа характеризует только преодоление силы тяжести, которая, в свою очередь, действует на груз.

В случае когда для подъема применяется какое-либо устройство, кроме силы тяжести булыжника, важно учесть еще и силу тяжести частей этого устройства. И кроме всего этого, важно помнить, что, выигрывая в силе, мы всегда будем проигрывать в пути. Все эти факты приводят к одному выводу, что затрачиваемая работа в любом варианте окажется больше полезной, Аз > Ап, вопрос как раз заключается в том, насколько её больше, ведь можно максимально сократить эту разницу и тем самым увеличить КПД, наш или нашего устройства.

Полезная работа — это часть затрачиваемой, которую мы совершаем, используя механизм. А КПД — это как раз та физическая величина, которая показывает, какую часть составляет полезная работа от всей затраченной.

Итог:

• Затрачиваемая работа Aз всегда больше полезной Ап.
• Чем больше отношение полезной к затрачиваемой, тем выше коэффициент, и наоборот.
• Ап находится произведением массы на ускорение свободного падения и на высоту подъема.

Физическая формула КПД

Существует определенная формула для нахождения КПД. Она звучит следующим образом: чтобы найти КПД в физике, нужно количество энергии разделить на проделанную системой работу. То есть КПД — это отношение затраченной энергии к выполненной работе. Отсюда можно сделать простой вывод, что тем лучше и эффективнее система или тело, чем меньше энергии затрачивается на выполнение работы.

Сама формула выглядит кратко и очень просто Ƞ будет равняться A/Q. То есть Ƞ = A/Q. В этой краткой формулы и фиксируют нужные нам элементы для вычисления. То есть A в этом случае является использованной энергией, которая потребляется системой во время работы, а большая буква Q, в свою очередь, будет являться затраченной A, или опять же затраченной энергией.

В идеале КПД равен единице. Но, как это обычно бывает, он её меньше. Так происходит по причине физики и по причине, конечно же, закона о сохранении энергии.

Все дело в том, что закон сохранения энергии предполагает, что не может быть получено больше А, чем получено энергии. И даже единице этот коэффициент будет равняться крайне редко, поскольку энергия тратится всегда. И работа сопровождается потерями: к примеру, у двигателя потеря заключается в его обильном нагреве.

Итак, формула КПД:

Ƞ=А/Q, где

• A — полезная работа, которую выполняет система.
• Q — энергия, которую потребляет система.

Применение в разных сферах физики

Примечательно, что КПД не существует как понятие нейтральное, для каждого процесса есть свой КПД, это не сила трения, он не может существовать сам по себе.

Рассмотрим несколько из примеров процессов с наличием КПД.

К примеру, возьмем электрический двигатель. Задача электрического двигателя — преобразовывать электрическую энергию в механическую. В этом случае коэффициентом будет являться эффективность двигателя в отношении преобразования электроэнергии в энергию механическую. Для этого случая также существует формула, и выглядит она следующим образом: Ƞ=P2/P1. Здесь P1 — это мощность в общем варианте, а P2 — полезная мощность, которую вырабатывает сам двигатель.

Нетрудно догадаться что структура формулы коэффициента всегда сохраняется, меняются в ней лишь данные, которые нужно подставить. Они зависят от конкретного случая, если это двигатель, как в случае выше, то необходимо оперировать затрачиваемой мощностью, если работа, то исходная формула будет другая.

Теперь мы знаем определение КПД и имеем представление об этом физическом понятии, а также об отдельных его элементах и нюансах. Физика — это одна из самых масштабных наук, но её можно разобрать на маленькие кусочки, чтобы понять. Сегодня мы исследовали один из этих кусочков.

Видео

Это видео поможет вам понять, что такое КПД.

16.15: Максимально полезная работа — Химия LibreTexts

1. Последнее обновление

2. Сохранить как PDF

• Эд Витц, Джон В. Мур, Джастин Шорб, Ксавьер Прат-Ресина, Тим Вендорф и Адам Хан
• Цифровая библиотека химического образования (ChemEd DL)

Свободная энергия Гиббса обладает еще одним очень полезным свойством. При протекании самопроизвольной химической реакции уменьшение свободной энергии ,–Δ G соответствует максимально возможному количеству полезной работы , w _max , которую можно получить . Символически,

\[-\Delta G = w_{max} \номер\]

Для реакции, которая не является самопроизвольной Δ 9{\ circ} _ {m} (298 \ text {K}) = -394,4 \ frac {\ text {кДж}} {\ text {моль}} \ nonumber \]

Таким образом, 1 моль углерода может выполнить почти ровно четверть работы, необходимой для разложения 1 моля Al ₂ O ₃ , и мы должны сжечь не менее 4 молей C для переработки каждого 1 моля Al ₂ O ₃ руды . (На практике процесс выплавки алюминия эффективен только на 17 процентов, поэтому необходимо сжечь почти в 6 раз больше теоретических 4 моль углерода.)

В контексте, который мы только что описали, бесплатная энергия – это энергия, которая доступна для выполнения полезной работы , а не энергия, которую мы можем получить даром. Когда происходит самопроизвольный процесс и происходит уменьшение свободной энергии, уменьшается доступность полезной энергии . Согласно первому закону термодинамики энергия не может потребляться ни в каком процессе, но согласно второму закону свободная (или доступная) энергия всегда потребляется в самопроизвольном процессе.

Когда мы говорим о потреблении энергетических ресурсов путем сжигания ископаемого топлива, речь идет о доступной энергии. Энергия, первоначально запасенная в топливе, преобразуется в тепловую энергию и рассеивается в окружающей среде. Как только это произошло, его полезность теряется. Невозможно абстрагировать эту энергию от окружающей среды и использовать ее для поднятия тяжестей или выполнения другой полезной работы, поскольку это соответствовало бы обращению спонтанного процесса вспять. Таким образом, второй закон добавляет очень важное уточнение к первому закону. В то время как первый закон говорит нам, что мы не можем уничтожить энергию, второй закон говорит, что мы также не можем ее использовать повторно.

Эта страница под названием 16.15: Максимально полезная работа распространяется под лицензией CC BY-NC-SA 4.0, авторами, ремиксами и/или кураторами являются Эд Витц, Джон У. Мур, Джастин Шорб, Ксавье Прат-Ресина, Тим Вендорф и Адам Хан.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   ХимПРАЙМ

   Лицензия

   CC BY-NC-SA

   Версия лицензии

   4,0

   Показать страницу TOC

   № на стр.

2. Теги

   1. свободная энергия
   2. Свободная энергия Гиббса
   3. работа

Свободная энергия Гиббса – равновесная термодинамика

Свободная энергия Гиббса определяется по:

Внутреннюю энергию U можно рассматривать как энергию, необходимую для создания
системы при отсутствии изменений температуры или объема. Окружающая среда с постоянной температурой T вносит вклад в величину TS
системы, уменьшая общие инвестиции, необходимые для создания системы. Этот
вклад чистой энергии для системы, созданной при температуре окружающей среды T от
пренебрежимо малый начальный объем представляет собой свободную энергию Гиббса.
Изменение свободной энергии Гиббса, ΔG, в реакции является очень полезным параметром.
Его можно рассматривать как максимальное количество работы, которое можно получить в результате реакции.

Энергия Гиббса Гри и химические реакции.
Изменение свободной энергии Гиббса
связанный с химической реакцией, является полезным индикатором того,
реакция пойдет самопроизвольно. Поскольку изменение свободной энергии равно
максимальная полезная работа, которую может совершить реакция. ΔG=Wмакс.
, то отрицательный ΔG, связанный с реакцией, указывает на то, что она может произойти
спонтанно. Это согласуется с обычным химическим соглашением о
рассматривая работу, совершаемую системой, как отрицательную работу. Наиболее распространенные реакции
можно оценить на спонтанность в стандартных условиях, просмотрев
соответствующие термодинамические величины для каждого из реагентов и продуктов.
ΔG=ΔH-TΔS.

Приложения.
Вы когда-нибудь хотели узнать, сколько энергии вам нужно для проведения диссоциации? Например, этот

Чтобы ответить на этот вопрос, у нас есть свободная энергия Гиббса.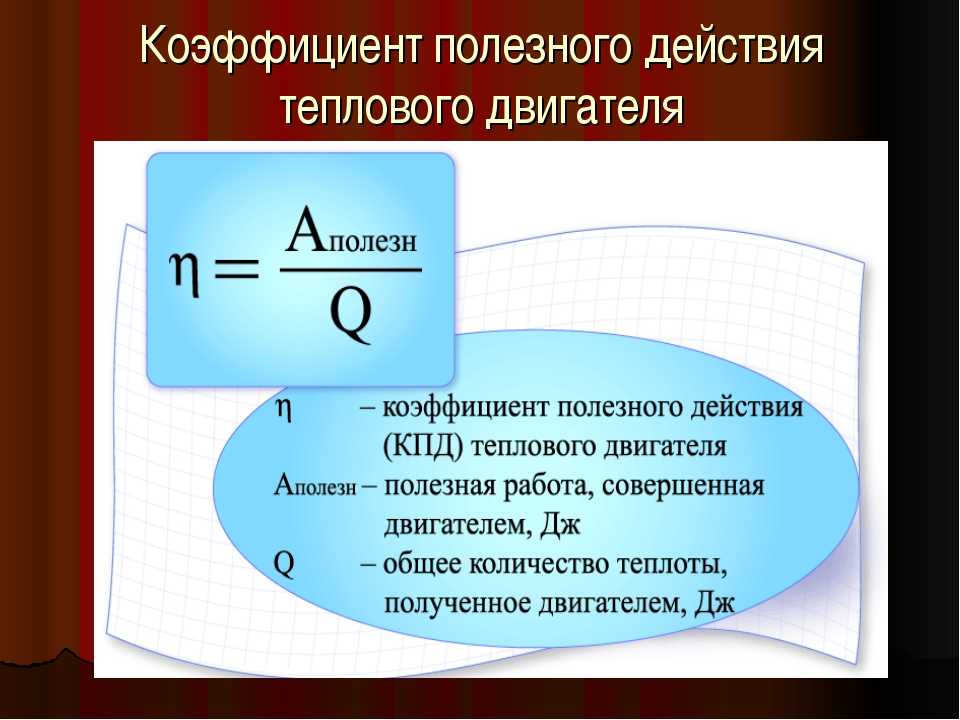
Свободная энергия Гиббса — это энергия, необходимая для совершения работы, и вот ее уравнение:
0172 ∆G = ∆H-T*∆S
для лучшего понимания энергии GIBBS У нас есть пример:
Микробный рост-это биологический процесс, который ранее рассматривался как химическая реакция, действующая в соответствии с уравнением свободной энергии GIBBS, разработанный во время 1870-е годы. Однако полное применение уравнения Гиббса к микробному росту произошло только в 1997 году, когда было экспериментально измерена энтропия дрожжевых клеток.
Доктор Эдвин Х. Баттли, заслуженный деятель Университета Стоуни-Брук и обладатель премии Дюбрунфо Международного общества биологической калориметрии (1994 г.) и медали Лавуазье (2010 г.), исследовал использование уравнения свободной энергии Гиббса для точного определения изменения энергии. сопровождающий клеточный рост.

Во многих системах значения некоторых переменных не могут быть определены экспериментально и поэтому должны рассчитываться на основе теоретически полученных значений. Изменение свободной энергии, сопровождающее клеточный рост, не может быть измерено напрямую, но, если теплота роста может быть измерена, а изменение энтропии, сопровождающее рост, может быть рассчитано косвенно из измерений теплоты, изменение свободной энергии может быть рассчитано с использованием уравнения свободной энергии Гиббса.
Рассчитайте термодинамику микробного роста!

*Используя свободную энергию Гиббса, вы можете узнать, находятся ли две фазы в равновесии.

Ссылки.
— Hyperphysics.phy (n.d.) Свободная энергия Гиббса. Получено с: http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/helmholtz.html#c2
— Bozeman Science (2011). Свободная энергия Гиббса. Получено с: http://youtu.be/DPjMPeU5OeM.
— Наука Бозмана (2014). Использование свободной энергии Гиббса.