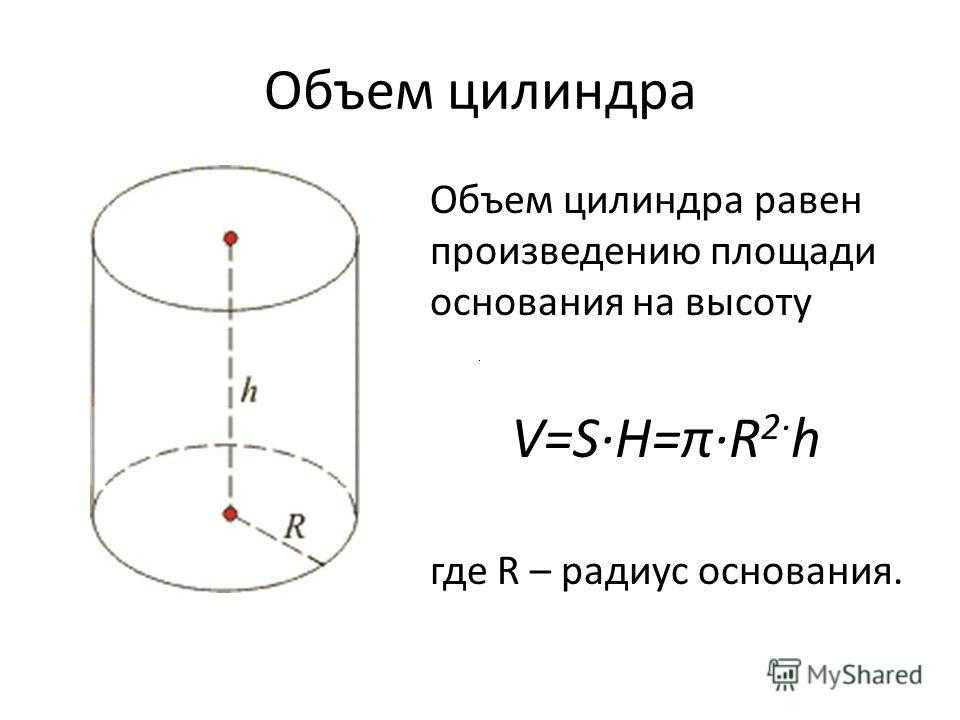
2} — это формула площади круга, а в нашем случае — площадь основания. Поэтому формулу объема цилиндра можно записать через площадь основания и высоту:

S (б.п.) = hP = 2πrh

— Если известна площадь бок. поверхности S (б.п.) и высота h цилиндра, радиус будет равен частному от деления S (б.п.) на произведение 2пи на высоту:

Формула вычисления объема цилиндра

1. Через площадь основания и высоту

Объем (V) цилиндра равняется произведению его высоты и площади основания.

V = S ⋅ H

2. Через радиус основания и высоту

Как мы знаем, в качестве оснований цилиндра (равны между собой) выступает круг, площадь которого вычисляется так: S = π ⋅ R². Следовательно, формулу для вычисления объема цилиндра можно представить в виде:

V = π ⋅ R² ⋅ H

Примечание: в расчетах значение числа π округляется до 3,14. 2.

Расшифровать формулу просто:

• V – объем цилиндра;
• π – 3,14;
• R – радиус цилиндра;
• D – диаметр.

То есть получается, что, если разделить объем на площадь основания, получится высота цилиндра.

Можно поступить проще. Для этого нам придется вычислить площадь боковой поверхности искомого цилиндра. Это легко сделать по формуле: S=2πRH. Слегка изменив формулу, получаем: H=S/2πR.

Таким образом, есть уже два способа, которые помогли вспомнить, как найти высоту цилиндра. Это нетрудно, когда перед глазами стройные формулы.

Способ расчета радиуса цилиндра:

Высота: Объем:

Высота: Площадь боковой поверхности:

Высота: Площадь полной поверхности:

Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра:
где V – объем цилиндра, h – высота

Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра:
где Sb – площадь боковой поверхности, h – высота

Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра:
где S – площадь полной поверхности, h – высота

S (п.п.) = S (б.п.) + 2S (осн.) = 2πrh + πr2=πr (2h+r)

Площадь боковой поверхности равняется длине окружности основания умноженной на высоту:

R = √V / πh

где V — объем цилиндра, h — высота.
Полная площадь поверхности цилиндра складывается из сумм площадей его боковой поверхности и двух оснований:

Примеры задач

Задание 1
Высота цилиндра равняется 5 см, а объем – 141,3 см³. Вычислите его радиус.

Решение:
Воспользуемся соответствующей формулой, подставив в нее известные по условиям задачи значения:

Задание 2
Найдите радиус цилиндра, если площадь его боковой поверхности равна 175,84 см², а высота составляет 7 см.

Решение:
Применим формулу, в которой задействованы заданные величины:

Задание 3
Рассчитайте радиус цилиндра, если полная площадь его поверхности – 602,88 см², а высота – 10 см.

Решение:
Используем третью формулу для нахождения неизвестной величины:

Через площадь боковой поверхности

Радиус цилиндра считается таким образом:

S_бок. – площадь боковой поверхности цилиндра; равна произведению длины окружности (2πR), являющейся основанием фигуры, на его высоту:

S = 2πRh

Площадь полной поверхности цилиндра через радиус основания и высоту

{S = 2pi r (h+r)}

Формула для нахождения полной поверхности цилиндра через высоту и радиус основания:

{S = 2pi r (h+r)}, где π — число Пи (3,14159…), r — радиус основания цилиндра, h — высота цилиндра.

Источники

• https://mnogoformul.ru/obem-cilindra
• https://infofaq.ru/radius-cilindra.html
• https://MicroExcel.ru/obyom-tsilindra/
• https://www.calc.ru/radius-tsilindra.html
• https://MicroExcel.ru/radius-tsilindra/
• https://mnogoformul.ru/ploshhad-poverkhnosti-cilindra

Калькулятор для цилиндра — intmag24.ru

Опубликовано 18.06.202025.11.2021 от Admin — Оставить комментарий

Онлайн калькулятор для цилиндра позволяет по известным данным вычислить:

• объем цилиндра,
• площадь основания, площадь боковой поверхности и  площадь полной поверхности цилиндра,
• элементы: радиус, диаметр и высоту.

Калькулятор для цилиндра: комментарий

Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью (называемой боковой поверхностью цилиндра) и не более чем двумя поверхностями (основаниями цилиндра).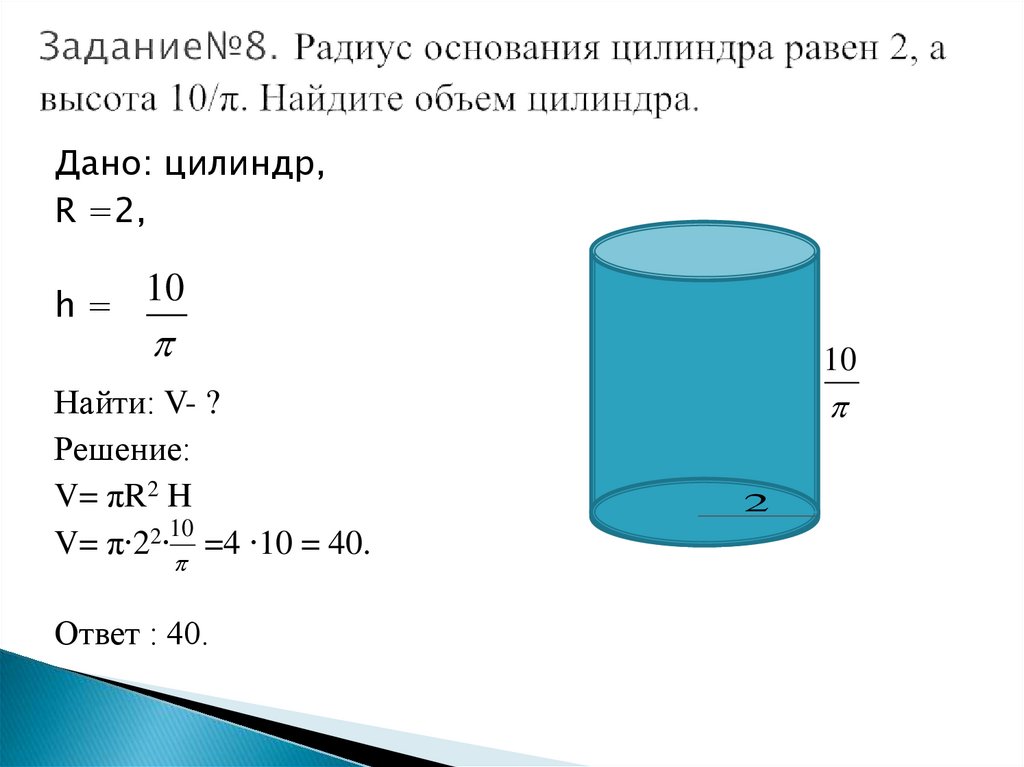

Обозначения для цилиндра:
R – радиус, D – диаметр,
V – объем,
Sо – площадь основания, Sб – площадь боковой поверхности, S – площадь полной поверхности,
h – высота прямого кругового цилиндра (h2 и h3 — минимальная  и максимальная высота)
π – число Пи которое всегда примерно равно 3,14.

Прямой круговой цилиндр

Круговым называется цилиндр, если его направляющая является окружностью. Прямым называется цилиндр, если его образующая перпендикулярна основаниям.

Формулы для прямого кругового цилиндра:

Найти объем цилиндра, если известны:

• радиус и высота цилиндра: V=πR²h
• диаметр и высота цилиндра: V=πD²/4h
• площадь и высота цилиндра: V=Sоh

Площадь(Sб) боковой поверхности прямого кругового цилиндра

Так как боковая поверхность представляет собой прямоугольник, то площадь боковой поверхности цилиндра определяется по формуле: Sб=2πR⋅h

Площадь(Sо) основания цилиндра

Основание цилиндра —круг, поэтому площадь одного основания находится по формуле площади круга: Sо=πR².

Площадь(S)  полной поверхности прямого кругового цилиндра

Площадь полной поверхности цилиндра определяется по формуле: S=2πRh+2πR²=2πR(h+R)

Формулы нахождения радиуса и диаметра по:

• высоте и объему: R=√(V/πh), D=2*√(V/πh)
• площади боковой поверхности и высоте: R=Sб/2πh, D=2*Sб/2πh
• площади основания и высоте: R=√(Sо/π), R=2*√(Sо/π)

Формулы нахождения высоты по:

• радиусу и объему: h=V/πR²
• площади боковой поверхности и радиусу: h=Sб/2πR
• площади полной поверхности и радиусу: h=S/2πR-R

Скошенный цилиндр

Прямой круговой цилиндр со скошенным основанием (скошенный цилиндр) определяется радиусом основания R, минимальной высотой h2 и максимальной высотой h3.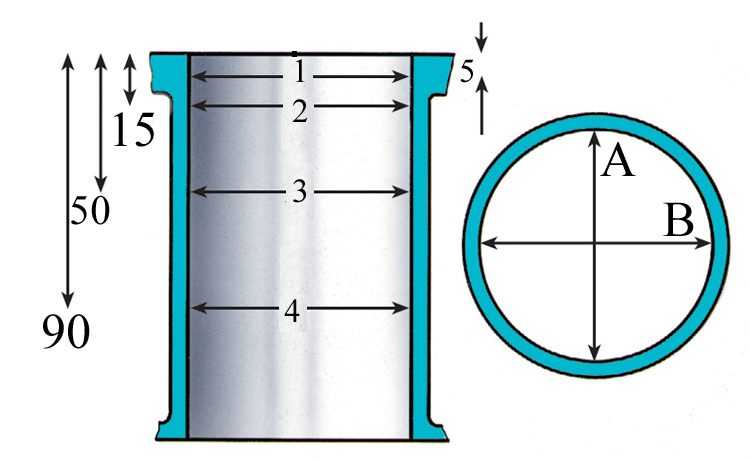

Формулы для скошенного цилиндра:

• Объем скошенного цилиндра: V=πR²(h2+h3)²
• Площадь(Sб) боковой поверхности скошенного цилиндра: Sб=πR(h2+h3)
• Площадь(Sо) оснований скошенного цилиндра: Sо=πR²+πR √(R2+((h2−h3)/2)²)
• Площадь(S) полной поверхности скошенного цилиндра  
  S=Sб+Sо= πR(h2+h3)+ πR²+πR √ (R²+((h2−h3)/2)²)  = πR[(h2+h3)+ R+√ (R²+((h2−h3)/2)²) ]

Список всех онлайн-конвертеров на странице «Калькуляторы«.

Рубрика: Калькуляторы

Метки Математика, Геометрия

Как измерить диаметр отверстия

Быстро. Вам нужны сменные подшипники, но вы не уверены, какие размеры вам нужны. Пришло время осмотреть старые подшипники и, возможно, провести несколько измерений.

Возможно, вам повезет. Если на подшипнике все еще есть выгравированный на нем видимый идентификационный номер, вы попали в сортировку. Просто позвоните в SMB Bearings и назовите этот код. Если нет, возможно, вы сможете откопать исходную документацию по заказу со ссылкой на из глубины вашей картотеки. Если ни то, ни другое невозможно, пришло время провести измерения.

Подшипник имеет три основных размера. Диаметр отверстия (иногда называемый внутренним диаметром или ID), внешний диаметр (OD) и ширина подшипника.

Хотя важны все три измерения, особое внимание уделяется диаметру отверстия, так как этот показатель полностью зависит от размера вала. Следует отметить, что диаметр вала не всегда равен диаметру отверстия . Во многих случаях диаметр вала часто немного больше, чем размер отверстия, чтобы подшипник со временем лучше подходил к валу. Это означает, что индукционные нагреватели необходимы для установки подшипников на вал, пока материал теплый и пластичный.

Чтобы получить эти три измерения, вы можете попытаться использовать линейку.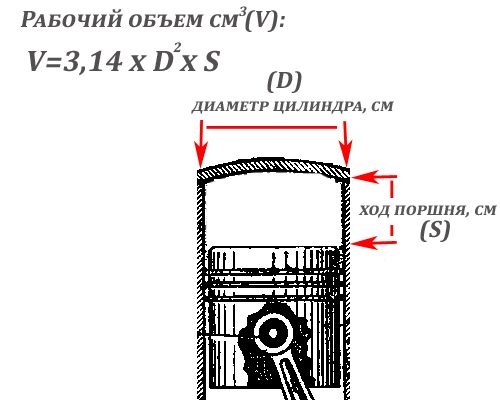 Так делают многие, но это не очень точно.

Лучший способ для большинства из нас измерить подшипники — использовать цифровые штангенциркули. Этот измерительный инструмент используется для измерения внутренних и внешних расстояний.

Хороший штангенциркуль имеет точность плюс-минус 0,02 мм или примерно одну десятитысячную долю дюйма. Внезапно линейка, которую вы захотели использовать, меркнет по сравнению с ней, хотя ни одна из них не конкурирует с манометрами, которые используют производители подшипников. Они могут иметь точность в пределах 0,0002 мм или менее 10 миллионных долей дюйма.

Большинство штангенциркулей позволяют переключаться между миллиметрами и дюймами одним нажатием кнопки, что позволяет измерять как дюймовые, так и метрические подшипники.

Готов к измерению диаметра отверстия ? Вот как это сделать.

Включите цифровые штангенциркули и обнулите показания данных в закрытом положении. Поместите подшипник на внутреннюю измерительную сторону штангенциркуля, раскатайте их настолько, насколько позволяет подшипник, и запишите отображаемые размеры. Вы должны покачивать суппорты внутри внутреннего кольца подшипника, чтобы убедиться, что они сидят в самой широкой части.

Повторите процесс, используя внешнюю сторону измерения штангенциркуля, чтобы вычислить внешний диаметр подшипника. На этот раз поверните штангенциркуль в направлении закрытия, чтобы получить измерение внешнего диаметра.

Используя внешнюю сторону измерения еще раз, измерьте ширину подшипника, что делается так же, как вы измеряете диаметр.

Имея на руках три измерения, вы можете связаться с SMB Bearings, чтобы узнать, какие подшипники со склада в Великобритании вам подходят.

Больше, чем размер подшипника

Даже при тщательном измерении диаметра и ширины необходимо учитывать еще несколько переменных:

• Имели ли исходные подшипники какие-либо экраны или уплотнения?
• Имеет ли он фланец на наружном кольце?
• Имеет ли внутреннее кольцо ту же ширину, что и наружное кольцо?
• Есть ли в подшипнике фиксатор?
• Из какого материала сделан подшипник?
• Подшипник содержал специальную смазку?

Чтобы быть в безопасности, вы также можете отправить нам соответствующий подшипник, чтобы наша команда рассмотрела его поближе. Вы можете найти наш почтовый адрес здесь, но сначала позвоните нам, чтобы мы знали, где его искать!

Если вам нужна дополнительная помощь, позвоните в команду SMB Bearings. У нас есть многолетний опыт поставок небольших и миниатюрных подшипников для различных отраслей промышленности. Позвоните нашим специалистам сегодня по телефону +44 (0) 1993 842 555 или по электронной почте [email protected].

Терминология: диаметр отверстия/диаметр канавки | Официальный журнал NRA

Вот определение, прямо из Справочника по огнестрельному оружию NRA . Это «… меньший внутренний диаметр бочки, который является диаметром круга, образованного верхушками земель». Это диаметр канала ствола, а диаметр нарезов — это «…диаметр окружности, описанной дном нарезов…»

Посмотрите на это так: оружейник начинает с толстостенной стальной трубы, когда он или она занимается изготовлением ствола для огнестрельного оружия. Трубка просверлена ружьем, прямая и соответствует размеру, который на несколько тысячных меньше диаметра пули. Этот размер будет примерно таким же, как диаметр канала ствола в готовом стволе. Затем он проталкивает или протягивает кнопку или резак через ствол вращательным движением, чтобы равномерно нанести спиральные канавки по каналу ствола. Это действие удаляет или смещает достаточное количество металла, чтобы образовались глубокие и равномерно расположенные канавки от края до края. Размер от дна канавки до дна противоположной канавки является диаметром канавки.

При выстреле пуля под большим давлением вдавливается в ствол. Пуля имеет диаметр, очень близкий к диаметру нареза ствола, поэтому она плотно прилегает. Расширяющиеся пороховые газы толкают его вперед, тем самым врезаясь в нарезы и заставляя его поворачиваться. Посадка достаточно плотная, чтобы предотвратить попадание пороховых газов вокруг пули, когда она пересекает ствол, поэтому она выходит из ствола, вращаясь со скоростью, определяемой скоростью закручивания этих спиральных канавок.

В бочке два диаметра. Больший (главный) диаметр — канавка; меньший (минор) — отверстие.

Даже после того, как их страна попала под контроль нацистов после капитуляции Франции в 1940 году, банды членов французского сопротивления продолжали сопротивляться, используя любое оружие, которое они могли добыть или получить.

Новости, исторические

Производители боеприпасов наращивают темпы удовлетворения потребительского спроса

В 2022 году не было недостатка в представлениях и объявлениях от компаний, производящих боеприпасы. это обещает сократить эти ужасные периоды нехватки боеприпасов или, по крайней мере, уменьшить их частоту.

Новости, Боеприпасы

Пистолет недели NRA: Smith & Wesson M&P Shield Plus из 30 моделей Super Carry с готовым оптическим затвором и патроном для одного из новейших на сегодняшний день патронов для самообороны, 30 Super Carry.

Новости, Оружие недели NRA

Стрелок, вопросы и ответы: Добыча липкого Мосина

Недавно я присоединился к числу владельцев винтовок модели Мосина-Нагана, в частности модели 91/30 калибра 7,62×54 мм R. Время от времени у меня возникали проблемы с экстракцией, которые обычно возникают после прогрева оружия. Можете ли вы порекомендовать что-нибудь, что можно сделать для устранения этой проблемы, или это конструктивная особенность, которую необходимо принять?

Новости, Винтовки

Вооруженный гражданин® 16 декабря 2022 г.

Прочтите сегодняшнюю статью «Вооруженный гражданин», чтобы узнать реальные истории законопослушных граждан прошлого и настоящего, которые использовали огнестрельное оружие для спасения жизней.

Вооруженный гражданин, Новости

Великое американское шоу под открытым небом возвращается в феврале 2023 года

Великое американское шоу под открытым небом воспевает традиции активного отдыха, которыми дорожат миллионы американцев и их семей, на площади 650 000 кв. футов. выставочное пространство, в котором примут участие более 1000 экспонентов, в том числе производители стрелкового оружия, экипировщики, продавцы лодок и домов на колесах, охотничьи и рыболовные продавцы и многие другие.