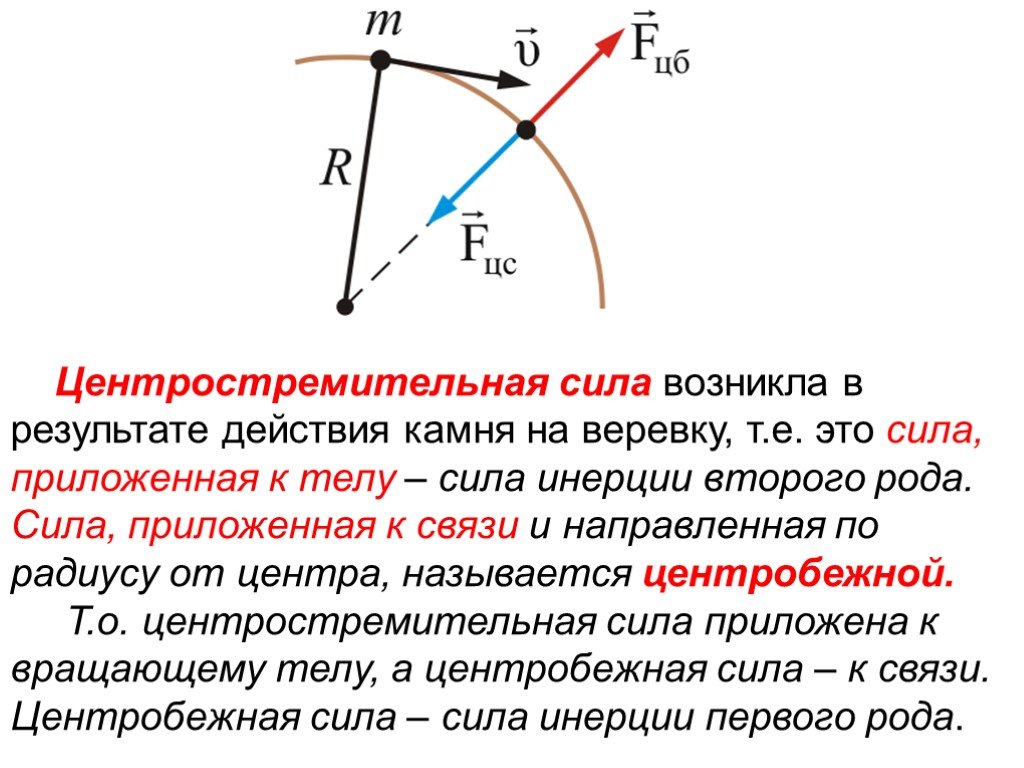
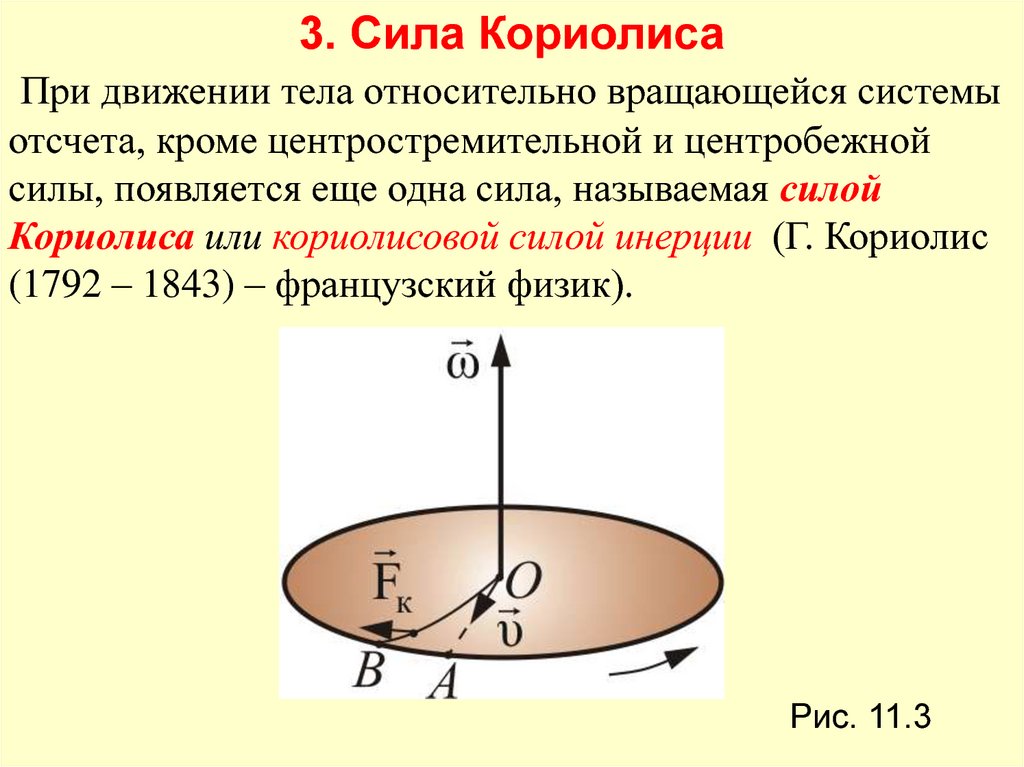
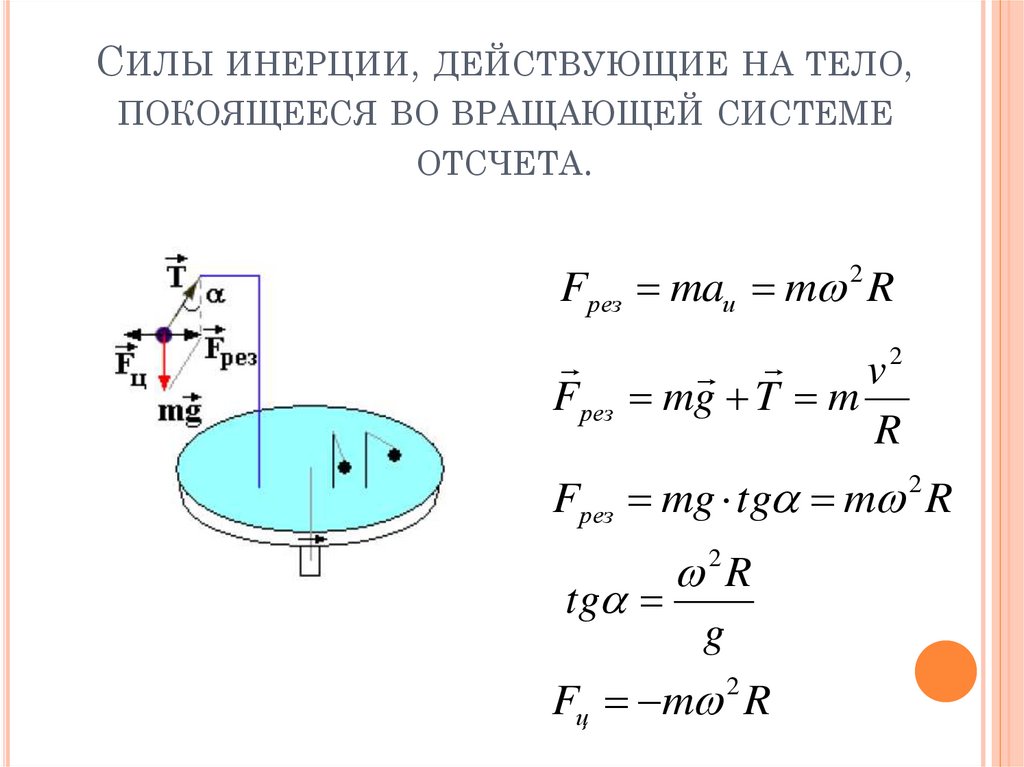
Физические основы механики

Представим себе диск, равномерно вращающийся с угловой скоростью . Вместе с диском вращается надетый на спицу шарик, соединенный с центром диска пружиной (рис. 8.3).

Рис. 8.3. Центробежная сила инерции в системе отсчета, связанной с вращающимся диском

Шарик покоится относительно диска и занимает на спице такое положение, при котором сила натяжения пружины оказывается равной произведению массы шарика на нормальное (центростремительное) ускорение (при равномерном вращении диска тангенциальное ускорение шарика, очевидным образом, равно нулю)

где — радиус-вектор, проведенный к шарику из центра диска (см. рис. 8.3). Но так рассуждает наблюдатель, смотрящий на вращение диска из инерциальной системы отсчета. Свяжем с диском вращающуюся неинерциальную систему отсчета К’, в которой диск вместе с шариком покоится. Условие равновесия шарика в этой системе имеет вид:

Наблюдатель во вращающейся системе отсчета объясняет равновесие шарика наличием силы инерции

направленной от центра диска 0′ по радиус-вектору .

Сила инерции, действующая на материальную точку в равномерно вращающейся с угловой скоростью ω системе отсчета, называется центробежной силой инерции:

Здесь — вектор, проведенный к материальной точке от оси вращения ортогонально последней. Мы ввели его, чтобы отличить от радиус-вектора в том случае, когда начало координат лежит на оси вращения, но не в плоскости вращения материальной точки.

Видео 8.4. Центробежная сила инерции: подвешенные шарики

При произвольном положении начала отсчета на оси вращения, радиус-вектор некоторой материальной точки всегда можно представить в виде

где _парал.— параллельная оси вращения, более того, лежащая на оси вращения (напомним: начинается вектор на оси вращения) составляющая радиус вектора , а — перпендикулярная к оси вращения его составляющая, начинающаяся на оси вращения, в центре той окружности, по которой движется рассматриваемая точка. С помощью известной формулы

учитывая, что векторное произведение и скалярное произведение равны нулю всегда, можно показать, что выражение для центробежной силы инерции представляется в виде

Таким образом, в общем случае, при произвольном выборе начала отсчета на оси вращения, для любого положения материальной точки, действующую на неё центробежную силу инерции, можно записать в виде

Видео 8.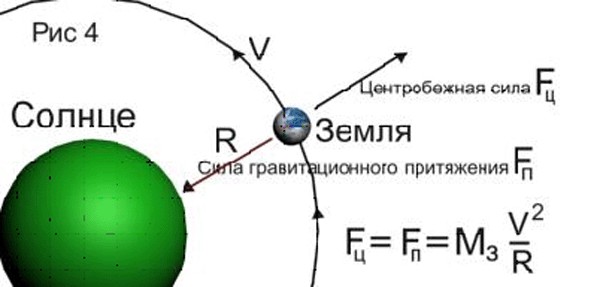 5. «Поразительное» поведение цепи — и здесь не обошлось без центробежной силы инерции. Цепь легкая, почти без трения между звеньями

Видео 8.6. «Поразительное» поведение цепи 2. Цепь тяжелая, с большим трением между звеньями

Пример. Сосуд с жидкостью вращается с угловой скоростью вокруг вертикальной оси (рис. 8.4). Найдем форму поверхности жидкости.

Рис. 8.4. Форма поверхности вращающейся жидкости

Задачу решаем в системе отсчета, вращающейся вместе с жидкостью. В этой системе жидкость неподвижна, но кроме силы тяжести на нее действует центробежная сила инерции. Поверхность жидкости симметрична относительно оси вращения. Рассмотрим сечение этой поверхности какой-нибудь вертикальной плоскостью, содержащей ось вращения, которую мы примем за ось .

Возьмем на поверхности элемент жидкости массой , расположенный в точке с координатой . На него действует сила тяжести и центробежная сила инерции (здесь координата есть расстояние от оси вращения, а и — единичные орты). Результирующая этих сил наклонена к вертикали под углом таким, что

Поверхность жидкости, описываемая функцией , всегда располагается ортогонально линии действия внешних сил. Как известно, тангенс того же угла можно найти как отношение приращений

то есть как производную. Получаем уравнение

которое легко интегрируется:

Это уравнение, как известно, описывает параболу. Вращение этой параболы задает параболоид вращения. Таким образом, поверхность вращающейся жидкости принимает форму параболоида вращения. При имеем , то есть плоскую горизонтальную поверхность.

Видео 8.7. Циркулярная «пила» из бумаги – неожиданное применение центробежной силы инерции

Видео 8.8. Сила Кориолиса: траектория движения шарика по вращающейся платформе

Дополнительная информация

http://www.plib.ru/library/book/14978.html — Сивухин Д.В. Общий курс физики, том 1, Механика Изд. Наука 1979 г.–— стр.349–353 (§66): детально обсуждается вес тел и проблема взвешивания на Земле.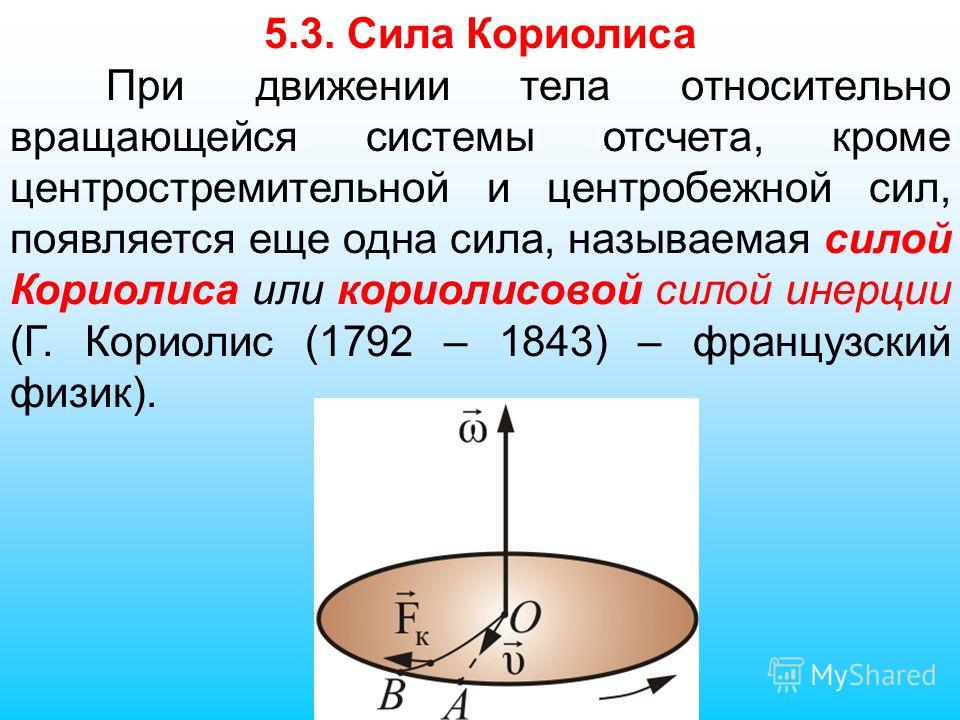

Центробежная сила или причина релятивистских поправок

• Главная
• Книга «Полевая физика»
• Том I
• Глава I
• Центробежная сила или причина релятивистских поправок

Рассмотрение обычных сил инерции и силы Кориолиса уже позволило нам объяснить природу всех известных поправок в обычной силе Лоренца. Мы нашли вихревое электрическое поле и магнитное поле. Казалось бы, другие поправки больше уже не нужны. Они просто не вписываются в обычную силу Лоренца! Однако это не так.

С подобным казусом мы столкнулись еще в самом начале этой главы (раздел 1.1), проводя аналогию сил инерции и электромагнитных сил. Сразу нашлась пара для обычной силы инерции и силы Кориолиса. Слагаемое с производной от угловой скорости мы вполне законно опустили, сославшись на равномерное вращение. И только центробежная сила пропала из красивой аналогии совершенно необоснованно. Что уже само по себе служит прямым намеком на ее особую роль в современной электродинамике! И теперь мы готовы понять эту роль.

Рассмотрим знакомое нам вращение механического диска. Как известно, центробежная сила действует перпендикулярно к оси вращения и направлена по радиусу. Эта сила связана с тем, что любой объект на вращающемся диске пытается сохранить свою линейную скорость и из-за вращения диска как бы выталкивается в сторону.

При движении одной заряженной частицы относительно другой соединяющая их полевая среда поворачивается (рисунок 1.10.1). В результате этого поворота возникает полевая центробежная сила, также направленная по радиусу вращения или по линии, соединяющей частицы. А именно по линии, соединяющей заряженные частицы, уже действует обычная электростатическая сила!

Рисунок 1.10.1. Релятивистские поправки к кулоновскому взаимодействию вызваны наличием центробежных сил в полевой среде.

Вот почему центробежная сила осталась незамеченной в классической электродинамике. Направление ее действия всегда совпадает с кулоновской компонентой и просто теряется на ее фоне! Это обстоятельство привело к тому, что центробежная сила не была оформлена в классической электродинамике в виде самостоятельного поля или силы, и до сих пор воспринимается лишь как искажение или поправка к электростатическому слагаемому!

Математически это выглядит так. В нашей формуле силы Лоренца (1.8.1) центробежное слагаемое имеет вид:

(1.10.1)

А как известно из механики, центробежную силу можно представить в виде градиента от квадрата линейной скорости вращения, а именно:

(1.10.2)

помня, что дифференцирование ведется по координатам частицы регистрации, и вектора v и ω при этом считаются постоянными.

Выразив теперь полевую массу через потенциал, мы получим:

(1.10.3)

Это поистине удивительное обстоятельство! Полевая центробежная сила имеет структуру обычной электростатической силы:

(1.10.4)

и просто «растворяется» в ней! Она то усиливает кулоновскую силу, то ослабляет ее. При этом возникает ощущение, что с обычной электродинамикой что-то не так. Но разрубить этот гордиев узел напрямую, решением «в лоб», эмпирически, путем уточнения экспериментов, или математически, путем усложнения формализма никак не получается. Выделить центробежную компоненту на фоне обычной кулоновской силы стало возможно только благодаря целостному пониманию системы электромагнитных добавок!

Примечательно, что величина поправки к электростатической силе за счет центробежной силы имеет знакомый порядок – отношение квадрата скорости частицы к квадрату скорости света. Это же порядок релятивистских поправок! Оставив для простоты в центробежной силе только первую часть со скоростью частицы-источника v, мы можем записать электростатическое слагаемое вместе с центробежной поправкой в виде:

(1. 10.5)

где v – модуль вектора скорости v.

Поправочный коэффициент при φ очень напоминает разложение известного релятивистского множителя (здесь мы для наглядности воспользовались приближенным выражением, хотя если учесть все нужные члены в нашей силе Лоренца, то соответствие будет точным):

(1.10.6)

Говоря о том, что при движении заряда к обычной электростатической силе добавляются только две поправки – вихревое электрическое поле и магнитная сила, мы временно опустили еще одно обстоятельство. Согласно современным представлениям при движении заряда сама электростатическая сила также должна измениться на величину релятивистского множителя, или, другими словами, потенциал следует преобразовать по формуле:

(1.10.7)

Вот где в классической силе Лоренца присутствует центробежная сила! Она не оформлена в виде самостоятельной силы или отдельного слагаемого, но она есть! И это один из существенных недочетов электродинамики. Потеря центробежной силы привела к неполноте всей электромагнитной системы. Это послужило поводом к появлению формального решения проблемы – теории относительности и преобразований Лоренца. Решению искусственному, позволяющему согласовать формулы, но не открывающему понимание природы вещей. Теперь мы готовы расставить все на свои места.

Полевая центробежная сила имеет структуру электростатической силы. Ее действие сводится к искажению кулоновского взаимодействия. Величина искажения имеет порядок релятивистских поправок. Поэтому потеря центробежной силы в классической электродинамике приводит к необходимости использования релятивистских преобразований для согласования формул.

1.8.1

Назад

1
…
2

3

4

5

6

7

8

9

10

11

12
…
13

Дальше

Centrifugal Force Calculator

, созданный Bogna Szyk

, рассмотренная Стивеном Вудлингом

Последнее обновление: 10 октября 2022 г.

СОДЕРЖАНИЕ:

• ЦЕНТРИФУГАЛЬНА делать дальше?
• Часто задаваемые вопросы

Калькулятор центробежной силы поможет вам найти силу, действующую на вращающийся объект, исходя из его массы, скорости и радиуса вращения. Вы можете использовать его не только для того, чтобы понять, как рассчитать центробежную силу, но и для ускорения и угловой скорости объекта. Читайте дальше, чтобы узнать, что такое определение центробежной силы и как применять уравнение центробежной силы.

Соотношение между силой и ускорением для объектов, движущихся по прямой линии, можно найти в нашем калькуляторе ускорения.

Определение центробежной силы

Центробежная сила – это сила инерции, возникающая в каждом вращающемся объекте. Оно требуется только во вращающейся системе отсчета — или, другими словами, когда мы смотрим на систему с точки зрения движущегося объекта.

Согласно первому закону Ньютона, если на объект не действует никакая сила, он движется прямолинейно. Чтобы произошло вращение, должна быть приложена центробежная сила, действующая наружу от центра вращения.

Например, вы можете представить себе камень, вращающийся на веревке. Центробежная сила — это сила, которая препятствует его движению к центру вращения (то есть к вашей руке).

Уравнение центробежной силы

Если вы знаете скорость объекта, просто используйте следующую формулу:

F = mv²/r

где:

• F — сила, выраженная в новых тоннах;
• м — масса объекта;
• v — скорость; и
• r это радиус.

Если вам известна только угловая скорость ω , вы можете пересчитать ее в нормальную скорость, просто умножив на длину окружности пути. Используйте следующее уравнение:

v = ω2πr

в случае, если ваш ω соответствует частоте Гц (1/с) .

Или формула:

v = ωr

для ω в рад/с .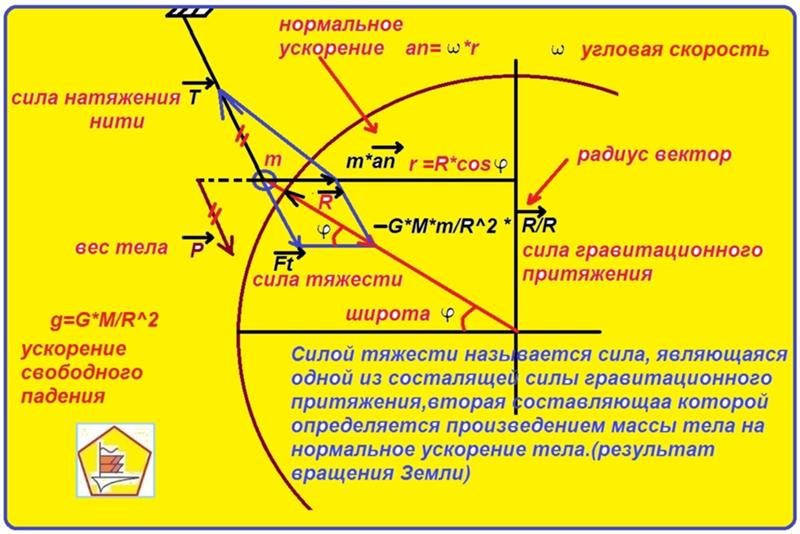

Или просто введите значения ω и r в наш калькулятор.

Для получения дополнительной информации о том, как найти длину окружности, посетите наш калькулятор длины окружности.

Как рассчитать центробежную силу

Выполните следующие простые шаги:

1. Найдите массу объекта — например, 10 кг .
2. Определить радиус вращения. Предположим, это 2 м .
3. Определить скорость объекта. Он может быть равен 5 м/с . Если вам известна только угловая скорость, вы можете использовать формулу v = ω ⋅ 2 ⋅ π ⋅ r для расчета скорости.
4. Используйте уравнение центробежной силы: F = m v² / r . В нашем примере она будет равна (10 кг) × (5 м/с)² / (2 м) = 125 кг⋅м/с² = 125 Н .
5. Или вместо этого вы можете просто ввести данные в наш калькулятор 🙂

Что делать дальше?

Наш калькулятор центробежной силы также можно использовать для нахождения центробежного ускорения a по простой формуле: a = F / m .

Он работает и в обратном порядке — например, вы можете найти массу объекта с заданной скоростью, центробежной силой и радиусом.

Поскольку вы знаете массу и скорость объекта, вы также можете найти его кинетическую энергию.

Кроме того, вы можете дополнительно изучить концепцию кинетической энергии, посетив наш калькулятор кинетической энергии.

Часто задаваемые вопросы

Что такое центробежная сила?

Центробежная сила вращающегося объекта — это внешняя сила, которая вытягивает объект из центра вращения. Это сила инерции, которая реагирует на центростремительную силу.

Как рассчитать центробежную силу поворачивающего автомобиля?

Вы можете попробовать калькулятор центробежной силы Omnicalculator или сделать следующее:

1. Узнать радиус кривизны. Допустим, 150 метров.
2. Определите скорость автомобиля. Это значение будет служить тангенциальной скоростью. Предположим, 50 км/ч

.

3. Умножьте массу автомобиля на квадрат скорости и разделите результат на радиус кривизны.
4. Результат 1286 ньютонов.

В чем разница между центробежной и центростремительной силой

Центробежная и центростремительная силы одинаковы, но направлены в противоположные стороны. В то время как центробежная сила направлена ​​в сторону, противоположную центру вращения, центростремительная сила направлена ​​к нему.

Какова центробежная сила на карусели радиусом 1 метр?

Для расчета центробежной силы нам нужны радиус центра, скорость вращения и масса объекта. Учитывая, что вы весите 70 кг и можете совершить один оборот на 360° за 2 секунды (30 оборотов в минуту или 30 об/мин), центробежная сила, с которой вы экспериментируете, составляет 960,9 ньютона.

Богна Шик

Масса (м)

Радиус (r)

Тангенциальная скорость (v)

Угловая скорость (ω)

Сила (F)

Центробежное ускорение (a)

Посмотрите 20 похожих калькуляторов вращательного и периодического движения 🌎

Угловое ускорениеУгловое смещениеУгловая частота, формула, определение Принцип, примеры (по сравнению с центростремительной силой)

4 мая 2022 г. 16 февраля 2022 г. Анупама Сапкота

Содержание

Определение центробежной силы

Центробежная сила — это внешняя фиктивная сила, которая действует на объект, движущийся по круговой траектории, направленной от центра вращения.

• Направление этой силы от оси вращения и параллельно оси вращения.
• Центробежная сила равна по величине и размерам другой силе (центростремительной), действующей по направлению к центру круговой траектории.
• Она называется фиктивной силой, потому что она проявляется только при наличии центростремительной силы. Эта сила возникает из-за инерционного свойства тела, движущегося по круговой траектории.
• Однако сила зависит от массы объекта, расстояния объекта от центра и скорости вращения.
• Концепция центробежной силы использовалась в различных вращающихся устройствах, таких как роторы центрифуг, дороги с насыпью и центробежные насосы.
• Единицей центробежной силы является Ньютон, а размерная формула M ¹ L ¹ T ^-2 .

Центробежная сила f формула

Формула для расчета центробежной силы приведена ниже.

Если скорость движущегося тела известна, то центробежную силу можно рассчитать по формуле:

где v — скорость движущегося тела, r — расстояние от движущегося тела до центр и м — масса движущегося тела.

Если известна угловая скорость движущегося объекта, то центробежную силу можно рассчитать по формуле:

где ω — угловая скорость, r — расстояние движущегося тела от центра и м — масса движущегося тела.

Принцип центробежной силы

• Как обсуждалось выше, центробежная сила является фиктивной или псевдо, поскольку она существует только при наличии центростремительной силы.
• Когда автомобиль с пассажирами поворачивает колесо, транспортное средство приводится в движение центростремительной силой, которая действует на все части транспортного средства.
• Однако пассажиры в автомобиле сохраняют свободу передвижения и, таким образом, сохраняют прямой путь, когда автомобиль начинает поворачивать.
• Это заставляет пассажиров двигаться к краю сиденья по направлению к двери, которая передает центростремительную силу пассажирам.
• Сила, с которой сталкиваются пассажиры вдали от автомобиля, является центробежной силой.
• Закон движения Ньютона не считает это реальной силой, так как согласно второму закону движения Ньютона ускорение вызывается силой.
• Когда камень на конце веревки, привязанный к шесту на земле, вращается, направление скорости камня постоянно меняется, что создает ускорение.
• Если струна порвется, камень сохранит свою инерцию и будет двигаться по прямой линии, касательной к круговой траектории.
• Если бы центробежная сила была реальной, камень двигался бы наружу, а не по касательной.

Как рассчитывается центробежная сила?

Для этого возьмем тот же пример с камнем на конце веревки, привязанной к шесту. Чтобы рассчитать центробежную силу, действующую на камень, можно выполнить следующие шаги:

1. Определите массу (m) камня. Допустим, масса 5 кг.
2. Определите длину строки. Допустим, длина 10 м.
3. Определите скорость камня. Предположим, что тангенциальная сила равна 5 м/с. Скорость может быть либо тангенциальной скоростью (v), либо угловой скоростью (ω). Если скорость является угловой скоростью, тангенциальная скорость может быть рассчитана как:

v = ω × r

4. Рассчитайте центробежную силу по данной формуле:

Таким образом, центробежная сила будет равна 12,5 Н. принцип центробежной силы. Центробежная сила, создаваемая роторами, создает в трубах градиент гидростатического давления, направленный перпендикулярно оси вращения. Это приводит к большим выталкивающим силам, которые толкают менее плотные частицы внутрь, в то время как более плотные частицы выталкиваются наружу. Этот принцип позволяет разделять частицы на основе их плотности.

Центробежные силы используются в различных аттракционах в парках развлечений, где сила прижимает райдеров к стене и позволяет пассажирам подняться над полом машин.

Примеры центробежной силы

Центробежная сила проявляется в различных процессах нашей повседневной жизни; некоторые примеры приведены ниже:

1. Сила, действующая на пассажиров наружу в автомобиле, когда автомобиль совершает поворот, является примером центробежной силы.
2. Когда камень, привязанный к веревке, вращается по кругу, сила, действующая на руки, также возникает из-за центробежной силы.
3. Земля сплющена на полюсе и выпукла на экваторе, потому что центробежная сила, действующая на частицы на экваторе, максимальна.
4. Когда ведро, наполненное водой, вращается по кругу, вода в ведре не падает, потому что вес ведра уравновешивается центробежной силой, действующей на ведро.
5. Грязь, налипшая на колеса автомобилей, под действием центробежной силы отбрасывается по касательной к брызговику.

Источник изображения: Wikia.

Центробежная сила против центростремительной силы

База сравнения	Центростремительная сила	Центробежная сила
Определение	Центростремительная сила — это сила, действующая на тело, движущееся по окружности по радиусу окружности и направленная к центру окружности.	Центробежная сила — это внешняя фиктивная сила, которая действует на объект, движущийся по круговой траектории, направленной от центра вращения.
Природа	Это реальная сила и реальные эффекты.	Считается фиктивной или псевдосилой, но имеет реальные последствия.
Направление	Направлен к центру окружности вращения.	Направлен от центра окружности вращения.
Роль	Круговое движение не существует без центростремительной силы.	Центробежная сила не имеет самостоятельного существования.
Происхождение	Возникновение центробежной силы связано с взаимодействием двух объектов.	Возникновение центробежной силы связано с инерцией.
Формула
Действие	Центростремительная сила действует как в инерциальной, так и в неинерциальной системе отсчета.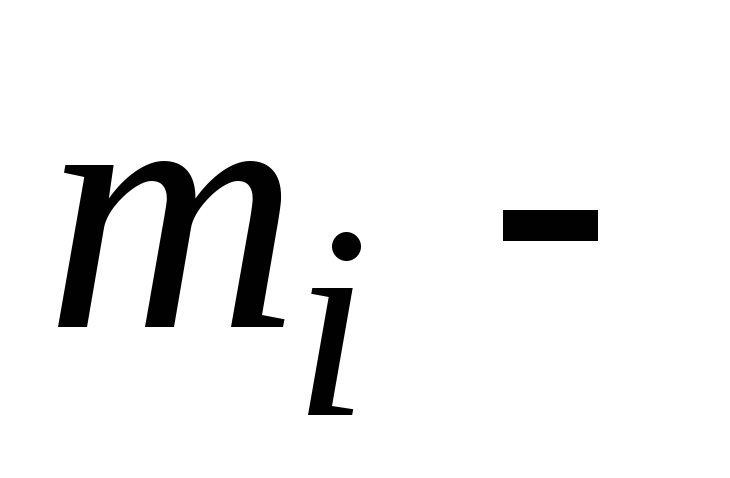	Центробежная сила действует только во вращающейся раме (неинерционные рамы).

Ссылки и источники

• Khatry MK et al. Принципы физики. Публикации Ааям.
• 3% – https://thefactfactor.com/facts/pure_science/physics/centripetal-force/6311/
• 2% — https://en.wikipedia.org/wiki/Centrifugal_force_(rotating_reference_frame)
• 1% – https://www.scienceabc.com/nature/what-is-centripetal-acceleration-what-is-centrifugal-force.html
• 1% – https://www.sarthaks.com/204136/stone-tied-string-length-whirled-vertical-circle-with-the-other-end-the-string-the-centre
• 1% – https://www.reference.com/science/centripetal-force-involved-operation-washing-machine-ee15394203b35628
• 1% – https://www.meritnation.com/ask-answer/question/a-stone-tied-at-the-end-of-string-is-whirled-in-a-circle-if/laws- движения/7284551
• 1% – https://www.ielts-mentor.com/writing-sample/writing-task-2/1313-ielts-writing-task-2-sample-323-the-private-motor-vehicle-has- значительно улучшенная индивидуальная свобода передвижения
• 1% – https://www.