Задачи на КПД теплового двигателя с решениями

У нас уже была внутренняя энергия и первое начало термодинамики, а сегодня разберемся с задачами на КПД теплового двигателя. Что поделать: праздники праздниками, но сессию ведь никто не отменял.

Присоединяйтесь к нам в телеграме и получайте полезную рассылку каждый день. А приступая к практике, не забывайте держать под рукой памятку по задачам и полезные формулы.

Задачи по физике на КПД теплового двигателя

Задача на вычисление КПД теплового двигателя №1

Условие 

Вода массой 175 г подогревается на спиртовке. Пока вода нагрелась от t1=15 до t2=75 градусов Цельсия, масса спиртовки уменьшилась с 163 до 157 г Вычислите КПД установки.

Решение

Коэффициент полезного действия можно вычислить как отношение полезной работы и полного количества теплоты, выделенного спиртовкой:

Полезная работа в данном случае – это эквивалент количества теплоты, которое пошло исключительно на нагрев. Его можно вычислить по известной формуле:

Полное количество теплоты вычисляем, зная массу сгоревшего спирта и его удельную теплоту сгорания.

Подставляем значения и вычисляем:

Ответ: 27%

Задача на вычисление КПД теплового двигателя №2

Условие

Старый двигатель совершил работу 220,8 МДж, при этом израсходовав 16 килограмм бензина. Вычислите КПД двигателя.

Решение

Найдем общее количество теплоты, которое произвел двигатель:

Теперь можно рассчитать КПД:

Или, умножая на 100, получаем значение КПД в процентах:

Ответ: 30%.

Задача на вычисление КПД теплового двигателя №3

Условие

Тепловая машина работает по циклу Карно, при этом 80% теплоты, полученной от нагревателя, передается холодильнику. За один цикл рабочее тело получает от нагревателя 6,3 Дж теплоты. Найдите работу и КПД цикла.

Решение

КПД идеальной тепловой машины:

По условию:

Вычислим сначала работу, а затем КПД:

Ответ: 20%; 1,26 Дж.

Задача на вычисление КПД теплового двигателя №4

Условие

На диаграмме изображен цикл дизельного двигателя, состоящий из адиабат 1–2 и 3–4, изобары 2–3 и изохоры 4–1. Температуры газа в точках 1, 2, 3, 4 равны T1 , T2 , T3 , T4 соответственно. Найдите КПД цикла.

Решение

Проанализируем цикл, а КПД будем вычислять через подведенное и отведенное количество теплоты. На адиабатах тепло не подводится и не отводится. На изобаре 2 – 3 тепло подводится, объем растет и, соответственно, растет температура. На изохоре 4 – 1 тепло отводится, а давление и температура падают.

Аналогично:

Получим результат:

Ответ: См. выше.

Задача на вычисление КПД теплового двигателя №5

Условие

Тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 2,94 кДж и отдаёт за один цикл охладителю количество теплоты Q2 = 13,4 кДж. Найдите КПД цикла.

Решение

Запишем формулу для КПД:

Отсюда:

Ответ: 18%

Вопросы на тему тепловые двигатели

Вопрос 1. Что такое тепловой двигатель?

Ответ. Тепловой двигатель – это машина, которая совершает работу за счет энергии, поступающей к ней в процессе теплопередачи. Основные части теплового двигателя: нагреватель, холодильник и рабочее тело.

Вопрос 2. Приведите примеры тепловых двигателей.

Ответ. Первыми тепловыми двигателями, получившими широкое распространение, были паровые машины. Примерами современного теплового двигателя могут служить:

• ракетный двигатель;
• авиационный двигатель;
• газовая турбина.

Вопрос 3. Может ли КПД двигателя быть равен единице?

Ответ. Нет. КПД всегда меньше единицы (или меньше 100%). Существование двигателя с КПД равным единице противоречит первому началу термодинамики.

КПД реальных двигателей редко превышает 30%.

Вопрос 4. Что такое КПД?

Ответ. КПД (коэффициент полезного действия) – отношение работы, которую совершает двигатель, к количеству теплоты, полученному от нагревателя.

Вопрос 5. Что такое удельная теплота сгорания топлива?

Ответ. Удельная теплота сгорания q – физическая величина, которая показывает, какое количество теплоты выделяется при сгорании топлива массой 1 кг. При решении задач КПД можно определять по мощности двигателя N и сжигаемому за единицу времени количеству топлива.

Задачи и вопросы на цикл Карно

Затрагивая тему тепловых двигателей, невозможно оставить в стороне цикл Карно – пожалуй, самый знаменитый цикл работы тепловой машины в физике. Приведем дополнительно несколько задач и вопросов на цикл Карно с решением.

Цикл (или процесс) Карно – это идеальный круговой цикл, состоящий из двух адиабат и двух изотерм. Назван так в честь французского инженера Сади Карно, который описал данный цикл в своем научном труде «О движущей силе огня и о машинах, способных развивать эту силу» (1894).

Задача на цикл Карно №1

Условие

Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 73,5 кДж. Температура нагревателя t1 =100° С, температура холодильника t2 = 0° С. Найти КПД цикла, количество теплоты, получаемое машиной за один цикл от нагревателя, и количество теплоты, отдаваемое за один цикл холодильнику.

Решение

Рассчитаем КПД цикла: 

С другой стороны, чтобы найти количество теплоты, получаемое машиной, используем соотношение:

Количество теплоты, отданное холодильнику, будет равно разности общего количества теплоты и полезной работы:

Ответ: 0,36; 204,1 кДж; 130,6 кДж.

Задача на цикл Карно №2

Условие

Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А=2,94 кДж и отдает за один цикл холодильнику количество теплоты Q2=13,4 кДж. Найти КПД цикла.

Решение

Формула для КПД цикла Карно:

Здесь A – совершенная работа, а Q1 – количество теплоты, которое понадобилось, чтобы ее совершить. Количество теплоты, которое идеальная машина отдает холодильнику, равно разности двух этих величин. Зная это, найдем:

Ответ: 17%.

Задача на цикл Карно №3

Условие

Изобразите цикл Карно на диаграмме и опишите его

Решение

Цикл Карно на диаграмме PV выглядит следующим образом:

• 1-2. Изотермическое расширение, рабочее тело получает от нагревателя количество теплоты q1;
• 2-3. Адиабатическое расширение, тепло не подводится;
• 3-4. Изотермическое сжатие, в ходе которого тепло передается холодильнику;
• 4-1. Адиабатическое сжатие.

Ответ: см. выше.

Вопрос на цикл Карно №1

Сформулируйте первую теорему Карно

Ответ. Первая теорема Карно гласит: КПД тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника, но не зависит ни от устройства машины, ни от вида или свойств её рабочего тела.

Вопрос на цикл Карно №2

Может ли коэффициент полезного действия в цикле Карно быть равным 100%?

Ответ. Нет. КПД цикла карно будет равен 100% только в случае, если температура холодильника будет равна абсолютному нулю, а это невозможно.

Если у вас остались вопросы по теме тепловых двигателей и цикла Карно, вы можете смело задавать их в комментариях. А если нужна помощь в решении задач или других примеров и заданий, обращайтесь в профессиональный студенческий сервис.

формула, чему равен термический, кратко и понятно

Содержание:

• 
  Что такое КПД 
  • 
    Понятие максимального значения

• 
  Как устроен тепловой двигатель
  • 
    Идеальный тепловой двигатель Карно

• 
  Расчет коэффициента полезного действия
• 
  Построение графика КПД теплового двигателя
• 
  Пример решения задачи

Содержание

• 
  Что такое КПД 
  • 
    Понятие максимального значения

• 
  Как устроен тепловой двигатель
  • 
    Идеальный тепловой двигатель Карно

• 
  Расчет коэффициента полезного действия
• 
  Построение графика КПД теплового двигателя
• 
  Пример решения задачи

Что такое КПД 

Коэффициент полезного действия (КПД) — это характеристика эффективности механизма преобразующего энергию. КПД обычно обозначается символом η, и представляет собой отношение полезной работы к полной работе.

Полная работа — это вся работа совершенная приложенной силой.

Полезная работа — это та работа, которая требуется от данного механизма.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Коэффициент полезного действия теплового двигателя подразумевает отношение полезной работы, совершенной данным двигателем, к количеству теплоты, полученному от нагревателя.

В науку и технику определение КПД двигателя ввёл в 1824 году французский инженер Сади Карно. 

Понятие максимального значения

В силу закона сохранения энергии часть теплоты при передаче неизбежно теряется. Также часть энергии всегда отдается холодильнику. Вывод: невозможно получить полезной работы больше или столько же, сколько затрачено энергии.

Значение КПД любого механизма всегда меньше единицы.

Как устроен тепловой двигатель

Любой тепловой двигатель состоит из трех основных частей:

• рабочего тела;
• нагревателя;
• холодильника.

В основе работы двигателя лежит циклический процесс.

Нагреватель с помощью, например, сгорания топливной смеси выделяет большое количество теплоты и передает ее рабочему телу.

Рабочее тело, например пар, газ или жидкость, при нагревании расширяется и совершает работу, к примеру, вращает турбину или перемещает поршень.

Холодильник нужен, чтобы вернуть рабочее тело в начальное состояние. Он поглощает часть энергии рабочего тела. Таким образом обеспечивается цикличность, и тепловой двигатель работает непрерывно.

Идеальный тепловой двигатель Карно

Модель двигателя Карно разработал французский физик С. Карно. 

Рабочая часть двигателя Карно — поршень в заполненном газом цилиндре. Двигатель Карно — идеальная машина, она возможна только в теории. Поэтому в ней силы трения между поршнем и цилиндром и тепловые потери считаются равными нулю.

Механическая работа максимальна, если рабочее тело выполняет цикл, состоящий из двух изотерм и двух адиабат. При изотермическом расширении работа газа совершается за счет внутренней энергии нагревателя. При адиабатном процессе — за счет внутренней энергии расширяющегося газа. В этом цикле нет контакта тел с разной температурой, поэтому исключена теплопередача без совершения работы. Такой цикл называют циклом Карно.

Адиабатический процесс — это термодинамический процесс, происходящий без теплообмена с окружающей средой (Q=0).

Изотермический процесс — это термодинамический процесс, происходящий при постоянной температуре. Так как у идеального газа внутренняя энергия зависит только от температуры, то переданное газу количество тепла Q идет полностью на совершение работы A (Q=A).

Функционирует двигатель Карно следующим образом:

1. Цилиндр вступает в контакт с горячим резервуаром, и газ расширяется при постоянной температуре. На этой фазе газ получает от горячего резервуара тепло.
2. Цилиндр окружается теплоизоляцией, за счет чего количество тепла, имеющееся у газа, сохраняется. Газ продолжает расширяться, пока его температура не упадет до температуры холодного теплового резервуара.
3. На третьей фазе теплоизоляция снимается. Газ в цилиндре, будучи в контакте с холодным резервуаром, сжимается, отдавая при этом часть тепла холодному резервуару.
4. Когда сжатие достигает определенной точки, цилиндр снова окружается теплоизоляцией. Газ сжимается за счет поднятия поршня до тех пор, пока его температура не сравняется с температурой горячего резервуара. После этого теплоизоляция удаляется, и цикл повторяется вновь с первой фазы.

Примечание

Чем больше разница между температурами нагревателя и холодильника, тем больше КПД двигателя Карно.

Расчет коэффициента полезного действия

Формула для расчета КПД теплового двигателя:

\(ɳ=\frac{Q_1-Q_2}{Q_1}\)

Где Q₁ — количество энергии, которую дает нагреватель; A — работу совершаемую рабочим телом; Q₂ — количество энергии, которая отдается холодильнику.

Для расчета КПД теплового двигателя, работающего по циклу Карно, формула приобретает следующий вид:

\(Elzrtln_k=\frac{T_1-T_2}{T_1}\)

Где T₁ — температура нагревателя; T₂ — температура холодильника.

Примечание

Формула Карно позволяет вычислить предельный (максимально возможный) КПД теплового двигателя.

Построение графика КПД теплового двигателя

Работа, которую производит рабочее тело, в циклическом процессе численно равна площади цикла на графике зависимости давления от объема. Если цикл проходит по часовой стрелке, работа численно равна со знаком «+», если против часовой, то со знаком «-».

Для построения такого графика необходимо:

1. Отложить объем рабочего тела (V) по оси абсцисс.
2. Отложить давление рабочего тела (p) по оси ординат.
3. Расположить на графике точки изотермы и адиабаты.

Для цикла Карно график будет выглядеть следующим образом:

Пример решения задачи

Задача № 1

Рассчитать КПД идеального теплового двигателя с температурой нагревания 1000º K и температурой холодильника равной 500° K.

Решение:

Применим формулу измерения КПД для идеального теплового двигателя: 

\(Elzrtln_k=\frac{T_1-T_2}{T_1}\)

T₁ = 1000

T₂ = 500

\(Elzrtln_k=\frac{1000-500}{1000}\)

\(Elzrtln_k=0,5\)

Ответ: КПД = 0,5

Насколько полезной была для вас статья?

Рейтинг: 5.00 (Голосов: 2)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

6.2: Двигатели и тепловая эффективность

1. Последнее обновление

2. Сохранить как PDF

• Том Вайдеман
• Калифорнийский университет, Дэвис

Простой двигатель

Циклические процессы позволяют иметь повторяющиеся способы преобразования тепловой энергии, поступающей в газ, в рабочую энергию, выходящую из газа.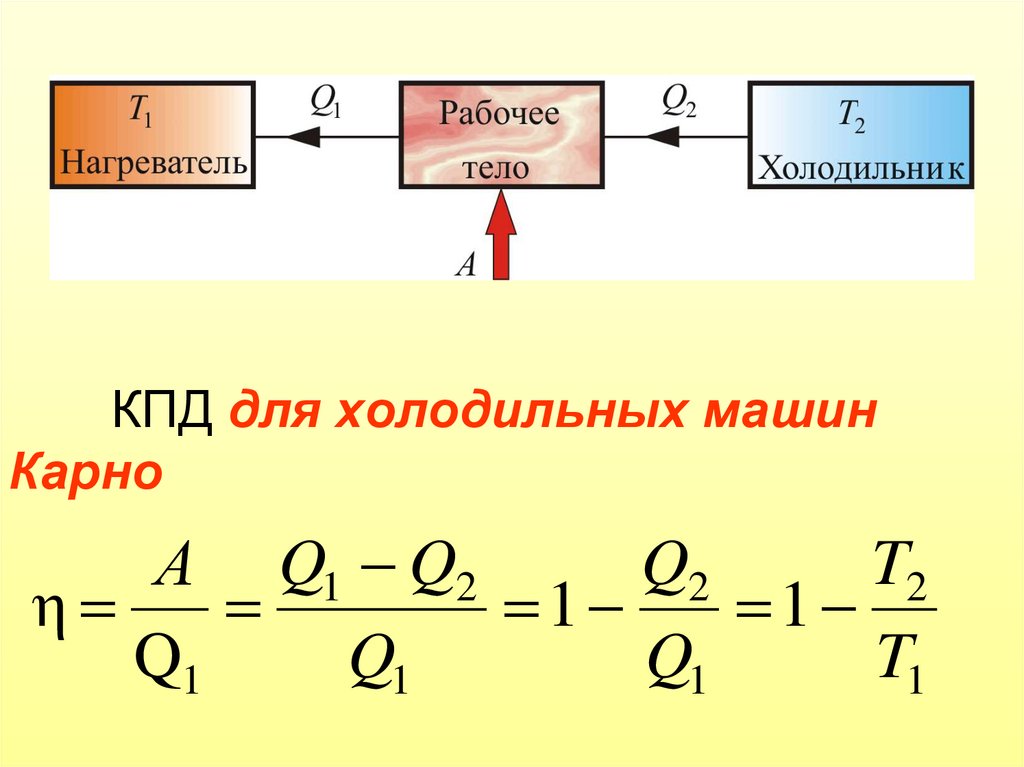 Мы знаем, что для теплообмена должна существовать разница температур, и правильно спроектированное устройство может работать в цикле, чтобы использовать разницу температур для получения полезной механической энергии. Такое устройство называется тепловой машиной . Конечно, для этого требуется циклический процесс, который проходит по часовой стрелке на диаграмме \(PV\). Теперь мы рассмотрим простейший вариант двигателя, который образует прямоугольник на своей диаграмме \(PV\). Мы будем делать акцент на том, чтобы визуализировать каждый этап цикла как физический процесс, в котором поршень обменивается теплом с тепловым резервуаром и/или взаимодействует с окружающей средой.

Рисунок 6.2.1 – Простой двигатель энергия не меняется в течение цикла, а это означает, что выходящая энергия работы (равная площади, ограниченной контуром) равна входящей тепловой энергии.

\[\Delta U = 0\; \;\;\Правая стрелка\;\;\; Q_{in} = W_{out} = \left(P_2-P_1\right)\left(V_2-V_1\right) \]

Теперь мы вычислим тепло, переданное во время всех четырех отдельных этапов циклического процесса, чтобы подтвердить этот результат.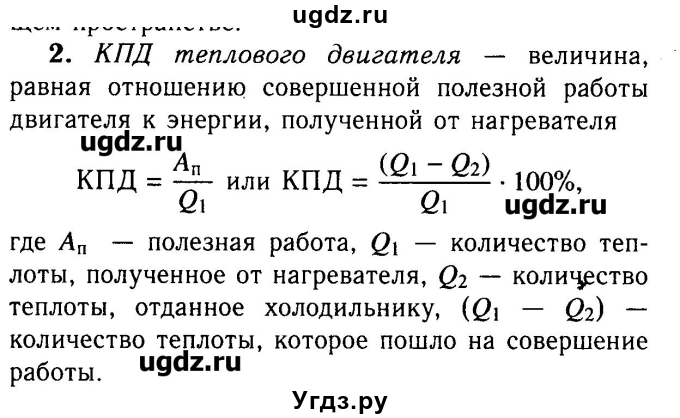 При этом мы будем включать диаграмму того, что происходит физически.

Рисунок 6.2.2a – Процесс A–B

это чуть теплее, чем газ в двигателе на каждом этапе процесса). Температура газа в процессе повышается, а объем увеличивается, при этом в систему поступает тепло. Количество переданного тепла:

\[Q_{AB} = nC_P\Delta T_{AB} = nC_P\left(\dfrac{P_2\Delta V_{AB}}{nR}\right)=\left(\dfrac{C_P}{R} P_2 \ right) \ left (v_2-v_1 \ right) \]

Рис. 6.2.2b-Процесс B-C

33

3333

333333 годы. и поскольку давление падает, это должно быть потому, что падает температура. Это может происходить только при неизменном объеме, когда тепло уходит из системы, а так как процесс квазистатический, то температура теплового резервуара на протяжении всего процесса несколько ниже температуры газа. Потеря тепла на этом этапе составляет:

\[Q_{BC} = nC_V\Delta T_{BC} = nC_V\left(\dfrac{\Delta P_{BC}V_2}{nR}\right)=\left(\dfrac{C_V}{R} V_2 \ справа) \ слева (P_1-P_2 \ Right) \]

Рис. 6.2.2C-Процесс C-D

Это Третий Лей. , на этот раз с падением температуры и объема. Опять же, этот квазистатический процесс требует, чтобы температура резервуара оставалась немного ниже температуры газа. Потери тепла:

\[Q_{CD} = nC_P\Delta T_{CD} = nC_P\left(\dfrac{P_2\Delta V_{CD}}{nR}\right)=\left(\dfrac{C_P}{R} P_1\right)\left(V_1-V_2\right) \]

температура за счет тепла, подведенного из термального резервуара, немного выше температуры газа. Передаваемое тепло:

\[Q_{DA} = nC_V\Delta T_{DA} = nC_V\left(\dfrac{\Delta P_{DA}V_1}{nR}\right)=\left(\dfrac{ C_V}{R}V_1\справа)\слева(P_2-P_1\справа) \]

Читателю предлагается в качестве упражнения по алгебре продемонстрировать, что сумма этих четырех теплопередач равна общей теплопередаче, как указано в уравнении 6. 2.1. При выполнении этого упражнения будет полезно помнить, что \(C_P = C_V + R\).

Двигатели реального мира

В ходе приведенных выше расчетов читателю могло прийти в голову, что постоянно возникало одно неудобное требование — тепловой резервуар всегда должен иметь бесконечно малую величину, отличную от температуры газа в двигателе. Как именно человек совершает такой подвиг? Резервуар становится немного теплее, увеличивая температуру газа до тех пор, пока они не придут к тепловому равновесию, затем резервуар снова становится немного теплее, так что он снова может отдавать небольшое количество тепла газу, и так далее? Этот процесс, очевидно, не может быть разумно сконструирован, и даже если бы это было возможно, тот факт, что скорость теплового потока связана с разницей температур, означает, что он будет мучительно медленным.

В реальном мире у нас обычно есть два термальных резервуара с фиксированными температурами для работы: один с высокой температурой, от которого двигатель получает тепло, и один с низкой температурой, куда двигатель отводит тепло. Обратите внимание, что в приведенном выше простом двигателе газ должен был как получать, так и отдавать тепло, хотя он получил чистое количество тепла, которое он преобразовал в работу. Это оказывается необходимой характеристикой всех двигателей (по причинам, которые мы рассмотрим позже) — двигатель не может просто брать тепло из одного горячего теплового резервуара и преобразовывать его в работу в цикле, не отдавая при этом тепло в другой. , более холодный термальный резервуар. Схема этого общего принципа двигателей показана ниже.

Рис. 6.2.3 – Реальная схема теплового двигателя Во-первых, процесс должен быть циклическим, что означает, что общее изменение внутренней энергии равно нулю, а общее поступающее тепло (тепло, поступающее из более теплого резервуара за вычетом тепла, отводимого в более холодный резервуар) равняется полной работе, которую необходимо совершить. выходит (технически есть еще работа, которая приходит, но эта схема включает только net работают, при этом отделяя «входящее» тепло от «исходящего» по причинам, которые вскоре станут ясны). Мы включили теплоты, обмениваемые с двумя резервуарами, в терминах их абсолютных значений, так что нам не нужно заботиться о условном обозначении подвода/отвода тепла. Ясно, что произведенная работа представляет собой разность общей тепловой энергии, поступающей из горячего резервуара, за вычетом общей тепловой энергии, отводимой в холодный тепловой резервуар.

Тепловая эффективность

Это правда, что в реальном мире когда мы берем тепло из одного резервуара и отдаем его в другой, более холодный, мы делаем два резервуара немного ближе по температуре. В идеале мы хотели бы избежать «траты впустую» любой из этой исходящей тепловой энергии, которая не делает ничего, кроме повышения температуры более холодного резервуара, а вместо этого просто преобразовать всю тепловую энергию, поступающую из горячего резервуара, непосредственно в работу. Достижение этой цели означало бы создание «совершенно эффективного двигателя», и мы бы сказали, что он имеет тепловой КПД 100%. Таким образом, определение процентной эффективности любого двигателя довольно очевидно — просто возьмите отношение извлекаемой работы к подведенному теплу:

\[ e = \dfrac{W_{net}}{Q_H} = \dfrac{\left|Q_H \right|-\left|Q_C\right|}{\left|Q_H\right|} = 1 — \dfrac{\left|Q_C\right|}{\left|Q_H\right|}\]

Должно следует отметить, что «извлеченная работа» — это чистая работа — работа, которая выходит в течение полного цикла, за вычетом вложенной работы (т. е. это площадь внутри замкнутого контура на PV-диаграмме по часовой стрелке). Заметьте также, что для этого двигателя температура не просто немного выше температуры газа в двигателе, и на самом деле сила, вызванная давлением газа, ненамного больше, чем внешняя сила, когда совершается работа. Таким образом, ни один из этих процессов не является квазистатическим. Но, как мы видели, это не помешает нам эффективно использовать модели квазистатических процессов.

Позже мы увидим, что двигатели максимально эффективны, когда процессы, за которыми они следуют, являются обратимыми, но, конечно, для некоторых процессов это требует, чтобы вовлеченный тепловой резервуар изменял свою температуру, чтобы оставаться бесконечно мало больше или меньше, чем температура двигателя. Это противоречит самому понятию «теплового резервуара», поэтому ясно, что реальный КПД двигателя будет хуже, чем у реверсивных двигателей, которые мы можем использовать для их моделирования. Тем не менее, мы можем использовать отношение общей работы к общему теплу для обратимой модели, чтобы вычислить максимальная возможная эффективность для смоделированного двигателя.

Пример \(\PageIndex{1}\)

В циклическом процессе для двигателя, показанного ниже, процесс от A до B увеличивает давление втрое, процесс от B до C является адиабатическим, а рабочий газ в двигатель одноатомный. Вычислите максимальный тепловой КПД этого двигателя.

Раствор

Обозначим объем газа на изохорном участке (\(A\стрелка вправо B\)) \(V_o\). Мы можем использовать адиабатический процесс, чтобы связать объем, занимаемый газом в точке С, с \(V_o\): 9{\ frac {3} {5}}V_o \right)\right] = -0,933P_oV_o \end{массив}\right\}\;\;\;\Rightarrow\;\;\; W_{net}=W_1+W_2 = 0,667P_oV_o\номер\]

Тепло уходит из системы во время изобарического процесса, а во время адиабатического процесса тепло не обменивается, поэтому все тепло, поступающее в двигатель, поступает во время изохорного процесса, и это легко вычислить для одноатомного идеального газа:

\[Q_{in} = \frac{3}{2}\Delta P V = 3P_oV_o \nonnumber\]

Эффективность определяется отношением полезной работы к теплу:

\[e = \dfrac{W_{net}}{Q_{in}} = \dfrac{0,667P_oV_o}{3P_oV_o} = 22,2\% \nonumber\]

 

Цикл Отто

Наш самый узнаваемый тип двигателя — это двигатель внутреннего сгорания, и наиболее распространенный циклический процесс, которому они следуют, называется Цикл Отто .

Предупреждение

В дальнейшем, когда слово «газ» относится к газу внутри поршня, который в основном представляет собой воздух. Говоря о бензине (наиболее распространенном топливе для сжигания топлива), мы будем называть его в этой длинной форме — мы не будем использовать сокращенную версию «газ».0169

Мы начнем с того, что построим диаграмму \(PV\), которая аппроксимирует процесс, а затем объясним каждую часть цикла.

Рис. 6.2.4-Цикл OTTO

Процесс A-B (Adiabatic Compression)

Процесс A-B (Adiabatic Compression)

Процесс A-B (Adiabatic Compression)

Процесс A-B (Adiabatic) с Aniabress) с Aniabress) с Aniabress). Среда ENTARERSALE). СМЕРИБА ИЛИ САМАЛИВА И ОРИКАЛЬНОЕ СОЦИАЛА). при прохладной (окружающей) температуре, когда над смесью совершается работа по ее сжатию. Это происходит очень быстро, так что газ не успевает обмениваться теплом с окружающей средой, что и побуждает рассматривать этот процесс как адиабатический.

процесс B-C (изохорный нагрев)

Бензин воспламеняется, что быстро изменяет температуру газа внутри поршня. Технически тепло поступает не снаружи двигателя, а скорее в результате экзотермического химического процесса, но это одно и то же. Это воспламенение происходит очень внезапно, прежде чем газ успеет расширить поршень, поэтому мы рассматриваем этот процесс как изохорный.

процесс C-D (адиабатическое расширение)

Нагретый газ теперь находится под очень высоким давлением, и это давление расширяет поршень, совершая работу. Опять же, скорость этого процесса настолько велика, что очень мало тепла успевает выйти из поршня, когда он происходит, поэтому мы рассматриваем этот процесс как адиабатический.

процесс D-A (изохорное охлаждение)

После полного расширения охлажденный, но еще более горячий, чем окружающая среда газ выбрасывается из двигателя, и в камеру поступает новая порция воздуха и паров бензина. Технически газ не «охлаждается изохорически», но это равносильно тому, что камера вскоре заполняется новым газом с более низкой температурой и тем же объемом.

Этот пример показывает, как мы можем использовать то, что мы узнали о термодинамических процессах, для анализа реальных ситуаций, даже если наше понимание основано на идеальных ситуациях, которых не существует в реальном мире. Мы просто смотрим на особенности реального процесса и максимально приближаем его к квазистатическому процессу. Во время этого процесса «сопоставления» мы заботимся о том, чтобы конечные точки совпадали правильно (поскольку это состояния равновесия) и чтобы тепло/работа, передаваемые во время процесса, имели смысл. В приведенном выше примере это состояло в том, чтобы спросить, произошел ли процесс быстро (нет времени для отвода тепла) или не изменился ли объем (нет выполненной работы). Вскоре мы снова увидим другую форму этого сопоставления.

Давайте посмотрим на эффективность этого цикла. Имейте в виду, что наша идеализированная версия будет более эффективной, чем то, что мы можем достичь в реальном мире, но это дает нам верхний предел того, на что мы можем надеяться.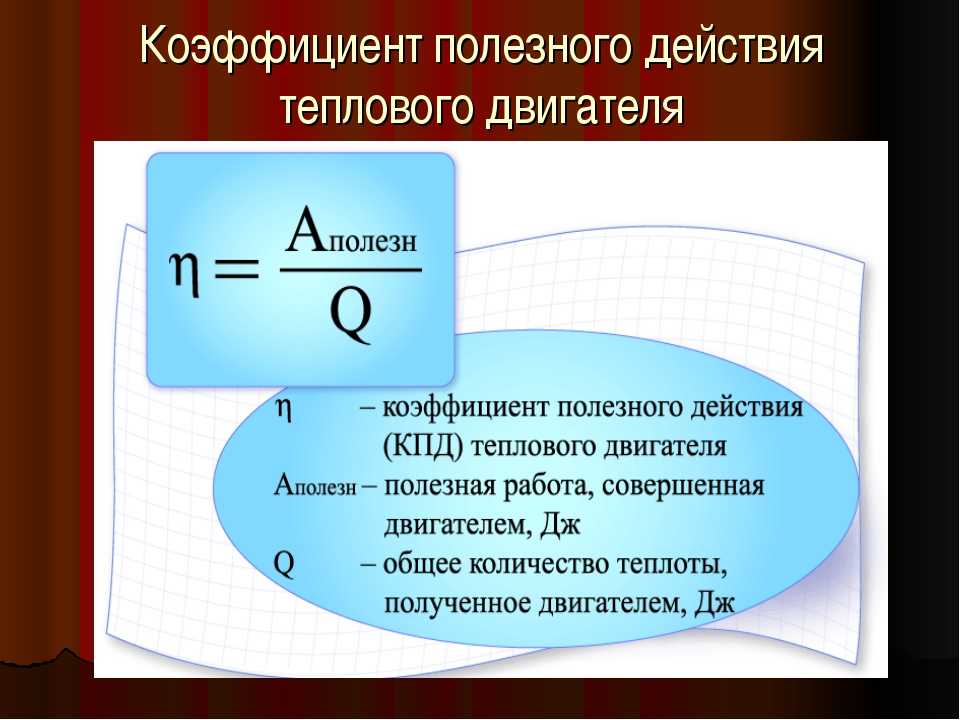 Чтобы получить КПД, нам нужно тепло, отдаваемое горячим резервуаром, и тепло, забираемое холодным резервуаром. В этом цикле теплообмен происходит только во время процессов B-C и DA, которые оба являются изохорными, поэтому теплообмен пропорционален изменениям температуры. Таким образом, эффективность определяется выражением:

\[e = 1 — \dfrac{\left|Q_C\right|}{\left|Q_H\right|} = 1 — \dfrac{nC_V\left(T_D — T_A\right)}{nC_V\left( T_C — T_B\right)} = 1 — \dfrac{\left(T_D — T_A\right)}{\left(T_C — T_B\right)} \]

Из этого результата должно быть ясно, что двигатель работает больше эффективно, когда разница температур между двумя тепловыми резервуарами больше. В данном случае это разница между температурой впрыскиваемого газа и воспламененного газа. Из диаграммы должно быть ясно, что эта разница может быть измерена как разность (или, правильнее сказать, отношение) двух объемов, занимаемых газом. С практической точки зрения, газ нельзя сжать до минимального объема, прежде чем воспламенить его, потому что повышение температуры из-за сжатия само по себе может самопроизвольно воспламенить газ. Топливо с более высоким октановым числом обеспечивает большую степень сжатия без нежелательного самовоспламенения, что повышает эффективность.

Как мы можем сделать вывод из вышеизложенного, КПД этого двигателя можно переписать в терминах переменной, которую нам легче измерить, чем температуры, а именно свойства самого двигателя. Два из четырех процессов являются изохорными, что означает, что объем изменяется только дважды в течение всего цикла, что означает, что нам нужно беспокоиться только о двух объемах — максимальном и минимальном. Максимум возникает при полном расширении поршня, а минимум при его полном сжатии. Нас даже не волнует, каковы эти значения, когда дело доходит до эффективности, а все, что нас волнует, это 9{1-\gamma}\]

Цикл Дизеля

Небольшим изменением цикла Отто можно несколько повысить КПД. Это изменение заключается в управлении процессом воспламенения таким образом, чтобы он происходил при постоянном давлении, а не при постоянном объеме. В этой конструкции двигателя используется так называемый дизельный цикл . Это, конечно, означает, что воспламенение должно происходить менее «взрывно», что снижает скорость, с которой может произойти цикл, и мы знаем из Физики 9А, что скорость, с которой производится работа, является мощностью цикла, поэтому, хотя это цикл получается более эффективным, он обеспечивает меньшую мощность.

Чтобы определить разницу в эффективности, нужно только изменить знаменатель уравнения 6.2.7, учитывающего процесс воспламенения (с B на C). Вместо того, чтобы происходить при постоянном объеме, это происходит при постоянном давлении, что просто изменяет \(C_V\) на \(C_P\), что дает:

\[e = 1-\dfrac{C_V\left(T_D-T_A\ right)}{C_P\left(T_C-T_B\right)}=1-\dfrac{1}{\gamma}\;\dfrac{T_D-T_A}{T_C-T_B}\]

Член, который вычитается из эффективность снижается на гамма-фактор, что приводит к более высокой эффективности. Кроме того, возможны более высокие степени сжатия, поскольку воздух сжимается без топлива (топливо добавляется постепенно, используя топливных форсунок в процессе воспламенения, поддерживая постоянное давление), устраняя проблему воспламенения топлива при сжатии. Конечно, хотя много лет назад этот процесс применялся исключительно для дизельных двигателей, в настоящее время впрыск топлива и сопровождающая его более высокая степень сжатия являются стандартом для автомобилей, работающих на бензине.

Цикл Карно

Мы смогли грамотно описать циклы Отто и Дизеля в терминах 4 квазистатических процессов, рассматривая воспламенение газа так, как если бы тепло добавлялось, а не возникало в результате химической реакции, и рассматривая замещение газа, как будто выделяется тепло. Без этих приемов сохранение квазистатических процессов сделало бы их очень медленными и не могло бы происходить между резервуарами с двумя фиксированными температурами, как показано на рис. чтобы и изохорический, и изобарический процессы происходили квазистатически, температура резервуара должна изменяться таким образом, чтобы она лишь бесконечно мало отличалась от температуры газа. Мы не можем получить что-то даром, и на самом деле процессы воспламенения и замещения газа необратимы, что делает эти процессы лишь приблизительно квазистатическими циклами, которые мы объявили.

Из этого анализа мы видим, что проблема с включением изохорных и изобарических процессов в «реальный» случай двигателя, вынужденного работать между двумя резервуарами с фиксированными температурами, заключается в том, что мы не можем сделать эти процессы обратимыми. Но даже при этом фиксированном температурном ограничении резервуаров есть два процесса, которые мы можем (в принципе) выполнять квазистатически. Адиабатический процесс вообще не включает теплопередачу, поэтому относительная температура двигателя и резервуара не имеет значения. Изотермический процесс оставляет температуру двигателя неизменной, поэтому, если она равна температуре резервуара, проблем не возникает.

В обсуждении, последовавшем за уравнением 5.8.20, мы отметили, что в любой данной точке на PV-диаграмме газа адиабата, проходящая через эту точку, круче, чем изотерма, которая также проходит через нее. Из-за этого мы можем создать циклический процесс, в котором используются два изотермических процесса (один вверху, один внизу диаграммы PV) и два адиабатических процесса (по одному на каждой стороне диаграммы PV), и этот цикл может быть приводимый в движение двумя резервуарами с фиксированной температурой. Это известно как Цикл Карно .

Рисунок 6.2.5 – Цикл Карно Отметив, что теплота не передается во время двух адиабатических процессов, и используя уравнение 5.8.16 для теплоты, переданной во время двух изотермических процессов, мы имеем:

\[ \left. \begin{массив}{l} \left|Q_H\right| = W_{out} = nRT_H\ln\left[\dfrac{V_B}{V_A}\right] \\ \left|Q_C\right| = -W_{in} = -nRT_C\ln\left[\dfrac{V_D}{V_C}\right]=nRT_C\ln\left[\dfrac{V_C}{V_D}\right] \\ e = 1 — \ dfrac{\left|Q_C\right|}{\left|Q_H\right|} \end{массив} \right\} \;\;\;\Rightarrow\;\;\; e = 1-\dfrac{T_C}{T_H}\dfrac{\ln\left[\dfrac{V_C}{V_D}\right]}{\ln\left[\dfrac{V_B}{V_A}\right]} \] 9{\gamma-1} \end{массив} \right\} \;\;\;\Rightarrow\;\;\; \dfrac{V_B}{V_A} = \dfrac{V_C}{V_D}\]

Подстановка их выше приводит к сокращению логарифмов в числителе и знаменателе, что делает эффективность цикла Карно простой функцией температур два резервуара:

\[e=1-\dfrac{T_C}{T_H} \]

Чем больше разница температур между двумя резервуарами, тем выше КПД двигателя Карно.

Холодильники

Одна вещь, которую мы постоянно видели в нашем обсуждении двигателей, это то, что циклы идут по часовой стрелке на диаграмме PV . Это гарантирует, что после полного цикла из системы выйдет работы из , а из тепла выйдет из . Что произойдет, если мы запустим цикл в обратном порядке? Затем идет работа и уходит тепло. Это основа холодильника . Естественно, это не значит, что мы можем взять двигатель внутреннего сгорания, включить его «задним ходом», и он превратится в кондиционер. Во-первых, мы не можем «не воспламенить» газ. Но мы можем осуществлять процессы в обратном направлении другими средствами. Во-первых, давайте посмотрим на схему холодильника, как мы сделали это для тепловой машины:

Рисунок 6.2.6 – Реальная схема холодильника состоит в том, чтобы отвести как можно больше тепла от холодного резервуара, совершая при этом как можно меньше работы. Поэтому мы определяем коэффициент полезного действия как отношение отводимой теплоты к требуемой работе:

\[K=\dfrac{\left|Q_C\right|}{W}=\dfrac{\left|Q_C\right|}{\left|Q_H\right|-\left|Q_C\right|}\ ]

Чрезвычайно упрощенный способ представить себе, как работает холодильник, таков: мы знаем, что если мы очень резко сожмем газ, он станет намного горячее (см. пример в самом конце раздела 5.8). Неудивительно, что верно и обратное: резкое расширение поршня газом приводит к сильному охлаждению газа. Предположим, мы хотим, чтобы внутри холодильника было холоднее, чем снаружи (да, это определение холодильника!). Начните с газа в поршне вне холодильника, сожмите его до небольшого объема и подождите сжатым, пока он не достигнет температуры наружного воздуха. Затем резко отпустите поршень и быстро отнесите его в холодильник. Если мы сожмем его достаточно, изменение температуры газа в поршне сделает его температуру ниже температуры внутри холодильника. Подождем немного, пока внутренняя часть холодильника отдает тепло холодному воздуху в поршне, тем самым охлаждая воздух внутри холодильника. Когда они достигают равновесия, мы выносим поршень наружу и повторяем процесс. Это транспортирует тепловую энергию из холодильника.

Работа, совершаемая газом при сжатии, превышает работу, совершаемую газом при расширении (т.е. необходимо приложить чистую работу). Процессы сжатия и расширения являются адиабатическими, а процессы «ожидания» — изохорными, поэтому PV-диаграмма выглядит примерно так:

Очевидно, мы пожертвовали реальностью ради этого понятного «холодильника». Очевидно, что нам не нужно транспортировать поршень в охлаждаемую камеру и из нее, и вместо этого мы можем подавать газ в нее и из нее, сжимая его на выходе и расширяя на входе. Но есть еще довольно большая проблема с этой конструкцией. Для того чтобы тепло передавалось в нужных направлениях в нужные моменты времени, нам нужно, чтобы температура газа после его охлаждения от расширения была ниже температуры окружающей среды в холодильнике. PV температуры внутри и снаружи холодильников более или менее соответствуют температурам состояний B и D соответственно. Это означает, что если мы проведем изотермы через точки B и D , то разрыв между этими изотермами представляет собой максимальный температурный разрыв, который мы можем поддерживать между горячей и холодной областями.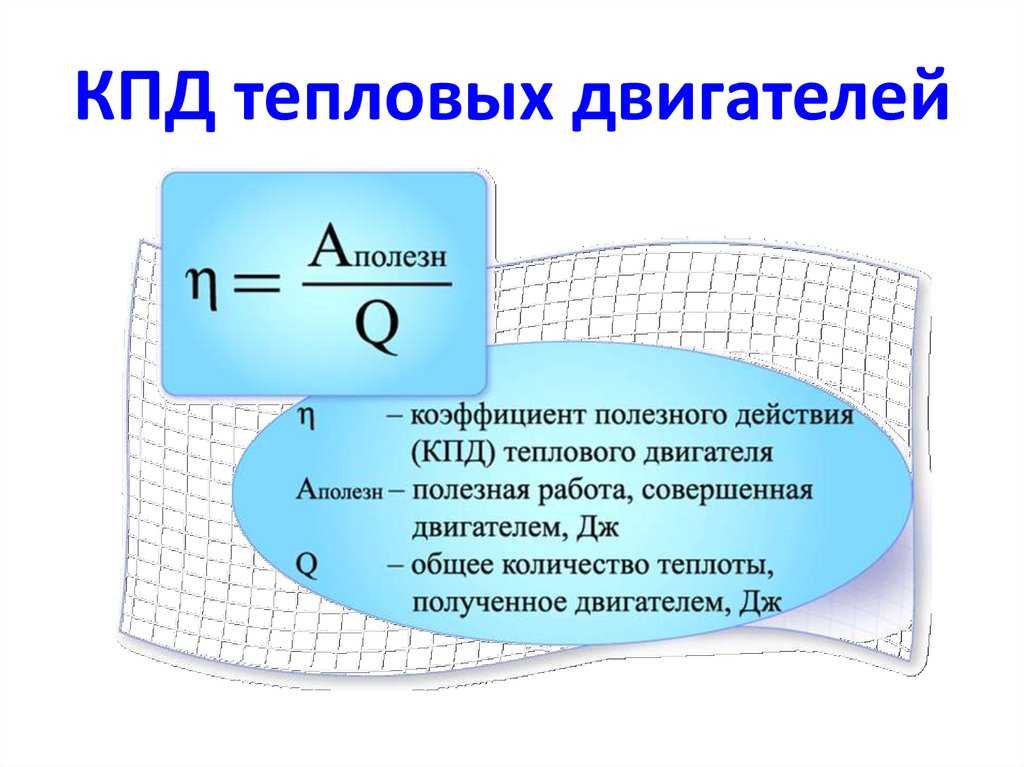 Очевидно, это зависит от разницы давлений, которую мы можем создать между сжатым газом и расширенным газом, но с практической точки зрения это является существенным препятствием.

Способ преодоления этого ограничения состоит в переносе большей части тепловой энергии в фазу хладагента. Мы знаем, что мы можем менять фазы, комбинируя сжатие/расширение и нагрев/охлаждение жидкости, а скрытая теплота парообразования значительна по сравнению с удельной теплоемкостью при небольшом изменении температуры. Это приводит к следующему основному процессу:

• компрессор превращает хладагент в жидкую фазу, которая нагревает его выше температуры наружного воздуха
• затем жидкость поступает в змеевик конденсатора , целью которого является увеличение площади контакта с наружным воздухом, ускорение процесса сброса тепла
• к тому времени, когда жидкость прошла через змеевик конденсатора, она находится под высоким давлением, но пришла в термическое равновесие с наружным воздухом, а затем проходит в расширительный клапан , где она адиабатически расширяется, изменяя фазу назад к газу и значительному падению температуры ниже температуры внутреннего воздуха
• затем газ проходит через змеевик испарителя , что увеличивает скорость, с которой тепло может попасть в хладагент из внутреннего воздуха, и в конце змеевика испарителя он снова поступает в компрессор, чтобы снова запустить цикл.

---

Эта страница под названием 6.2: Двигатели и тепловая эффективность распространяется по лицензии CC BY-SA 4.0 и была создана, изменена и/или курирована Томом Вайдеманом непосредственно на платформе LibreTexts.

1. Наверх
• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Том Вайдеман

   Лицензия

   CC BY-SA

   Версия лицензии

   4,0

   Показать оглавление

   нет

2. Теги

   1. тепловая машина
   2. источник@родной
   3. Тепловой КПД

Измерение тепловой эффективности с использованием принципа Карно

Благодаря работе 19инженером 19-го века по имени Сади Карно, вы можете применить закон сохранения энергии для измерения теплового КПД двигателя.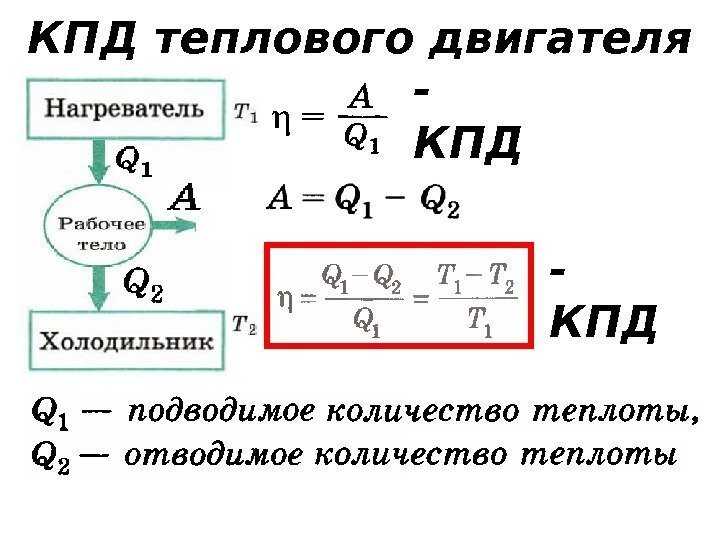

Зная количество работы, которую выполняет тепловая машина, и ее КПД, вы можете рассчитать, сколько теплоты уходит и сколько уходит (наряду с небольшой помощью закона сохранения энергии, который связывает работу, теплоту и теплоту). вышли вместе). Но почему бы не создать тепловые двигатели со 100-процентным КПД? Было бы неплохо преобразовать все тепло, которое уходит в тепловую машину, в работу, но в реальном мире так не бывает. Тепловые двигатели имеют некоторые неизбежные потери, например, из-за трения о поршни в паровой машине.

Изучая эту проблему, Карно пришел к выводу, что лучшее, что вы можете сделать эффективно, — это использовать двигатель, в котором таких потерь нет. Если в двигателе нет потерь, система вернется в состояние, в котором она находилась до начала процесса. Это называется обратимым процессом . Например, если тепловая машина теряет энергию на преодоление трения, в ней нет обратимого процесса, потому что она не приходит в то же состояние, когда процесс завершен. У вас есть наиболее эффективный тепловой двигатель, когда двигатель работает реверсивно.

Принцип Карно гласит, что ни один нереверсивный двигатель не может быть таким же эффективным, как реверсивный, и что все реверсивные двигатели, работающие при одних и тех же температурах, имеют одинаковую эффективность. Вот в чем фишка: идеально обратимого двигателя не существует, поэтому Карно придумал идеальный.

В двигателе Карно , тепло, поступающее от источника тепла, подводится при постоянной температуре T _ч . Тем временем отводимое тепло уходит в радиатор, который имеет постоянную температуру T _c . Поскольку источник тепла и радиатор всегда имеют одинаковую температуру, вы можете сказать, что отношение отданного и отведенного тепла равно отношению этих температур (выраженное в градусах Кельвина):

А поскольку КПД тепловой машины равен

КПД двигателя Карно равен

.

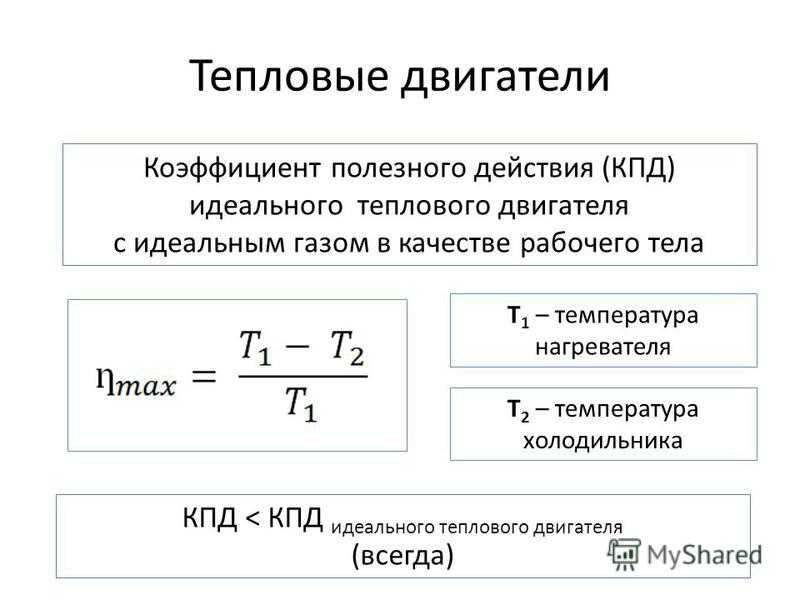
Это уравнение представляет максимально возможный КПД тепловой машины. Вы не можете сделать ничего лучше этого. И, как гласит третий закон термодинамики, вы не можете достичь абсолютного нуля; следовательно, T _c никогда не равно 0, поэтому эффективность всегда равна 1 минус некоторое число. У вас никогда не будет теплового двигателя со 100-процентным КПД.

Применение уравнения для максимально возможной эффективности

легко. Например, скажем, вы придумали потрясающее новое изобретение: двигатель Карно, использующий воздушный шар для соединения земли (27 градусов по Цельсию) в качестве источника тепла с воздухом на высоте 33 000 футов (около -25 градусов по Цельсию). использовать в качестве теплоотвода. Какой максимальный КПД вы можете получить для своего теплового двигателя? После преобразования температуры в кельвины подстановка чисел дает

Ваш двигатель Карно может иметь КПД не более 17,3% — не слишком впечатляюще. С другой стороны, предположим, что вы можете использовать поверхность Солнца (около 5800 кельвинов) в качестве источника тепла и межзвездное пространство (около 3,40 кельвина) в качестве поглотителя тепла (из чего состоят научно-фантастические рассказы). У вас была бы совсем другая история:

Вы получаете теоретический КПД вашего двигателя Карно — 99,9 процента.

Вот еще один пример. Вы на Гавайях, берете заслуженный отпуск с другими трудолюбивыми физиками. Лето было жарким, и, отдыхая на пляже, вы читаете статью об энергетическом кризисе, вызванном всеми этими жужжащими кондиционерами. Вы откладываете газету, когда счастливые физики, качающиеся в прибое, зовут вас, говоря, что вы должны зайти окунуться.

«Насколько тепло?» ты спрашиваешь.

«Очень», — говорят они, подпрыгивая. «Около 300 кельвинов».

Хм, вы думаете. Если бы вы могли создать двигатель Карно и использовать поверхность океана в качестве источника тепла (300 кельвинов) и дно океана (около 7 градусов Цельсия или 280 кельвинов) в качестве поглотителя тепла, какова была бы эффективность такого двигателя? двигатель быть? И сколько входного тепла вам потребуется для обеспечения всех энергетических потребностей США в течение одного года

математика, чтобы найти эффективность:

Хм, эффективность 6,7%.