Угловая скорость и угловое ускорение

Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела в теории и на примерах решения задач.

Угловая скорость

Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени.

Обозначение угловой скорости: ω (омега).

Рассмотрим некоторое твердое тело, вращающееся относительно неподвижной оси.

С этим телом свяжем воображаемую плоскость П, которая совершает вращение вместе с заданным телом.

Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Изменение этого угла с течением времени есть закон вращательного движения:

Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения Oz. Угол измеряется в радианах.

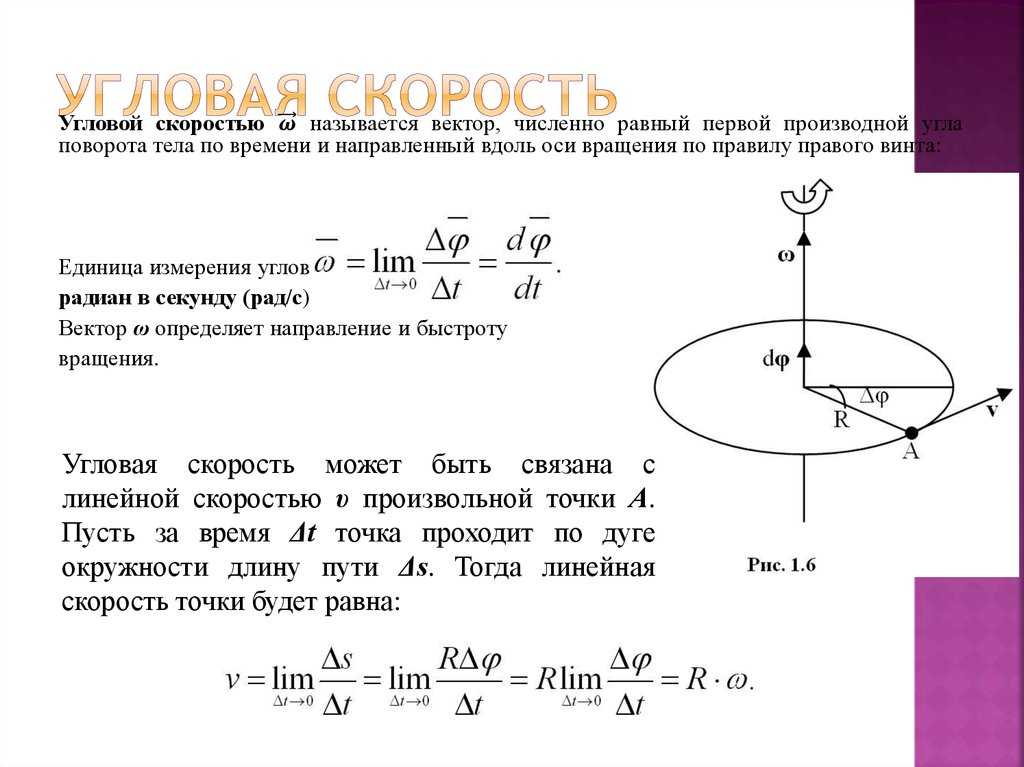
Быстрота изменения угла φ (перемещения плоскости П из положения П₁ в положение П₂) – это и есть угловая скорость:

Приняв вектор k как единичный орт положительного направления оси, получим:

Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.

Формулы угловой скорости

Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:

1. если известно количество оборотов n за единицу времени t:
2. если задан угол поворота φ за единицу времени:
3. если известна окружная скорость точки тела v и расстояние от оси вращения до этой точки r:

Размерности угловой скорости:

• Количество оборотов за единицу времени [об/мин], [c^-1].
• Угол поворота за единицу времени [рад/с].

Определение угловой скорости

Пример: Диск вращается относительно своего центра.
Известна скорость v некоторой точки A, расположенной на расстоянии r от центра вращения диска.

Определить величину и направление угловой скорости диска ω, если v = 5 м/с, r = 70 см.

Таким образом, угловая скорость диска составляет 7,14 оборотов в секунду. Направление угловой скорости можно определить по направлению скоростей её точек.

Вектор скорости точки A стремится повернуть диск относительно центра вращения против хода часовой стрелки, следовательно, направление угловой скорости вращения диска имеет такое же направление.

Другие примеры решения задач >

Угловое ускорение

Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:

Обозначение: ε (Эпсилон)

Единицы измерения углового ускорения: [рад/с²], [с^-2]

Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.

Другими словами, при положительном ускорении угловая скорость нарастает (вращение ускоряется), а при отрицательном — уменьшается (вращение замедляется).

Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:

• равномерное вращение (ω — const)
• равнопеременное вращение (ε — const)

Расчет углового ускорения

Пример: По заданному значению касательной составляющей полного ускорения a_τ точки B, расположенной на расстоянии r от центра вращения колеса.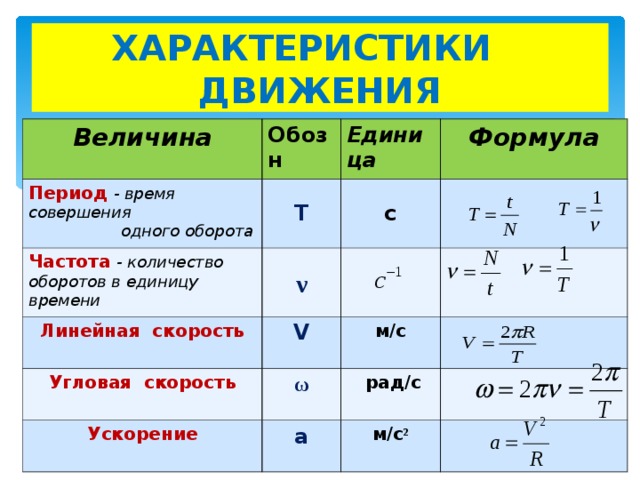

Требуется определить величину и направление углового ускорения колеса ε, если a_τ = 10 м/с², r = 50 см.

Угловое ускорение колеса в заданный момент времени составляет 20 оборотов за секунду в квадрате. Направление углового ускорения определяется по направлению тангенциального ускорения точки.

Здесь, угловое ускорение направлено противоположно направлению угловой скорости вращения колеса. Это означает, что вращение колеса замедляется.

В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:

Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость

ω = 1,5 с^-1 = 9,42 рад/с.

Смотрите также:

• Примеры расчета угловой скорости и ускорения
• Скорости и ускорения точек вращающегося тела

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

ВЫБЕРИТЕ РАЗДЕЛ МЕХАНИКИ

• Техническая механика (техмех)
• Теоретическая механика (теормех)
• Сопротивление материалов (сопромат)
• Строительная механика (строймех)
• Теория механизмов и машин (ТММ)
• Детали машин и ОК (ДМ)
• Инженерная механика (инжмех)

НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ

На нашем сайте можно бесплатно скачать:

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Сохранить или поделиться с друзьями

Помощь с решением

Поиск формул и решений задач

Угловая скорость — frwiki.

wiki

«Скорость вращения» перенаправляется сюда. Для других значений см Скорость (значения) и Вращение .

«Угловая частота» перенаправляется сюда. Для других значений, см. Частота (значения) .

Угловая скорость (или скорость вращения ) представляет собой величину, которая представляет собой отношение от угла поворота в момент . Это является аналогом, для вращательного движения, от скорости для поступательного движения .

• Когда время ограничено, мы говорим о средней угловой скорости .
• Когда время бесконечно мало, мы говорим о мгновенной угловой скорости или просто об угловой скорости . Затем угловая скорость определяется как производная по времени от углового положения вращающегося объекта. Производная по времени от угловой скорости — это угловое ускорение .

Резюме

• 1 шт.
  • 1.1 Эквивалентность единиц
• 2 измерение
• 3 Вектор угловой скорости
• 4 Примечания и ссылки
• 5 См. Также
  • 5.1 Библиография
  • 5.2 Статьи по теме

Единицы измерения

Единица угловой скорости в Международной системе является радиан в секунду (рад / с или рад с ^-1 ). Его не следует выражать в герцах (Гц), до которых нельзя привести радиан в секунду.

В области промышленной механики и повседневной жизни это часто выражается в оборотах в минуту (об / мин).

Вы также можете использовать градусы в секунду и обороты в секунду.

Эквивалентность единиц

Полный оборот, совершенный за период T, равен 2π радиан. Следовательно, пройден радиан . Угловая скорость, которая описывает количество угловых единиц, пройденных за единицу времени, является обратной, поскольку частота f является обратной по отношению к периоду. Другими словами:
Т2π{\ displaystyle {\ frac {T} {2 \ pi}}}ωзнак равно2πТзнак равно2πж{\ displaystyle \ omega = {\ frac {2 \ pi} {T}} = 2 \ pi f}

В международной системе единиц время выражается в секундах, а частота — в герцах . {- 1}}это размерность частоты .

Поскольку углы являются безразмерными величинами, их можно передать просто в с ^-1, но этого следует избегать, если единица измерения угла не является совершенно ясной.

Вектор угловой скорости

Иногда используется вектор угловой скорости . Это вектор:
ω→{\ displaystyle {\ vec {\ omega}}}

• перпендикулярно плоскости вращения;
• ориентированы так, чтобы движение было в положительном направлении, обычно задаваемом правилом правой руки  ;
• норма которого равна ω .

Таким образом, вектор угловой скорости определяет как ось, вокруг которой вращается объект, так и скорость его вращения. Это не совсем вектор, а псевдовектор, поскольку симметричное в зеркале инвертировано.

Использование вектора угловой скорости позволяет применять методы вычисления вектора к объектам, вращающимся относительно друг друга.

Он позволяет составлять угловые скорости путем сложения векторов и вычислять линейные скорости из угловых скоростей.

Циркулярный перевод:

В объекте, вращающемся вокруг опоры, который сам вращается, сложение векторов угловой скорости дает движение объекта.

Если два вектора угловой скорости направлены в одном направлении, но в противоположном направлении, их сложение дает нулевой вектор. Объект описывает круг, не меняя ориентации, в круговом поступательном движении .

Примечания и ссылки

1. ↑ Dubesset 2000, стр.  4 ( онлайн ), стр.  122 ( онлайн ).
2. ↑ Dubesset 2000, стр.  104.
3. ↑ «На практике символы rad и sr используются по мере необходимости», Международное бюро мер и весов, Единицы со специальными названиями и специальными символами .

Смотрите также

Библиография

 : документ, использованный в качестве источника для этой статьи.

• Ричард Тайлле, Лоик Злодей и Паскаль Февр, Физический словарь, Брюссель, Де Бок ,2013, 3 ^е  изд. , Х-899  с. ( ISBN  978-2-8041-7554-2, читать онлайн ) :
  • п.  561 , «Пульсация» ,
  • п.  723 «Угловая скорость» ,
  • [ Дик. Phys. , изд. 2008  (страница консультации по 23 июля 2014)] ( ( ISBN  978-2-8041-5688-6 ) (уведомление BnF п ^о  FRBNF41256105 ), соответственно. P.  405 и стр.  523 .
• Мишель Дюбессе, Руководство Международной системы единиц: лексика и преобразования, Париж, Technip, колл.  «Публикации Французского нефтяного института  »,2000 г., 169  с. ( ISBN  2-7108-0762-9, уведомление BnF п ^о  FRBNF37624276, читать онлайн )

Статьи по Теме

• Момент (механический)
• Вектор угловой скорости
• Аналогия между вращением и перемещением

<img src=»//fr.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>

условных единиц — Единица угловой скорости

спросил
5 лет, 2 месяца назад

Изменено
5 лет, 2 месяца назад

Просмотрено
812 раз

$\begingroup$

На этот вопрос уже есть ответы здесь :

Почему радианы более естественны, чем любые другие угловые единицы?

(7 ответов)

Закрыта 5 лет назад.

Почему угловая скорость $\omega$ всегда указывается в $rad/sec$? Что-то не так, если я напишу в $градусах/сек$? Если нет, то почему почти во всех книгах он указан как $rad/sec$??

• условные обозначения
• шт.
• размерный анализ
• угловая скорость

$\endgroup$

3

$\begingroup$

$w $ — это угловая скорость, а не угловое смещение. Вы можете записать это в град/сек, если хотите. Причина, по которой используются рад/сек, заключается в том, что тождества $\frac{d}{dx}\cos(x) = -\sin(x) $ и $ \frac{d}{dx}\sin(x) = \ cos(x)$ справедливы только тогда, когда x измеряется в радианах. 9{i\pi\omega t/180}$. Эти дополнительные факторы вступят в силу, когда вы будете брать производные или выполнять интегралы, а также решать любые дифференциальные уравнения, поэтому вскоре я буду на коленях умолять вернуть радианы.

Но, если вы не в классе, где инструктор требует, чтобы вы использовали радианы в секунду (и не поймите меня неправильно — если бы вы были в моем классе, я бы сделал это требованием), тогда вы’ Вы вольны сделать свою жизнь настолько неудобной, насколько захотите.

$\endgroup$

4

$\begingroup$

Радиан — стандартная единица измерения угла. Угловая скорость — это просто угол, на который проходит частица или тело в единицу времени. Вы можете задать ему любую разумную единицу, которая, очевидно, должна обозначать угол, пройденный за единицу времени. Поэтому вы можете использовать единицу измерения $град/с$.

Единица измерения $рад/с$ обычно используется, потому что это единица СИ, а соотношение типа $v=\omega r$ выводится для угловой скорости в $рад/с$.

$\endgroup$

$\begingroup$

Вы можете писать угловую скорость как угодно, если это имеет смысл и вы указываете единицы измерения. Вы можете свободно записывать это как градусы в секунду, обороты в час или что-то в этом роде. Причина, по которой ω выражается в рад/сек, заключается в том, что с ним гораздо проще проводить дифференцирование и интегрирование (находить угловое ускорение или угловое смещение). Дифференциация треугольников с единицами измерения, отличными от радианов, не будет работать.

$\endgroup$

Очень активный вопрос . Заработайте 10 репутации (не считая бонуса ассоциации), чтобы ответить на этот вопрос. Требование к репутации помогает защитить этот вопрос от спама и отсутствия ответа.

Угловая частота — TCS Wiki

В физике угловая частота. ω. (также называется угловая скорость , радиальная частота и частота в радианах) — это мера скорости вращения. Высокая скорость угловой частоты означает, что что-то вращается очень быстро. Угловая частота представляет собой величину векторной величины угловой скорости , которая также известна как вектор угловой частоты [math]\displaystyle{ \vec{\omega}}[/math].

Файл:Angularvelocity.svg

Угловая частота — это мера скорости вращения объекта.

Она полезна во многих областях математики и естественных наук, поскольку позволяет понять многие свойства физических объектов в нашем мире. В единицах СИ угловая частота измеряется в радианах в секунду с размерами t 9{-1} }[/math]), так как с ним легче работать. Таким образом, угловая частота определяется выражением

 [математика]\displaystyle{ \omega = \frac{2\pi}{T} = 2 \pi f }[/math]
 

где [math]\displaystyle{ T }[/math] — время (период) одного вращения (оборота), а [math]\displaystyle{ f }[/math] — частота.

Если колесо поворачивается на угол [math]\displaystyle{ \theta }[/math] за время [math]\displaystyle{ t }[/math], то угловая частота в любой момент определяется выражением,

 [математика]\displaystyle{ \omega = \frac{d\theta}{dt} }[/math]
 

Если скорость вращения постоянна, это становится

 [математика]\displaystyle{ \omega = \frac{\theta}{t}}[/math]
 

а так похоже на скорость.

Для объектов, движущихся по кругу, угловая частота также может быть указана как (в радианах),

 [математика]\displaystyle{ \omega = \frac{v}{r} }[/math]
 

где [math]\displaystyle{ v }[/math] — скорость, а [math]\displaystyle{ r }[/math] — расстояние от середины круга.

Примеры

Угловая частота важна для определения того, может ли объект оставаться над землей, преодолевая гравитацию, или может ли волчок оставаться на месте. Это также важно для создания частоты подачи электроэнергии в сеть и снижения нагрева из-за трения в двигателях.

Спутники

Объекты притягиваются к земле под действием гравитации. Чтобы противостоять этому, спутник должен лететь достаточно быстро, чтобы не касаться земли. Чтобы силы были равны друг другу,
93} }[/математика]

, что приводит к одному из законов Иоганна Кеплера.

Электроснабжение

Генераторы на электростанциях вращаются с определенной частотой. Скорость, с которой они вращаются, дает нам частоту, на которой находятся наши источники электроэнергии.