Угловая скорость | это… Что такое Угловая скорость?
Угловая скорость (синяя стрелка) в одну единицу по часовой стрелке
Угловая скорость (синяя стрелка) в полторы единицы по часовой стрелке
Угловая скорость (синяя стрелка) в одну единицу против часовой стрелки
Углова́я ско́рость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:
- ,
а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону.
Единица измерения угловой скорости, принятая в системах СИ и СГС — радианы в секунду. (Примечание: радиан, как и любые единицы измерения угла, — физически безразмерен, поэтому физическая размерность угловой скорости — просто [1/секунда]). В технике также используются обороты в секунду, намного реже — градусы в секунду, грады в секунду. Пожалуй, чаще всего в технике используют обороты в минуту — это идёт с тех времён, когда частоту вращения тихоходных паровых машин определяли просто «вручную», подсчитывая число оборотов за единицу времени.
В технике также используются обороты в секунду, намного реже — градусы в секунду, грады в секунду. Пожалуй, чаще всего в технике используют обороты в минуту — это идёт с тех времён, когда частоту вращения тихоходных паровых машин определяли просто «вручную», подсчитывая число оборотов за единицу времени.
Вектор (мгновенной) скорости любой точки (абсолютно) твердого тела, вращающегося с угловой скоростью , определяется формулой:
где — радиус-вектор к данной точке из начала координат, расположенного на оси вращения тела, а квадратными скобками обозначено векторное произведение. Линейную скорость (совпадающую с модулем вектора скорости) точки на определенном расстоянии (радиусе) от оси вращения можно считать так: Если вместо радианов применять другие единицы углов, то в двух последних формулах появится множитель, не равный единице.
- В случае плоского вращения, то есть когда все векторы скоростей точек тела лежат (всегда) в одной плоскости («плоскости вращения»), угловая скорость тела всегда перпендикулярна этой плоскости, и по сути — если плоскость вращения заведомо известна — может быть заменена скаляром — проекцией на ось, ортогональную плоскости вращения.
 В этом случае кинематика вращения сильно упрощается, однако в общем случае угловая скорость может менять со временем направление в трехмерном пространстве, и такая упрощенная картина не работает.
В этом случае кинематика вращения сильно упрощается, однако в общем случае угловая скорость может менять со временем направление в трехмерном пространстве, и такая упрощенная картина не работает. - Производная угловой скорости по времени есть угловое ускорение.
- Движение с постоянным вектором угловой скорости называется равномерным вращательным движением (в этом случае угловое ускорение равно нулю).
- Угловая скорость (рассматриваемая как свободный вектор) одинакова во всех инерциальных системах отсчета, однако в разных инерциальных системах отсчета может различаться ось или центр вращения одного и того же конкретного тела в один и тот же момент времени (то есть будет различной «точка приложения» угловой скорости).
- В случае движения одной единственной точки в трехмерном пространстве можно написать выражение для угловой скорости этой точки относительно выбранного начала координат:
- , где — радиус-вектор точки (из начала координат), — скорость этой точки.
 — векторное произведение, — скалярное произведение векторов. Однако эта формула не определяет угловую скорость однозначно (в случае единственной точки можно подобрать и другие векторы , подходящие по определению, по другому — произвольно — выбрав направление оси вращения), а для общего случая (когда тело включает более одной материальной точки) — эта формула не верна для угловой скорости всего тела (так как дает разные для каждой точки, а при вращении абсолютно твёрдого тела по определению угловая скорость его вращения — единственный вектор). При всём при этом, в двумерном случае (случае плоского вращения) эта формула вполне достаточна, однозначна и корректна, так как в этом частном случае направление оси вращения заведомо однозначно определено.
— векторное произведение, — скалярное произведение векторов. Однако эта формула не определяет угловую скорость однозначно (в случае единственной точки можно подобрать и другие векторы , подходящие по определению, по другому — произвольно — выбрав направление оси вращения), а для общего случая (когда тело включает более одной материальной точки) — эта формула не верна для угловой скорости всего тела (так как дает разные для каждой точки, а при вращении абсолютно твёрдого тела по определению угловая скорость его вращения — единственный вектор). При всём при этом, в двумерном случае (случае плоского вращения) эта формула вполне достаточна, однозначна и корректна, так как в этом частном случае направление оси вращения заведомо однозначно определено.
- В случае равномерного вращательного движения (то есть движения с постоянным вектором угловой скорости) декартовы координаты точек вращающегося так тела совершают гармонические колебания с угловой (циклической) частотой, равной модулю вектора угловой скорости.

- При измерении угловой скорости в оборотах в секунду (об/с), модуль угловой скорости равномерного вращательного движения совпадает с частотой вращения f, измеренной в герцах (Гц), то есть в таких единицах . В случае использования обычной физической единицы угловой скорости — радианов в секунду — модуль угловой скорости связан с частотой вращения так: . Наконец, при использовании градусов в секунду связь с частотой вращения будет: .
Связь с конечным поворотом в пространстве
- Пусть поворот, изменяющийся во времени, задан величиной угла и ортом оси конечного поворота в пространстве . Тогда угловая скорость, соответствующая этому повороту, равна
- .
- Если поворот задан матрицей поворота , где — символ Кронекера, — символ Леви-Чивиты (суммирование ведется по правилу Эйнштейна от 1 до 3), выражение для элементов которой через и могут быть получены, например, с помощью формулы Родрига, то угловая скорость равна
- .

- Если для описания поворота используется кватернион, выражаемый через угол и орт оси поворота как , то угловая скорость находится из выражения .
- В случае, когда поворот описывается с помощью вектора , изменяющегося во времени, обозначим , а также — матрица половинного поворота , — квадрат модуля вектора . Тогда угловая скорость:
- .
См. также
- Угловая частота
- Угловое ускорение
- Момент импульса
Литература
- Лурье А. И. Аналитическая механика\\ А. И. Лурье. — М.: ГИФМЛ, 1961. — С. 100-136
Формула угловой скорости в физике
Содержание:
- Определение и формула угловой скорости
- Равномерное вращение
- Формула, связывающая линейную и угловую скорости
- Единицы измерения угловой скорости
- Примеры решения задач
Определение и формула угловой скорости
Определение
Круговым движением точки вокруг некоторой оси называют движение, при котором траекторией точки является окружность
с центром, который лежит на оси вращения, при этом плоскость окружности перпендикулярна этой оси.
Вращением тела вокруг оси называют движение, при котором все точки тела совершают круговые движения около этой оси.
Перемещение при вращении характеризуют при помощи угла поворота
$(\varphi)$ . Часто используют вектор элементарного поворота
$\bar{d\varphi}$ , который равен по величине элементарному углу поворота тела
$(d \varphi)$ за маленький отрезок времени dt и направлен по мгновенной оси вращения в сторону,
откуда этот поворот виден реализующимся против часовой стрелки. Надо отметить, что только элементарные угловые перемещения являются векторами.
Углы вращения на конечные величины векторами не являются.
Определение
Угловой скоростью называют скорость изменения угла поворота и обозначают ее обычно буквой
$\omega$ . Математически определение угловой скорости записывают так:
$$\bar{\omega}=\frac{d \bar{\varphi}}{d t}=\dot{\bar{\varphi}}(1)$$
Угловая скорость — векторная величина (это аксиальный вектор). Она имеет направление вдоль мгновенной оси вращения совпадающее
Она имеет направление вдоль мгновенной оси вращения совпадающее
с направлением поступательного правого винта, если его вращать в сторону вращения тела (рис.1).
Вектор угловой скорости может претерпевать изменения как за счет изменения скорости вращения тела вокруг оси (изменение модуля угловой скорости),
так и за счет поворота оси вращения в пространстве ($\bar{\omega}$ при этом изменяет направление).
Равномерное вращение
Если тело за равные промежутки времени поворачивается на один и тот же угол,
то такое вращение называют равномерным. При этом модуль угловой скорости находят как:
$$\omega=\frac{\varphi}{t}(2)$$
где $(\varphi)$ – угол поворота, t – время, за которое этот поворот совершён.
Равномерное вращение часто характеризуют при помощи периода обращения (T), который является временем, за которое тело производит один оборот
($\Delta \varphi=2 \pi$). Угловая скорость связана с периодом обращения как:
$$\omega=\frac{2 \pi}{T}(3)$$
С числом оборотов в единицу времени ($\nu) угловая скорость связана формулой:
$$\omega=2 \pi \nu(4)$$
Понятия периода обращения и числа оборотов в единицу времени иногда используют и для описания неравномерного вращения,
но понимают при этом под мгновенным значением T, время за которое тело делало бы один оборот, если бы оно вращалось равномерно
с данной мгновенной величиной скорости. {3} \approx 20(\mathrm{rad})$$
{3} \approx 20(\mathrm{rad})$$
Ответ. $\varphi = 20$ рад.
Читать дальше: Формула удельного веса.
Угловая скорость | Medical Journals
В физике угловая скорость означает, насколько быстро объект вращается или вращается относительно другой точки, т. е. насколько быстро угловое положение или ориентация объекта изменяется со временем. Есть два типа угловой скорости: орбитальная угловая скорость и спиновая угловая скорость. Угловая скорость вращения относится к тому, насколько быстро твердое тело вращается относительно своего центра вращения. Орбитальная угловая скорость относится к тому, как быстро точечный объект вращается вокруг фиксированного начала координат, то есть к скорости изменения его углового положения относительно начала координат. Угловая скорость вращения не зависит от выбора начала координат, в отличие от орбитальной угловой скорости, которая зависит от выбора начала координат.
Как правило, угловая скорость измеряется в углах в единицу времени, т. е. радиан в секунду (угол заменяет расстояние от линейной скорости общим временем). Единица угловой скорости в системе СИ выражается в радианах в секунду, при этом радиан имеет безразмерное значение, равное единице, поэтому единицы измерения угловой скорости в системе СИ указаны как 1/с или с-1. Угловая скорость обычно обозначается символом омега (ω, иногда Ω). По соглашению, положительная угловая скорость указывает на вращение против часовой стрелки, а отрицательная — по часовой стрелке.
е. радиан в секунду (угол заменяет расстояние от линейной скорости общим временем). Единица угловой скорости в системе СИ выражается в радианах в секунду, при этом радиан имеет безразмерное значение, равное единице, поэтому единицы измерения угловой скорости в системе СИ указаны как 1/с или с-1. Угловая скорость обычно обозначается символом омега (ω, иногда Ω). По соглашению, положительная угловая скорость указывает на вращение против часовой стрелки, а отрицательная — по часовой стрелке.
Например, геостационарный спутник совершает один оборот в день над экватором, или 360 градусов за 24 часа, и имеет угловую скорость ω = (360°)/(24 ч) = 15°/ч, или (2π рад) /(24 ч) ≈ 0,26 рад/ч. Если угол измеряется в радианах, линейная скорость равна радиусу, умноженному на угловую скорость, {\ displaystyle v = r \ omega {\ displaystyle v = r \ omega}. Таким образом, при радиусе орбиты 42 000 км от центра Земли скорость спутника в космосе составляет v = 42 000 км × 0,26 / ч ≈ 11 000 км / ч. Угловая скорость положительна, поскольку спутник движется на восток с вращением Земли (против часовой стрелки от северного полюса). В трех измерениях угловая скорость представляет собой псевдовектор, величина которого измеряет скорость, с которой объект вращается или вращается, и его направление указывает перпендикуляр к мгновенной плоскости вращения или углового смещения. Ориентация угловой скорости условно задается правилом правой руки.
В трех измерениях угловая скорость представляет собой псевдовектор, величина которого измеряет скорость, с которой объект вращается или вращается, и его направление указывает перпендикуляр к мгновенной плоскости вращения или углового смещения. Ориентация угловой скорости условно задается правилом правой руки.
В физике угловая скорость означает, насколько быстро объект вращается или вращается относительно другой точки, т. е. насколько быстро угловое положение или ориентация объекта изменяется со временем. Есть два типа угловой скорости: орбитальная угловая скорость и спиновая угловая скорость. Угловая скорость вращения относится к тому, насколько быстро твердое тело вращается относительно своего центра вращения. Орбитальная угловая скорость относится к тому, как быстро точечный объект вращается вокруг фиксированного начала координат, то есть к скорости изменения его углового положения относительно начала координат. Угловая скорость вращения не зависит от выбора начала координат, в отличие от орбитальной угловой скорости, которая зависит от выбора начала координат.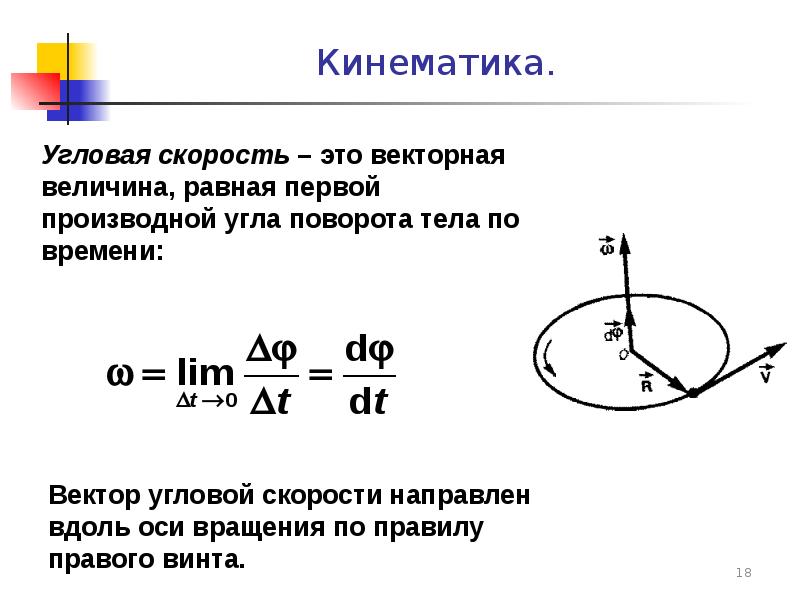
Как правило, угловая скорость измеряется в углах в единицу времени, т.е. радиан в секунду (угол заменяет расстояние от линейной скорости общим временем). Единица угловой скорости в системе СИ выражается в радианах в секунду, при этом радиан имеет безразмерное значение, равное единице, поэтому единицы измерения угловой скорости в системе СИ указаны как 1/с или с-1. Угловая скорость обычно обозначается символом омега (ω, иногда Ω). По соглашению, положительная угловая скорость указывает на вращение против часовой стрелки, а отрицательная — по часовой стрелке.
Например, геостационарный спутник совершает один оборот в день над экватором, или 360 градусов за 24 часа, и имеет угловую скорость ω = (360°)/(24 ч) = 15°/ч, или (2π рад) /(24 ч) ≈ 0,26 рад/ч. Если угол измеряется в радианах, линейная скорость равна радиусу, умноженному на угловую скорость, {\ displaystyle v = r \ omega {\ displaystyle v = r \ omega}. Таким образом, при радиусе орбиты 42 000 км от центра Земли скорость спутника в космосе составляет v = 42 000 км × 0,26 / ч ≈ 11 000 км / ч. Угловая скорость положительна, поскольку спутник движется на восток с вращением Земли (против часовой стрелки от северного полюса). В трех измерениях угловая скорость представляет собой псевдовектор, величина которого измеряет скорость, с которой объект вращается или вращается, и его направление указывает перпендикуляр к мгновенной плоскости вращения или углового смещения. Ориентация угловой скорости условно задается правилом правой руки.
Угловая скорость положительна, поскольку спутник движется на восток с вращением Земли (против часовой стрелки от северного полюса). В трех измерениях угловая скорость представляет собой псевдовектор, величина которого измеряет скорость, с которой объект вращается или вращается, и его направление указывает перпендикуляр к мгновенной плоскости вращения или углового смещения. Ориентация угловой скорости условно задается правилом правой руки.
Соответствующие разделы общей науки
Преобразователь угловой скорости и частоты вращения • Механика • Определения единиц измерения • Онлайн-конвертеры единиц измерения
Преобразователь длины и расстоянияПреобразователь массыСухой объем и общие измерения для приготовления пищиКонвертер площадиКонвертер объема и общего измерения для приготовления пищиПреобразователь температурыПреобразователь давления, напряжения, модуля ЮнгаПреобразователь энергии и работыПреобразователь мощностиПреобразователь силыПреобразователь силыПреобразователь времениПреобразователь линейной скорости и скоростиПреобразователь углаПреобразователь эффективности использования топлива, расхода топлива и экономии топливаПреобразователь чиселКонвертер единиц информации и Хранение данныхКурсы обмена валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияПреобразователь ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер импульсаИмпульс крутящего моментаКонвертер удельной энергии, теплоты сгорания (в расчете на массу)Конвертер удельной энергии, теплоты сгорания (в объеме) Конвертер температуры Конвертер интервала Конвертер коэффициента теплового расширенияКонвертер теплового сопротивленияТеплопровод Конвертер удельной теплоемкостиПлотность теплоты, плотность пожарной нагрузкиКонвертер плотности теплового потокаКонвертер коэффициента теплопередачиКонвертер объемного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер массового потокаКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкости Конвертер кинематической вязкости Конвертер поверхностного натяженияМодерация проницаемости, проницаемости, паропроницаемости Преобразователь скорости пропускания паровПреобразователь уровня звукаПреобразователь чувствительности микрофонаПреобразователь уровня звукового давления (SPL)Преобразователь уровня звукового давления с выбираемым эталонным давлениемПреобразователь яркостиПреобразователь силы светаПреобразователь освещенностиПреобразователь разрешения цифрового изображенияПреобразователь частоты и длины волныПреобразователь оптической силы (диоптрий) в фокусное расстояниеПреобразователь оптической силы (диоптрий) в увеличение (X)Электрический заряд КонвертерКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаОбъемный заряд De Преобразователь электрического токаПреобразователь линейной плотности токаПреобразователь поверхностной плотности токаПреобразователь напряженности электрического поляПреобразователь электрического потенциала и напряженияПреобразователь электрического сопротивленияПреобразователь удельного электрического сопротивленияПреобразователь электрической проводимостиПреобразователь электропроводностиПреобразователь емкостиПреобразователь емкостиПреобразователь индуктивностиПреобразователь реактивной мощности переменного токаПреобразователь калибров проводов в СШАПреобразование уровней в дБм, дБВ, Ватт и других единицахПреобразователь силы магнитного поля КонвертерПлотность магнитного потокаМощность поглощенной дозы излучения, Мощность общей дозы ионизирующего излучения КонвертерРадиоактивность. Преобразователь радиоактивного распадаПреобразователь радиационного воздействияИзлучение. Конвертер поглощенной дозыКонвертер метрических префиксовКонвертер передачи данныхКонвертер типографских и цифровых изображенийКонвертер единиц измерения объема пиломатериаловКалькулятор молярной массыПериодическая таблица
Преобразователь радиоактивного распадаПреобразователь радиационного воздействияИзлучение. Конвертер поглощенной дозыКонвертер метрических префиксовКонвертер передачи данныхКонвертер типографских и цифровых изображенийКонвертер единиц измерения объема пиломатериаловКалькулятор молярной массыПериодическая таблица
радиан в секунду
A радиан в секунду (рад·с⁻¹, рад/с) — единица измерения скорости вращения или угловой скорости в системе СИ и СГС. Радиан в секунду также является единицей угловой частоты. Один радиан в секунду определяется как изменение ориентации объекта на один радиан каждую секунду.
радиан/день
A радиан в день (рад·д⁻¹, рад/д) – метрическая единица скорости вращения или угловой скорости. Радиан в сутки также является единицей угловой частоты. Один радиан в день определяется как изменение ориентации объекта на один радиан каждые 24 часа.
радиан/час
A радиан в час (рад·ч⁻¹, рад/ч) — метрическая единица скорости вращения или угловой скорости. Радиан в час также является единицей угловой частоты. Один радиан в час определяется как изменение ориентации объекта на один радиан каждый час.
Радиан в час также является единицей угловой частоты. Один радиан в час определяется как изменение ориентации объекта на один радиан каждый час.
радиан/минута
A радиан в минуту (рад·мин⁻¹, рад/мин) — метрическая единица скорости вращения или угловой скорости. Радиан в минуту также является единицей угловой частоты. Один радиан в минуту определяется как изменение ориентации объекта на один радиан каждую минуту.
градус/день
A градус в день (градус·d⁻¹, градус/d) — метрическая единица скорости вращения или угловой скорости. Градус в сутки также является единицей угловой частоты. Один градус в день определяется как изменение ориентации объекта на один градус каждые 24 часа.
градус/час
A градус в час (градус·ч⁻¹, градус/ч) — метрическая единица скорости вращения или угловой скорости. Градус в час также является единицей угловой частоты. Один градус в час определяется как изменение ориентации объекта на один градус каждый час.
Один градус в час определяется как изменение ориентации объекта на один градус каждый час.
град/мин
A градус в минуту (градус·мин⁻¹, градус/мин) — метрическая единица скорости вращения или угловой скорости. Градус в минуту также является единицей угловой частоты. Один градус в минуту определяется как изменение ориентации объекта на один градус каждую минуту.
градусов в секунду
A градуса в секунду (градус·с⁻¹, градус/с) — метрическая единица скорости вращения или угловой скорости. Градус в секунду также является единицей угловой частоты. Один градус в секунду определяется как изменение ориентации объекта на один градус каждую секунду.
оборотов/день
оборотов в день (r·d⁻¹, r/d, 1/d, d⁻¹) — метрическая единица скорости вращения или угловой скорости. Оборот в сутки также является единицей угловой частоты. Один оборот в день определяется как изменение ориентации объекта на один полный оборот каждые 24 часа.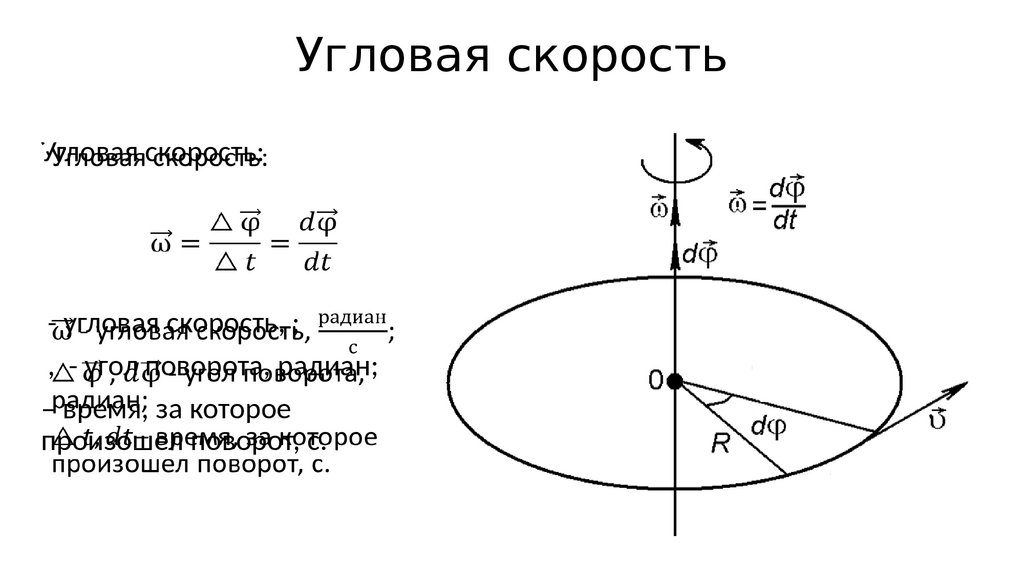
оборотов в час
A оборотов в час (r·h⁻¹, r/h, 1/h, h⁻¹) — метрическая единица скорости вращения или угловой скорости. Оборот в час также является единицей угловой частоты. Один оборот в час определяется как изменение ориентации объекта на один полный оборот каждый час.
оборотов в минуту
A оборотов в минуту (об/мин⁻¹, об/мин, 1/мин, мин⁻¹) — метрическая единица скорости вращения или угловой скорости. Оборот в минуту также является единицей угловой частоты. Один оборот в минуту определяется как изменение ориентации объекта на один полный оборот каждую минуту.
оборотов в секунду
A оборотов в секунду (r·s⁻¹, r/s) — метрическая единица скорости вращения или угловой скорости. Оборот в секунду также является единицей угловой частоты. Один оборот в секунду определяется как изменение ориентации объекта на один полный оборот каждую секунду.
оборотов в год
оборотов в год (r·y⁻¹, r/y, 1/y, y⁻¹) — метрическая единица скорости вращения или угловой скорости. Оборот в год также является единицей угловой частоты. Один оборот в год определяется как изменение ориентации объекта на один полный оборот каждый год.
оборотов в месяц
оборотов в месяц (об/м⁻¹, об/м, 1/м, м⁻¹) — метрическая единица скорости вращения или угловой скорости. Оборот в месяц также является единицей угловой частоты. Один оборот в месяц определяется как изменение ориентации объекта на один полный оборот каждый месяц.
оборотов в неделю
оборотов в неделю (r·w⁻¹, r/w, 1/w, w⁻¹) — метрическая единица скорости вращения или угловой скорости. Оборот в неделю также является единицей угловой частоты. Один оборот в неделю определяется как изменение ориентации объекта на один полный оборот каждую неделю.
градус/год
A градус в год (градус·г⁻¹, градус/год) – метрическая единица скорости вращения или угловой скорости. Градус в год также является единицей угловой частоты. Один градус в год определяется как изменение ориентации объекта на один градус каждый год.
градус/месяц
A градус в месяц (градус·м⁻¹, градус/м) — метрическая единица скорости вращения или угловой скорости. Градус в месяц также является единицей угловой частоты. Один градус в месяц определяется как изменение ориентации объекта на один градус каждый месяц.
градусов в неделю
A градуса в неделю (градус·w⁻¹, градус/w) — метрическая единица скорости вращения или угловой скорости. Градус в неделю также является единицей угловой частоты. Один градус в неделю определяется как изменение ориентации объекта на один градус каждую неделю.
радиан/год
A радиан в год (рад·г⁻¹, рад/год, 1/год, y⁻¹) — метрическая единица скорости вращения или угловой скорости.

 В этом случае кинематика вращения сильно упрощается, однако в общем случае угловая скорость может менять со временем направление в трехмерном пространстве, и такая упрощенная картина не работает.
В этом случае кинематика вращения сильно упрощается, однако в общем случае угловая скорость может менять со временем направление в трехмерном пространстве, и такая упрощенная картина не работает.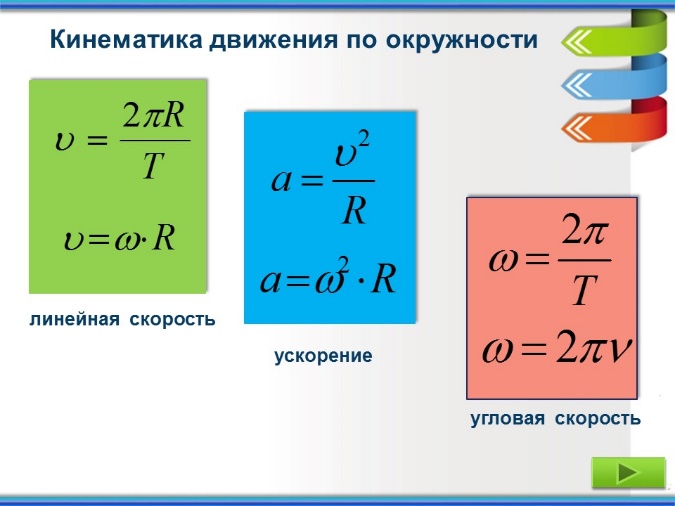 — векторное произведение, — скалярное произведение векторов. Однако эта формула не определяет угловую скорость однозначно (в случае единственной точки можно подобрать и другие векторы , подходящие по определению, по другому — произвольно — выбрав направление оси вращения), а для общего случая (когда тело включает более одной материальной точки) — эта формула не верна для угловой скорости всего тела (так как дает разные для каждой точки, а при вращении абсолютно твёрдого тела по определению угловая скорость его вращения — единственный вектор). При всём при этом, в двумерном случае (случае плоского вращения) эта формула вполне достаточна, однозначна и корректна, так как в этом частном случае направление оси вращения заведомо однозначно определено.
— векторное произведение, — скалярное произведение векторов. Однако эта формула не определяет угловую скорость однозначно (в случае единственной точки можно подобрать и другие векторы , подходящие по определению, по другому — произвольно — выбрав направление оси вращения), а для общего случая (когда тело включает более одной материальной точки) — эта формула не верна для угловой скорости всего тела (так как дает разные для каждой точки, а при вращении абсолютно твёрдого тела по определению угловая скорость его вращения — единственный вектор). При всём при этом, в двумерном случае (случае плоского вращения) эта формула вполне достаточна, однозначна и корректна, так как в этом частном случае направление оси вращения заведомо однозначно определено.
