Реактивная мощность | это… Что такое Реактивная мощность?
ТолкованиеПеревод
- Реактивная мощность
Электри́ческая мо́щность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии.
Содержание
- 1 Мгновенная электрическая мощность
- 2 Мощность постоянного тока
- 3 Мощность переменного тока
- 3.1 Активная мощность
- 3.2 Реактивная мощность
- 3.3 Полная мощность
- 4 Измерения
- 5 Литература
- 6 Ссылки
- 7 См. также
Мгновенная электрическая мощность
Мгновенная электрическая мощность P (t), выделяющаяся на элементе электрической цепи — произведение мгновенных значений напряжения U (t) и силы тока I (t) на этом элементе:
Если элемент цепи — резистор c электрическим сопротивлением R, то
Мощность постоянного тока
Так как значения силы тока и напряжения постоянны и равны мгновенным значениям в любой момент времени, то среднюю мощность можно вычислить по формулам:
Мощность переменного тока
Активная мощность
Среднее за период Т значение мгновенной мощности называется активной мощностью: .
 В цепях однофазного синусоидального тока , где U и I — действующие значения напряжения и тока, φ — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле . В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S активная связана соотношением . Единица активной мощности — ватт (W, Вт). Для СВЧ электромагнитного сигнала, в линиях передачи, аналогом активной мощности является мощность, поглощаемая нагрузкой.
В цепях однофазного синусоидального тока , где U и I — действующие значения напряжения и тока, φ — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле . В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S активная связана соотношением . Единица активной мощности — ватт (W, Вт). Для СВЧ электромагнитного сигнала, в линиях передачи, аналогом активной мощности является мощность, поглощаемая нагрузкой.
Реактивная мощность
Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи переменного тока, равна произведению действующих значений напряжения U и тока I, умноженному на синус угла сдвига фаз φ между ними: Q = UI sin φ. Единица реактивной мощности — вольт-ампер реактивный (var, вар). Реактивная мощность связана с полной мощностью S и активной мощностью Р соотношением: . Реактивная мощность в электрических сетях вызывает дополнительные активные потери (на покрытие которых расходуется энергия на электростанциях) и потери напряжения (ухудшающие условия регулирования напряжения). В некоторых электрических установках реактивная мощность может быть значительно больше активной. Это приводит к появлению больших реактивных токов и вызывает перегрузку источников тока. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности.
 Для СВЧ электромагнитного сигнала, в линиях передачи, аналогом реактивной мощности является мощность, отраженная от нагрузки.
Для СВЧ электромагнитного сигнала, в линиях передачи, аналогом реактивной мощности является мощность, отраженная от нагрузки.Необходимо отметить, что величина sinφ для значений φ от 0 до плюс 90 ° является положительной величиной. Величина sinφ для значений φ от 0 до минус 90 ° является отрицательной величиной. В соответствии с формулой Q = UI sinφ реактивная мощность может быть отрицательной величиной. Но отрицательное значение мощности нагрузки характеризует нагрузку как генератор энергии. Активное, индуктивное, емкостное сопротивление не могут быть источниками постоянной энергии. Модуль величины Q = UI sinφ приблизительно описывает реальные процессы преобразования энергии в магнитных полях индуктивностей и в электрических полях емкостей. Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии возвращаемой от индуктивной и емкостной нагрузки в источник переменного напряжения.
 Измерительные преобразователи реактивной мощности, использующие формулу Q = UI sinφ, более просты и значительно дешевле измерительных преобразователей на микропроцессорной технике.
Измерительные преобразователи реактивной мощности, использующие формулу Q = UI sinφ, более просты и значительно дешевле измерительных преобразователей на микропроцессорной технике.Полная мощность
Полная мощность — величина, равная произведению действующих значений периодического электрического тока в цепи I и напряжения U на её зажимах: S = U×I; связана с активной и реактивной мощностями соотношением: , где Р — активная мощность, Q — реактивная мощность (при индуктивной нагрузке Q > 0, а при ёмкостной Q < 0). Единица полной электрической мощности — вольт-ампер (VA, ВА).
Векторная зависимость между полной, активной и реактивной мощностью выражается формулой:
Измерения
- Для измерения электрической мощности применяются ваттметры и варметры, можно также использовать косвенный метод, с помощью вольтметра и амперметра.
- Для измерения коэффициента реактивной мощности применяют фазометры
Литература
- Бессонов Л.
 А. — Теоретические основы электротехники: Электрические цепи — М.: Высш. школа, 1978
А. — Теоретические основы электротехники: Электрические цепи — М.: Высш. школа, 1978
Ссылки
- Преобразование энергии в электрической цепи
- Для чего нужна компенсация реактивной мощности
- Измерение энергопотребления компьютеров
- Общие основы электротехники
См. также
- Мощность (физика)
- Ваттметр
- Электрический ток
- Коэффициент мощности
- Список параметров напряжения и силы электрического тока
Wikimedia Foundation.
2010.
Игры ⚽ Нужно решить контрольную?
- Реактивная броня
- Реактивная система залпового огня
Полезное
Компенсация реактивной мощности
ТОЭ переменный ток
В электрических цепях переменного тока присутствуют два вида мощности – активная и реактивная. Активная мощность является полезной и расходуется непосредственно на совершение полезной работы.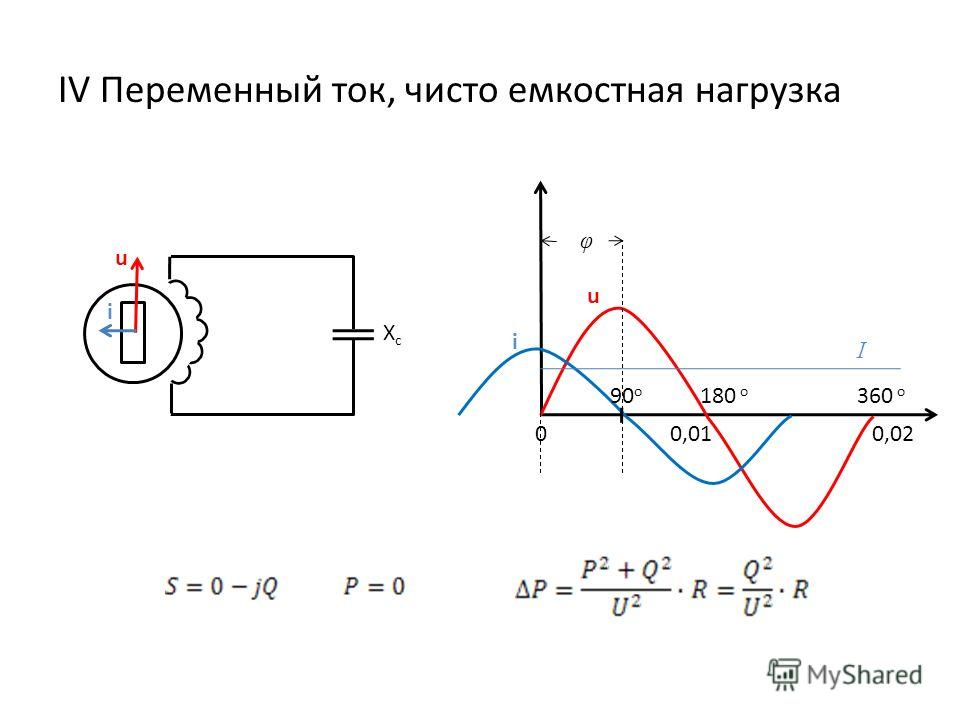 Реактивная мощность чаще имеет отрицательное воздействие, в связи с чем, требуется компенсация реактивной мощности.
Реактивная мощность чаще имеет отрицательное воздействие, в связи с чем, требуется компенсация реактивной мощности.
Реактивная мощность
Реактивная мощность возникает при наличии реактивных элементов в цепи, таких как катушка или конденсатор. При этом часть энергии полученной от источника возвращается обратно к нему.
При наличии в цепи и катушки и конденсатора, суммарная реактивная мощность оказывается меньше, чем в цепях, в которых эти элементы расположены по отдельности. Это связано с тем, что индуктивная QL и емкостная QC мощности имеют разные знаки. При равенстве этих мощностей наблюдается явление резонанса, при котором реактивная мощность равна нулю. В этом случае энергия не поступает к источнику, а циркулирует между катушкой и конденсатором.
Реактивная мощность в промышленных установках
В промышленности большая часть оборудования обладает индуктивностью, а следовательно и реактивной мощностью. Примером таких установок может служить трансформаторы, двигатели, индукционные нагревательные установки и т.д. Чем больше величина реактивной мощности, тем меньше коэффициент мощности cosϕ, который определяется как отношение активной мощности к полной. Чем больше число установок, тем больше их суммарная реактивная мощность, следовательно, потери связанные с реактивной мощностью больше.
Примером таких установок может служить трансформаторы, двигатели, индукционные нагревательные установки и т.д. Чем больше величина реактивной мощности, тем меньше коэффициент мощности cosϕ, который определяется как отношение активной мощности к полной. Чем больше число установок, тем больше их суммарная реактивная мощность, следовательно, потери связанные с реактивной мощностью больше.
Реактивная мощность также влияет на токи в цепи. На примере асинхронного двигателя ток определяется как
При увеличении реактивной мощности (Q) ток также будет увеличиваться, что приводит к необходимости выбора проводов большего сечения, а следовательно к лишним затратам. Кроме того, увеличение тока приводит к увеличению тепловых потерь, а следовательно к дополнительному нагреву двигателя.
Компенсация реактивной мощности
Как было сказано ранее, большие значения реактивной мощности приводят к значительным экономическим и трудовым затратам. Поэтому, на практике стараются максимально уменьшить её значение.
Уменьшение реактивной мощности может достигаться несколькими способами. Самым эффективным считается правильный подбор мощности двигателей и трансформаторов и нахождение эффективного режима нагрузки, без холостого хода и недогрузки. Такой способ не требует дополнительных материальных затрат, но им не всегда получается достигнуть оптимальных значений и прибегают к искусственным способам компенсации реактивной мощности.
Одним из таких способов является включение батареи конденсаторов параллельно к приемнику.
С помощью использования батареи конденсаторов можно добиться полной компенсации реактивной мощности. Но на практике затраты на дополнительное оборудование могут значительно превысить затраты на реактивную мощность, из-за дороговизны конденсаторов. Поэтому чаще всего, добиваются лишь частичной компенсации реактивной мощности.
Компенсацию реактивной мощности рассмотрим на примере асинхронного двигателя.
До включения батареи конденсаторов параллельно двигателю, значение реактивной мощности было равно Q1, а ток в питающих проводах двигателя был равен I1. При включении батареи, это значение снизилось до Q2, так как часть индуктивной мощности была скомпенсирована емкостной.
При включении батареи, это значение снизилось до Q2, так как часть индуктивной мощности была скомпенсирована емкостной.
Ток значительно уменьшается до величины I2, благодаря появлению тока Ic, который можно рассчитать по формуле
Емкость батареи
Мощность батареи
Таким образом, компенсация реактивной мощности играет важную роль с точки зрения сокращения расходов предприятия.
Мощность в цепи переменного тока – активная мощность, реактивная мощность, полная мощность
В электрических и электронных схемах мощность является одной из наиболее важных величин, используемых для анализа цепей для практических приложений. Электрическая мощность определяется как скорость расширения или поглощения энергии в цепи во времени, т. е.
$$\mathrm{Power,P=\frac{Energy \;expanded\; или же\; поглощенный (𝑊)}{Time(𝑡)}}. ….(1)$$
….(1)$$
Эта статья предназначена для объяснения отношения мощности в цепях переменного тока . Где цепь переменного тока — это цепь, которая возбуждается от источника переменного напряжения.
Мгновенная мощность в цепи переменного тока
Значение электрической мощности в цепи переменного тока, измеренное в определенный момент времени, называется
мгновенная мощность . Обычно обозначается строчной буквой $p$. В целом,
мгновенная мощность в цепи переменного тока получается путем умножения мгновенного напряжения на
мгновенный ток, т. е.
$$\mathrm{Мгновенная \;мощность, 𝑝 = \upsilon. i\;\;}….(2)$$
Рассмотрим любую цепь переменного тока, если мгновенные значения напряжения и тока в цепи заданы формулой
$$\mathrm{\upsilon=V_{m}\ sin\left({wt}\right)}….(3)$$
$$\mathrm{i=I_{m}\sin\left({wt-\phi}\right)}.. ..(4)$$
Где $\mathrm{\phi}$ — фазовый угол между напряжением и током в любой момент времени. Где $\mathrm{\phi}$ имеет отрицательное значение, когда ток отстает от напряжения, положительное значение, когда ток опережает напряжение, и ноль, когда ток и напряжение находятся в одной фазе.
Следовательно, по определению мгновенная мощность определяется выражением
$$\mathrm{p=vi=V_{m}\sin(wt).I_{m}\sin(wt-\phi)}$ $
$$\mathrm{\Rightarrow\; p=\frac{1}{2}\times2\times\; V_{m}I_{m}\sin wt \sin (wt-\phi)}$$
$$\mathrm{\Rightarrow\; p=\frac{V_{m}I_{m}}{2}[\cos\phi-\cos(2wt-\phi)]}$$
$$\mathrm{\следовательно\; p=\frac{V_{m}I_{m}}{2}\cos\phi-\frac{V_{m}I_{m}}{2}\cos(2wt-\phi)}…. ..(5)$$
Здесь второе слагаемое в правой части уравнения (5) содержит удвоенный частотный член, а модуль среднего значения этого члена равен нулю, поскольку среднее значение синусоидальной величины по полному цикл нулевой. Таким образом, мгновенная мощность состоит только из первого члена уравнения (5), т. е.
$$\mathrm{P=\frac{1}{2}\;V_{m}I_{m}\cos\phi……(6)}$$
Этот термин равен средняя мощность в цепи переменного тока. Кроме того, средняя мощность в цепи переменного тока может быть выражена через среднеквадратичные значения напряжения и тока следующим образом:
$$\mathrm{P=\frac{V_{m}}{\sqrt{2}}\frac{I_ {m}}{\sqrt{2}}\cos\phi}$$
$$\mathrm{\следовательно \;P=VI\cos\phi. ….(7)}$$
….(7)}$$
Где , $\mathrm{\cos\phi}$ известен как коэффициент мощности схемы.
В электрической цепи переменного тока различают следующие три вида электроэнергии −
- Активная мощность
- Реактивная мощность
- Полная мощность
Активная мощность
Активная мощность – это количество полной электроэнергии в электрической цепи переменного тока, которая фактически потребляется или используется. Его также называют реальной мощностью или реальной мощностью . Активная мощность измеряется в ваттах (Вт). Более крупными единицами активной мощности являются киловатт (кВт), мегаватт (МВт), гигаватт (ГВт) и так далее.
Технически, когда в электрической цепи переменного тока угол сдвига фаз становится равным нулю, т.е. коэффициент мощности становится равным единице, то мощность, потребляемая в цепи, называется 9{\circ}}$$
$$\mathrm{\следовательно, Active\;Power,P=VI}$$
На практике активная мощность используется для определения номинальных характеристик электрических нагрузок, таких как двигатели, лампочки, утюги, и т. д.
д.
Реактивная мощность
Реактивная мощность — это количество общей электрической мощности, которая остается неиспользованной в электрической цепи переменного тока и течет туда и обратно в электрической системе от нагрузки к источнику и наоборот . Обозначается буквой Q и измеряется в Вольт-ампер реактивный (ВАР) .
Реактивная мощность в цепи переменного тока также может быть определена как произведение среднеквадратичных значений напряжения и тока на синус фазового угла, т. е.
$$\mathrm{Q=VI\sin\phi}$$
Реактивная мощность также известна как мощность Вт или квадратурная мощность . Для индуктивной нагрузки потребляемая реактивная мощность равна отстающей реактивной мощности , а потребляемая конденсатором — опережающей реактивной мощности . Следовательно, есть два элемента цепи переменного тока, а именно индуктор и конденсатор, которые отвечают за поток реактивной мощности в цепи.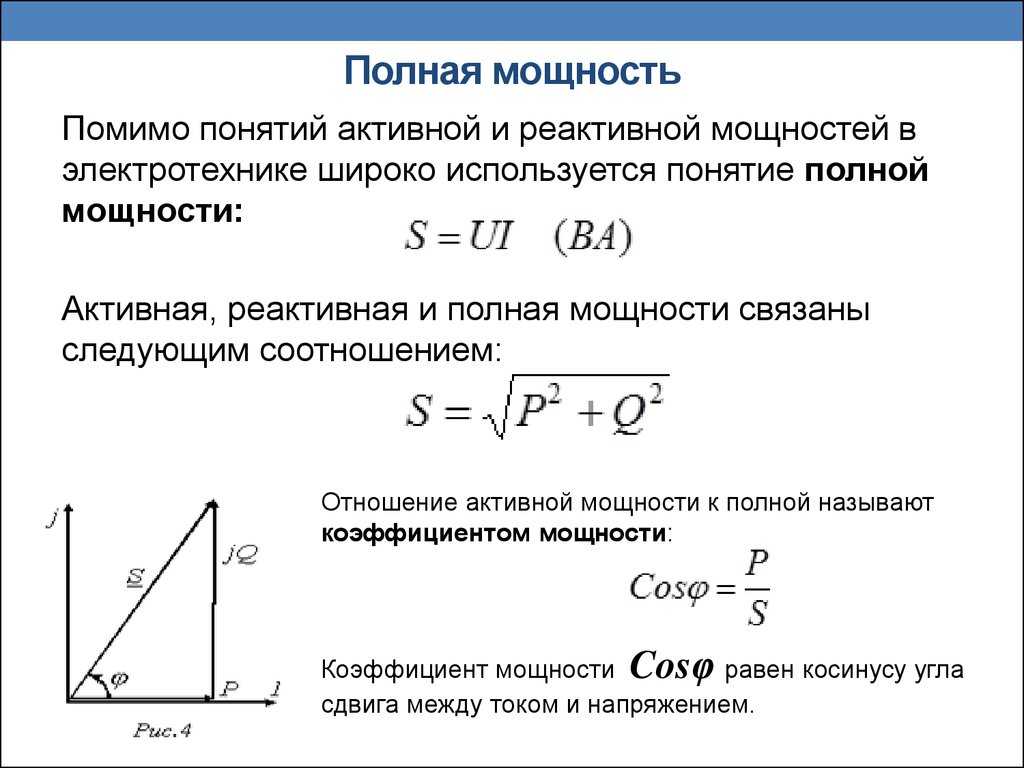
Реактивная мощность отвечает за работу всех электромагнитных машин, таких как двигатели, генераторы и т. д., поскольку она создает в этих машинах необходимое магнитное возбуждение.
Полная мощность
Полная мощность, производимая источником переменного тока, равна полной мощности . Он измеряется как произведение среднеквадратичных значений напряжения и тока. Полная мощность обозначается буквой S и измеряется в Вольт-ампер (ВА) .
$$\mathrm{Полная\;мощность,\;S=VI}$$
Полная мощность также определяется суммой векторов активной и реактивной мощностей, т.е.
$$\mathrm{S=P +jQ}$$
На практике полная мощность используется для определения номинальных характеристик электрических устройств, которые действуют как источники и передатчики энергии, таких как генераторы, генераторы переменного тока, трансформаторы и т. д.
Числовой пример
Если значения RMS тока и напряжения в цепи переменного тока составляют 220 В и 5 А. Если между напряжением и током имеется разность фаз 60°. Определить активную мощность, реактивную мощность и полную мощность в цепи.
Если между напряжением и током имеется разность фаз 60°. Определить активную мощность, реактивную мощность и полную мощность в цепи.
Решение
Данные,
Следовательно, активная мощность в данной цепи равна,
$$\mathrm{P=VI\cos\phi}$$
$$\mathrm\Rightarrow{P=220 \times5\times\cos60}$$
$$\mathrm{\следовательно\;P=550W}$$
Реактивная мощность, протекающая по цепи, равна,
$$\mathrm{Q=VI\sin\ phi}$$
$$\mathrm{Q=220\times5\times\sin60}$$
$$\mathrm{\следовательно Q = 952,63 \;VAR}$$
Полная мощность, подводимая к схема,
$$\mathrm{S = VI = 220\times5}$$
$$\mathrm{\следовательно S = 1100 \;VA}$$
Заключение
В этой статье мы обсудили три основных типа электрических мощностей, а именно активной мощности, реактивной мощности и полной мощности в цепи переменного тока. Основная причина такой классификации мощностей заключается в том, что в цепи переменного тока электрическая мощность зависит от коэффициента мощности.
ac — Как возникают колебания реактивной мощности между источником и нагрузкой?
Чтобы мощность колебалась в обратном направлении и между источником и катушкой индуктивности, источник должен быть емкостным. То есть он должен либо содержать конденсатор достаточной емкости, либо должен вести себя так, как если бы он был конденсатором. Синхронные генераторы поля возбуждения можно заставить вести себя так, как если бы они были конденсаторами, регулируя ток возбуждения. Любой другой тип генератора или источника переменного тока требует наличия конденсатора для питания индуктивной нагрузки.
Ключевой концепцией здесь является то, что энергия хранится в конденсаторах и катушках индуктивности. Поскольку ток опережает напряжение в конденсаторе и отстает от напряжения в индукторе, энергия может «колебаться» или передаваться туда и обратно между конденсатором и индуктором. Это должно обеспечить достойное интуитивное понимание утверждения «Реактивная мощность — это мощность, которая постоянно колеблется между источником и нагрузкой». В основном это концепция, которая важна при производстве, передаче, распределении и использовании электроэнергии переменного тока. В мире сигналов на это можно смотреть по-разному.
В основном это концепция, которая важна при производстве, передаче, распределении и использовании электроэнергии переменного тока. В мире сигналов на это можно смотреть по-разному.
Обратите внимание, что также полезно понимать математику, представленную во временной области @Andy aka. В какой-то момент вам также понадобится разобраться в представлениях векторов.
Понимание того, как синхронная машина с раневым полем может действовать как конденсатор, важно, но выходит за рамки этого вопроса.
Подробнее
Чтобы более подробно рассмотреть проблему, обратитесь к диаграмме ниже.
При нулевом фазовом угле ток равен нулю, поэтому магнитное поле индуктора равно нулю и энергия не сохраняется. Приложенное напряжение вызывает рост тока, и энергия передается результирующему магнитному полю в индукторе. Скорость передачи энергии от источника к нагрузке показана кривой мощности. Мощность в каждый момент времени равна напряжению в этот момент времени, умноженному на ток в это время. Фактическая запасенная энергия представляет собой площадь под кривой.
Фактическая запасенная энергия представляет собой площадь под кривой.
При 90 градусах напряжение меняется на противоположное, ток начинает уменьшаться и энергия передается от катушки индуктивности обратно к источнику. Мощность отрицательна, потому что направление передачи энергии изменилось на противоположное.
При 180 градусах ток меняет направление, что приводит к еще одному изменению направления потока энергии.
Поток энергии продолжается вперед и назад, как показано на рисунке.
Если считать источник переменного тока идеальным, можно просто сказать, что он принимает возвращаемую энергию. Реальный источник энергии должен иметь физический механизм для приема возвращенной энергии. В комментарии было предложено, что генератор просто просит как двигатель и ускоряет свою собственную инерцию и инерцию, если приводной двигатель слегка каждый раз, когда он получает возвращенную энергию. Это возможно, но, как минимум, проблематично и неэффективно. Что происходит в системах распределения электроэнергии, так это то, что емкость встроена в источник, чтобы дополнить индуктивность нагрузки, накапливая энергию, когда нагрузка возвращает ее, и возвращая ее обратно в нагрузку по мере необходимости.

 В цепях однофазного синусоидального тока , где U и I — действующие значения напряжения и тока, φ — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле . В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S активная связана соотношением . Единица активной мощности — ватт (W, Вт). Для СВЧ электромагнитного сигнала, в линиях передачи, аналогом активной мощности является мощность, поглощаемая нагрузкой.
В цепях однофазного синусоидального тока , где U и I — действующие значения напряжения и тока, φ — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле . В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S активная связана соотношением . Единица активной мощности — ватт (W, Вт). Для СВЧ электромагнитного сигнала, в линиях передачи, аналогом активной мощности является мощность, поглощаемая нагрузкой.
 Для СВЧ электромагнитного сигнала, в линиях передачи, аналогом реактивной мощности является мощность, отраженная от нагрузки.
Для СВЧ электромагнитного сигнала, в линиях передачи, аналогом реактивной мощности является мощность, отраженная от нагрузки. Измерительные преобразователи реактивной мощности, использующие формулу Q = UI sinφ, более просты и значительно дешевле измерительных преобразователей на микропроцессорной технике.
Измерительные преобразователи реактивной мощности, использующие формулу Q = UI sinφ, более просты и значительно дешевле измерительных преобразователей на микропроцессорной технике.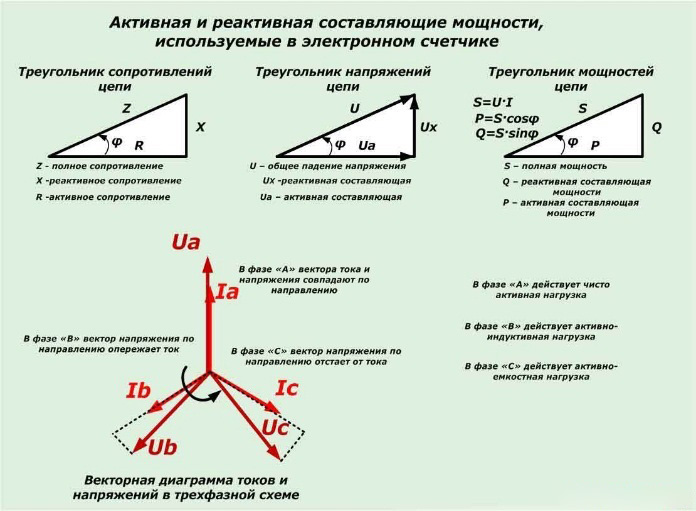 А. — Теоретические основы электротехники: Электрические цепи — М.: Высш. школа, 1978
А. — Теоретические основы электротехники: Электрические цепи — М.: Высш. школа, 1978