Расчет крутящего момента на валу гидронасоса | Мир гидравлики

Инженерно-проектный центр

• О нас
• Наши проекты
• Формы заказа
  • Выбор гидроагрегата
    • Гидроагрегат, Гидростанция, Маслонапорная установка, Насосная станция или Насосная установка
  • Выбор пресса
    • Гидравлические прессы
  • Выбор вулканизационного пресса
    • Вулканизационные пресса
  • Выбор гидроцилиндра
    • Гидравлические цилиндры
• Модернизация оборудования
• Проектирование гидравлических систем
• Услуги оказываемые нашей компанией
• Опросные листы
• Сотрудничество
• Техническая информация
  • Руководство по эксплуатации БГ12-4 РЭ
  • Паспорт. П-КРМ.000 ПС
  • Паспорт. Пневмораспределитель 5Р2.00.000 ПС
  • ГОСТ 6911-71
  • Паспорт на станцию смазочную СДР
  • Таблица аналогов гидравлических схем для гидрораспределителей Российского и зарубежного производства
  • Таблица аналогов маркировок гидрораспределителей отечественных и импортных
  • Калькуляторы
    • Расчет гидропривода
    • Расчет мощности, расхода и давления гидропривода
    • Расчет подачи насоса
    • Расчет крутящего момента на валу гидронасоса
    • Расчет оборотов гидромотора
    • Расчет крутящего момента гидромотора
    • Расчет параметров гидравлического цилиндра по размерным характеристикам
    • Расчет размеров гидравлического цилиндра по техническим параметрам
    • Расчет диаметра трубопровода, скорости потока рабочей жидкости
  • Литература
    • Станочные гидроприводы. В.К. Свешников, А.А. Усов
    • Станочные гидроприводы. В.К. Свешников
    • Гидрооборудование. Международный справочник. В.К. Свешников
    • Гидравлика. Гидромашины и гидроприводы. Т.М. Башта
    • Объёмные гидравлические и пневматические приводы. Никитин
    • Металлорежущие станки. Тепинкичиев В.К
    • Учебный курс по гидравлике. Том 1. Rexroth Bosch Group
    • Гидравлические системы станков и автоматических линий. М.М. Кузнецов
    • Гидравлическое оборудование металлорежущих станков
    • Рекомендуемые рабочие жидкости для гидросистем
    • Гидронасосы и гидромоторы
    • ГОСТ 15150-69
• Контакты

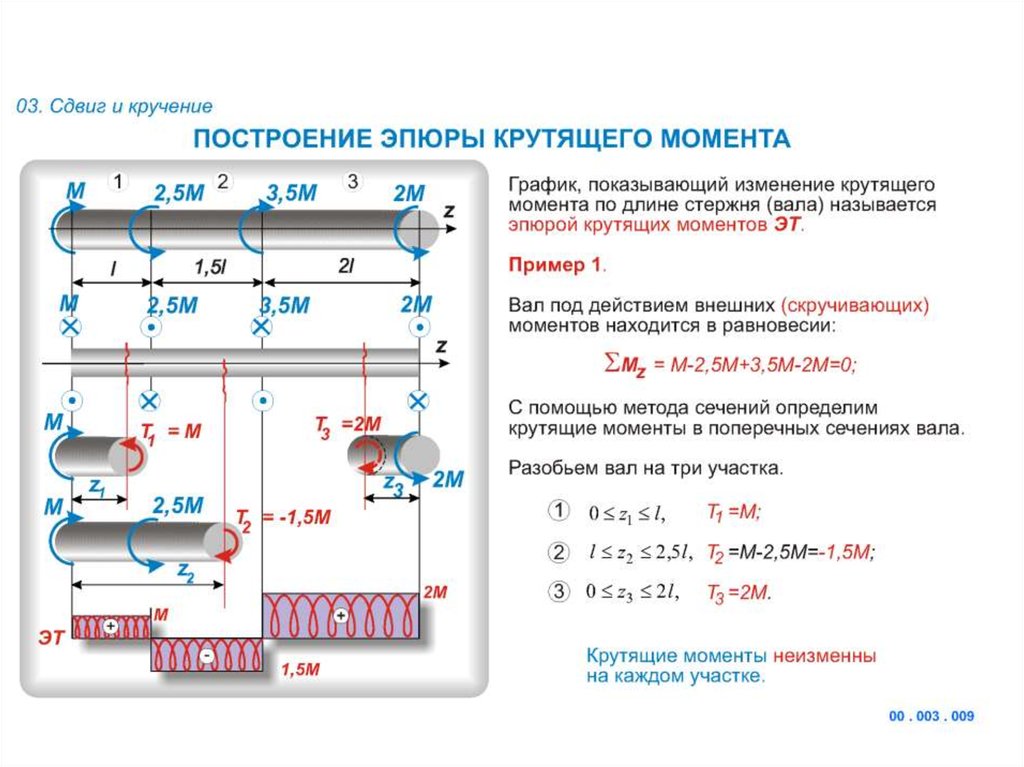
8 Расчет крутящих моментов на валах

8.1 Расчет крутящего момента
на валу электродвигателя

Для
определения крутящего момента на валу
электродвигателя привода главного
движения используется номинальная
мощность и номинальная частота вращения:

где
– мощность электродвигателя, кВт:

–номинальная
частота вращения электродвигателя,
мин^-1:

.

.

8.2 Расчет крутящего момента на валах
привода

Крутящий
момент на валах привода рассчитывается
по формуле:

где

– мощность электродвигателя, кВт:

–КПД
участка привода от электродвигателя
до соответствующего вала;

–расчетная
частота вращения соответствующего
вала, принимается по графику частот,
мин^-1.

8.3 Расчет крутящего момента на первом
валу привода

Крутящий
момент на первом валу привода рассчитывается
по формуле:

где
– мощность электродвигателя, кВт:

–КПД
участка привода от электродвигателя
до 1-го вала;

–расчетная
частота вращения на 1-ом валу, принимаем
по графику частот, мин^-1:
= 2850 мин^-1.

КПД
участка привода до первого вала
рассчитывается по формуле:

где
– КПД зубчатой муфты;

–КПД
пары подшипников;

8.4 Расчет крутящего момента на втором
валу привода

Крутящий
момент на втором валу привода рассчитывается
по формуле:

где
– мощность электродвигателя, кВт:

–КПД
участка привода от электродвигателя
до 2-го вала;

–расчетная
частота вращения на 1-ом валу, принимаем
по графику частот, мин^-1:
= 630 мин^-1.

КПД
участка привода до второго вала
рассчитывается по формуле:

где
–
КПД зубчатой муфты;

–КПД
пары подшипников;

—
КПД зацепления зубчатых колес;
.

8.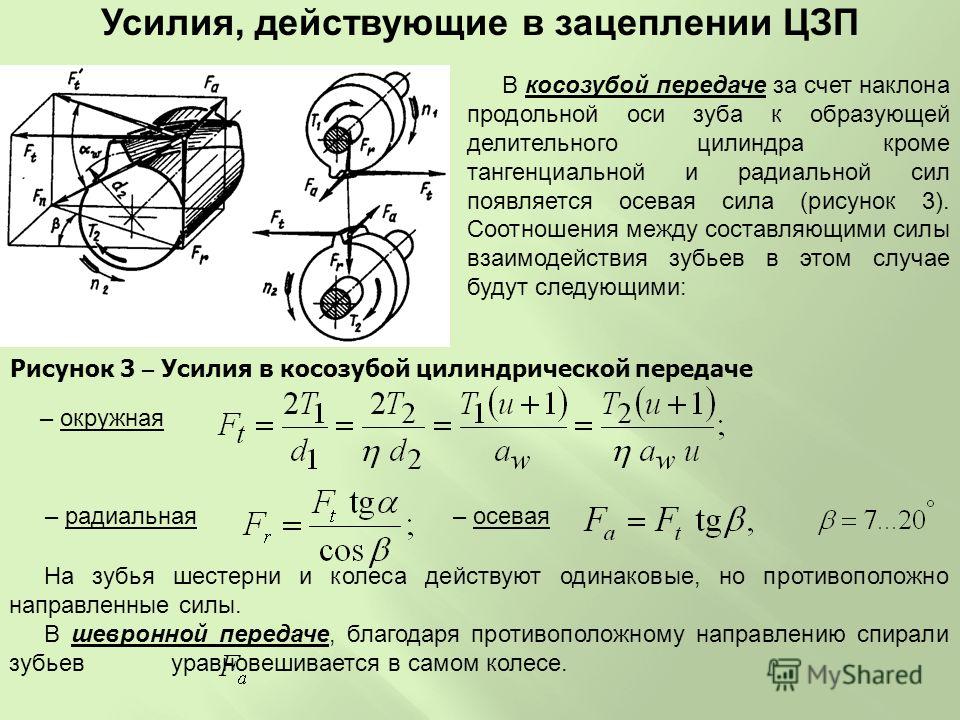 5 Расчет крутящего момента на третьем
валу привода

Крутящий
момент на третьем валу привода
рассчитывается по формуле:

где
– мощность электродвигателя, кВт:

–КПД
участка привода от электродвигателя
до 3-го вала;

–расчетная
частота вращения на 1-ом валу, принимаем
по графику частот, мин^-1:
= 160 мин^-1.

КПД
участка привода до третьего вала
рассчитывается по формуле:

где
–
КПД зубчатой муфты;

–КПД
пары подшипников;

—
КПД зацепления зубчатых колес;
.

8.6 Расчет крутящего момента на четвертом
валу привода

Крутящий
момент на четвертом валу привода
рассчитывается по формуле:

где
– мощность электродвигателя, кВт:

–КПД
участка привода от электродвигателя
до 4-го вала;

–расчетная
частота вращения на 4-ом валу, определяется
по формуле:

где
– минимальная частота вращения четвертого
вала, мин^-1:

мин^-1;

–максимальная
частота вращения четвертого вала, мин^-1:

мин^-1.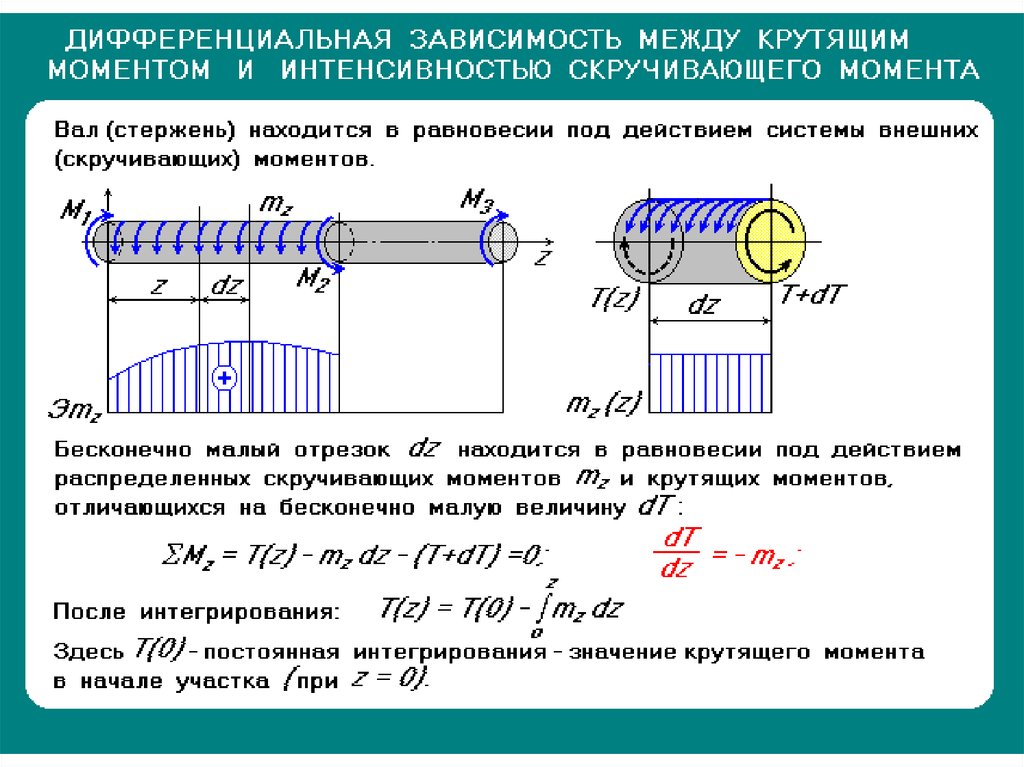

КПД
участка привода до четвертого вала
рассчитывается по формуле:

где
–
КПД зубчатой муфты;

–КПД
пары подшипников;

–КПД
зацепления зубчатых колес;
.

Крутящий
момент на шпинделе рассчитывается по
формуле:

где
– мощность электродвигателя, кВт:

–КПД
участка привода от электродвигателя
до шпинделя;

–расчетная
частота вращения шпинделя, определяется
по формуле:

где
– минимальная частота вращения четвертого
вала, мин^-1:

мин^-1;

–диапазон
регулирования частот вращения шпинделя:

КПД
участка привода до шпинделя рассчитывается
по формуле:

где
–
КПД зубчатой муфты;

–КПД
пары подшипников;

–КПД
зацепления зубчатых колес;
.

9 Проектный расчет передач

9.1 Расчет цилиндрической прямозубой
постоянной передачиz₁–z₂

9.1.1
Исходные данные

1.
Расчетный крутящий момент на первом
валу привода, H·м:

Т₁
=
13 Н·м;

2.
Число зубьев шестерни: z₁
=
18;

3.
Число зубьев колеса: z₂
=
83;

4.
Передаточное число передачи: u₁
=
4,76.

9.1.2
Выбор материала и термической обработки
зубчатых
колес

В
качестве материала для зубчатых колес
передачи выбираем сталь 40Х, которая
отвечает необходимым техническим и
эксплуатационным требованиям. В качестве
термической обработки выбираем объемную
закалку, позволяющую получить твердость
зубьев 40..50HRC_э.

9.1.3
Проектный расчет постоянной прямозубой
зубчатой передачи
на контактную выносливость

Диаметр
начальной окружности шестерни
рассчитывается по формуле:

где

вспомогательный
коэффициент: для прямозубых передач

—
расчётный крутящий момент на первом
валу, Н·м: Т₁=13
Н·м;

коэффициент
нагрузки для шестерни, равный 1,3. .1,5:
принимаем

—
передаточное число:

отношение
рабочей ширины венца передачи к начальному
диаметру шестерни:

допускаемое
контактное напряжение, МПа.

Допускаемое
контактное напряжение для прямозубых
передач рассчитывается по формуле:

где

базовый
предел контактной выносливости
поверхностей зубьев, соответствующий
базовому числу циклов перемены напряжений,
МПа;

МПа;

S_H
– коэффициент безопасности: S_H
= 1,1.

Коэффициент
отношения рабочей ширины венца передачи
к начальному диаметру шестерни может
приниматься в пределах

или
определяется
по формуле:

отношение
рабочей ширины венца передачи к модулю:
принимаем

число
зубьев шестерни: z₁
= 18.

что
находится в допустимых пределах
.

Таким
образом, диаметр начальной окружности
шестерни равен:

Модуль
постоянной прямозубой передачи
определяется из условия расчета на
контактную выносливость зубьев по
рассчитанному значению диаметра
начальной окружности шестерни по
формуле:

где

диаметр
начальной окружности шестерни, мм:d_w1
=
38,75 мм;

число
зубьев шестерни: z₁
= 18.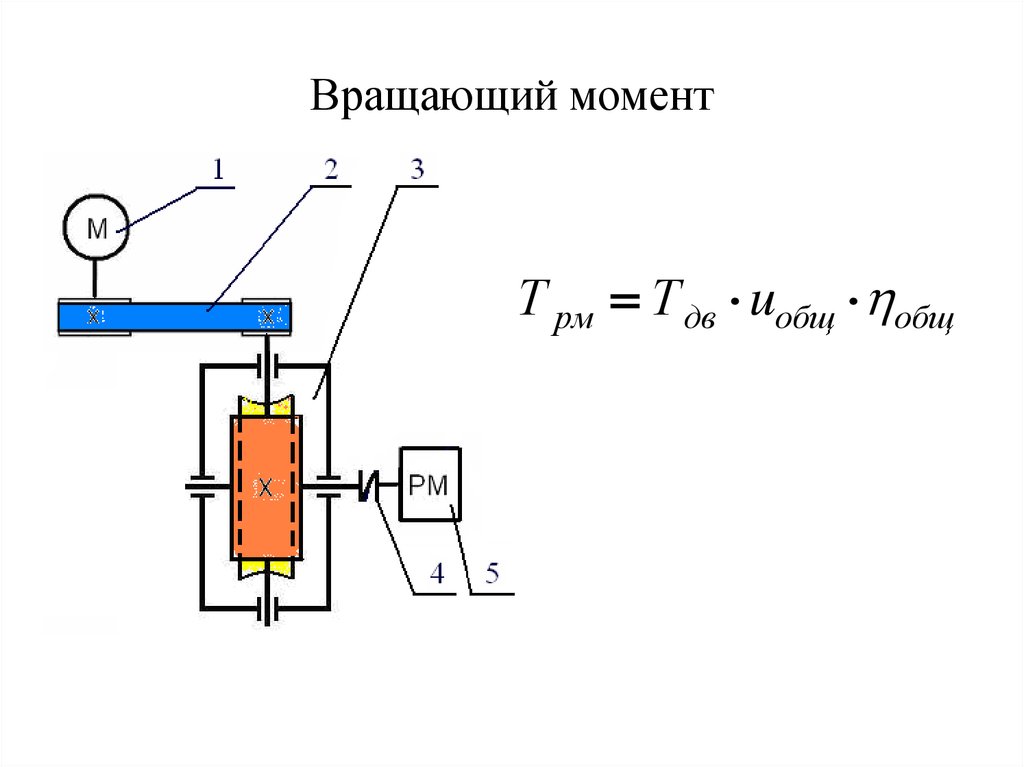

Как рассчитать крутящий момент на валу

Обновлено 22 декабря 2020 г.

Кевин Бек

Вся физика занимается описанием того, как движутся объекты и как определенные величины, которыми они обладают (например, энергия, импульс), обмениваются друг с другом и окружающая среда. Возможно, самой фундаментальной величиной, управляющей движением, является сила, которая описывается законами Ньютона.

Когда вы представляете силы, вы, вероятно, представляете объекты, которые толкают или тянут по прямой линии. На самом деле, когда вы впервые знакомитесь с концепцией силы в курсе физических наук, вам представляют такой сценарий, потому что он самый простой.

Но физические законы, управляющие вращательным движением, включают совершенно другой набор переменных и уравнений, даже если лежащие в их основе принципы одни и те же. Одной из таких специальных величин является крутящий момент , который часто действует для вращения валов в машинах.

Что такое Сила?

Проще говоря, сила — это толчок или тяга. Если суммарный эффект всех сил, действующих на объект, не компенсируется, то эта результирующая сила заставит объект ускоряться или изменять его скорость.

Возможно, вопреки вашей собственной интуиции, а также представлениям древних греков, для перемещения объекта с постоянной скоростью не требуется сила, ибо ускорение определяется как скорость изменения скорости.

Если ​ a ​ = 0, измените ​ v ​ = 0 и никакая сила не требуется для того, чтобы объект продолжал двигаться, при условии, что на него не действуют другие силы (включая сопротивление воздуха или трение).

В закрытой системе, если сумма всех действующих сил равна нулю ​ и ​ сумма всех присутствующих крутящих моментов также равна нулю, система считается ​ равновесной ​, так как ничто не заставляет ее изменить свое движение.

Крутящий момент Объяснение

Вращательный аналог силы в физике представляет собой крутящий момент, представленный ​ ​ T ​ ​.

Крутящий момент является важнейшим компонентом практически любого мыслимого инженерного приложения; каждая машина с вращающимся валом включает в себя компонент крутящего момента, на долю которого приходится почти весь транспортный мир, наряду с сельскохозяйственным оборудованием и многим другим в промышленном мире.

Общая формула для крутящего момента имеет вид . Поскольку sin 0° = 0 и sin 90° = 1, вы можете видеть, что крутящий момент максимизируется, когда сила приложена перпендикулярно к рычагу. Когда вы думаете о любом опыте работы с длинными гаечными ключами, который у вас может быть, это, вероятно, интуитивно понятно.

• Крутящий момент имеет те же единицы измерения, что и энергия (ньютон-метр), но в случае крутящего момента это никогда не называют «Джоулями». И в отличие от энергии, крутящий момент является векторной величиной.

Формула крутящего момента на валу

Чтобы рассчитать крутящий момент на валу, например, если вы ищете формулу крутящего момента на распределительном валу, сначала необходимо указать тип вала, о котором вы говорите.

Это связано с тем, что валы, которые, например, полые и содержат всю свою массу в цилиндрическом кольце, ведут себя иначе, чем сплошные валы того же диаметра.

Для кручения как полых, так и сплошных валов в игру вступает величина, называемая напряжением сдвига , , представленная τ (греческая буква тау). Кроме того, полярный момент инерции площади , Дж , величина, скорее похожая на массу в задачах вращения, входит в смесь и специфична для конфигурации вала.

Общая формула для крутящего момента на валу:

T = τ × \frac{J}{r}

, где ​ r ​ длина и направление плеча рычага. Для сплошного вала J ​ имеет значение (π/2)​ r ​ ⁴ .

Для полого вала ​ J ​ вместо (π/2)(​ r ​ _o ⁴ – ​ r ​ _{i 9002 4909), где 2 i 9002 4909 r o и r o — внешний и внутренний радиусы вала (твердая часть снаружи пустого цилиндра).}

Как рассчитать диаметр вала по крутящему моменту?

Когда вал передает мощность от приводного оборудования к ведомому оборудованию, необходимо рассчитать диаметр вала по крутящему моменту на основе максимального крутящего момента, который может быть передан через вал, или максимальной степени крутки вала. В противном случае вал может не удовлетворять функциональным возможностям оборудования.

Как известно, уравнение кручения (подробнее об уравнении кручения читайте здесь)

Где

τ  = напряжение кручения, возникающее на внешней поверхности вала (максимальное напряжение сдвига).

r  = Радиус вала.

T  = крутящий момент или крутящий момент.

Дж  = полярный момент инерции.

Эмпирическое правило Для определения F…

Включите JavaScript

C  = Модуль жесткости материала вала.

l   = длина вала.

θ  = угол закручивания в радианах по длине.

Из уравнения кручения мы можем рассмотреть

Можно записать как

Полярный момент инерции будет рассчитан из следующего уравнения.

Полярный момент инерции для круглого поперечного сечения равен

Отсюда максимальный крутящий момент, который может быть передан через вал, можно записать как

Из приведенного выше уравнения мы можем вычислить неизвестные факторы. В нашем случае диаметр вала является неизвестным фактором.

Таким образом, нам нужны следующие входные данные

• Максимальный крутящий момент, который будет передаваться через вал (Мы также можем рассчитать крутящий момент из мощности и скорости)
• Напряжение сдвига при кручении материала

Возьмем Пример задачи для расчета диаметра вала по крутящему моменту.

Проблема: Вал передает мощность 200 кВт при 1200 об/мин.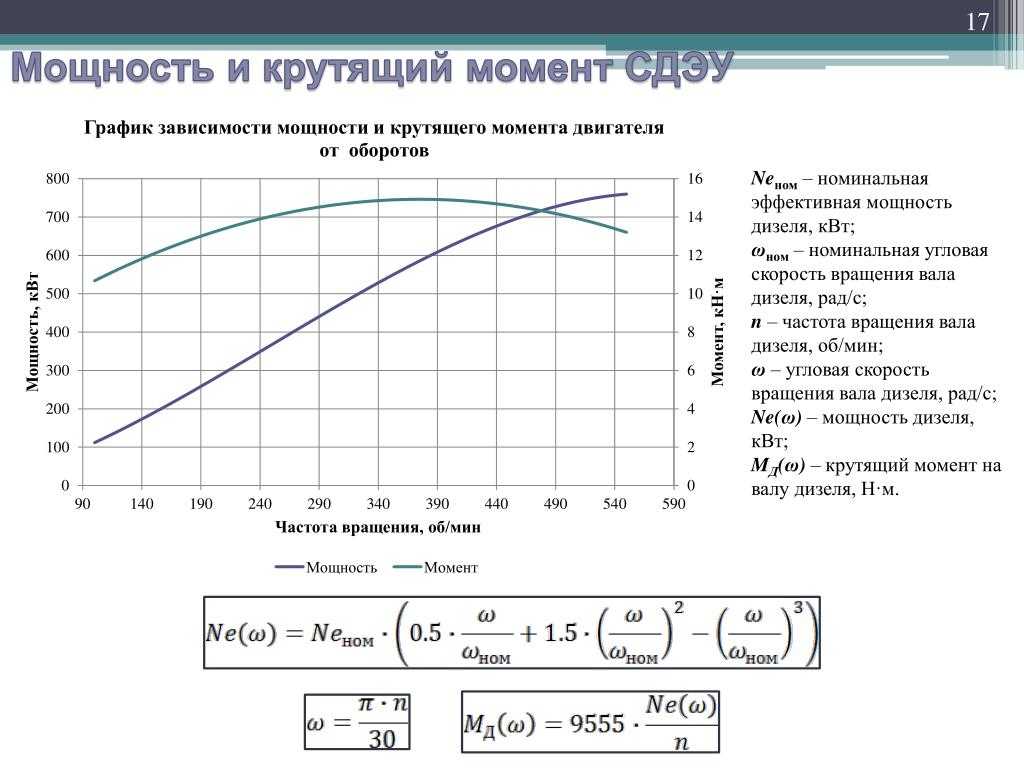 Найдите подходящий диаметр вала, если максимальный передаваемый крутящий момент превышает средний на 30 %. Максимально допустимое касательное напряжение принять равным 70 МПа.

ОТВЕТ:

. Данные

Power (P) = 200 кВт = 200 x 10 ³ W

Скорость (N) = 1200 об / мин

Рабочий крутящий момент (T _работа ) =?

Максимальный крутящий момент, который может быть приложен к валу = 30% от рабочего крутящего момента

T _Макс. = 1,3 x T _{Рабочий}

Мощность(P) = (2 π N T)/60 = ( 2 x 3,14 x 1200 x T)/60

200 x 10 ³ = 125,6 x T

T = 1592.36 N-m (Torque Calculator)

Operating Torque (T _Operating ) = 1592.36 N-m

Where T _Max = 1.3 x T _Operating

T _Max = 1.3 x  1592.36

T _Max = 2070,06 Н-м

Максимальный крутящий момент, который может быть приложен к валу (T _Max ) = 2070,06 Н-м

Исходя из этого максимального рабочего крутящего момента, мы можем найти диаметр вала с помощью приведенного выше уравнения

2070,06 x 10 ³ N-MM = (70 МПа (N-MM ² ) x π x D ³ ) 16

D ³ = 150687,075 мм

D = 53,19 мм

. Обязательный диаграмм будет будет диаметром A 53 33

D = 53,19 мм

. мм вал

Вот онлайн-калькулятор, который поможет вам рассчитать диаметр вала. Попробуйте, будет весело 🙂

(Калькулятор крутящего момента)

Здесь мы рассматриваем только максимальный крутящий момент, который может быть передан через вал, как известный фактор для расчета диаметра вала. Мы также можем найти диаметр вала с максимальным допустимым угловым скручиванием вала, учитывая жесткость вала (C) и отношение крутящего момента (приведенное ниже) из уравнения кручения.

Попробуйте выполнить следующее упражнение и опубликуйте свой ответ в поле для комментариев ниже! Посмотрим, кто сможет опубликовать правильный ответ.

Задача на упражнение: Вал передает мощность 97,5 кВт при 180 об/мин. Если допустимое напряжение сдвига в материале 60 МПа, подберите подходящий диаметр вала. Вал не должен скручиваться более чем на 1° на длине 3 метра. Принять C = 80 ГПа.

А если вал подвергается изгибу, то и диаметр вала можно рассчитать.