Работа, мощность, энергия — Физика — Теория, тесты, формулы и задачи
Оглавление:
- Основные теоретические сведения
- Механическая работа
- Мощность
- Кинетическая энергия
- Потенциальная энергия
- Коэффициент полезного действия
- Закон сохранения механической энергии
- Некоторые рекомендации к решению задач на работу
- Закон сохранения энергии и динамика вращательного движения
- Неупругие соударения
- Абсолютно упругий удар
- Рекомендации к решению некоторых сложных задач на законы сохранения
Механическая работа
К оглавлению…
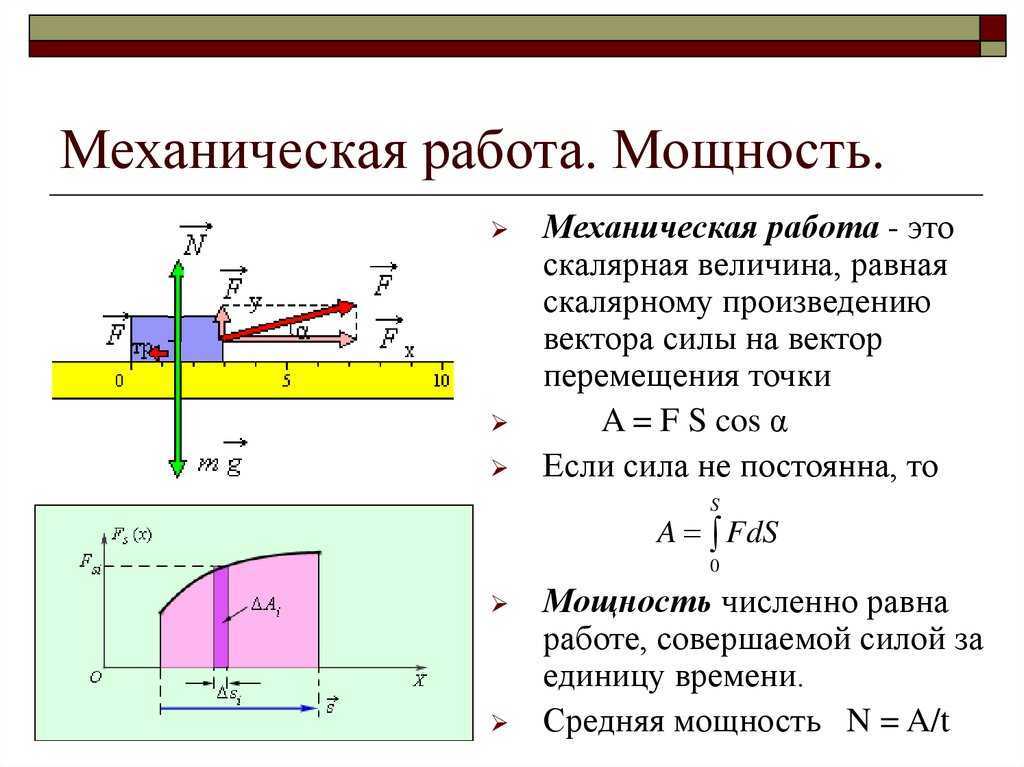
Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы. Работой, совершаемой постоянной силой F, называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла между векторами силы F и перемещения S:
Работа является скалярной величиной. Она может быть как положительна (0° ≤ α < 90°), так и отрицательна (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю. В системе СИ работа измеряется в джоулях (Дж). Джоуль равен работе, совершаемой силой в 1 ньютон на перемещении 1 метр в направлении действия силы.
Она может быть как положительна (0° ≤ α < 90°), так и отрицательна (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю. В системе СИ работа измеряется в джоулях (Дж). Джоуль равен работе, совершаемой силой в 1 ньютон на перемещении 1 метр в направлении действия силы.
Если же сила изменяется с течением времени, то для нахождения работы строят график зависимости силы от перемещения и находят площадь фигуры под графиком – это и есть работа:
Примером силы, модуль которой зависит от координаты (перемещения), может служить сила упругости пружины, подчиняющаяся закону Гука (Fупр = kx).
Мощность
К оглавлению…
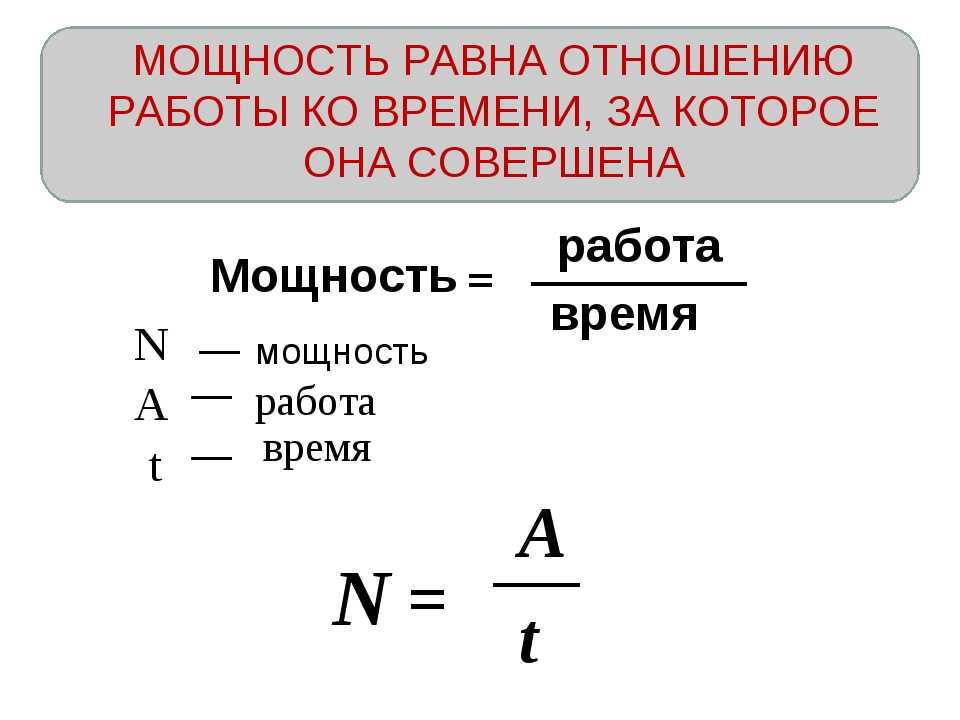
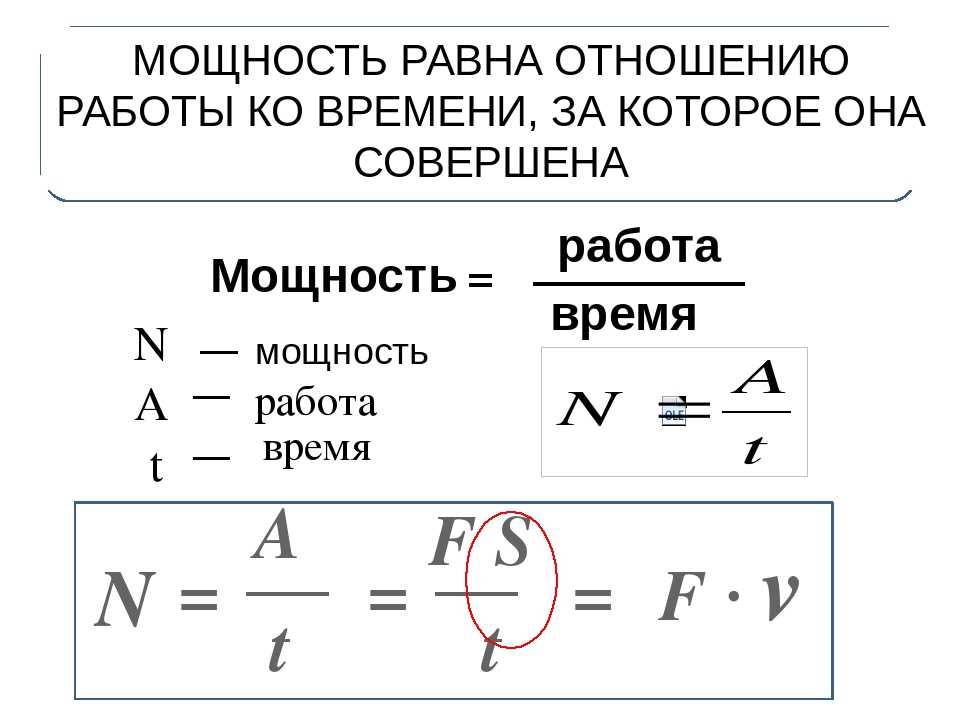
Работа силы, совершаемая в единицу времени, называется мощностью. Мощность P (иногда обозначают буквой N) – физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа:
По этой формуле рассчитывается средняя мощность, т. е. мощность обобщенно характеризующая процесс. Итак, работу можно выражать и через мощность: A = Pt (если конечно известна мощность и время совершения работы). Единица мощности называется ватт (Вт) или 1 джоуль за 1 секунду. Если движение равномерное, то:
е. мощность обобщенно характеризующая процесс. Итак, работу можно выражать и через мощность: A = Pt (если конечно известна мощность и время совершения работы). Единица мощности называется ватт (Вт) или 1 джоуль за 1 секунду. Если движение равномерное, то:
По этой формуле мы можем рассчитать мгновенную мощность (мощность в данный момент времени), если вместо скорости подставим в формулу значение мгновенной скорости. Как узнать, какую мощность считать? Если в задаче спрашивают мощность в момент времени или в какой-то точке пространства, то считается мгновенная. Если спрашивают про мощность за какой-то промежуток времени или участок пути, то ищите среднюю мощность.
КПД – коэффициент полезного действия, равен отношению полезной работы к затраченной, либо же полезной мощности к затраченной:
Какая работа полезная, а какая затраченная определяется из условия конкретной задачи путем логического рассуждения. К примеру, если подъемный кран совершает работу по подъему груза на некоторую высоту, то полезной будет работа по поднятию груза (так как именно ради нее создан кран), а затраченной – работа, совершенная электродвигателем крана.
Итак, полезная и затраченная мощность не имеют строгого определения, и находятся логическим рассуждением. В каждой задаче мы сами должны определить, что в этой задаче было целью совершения работы (полезная работа или мощность), а что было механизмом или способом совершения всей работы (затраченная мощность или работа).
В общем случае КПД показывает, как эффективно механизм преобразует один вид энергии в другой. Если мощность со временем изменяется, то работу находят как площадь фигуры под графиком зависимости мощности от времени:
Кинетическая энергия
К оглавлению…
Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела (энергией движения):
То есть если автомобиль массой 2000 кг движется со скоростью 10 м/с, то он обладает кинетической энергией равной Ек = 100 кДж и способен совершить работу в 100 кДж. Эта энергия может превратиться в тепловую (при торможении автомобиля нагревается резина колес, дорога и тормозные диски) или может быть потрачена на деформацию автомобиля и тела, с которым автомобиль столкнулся (при аварии). При вычислении кинетической энергии не имеет значения куда движется автомобиль, так как энергия, как и работа, величина скалярная.
При вычислении кинетической энергии не имеет значения куда движется автомобиль, так как энергия, как и работа, величина скалярная.
Тело обладает энергией, если способно совершить работу. Например, движущееся тело обладает кинетической энергией, т.е. энергией движения, и способно совершать работу по деформации тел или придания ускорения телам, с которыми произойдёт столкновение.
Физический смысл кинетической энергии: для того чтобы покоящееся тело массой m стало двигаться со скоростью v необходимо совершить работу равную полученному значению кинетической энергии. Если тело массой m движется со скоростью v, то для его остановки необходимо совершить работу равную его первоначальной кинетической энергии. При торможении кинетическая энергия в основном (кроме случаев соударения, когда энергия идет на деформации) «забирается» силой трения.
Теорема о кинетической энергии: работа равнодействующей силы равна изменению кинетической энергии тела:
Теорема о кинетической энергии справедлива и в общем случае, когда тело движется под действием изменяющейся силы, направление которой не совпадает с направлением перемещения. Применять данную теорему удобно в задачах на разгон и торможение тела.
Применять данную теорему удобно в задачах на разгон и торможение тела.
Потенциальная энергия
К оглавлению…
Наряду с кинетической энергией или энергией движения в физике важную роль играет понятие потенциальной энергии или энергии взаимодействия тел.
Потенциальная энергия определяется взаимным положением тел (например, положением тела относительно поверхности Земли). Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения тела и определяется только начальным и конечным положениями (так называемые консервативные силы). Работа таких сил на замкнутой траектории равна нулю. Таким свойством обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии.
Потенциальная энергия тела в поле силы тяжести Земли рассчитывается по формуле:
Физический смысл потенциальной энергии тела: потенциальная энергия равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень (h – расстояние от центра тяжести тела до нулевого уровня).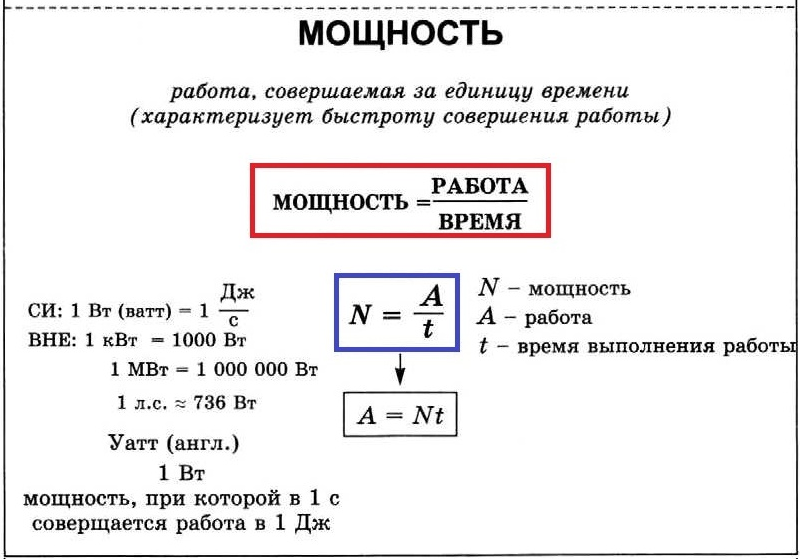 Если тело обладает потенциальной энергией, значит оно способно совершить работу при падении этого тела с высоты h до нулевого уровня. Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком:
Если тело обладает потенциальной энергией, значит оно способно совершить работу при падении этого тела с высоты h до нулевого уровня. Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком:
Часто в задачах на энергию приходится находить работу по поднятию (переворачиванию, доставанию из ямы) тела. Во всех этих случаях нужно рассматривать перемещение не самого тела, а только его центра тяжести.
Потенциальная энергия Ep зависит от выбора нулевого уровня, то есть от выбора начала координат оси OY. В каждой задаче нулевой уровень выбирается из соображения удобства. Физический смысл имеет не сама потенциальная энергия, а ее изменение при перемещении тела из одного положения в другое. Это изменение не зависит от выбора нулевого уровня.
Потенциальная энергия растянутой пружины рассчитывается по формуле:
где: k – жесткость пружины. Растянутая (или сжатая) пружина способна привести в движение прикрепленное к ней тело, то есть сообщить этому телу кинетическую энергию.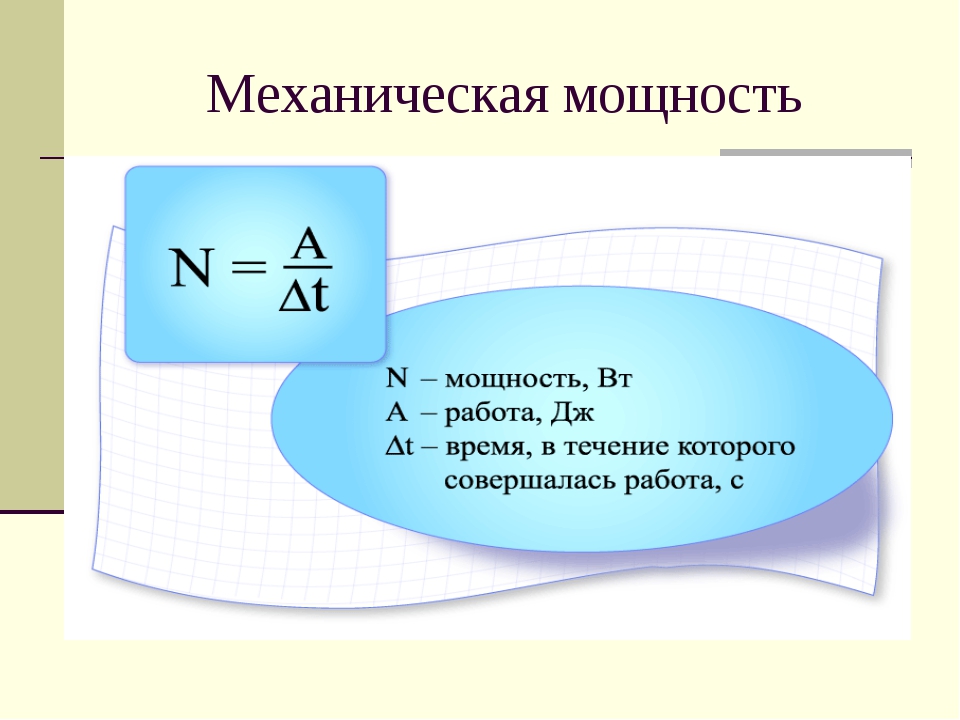 Следовательно, такая пружина обладает запасом энергии. Растяжение или сжатие х надо рассчитывать от недеформированного состояния тела.
Следовательно, такая пружина обладает запасом энергии. Растяжение или сжатие х надо рассчитывать от недеформированного состояния тела.
Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией. Если в начальном состоянии пружина уже была деформирована, а ее удлинение было равно x1, тогда при переходе в новое состояние с удлинением x2 сила упругости совершит работу, равную изменению потенциальной энергии, взятому с противоположным знаком (так как сила упругости всегда направлена против деформации тела):
Потенциальная энергия при упругой деформации – это энергия взаимодействия отдельных частей тела между собой силами упругости.
Работа силы трения зависит от пройденного пути (такой вид сил, чья работа зависит от траектории и пройденного пути называется: диссипативные силы). Понятие потенциальной энергии для силы трения вводить нельзя.
Коэффициент полезного действия
К оглавлению…
Коэффициент полезного действия (КПД) – характеристика эффективности системы (устройства, машины) в отношении преобразования или передачи энергии. Он определяется отношением полезно использованной энергии к суммарному количеству энергии, полученному системой (формула уже приведена выше).
КПД можно рассчитывать как через работу, так и через мощность. Полезная и затраченная работа (мощность) всегда определяются путем простых логических рассуждений.
В электрических двигателях КПД – отношение совершаемой (полезной) механической работы к электрической энергии, получаемой от источника. В тепловых двигателях – отношение полезной механической работы к затрачиваемому количеству теплоты. В электрических трансформаторах – отношение электромагнитной энергии, получаемой во вторичной обмотке, к энергии, потребляемой первичной обмоткой.
В силу своей общности понятие КПД позволяет сравнивать и оценивать с единой точки зрения такие различные системы, как атомные реакторы, электрические генераторы и двигатели, теплоэнергетические установки, полупроводниковые приборы, биологические объекты и т. д.
д.
Из–за неизбежных потерь энергии на трение, на нагревание окружающих тел и т.п. КПД всегда меньше единицы. Соответственно этому КПД выражается в долях затрачиваемой энергии, то есть в виде правильной дроби или в процентах, и является безразмерной величиной. КПД характеризует как эффективно работает машина или механизм. КПД тепловых электростанций достигает 35–40%, двигателей внутреннего сгорания с наддувом и предварительным охлаждением – 40–50%, динамомашин и генераторов большой мощности – 95%, трансформаторов – 98%.
Задачу, в которой нужно найти КПД или он известен, надо начать с логического рассуждения – какая работа является полезной, а какая затраченной.
Закон сохранения механической энергии
К оглавлению…
Полной механической энергией называется сумма кинетической энергии (т.е. энергии движения) и потенциальной (т.е. энергии взаимодействия тел силами тяготения и упругости):
Если механическая энергия не переходит в другие формы, например, во внутреннюю (тепловую) энергию, то сумма кинетической и потенциальной энергии остаётся неизменной. Если же механическая энергия переходит в тепловую, то изменение механической энергии равно работе силы трения или потерям энергии, или количеству выделившегося тепла и так далее, другими словами изменение полной механической энергии равно работе внешних сил:
Если же механическая энергия переходит в тепловую, то изменение механической энергии равно работе силы трения или потерям энергии, или количеству выделившегося тепла и так далее, другими словами изменение полной механической энергии равно работе внешних сил:
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему (т.е. такую в которой не действует внешних сил, и их работа соответственно равна нолю) и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной:
Это утверждение выражает закон сохранения энергии (ЗСЭ) в механических процессах. Он является следствием законов Ньютона. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой силами упругости и тяготения. Во всех задачах на закон сохранения энергии всегда будет как минимум два состояния системы тел. Закон гласит, что суммарная энергия первого состояния будет равна суммарной энергии второго состояния.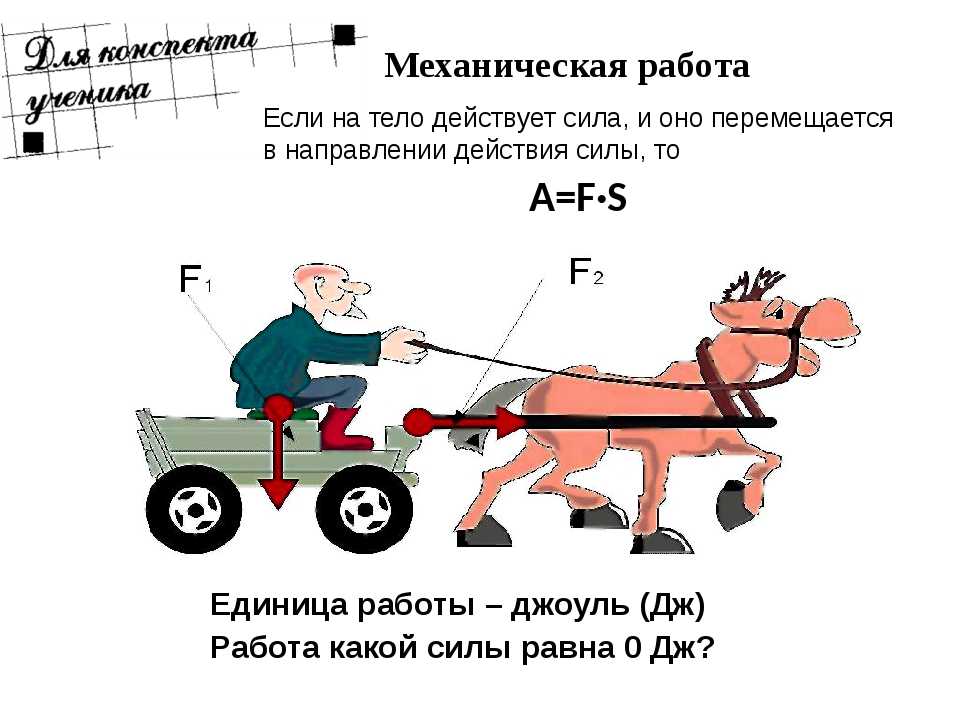
Алгоритм решения задач на закон сохранения энергии:
- Найти точки начального и конечного положения тела.
- Записать какой или какими энергиями обладает тело в данных точках.
- Приравнять начальную и конечную энергию тела.
- Добавить другие необходимые уравнения из предыдущих тем по физике.
- Решить полученное уравнение или систему уравнений математическими методами.
Важно отметить, что закон сохранения механической энергии позволил получить связь между координатами и скоростями тела в двух разных точках траектории без анализа закона движения тела во всех промежуточных точках. Применение закона сохранения механической энергии может в значительной степени упростить решение многих задач.
В реальных условиях практически всегда на движущиеся тела наряду с силами тяготения, силами упругости и другими силами действуют силы трения или силы сопротивления среды. Работа силы трения зависит от длины пути.
Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание). Таким образом энергия в целом (т.е. не только механическая) в любом случае сохраняется.
При любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую. Этот экспериментально установленный факт выражает фундаментальный закон природы – закон сохранения и превращения энергии.
Одним из следствий закона сохранения и превращения энергии является утверждение о невозможности создания «вечного двигателя» (perpetuum mobile) – машины, которая могла бы неопределенно долго совершать работу, не расходуя при этом энергии.
Разные задачи на работу
К оглавлению…
Если в задаче требуется найти механическую работу, то сначала выберите способ её нахождения:
- Работу можно найти по формуле: A = FS∙cosα.
 Найдите силу, совершающую работу, и величину перемещения тела под действием этой силы в выбранной системе отсчёта. Обратите внимание, что угол должен быть выбран между векторами силы и перемещения.
Найдите силу, совершающую работу, и величину перемещения тела под действием этой силы в выбранной системе отсчёта. Обратите внимание, что угол должен быть выбран между векторами силы и перемещения. - Работу внешней силы можно найти, как разность механической энергии в конечной и начальной ситуациях. Механическая энергия равна сумме кинетической и потенциальной энергий тела.
- Работу по подъёму тела с постоянной скоростью можно найти по формуле: A = mgh, где h – высота, на которую поднимается центр тяжести тела.
- Работу можно найти как произведение мощности на время, т.е. по формуле: A = Pt.
- Работу можно найти, как площадь фигуры под графиком зависимости силы от перемещения или мощности от времени.
Закон сохранения энергии и динамика вращательного движения
К оглавлению…
Задачи этой темы являются достаточно сложными математически, но при знании подхода решаются по совершенно стандартному алгоритму. Во всех задачах Вам придется рассматривать вращение тела в вертикальной плоскости. Решение будет сводиться к следующей последовательности действий:
Во всех задачах Вам придется рассматривать вращение тела в вертикальной плоскости. Решение будет сводиться к следующей последовательности действий:
- Надо определить интересующую Вас точку (ту точку, в которой необходимо определить скорость тела, силу натяжения нити, вес и так далее).
- Записать в этой точке второй закон Ньютона, учитывая, что тело вращается, то есть у него есть центростремительное ускорение.
- Записать закон сохранения механической энергии так, чтобы в нем присутствовала скорость тела в той самой интересной точке, а также характеристики состояния тела в каком-нибудь состоянии про которое что-то известно.
- В зависимости от условия выразить скорость в квадрате из одного уравнения и подставить в другое.
- Провести остальные необходимые математические операции для получения окончательного результата.
При решении задач надо помнить, что:
- Условие прохождения верхней точки при вращении на нити с минимальной скоростью – сила реакции опоры N в верхней точке равна 0.
 Такое же условие выполняется при прохождении верхней точки мертвой петли.
Такое же условие выполняется при прохождении верхней точки мертвой петли. - При вращении на стержне условие прохождения всей окружности: минимальная скорость в верхней точке равна 0.
- Условие отрыва тела от поверхности сферы – сила реакции опоры в точке отрыва равна нулю.
Неупругие соударения
К оглавлению…
Закон сохранения механической энергии и закон сохранения импульса позволяют находить решения механических задач в тех случаях, когда неизвестны действующие силы. Примером такого рода задач является ударное взаимодействие тел.
Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения. Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин.
С ударным взаимодействием тел нередко приходится иметь дело в обыденной жизни, в технике и в физике (особенно в физике атома и элементарных частиц). В механике часто используются две модели ударного взаимодействия – абсолютно упругий и абсолютно неупругий удары.
Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.
При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание). Для описания любых ударов Вам нужно записать и закон сохранения импульса, и закон сохранения механической энергии с учетом выделяющейся теплоты (предварительно крайне желательно сделать рисунок).
Абсолютно упругий удар
К оглавлению…
Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел. Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара. При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии. Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя.
Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара. При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии. Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя.
Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров. Таким образом, пользуясь законами сохранения механической энергии и импульса, можно определить скорости шаров после столкновения, если известны их скорости до столкновения. Центральный удар очень редко реализуется на практике, особенно если речь идет о столкновениях атомов или молекул. При нецентральном упругом соударении скорости частиц (шаров) до и после столкновения не направлены по одной прямой.
Частным случаем нецентрального упругого удара может служить соударения двух бильярдных шаров одинаковой массы, один из которых до соударения был неподвижен, а скорость второго была направлена не по линии центров шаров. В этом случае векторы скоростей шаров после упругого соударения всегда направлены перпендикулярно друг к другу.
В этом случае векторы скоростей шаров после упругого соударения всегда направлены перпендикулярно друг к другу.
Законы сохранения. Сложные задачи
К оглавлению…
Несколько тел
В некоторых задачах на закон сохранения энергии тросы с помощью которых перемещаются некие объекты могут иметь массу (т.е. не быть невесомыми, как Вы могли уже привыкнуть). В этом случае работу по перемещению таких тросов (а именно их центров тяжести) также нужно учитывать.
Если два тела, соединённые невесомым стержнем, вращаются в вертикальной плоскости, то:
- выбирают нулевой уровень для расчёта потенциальной энергии, например на уровне оси вращения или на уровне самой нижней точки нахождения одного из грузов и обязательно делают чертёж;
- записывают закон сохранения механической энергии, в котором в левой части записывают сумму кинетической и потенциальной энергии обоих тел в начальной ситуации, а в правой части записывают сумму кинетической и потенциальной энергии обоих тел в конечной ситуации;
- учитывают, что угловые скорости тел одинаковы, тогда линейные скорости тел пропорциональны радиусам вращения;
- при необходимости записывают второй закон Ньютона для каждого из тел в отдельности.

Разрыв снаряда
В случае разрыва снаряда выделяется энергия взрывчатых веществ. Чтобы найти эту энергию надо от суммы механических энергий осколков после взрыва отнять механическую энергию снаряда до взрыва. Также будем использовать закон сохранения импульса, записанный, в виде теоремы косинусов (векторный метод) или в виде проекций на выбранные оси.
Столкновения с тяжёлой плитой
Пусть навстречу тяжёлой плите, которая движется со скоростью v, движется лёгкий шарик массой m со скоростью uн. Так как импульс шарика много меньше импульса плиты, то после удара скорость плиты не изменится, и она будет продолжать движение с той же скоростью и в том же направлении. В результате упругого удара, шарик отлетит от плиты. Здесь важно понять, что не поменяется скорость шарика относительно плиты. В таком случае, для конечной скорости шарика получим:
Таким образом, скорость шарика после удара увеличивается на удвоенную скорость стены.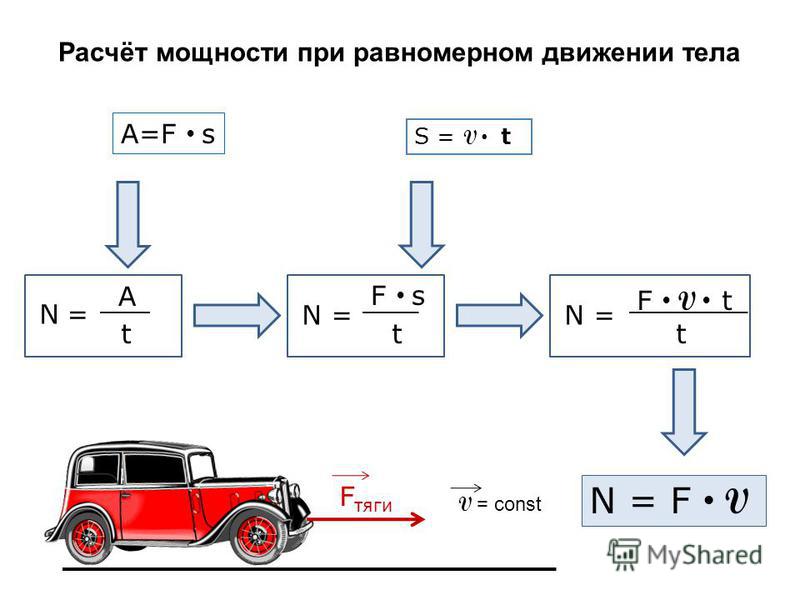 Аналогичное рассуждение для случая, когда до удара шарик и плита двигались в одном направлении, приводит к результату согласно которому скорость шарика уменьшается на удвоенную скорость стены:
Аналогичное рассуждение для случая, когда до удара шарик и плита двигались в одном направлении, приводит к результату согласно которому скорость шарика уменьшается на удвоенную скорость стены:
Задачи о максимальных и минимальных значениях энергии сталкивающихся шаров
В задачах такого типа главное понять, что потенциальная энергия упругой деформации шаров максимальна, если кинетическая энергия их движения минимальна – это следует из закона сохранения механической энергии. Сумма кинетических энергий шаров минимальна в тот момент, когда скорости шаров будут одинаковы по величине и направлены в одном направлении. В этот момент относительная скорость шаров равна нулю, а деформация и связанная с ней потенциальная энергия максимальна.
Механическая работа — определение, формула, виды, свойства
Для нас привычно понятие «работа» в бытовом смысле. Работая, мы совершаем какое-либо действие, чаще всего полезное. В физике (если точнее, то в механике) термин «работа» показывает, какую силу в результате действия приложили, и на какое расстояние тело в результате действия этой силы переместилось.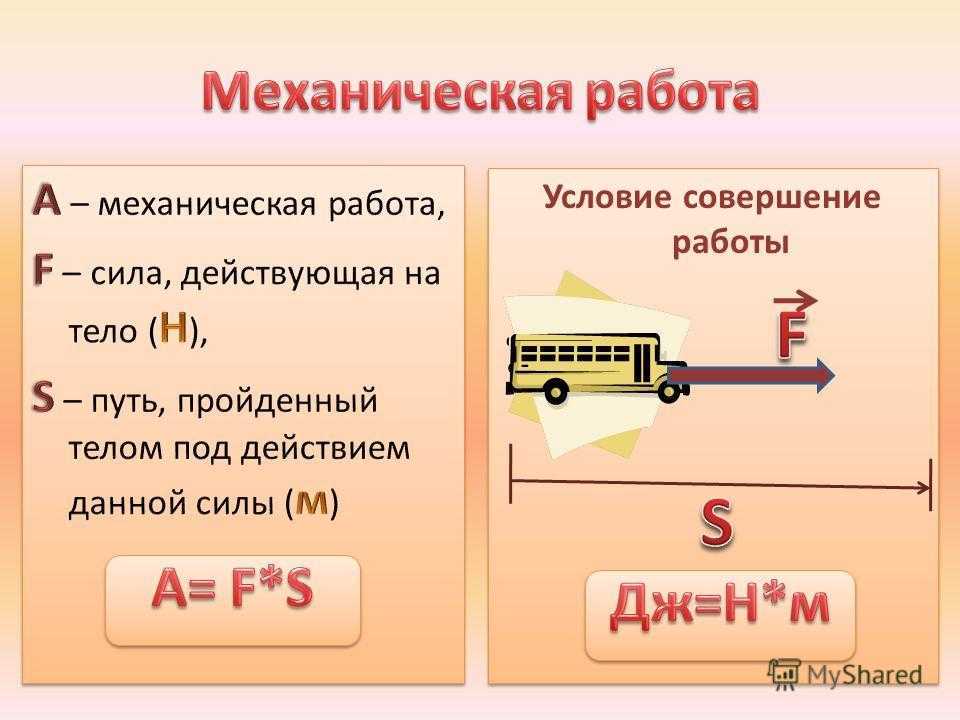
Например, нам нужно поднять велосипед по лестнице в квартиру. Тогда работа будет определяться тем, сколько весит велосипед и на каком этаже (на какой высоте) находится квартира.
Механическая работа — это физическая величина, прямо пропорциональная приложенной к телу силе и пройденному телом пути.
Чтобы рассчитать работу, нам необходимо умножить численное значение приложенной к телу силы F на путь, пройденный телом в направлении действия силы S. Работа обозначается латинской буквой А.
Механическая работа А = FS A — механическая работа [Дж] F — приложенная сила [Н] S — путь [м] |
Если под действием силы в 1 ньютон тело переместилось на 1 метр, то данной силой совершена работа в 1 джоуль.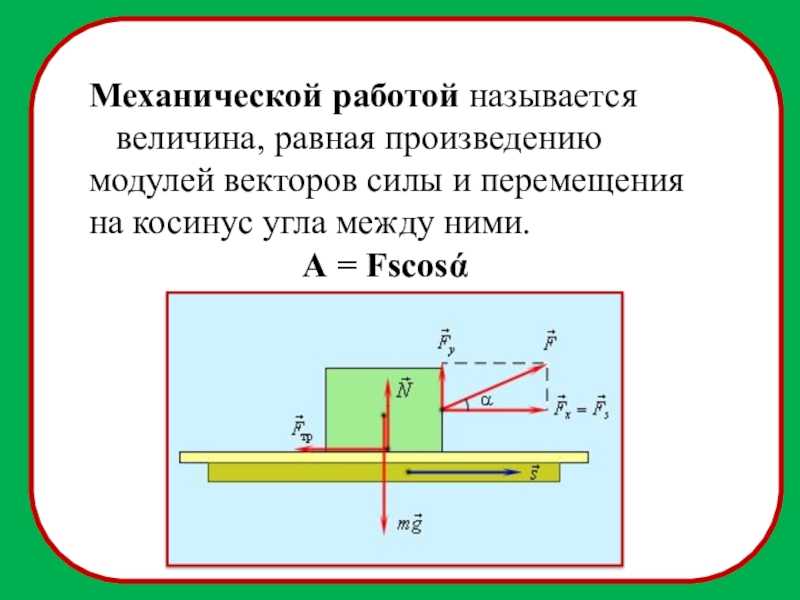
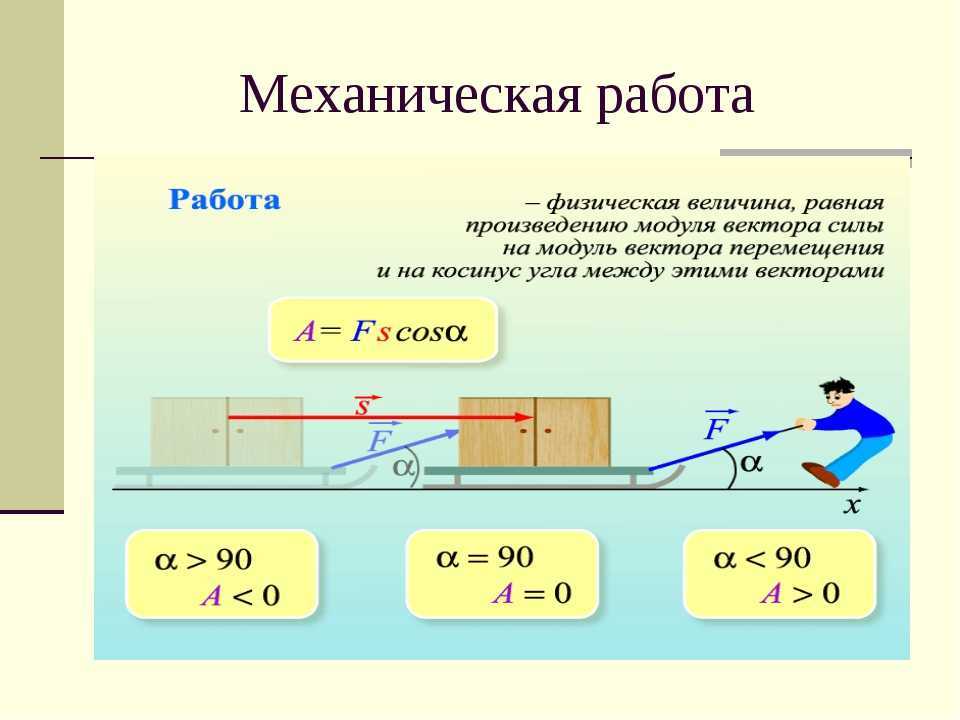
Поскольку сила и путь — векторные величины, в случае наличия между ними угла формула принимает вид.
Механическая работа А = FScosα A — механическая работа [Дж] F — приложенная сила [Н] S — путь [м] α — угол между векторами силы и перемещения [°] |
Числовое значение работы может становиться отрицательным, если вектор силы противоположен вектору скорости. Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае сила называется противодействующей.
Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае сила называется противодействующей.
Для совершения работы необходимы два условия:
- чтобы на тело действовала сила,
- чтобы происходило перемещение тела.
Сила, действующая на тело, может и не совершать работу. Например, если кто-то безуспешно пытается сдвинуть с места тяжелый шкаф. Сила, с которой человек действует на шкаф, не совершает работу, поскольку перемещение шкафа равно нулю.
Запомнить!
Работа равна нулю, если:
- при приложенной силе перемещение отсутствует;
- сила не приложена и тело перемещается по инерции;
- угол между векторами силы и перемещения равен 90°.

Полезная и затраченная работа
Был такой мифологический персонаж у древних греков — Сизиф. За то, что он обманул богов, те приговорили его после смерти вечно таскать огромный булыжник вверх по горе, откуда этот булыжник скатывался — и так без конца. В общем, Сизиф делал совершенно бесполезное дело с нулевым КПД. Поэтому бесполезную работу и называют «сизифов труд».
Чтобы разобраться в понятиях полезной и затраченной работы, давайте пофантазируем и представим, что Сизифа помиловали и камень больше не скатывается с горы, а КПД перестал быть нулевым.
Полезная работа в этом случае равна потенциальной энергии, приобретенной булыжником. Потенциальная энергия, в свою очередь, прямо пропорциональна высоте: чем выше расположено тело, тем больше его потенциальная энергия. Выходит, чем выше Сизиф прикатил камень, тем больше полезная работа.
Потенциальная энергия Еп = mgh m — масса тела [кг] g — ускорение свободного падения [м/с2] h — высота [м] На планете Земля g ≈ 9,8 м/с2 |
Затраченная работа в нашем примере — это механическая работа Сизифа. Механическая работа зависит от приложенной силы и пути, на протяжении которого эта сила была приложена.
Механическая работа зависит от приложенной силы и пути, на протяжении которого эта сила была приложена.
Механическая работа А = FS A — механическая работа [Дж] F — приложенная сила [Н] S — путь [м] |
И как же достоверно определить, какая работа полезная, а какая затраченная?
Все очень просто! Задаем два вопроса:
За счет чего происходит процесс?
Ради какого результата?
В примере выше процесс происходит ради того, чтобы тело поднялось на какую-то высоту, а значит — приобрело потенциальную энергию (для физики это синонимы).
Происходит процесс за счет энергии, затраченной Сизифом — вот и затраченная работа.
Мощность
На заводах по всему миру большинство задач выполняют машины. Например, если нам нужно закрыть крышечками тысячу банок колы, аппарат сделает это в считанные минуты. У человека эта задача заняла бы намного больше времени. Получается, что машина и человек выполняют одинаковую работу за разные промежутки времени. Для того, чтобы описать скорость выполнения работы, нам потребуется понятие мощности.
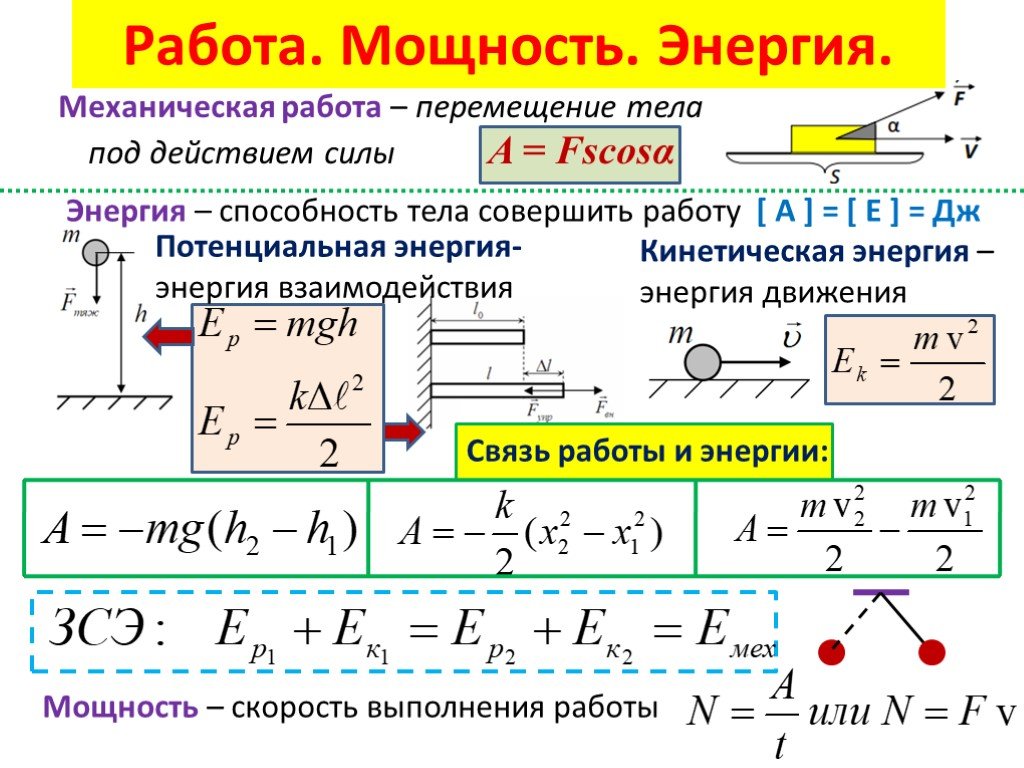
Мощностью называется физическая величина, равная отношению работы ко времени ее выполнения.
Мощность N = A/t N — мощность [Вт] A — механическая работа [Дж] t — время [с] |
Один ватт — это мощность, при которой работа в один джоуль совершается за одну секунду.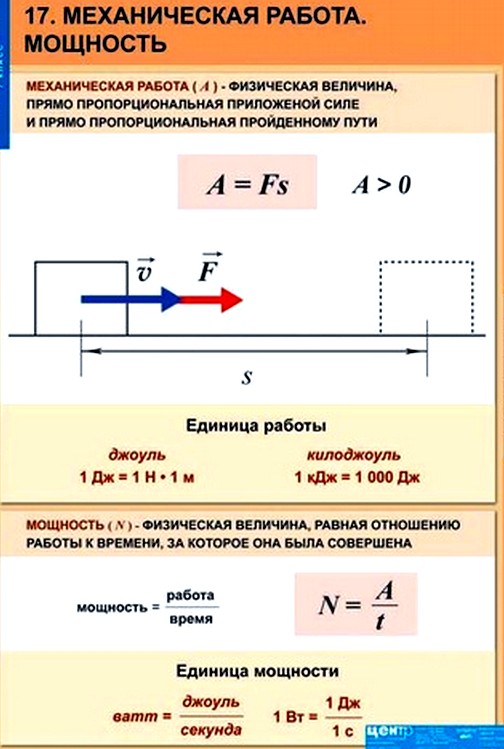
Также для мощности справедлива другая формула:
Мощность N = Fv N — мощность [Вт] F — приложенная сила [Н] v — скорость [м/с] |
Как и для работы, для мощности справедливо правило знаков: если векторы направлены противоположно, значение мощности будет отрицательным.
Поскольку сила и скорость — векторные величины, в случае наличия между ними угла формула принимает следующий вид:
Мощность N = Fvcosα N — мощность [Вт] F — приложенная сила [Н] v — скорость [м/с] α — угол между векторами силы и скорости [°] |
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Запишитесь и участвуйте в розыгрыше 8 уроков
Примеры решения задач
Задача 1
Ложка медленно тонет в большой банке меда. На нее действуют сила тяжести, сила вязкого трения и выталкивающая сила. Какая из этих сил при движении тела совершает положительную работу? Выберите правильный ответ:
Выталкивающая сила.
Сила вязкого трения.
Сила тяжести.
Ни одна из перечисленных сил.
Решение
Поскольку ложка падает вниз, перемещение направлено вниз. В ту же сторону, что и перемещение, направлена только сила тяжести. Это значит, что она совершает положительную работу.
Ответ: 3.
Задача 2
Ящик тянут по земле за веревку по горизонтальной окружности длиной L = 40 м с постоянной по модулю скоростью. Модуль силы трения, действующей на ящик со стороны земли, равен 80 H. Чему равна работа силы тяги за один оборот?
Модуль силы трения, действующей на ящик со стороны земли, равен 80 H. Чему равна работа силы тяги за один оборот?
Решение
Поскольку ящик тянут с постоянной по модулю скоростью, его кинетическая энергия не меняется. Вся энергия, которая расходуется на работу силы трения, должна поступать в систему за счет работы силы тяги. Отсюда находим работу силы тяги за один оборот:
Ответ: 3200 Дж.
Задача 3
Тело массой 2 кг под действием силы F перемещается вверх по наклонной плоскости на расстояние l = 5 м. Расстояние тела от поверхности Земли при этом увеличивается на 3 метра. Вектор силы F направлен параллельно наклонной плоскости, модуль силы F равен 30 Н. Какую работу при этом перемещении в системе отсчета, связанной с наклонной плоскостью, совершила сила F?
Решение
В данном случае нас просят найти работу силы F, совершенную при перемещении тела по наклонной плоскости.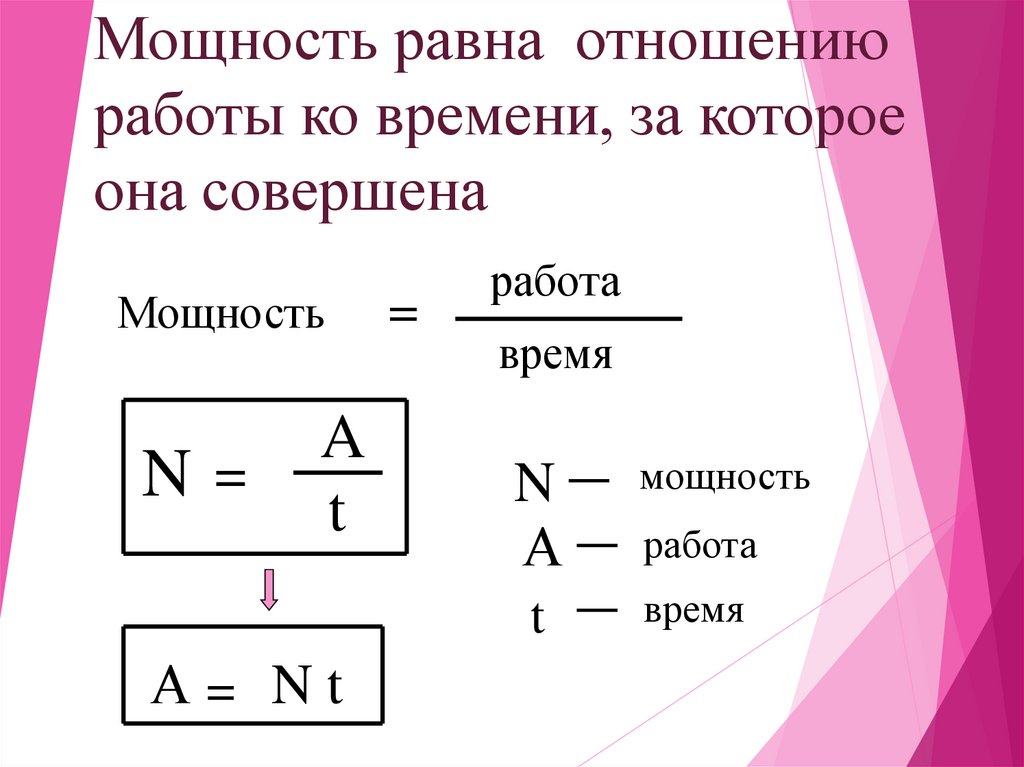 Это значит, что нас интересуют сила F и пройденный путь. Если бы нас спрашивали про работу силы тяжести, мы бы считали через силу тяжести и высоту.
Это значит, что нас интересуют сила F и пройденный путь. Если бы нас спрашивали про работу силы тяжести, мы бы считали через силу тяжести и высоту.
Работа силы определяется как скалярное произведение вектора силы и вектора перемещения тела. Следовательно:
A = Fl = 30 * 5 = 150 Дж
Ответ: 150 Дж.
Задача 4
Тело движется вдоль оси ОХ под действием силы F = 2 Н, направленной вдоль этой оси. На рисунке приведен график зависимости проекции скорости vx тела на эту ось от времени t. Какую мощность развивает эта сила в момент времени t = 3 с?
Решение
На графике видно, что проекция скорости тела в момент времени 3 секунды равна 5 м/с.
Мощность можно найти по формуле N = Fv.
N = FV = 2×5 = 10 Вт
Ответ: 10 Вт.
Попробуйте онлайн-курс подготовки к ЕГЭ по физике с опытным преподавателем в Skysmart!
9.1 Работа, мощность и теорема о работе-энергии. Физика
Раздел Цели обучения
К концу этого раздела вы сможете делать следующее:
- Описывать и применять теорему работа-энергия
- Описать и рассчитать работу и мощность
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:
- (6) Научные концепции. Учащийся знает, что изменения происходят в физической системе, и применяет законы сохранения энергии и импульса. Ожидается, что студент:
- (А)
описывать и применять теорему работа-энергия; - (С)
описать и вычислить работу и мощность.
- (А)
Кроме того, Руководство по физике для средней школы касается следующих стандартов:
- (6) Научные концепции. Учащийся знает, что изменения происходят в физической системе, и применяет законы сохранения энергии и импульса. Ожидается, что студент:
- (С)
рассчитать механическую энергию, мощность, генерируемую внутри, приложенный к ней импульс и импульс физической системы.
- (С)
Используйте лабораторную работу под названием «Работа и энергия» в качестве дополнения к материалам этого раздела.
Основные термины раздела
| энергия | гравитационная потенциальная энергия | джоулей | кинетическая энергия | механическая энергия |
| потенциальная энергия | мощность | Вт | работа | теорема работа-энергия |
Поддержка учителей
Поддержка учителей
В этом разделе учащиеся узнают, как работа определяет изменения кинетической энергии и что мощность — это скорость выполнения работы.
[BL][OL] Повторить понимание массы, скорости и ускорения под действием силы тяжести. Дайте общее определение слов потенциальный и кинетический .
[AL][AL] Напомните учащимся уравнение W=PEe=fmgW=PEe=fmg . Укажите, что ускорение свободного падения постоянно, поэтому PE e , которая является результатом работы силы тяжести, также будет постоянной. Сравните это с ускорением за счет других сил, таких как приложение мышц для подъема камня, которое может быть непостоянным.
Теорема о работе и энергии
В физике термин работа имеет очень конкретное определение. Работа — это приложение силы ff для перемещения объекта на расстояние d в направлении приложения силы. Работа, Вт , описывается уравнением
W=fd.W=fd.
Некоторые вещи, которые мы обычно считаем работой, не являются работой в научном смысле этого слова. Рассмотрим несколько примеров. Подумайте, почему каждое из следующих утверждений верно.
Рассмотрим несколько примеров. Подумайте, почему каждое из следующих утверждений верно.
- Домашнее задание не работа.
- Поднять камень вверх над землей — это работа.
- Нести камень по прямой траектории через газон с постоянной скоростью не работа.
Первые два примера довольно просты. Домашняя работа не является работой, потому что объекты не перемещаются на расстояние. Поднять камень над землей — это работа, потому что камень движется в направлении приложения силы. Последний пример менее очевиден. Напомним из законов движения, что сила равна , а не требуется для перемещения объекта с постоянной скоростью. Поэтому, хотя может быть приложена некоторая сила, чтобы удерживать камень над землей, результирующая сила не прилагается, чтобы поддерживать движение камня вперед с постоянной скоростью.
Поддержка учителей
Поддержка учителей
[BL][OL] Объясните, что когда эта теорема применяется к объекту, который сначала покоится, а затем ускоряется, член 12mv1212mv12 равен нулю.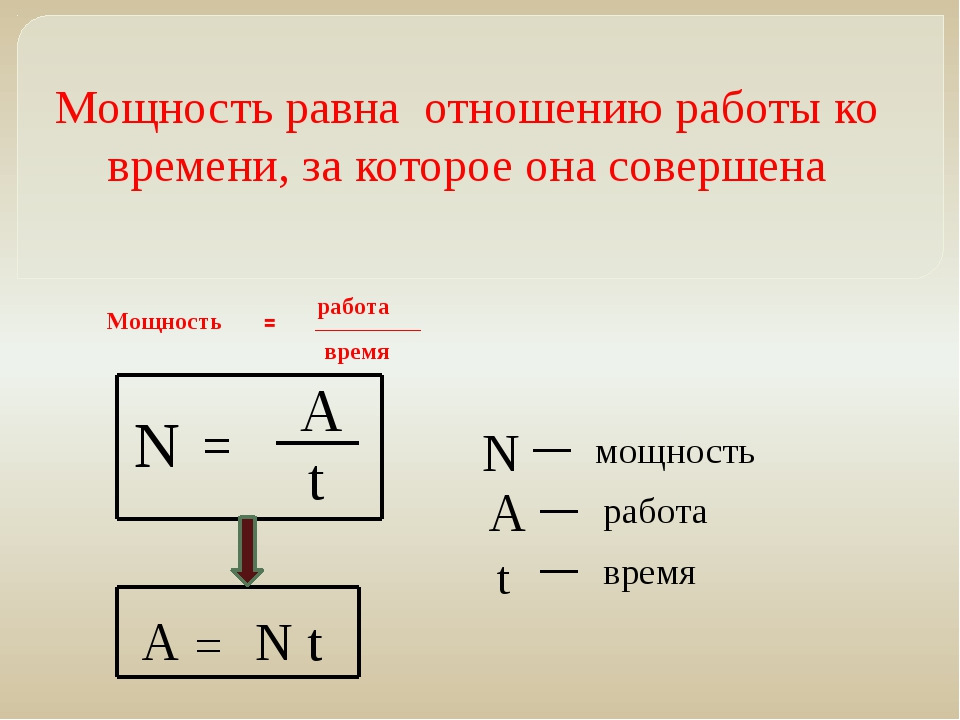
[OL][AL] Работа измеряется в джоулях и W=fdW=fd . Сила измеряется в ньютонах, а расстояние в метрах, поэтому джоули эквивалентны ньютон-метрам (Н⋅м)(Н⋅м)
Работа и энергия тесно связаны. Когда вы совершаете работу по перемещению объекта, вы изменяете энергию объекта. Вы (или объект) также тратите энергию на выполнение работы. Фактически энергию можно определить как способность совершать работу. Энергия может принимать различные формы, и одна форма энергии может трансформироваться в другую. В этой главе нас будет интересовать механическая энергия, которая существует в двух формах: кинетическая энергия и потенциальная энергия.
- Кинетическая энергия также называется энергией движения. Движущийся объект обладает кинетической энергией.
- Потенциальная энергия, иногда называемая запасенной энергией, бывает нескольких видов. Гравитационная потенциальная энергия — это накопленная энергия, которой обладает объект в результате его положения над поверхностью Земли (или другого объекта в космосе).
 Автомобиль американских горок на вершине холма обладает гравитационной потенциальной энергией.
Автомобиль американских горок на вершине холма обладает гравитационной потенциальной энергией.
Давайте посмотрим, как выполнение работы над объектом изменяет энергию объекта. Если мы приложим силу, чтобы поднять камень с земли, мы увеличим потенциальную энергию камня, PE 9.0080 . Если мы уроним камень, сила гравитации увеличит кинетическую энергию камня по мере его движения вниз, пока он не упадет на землю.
Сила, которую мы прикладываем, чтобы поднять камень, равна его весу, w , что равно его массе, m , умноженной на ускорение свободного падения, g .
f=w=mgf=w=mg
Работа, которую мы совершаем над камнем, равна силе, которую мы прикладываем, умноженной на расстояние d , на которое мы поднимаем камень. Работа, которую мы совершаем над камнем, также равна выигрышу камня в гравитационной потенциальной энергии, РЕ и .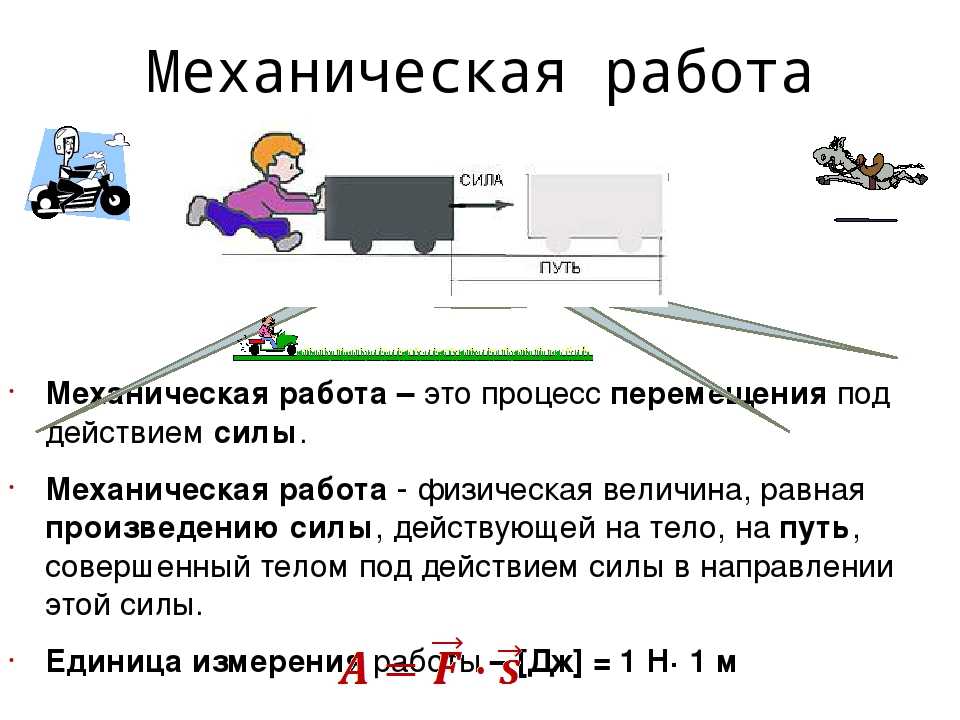
W=PEe=mgdW=PEe=mgd
Кинетическая энергия зависит от массы объекта и его скорости, v .
KE=12mv2KE=12mv2
Когда мы бросаем камень, сила тяжести заставляет камень падать, придавая камню кинетическую энергию. Когда работа, совершаемая над телом, увеличивает только его кинетическую энергию, то чистая работа равна изменению величины величины 12mv212mv2. Это формулировка теоремы работа-энергия, которая математически выражается как
W=ΔKE = 12mv22−12mv12.W=ΔKE = 12mv22−12mv12.
Нижние индексы 2 и 1 указывают конечную и начальную скорость соответственно. Эта теорема была предложена и успешно проверена Джеймсом Джоулем (рис. 9.2).
Имя Джоуль звучит знакомо? Джоуль (Дж) является метрической единицей измерения как работы, так и энергии. Измерение работы и энергии в одних и тех же единицах подтверждает идею о том, что работа и энергия связаны и могут быть преобразованы друг в друга. 1,0 Дж = 1,0 Н∙м, единица силы, умноженная на расстояние. 1,0 Н = 1,0 кг∙м/с 2 , поэтому 1,0 Дж = 1,0 кг∙м 2 /с 2 . Анализ единиц слагаемого (1/2) m v 2 даст те же единицы для джоулей.
1,0 Н = 1,0 кг∙м/с 2 , поэтому 1,0 Дж = 1,0 кг∙м 2 /с 2 . Анализ единиц слагаемого (1/2) m v 2 даст те же единицы для джоулей.
Рисунок
9.2
Джоуль назван в честь физика Джеймса Джоуля (1818–1889). (Ч. Х. Джинс, Wikimedia Commons)
Смотреть физику
Работа и энергия
В этом видео объясняется теорема об энергии работы и обсуждается, как работа, выполняемая над объектом, увеличивает КЭ объекта.
Проверка захвата
Верно или неверно — прирост энергии объекта, на который действует только гравитационная сила, равен произведению веса объекта на расстояние, на которое он падает.
- Правда
- Ложь
Поддержка учителей
Поддержка учителей
Повторите информацию о кинетической и потенциальной энергии, обсуждавшуюся ранее в этом разделе. Попросите учащихся различать и понимать два способа увеличения энергии объекта (1) приложение горизонтальной силы для увеличения KE и (2) приложение вертикальной силы для увеличения PE.
Попросите учащихся различать и понимать два способа увеличения энергии объекта (1) приложение горизонтальной силы для увеличения KE и (2) приложение вертикальной силы для увеличения PE.
Расчеты с использованием работы и мощности
В приложениях, связанных с работой, нас часто интересует, насколько быстро выполняется работа. Например, при проектировании американских горок важным фактором является время, необходимое для подъема автомобиля с американских горок на вершину первого холма. Полчаса подъема наверняка вызовут раздражение у райдеров и снизят продажи билетов. Давайте посмотрим, как рассчитать время, необходимое для выполнения работы.
Вспомните, что ставка может использоваться для описания количества, например работы, за период времени. Мощность – это скорость, с которой совершается работа. В этом случае скорость означает в единицу времени . Мощность рассчитывается путем деления выполненной работы на время, затраченное на эту работу.
P=WtP=Wt
Давайте рассмотрим пример, который поможет проиллюстрировать разницу между работой, силой и мощностью. Предположим, что женщина на рис. 9.3, поднимающая телевизор с помощью шкива, поднимает телевизор на четвертый этаж за две минуты, а мужчине, несущему телевизор по лестнице, требуется пять минут, чтобы добраться до того же места. Они проделали одинаковую работу (fd)(fd) на телевидении, потому что они переместили одинаковую массу на одно и то же расстояние по вертикали, что требует такой же величины восходящей силы. Однако женщина, использующая шкив, произвела больше энергии. Это потому, что она выполнила работу за меньшее время, поэтому знаменатель формулы мощности т , меньше. (Для простоты мы пока оставим в стороне тот факт, что человек, поднимающийся по лестнице, также проделал работу над собой.)
Рисунок
9.3
Как бы вы не перенесли телевизор на четвертый этаж, объем выполняемой работы и потенциальный прирост энергии одинаков.
Мощность может быть выражена в ваттах (Вт). Эта единица может использоваться для измерения мощности, связанной с любой формой энергии или работы. Вы, скорее всего, слышали этот термин, используемый в отношении электрических устройств, особенно лампочек. Умножение мощности на время дает количество энергии. Электричество продается в киловатт-часах, потому что это равно количеству потребляемой электроэнергии.
Единица измерения ватт была названа в честь Джеймса Уатта (1736–1819) (см. рис. 9.4). Он был шотландским инженером и изобретателем, который открыл, как увеличить мощность паровых двигателей.
Рисунок
9.4
Думает ли Джеймс Уатт о ваттах? (Карл Фредерик фон Бреда, Wikimedia Commons)
Поддержка учителей
Поддержка учителей
[BL][OL] Рассмотрите понятие о том, что работа изменяет энергию объекта или системы. Вспомните единицы работы, энергии, силы и расстояния. Используйте уравнения для механической энергии и работы, чтобы показать, что является работой, а что нет.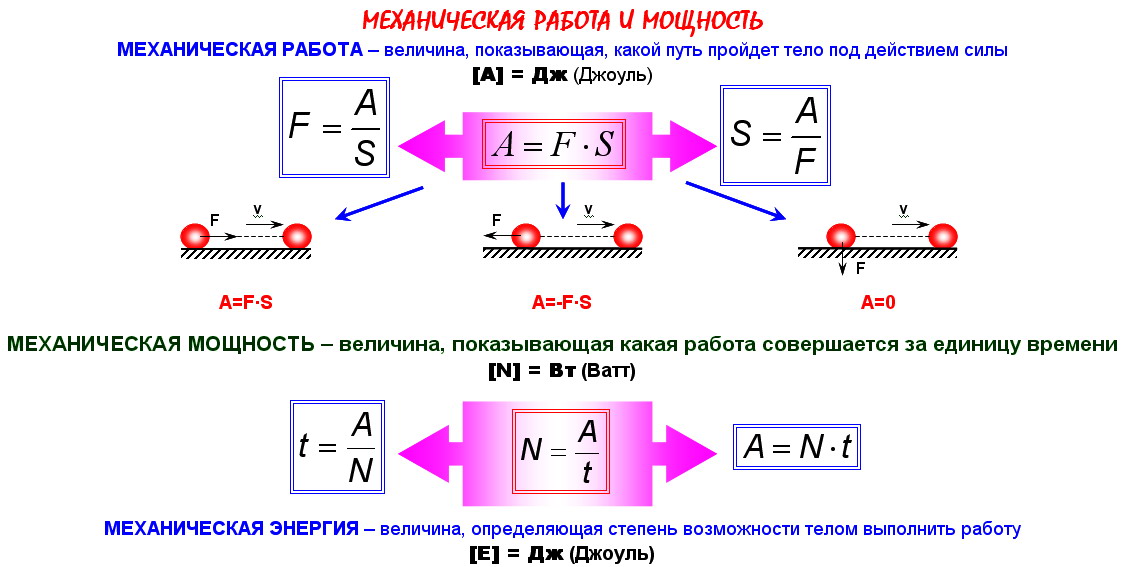 Объясните, почему держать что-то над землей или нести что-то по ровной поверхности — это не работа в научном смысле.
Объясните, почему держать что-то над землей или нести что-то по ровной поверхности — это не работа в научном смысле.
[ПР] Попросите учащихся использовать уравнения механической энергии, чтобы объяснить, почему каждое из них работает или не работает. Попросите их привести больше примеров, пока они не поймут разницу между научным термином работа и задачей, которая просто трудна, но не буквально работает (в научном смысле).
[BL][OL] Подчеркните, что мощность — это скорость, и эта скорость означает «в единицу времени». В метрической системе это обычно секунды. Завершите раздел, устранив любые неверные представления о различиях между силой, работой и мощностью.
[AL] Объясните отношения между единицами силы, работы и мощности. Если W=fdW=fd и работа может быть выражена в Дж, то P=Wt=fdtP=Wt=fdt, поэтому мощность может быть выражена в единицах N⋅msN⋅ms
Также объясните, что мы покупаем электроэнергию в киловатт-часах, потому что , когда мощность умножается на время, единицы времени сокращаются, остается работа или энергия.
Смотреть физику
Роль Уатта в промышленной революции
Это видео демонстрирует, как ватты, полученные в результате изобретений Уатта, помогли сделать промышленную революцию возможной и позволили Англии вступить в новую историческую эру.
Проверка захвата
Какой вид механической энергии вырабатывает паровая машина?
- Потенциальная энергия
- Кинетическая энергия
- Атомная энергия
- Солнечная энергия
Прежде чем продолжить, убедитесь, что вы понимаете различия между силой, работой, энергией и мощностью. Сила, действующая на объект на расстоянии, работает. Работа может увеличивать энергию, а энергия может выполнять работу. Мощность – это скорость, с которой совершается работа.
Рабочий пример
Применение теоремы о работе и энергии
Фигуристка массой 50 кг скользит по льду со скоростью 8 м/с, когда ее друг подходит сзади и толкает ее, в результате чего ее скорость увеличивается до 12 м/с. Сколько работы сделал друг на фигуристке?
Сколько работы сделал друг на фигуристке?
Стратегия
К задаче можно применить теорему о работе-энергии. Напишите уравнение теоремы и упростите его, если возможно.
W=ΔKE = 12mv22−12mv12W=ΔKE = 12mv22−12mv12
Упростить до W=12m(v22−v12) Упростить до W=12m(v22−v12)
Решение
Определите переменные.
м = 50 кг,
v2=12мс, иv1=8мсv2=12мс, иv1=8мс
9,1
Замена.
W=1250(122−82)=2000 JW=1250(122−82)=2000 Дж
9.2
Обсуждение
Работа над объектом или системой увеличивает ее энергию. В этом случае увеличивается кинетическая энергия фигуриста. Отсюда следует, что прирост энергии должен быть равен разнице КЭ до и после толчка.
Советы для успеха
Эта задача иллюстрирует общий метод решения задач, требующих применения формул: определить неизвестные и известные переменные, выразить неизвестные переменные через известные переменные, а затем ввести все известные значения.
Поддержка учителей
Поддержка учителей
Определите три переменные и выберите соответствующее уравнение. Различайте начальную и конечную скорость и обращайте внимание на знак минус.
Определите переменные. м = 50 кг,
v2=12мс, иv1=8мсv2=12мс, иv1=8мс
Замена.
W=1250(122−82)=2000 JW=1250(122−82)=2000 J
Практические задачи
1.
(кредит: модификация работы Pass My Exams, CC BY-SA 4.0)
Рисунок
9.6
Тяжелоатлет поднимает с пола штангу массой 200 Н на высоту 2 м. Сколько работы сделано?
0\,\текст{J}
100\,\text{J}
200\,\text{J}
400\,\text{J}
2.
Определите, какое из следующих действий генерирует больше энергии. Показать свою работу.
- перенос телевизора 100\,\text{N} на второй этаж через 50\,\text{s} или
- нести 24\,\text{N} арбуз на второй этаж в 10\,\text{s}?
Перенос 100\,\text{N} телевизора генерирует больше энергии, чем перенос 24\,\text{N} арбуза на ту же высоту, потому что мощность определяется как проделанная работа, умноженная на временной интервал.
Перенос 100\,\text{N} телевизора генерирует больше энергии, чем перенос 24\,\text{N} арбуза на ту же высоту, потому что мощность определяется как отношение выполненной работы к интервалу времени.
Перенос 24\,\text{N} арбуза генерирует больше энергии, чем перенос 100\,\text{N} телевизора на ту же высоту, потому что мощность определяется как проделанная работа, умноженная на временной интервал.

Перенос 24\,\text{N} арбуза генерирует больше энергии, чем перенос 100\,\text{N} телевизора на ту же высоту, потому что мощность определяется как отношение выполненной работы к временному интервалу.
Проверьте свое понимание
3.
Укажите два свойства, которые выражаются в джоулях.
работа и сила
энергия и вес
работа и энергия
вес и сила
4.
Когда кокос падает с дерева, над ним выполняется работа W , когда он падает на пляж. Эта работа описывается уравнением
W= Fd = 12mv22−12mv12.W= Fd = 12mv22−12mv12.
9.3
Определите количества F , d , m , v 1 и v 7 2 в этом событии.
- F — сила тяжести, равная весу кокоса, d — расстояние, на которое падает орех, м — масса земли, v 1 — начальная скорость, а v 2 — скорость, с которой он ударяется о берег.
- F — сила тяжести, равная весу кокоса, d — расстояние, на которое падает орех, м — масса кокоса, v 1 — начальная скорость, а v 2 — скорость, с которой он достигает берега.

- F — сила тяжести, равная весу кокоса, d — расстояние, на которое падает орех, м — масса земли, v 1 — скорость с которой он попадает на берег, а v 2 — начальная скорость.
- F — сила тяжести, равная весу кокоса, d — расстояние, на которое падает орех, м — масса кокоса, v 1 — скорость, с которой он падает на пляж, v 2 — начальная скорость.
Поддержка учителей
Поддержка учителей
Используйте вопросы «Проверить ваше понимание», чтобы оценить достижение учащимися учебных целей раздела. Если учащиеся испытывают трудности с выполнением определенной задачи, функция «Проверить понимание» поможет определить, какая из них, и направит учащихся к соответствующему содержанию.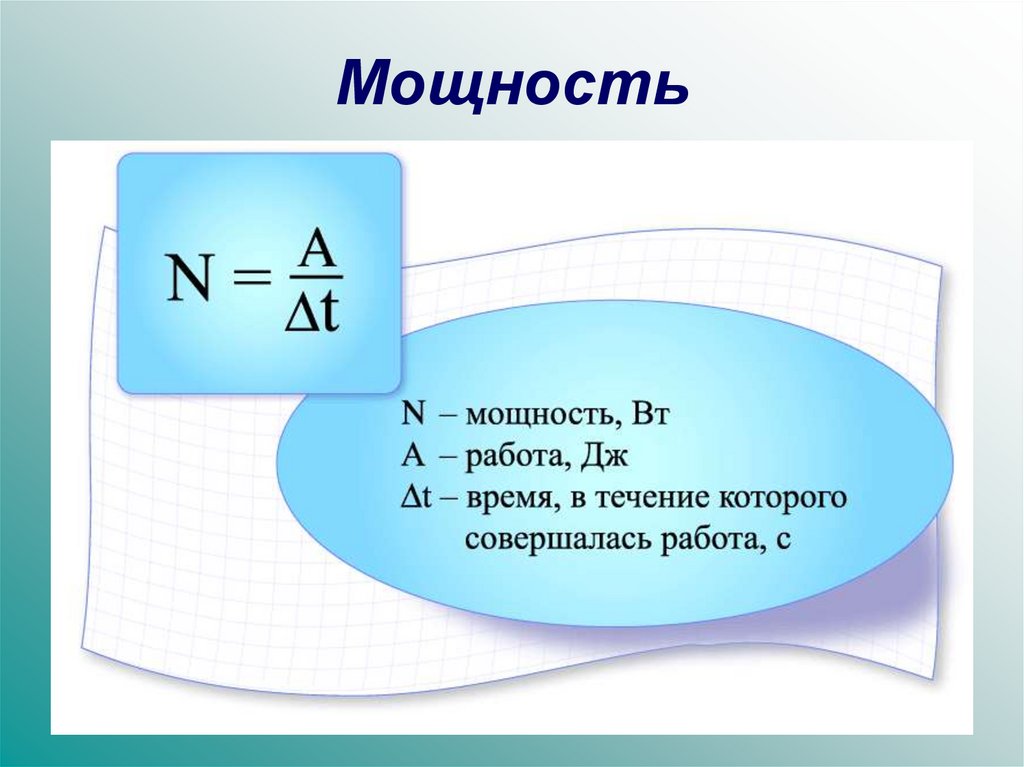
Мощность
Количественная работа связана с силой, вызывающей перемещение. Работа не имеет ничего общего с количеством времени, в течение которого эта сила действует, вызывая смещение. Иногда работа выполняется очень быстро, а иногда работа выполняется довольно медленно. Например, скалолазу требуется аномально много времени, чтобы поднять свое тело на несколько метров вверх по склону утеса. С другой стороны, турист (который выбирает более легкий путь в гору) может поднять свое тело на несколько метров за короткий промежуток времени. Два человека могут выполнить один и тот же объем работы, но турист сделает ее за значительно меньшее время, чем скалолаз. Величина, связанная со скоростью, с которой выполняется определенный объем работы, называется мощностью. У туриста больше номинальная мощность , чем скалолаз.
Мощность — это скорость выполнения работы. Это соотношение работа/время. Математически это вычисляется с использованием следующего уравнения.
или
P = Вт/т
Стандартной метрической единицей мощности является Вт . Как следует из уравнения мощности, единица мощности эквивалентна единице работы, деленной на единицу времени. Таким образом, ватт эквивалентен джоулю в секунду. По историческим причинам лошадиных сил иногда используется для описания мощности, выдаваемой машиной. Одна лошадиная сила эквивалентна примерно 750 Вт.
Большинство машин спроектированы и изготовлены для работы с объектами. Все машины обычно описываются номинальной мощностью. Номинальная мощность указывает скорость, с которой эта машина может работать с другими объектами. Таким образом, мощность машины — это отношение работы к времени для этой конкретной машины. Автомобильный двигатель является примером машины, которой присваивается номинальная мощность. Номинальная мощность относится к тому, насколько быстро автомобиль может разогнать автомобиль.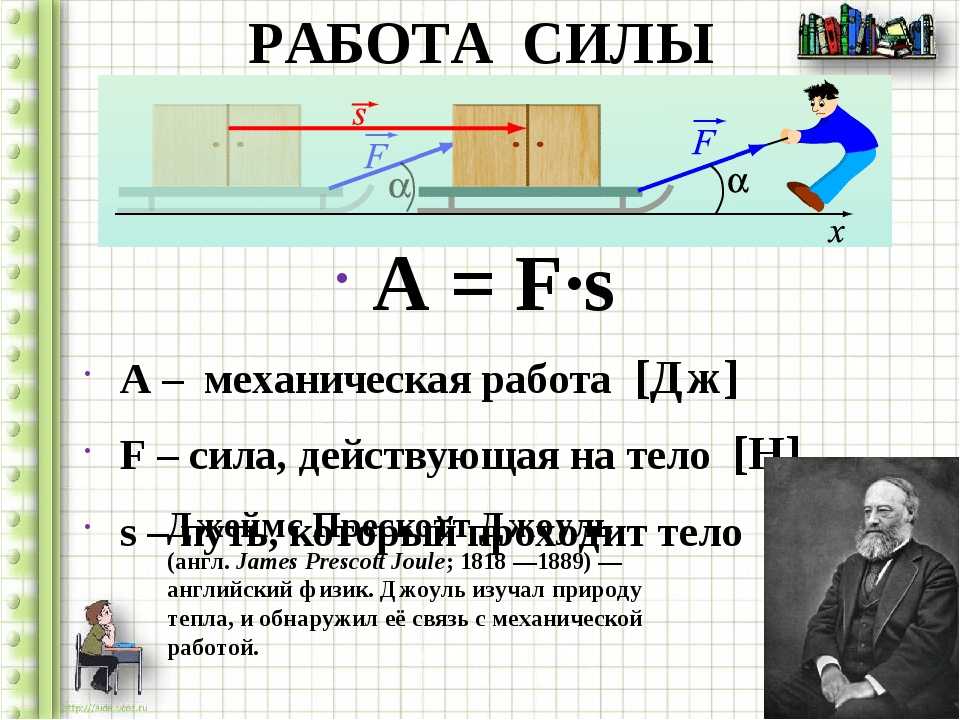 Предположим, что двигатель мощностью 40 лошадиных сил может разогнать автомобиль с 0 до 60 миль/ч за 16 секунд. Если бы это было так, то автомобиль, мощность которого в четыре раза превышала бы мощность, мог бы выполнить тот же объем работы за четверть времени. То есть 160-сильный двигатель мог разогнать тот же автомобиль с 0 до 60 миль/ч за 4 секунды. Дело в том, что при одном и том же объеме работы мощность и время обратно пропорциональны. Уравнение мощности предполагает, что более мощный двигатель может выполнить тот же объем работы за меньшее время.
Предположим, что двигатель мощностью 40 лошадиных сил может разогнать автомобиль с 0 до 60 миль/ч за 16 секунд. Если бы это было так, то автомобиль, мощность которого в четыре раза превышала бы мощность, мог бы выполнить тот же объем работы за четверть времени. То есть 160-сильный двигатель мог разогнать тот же автомобиль с 0 до 60 миль/ч за 4 секунды. Дело в том, что при одном и том же объеме работы мощность и время обратно пропорциональны. Уравнение мощности предполагает, что более мощный двигатель может выполнить тот же объем работы за меньшее время.
Человек также является машиной с номинальной мощностью . Некоторые люди обладают большей силой, чем другие. То есть некоторые люди способны выполнять тот же объем работы за меньшее время или больший объем работы за то же время. Обычная физическая лаборатория включает в себя быстрый подъем по лестнице и использование информации о массе, росте и времени для определения личной силы студента. Несмотря на диагональное движение по лестнице, часто предполагается, что горизонтальное движение является постоянным, и вся сила от ступеней используется для подъема ученика вверх с постоянной скоростью. Таким образом, вес ученика равен силе, совершающей работу над учеником, а высота лестницы — смещению вверх. Предположим, что Бен Пумпинирон поднимает свое 80-килограммовое тело по 2,0-метровой лестнице за 1,8 секунды. Если бы это было так, то мы могли бы вычислить 9 Бена.0507 номинальная мощность . Можно предположить, что Бен должен приложить к лестнице направленную вниз силу в 800 ньютонов, чтобы поднять свое тело. При этом лестница будет толкать тело Бена вверх с достаточной силой, чтобы поднять его тело вверх по лестнице. Также можно предположить, что угол между силой лестницы, действующей на Бена, и смещением Бена равен 0 градусов. С этими двумя приближениями номинальная мощность Бена может быть определена, как показано ниже.
Таким образом, вес ученика равен силе, совершающей работу над учеником, а высота лестницы — смещению вверх. Предположим, что Бен Пумпинирон поднимает свое 80-килограммовое тело по 2,0-метровой лестнице за 1,8 секунды. Если бы это было так, то мы могли бы вычислить 9 Бена.0507 номинальная мощность . Можно предположить, что Бен должен приложить к лестнице направленную вниз силу в 800 ньютонов, чтобы поднять свое тело. При этом лестница будет толкать тело Бена вверх с достаточной силой, чтобы поднять его тело вверх по лестнице. Также можно предположить, что угол между силой лестницы, действующей на Бена, и смещением Бена равен 0 градусов. С этими двумя приближениями номинальная мощность Бена может быть определена, как показано ниже.
Мощность Бена составляет 871 Вт. Он довольно лошадь .
Другая формула мощности
Выражением мощности является работа/время. А поскольку выражение для работы есть сила*смещение, выражение для мощности можно переписать как (сила*смещение)/время. Поскольку выражение для скорости есть перемещение/время, выражение для мощности можно еще раз переписать как сила*скорость. Это показано ниже.
Поскольку выражение для скорости есть перемещение/время, выражение для мощности можно еще раз переписать как сила*скорость. Это показано ниже.
Это новое уравнение для мощности показывает, что мощная машина одновременно мощная (большая сила) и быстрая (большая скорость). Мощный автомобильный двигатель силен и быстр. Мощная сельскохозяйственная техника надежна и быстра. Мощный тяжелоатлет силен и быстр. Сильный лайнсмен в футбольной команде силен и быстр. А 9Машина 0507 , которая достаточно мощна, чтобы приложить большую силу, чтобы вызвать перемещение за небольшой промежуток времени (т. е. с большой скоростью), является мощной машиной.
Проверьте свое понимание
Используйте свое понимание работы и мощности, чтобы ответить на следующие вопросы. Когда закончите, нажмите кнопку, чтобы просмотреть ответы.
1. Два студента-физика, Уилл Н. Эндэйбл и Бен Пампинирон, в зале тяжелой атлетики. Уилл поднимает над головой 100-фунтовую штангу 10 раз за одну минуту; Бен поднимает 100-фунтовую штангу над головой 10 раз за 10 секунд. Кто из учеников больше всего работает? ______________ Кто из учеников проявляет наибольшую силу? ______________ Объясните свои ответы.
Эндэйбл и Бен Пампинирон, в зале тяжелой атлетики. Уилл поднимает над головой 100-фунтовую штангу 10 раз за одну минуту; Бен поднимает 100-фунтовую штангу над головой 10 раз за 10 секунд. Кто из учеников больше всего работает? ______________ Кто из учеников проявляет наибольшую силу? ______________ Объясните свои ответы.
2. Во время физического кабинета Джек и Джилл взбежали на холм. Джек вдвое массивнее Джилл; однако Джилл преодолевает то же расстояние вдвое быстрее. Кто работал больше всех? ______________ Кто приложил больше всего усилий? ______________ Объясните свои ответы.
3. Усталая белка (массой около 1 кг) отжимается, прикладывая силу, поднимающую ее центр масс на 5 см, чтобы совершить работу всего лишь в 0,50 Дж. Если усталая белка проделает всю эту работу за 2 секунды, то определите ее мощность.
4.

 Найдите силу, совершающую работу, и величину перемещения тела под действием этой силы в выбранной системе отсчёта. Обратите внимание, что угол должен быть выбран между векторами силы и перемещения.
Найдите силу, совершающую работу, и величину перемещения тела под действием этой силы в выбранной системе отсчёта. Обратите внимание, что угол должен быть выбран между векторами силы и перемещения.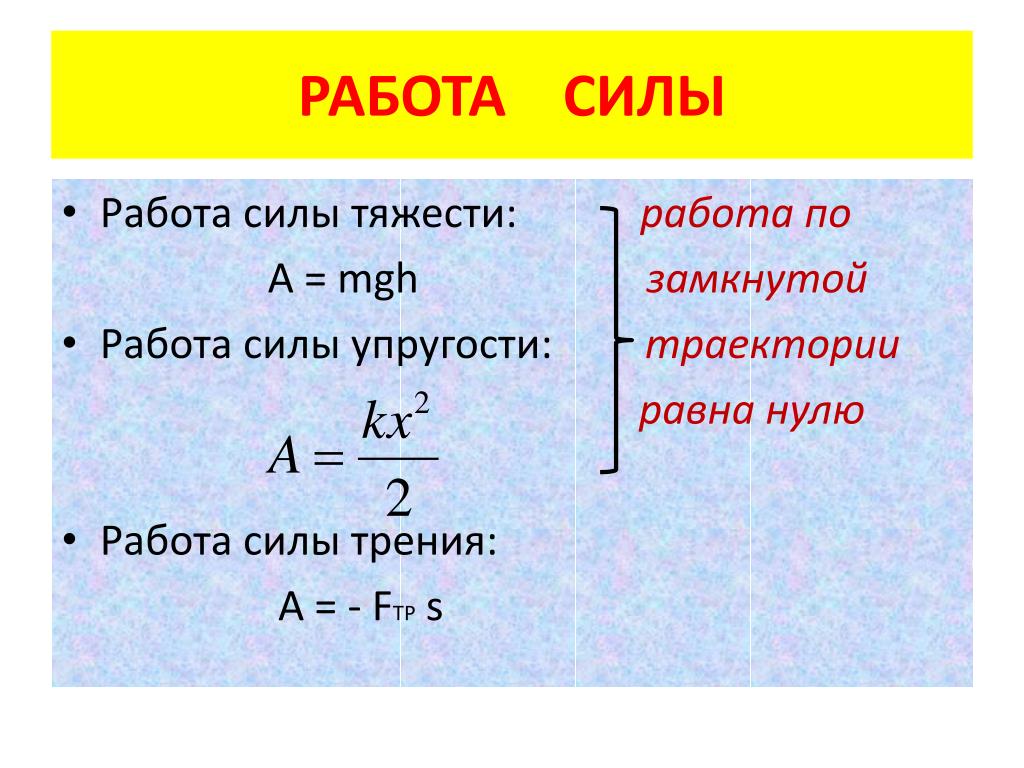 Такое же условие выполняется при прохождении верхней точки мертвой петли.
Такое же условие выполняется при прохождении верхней точки мертвой петли.

 Автомобиль американских горок на вершине холма обладает гравитационной потенциальной энергией.
Автомобиль американских горок на вершине холма обладает гравитационной потенциальной энергией.