Основные параметры зубчатых колес — Энциклопедия по машиностроению XXL
ОСНОВНЫЕ ПАРАМЕТРЫ ЗУБЧАТЫХ КОЛЕС Колеса (катки) фрикционной цилиндрической передачи прижаты друг к другу. Поэтому при вращении одного колеса (в результате возникновения сил трения) приводится во вращение и другое [c.216]
Модуль является основным параметром зубчатого колеса и его величины установлены СТ СЭВ 310—76. Многие размеры зубчатого колеса зависят от величины модуля, например, размеры зуба, венца, ступицы и т. д. [c.206]
Основным параметром зубчатых колес является модуль. Модуль т — это длина диаметра делительной окружности, приходящаяся на один зуб колеса. Стандартом установлен ряд чисел модулей (табл. 58). [c.147]
Модуль зубьев — основной параметр зубчатого колеса. Для пары колес, находящихся в зацеплении, модуль должен быть одинаковым. Модули зубьев для цилиндрических и конических передач регламентированы ГОСТ 9563—60. Значения стандартных модулей от 1 до 14 мм приведены в табл. 71.
[c.114]
Значения стандартных модулей от 1 до 14 мм приведены в табл. 71.
[c.114]
Все основные параметры зубчатых колес выражают через модули, а именно шаг зубьев [c.115]
Заполненный бланк 1, содержащий таблицу основных параметров зубчатых колес и зацепления для оптимального значения с, график зависимости е = / (с), кальку с эскизом зубчатого зацепления. [c.49]
На сборочном чертеже должны быть указаны габаритные, установочные и присоединительные размеры, расчетные размеры, основные параметры зубчатых колес, шкал и других составных частей и их элементов, непосредственно связанных с эксплуатацией оборудования. В необходимых случаях должны быть указаны также размеры ответственных деталей, предельные отклонения этих размеров, материал, твердость, покрытие, шероховатость обработанных поверхностей и другие технические данные. [c.36]
ОСНОВНЫЕ ПАРАМЕТРЫ ЗУБЧАТЫХ КОЛЕС И РЕДУКТОРОВ
[c. 403]
403]
Основные параметры зубчатых колес [c.451]
В работе студент должен научиться определять основные параметры зубчатых колес с эвольвентным профилем зуба. Основными параметрами зубчатого колеса с эвольвентным профилем являются модуль (т). число зубьев г и угол профиля производящей рейки Лр). Все остальные величины зубчатых колес могут быть [c.32]
Основные параметры зубчатых колес и редукторов [c.351]
Основные параметры зубчатого колеса показаны на рис. 1. [c.247]
Расчет основных параметров зубчатых колес. [c.35]
РАСЧЕТ ОСНОВНЫХ ПАРАМЕТРОВ ЗУБЧАТЫХ КОЛЕС [c.40]
Выбор основных параметров зубчатых колес и передач [c.17]
Рассмотрим основные параметры зубчатого колеса. На рис. 47, в дано пространственное изображение части зубчатого колеса с внешним расположением зубьев, а на рис. 47, г — его конструктивное изображение в ортогональной проекции. [c.89]
[c.89]
Подсчет основных параметров зубчатого колеса. Чтобы условно изобразить зубчатый венец, определяют диаметр трех окружностей.
[c.154]
Основные параметры зубчатых колес (диаметр, ширина, модуль, число зубьев и пр.) определяют при проектировании передачи (см. гл. XIV). Ниже рассматриваются вопросы, связанные с конструктивной формой зубчатых колес. [c.325]
Основные параметры зубчатого колеса электростартера [c.166]
Методы и периодичность текущего контроля основных параметров зубчатых колес и параметров технологического процесса после химико-термической обработки [c.448]
Г. 16530-83, 16531-83, 16532-83 — основные параметры зубчатых колес [c.11]
Одним из основных параметров зубчатых колес является модуль [c.254]
Освоить методику измерения основных параметров зубчатых колес.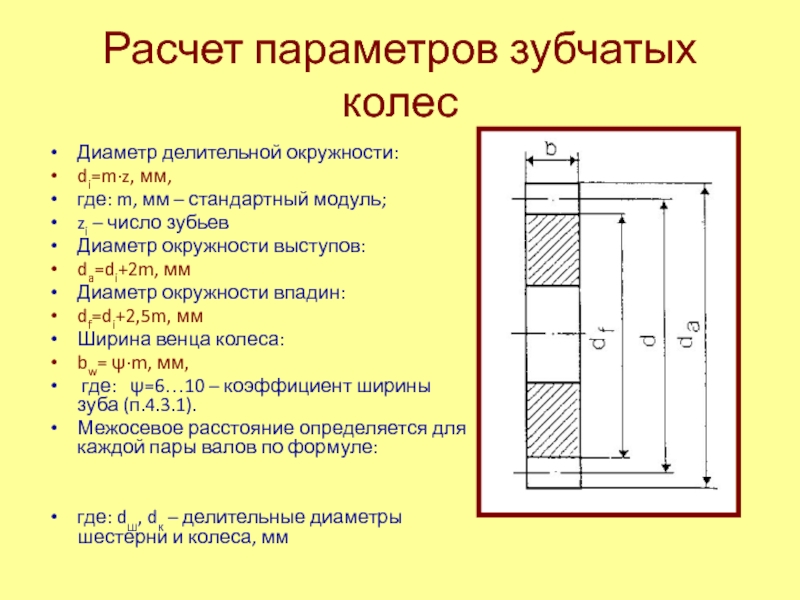 [c.178]
[c.178]
Задание основных параметров зубчатого колеса. Для выполнения этого этапа конструирования из главного экранного меню вызывают подменю функций задания основных параметров зубчатого колеса, в котором представлены строки вызова функции диалога для ввода необходимых параметров соответственно зубчатого зацепления, зубчатого венца, отверстия в ступице, ступицы, диска зубчатого колеса. [c.440]
Основные параметры зубчатых колес (число зубьев, модуль, диаметр, ширина зубчатого венца) определяются при расчете передачи. Ниже рассматриваются вопросы, связанные с конструктивной формой зубчатых колес. [c.261]
Модуль зацепления является одним из основных параметров зубчатого колеса и выражается в миллиметрах. С целью сокращения количества инструмента значение модулей m стандартизовано по ГОСТ. Размеры инструментальной рейки, так называемый исходный контур инструментальной рейки, также стандартизованы в долях модуля зацепления (рис.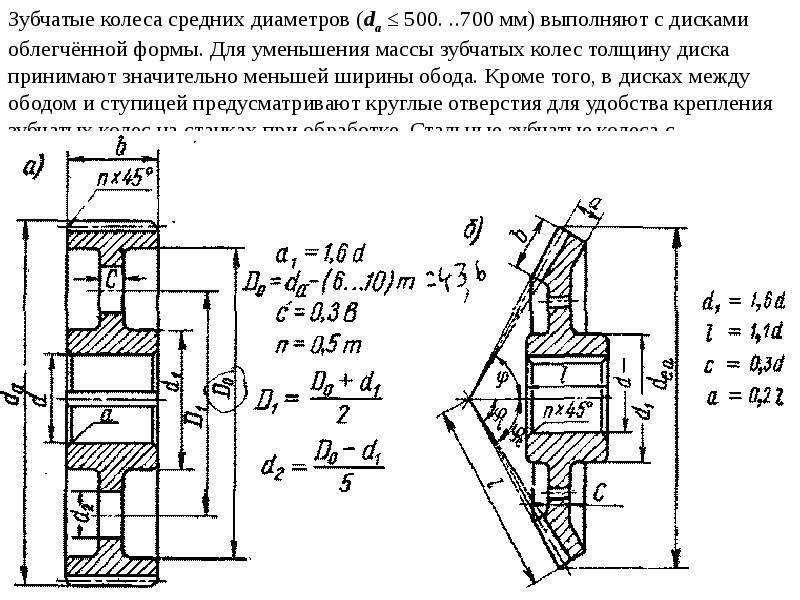 67).
[c.121]
67).
[c.121]
Отсюда видно, что шаг зацепления всегда выражается через радиус НЛП через диаметр окружности несоизмеримым числом, так как в правую часть входит трансцендентное число л. Это затрудняет подбор размеров зубчатых колес % при проектировании колес и практическое их измерение. Поэтому для определения основных размеров зубчатых колес в качестве основной единицы принят некоторый параметр, называемый модулем зацепления. Модуль зацепления измеряется в миллиметрах и обозначается буквой т. Величина модуля равна [c.429]
Делительные диаметры удобны для расчетов, связанных с проектированием зубчатых передач, вычерчиванием и изготовлением зубчатых колес. От делительного диаметра числа зубьев z зависит один из основных параметров зубчатых зацеплений, так называемый модуль т [c.185]
Раньше были приведены формулы для определения основных параметров зубчатых колес при условии, что стандартный модуль соответствует их начальным окружностям, совпадающим с делительными окружностями. Однако это условие накладывает некоторые ограничения и вызывает трудности, возникающие при конструировании зубчатых передач. Например, уменьшение числа зубьев колеса удешевляет производство зубчатых колес, уменьшает вес конструкции, делает ее более компактной и т, д. Но уменьшение числа зубьев при нормальном зубчатом зацеплении можегг вызвать подрез зубьев. Поэтому для улучшения условий работы зубчатых колес — устранения заострения вершин зубьев и возможного заклинивания зубчатого зацепления, а также для повышения контактной и изгибной прочности, вписывания проектируемой зубчатой передачи в заданный габарит и т. д. — нормальное зубчатое зацепление, как не удовлетворяющее предъявляемым требованиям, необходимо заменять исправленным зацеплением. Зубчатые колеса с геометрическими параметрами, отличающимися от нормальных, называют исправленными, или корригированными.
[c.202]
Однако это условие накладывает некоторые ограничения и вызывает трудности, возникающие при конструировании зубчатых передач. Например, уменьшение числа зубьев колеса удешевляет производство зубчатых колес, уменьшает вес конструкции, делает ее более компактной и т, д. Но уменьшение числа зубьев при нормальном зубчатом зацеплении можегг вызвать подрез зубьев. Поэтому для улучшения условий работы зубчатых колес — устранения заострения вершин зубьев и возможного заклинивания зубчатого зацепления, а также для повышения контактной и изгибной прочности, вписывания проектируемой зубчатой передачи в заданный габарит и т. д. — нормальное зубчатое зацепление, как не удовлетворяющее предъявляемым требованиям, необходимо заменять исправленным зацеплением. Зубчатые колеса с геометрическими параметрами, отличающимися от нормальных, называют исправленными, или корригированными.
[c.202]
При этом положения точек пересечения эвольвентных профилей с линией зацепления рассматриваются для каждого из колес относительно своего начала координат. Неточность процесса зубообразования вызовет появление погрешностей основных параметров зубчатых колес, причем в дальнейших рассуждениях не будем учитывать влияния погрешности радиусов основных окружностей и погрешностей формы эвольвентных профилей колес на изменения угла зацепления зубчатой передачи. Принятые допущения позволяют утверждать, что положение каждого колеса может быть взаимно однозначно определено положением конечного числа точек пересечения эвольвент профилей с линией зацепления (рис. 1.26). При этом будем считать, что линия зацепления при движении колес неподвижна в системе координат, связанной с осями колес.
[c.68]
Неточность процесса зубообразования вызовет появление погрешностей основных параметров зубчатых колес, причем в дальнейших рассуждениях не будем учитывать влияния погрешности радиусов основных окружностей и погрешностей формы эвольвентных профилей колес на изменения угла зацепления зубчатой передачи. Принятые допущения позволяют утверждать, что положение каждого колеса может быть взаимно однозначно определено положением конечного числа точек пересечения эвольвент профилей с линией зацепления (рис. 1.26). При этом будем считать, что линия зацепления при движении колес неподвижна в системе координат, связанной с осями колес.
[c.68]
Расчет кинематической пвгрешности. На рис. 6.21 изображена планетарная передача 2/С — Л с двухвенцовым сателлитом. Основные параметры зубчатых колес приведены в табл. 6.9..
[c.184]
Отдельной составной частью руководства является паспорт станка, оформленный на специальных стандартных бланках. Паспорт содержит осАовиые данные станка (характеристику) спецификацию сборочных единиц (узлов) станка таблицу основных параметров зубчатых колес, червяков, винтов и гаек кинематическую схему станка таблицу механики главного движения (положение рукояток и соответствующие им частоты вращения шпинделя, наибольшие допускаемые крутящие моменты, мощности, к.п.д., указания о слабых звеньях) таблицу механизма подачи (положение рукояток и соответствующие им величины подачи и шагов резьб), схему расположения и спецификацию подшипников. К Руководству прилагаются чертежи наиболее часто заменяемых деталей станка.
[c.107]
Паспорт содержит осАовиые данные станка (характеристику) спецификацию сборочных единиц (узлов) станка таблицу основных параметров зубчатых колес, червяков, винтов и гаек кинематическую схему станка таблицу механики главного движения (положение рукояток и соответствующие им частоты вращения шпинделя, наибольшие допускаемые крутящие моменты, мощности, к.п.д., указания о слабых звеньях) таблицу механизма подачи (положение рукояток и соответствующие им величины подачи и шагов резьб), схему расположения и спецификацию подшипников. К Руководству прилагаются чертежи наиболее часто заменяемых деталей станка.
[c.107]
Основным параметром зубчатого колеса является делительная окружность. Диаметр делительной окружности обозначается буквой с1 и называется делительным. По делительной окружности откладывается окружной шаг зубьев, обозначаемый р, и представляюший собой расстояние по дуге делительной окружности между соседними (смежными) зубьями колеса (рис. 440). Таких шагов можно отложить столько, сколько зубьев имеет колесо, иначе говоря, отрезки, равные шагу р,, делят делительную окружность на I частей, отсюда ее название — делительная. [c.254]
[c.254]
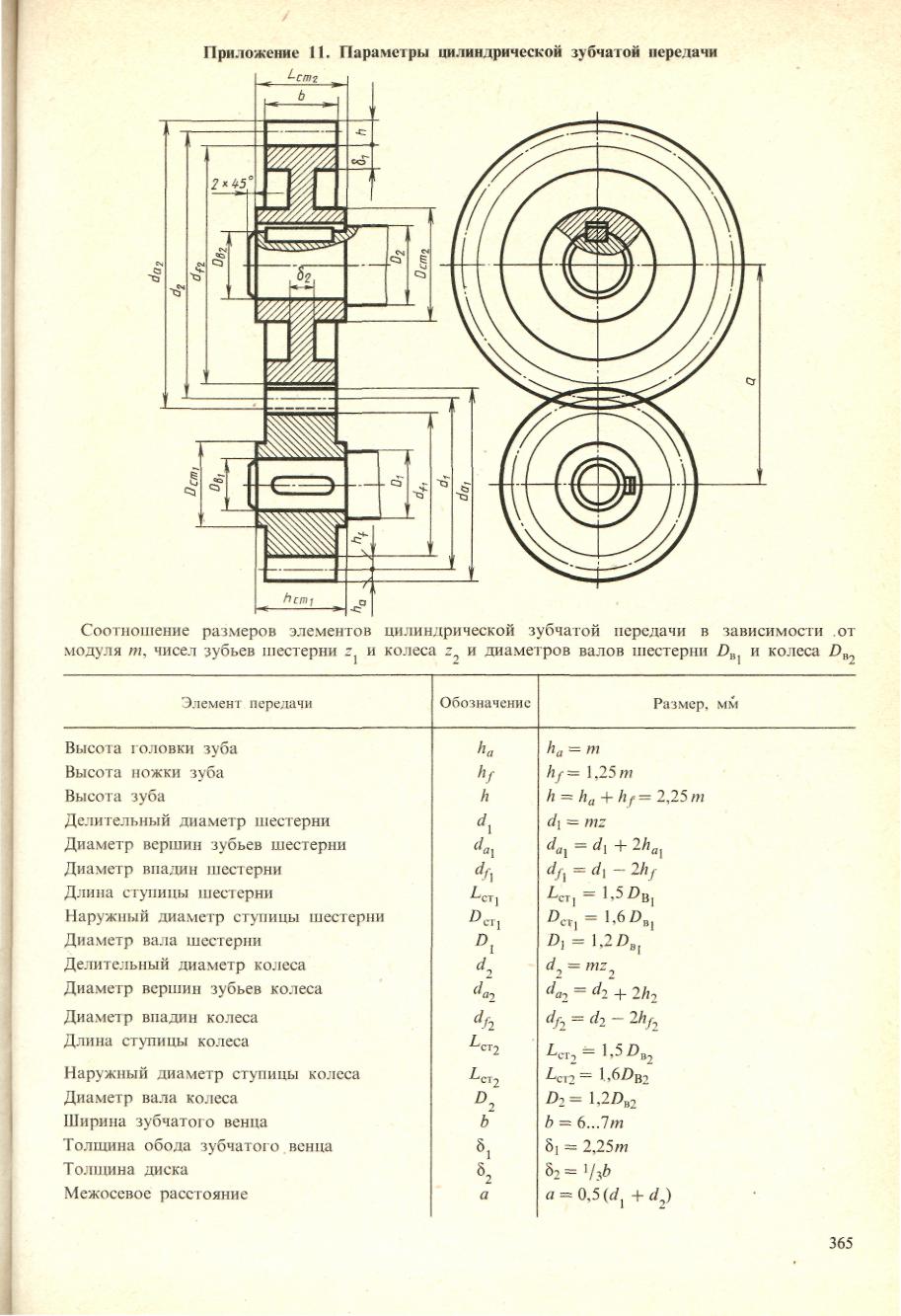
Основные параметры зубчатого цилиндрического колеса
Геометрические | Обозначение | Расчетная формула |
Высота головки | ha | ha |
Высота ножки | hr | hf=1.25m |
Высота зуба | h | h |
Делительный | d | d=mz |
Диаметр вершин | da | da=d+2ha=m(z+2) |
Диаметр впадин | df | df=d-2hf=m(z-2,5) |
Окружной шаг | Pt | Pt= |
Окружная толщина | St | St=0. |
Окружная ширина | et | et=0.5Pt= |
Радиус кривизны | Rf | Rf= |
Табл.3
Конструктивные | Расчетная формула |
Ширина зубчатого | b=(6/8)m |
Толщина обода | δ1=(2,5/3)m |
Наружный диаметр | Dст=(1,6/1,8)DB |
Толщина диска | δ2=(3/3,6)m |
Диаметр, | D1=0,5(DK+Dст) |
Диаметр отверстий | D0=(DK-Dст)/2,5/3 |
Длина ступицы | Lст=1,5DB |
Фаска | 0,5mX45o |
Размеры паза под | Выбираются по |
Примечание. | |
Если зубчатое
колесо изготовлено так, что высота зуба
h=2,25m,
то колесо называется выполненным без
смещения исходного контура (некоррегированное
колесо). Если колесо изготовлено с
высотой зуба h=2,25m,
то колесо называется выполненным со
смещением исходного контура (корригированное
колесо).
Смещение исходного
контура характеризуется коэффициентом
смещения исходного контура, обозначаемым
по ГОСТ 16531-70 буквой х.
Для некоррегированного колеса коэффициент
смещения исходного контура х=0.
При выполнении
учебных чертежей обычно ориентируются
на применение некоррегированных колес
нормального эволвентного зацепления,
параметры которых находятся в определенной
зависимости от модуля т и числа зубьев
(см. табл. 2).
3. Конструктивные разновидности зубчатых колес
В современном
машиностроении применяются зубчатые
колеса самых разнообразных конструкций,
отличающиеся друг от друга технологией
изготовления, материалом и конструктивными
особенностями.
Конструктивные
форма и размеры зубчатого колеса зависят
от нагрузок, действующих на его зубья,
требований технологии их изготовления,
удобства монтажа и эксплуатации,
уменьшения массы (веса) зубчатых колес,
бесшумности работы и др.
Наиболее часто
встречающиеся формы цилиндрических
зубчатых колес с прямыми зубьями
представлены на рис. 1, д-ж.
Цилиндрическое
зубчатое колесо малого диаметра (рис.
1, д-ж) обычно имеет форму сплошного
цилиндра с отверстием для установки на
вал.
При несколько
большем диаметре колеса для облегчения
его конструкции выполняются массивными
только обод и ступица (втулка) с отверстием
для вала. Остальная часть колеса
представляет собой тонкий диск с
отверстиями (или без отверстий). Диск
может выполняться с ребрами жесткости.
Если диаметр колеса
достаточно велик, диск заменяется
несколькими спицами, соединяющими обод
со ступицей.
Форма спиц может быть различной. Форма
Форма
поперечного сечения спиц тоже различна:
круглая, овальная, прямоугольная,
двутавровая, крестообразная и др.
Колеса большого
диаметра для удобства монтажа’и упрощения
технологии изготовления иногда выполняют
разъемными из двух половин, скрепляемых
болтами (рис. 5, а).
Рис.5
Если в конструкции
необходимо применить внутреннее
зацепление, то большое колесо изготовляют
с внутренними зубьями (рис. 5, б). Для
поворота вала на какой-либо заданный
угол применяют зубчатый сектор (рис. 5,
в).
Зубья колес могут
быть прямыми (рис. 5, а-в) косыми (рис. 5,
г), шевронными и криволинейными (рис. 5,
д). Термины, определения и обозначения
элементов зубчатых передач установлены
ГОСТ 16536-78 и ГОСТ 16561-76.
Рис. 5
Геометрические параметры зубчатых колёс.
Кинематическими характеристиками всякого колеса являются число зубьев и шаг зацепления .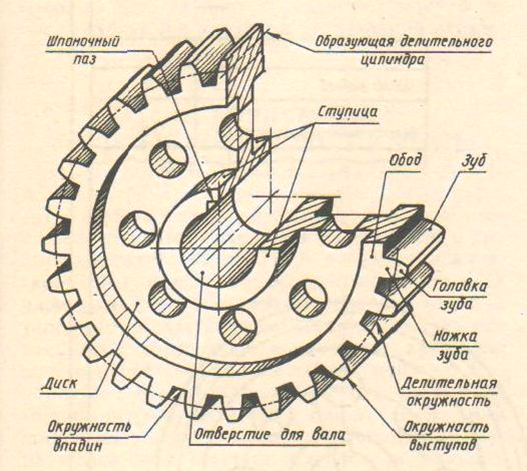
1 – наружная окружность .
2 – делительная окружность .
3 – окружность впадин .
Если дано число зубьев и длина шага, то длину делительной окружности можно найти по формуле: , тогда диаметр делительной окружности определяется с помощью выражения , где — модуль зацепления, то есть .
Через модуль зацепления выражаются все геометрические параметры зубчатого колеса и межосевые расстояния передач. Модуль зацепления является гостированной величиной, поскольку профильный инструмент для изготовления зубчатых колёс и измерительные инструменты дорогостоящи.
Делительная окружность делит зуб на две части: ; ; .
Определяем диаметры колёс:
;
.
— толщина зуба.
— ширина впадины.
Теоретически толщина зуба должна быть равна ширине впадины, но, чтобы не было защемления при зацеплении, на практике ширина впадины делается больше, чем толщина зуба в пределах допуска на боковой зазор.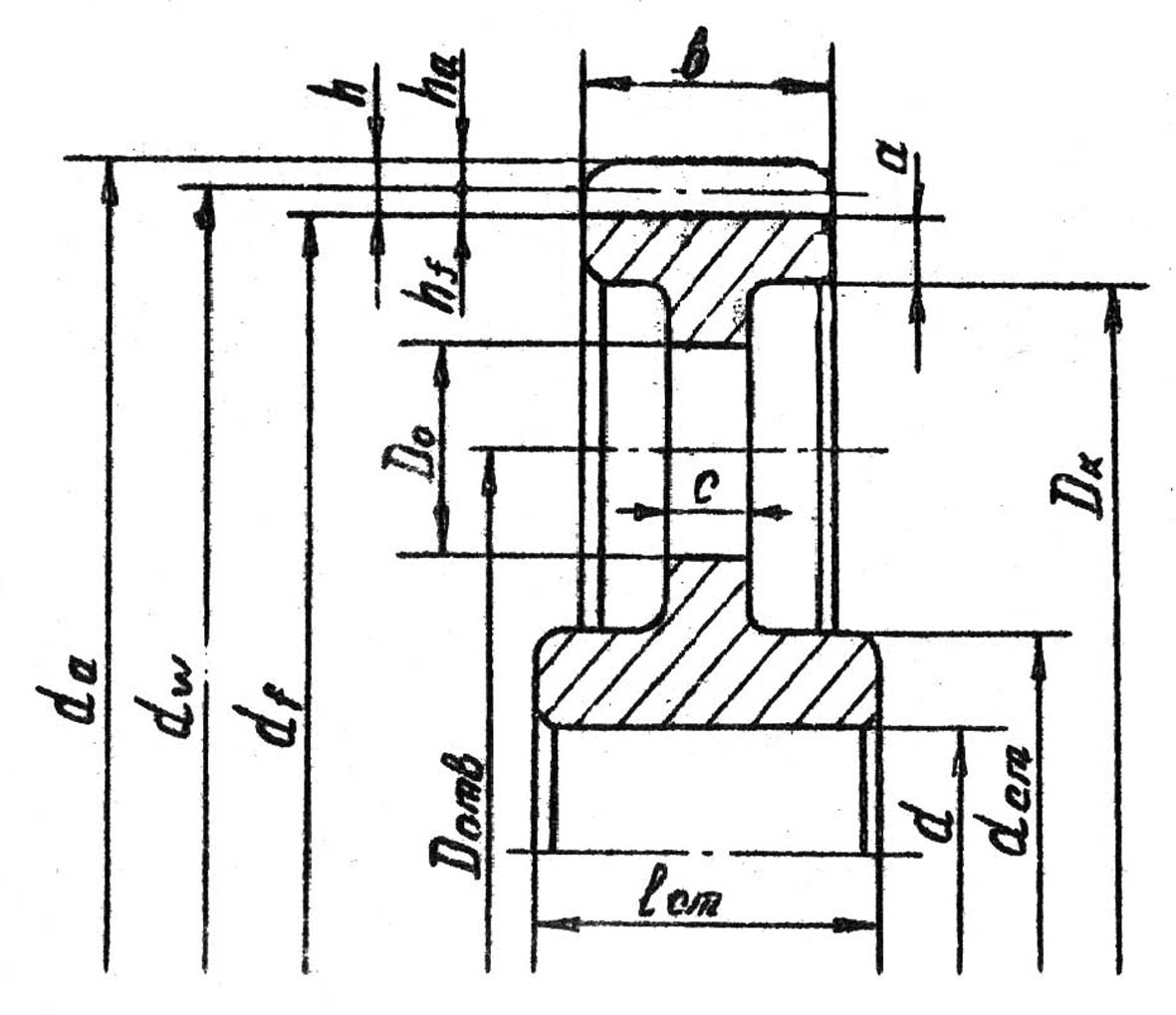
Межосевое расстояние в передачах принято обозначать : .
Основная теорема зацепления.
Теорема Виллиса.
; .
— время полного контакта двух сопряжёно работающих зубьев, от встречи до расставания. Внутри этого промежутка заметно, что передаточное отношение будет переменным. Если зубчатая передача быстроходна, то такие передачи непригодны.
Теорема Виллиса.
Какой кривой необходимо очертить профили зубьев, чтобы мгновенное передаточное отношение было постоянным?
Известны угловые скорости и .
; .
; .
.
Через точку проведём общую касательную к сопряжённым профилям. Разложим вектора скоростей на нормальные и тангенциальные составляющие, и сравним нормальные составляющие скоростей. Возможны следующие варианты:
1. — первый профиль «внедрится» во второй, что приведёт к их разрушению.
2. — профили работают в контакте.
Так как , а , следовательно, , что допустимо и имеет место на практике. В процессе зацепления происходит не чистое обкатывание профилей, а соскальзывание, что приводит к износу зубьев по профилю.
Сравним треугольники и . Эти треугольники подобны, поэтому очевидно равенство , следовательно, .
Обозначим , .
Аналогично: .
Исходя из того, что , получим: .
Рассмотрим треугольники и . Они подобны, как прямоугольные со смежными сторонами.
Обозначим: ; .
Тогда: .
Следовательно, положение точки на линии центров в процессе зацепления должно быть неизменным.
Для постоянства передаточного отношения в зубчатой передаче необходимо, чтобы общая нормаль к профилям зубьев всегда проходила бы через одну и ту же точку (полное зацепление) на линии центров , и делила бы линию центров в отношении обратно пропорциональном отношению угловых скоростей.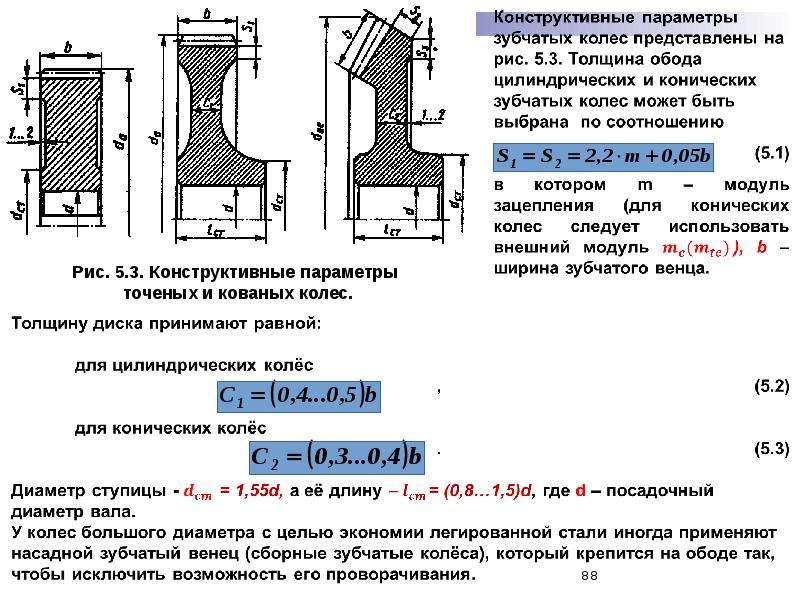
Следствия:
1. Чтобы в зубчатой передаче иметь постоянным передаточное отношение, необходимо профили зубьев очертить тонкими кривыми, которые отвечали бы требованиям основной теоремы зацепления.
2. Требованиям основной теоремы зацепления соответствует эвольвента, образующая эвольвентное зацепление и сочетание эпициклоиды и гипоциклоиды, образующей циклоидное зацепление.
Эвольвента является бесконечной спиралью вне данной окружности.
Проведём обкатывание вспомогательных окружностей и без скольжения по начальной окружности, и получим эпициклоиду и гипоциклоиду.
Ножка зуба оформляется по гипоциклоиде, а головка зуба оформляется по эпициклоиде.
Узнать еще:
Основные элементы и параметры зубчатых колес
Содержание:
Основные элементы и параметры зубчатых колес
- В зубчатых передачах вращение тяги достигается за счет взаимодействия одного выступа тяги (зубьев) и другого зуба тяги (выступов).
 Основными деталями таких зубчатых колес являются зубчатые колеса, объемными элементами которых являются корпус зубчатого колеса, зубчатое колесо и желоб. Конструкция зубчатой передачи зависит от типа зубчатой передачи. Основные типы: цилиндрическая, коническая, гипоидная, червячная, червячная и др.
Основными деталями таких зубчатых колес являются зубчатые колеса, объемными элементами которых являются корпус зубчатого колеса, зубчатое колесо и желоб. Конструкция зубчатой передачи зависит от типа зубчатой передачи. Основные типы: цилиндрическая, коническая, гипоидная, червячная, червячная и др.
Цилиндрические зубчатые колеса подразделяются на цилиндрические цилиндрические зубчатые колеса, косозубые зубчатые колеса, угловые зубчатые колеса и т. Д., А также эвольвентные, циклоидальные и другие типы зубьев. Рисунок 123. Сетка эвольвентного цилиндрического зубчатого колеса: зубная паста Расширенный цилиндр На рисунке показан наиболее поврежденный вентиляционный механизм и главный полицейский, а также параметры этого механизма. Профиль эвольвентного зубца 123 формируется путем скатывания по основной окружности колеса без скольжения по прямой линии.
Класс точности характеризует характеристики измерительного прибора, но не является показателем точности измерения, так как при определении погрешности измерения необходимо учитывать погрешность метода, настройки и т.
д.
Людмила Фирмаль
Основная окружность колеса 1 представляет собой круг, а его развертка представляет собой теоретический профиль зуба. Начальная окружность 2 представляет собой окружность, в которой заданная пропорция угловой скорости колеса обеспечивается за счет фрикционного сцепления с окружностью другого передаточного колеса: = d s . Разделить круг— Круг, который является основой для определения элементов и размеров зуба. Для некоррелированных передач начальный круг и круг основного тона совпадают. Линия 3 сетки это путь к общей точке контакта зубов. Угол зацепления е это угол между линией зацепления и прямой, перпендикулярной центральной линии.
- Основным круговым шагом зубца P1b является расстояние между одноименными профилями от соседних зубьев вдоль дуги первого круга. В принципе Нормальный шаг Pn это расстояние между параллельными касательными для двух одинаковых профилей зубьев. Нормальный модуль зубца t представляет собой линейное значение, в 1 раз превышающее нормальный шаг зуба Через модуль определяются все размеры редуктора.
 Например, d = tg. Где r количество зубьев шестерни. Значения модуля стандартизированы в диапазоне 0,5 100 мм. Точность зубчатых колес и зубчатых колес установлена на 12 градусов и показана в порядке увеличения от 1 до 12 (ГОСТ 1643 81).
Например, d = tg. Где r количество зубьев шестерни. Значения модуля стандартизированы в диапазоне 0,5 100 мм. Точность зубчатых колес и зубчатых колес установлена на 12 градусов и показана в порядке увеличения от 1 до 12 (ГОСТ 1643 81).
Каждая точность соответствует следующему. Стандарт кинематической точности, ограничивающий погрешность угла поворота колеса. Ограничивает норму плавности работы, неравномерность движения колеса за оборот. Определяет стандарт контакта зуба и целостность рабочих поверхностей зуба друг с другом. Метрики критериев кинематической ошибки включают погрешность шага зубчатого колеса, радиальное биение зубчатого венца и нормальную вибрацию нормальной длины. Индикаторы на основе гладкости локальная ошибка движения, отклонение шага, ошибка профиля зуба и т. Д.
В начале измерения зубчатое колесо вращается так, что стрелка индикатора устанавливается на ноль, а измерительный наконечник рычага входит в контакт с основанием боковой части измерительных зубьев.
Людмила Фирмаль
Индикаторы критериев контакта с зубами индикаторы, обеспечивающие гарантированный боковой зазор, такой как общее пятно контакта, ошибка направления зуба, ошибка линии контакта, отклонение межосевого расстояния, общая нормальная длина Отклонение, отклонение толщины зуба и т. Д. Стоматологические измерительные приборы делятся на два типа: мольберт, на котором установлены проверенные колеса, и депозит, прикрепленный к колесам, проверенный зубцами или желобами.
Смотрите также:
Предмет метрология
Основные параметры зубчатого зацепления — Студопедия
Рассмотрение ограничим зубчатыми передачами с круглыми колесам.
Расстояние между одноименными точками профилей соседних зубьев, измеренное по дуге окружности с центром на оси вращения колеса, называется окружным шагом.
На рис.6.11 показаны сечения зубьев колеса осевой 2, торцовой 1 плоскостями. Дана также одна из соосных цилиндрических поверхностей, например делительная поверхность 3.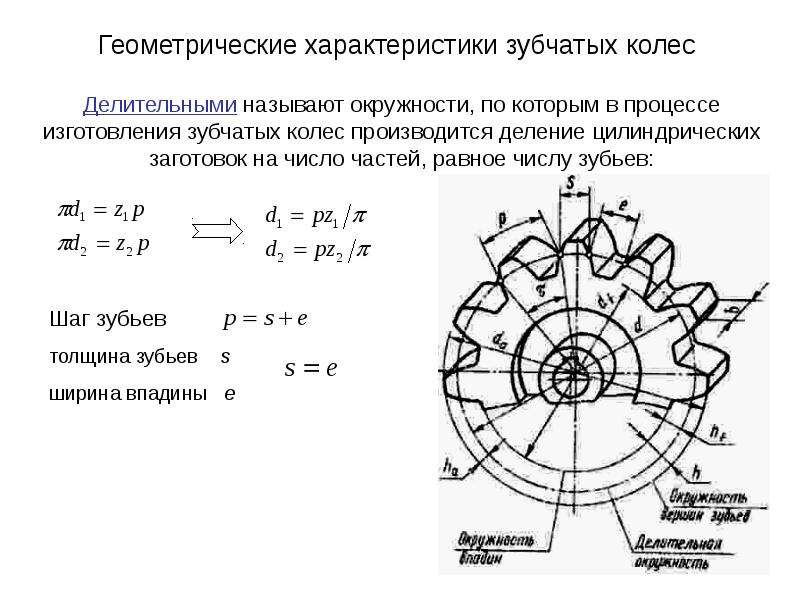 Различают шаг окружной рt, осевой рx, нормальный рn. В зависимости от вида поверхности 3 каждый из перечисленных шагов может быть делительным, начальным и т. п. Центральный угол, соответствующий дуге рt,называют угловым шагом τ, τ = 2π/z;, где z — число зубьев.
Различают шаг окружной рt, осевой рx, нормальный рn. В зависимости от вида поверхности 3 каждый из перечисленных шагов может быть делительным, начальным и т. п. Центральный угол, соответствующий дуге рt,называют угловым шагом τ, τ = 2π/z;, где z — число зубьев.
Рис.6.11
Очевидно, что окружной шаг меняется с диаметром окружности, на которой его измеряют.
Если число зубьев колеса z , радиус начальной окружности rw,шаг зубьев по начальной окружности pt , то длина окружности: 2π rw = z рt
Для двух находящихся в зацеплении колес должно выполняться
pt = 2πrw1/z1 = 2πrw2/z2 (6.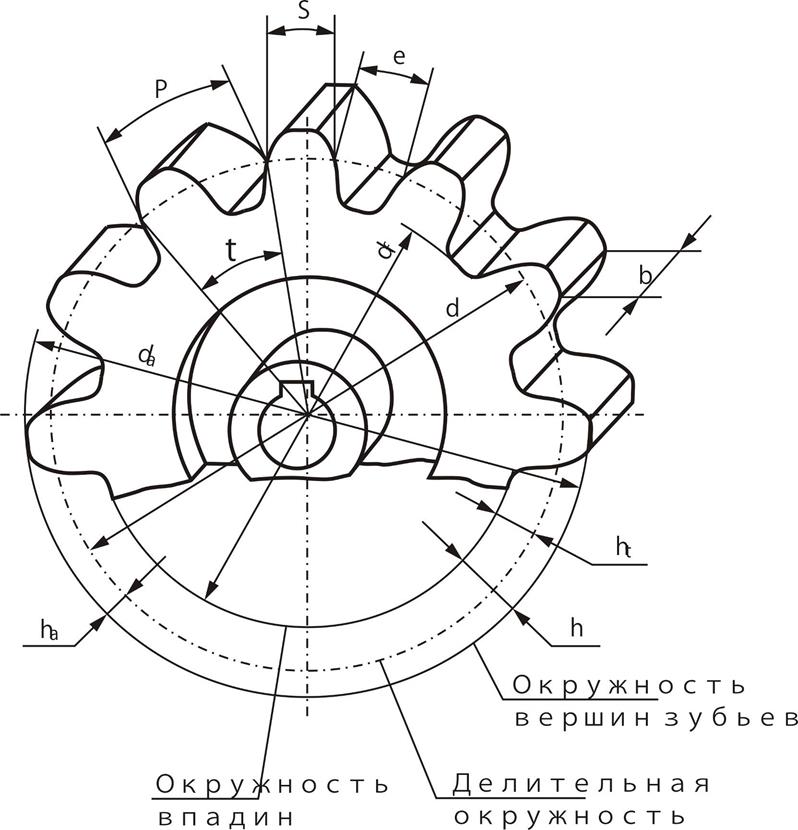 10)
10)
Следовательно, основной кинематической параметр — передаточное отношение зубчатой передачи может быть определено:
i12 = rw2/rw1 = z2/z1 (6.11)
Для одной пары зубчатых колес предусматривается понятие передаточное число зубчатой передачи
u =z2/ z1
где z2 — число зубьев зубчатого колеса; z1— число зубьев шестерни. Под шестерней понимается зубчатое колесо с меньшим числом зубьев, а при равенстве чисел зубьев — ведущее колесо. При ведущей шестерне
u =│i12│.
Одноступенчатые передачи обычно применяются при передаточных отношениях i ≤ 12 — в приборах, i ≤ 6 — в машинах. Передаточное отношение передачи (рис. 6.12 а)
Передаточное отношение передачи (рис. 6.12 а)
i12 = — ω2/ ω 1= —z2/ z1
а) б)
в)
Рис. 6.12
Многоступенчатые передачи применяют в тех случаях, когда требуется осуществить большие передаточные отношения. Для трехступенчатой передачи (рис. 6.12 б)
где k = 3 — число пар внешнего зацепления.
В рядовой передаче (рис.6.12 в) с последовательным соединением колес числа зубьев промежуточных колес не влияют на передаточное отношение механизма:
i14=(-1)кω4 / ω1=(-1)3 i12 i 23i34=- (z2 / z1)( z3 /z2)( z4 /z3)= — z4 / z1
Такие колеса называются паразитными. Они применяются для получения требуемого направления вращения или для передачи движения между далеко отстоящими валами.
Они применяются для получения требуемого направления вращения или для передачи движения между далеко отстоящими валами.
Учитывая, что 2π×rw = z×рt , получим dw= z рt/ π. Из (6.10) видно, что для двух сопряженных колес отношение рt/ π будет постоянным. Отношение рt/π = m [мм], называется модулем зацепления. Значения модуля, как основного параметра зубчатого зацепления стандартизованы (СТ СЭВ 310-76). Стандартным значение модуля будет только для одной окружности, называемой делительной. Делительная окружность делит зуб на головку и ножку.
Делительная окружность — это базовая окружность для опрвделения размеров зубьев. Она является характеристикой одного зубчатого колеса, диаметр этой окружности имеет постоянную величину. Начальные окружности дают характеристику зацепления двух зубчатых колес, диаметры этих колес зависят от межосевого расстояния.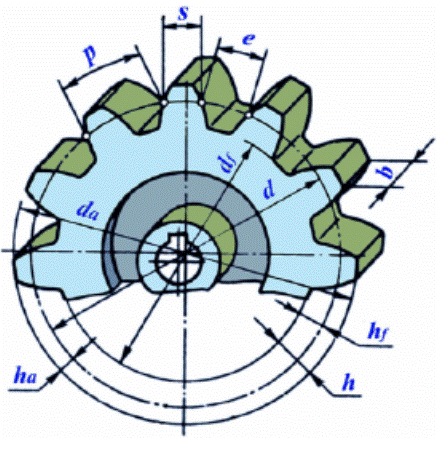 Для зубчатых колес без смещения (нулевое колесо) делительная и начальная окружности совпадают.
Для зубчатых колес без смещения (нулевое колесо) делительная и начальная окружности совпадают.
Для нулевых колес dw= d.
Внешняя окружность зубчатого колеса, очерчивающая вершины зубьев, называется окружностью вершин(диаметр окружности вершин da). (рис. 6.13).
Окружность, ограничивающая основание впадин, называется окружностью впадин(диаметр окружности впадин df).
Элемент зуба, расположенный с внешней стороны делительной окружности для внешнего зацепления (с внутренней стороны делительной окружности для внутреннего зацепления), называется головкой зуба(высота головки зуба ha),а с внутренней стороны этой окружности для внешнего зацепления (с наружной стороны делительной окружности – для внутреннего зацепления)-ножкой зуба ( высота ножки зуба hf ).
Рис. 6.13
Выбранный модуль зацепления является основным параметром для определенияразмеров зубчатого зацепления.
Высота головки зуба
ha=ha*m (6.11)
где ha* — коэффициент высоты головки зуба:
ha*= 1 — для нормального зуба;
ha*= 0,8 — для укороченного зуба.
Высота ножки зуба
hf=(ha*+c*)m (6.12)
где c* — коэффициент радиального зазора.
Этот зазор нужен для того, чтобы не происходило заклинивание зуба во впадине, а так же для компенсации температурных деформаций.
При ha*= I и т> 1 с*= 0.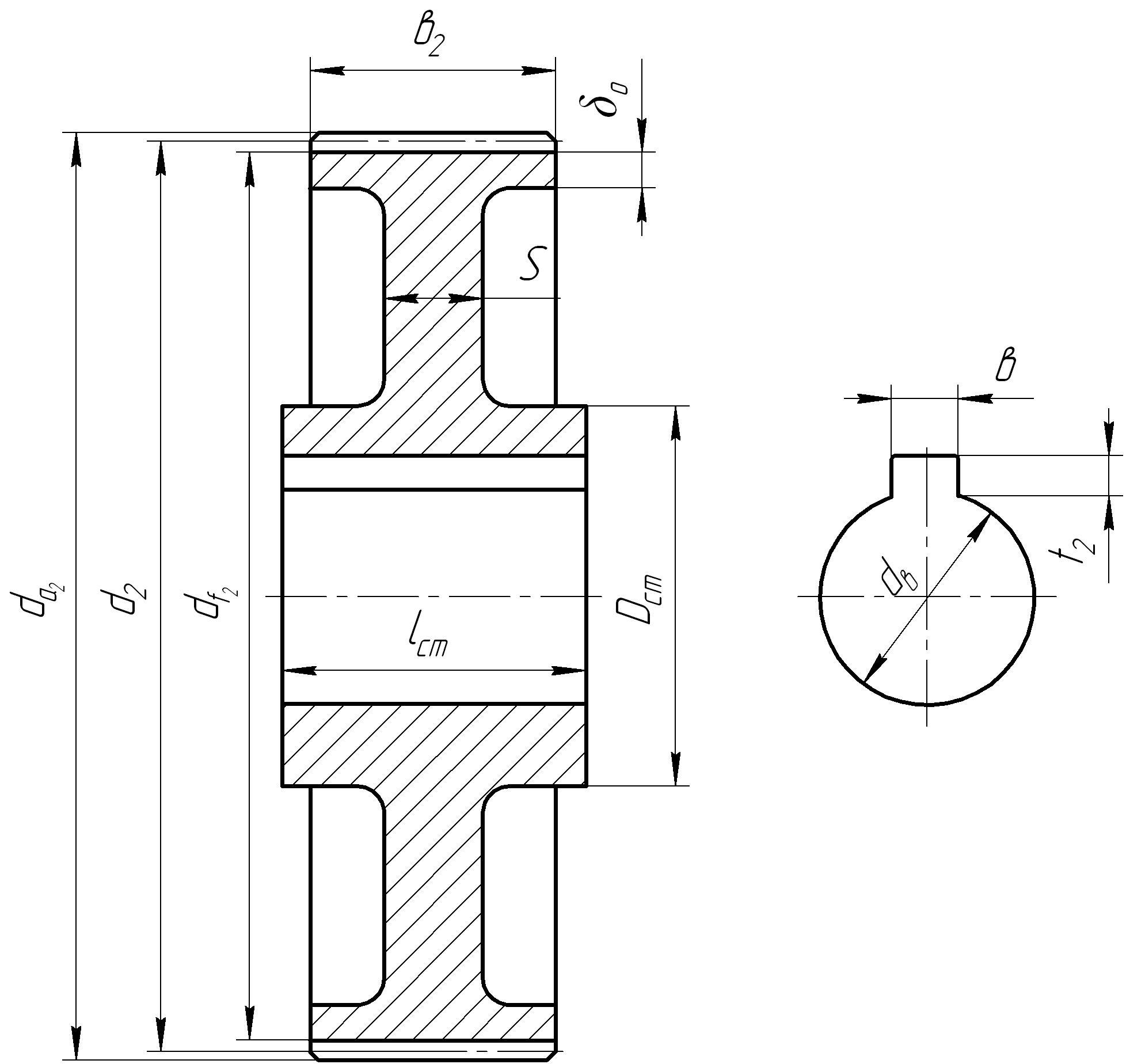 25 радиальный зазор
25 радиальный зазор
с=с*т (6.13)
Диаметр окружности вершин
da=d±2ha= т(z±2ha*) (6.14)
Диаметр окружности впадин
df= d±2 hf= т[z±2( ha*+ с*)](6.15)
Межосевое расстояние
aw=0,5(dw2±dw1)=0,5m(z2±z1) (6.16)
В (6.14) и (6.16) знак + для внешнего зацепления, знак – для внутреннего зацепления.
В (6.15) знак + для внутреннего зацепления, знак- для внешнего зацепления.
Высота зуба
h=ha+hf=m(2ha*+c*) (6.17)
Вопросы для самоконтроля:
1. Что называется окружным шагом ?
2. Что такое передаточное число зубчатой передачи?
Что такое передаточное число зубчатой передачи?
3. Как определить передаточное отношение многоступенчатой зубчатой передачи ?
4. От чего зависит передаточное отношение рядовой передачи с последовательным соединением колес ?
5. Какая окружность зубчатого колеса называется делительной?
6. Какая часть зуба называется головкой?
7. Какая часть зуба называется ножкой?
8. Какая величина называется модулем зацепления?
9. Могут ли два колеса, находящиеся в зацеплении иметь разный модуль?
10. Какая окружность называется окружностью вершин?
11. Какая окружность называется окружностью впадин?
12. Чему равна высота головки зуба?
13. Чему равна высота ножки зуба?
14. Каково соотношение между высотой головки и ножки зуба?
15. Как рассчитать диаметр окружности вершин?
16. Как рассчитать диаметр окружности впадин?
Модуль шестерни.
 Что это такое? — Справочная информация
Что это такое? — Справочная информация
Основные сведения об эвольвентном зацеплении
Профиль боковых сторон зубьев зубчатых колес с эвольвентным зацеплением представляет собой две симметрично расположенные эвольвенты.
Эвольвента — это плоская кривая с переменным радиусом кривизны, образованная некоторой точкой на прямой, обкатывающейся без скольжения по окружности, диаметром (радиусом) db(rb) называемой основной окружностью.
Основные параметры эвольвентного зацепления. На рис. 1.1 показано зацепление двух зубчатых колес с эвольвентным профилем. Рассмотрим основные параметры зацепления, их определения и стандартные обозначения.
В отличие от принятого ранее, обозначение всех параметров производится строчными, а не заглавными буквами с индексами, указывающими их принадлежность колесу, инструменту, типу окружности и виду сечения.
Стандартом предусмотрены три группы индексов:
- первая группа: n, t, x — означает вид сечения, соответственно нормальный, торцовый (окружной), осевой;
- вторая группа: a,f,b,w,y- означает, что параметр относится соответственно к окружностям выступов, впадин, основной, начальной и любой концентричной окружности.
 Для делительной окружности индекс не указывается;
Для делительной окружности индекс не указывается; - третья группа: 1, 2, 0 — означает, что параметр относится соответственно к шестерне, колесу, зуборезному инструменту.
Порядок использования индексов определяется номером группы, т.е. вначале предпочтение отдается индексам первой группы, затем второй и т.д.
Некоторые индексы разрешается опускать в случаях, исключающих возникновение недоразумений или не имеющих применения по определению. Например, у прямозубых цилиндрических колес не используются индексы первой группы. В ряде случаев некоторые индексы с целью сокращения записи также опускаются.
Некоторые индексы разрешается опускать в случаях, исключающих возникновение недоразумений или не имеющих применения по определению. Например, у прямозубых цилиндрических колес не используются индексы первой группы. В ряде случаев некоторые индексы с целью сокращения записи также опускаются.
Рассмотрим зацепление двух прямозубых цилиндрических (рис. 1.1) колес: с меньшим числом зубьев (z1), называемого шестерней, и с большим числом зубьев (z2), называемого колесом; соответственно с центрами колес в точках О1 и О2. В процессе обката шестерни с колесом происходит качение без скольжения двух центроид — окружностей, соприкасающихся в полюсе зацепления — Р. Эти окружности называются начальными, а их диаметры (радиусы) обозначаются с индексом w: dwl (rwl), dw2 (rw2). Для некорригированных колес эти окружности совпадают с делительными окружностями, обозначение диаметров (радиусов) которых дается без индексов первой и второй групп, т.е. для шестерни — d1(r1), для колеса — d2(r2).
1.1) колес: с меньшим числом зубьев (z1), называемого шестерней, и с большим числом зубьев (z2), называемого колесом; соответственно с центрами колес в точках О1 и О2. В процессе обката шестерни с колесом происходит качение без скольжения двух центроид — окружностей, соприкасающихся в полюсе зацепления — Р. Эти окружности называются начальными, а их диаметры (радиусы) обозначаются с индексом w: dwl (rwl), dw2 (rw2). Для некорригированных колес эти окружности совпадают с делительными окружностями, обозначение диаметров (радиусов) которых дается без индексов первой и второй групп, т.е. для шестерни — d1(r1), для колеса — d2(r2).
Рис. 1.1. Эвольвентное зацепление зубчатых колес
Делительная окружность — окружность, на которой шаг между зубьями и угол профиля равны им же на делительной прямой зубчатой рейки, сцепленной с колесом. При этом шаг (Р = π · m) — расстояние между двумя соседними одноименными сторонами профиля. Отсюда диаметр делительной окружности колеса d = P · Z / π = m · Z
При этом шаг (Р = π · m) — расстояние между двумя соседними одноименными сторонами профиля. Отсюда диаметр делительной окружности колеса d = P · Z / π = m · Z
Модуль зуба (m = P / π) — величина условная, имеющая размерность в миллиметрах (мм) и используемая как масштаб для выражения многих параметров зубчатых колес. В зарубежной практике в этом качестве используется питч — величина, обратная модулю.
Основная окружность — это окружность, от которой образуется эвольвента. Все параметры, относящиеся к ней, обозначаются с индексом b например, диаметры (радиусы) колес в зацеплении: db1 (rbl), db2 (rb).
Касательно к основным окружностям через полюс зацепления Р проходит прямая N-N, а ее участок N1-N2 называется линией зацепления, по которой в процессе обката перемещается точка контакта сопрягаемых профилей колес. N1-N2 называется номинальной (теоретической) линией зацепления, обозначаемой буквой g.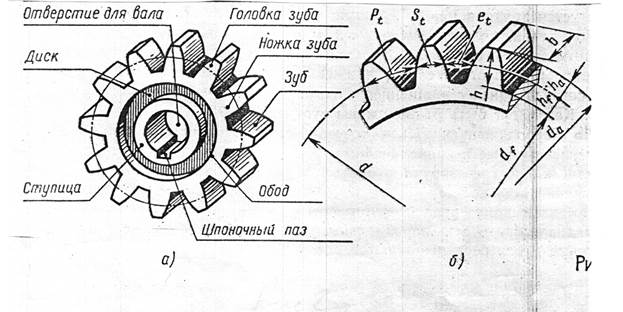 Расстояние между точками пересечения ее с окружностями выступов колес называется рабочим участком линии зацепления и обозначается ga.
Расстояние между точками пересечения ее с окружностями выступов колес называется рабочим участком линии зацепления и обозначается ga.
В процессе обката зубчатых колес точка контакта профилей перемещается в пределах активного (рабочего) участка линии зацепления ga, которая является нормалью к профилям обоих колес в этих точках и одновременно общей касательной к обеим основным окружностям.
Угол между линией зацепления и перпендикуляром к линии, соединяющей центры сопрягаемых колес, называется углом зацепления. У корригированных колес этот угол обозначается αw12; для некорригированных колес αw12 = α0.
Межцентровое расстояние некорригированных колес
aW12 = rW1 + rW2 = r1 + r2 = m ·( Z1 + Z2 ) / 2
Окружности выступов и впадин — окружности, проходящие соответственно через вершины и впадины зубьев колес. Их диаметры (радиусы) обозначаются: da1 ( ra1 ), df1 ( rf1 ), da2 ( ra2 ), df2( rf2 ).
Их диаметры (радиусы) обозначаются: da1 ( ra1 ), df1 ( rf1 ), da2 ( ra2 ), df2( rf2 ).
Шаги зубьев колес — Pt Рb, Рn, Рх — это расстояния между одноименными сторонами профиля, замеренные:
- по дуге делительной окружности в торцовом сечении — окружной (торцевый) шаг Pt = d / Z;
- по дуге основной окружности — основной шаг Pb = db / Z;
- по контактной нормали (линии зацепления) — основной нормальный шаг Рbn;
- по нормали к направлению зубьев и по оси (у винтовых передач) — нормальный шаг Рn и осевой шаг Рх.
Коэффициент перекрытия, ε — отношение активной (рабочей) части линии зацепления к основному нормальному шагу:
ε = ga / Pbn
Окружная (торцовая) толщина зуба, St — длина дуги делительной окружности, заключенная между двумя сторонами зуба.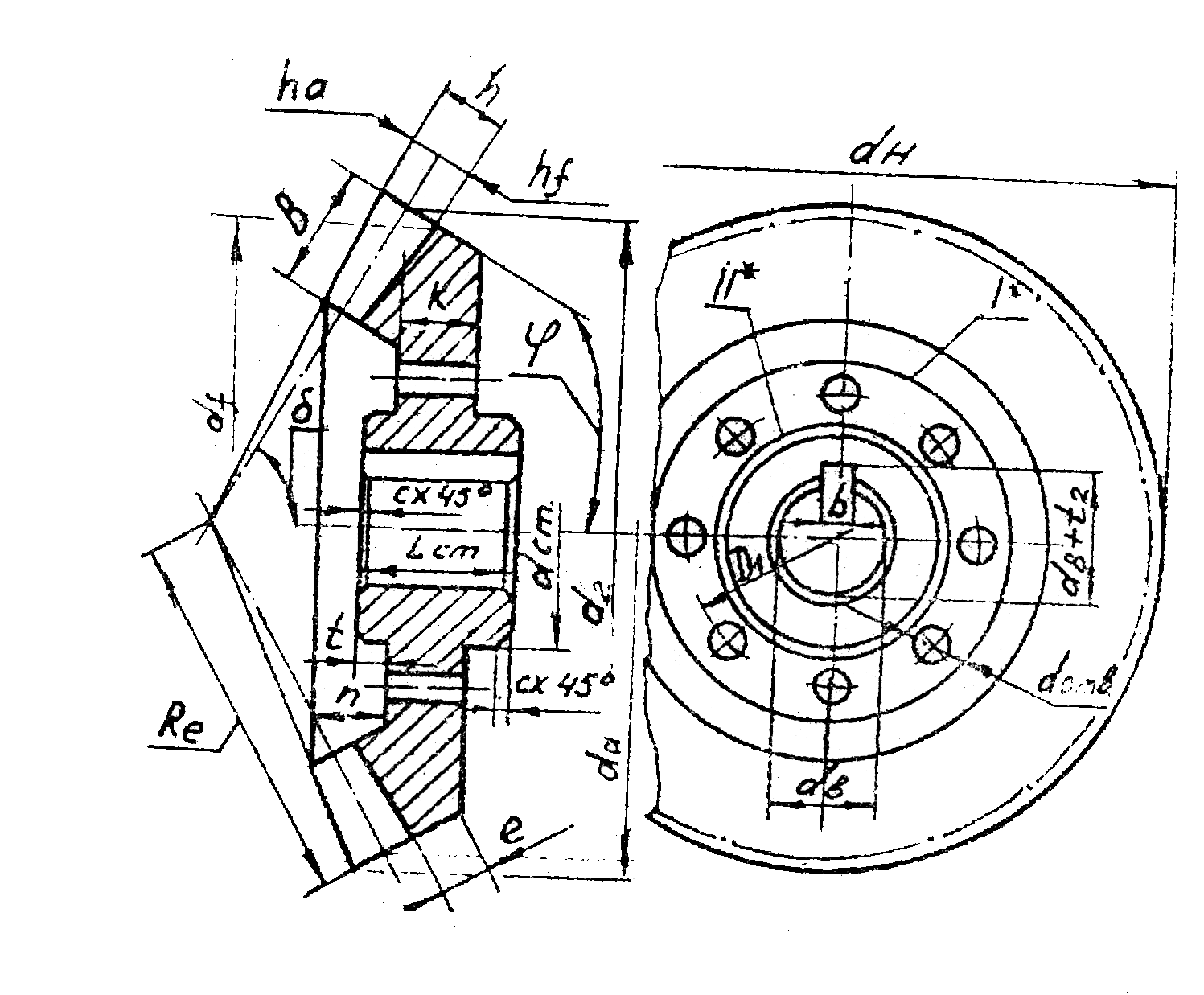
Окружная ширина впадины между зубьями, е — расстояние между разноименными сторонами профиля по дуге делительной окружности.
Высота головки зуба, ha — расстояние между окружностями выступов и делительной:
ha = ra — r
Высота ножки зуба hf — расстояние между окружностями делительной и впадин:
hf = r — rf
Высота зуба:
h = ha + hf
Рабочий участок профиля зуба — геометрическое место точек контакта профилей сопрягаемых колес, определяется как расстояние от вершины зуба до точки начала эвольвенты. Ниже последней следует переходная кривая.
Переходная кривая профиля зуба — часть профиля от начала эвольвенты, т.е. от основной окружности до окружности впадин. При методе копирования соответствует форме головки зуба инструмента, а при методе обкатки образуется вершинной кромкой режущего инструмента и имеет форму удлиненной эвольвенты (для инструментов реечного типа) или эпициклоиды (для инструментов типа колеса).
Рис. 1.2. Зацепление зубчатой рейки с колесом
Понятие об исходном контуре рейки
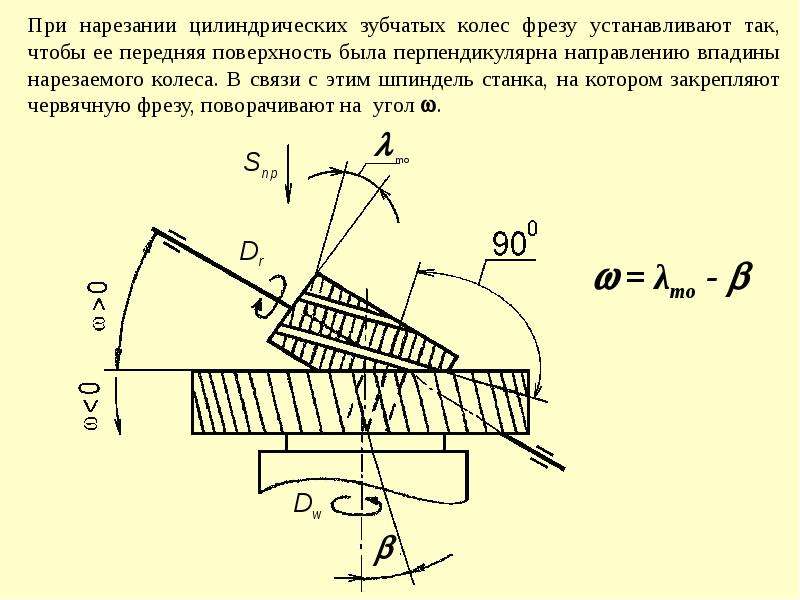
Как было показано выше, частным случаем эвольвенты при z = (бесконечность) является прямая линия. Это дает основание использовать в эвольвентном зацеплении рейку с прямобочными зубьями. При этом любое зубчатое колесо данного модуля независимо от числа зубьев может быть сцеплено с рейкой того же модуля. Отсюда возникла идея обработки колес методом обкатки. В зацеплении колеса с рейкой (рис. 1.2) радиус начальной окружности последней равен бесконечности, а сама окружность превращается в начальную прямую рейки. Линия зацепления N1N2Так как профиль зубьев рейки — прямая линия, это в значительной мере упрощает контроль линейных параметров зубьев и угла профиля. С этой целью стандартами установлено понятие исходного контура зубчатой рейки (рис. 1.4, а) проходит через полюс Р касательно к основной окружности колеса и перпендикулярно к боковой стороне профиля зуба рейки. В процессе зацепления начальная окружность колеса обкатывается по начальной прямой рейки, а угол зацепления становится равным углу профиля зуба рейки α .
В процессе зацепления начальная окружность колеса обкатывается по начальной прямой рейки, а угол зацепления становится равным углу профиля зуба рейки α .
Так как профиль зубьев рейки — прямая линия, это в значительной мере упрощает контроль линейных параметров зубьев и угла профиля. С этой целью стандартами установлено понятие исходного контура зубчатой рейки (рис. 1.3, а)
В соответствии со стандартами, принятыми в нашей стране для эвольвентного зацепления, исходный контур имеет следующие параметры зубьев в зависимости от модуля:
- угол профиля α = 20°;
- коэффициент высоты головки h*a = 1;
- коэффициент высоты ножки h*f = 1,25;
- коэффициент радиального зазора с* = 0,25 или 0,3;
- коэффициент граничной (рабочей) высоты зуба h*L = 2;
- шаг зубьев Р = π · m;
- толщина зуба S и ширина впадины е: S = е = 0,5Р = π · m / 2.

Делительная прямая рейки проходит по середине рабочей высоты зуба hL.
Для зуборезных инструментов основные параметры зубьев по аналогии с изложенным выше задаются параметрами исходной инструментальной рейки (рис. 1.3, б). Так как зубья режущего инструмента обрабатывают впадину между зубьями колеса и могут нарезать колеса с модифицированным (фланкированным) профилем, между названными исходными контурами имеются существенные различия:
- Высота головки зуба исходной инструментальной рейки ha0 = (h*f0 + с0 )m = 1,25 m, т.е. коэффициент высоты головки й h*a0 =1,25. Высота ножки зуба hf0 = 1,25 m, а полная высота зуба h0 = ha0 + hf0 = 2,5 m.
- Если нарезаемое колесо имеет срез у головки (модифицированный профиль), то ножка зуба инструментальной рейки должна иметь утолщение с параметрами h ф 0 , α ф 0 , n ф 0.

- Толщина зуба у зубчатой рейки S = π · m / 2 ,
а у инструментальной рейки при нарезании колес с модифицированным профилем зубьев S0 = π · m / 2 ± ΔS0Рис. 1.3. Исходные контуры:
а — зубчатой рейки; б — инструментальной рейки
Поправка ΔS 0 берется из справочников [23, 24] в зависимости от величины модуля зуба. Знак «+» берется для чистовых, а знак «-« — для черновых инструментов. В первом случае происходит утонение зубьев нарезаемого колеса с целью создания бокового зазора между зубьями сцепляемых колес, во втором случае утолщение, в результате чего нарезаемые зубья получают припуск на чистовую обработку.
У колес с обычным (модифицированным) профилем зубьев изменение толщины нарезаемых зубьев можно получить путем смещения инструментальной рейки относительно центра колеса и утолщение ее зубьев у ножки не требуется.
Параметры зацепления корригированных зубчатых колес.
 Корригирование (исправление) колес дает возможность улучшить зубчатое зацепление по сравнению с нормальным зацеплением в отношении трения, износа и прочности зубьев, уменьшить вероятность подреза ножки зубьев при малом их числе и др.
Корригирование (исправление) колес дает возможность улучшить зубчатое зацепление по сравнению с нормальным зацеплением в отношении трения, износа и прочности зубьев, уменьшить вероятность подреза ножки зубьев при малом их числе и др.Применительно к долбякам корригирование дает возможность получения задних углов на режущих кромках (см. ниже).
Из известных методов корригирования на практике наибольшее применение нашло высотное корригирование, которое осуществляется путем смещения профиля исходной инструментальной рейки относительно центра нарезаемого колеса. Такое смещение принято считать положительным, если рейка отводится от центра колеса, и отрицательным, когда она приближается к его центру (рис. 1.4).
Рис. 1.4. Схема высотного корригирования зубчатого колеса:
1 — положительное смещение; 2 — нулевое смещение; 3 — отрицательное смещение
Величина смещения оценивается произведением хо · m, где х0 — коэффициент смещения
При положительном смещении высота головки зуба нарезаемого колеса h‘a1 увеличивается на величину хот, а высота ножки h‘f1 уменьшается на ту же величину.
 При отрицательном смещении, наоборот, высота головки зуба уменьшается, а высота ножки увеличивается. Полная высота зуба колеса в обоих случаях остается неизменной.
При отрицательном смещении, наоборот, высота головки зуба уменьшается, а высота ножки увеличивается. Полная высота зуба колеса в обоих случаях остается неизменной.Так как при этом положение делительной и основной окружностей колеса постоянно и не зависит от величины смещения, то неизбежно изменение толщины зуба нарезаемого колеса по делительной окружности из-за смещения делительной прямой рейки относительно начального положения на величину ± хо · m. Как видно из рис. 1.5, толщина зуба по делительной окружности у корригированного колеса при смещении рейки инструмента
S‘1, 3 = π · m / 2 ± 2 · x0 · m · tg α0
где ΔS = x0 · m · tg α 0.
Знак «+» берется при положительном, а знак «-« — при отрицательном смещении.
При расчетах зуборезных инструментов, например долбяков, зубья которых корригированы, возникает необходимость определения толщины зуба на окружности любого радиуса — rу, концентричной с делительной окружностью радиусом r.

Рис. 1.5. Изменение толщины зуба на делительной окружности при положительном смещении инструментальной рейки.
Зацепления зубчатые относятся к передачам (подвижным
соединениям) и передают движение от двигателя к исполнительным механизмам. К
составным частям зубчатых передач относятся зубчатые колеса (цилиндрические,
конические), червяки, рейки.
Диаметр делительной окружности d является одним
из основных параметров, по которому производят расчет зубчатого колеса:
d = m × z,
где z – число зубьев;
m – модуль.
Модуль зацепления m – это часть диаметра делительной окружности, приходящейся на один зуб:
m = t / π,
где t – шаг зацепления.
Высота
зуба:
h = ha + hf,
где ha – высота головки зуба, ha = m; hf – высота ножки зуба, hf = 1,25m.
Диаметр
окружности выступов зубьев:
da = d + 2ha = m (z + 2).
Диаметр
окружности впадин:
df = d – 2hf = m (z – 2,5).
Служит для передачи вращения при
параллельных осях валов.
ГОСТ 9563-60 предусматривает два ряда модулей m= 0,05…100 мм.
Ряд 1: … 0,5;
0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375;
1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …
Примечание. Ряд 1
следует предпочитать ряду 2.
Служит для преобразования вращательного
движения в возвратно-поступательное.
ГОСТ 9563-60 предусматривает два ряда
модулей m = 0,05…100 мм.
Ряд 1: … 0,5;
0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375;
1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …
Примечание. Ряд 1
Ряд 1
следует предпочитать ряду 2.
Служит для передачи
вращательного движения между валами со скрещивающимися осями.
ГОСТ 19672-74
устанавливает два ряда значений модулей m (мм).
Ряд 1: … 1;
1,25; 1,6; 2; 2,5; 3,15; 4; 5; 6,3; 8; 10 …
Ряд 2: … 1,5; 3;
3,5; 6; 7 …
Примечание. Ряд 1 следует предпочитать ряду 2.
Служит для передачи вращения при
пересекающихся осях валов.
ГОСТ 9563-60 предусматривает два ряда
модулей m= 0,05…100 мм.
Ряд 1: … 0,5;
0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375;
1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …
Примечание. Ряд 1
следует предпочитать ряду 2.
Знать о параметрах, определяющих форму зубчатых колес
Понимание различных технических терминов необходимо при проектировании шестерен.
В этой главе мы объясняем термины и их значение для параметров передачи.
1. Зубчатые передачи
Как правило, для придания формы зубчатым колесам используются профили зубьев с эвольвентными кривыми. (Рисунок 4-1)
«Эвольвентная кривая» — это кривая, нарисованная концом нити, разматываемой с цилиндра под натяжением.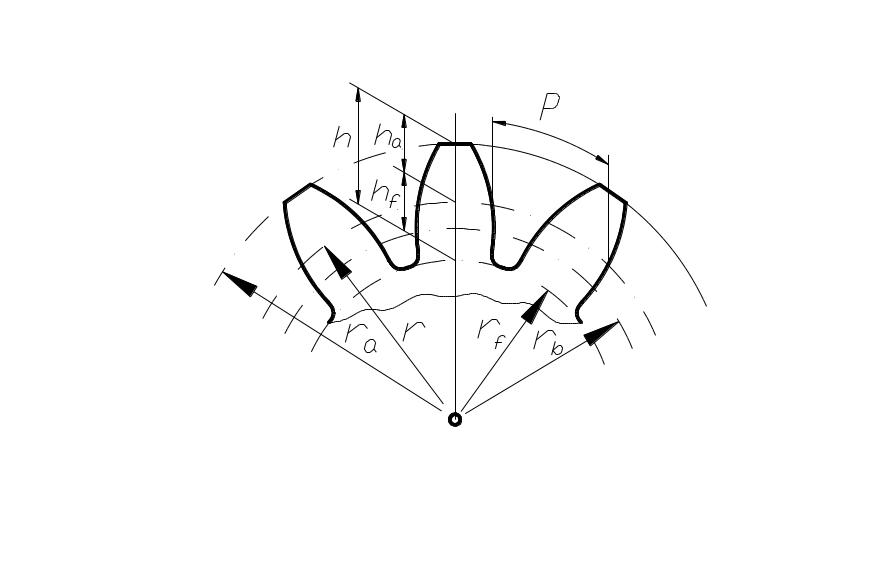
Характеристики эвольвентных кривых:
- Сетка правильно, даже если расстояние между валами имеет небольшую погрешность
- Легко сформировать правильный профиль зуба
- Вращается плавно, так как шестерни зацепляются при качении по кривой
Рисунок 4-1 Эвольвентная кривая
2. Типы конструктивных параметров, необходимых для конструирования зубчатых передач
Параметры, необходимые для конструкции редуктора, показаны ниже.(Рисунок 4-2)
1. Окружность наконечника
2. Контрольная окружность
3. Базовая окружность
4. Корневой круг
5. Диаметр вершины
6. Контрольный диаметр
7. Базовый диаметр
8. Диаметр основания
9. Приложение
10. Dedendum
11. Глубина зуба
12. Ширина лица
13. Центральная линия
14. Межосевое расстояние
15. Базовый шаг
16. Точка тангажа
17. Точка пересечения
18. Люфт
19. Длина пути контакт
(линия действий)
Рисунок 4-2 Параметры, необходимые для конструкции редуктора
3.
 Основные параметры, необходимые для конструкции редуктора
Основные параметры, необходимые для конструкции редуктора
1. Модуль
Модуль размером с зуб в мм.
Поскольку модуль не может быть измерен непосредственно штангенциркулем или шкалой, начинающие конструкторы могут быть озадачены модулем вначале при проектировании шестерни.
Модуль — это числовое значение, полученное путем деления среднего диаметра на количество зубьев и выражаемое следующей формулой:
m = d / z
m: модуль, d: делительный диаметр, z: количество зубьев
Стоимость модуля определяется стандартными числами.
Стандартное число — это числовое значение, которое обычно используется при производстве промышленных товаров.
В соответствии с JIS B 1701: 2017 стандартные значения модуля для эвольвентных зубчатых колес установлены, как показано ниже. Предпочтительно использование модулей серии I. (Таблица 4-1)
Таблица 4-1 Обычно используемые значения модулей (JIS B 1701-2017)
| Я серия | 0,1 0,2 0,3 0,4 0,5 0,6 0,8 1 1,25 1,5 2 2,5 3 4 5 6 8 10 12 16 20 25 32 40 50 |
| II серия | 0. 15 0,25 0,35 0,45 0,55 0,7 0,75 0,9 1,125 1,375 1,75 2,25 2,75 3,5 4,5 5,5 (6,5) 7 9 11 14 18 22 28 36 45 15 0,25 0,35 0,45 0,55 0,7 0,75 0,9 1,125 1,375 1,75 2,25 2,75 3,5 4,5 5,5 (6,5) 7 9 11 14 18 22 28 36 45 |
Модуль меняется в зависимости от значений PV.
Значение PV получается путем умножения давления нагрузки P на скорость скольжения V.
Следовательно, модуль необходимо устанавливать больше по мере увеличения нагрузки на шестерню и увеличения ее скорости вращения. С другой стороны, модуль можно установить меньше по мере того, как нагрузка, прикладываемая к шестерне, и ее скорость вращения уменьшаются.
При первом проектировании зубчатых колес, должно быть, очень сложно выбрать размер модуля. Конструкторы должны продолжить работу по проектированию, отрегулировав различные значения параметров, включая модуль, а также проверив размер и прочность.
Есть два способа временно определить значение модуля.
1. Определить значение модуля временно опытным путем
Понимание модулей шестерен, используемых в различных продуктах, помогает определить стоимость модуля.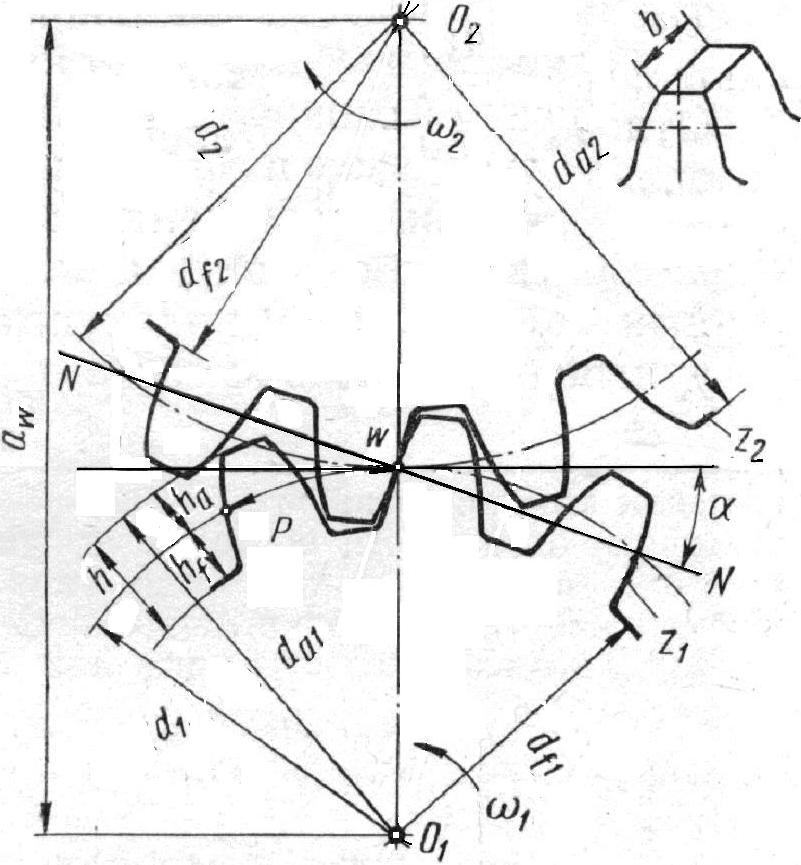
EX)
Наручные часы … прибл. 0,05 — 0,2
Принтеры и копировальные аппараты в офисе … прибл. 0,6 — 1,0
Рейки и шестерни для рулевого управления автомобиля … прибл. 1,75 — 2,5
Трансмиссия для автомобиля … прибл. 1,5 — 3,0
2. Определите значение модуля временно из каталога стандартных коммерческих шестерен
В каталогах указаны допустимые значения крутящего момента для материалов или модулей. Вы можете обратиться к значениям для временного определения модуля.
2.Угол давления
Угол давления — это угол, под которым зуб наклоняется относительно нормали к делительной линии. (Рисунок 4-3)
Обычно используется угол давления 20 °. Однако иногда также используются углы давления 14,5 ° или 17,5 °. Чем больше угол давления, тем шире сухожилие и повышается прочность.
1. Дополнение
2. Поверхность зуба
3. Основание
4. Нормальная линия к делительной линии
5. Угол давления
6.Участок
7. Линия поля
Линия поля
Изображение 4-3 Угол давления (стандартный профиль зуба базовой рейки)
3. Количество зубьев
Вам необходимо определить количество зубьев пары зубчатых колес, чтобы рассчитать передаточное число, как описано во второй статье. Будьте осторожны с минимальным количеством зубов (кроме червяка).
Количество зубьев шестерни необходимо уменьшить, насколько это возможно, для увеличения уменьшения скорости или увеличения передаточного числа. Однако наконечник инструмента типа рейки может перекрывать нижнюю часть ножки, а наконечник может измерять нижнюю часть ножки, если количество зубцов ниже определенного значения.(Рисунок 4-4)
«Дедендум выглядит хрупким и может сломаться, когда число зубцов равно 10 …»
Рисунок 4-4 Зуб сужен к нижнему краю из-за подрезки
Это называется «интерференцией зуба», а зуб, сужающийся к сухожилию, называется «поднутрением». (Рисунок 4-5)
Рисунок 4-5 Выточка
Предел количества зубьев для предотвращения поднутрения определяется по следующей формуле.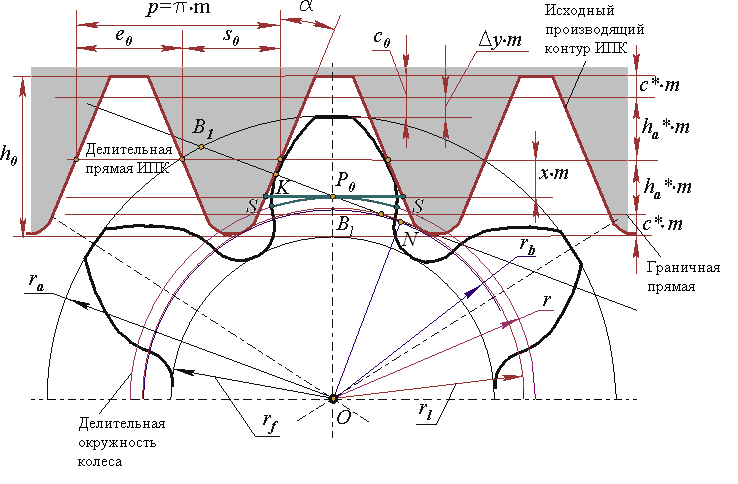 При угле давления α = 20 ° предельное число равно 17.
При угле давления α = 20 ° предельное число равно 17.
г = 2 / sin2α
Однако это не означает, что шестерня с подрезкой бесполезна. Как правило, практическое минимальное количество зубьев — 14.
Чтобы предотвратить подрезку, вы можете использовать «смещение» (изменение расстояния между зуборезным инструментом и зубчатым колесом).
Из-за ограничения минимального количества зубьев диаметр шестерни не может быть очень маленьким. Поэтому, если вы хотите увеличить передаточное число, зубчатое зацепление становится большим, и вам нужно учитывать пространство, необходимое в вашей конструкции.
4. Направление крутки
Зубья шестерни с правыми зубьями наклонены вправо относительно вала шестерни, когда вы держите вал в вертикальном положении, а шестерни с левыми зубьями имеют зубцы, наклоненные влево. Что касается реек и червяков, зубья шестерен с правыми зубьями поднимаются вправо, когда вы держите вал в вертикальном положении, а шестерни с левыми зубьями поднимаются влево.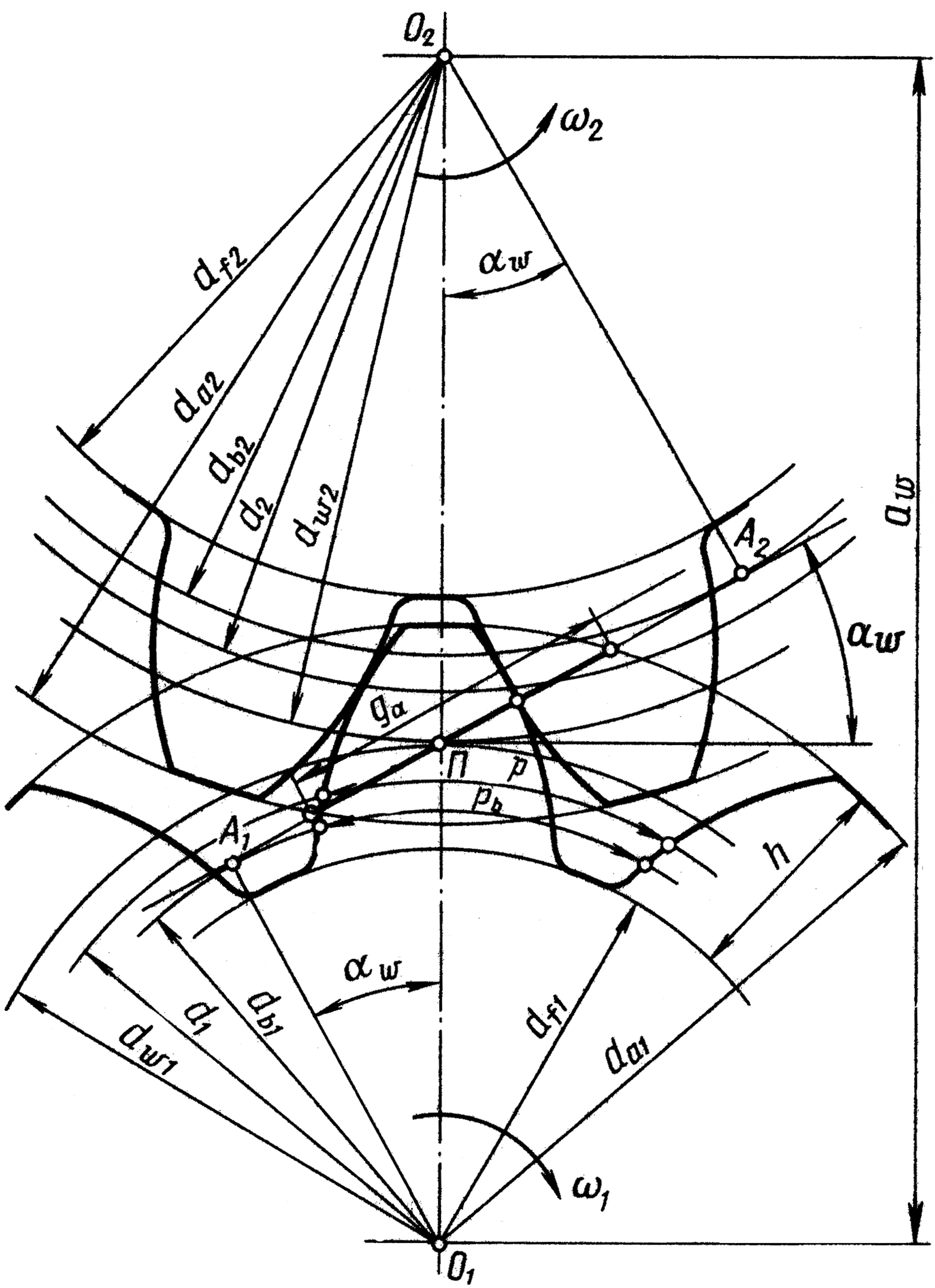
Пара косозубых шестерен или спирально-конических зубчатых колес должна иметь одинаковый модуль и угол прижима, но, кроме того, нужно обращать внимание на направление закручивания.
Что касается зубьев косозубых шестерен, спирально-конических шестерен и реек, то направление закручивания шестерен должно быть противоположным друг другу для зацепления. (Рисунок 4-6)
Две косозубые шестерни, зубья которых наклонены в одном направлении, никогда не входят в зацепление, поэтому вам нужно подготовить две косозубые шестерни, направления вращения которых противоположны.
Правые зубы / Левые зубы
Шестерня: левый зубец, Рейка: правый зубец
Шестерня: правые зубья, Рейка: левая зубья
Правые зубы / Левые зубы
Рисунок 4-6 Шестерни противоположного направления вращения
С другой стороны, направления закручивания зубьев шестерен винтовых или червячных шестерен, используемых для косых валов, должны быть одинаковыми для зацепления. (Рисунок 4-7)
(Рисунок 4-7)
Правые зубы / Левые зубы
Правые зубья / Левые зубья
a) Винтовая шестерня
Правые зубы / Левые зубы
Правые зубья / Левые зубья
б) Червячная шестерня
Рисунок 4-7 Шестерни с одинаковыми направлениями закручивания
«Направление скручивания зацепления зависит от типа шестерни!»
5. Угол кручения
Зуб наклонен относительно оси цилиндра.
Эта величина наклона называется «торсионным углом». (Рисунок 4-8)
Винтовые шестерни, показанные на Рисунке 4-7, имеют угол кручения 45 °.
Вы можете свободно определять угол кручения для зацепления двух шестерен, но обратите внимание, что составляющая направления осевого усилия (осевого направления) увеличивается с увеличением угла кручения, и в результате эффективность машины снижается. Для обычных косозубых зубчатых колес желательно значение ниже 25 °, чтобы избежать слишком большого усилия.
Изображение 4-8 Угол кручения косозубой шестерни
Мы обсудили параметры, необходимые для конструкции редуктора, и их значения.
Далее мы объясним типы материала зубчатых колес.
(продолжение следует …)
* Иллюстрация: KAOSUN
ОТКАЗ ОТ ОТВЕТСТВЕННОСТИ
Целью написания этой статьи было ознакомить читателей с элементарным уровнем зубчатой техники.
Мы надеемся, что фактическое проектирование и производство зубчатых колес и механизмов, в которых используются зубчатые колеса, выполняются с достаточными техническими и специализированными соображениями при полной ответственности пользователя.
Мы отказываемся от какой-либо ответственности и не будем компенсировать прямой или косвенный ущерб, причиненный механизмами, разработанными пользователями, которые прочитали эту статью.
Базовая терминология и расчет зубчатых передач
2. Терминология и расчет базовой передачи / Давайте изучим основы технологии базовой передачи!
Размер шестерни, угол сжатия, количество зубьев… мы вводим базовую терминологию, измерения и выражения, необходимые для понимания базовой технологии передачи.
Сравнительный размер зубьев шестерни
В соответствии с рекомендациями ISO (Международной организации по стандартизации), размер модуля определяется как единица измерения размеров зубьев шестерни.Однако используются и другие методы.
Модуль (м)
м = 1 (p = 3,1416)
м = 2 (p = 6,2832)
м = 4 (p = 12,566)
Рис. 2.1 Профили зубьев стоек
Если вы умножите Модуль на Пи, вы можете получить Шаг (p). Шаг — это расстояние между соответствующими точками на соседних зубах.
p = Pi x Модуль = πm (2,1)
Пример расчета
Каков размер шага (p) шестерни с модулем m = 3?
р = πm = 9.4248
CP (круговой шаг)
Круговой шаг (CP) обозначает эталонный шаг (p).
Например, вы можете производить шестерни с точным интегральным значением, таким как CP5 / CP10 / CP15 / CP20.
Преобразование из CP в модуль
m = CP / π (2.2)
Пример расчета
CP10 преобразуется в модуль следующим образом;
м = 10 / 3,1416 = 3,1831
DP (диаметральный шаг)
DP обозначает диаметр диаметра.
По стандартам ISO единица измерения миллиметр (мм) предназначена для выражения длины, однако единицы измерения дюйм используются в США, Великобритании и других странах; Диаметр диаметра также используется в этих странах.
Преобразование из DP в модуль
m = 25,4 / DP (2,3)
Пример расчета
DP 8 преобразуется в модуль следующим образом;
м = 25,4 / 8 = 3,175
Угол давления (α)
Угол давления — это угол наклона зуба шестерни, который определяет профиль зуба.
В последнее время угол давления (α) обычно устанавливается на 20 °, однако преобладали шестерни 14,5 °.
Рис. 2.2 Нормализованный профиль зуба каталожного номера
(важная терминология передач и номенклатура передач на рис.2)
- Ссылка
- Угол давления
- Нормальная опорная линия
- Шаг
- Поверхность зуба
- Корневая поверхность
- Верхний край
Количество зубьев
Число зубцов обозначает количество зубьев шестерни.
Они подсчитываются, как показано на Рисунке 2.3. Количество зубьев этой шестерни 10.
Рис. 2.3 Количество зубьев
Модуль (м), угол давления (α) и количество зубцов, представленные здесь, являются тремя основными элементами в составе шестерни.На основании этих элементов рассчитываются размеры шестерен.
Глубина и толщина зуба
Глубина зуба определяется размером модуля (м). Здесь представлены профили зубьев (полная глубина), соответствующие стандартам ISO и JIS (Японские промышленные стандарты).
Пожалуйста, см. Рисунок 2.4 ниже для объяснения глубины зуба (h) / дополнения (га) / Dedendum (hf).
Глубина зуба (h) — это расстояние между вершиной зуба и корнем зуба.
h = 2,25 м
(= Дополнение + Dedendum) (2.4)
Рис. 2.4 Глубина и толщина зуба
(важная терминология зубчатых колес и номенклатура зубчатых колес на рис. 2.4)
- Ссылка
- Шаг
- Толщина зуба
- Дополнение
- Dedendum
- Глубина зуба
- Наконечник зуба
- Корень зуба
Дополнение (га) — это расстояние между контрольной линией и вершиной зуба.
Dedendum (hf) — это расстояние между опорной линией и корнем зуба.
Толщина зуба в основном составляет половину значения шага (p). * Шаг (p) = πm
Примеры расчетов
Ниже приведены расчеты глубины зуба (h) / дополнения (га) / отклонения (hf) для шестерни с модулем 2.
h = 2,25 м = 2,25 × 2 = 4,50
га = 1,00 м = 1,00 × 2 = 2,00
hf = 1,25 м = 1,25 × 2 = 2,50
На предыдущих страницах мы познакомили с основами зубчатых колес, включая «Модуль», «Угол давления», «Число зубцов» и «Глубину и толщину зубьев».В этом разделе мы познакомимся с основными частями цилиндрических зубчатых колес и расчетами размеров.
Диаметр шестерен (размер)
Размер шестерен определяется в соответствии с контрольным диаметром (d) и определяется этими другими факторами; основной круг, Шаг, Толщина зуба, Глубина зуба, Дополнение и Dedendum.
Контрольный диаметр (d)
Диаметр наконечника (да)
Диаметр корня (df)
Рис.2.5 Диаметр шестерен
(важная терминология зубчатых колес и номенклатура зубчатых колес на рис. 2.5)
- Дополнение
- Dedendum
- Диаметр корня
- Контрольный диаметр
- Диаметр наконечника
Добавленная и нижняя окружность, представленные здесь, представляют собой контрольную окружность, которую нельзя увидеть на шестерне, поскольку это виртуальный круг, определяемый размером шестерни.
Примеры расчетов
Ниже приведены расчеты эталонного диаметра / диаметра наконечника / диаметра корня цилиндрической шестерни с модулем (м) 2 и 20 зубьями (z).
d = zm = 20 x 2 = 40
da = d + 2 m = 40 + 4 = 44
df = d — 2,5 м = 40-5 = 35
Практический тест:
Технические характеристики цилиндрического зубчатого колеса
Модуль (м) = 4
Количество зубьев (z) = 40 (угол давления α = 20 °)
| Контрольный диаметр | d = | |
| Диаметр наконечника | да = | |
| Диаметр корня | df = |
Рис.2.6 Номенклатура рабочего оборудования
(важная терминология зубчатых колес и номенклатура зубчатых колес на рис. 2.6)
- Диаметр наконечника
- Контрольный диаметр
- Диаметр основания
- Диаметр корня
- Ширина лица
- Толщина зуба
- Контрольный шаг
- Центральная линия
- Угол давления
- Люфт
- Глубина зуба
- Дополнение
- Dedendum
- Межосевое расстояние
- Зазор кончика и корня
Таблица 2.1 Символы и номенклатура шестерен
| Условия | Символы | Условия | Символы |
|---|---|---|---|
| Модуль | м | Толщина зуба | с |
| Угол давления | α | Справочный диаметр | г |
| Число зубьев | z | Диаметр наконечника | da |
| Шаг | с. | Диаметр корня | df |
| Глубина зуба | ч | Межосевое расстояние | a |
| Приложение | га | Люфт | j |
| Dedendum | hf | Зазор кончика и корня | с |
Межосевое расстояние и люфт
Когда пара шестерен находится в зацеплении так, что их контрольные окружности соприкасаются, межосевое расстояние (a) составляет половину суммы их контрольных диаметров.
Межосевое расстояние (а)
а = (d1 + d2) / 2 (2,11)
Рис. 2.7 Межосевое расстояние
Шестерни
могут зацепляться, как показано на рисунке 2.6, однако важно учитывать надлежащий люфт (люфт), чтобы шестерни могли работать плавно. Люфт — это люфт между поверхностями зубьев парных шестерен в зацеплении.
Сопрягаемые шестерни также имеют зазор (люфт) вертикальный по отношению к глубине зуба. Это называется зазором между вершиной и корнем (c), расстоянием между корнем зуба и вершиной зуба сопряженных шестерен.
Зазор кончика и корня (c)
c = 1,25 м — 1,00 м
= 0,25 м (2,12)
Рис. 2.8 Зазор кончика и корня
(важная терминология зубчатых колес и номенклатура зубчатых колес на рис. 2.8)
- Дополнение по кругу
- Dedendum круг
- Зазор кончика и корня
Примеры расчетов
Ниже приведены расчеты для межосевого расстояния (a) и зазора между концом и корнем (c), когда модуль m = 2, шестерня z1 = 20, шестерня z2 = 40
Базовый диаметр шестерни d1 = 20 × 2 = 40
Базовый диаметр шестерни d2 = 40 × 2 = 80
Межосевое расстояние a = (40 + 80) / 2 = 60
c = 0.25 × 2 = 0,5
Примеры расчетов
Попрактикуйтесь в вычислении размеров шестерен.
| Условия | Символы | Формула | Шестерня | Шестерня |
|---|---|---|---|---|
| Модуль | м | – | 2,5 | |
| Угол давления | α | 20 ° | ||
| Число зубцов | z | 15 | 30 | |
| Контрольный диаметр | г | г м | 37.5 | 75 |
| Приложение | га | 1,00 м | 2,5 | 2,5 |
| Dedendum | hf | 1,25 м | 3,125 | 3,125 |
| Глубина зуба | ч | 2,25 м | 5,625 | 5,625 |
| Диаметр наконечника | da | д + 2 м | 42.5 | 80 |
| Диаметр корня | df | d — 2,5 м | 31,25 | 68,75 |
| Межосевое расстояние | a | d1 + d2 / 2 | 56,25 | |
Практический тест:
Расчеты размеров шестерен.
| Условия | Символы | Формула | Шестерня | Шестерня |
|---|---|---|---|---|
| Модуль | м | – | 4 | |
| Угол давления | α | 20 ° | ||
| No.зубцов | z | 12 | 60 | |
| Контрольный диаметр | г | г м | ||
| Приложение | га | 1,00 м | ||
| Dedendum | hf | 1,25 м | ||
| Глубина зуба | ч | 2,25 м | ||
| Диаметр наконечника | da | д + 2 м | ||
| Диаметр корня | df | д — 2.5 м | ||
| Межосевое расстояние | a | d1 + d2 / 2 | ||
Винтовая шестерня
Цилиндрические зубчатые колеса с геликоидальными зубьями называются косозубыми шестернями.
Большинство расчетов для цилиндрических зубчатых колес можно применить и к косозубым зубчатым колесам. Этот тип шестерни имеет два вида профилей зубьев в соответствии с базовой поверхностью. (Рисунок 2.9)
Рис. 2.9 Правосторонняя косозубая шестерня
(важная терминология передач и номенклатура передач на рис.9)
- Нормальный модуль
- Поперечный модуль
- Угол наклона винтовой линии β
(a) Поперечная система (поперечный модуль / угол давления) * Поперечная ось обозначает центральную линию шестерни.
(b) Нормальная система (нормальный модуль / угол давления)
Выражение отношения: поперечный модуль (mt) и нормальный модуль (mn)
Обе системы используются в редукторах KHK Stock Gears.
Поперечная система : Заземляющие цилиндрические зубчатые колеса KHG
Нормальная система : Цилиндрические зубчатые колеса SH
Контрольный диаметр (d) косозубой шестерни с поперечной системой можно рассчитать по уравнению (2.8).
Контрольный диаметр (d) косозубой шестерни с нормальной системой можно рассчитать по уравнению (2.14).
Примеры расчетов
Ниже приводится расчет эталонного диаметра косозубой шестерни с:
Поперечный модуль mt = 2, количество зубьев z = 30, угол наклона спирали β = 15 ° (R)
Базовый диаметр d = zmt = 30 × 2 = 60
Ниже приводится расчет эталонного диаметра косозубой шестерни с:
Нормальный модуль mn = 2, количество зубьев z = 30, угол наклона спирали β = 15 ° (R)
Базовый диаметр d = zmn / cos β = 30 × 2 / cos 15 ° = 62.117
Практический тест:
Технические характеристики винтовой передачи
Нормальный модуль (мн) = 4 Угол наклона спирали (β) = 15 °
Поперечный модуль mt =
Устранение неполадок передач: объяснение терминологии
Питтинг
Когда поверхность шестерни многократно подвергается нагрузке и сила в точке контакта превышает предел выносливости материала, возникают мелкие трещины, которые в конечном итоге переходят в отслоение мелких деталей, в результате чего образуются ямки (кратеры).
Начальная стадия питтинга
Первоначальная причина возникает из-за того, что небольшие выпуклые части поверхностей зубчатых колес контактируют друг с другом, а местная нагрузка превышает предел усталости. Когда шестерни приводятся в движение и поверхности изнашиваются, локальные выпуклые участки исчезают, нагрузка выравнивается, и точечная коррозия прекращается.
Прогрессивный питтинг
Даже после того, как поверхности шестерен изношены и нагрузка выровнена, со временем начинает происходить точечная коррозия и ямки увеличиваются.
(1) Когда существует состояние перегрузки и нагрузка на поверхность шестерни превышает предел выносливости материала.
(2) Во время движения распределение нагрузки по поверхности шестерни может стать неравномерным из-за прогиба различных деталей, что приведет к превышению предела выносливости.
Это некоторые из возможных причин прогрессирующей точечной коррозии.
Подсчет очков
Это состояние, при котором смазочное покрытие разрушается из-за перегрева локальных контактных областей, вызывая износ поверхности шестерни от контакта металла с металлом. Это состояние может прогрессировать от умеренного до тяжелого.
Прорези
В направлении скольжения шестерни появляется канавка. Это часть абразивного износа, возможны следующие причины.
(1) Износ из-за попадания твердого постороннего предмета размером больше толщины масляной пленки в зацепление шестерни.
(2) Износ из-за твердого постороннего предмета, по какой-то причине закопанного в противоположном зубе шестерни.
(3) Износ из-за твердой выпуклой части зуба противоположной шестерни, врезающейся в зацепляющуюся шестерню.
Абразивный износ
Износ, который выглядит как травма от истирания или имеет вид притирки.Ниже приведены некоторые из причин.
(1) Возможный износ из-за примешивания к смазке твердых посторонних предметов (таких как металлические частицы износа, заусенцы, окалина, песок и т. Д.).
(2) Износ из-за разницы в твердости двух зацепляющихся шестерен, у которых твердая выпуклая часть вонзается в более мягкую поверхность шестерни.
Адгезионный износ
Износ, обычно возникающий между металлами при скользящем контакте. Снижение износа зависит от типа, давления, скорости, расстояния и смазки.
Мельчайшая часть материала в контактных сварных швах (прилипании) и механизме износа возникает в результате отслаивания их под действием силы сдвига.
Выкрашивание
Это относится к признаку падения относительно большой металлической стружки с поверхности шестерни из-за усталости материала под поверхностью из-за высокой нагрузки. Вогнутая часть поверхности шестерни имеет большие размеры, а форма и глубина — неправильные. Поскольку приложенная сила сдвига превышает предел выносливости материала, возникают и растут усталостные трещины, что может привести к поломке зуба.
Чрезмерный износ
Износ поверхности шестерни, подвергающейся интенсивному повторяющемуся контакту металла с металлом, который происходит, когда масляная пленка тонкая, а смазка недостаточна по сравнению с нагрузкой и шероховатостью поверхности шестерни.Это состояние обычно возникает при работе с очень низкой скоростью и высокой нагрузкой.
Перегрузка Обрыв
Поломка, вызванная неожиданно большой нагрузкой в течение одного или нескольких циклов действия (обычно ошибки при проектировании или производстве не учитываются). Поверхность излома расширяется волокнами от начальной точки и указывает на внезапное расщепление. Причина в том, что нагрузка превышает предел прочности материала шестерни. Это может произойти из-за первичного двигателя, ведомого механизма или поломки подшипников или других шестерен, что может вызвать заклинивание зубьев, внезапную остановку или концентрацию нагрузки из-за неравномерного контакта зубьев.
Усталостная поломка
Это случай, когда корневые части шестерни подвергаются повторяющейся нагрузке, превышающей предел выносливости материала. Трещина, которая начинается в углу корня шестерни, распространяется до тех пор, пока зуб не сломается. Поверхность с трещинами относительно гладкая, и отправную точку часто можно определить по отметке пляжа (ракушечному рисунку) вокруг нее.
Поломка при сдвиге
Это описывает, когда зуб отделяется от тела в результате срезания из-за однократной экстремальной перегрузки.Поломка прямая в окружном направлении и выглядит плоской, как если бы она была обработана. В близлежащей зоне видна пластическая деформация. Это происходит, когда приложенная сила превышает прочность материала на сдвиг. Это происходит, когда шестерня с высокой жесткостью и прочностью входит в зацепление с шестерней, которая имеет относительно низкий модуль упругости и слабый материал.
Ссылки по теме:
Знать о параметрах, определяющих форму зубчатых колес
Калькулятор свободного хода
Терминология зубчатых колес
Типы зубчатых колес и терминология
Расчет размеров зубчатых колес
齿轮 的 基本 用语 和 尺寸 计算 — 中文 页
Какие основные параметры Gears?
Введение
Зубчатые колеса — довольно сложные элементы машин, и их понимание довольно сложно.Прежде чем приступить к проектированию шестерен, необходимо хорошо знать основные параметры, которыми обозначается шестерня, чтобы продолжить рассмотрение сложных аспектов шестерен.
Даже не инженер, у которого есть редуктор, работающий на его оборудовании, должен знать основы передачи, чтобы помочь ему в случае поломки.
Давайте теперь посмотрим, какие основные параметры необходимо учитывать в следующем разделе
5 Основные параметры передачи
1. Тип зубчатой передачи **: ** Необходимо знать тип используемой зубчатой передачи. Система передач может принадлежать к различным подкатегориям, таким как зубчатые передачи с параллельными осями, зубчатые колеса с перпендикулярной осью, планетарные зубчатые передачи и т. Д. Щелкните здесь, чтобы просмотреть подробную статью о классификации зубчатых колес
2. Передаточное число: важных параметров, которые нужно знать о шестернях. Передаточное число называется соотношением между количеством зубьев шестерни (, как правило, меньше по диаметру, а ведущий элемент ) и количеством зубьев на шестерне (, как правило, больше по диаметру, и ведомый элемент ). ).Математически это может быть выражено как Соотношение = количество зубьев шестерни / количество зубьев шестерни. Обозначается термином « i ».
3. Модуль: Это важный параметр в передаче. Размер зуба шестерни определяется модулем. Чем меньше размер зубьев шестерни, тем меньше модуль, и чем больше размер зубьев шестерни, тем больше модуль. Это обозначается термином « M ».
4. Межосевое расстояние: Межосевое расстояние — еще один важный параметр, предназначенный для определения зубчатой пары. Это расстояние между центром шестерни и центром шестерни. Обычно это обозначается термином « a ». Это характерно для большинства основных типов зубчатых колес, за исключением конических.
5. Угол наклона винтовой линии: Это угол наклона зубьев. Это применимо только для косозубых шестерен.Для прямозубых шестерен угол наклона винтовой линии обычно составляет 0 градусов. Это обозначается термином « β ».
Это некоторые общие термины в терминологии зубчатых передач. Прежде чем приступить к выбору передач и проектированию, нужно действительно знать все эти термины.
Глава 7. Шестерни
И Чжан Содержание Шестерни — это элементы машин, которые передают движение посредством 7.1 Классификация передачШестерни можно классифицировать по относительному положению
Вот краткий список распространенных форм. Обсудим каждый Шестерни для соединения параллельных валов
Шестерни для соединения пересекающихся валов
Ни параллельные, ни пересекающиеся валы
7.2 Зубчатая передача7.2.1 Основной закон действия зубчатого колесаНа рис. 7-2 показаны два сопряженных зубца шестерни.
Изображение 7-2 Два профиля зубьев шестерниХотя два профиля имеют разные скорости (7-1) или же (7-2) Заметим, что пересечение касания (7-3) Таким образом, соотношение угловых скоростей движущихся (7-4) Точка P очень важна для соотношения скоростей, и это 7.2.2 Постоянный коэффициент скоростиДля постоянного передаточного числа положение P должно оставаться Теперь можно сформулировать фундаментальный закон действия зубчатого колеса .
7.2.3 Сопряженные профилиЧтобы получить ожидаемое отношение скоростей двух профилей зубьев, Хотя возможны многие формы зубов, для которых сопряженный зуб может 7.3 Эвольвентная криваяСледующие примеры представляют собой эвольвентные цилиндрические зубчатые колеса. Мы используем слово Файл SimDesign для этих шестерен — simdesign / gear15.30.sim. Другие примеры шестерен 7.3.1 Построение эвольвентной кривой |
| Крупная смола | 2 | 2,25 | 2,5 | 3 | 4 | 6 | 8 | 10 | 12 | 16 |
| Мелкий шаг | 20 | 24 | 32 | 40 | 48 | 64 | 96 | 120 | 150 | 200 |
Таблица 7-2 Обычно используемые диаметральные шаги
Вместо использования теоретической делительной окружности в качестве показателя размера зуба, базовая окружность, которая является более фундаментальной окружностью,
может быть использован.Результат называется базовым шагом .
p b , и это связано с круговым шагом p
по уравнению
(7-8)
7,5 Условия для правильного создания сетки
На рис. 7-5 показаны две зацепляющие шестерни, контактирующие в
точка K 1 и K 2 .
Рисунок 7-5 Две зацепляющие шестерни
Чтобы получить правильную сетку, расстояние
K 1 K 2 на передаче 1 должно быть таким же, как и на
расстояние K 1 K 2 на передаче 2.В виде
K 1 K 2 на обеих шестернях равны базовому шагу их шестерен, соответственно. Следовательно
(7-9)
С
(7-10)
а также
(7-11)
Таким образом
(7-12)
Чтобы удовлетворить вышеприведенному уравнению, пара зацепляющих шестерен должна удовлетворять
следующее условие:
(7-13)
7.6 Обычные зубчатые передачи
Зубчатые передачи состоят из двух или более шестерен для
передача движения от одной оси к другой. Обычная передача
поезда имеют оси относительно рамы для всех шестерен, содержащих
поезд. На рисунке 7-6a показан простой
обычный поезд , в котором только одна шестерня на каждую ось. В
Рис. 7-6b: составной обычный поезд
рассматривается как одно, в котором две или более шестерен могут вращаться вокруг одной
ось.
Рисунок 7-6 Обычные зубчатые передачи
7.6.1 Передаточное число
Мы знаем, что соотношение скоростей пары шестерен — это
обратная пропорция диаметров их шага
окружности, а диаметр делительной окружности равен числу
зубцов, разделенных на диаметральный шаг.Также,
мы знаем, что необходимо, чтобы сопрягаемые шестерни имели одинаковые
диаметральный шаг так, чтобы удовлетворять условию правильного
сетка. Таким образом, мы заключаем, что отношение скоростей пары
шестерни — это обратное соотношение их числа зубьев.
Для обычных зубчатых передач на рис. 7-6а мы имеем
(7-14)
Эти уравнения можно объединить, чтобы получить отношение скоростей
от первой передачи в поезде до последней передачи:
(7-15)
Примечание:
- Номера зубьев в числителе соответствуют ведомым шестерням,
а номера зубьев в знаменателе принадлежат водителю
шестерни. - Шестерни 2 и 3 обе ведущие и, в свою очередь, ведомые. Таким образом, они
называется промежуточные шестерни . Поскольку их номера зубов отменяются, бездельник
шестерни не влияют на величину передаточного отношения вход-выход, но они
меняйте направление вращения. Обратите внимание на стрелки направления на
фигура. Холостые передачи также позволяют сэкономить место и
деньги (Если шестерни 1 и 4 зацепляются прямо на большом центральном расстоянии,
их начальный круг будет намного больше.) - Есть два способа определить направление поворотного
направление.Первый способ — обозначить стрелки для каждой шестерни, как показано на рисунке 7-6. Второй способ — несколько
м -й степени « -1 » с общим коэффициентом скоростного режима. Где
м — количество пар внешних
контактные шестерни (зубчатые пары с внутренним контактом)
не меняйте направление вращения). Однако второй метод не может
применяться к пространственным зубчатым колесам.
Таким образом, получить передаточное число зубчатой передачи несложно.
на рисунке 7-6b:
(7-16)
7.7 планетарных зубчатых передач
Планетарные зубчатые передачи , также называемые планетарными зубчатыми колесами
поезда — это те, в которых одна или несколько шестерен вращаются вокруг
центральная ось поезда. Таким образом, они отличаются от обычного поезда тем, что
имеющий подвижную ось или оси. На рис. 7-8 показан
базовая компоновка, которая функционирует сама по себе или когда используется как часть
более сложной системы. Шестерня 1 называется солнечной шестерней , шестерня
2 — это планета , звено H — плечо или планета
Перевозчик .
Рисунок 7-8 Планетарные зубчатые передачи
Рисунок 7-7 Планетарные шестерни, смоделированные с помощью SimDesign
Файл SimDesign — simdesign / gear.planet.sim. Поскольку
солнечная шестерня (самая большая шестерня) зафиксирована, степень свободы указанного механизма
это один. Когда вы тянете за руку или планету, у механизма появляется
определенное движение. Если солнечная шестерня не замерзла, относительное движение
трудно контролировать.
7.7.1 Коэффициент скорости
Определить передаточное отношение планетарных зубчатых передач несколько сложнее.
анализ, чем требуется для обычного снаряжения
поезда.Будем следовать процедуре:
- Переверните механизм планетарной зубчатой передачи, представив
приложение вращательного движения с угловой скоростью H к
механизм. Разберем движение до и после инверсии.
с таблицей 7-3:Таблица 7-3 Инверсия планетарных зубчатых передач.
Примечание: H — поворотный
скорость шестерни i в воображаемом механизме.Обратите внимание, что в воображаемом механизме рука
H является стационарным и выполняет функцию рамы.Ни одна ось шестерни не движется
более. Следовательно, воображаемый механизм — это обычный
зубчатая передача. - Примените уравнение отношения скоростей обыкновенного
зубчатые передачи к воображаемому механизму. Мы получили(7-17)
или же
(7-18)
7.7.2 Пример
Возьмите планетарную зубчатую передачу на Рисунке 7-8.
В качестве примера. Предположим, N 1 = 36, N 2 = 18, 1 = 0, 2 = 30. Что такое
значение N ?
С применением уравнения отношения скоростей планетарного
зубчатых передач, имеем следующее уравнение:
(7-19)
Из уравнения и заданных условий мы можем получить ответ:
N = 10.
Содержание
Полное содержание
- 1 Физические принципы
- 2 Механизмы и простые машины
- 3 Подробнее о машинах и механизмах
- 4 Основная кинематика жестких тел с ограничениями
- 5 планарных рычагов
- 6 кулачков
- 7 передач
- 7.1 Классификация передач
- 7.2 Зубчатая передача
- 7.2.1 Основной закон действия зубчатого колеса
- 7.2.2 Постоянный коэффициент скорости
- 7.2.3 Сопряженные профили
- 7.3.1 Построение инволютной кривой
- 7.3.2 Свойства эвольвентных кривых
- 7.6.1 Коэффициент скорости
sfinger@ri.cmu.edu
Терминология и формулы цилиндрического зубчатого колеса
Что такое прямозубая шестерня?
Цилиндрическая зубчатая передача — один из самых простых и распространенных типов цилиндрических зубчатых колес.Прямозубые шестерни имеют прямые зубья, идущие параллельно валу.
Эти шестерни просты в изготовлении и могут использоваться в самых разных областях. Эти приложения включают увеличение или уменьшение скорости, умножение крутящего момента и повышение точности систем позиционирования.
В этом блоге мы собираемся дать определение терминологии прямозубого зубчатого колеса и предоставить формулы для определения значений этих терминов.
Цилиндрические зубчатые колеса — термины, определения и расчеты
Следующие термины относятся к цилиндрическим зубчатым колесам:
- Приложение : Высота зуба над делительной окружностью.
- Люфт : зазор между двумя сопряженными зубьями отдельных шестерен.
- Базовая окружность : теоретическая окружность, используемая для создания эвольвентной кривой при создании профилей зубьев.
- Межосевое расстояние : Расстояние между центральными валами двух шестерен.
- Хордовое приложение : Расстояние между хордой, проходящей через точки, где
- делительная окружность пересекает профиль зуба и вершину зуба.
- Толщина хорды : Толщина зуба, измеренная по хорде, проходящей через точки, где делительная окружность пересекает профиль зуба.
- Шаг окружности : Измерение длины дуги делительной окружности от одной точки на зубе до той же точки на соседнем зубе.
- Толщина круга : толщина зуба на делительной окружности.
- Зазор : Зазор между малым диаметром одной шестерни и большим диаметром ответной шестерни.
- Dedendum : Глубина зуба между делительной окружностью и малым диаметром.
- Диаметр делительного шага : Число зубьев на дюйм делительного диаметра.
- Скругление : Малый радиус, соединяющий профиль зуба с корневой окружностью.
- Модуль : количество зубьев на миллиметр делительного диаметра.
- Внешний диаметр : Наибольший диаметр шестерни.
- Шестерня : шестерня меньшего размера в любой паре с зацеплением.
- Окружность шага : Окружность, радиус которой равен расстоянию от центра шестерни до точки тангажа. Здесь измеряется скорость передачи.
- Диаметр шага : Диаметр делительной окружности.
- Точка тангажа : Точка касания делительных окружностей пары сопряженных шестерен.
- Угол давления : угол между линией воздействия и линией, перпендикулярной линии центров.
- Окружность корня (или дендендума) : Меньший диаметр зуба.
- Передаточное число : Отношение оборотов входной шестерни к оборотам выходной шестерни в течение заданного промежутка времени.
- Вся глубина : Высота зуба от большого диаметра до меньшего диаметра шестерни.
- Рабочая глубина : Глубина, на которую зуб входит в пространство между зубьями ответной шестерни.
Формулы для определения некоторых из этих терминов включают:
| Дополнение | 1.0 ÷ диаметральный шаг |
| Клиренс | 0,157 ÷ диаметральный шаг |
| Диаметр диаметра | Число зубьев ÷ делительный диаметр |
| Число зубцов | Диаметр шага * диаметральный шаг |
| Внешний диаметр | (Количество зубьев + 2) ÷ диаметральный шаг |
| Диаметр шага | Количество зубьев ÷ диаметральный шаг |
| Толщина зуба | 1.5708 ÷ диаметральный шаг |
| Вся глубина | 2,157 ÷ диаметральный шаг |
| Рабочая глубина | 2 ÷ диаметральный шаг |
Обзор цилиндрических зубчатых колес
Прямозубые шестерни обратного инжиниринга
Нас часто спрашивают, как реконструировать цилиндрические зубчатые колеса и есть ли у нас возможности для этого. Ответ — да, мы можем перепроектировать образцы клиентов. Мы используем координатно-измерительную машину (КИМ) в сочетании со специализированным программным обеспечением для зубчатых колес для определения точных параметров данной цилиндрической зубчатой передачи.
Хотя можно реконструировать прямозубое цилиндрическое зубчатое колесо с помощью простых измерительных инструментов и некоторых быстрых вычислений, этот метод можно использовать только для стандартных зубчатых колес. Часто зубчатое колесо будет изготовлено на заказ для конкретного применения, и некоторые размеры или допуски будут изменены. Поэтому для определения истинных параметров зубчатого колеса необходимо использовать КИМ или специальный прибор для проверки зубчатых колес. Для получения информации об этом процессе посетите наше руководство по цилиндрическим зубчатым колесам с обратной конструкцией.
Производство необходимого снаряжения в Grob
В Grob мы можем создать холоднокатаные прямозубые цилиндрические зубчатые колеса, которые точно соответствуют спецификациям вашего проекта.Наши стандартные шестерни доступны из углеродистой стали с низким и средним содержанием углерода или алюминия, и они доступны с углами давления 14,5 ° или 20 °.
Мы — семейная компания, которая работает в течение 90 лет, и в нашем производственном предприятии и штаб-квартире, расположенных в Графтоне, штат Висконсин, работают 60 технических специалистов и инженеров. Мы обладаем опытом и навыками, необходимыми для производства качественной продукции в сроки выполнения вашего проекта.
Для получения дополнительной информации о наших возможностях по производству зубчатых колес, свяжитесь с нами.
Понимание профиля зуба шестерни и формулы модуля шестерни
Геометрия простого прямозубого зубчатого колеса сложна. Многочисленные размерные параметры определяют форму профиля зуба, определяют, как шестерни подходят друг к другу, и определяют места, где силы действуют на зубья шестерни. Два наиболее важных параметра, которые часто путают друг с другом, — это делительный диаметр (или средний диаметр резьбы), обычно обозначаемый как (d), и модуль (или модуль), обычно обозначаемый как (м).
Делительный диаметр, проще говоря, — это диаметр невидимого цилиндра, который проходит приблизительно через «середину» зубьев шестерни, определяя то, что обычно называют «делительной окружностью». Кроме того, эта делительная окружность определяется как окружность с центром на оси шестерни, которая проходит через точку деления на зубьях прямозубой шестерни. Эта точка деления расположена между основанием зуба прямозубой шестерни, которое обозначает малый диаметр, и вершиной зуба цилиндрической шестерни, которая обозначает большой диаметр зуба прямозубой шестерни.Этот диаметр относительно легко определить в типичных размерах шестерен типичной Американской ассоциации производителей зубчатых колес (AGMA), поскольку он указан как диаметр где-то между малым и большим диаметрами зубчатого колеса.
Не вдаваясь в подробности, делительный диаметр также определяет приблизительную зону сопряжения двух шестерен, а это означает, что зубья будут входить в зацепление по делительному диаметру. Таким образом, он также определяет важное понятие, называемое линией действия или линией давления. Эта линия определяет направление силы, действующей на каждый зуб.Делительный диаметр также является основой для определения угла давления зуба, толщины зуба и угла наклона винтовой линии зубчатого колеса.
К сожалению, средний диаметр не может быть измерен непосредственно на физическом зубчатом колесе. Как правило, адекватное приближение к измерениям делительного диаметра можно получить путем измерения штангенциркулем на двух установочных штифтах, помещенных между зубьями шестерни в противоположных местах на шестерне. Затем диаметр одного из штифтов вычитается из измерения, полученного штангенциркулем, чтобы получить оценку делительного диаметра.
Это одна из причин, по которой была введена концепция модуля (m) шестерни. Проще говоря, это отношение делительного диаметра (d) к количеству зубьев (N) на шестерне:
Модуль обычно указывается в стандартных таблицах размеров зубчатых колес с подразумеваемыми единицами длины: либо (мм) для единиц СИ, либо (дюймов) для единиц BG. В некотором смысле, это мера единичного размера шестерни на основе количества зубьев на шестерне. Полезная аналогия заключается в том, что модуль определяет «размер» каждого зуба как часть «круговой диаграммы» диаметра деления.На самом деле это означает, что каждый зуб обладает «модульной» единицей части общего делительного диаметра. Например, шестерня с модулем 10 (указана в единицах СИ) буквально означает, что каждый зуб «использует» 10 (мм) от общего делительного диаметра.
Таким образом, модуль представляет собой очень простой параметр, позволяющий определить, смогут ли две шестерни с разным диаметром шага сопрягаться вместе; две шестерни с разными модулями не будут соединяться вместе, потому что размер единицы шестерни, как обсуждалось выше, должен совпадать, чтобы шестерни могли соединяться вместе,
Наконец, учитывая только модуль зубчатой передачи, можно рассчитать ряд других геометрических параметров зубчатой передачи, например диаметральный шаг и круговой шаг.И диаметр шага зубчатого колеса, и модуль зубчатого колеса — это два связанных, но различных параметра, которые очень полезно знать для выбора и определения размеров зубчатых колес, поскольку международные стандарты зубчатых передач и общие правила проектирования теперь в значительной степени зависят от использования этих параметров.
Helical Gears — обзор
Helical Gears
Цилиндрические шестерни были разработаны на основе цилиндрических шестерен, и их зубья расположены под углом к оси вала. Контакт между зубьями в сетке действует по диагональным поверхностям лица прогрессивным образом; ни в коем случае ни один зуб не задействуется по всей длине.Прежде чем контакт между одной парой зубов прекращается, начинается зацепление между следующей парой. Таким образом, зацепление является непрерывным, и этот факт приводит к уменьшению удара, который возникает, когда прямые зубья работают под большими нагрузками. Спиральные зубья обеспечивают плавную и бесшумную работу при высоких нагрузках; значительно снижен люфт; и за счет увеличения длины зуба при той же толщине зубчатого колеса прочность зуба повышается.
Рис. 31.20 иллюстрирует угол подъема и наклона винтовой линии, применяемый к косозубой шестерне.Для одинарных косозубых шестерен угол наклона винтовой линии обычно составляет 12–20 °.
Рис. 31.20. Угол подъема и винтовой линии косозубой шестерни.
Поскольку зубья расположены под углом, при зацеплении двух шестерен возникает боковой или торцевой упор, который имеет тенденцию разделять шестерни. На рис. 31.21 показаны две шестерни на параллельных валах и расположение подходящих упорных подшипников. Обратите внимание, что положение упорных подшипников зависит от направления вращения вала и «руки» спирали.
Рис.31.21. Цилиндрические шестерни с упорными подшипниками.
Для того, чтобы исключить серьезное влияние концевой тяги, пары шестерен могут быть расположены, как показано на рис. 31.22, где в двойной косозубой шестерне используется левая и правая спираль. Вместо использования двух шестерен можно нарезать две спирали на одной и той же заготовке шестерни.

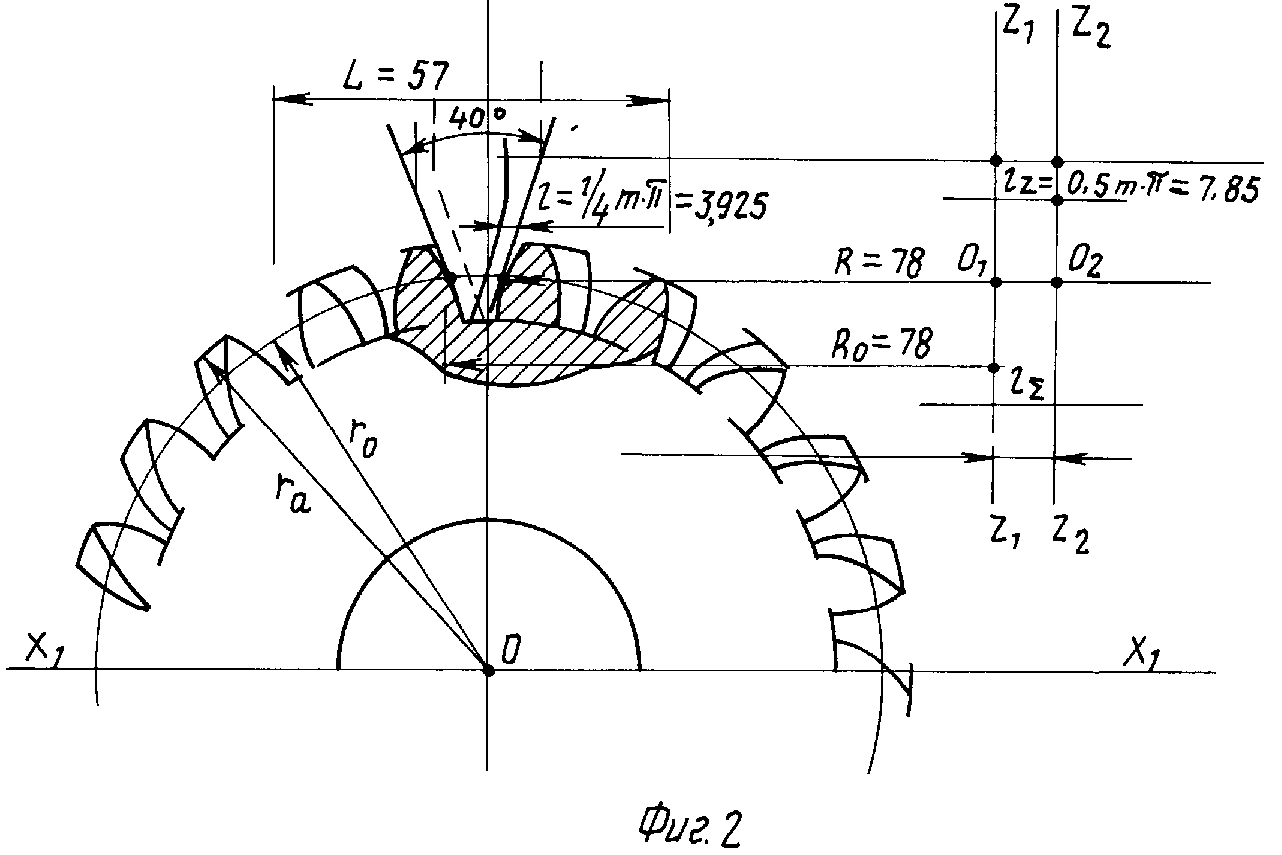 5Pt=
5Pt=
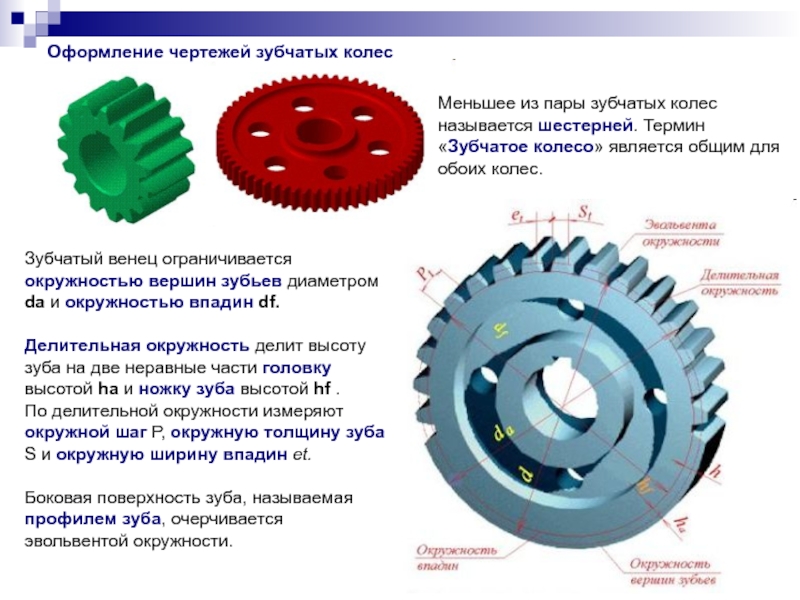 Основными деталями таких зубчатых колес являются зубчатые колеса, объемными элементами которых являются корпус зубчатого колеса, зубчатое колесо и желоб. Конструкция зубчатой передачи зависит от типа зубчатой передачи. Основные типы: цилиндрическая, коническая, гипоидная, червячная, червячная и др.
Основными деталями таких зубчатых колес являются зубчатые колеса, объемными элементами которых являются корпус зубчатого колеса, зубчатое колесо и желоб. Конструкция зубчатой передачи зависит от типа зубчатой передачи. Основные типы: цилиндрическая, коническая, гипоидная, червячная, червячная и др. д.
д. Например, d = tg. Где r количество зубьев шестерни. Значения модуля стандартизированы в диапазоне 0,5 100 мм. Точность зубчатых колес и зубчатых колес установлена на 12 градусов и показана в порядке увеличения от 1 до 12 (ГОСТ 1643 81).
Например, d = tg. Где r количество зубьев шестерни. Значения модуля стандартизированы в диапазоне 0,5 100 мм. Точность зубчатых колес и зубчатых колес установлена на 12 градусов и показана в порядке увеличения от 1 до 12 (ГОСТ 1643 81).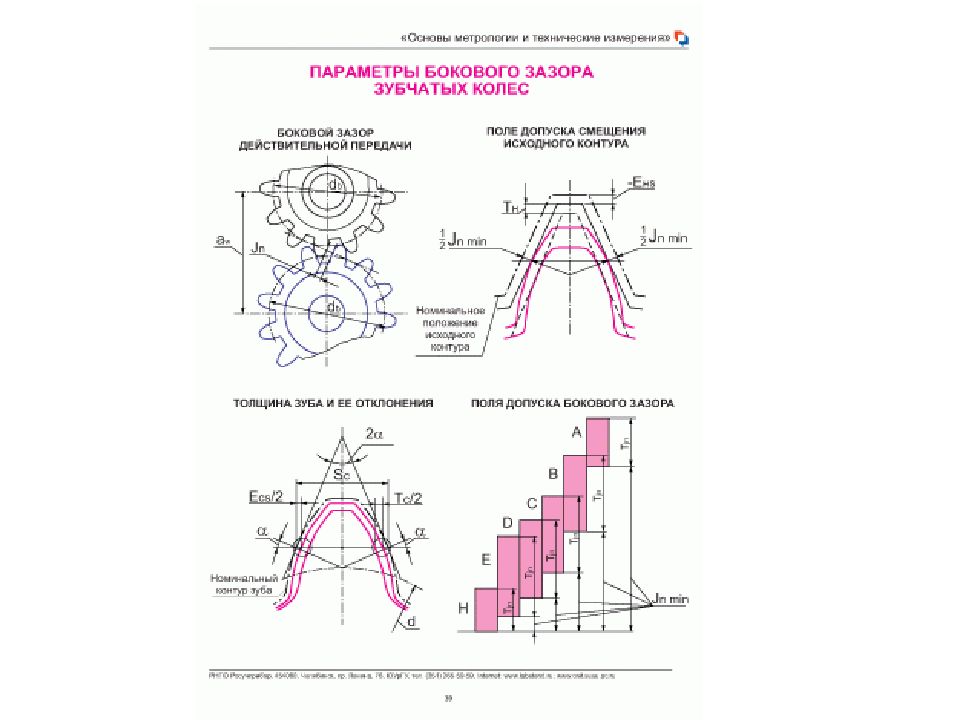
 Для делительной окружности индекс не указывается;
Для делительной окружности индекс не указывается;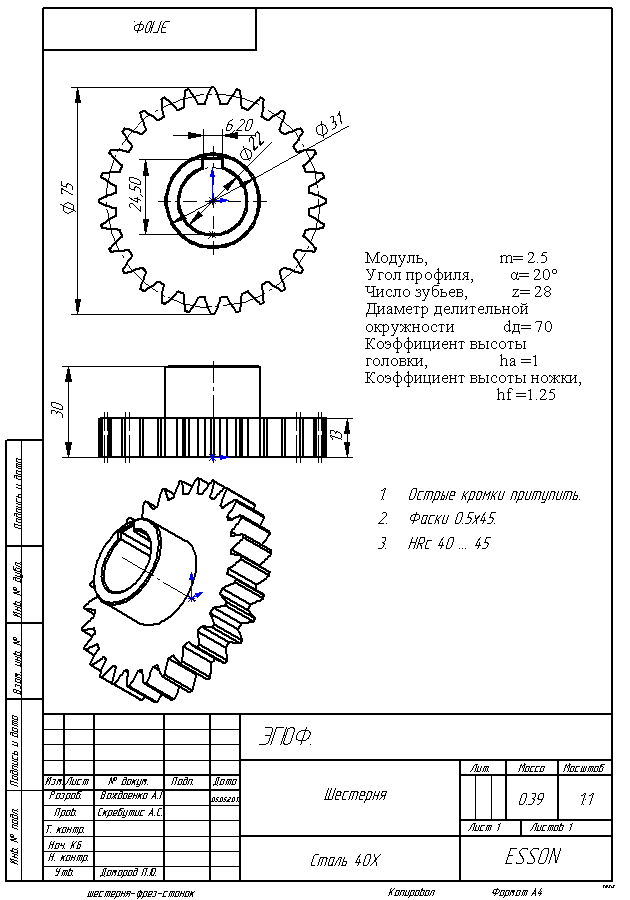
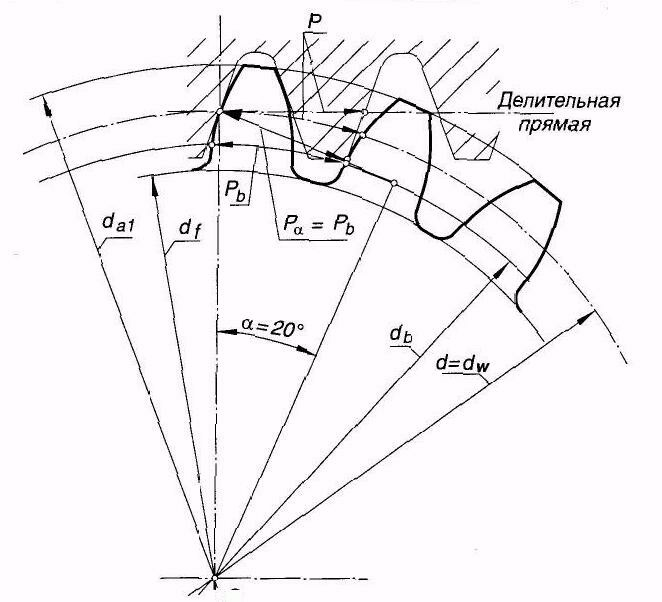
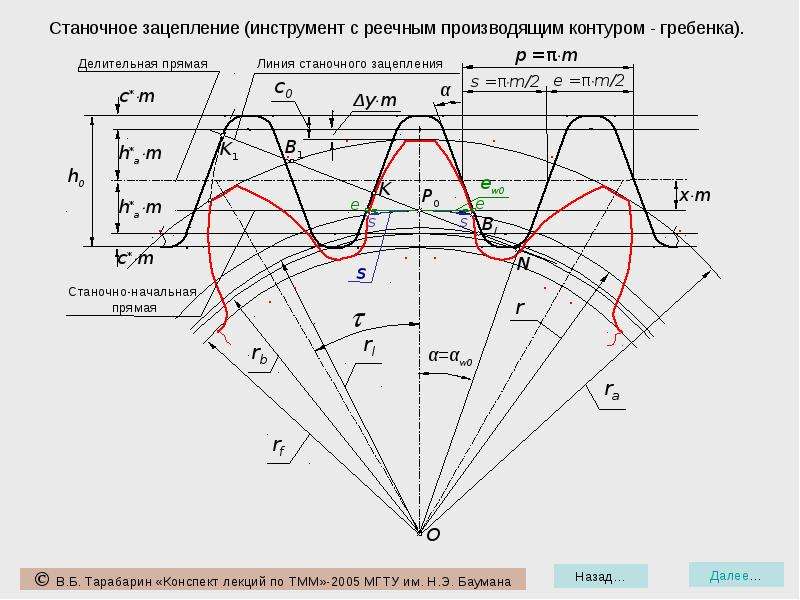 Корригирование (исправление) колес дает возможность улучшить зубчатое зацепление по сравнению с нормальным зацеплением в отношении трения, износа и прочности зубьев, уменьшить вероятность подреза ножки зубьев при малом их числе и др.
Корригирование (исправление) колес дает возможность улучшить зубчатое зацепление по сравнению с нормальным зацеплением в отношении трения, износа и прочности зубьев, уменьшить вероятность подреза ножки зубьев при малом их числе и др.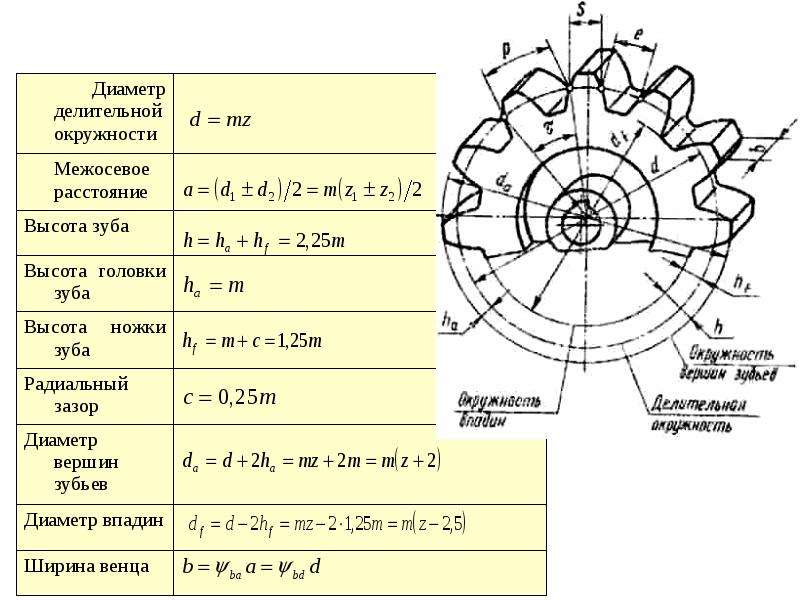 При отрицательном смещении, наоборот, высота головки зуба уменьшается, а высота ножки увеличивается. Полная высота зуба колеса в обоих случаях остается неизменной.
При отрицательном смещении, наоборот, высота головки зуба уменьшается, а высота ножки увеличивается. Полная высота зуба колеса в обоих случаях остается неизменной.