Модуль зубьев зубчатого колеса: расчет, стандартные, определение
Зубчатая передача впервые была освоена человеком в глубокой древности. Имя изобретателя осталось скрыто во тьме веков. Первоначально зубчатые передачи имели по шесть зубьев — отсюда и пошло название «шестерня». За многие тысячелетия технического прогресса передача многократно усовершенствовалась, и сегодня они применяются практически в любом транспортном средстве от велосипеда до космического корабля и подводной лодки. Используются они также в любом станке и механизме, больше всего шестеренок используется в механических часах.
Зубчатое колесо
Содержание
Что такое модуль зубчатого колеса
Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров
Каждую шестеренку характеризует несколько основных параметров
- диаметр;
- число зубьев;
- шаг;
- высота зубца;
- и некоторые другие.
Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида — основной и торцевой.
Скачать ГОСТ 9563-60
В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров.
Для расчета этого параметра применяют следующие формулы:
m=t/π,
где t — шаг.
Параметры зубчатых колес
Модуль зубчатого колеса можно рассчитать и следующим образом:
m=h/2,25,
где h — высота зубца.
И, наконец,
m=De/(z+2),
где De — диаметр окружности выступов,а z — число зубьев.
Что же такое модуль шестерни?
это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.
Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.
Формула расчета параметров прямозубой передачи
Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.
Расчет модуля зубчатого колеса
Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:
π×D=t×z,
проведя преобразование, получим:
D=(t /π)×z
Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.
t/π=m,
размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:
В=m×z;
выполнив преобразование, находим:
m=D / z.
Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса.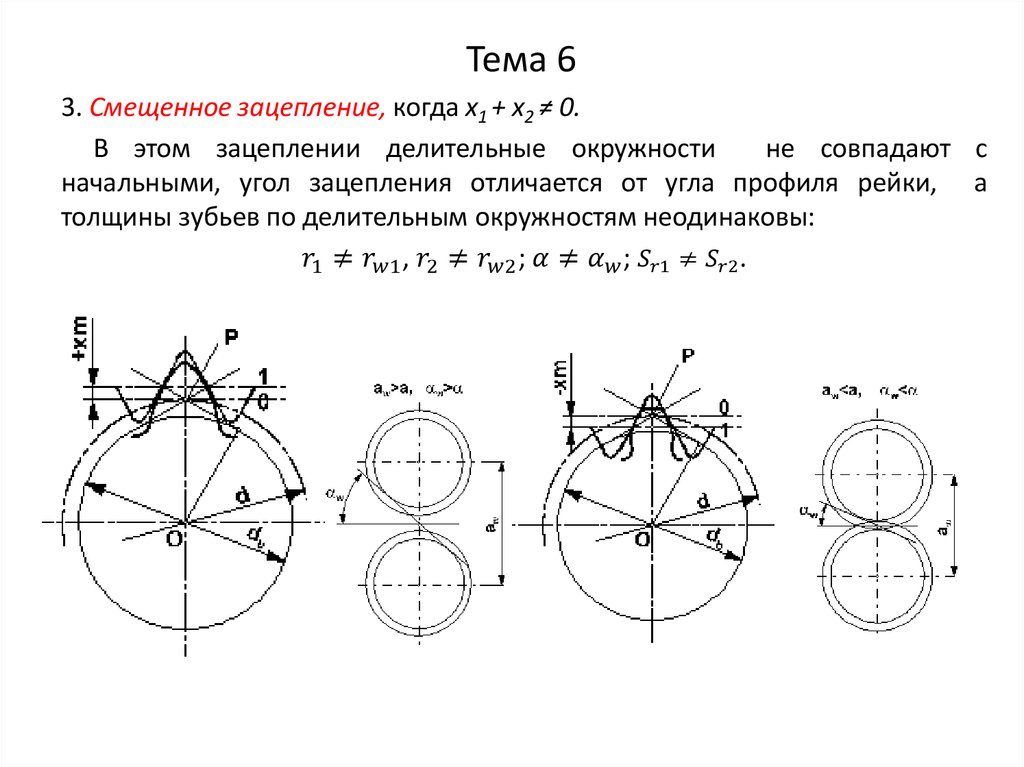 Диаметр окружности выступов De получается равным
Диаметр окружности выступов De получается равным
De=d+2× h’,
где h’- высота головки.
Высоту головки приравнивают к m:
h’=m.
Проведя математические преобразования с подстановкой, получим:
De=m×z+2m = m(z+2),
откуда вытекает:
m=De/(z+2).
Диаметр окружности впадин Di соответствует De за вычетом двух высот основания зубца:
Di=D-2h“,
где h“- высота ножки зубца.
Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:
h’ = 1,25m.
Устройство зубчатого колеса
Выполнив подстановку в правой части равенства, имеем:
Di = m×z-2×1,25m = m×z-2,5m;
что соответствует формуле:
Di = m(z-2,5m).
Полная высота:
h = h’+h“,
и если выполнить подстановку, то получим:
h = 1m+1,25m=2,25m.
Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.
Следующий важный размер, толщину зубца s принимают приблизительно равной:
- для отлитых зубцов: 1,53m:
- для выполненных путем фрезерования-1,57m, или 0,5×t
Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины sв, получаем формулы для ширины впадины
- для отлитых зубцов: sв=πm-1,53m=1,61m:
- для выполненных путем фрезерования- sв= πm-1,57m = 1,57m
Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:
- усилия, прикладываемые к детали при эксплуатации;
- конфигурация деталей, взаимодействующих с ней.

Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.
Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.
Исходные данные и замеры
На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.
Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.
Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.
Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.
Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.
Результаты расчетов
Для более крупных потребуются измерения и вычисления.
Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:
m=De/(z+2)
Последовательность действий следующая:
- измерить диаметр штангенциркулем;
- сосчитать зубцы;
- разделить диаметр на z+2;
- округлить результат до ближайшего целого числа.

Зубец колеса и его параметры
Данный метод подходит как для прямозубых колес, так и для косозубых.
Расчет параметров колеса и шестерни косозубой передачи
Расчетные формулы для важнейших характеристик шестерни косозубой передачи совпадают с формулами для прямозубой. Существенные различия возникают лишь при прочностных расчетах.
Что такое модуль зубчатого колеса? Как вычислить модуль зубчатого колеса
Содержание
- История
- Модуль зубьев зубчатого колеса
- Что такое модуль зубчатого колеса
- Чему равен модуль зубчатого колеса?
- Для чего нужен модуль зубчатого колеса?
- Как определить параметры шестерни?
- Как найти модуль шестерни?
- Как найти делительный диаметр шестерни?
- Как найти модуль зуба?
- Какие бывают модули зубчатых колес?
- Цилиндрические зубчатые колёса
- Продольная линия зуба
- Прямозубые колёса
- Косозубые колёса
- Шевронные колеса
- Колёса с круговыми зубьями
- Винтовые шестерни
- Секторные колёса
- Зубчатые колёса с внешним и внутренним зацеплением
- Звездочка
- Реечная передача (кремальера)
- Коронные колёса
- Конические зубчатые колёса
- Зубчатые передачи
- Типы зубчатых передач
- Эвольвентное зацепление
- Форма зубьев
- Коррегирование зубчатого зацепления
- Зубчатые передачи с точно заданным межосевым расстоянием
- Зубчатые передачи с изменяемым межосевым расстоянием
- Расчетные формулы для зубчатых передач
- Основные параметры зубчатых цилиндрических передач
- Межосевые расстояния
- Межосевые расстояния для двухступенчатых несоосных редукторов общего назначения
- Коэффициент запаса прочности при работе зуба двумя сторонами
- Межосевые расстояния для трехступенчатых несоосных редукторов общего назначения
- Номинальные передаточные числа
- Почему шестерни часто выполняют заодно с валом?
История
Сама по себе идея механической передачи восходит к идее колеса. Применяя систему из двух колёс разного диаметра, можно не только передавать, но и преобразовывать движение. Если ведомым будет большее колесо, то на выходе мы потеряем в скорости, но зато крутящий момент этой передачи увеличится. Эта передача удобна там, где требуется «усилить движение», например, при подъеме тяжестей. Но сцепление между передаточными колесами с гладким ободом недостаточно жесткое, колёса проскальзывают. Поэтому вместо гладких колес начали использовать зубчатые.
Применяя систему из двух колёс разного диаметра, можно не только передавать, но и преобразовывать движение. Если ведомым будет большее колесо, то на выходе мы потеряем в скорости, но зато крутящий момент этой передачи увеличится. Эта передача удобна там, где требуется «усилить движение», например, при подъеме тяжестей. Но сцепление между передаточными колесами с гладким ободом недостаточно жесткое, колёса проскальзывают. Поэтому вместо гладких колес начали использовать зубчатые.
В Древнем Египте для орошения земель уже использовались приводимые в действие быками устройства, состоявшие из деревянной зубчатой передачи и колеса с большим числом ковшей.
Вместо зубьев первоначально использовали деревянные цилиндрические или прямоугольные пальцы, которые устанавливали по краю деревянных ободьев.
Изготовленный в I веке до н.э. Антикитерский механизм состоял из десятков металлических зубчатых колес [4] .
Модуль зубьев зубчатого колеса
Зубчатая передача впервые была освоена человеком в глубокой древности.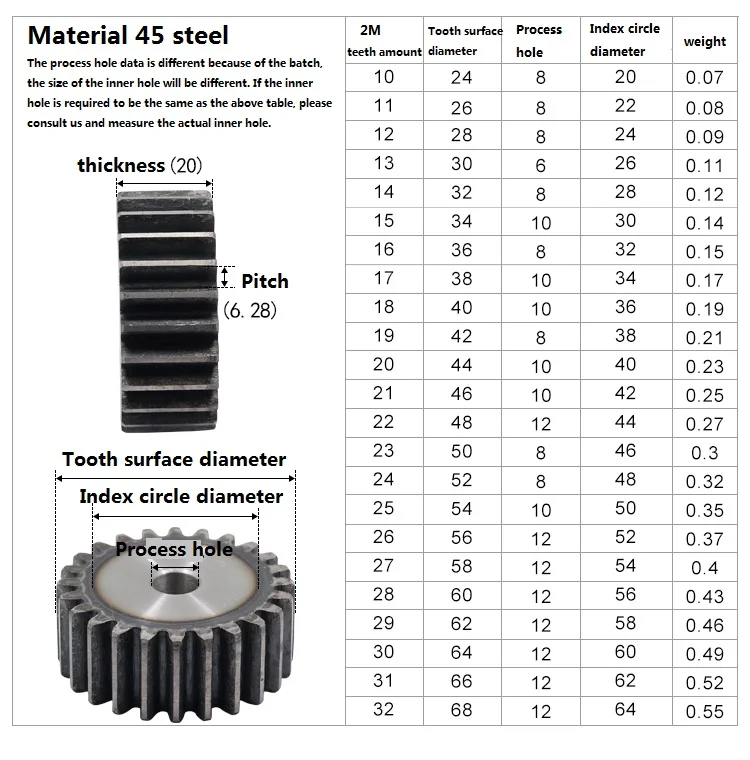 Имя изобретателя осталось скрыто во тьме веков. Первоначально зубчатые передачи имели по шесть зубьев — отсюда и пошло название «шестерня». За многие тысячелетия технического прогресса передача многократно усовершенствовалась, и сегодня они применяются практически в любом транспортном средстве от велосипеда до космического корабля и подводной лодки. Используются они также в любом станке и механизме, больше всего шестеренок используется в механических часах.
Имя изобретателя осталось скрыто во тьме веков. Первоначально зубчатые передачи имели по шесть зубьев — отсюда и пошло название «шестерня». За многие тысячелетия технического прогресса передача многократно усовершенствовалась, и сегодня они применяются практически в любом транспортном средстве от велосипеда до космического корабля и подводной лодки. Используются они также в любом станке и механизме, больше всего шестеренок используется в механических часах.
Что такое модуль зубчатого колеса
Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров
- диаметр;
- число зубьев;
- шаг;
- высота зубца;
- и некоторые другие.

Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида — основной и торцевой.
В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров.
Для расчета этого параметра применяют следующие формулы:
Параметры зубчатых колес
Модуль зубчатого колеса можно рассчитать и следующим образом:
где h — высота зубца.
где De — диаметр окружности выступов,а z — число зубьев.
Чему равен модуль зубчатого колеса?
Модуль зубчатого колеса Модуль зубчатого колеса, геометрический параметр зубчатых колёс. Для прямозубых цилиндрических зубчатых колёс модуль m равен отношению диаметра делительной окружности dд к числу зубьев z или отношению шага t по делительной окружности к числу: m = dд/z = ts/p.
Для чего нужен модуль зубчатого колеса?
Что же такое модуль шестерни? это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.
Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.
Как определить параметры шестерни?
Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр. Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.
Как найти модуль шестерни?
Как определить модуль косозубой шестерни.
Измеряем диаметр:
- Диаметр окружности выступов (De) равен 28,6 мм.
- Считаем количество зубьев. Z=25.
- Делительный диаметр (De) делим на количество зубьев 25 +2. Равно 28,6 разделить на 27=1,05925925925926.
- Округляем до ближнего модуля. Получается модуль 1.
Как найти делительный диаметр шестерни?
Диаметр делительной окружности d является одним из основных параметров, по которому производят расчет зубчатого колеса: d = m × z, где z – число зубьев; m – модуль.
Как найти модуль зуба?
Модуль = De/Z+2. То есть диаметр окружности выступов разделить на количество зубьев плюс 2. Измеряем диаметр: Диаметр окружности выступов (De) равен 28,6 мм.
Какие бывают модули зубчатых колес?
Модуль — это линейная величина, в π раз меньшая шага зубьев p (окружного pt, осевого рx, нормального рn и других шагов) эвольвентного зубчатого колеса m = р/π. Соответственно различают модули: окружной mt, осевой mx, нормальный mn и др.
Цилиндрические зубчатые колёса
Параметры зубчатого колеса
Профиль зубьев колёс как правило имеет эвольвентную боковую форму. Однако существуют передачи с круговой формой профиля зубьев (передача Новикова с одной и двумя линиями зацепления) и с циклоидальной. Кроме того, в храповых механизмах применяются зубчатые колёса с несимметричным профилем зуба.
Параметры эвольвентного зубчатого колеса:
- m — модуль колеса. Модулем зацепления называется линейная величина в π раз меньшая окружного шага P или отношение шага по любой концентрической окружности зубчатого колеса к π, то есть модуль — число миллиметров диаметра делительной окружности приходящееся на один зуб.
 Тёмное и светлое колёсо имеют одинаковый модуль. Самый главный параметр, стандартизирован, определяется из прочностного расчёта зубчатых передач. Чем больше нагружена передача, тем выше значение модуля. Через него выражаются все остальные параметры. Модуль измеряется в миллиметрах, вычисляется по формуле:
Тёмное и светлое колёсо имеют одинаковый модуль. Самый главный параметр, стандартизирован, определяется из прочностного расчёта зубчатых передач. Чем больше нагружена передача, тем выше значение модуля. Через него выражаются все остальные параметры. Модуль измеряется в миллиметрах, вычисляется по формуле:
- z — число зубьев колеса
- p — шаг зубьев (отмечен сиреневым цветом)
- d — диаметр делительной окружности (отмечена жёлтым цветом)
- da — диаметр окружности вершин тёмного колеса (отмечена красным цветом)
- db — диаметр основной окружности — эвольвенты (отмечена зелёным цветом)
- df — диаметр окружности впадин тёмного колеса (отмечена синим цветом)
- haP+hfP — высота зуба тёмного колеса, x+haP+hfP — высота зуба светлого колеса
Для целей стандартизации, удобства изготовления и замены зубчатых колёс в машиностроении приняты определённые значения модуля зубчатого колеса m, представляющие собой ряд из чисел на выбор: 0,05; 0,06; 0,08; 0,1; 0,12; 0,15; 0,2; 0,25; 0,3; 0,4; 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 25; 32; 40; 50; 60; 80; 100.

Зубчатые колеса могут быть изготовлены с различным смещением режущей рейки: без смещения (нулевое зубчатое колесо или «с нулевыми зубцами»), с положительным смещением (смещение в сторону увеличения материала), с отрицательным смещением (смещение в сторону уменьшения материала).
Высота головки зуба — haP и высота ножки зуба — hfP — в случае нулевого зубчатого колеса соотносятся с модулем m следующим образом: haP = m; hfP = 1,25 m, то есть:
Отсюда получаем, что высота зуба h (на рисунке не обозначена):
Вообще из рисунка ясно, что диаметр окружности вершин da больше диаметра окружности впадин df на двойную высоту зуба h. Исходя из всего этого, если требуется практически определить модуль m зубчатого колеса, не имея нужных данных для вычислений (кроме числа зубьев z), то необходимо точно измерить его наружный диаметр da и результат разделить на число зубьев z плюс 2:
Продольная линия зуба
Цилиндрические зубчатые колеса классифицируются в зависимости от формы продольной линии зуба на:
| ПРЯМОЗУБЫЕ | КОСОЗУБЫЕ | ШЕВРОННЫЕ | ЗУБЬЯ НОВИКОВА |
Прямозубые колёса
Зубья расположены в радиальных плоскостях, а линия контакта зубьев обеих шестерён параллельна оси вращения. При этом оси обеих шестерён также должны располагаться строго параллельно. Прямозубые колеса имеют наименьшую стоимость, их работа имеет наивысший КПД, но, в то же время, предельный передаваемый крутящий момент таких колес ниже, чем косозубых и шевронных.
При этом оси обеих шестерён также должны располагаться строго параллельно. Прямозубые колеса имеют наименьшую стоимость, их работа имеет наивысший КПД, но, в то же время, предельный передаваемый крутящий момент таких колес ниже, чем косозубых и шевронных.
Косозубые колёса
Зубья располагаются под углом к оси вращения, а по форме образуют часть винтовой линии. Зацепление таких колёс происходит плавнее, чем у прямозубых, и с меньшим шумом. Также увеличена площадь контакта, что при тех же размерах с прямозубыми позволяет передавать больший крутящий момент. При работе косозубой пары зацепления возникает механическая осевая сила, направленная вдоль оси вращения каждого колеса и стремящаяся раздвинуть оба колеса в противоположные стороны от плоскости контакта, что обязательно требует применения упорных подшипников. Увеличенная площадь трения зубьев косозубого зацепления вызывает дополнительные потери мощности на нагрев. В целом, косозубые колёса применяются в механизмах, требующих передачи большого крутящего момента на высоких скоростях, либо имеющих жёсткие ограничения по шумности.
Шевронные колеса
Изобретение шевронного профиля зуба часто приписывают Андре Ситроену, однако на самом деле он лишь выкупил патент на более совершенную схему, которую придумал польский механик-самоучка [6] . Зубья таких колёс изготавливаются в виде буквы «V» (либо они получаются стыковкой двух косозубых колёс со встречным расположением зубьев). Шевронные колёса решают проблему осевой силы. Осевые силы обеих половин такого колеса взаимно компенсируются, поэтому отпадает необходимость в установке валов на упорные подшипники. При этом передача является самоустанавливающейся в осевом направлении, по причине чего в редукторах с шевронными колесами один из валов устанавливают на плавающих опорах (как правило — на подшипниках с короткими цилиндрическими роликами).
Колёса с круговыми зубьями
Передача на основе колёс с круговыми зубьями (Передача Новикова) имеет ещё более высокие ходовые качества, чем косозубые — высокую нагрузочную способность зацепления, высокую плавность и бесшумность работы. Однако они ограничены в применении сниженными, при тех же условиях, КПД и ресурсом работы, такие колёса заметно сложнее в производстве. Линия зубьев у них представляет собой окружность радиуса, подбираемого под определённые требования. Контакт поверхностей зубьев происходит в одной точке на линии зацепления, расположенной параллельно осям колёс.
Однако они ограничены в применении сниженными, при тех же условиях, КПД и ресурсом работы, такие колёса заметно сложнее в производстве. Линия зубьев у них представляет собой окружность радиуса, подбираемого под определённые требования. Контакт поверхностей зубьев происходит в одной точке на линии зацепления, расположенной параллельно осям колёс.
Винтовые шестерни
Шестерни имеют форму цилиндра с расположенными на нем зубьями по винтовой линии. Эти шестеренки используются на непересекающихся валах, которые располагаются перпендикулярно друг друга, угол между ними 90°.
Секторные колёса
Секторное колесо представляет собой часть обычного цилиндрического колеса с зубьями любого типа. Такие колёса применяются в тех случаях, когда не требуется вращение звена на полный оборот, и поэтому можно сэкономить на его габаритах.
Зубчатые колёса с внешним и внутренним зацеплением
Пара зубчатых колёс с ВНЕШНИМ зацеплением. Передаточное число — 3 (42/14). Вращение колёс происходит противонаправлено. | Пара зубчатых колёс с ВНУТРЕННИМ зацеплением. Передаточное число — 3 (42/14). Вращение колёс происходит сонаправленно. |
Звездочка
Шестерня-звезда – это основная деталь цепной передачи, которая используется совместно с гибким элементом – цепью для передачи механической энергии.
Реечная передача (кремальера)
Реечная передача (кремальера)
Реечная передача (кремальера) применяется в тех случаях, когда необходимо преобразовать вращательное движение в поступательное и обратно. Состоит из обычной прямозубой шестерни и зубчатой планки (рейки). Работа такого механизма показана на рисунке.
Зубчатая рейка представляет собой часть колеса с бесконечным радиусом делительной окружности. Поэтому делительная окружность, а также окружности вершин и впадин превращаются в параллельные прямые линии. Эвольвентный профиль рейки также принимает прямолинейное очертание. Такое свойство эвольвенты оказалось наиболее ценным при изготовлении зубчатых колёс.
Такое свойство эвольвенты оказалось наиболее ценным при изготовлении зубчатых колёс.
Также реечная передача применяется в зубчатой железной дороге.
Цевочная передачаКоронная шестерня
Коронные колёса
Коронное колесо — особый вид колёс, зубья которых располагаются на боковой поверхности. Такое колесо, как правило, стыкуется с обычным прямозубым, либо с барабаном из стержней (цевочное колесо), как в башенных часах. Передачи с цевочным колесом — одни из самых ранних и просты в изготовлении, но характеризуются очень большими потерями на трение.
Конические зубчатые колёса
Главная передача в заднеприводном автомобиле
Во многих машинах осуществление требуемых движений механизма связано с необходимостью передать вращение с одного вала на другой при условии, что оси этих валов пересекаются. В таких случаях применяют коническую зубчатую передачу. Различают виды конических колёс, отличающихся по форме линий зубьев: с прямыми, тангенциальными, круговыми и криволинейными зубьями. Конические колёса с круговым зубом, например, применяются в автомобильных главных передачах коробки передач.
Конические колёса с круговым зубом, например, применяются в автомобильных главных передачах коробки передач.
Зубчатые передачи
Зубчатые передачи — это механизм или часть механизма механической передачи, в состав которого входят зубчатые колёса. Зубчатые передачи служат для того, чтобы непрерывно передавать силу и крутящий момент двух валов, расположение которых определяет тип имеющейся зубчатой передачи. Вот о том, что представляют зубчатые передачи, мы и поговорим в этой статье.
Типы зубчатых передач
Эвольвентное зацепление
Все прямозубые цилиндрические передачи с одинаковым модулем зацепления могут изготавливаться на одном оборудовании, независимо от количества зубьев и размеров головки.
Модули зацепления цилиндрических и конических зубчатых колес стандартизированы по DIN 780; модули зацепления червячных передач по DIN 780; модули шлицевых соединений по DIN 5480; модули зубчатого зацепления нормального профиля для шестерен со спиральными зубьями по DIN 780.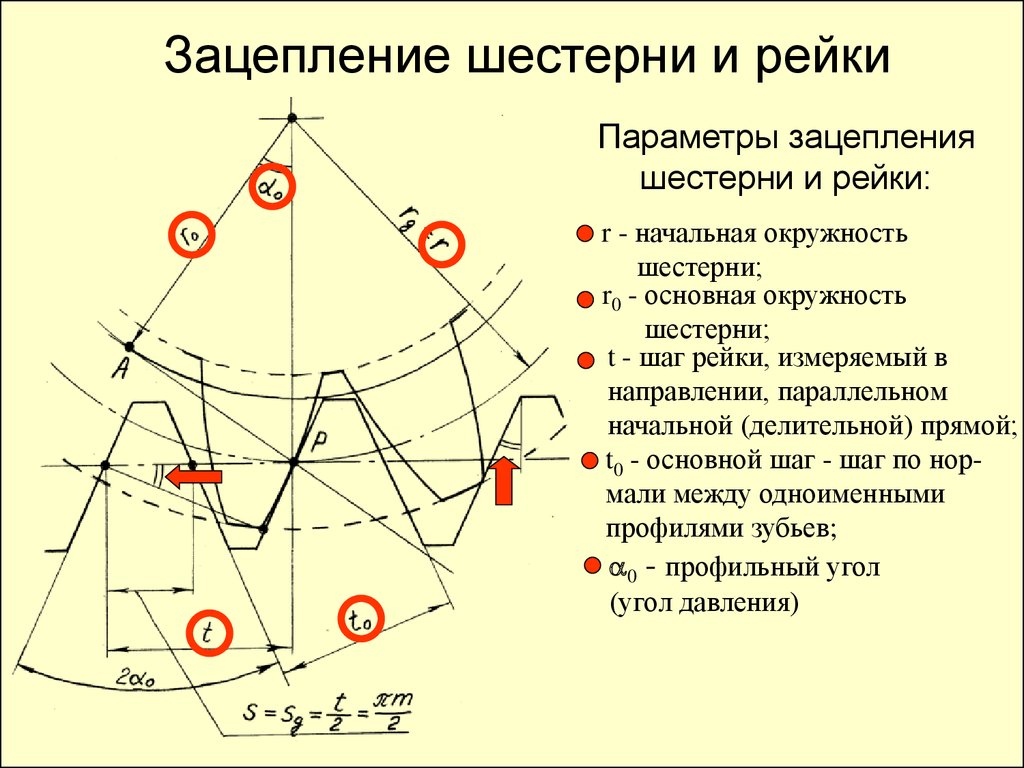
Форма зубьев
Для прямозубых цилиндрических передач форма зубьев определяется DIN 867, DIN 58400; конических передач — DIN 3971; червячных передач — DIN 3975; шлицевых соединений — DIN 5480 (см. рис. «Прямые и косые зубья (наружное зацепление)» ).
Форма зубьев гипоидных передач регламентируется стандартом DIN 867. В дополнение к стандартным углам зацепления (20° для зубчатых передач и 30° для шлицевых соединений) применяются также и углы зацепления 12°, 14°30 15°, 17°30′| 22°30′ и 25°.
Коррегирование зубчатого зацепления
Коррегирование зубчатого зацепления (изменение высоты головки зуба (см. рис. «Коррегирование зубчатого зацепления прямозубой цилиндрической передачи (циклоидное зацепление)» ) применяется для предотвращения подрезания у шестерен с малым количеством зубьев. Оно позволяет увеличить прочность ножки зуба и точно обеспечить межосевое расстояние.
Зубчатые передачи с точно заданным межосевым расстоянием
У зубчатых пар с точно заданным межосевым расстоянием изменение высоты головки зуба для шестерни и зубчатого колеса производится на одинаковую величину, но в противоположных направлениях, что позволяет сохранить межосевое расстояние неизменным. Такое решение применяется в гипоидных и косозубых передачах.
Такое решение применяется в гипоидных и косозубых передачах.
Зубчатые передачи с изменяемым межосевым расстоянием
Изменение высоты головки зуба для шестерни и зубчатого колеса производится независимо друг от друга, поэтому межосевое расстояние передачи может изменяться. Допускаемые отклонения линейных размеров зубчатых передач регламентированы. Для прямозубых цилиндрических передач — DIN 3960, DIN 58405; для конических передач — DIN 3971; червячных передач — DIN 3975.
Подставляя jη = 0 в приведенные ниже формулы, рассчитывают параметры зацепления без зазора между зубьями. Для определения зазора между зубьями допускаемые отклонения толщины зубьев и зоны их зацепления принимают в соответствии со стандартами DIN 3967 и DIN 58405 в зависимости от требуемой степени точности зубчатой передачи.
Следует отметить, что не обязательно стремиться к нулевому зазору между зубьями. Для компенсации имеющихся отклонений размеров зубьев и сборки шестерен достаточно иметь минимальный зазор, который, кроме того, предотвращает возможность заклинивания зубчатых колес.
Допускаемые отклонения других расчетных параметров (зазор между ножками двух смежных зубьев, межцентровое расстояние) приведены в стандартах DIN 3963, DIN 58405, DIN 3962 Т2, DIN 3967, DIN 3964.
Расчетные формулы для зубчатых передач
Основные параметры зубчатых цилиндрических передач
Стандарт распространяется на цилиндрические передачи внешнего зацепления для редукторов и ускорителей, в том числе и комбинированных (коническо-цилиндрических, цилиндро-червячных и др.), выполняемых в виде самостоятельных агрегатов. Стандарт не распространяется на передачи редукторов специального назначения и специальной конструкции Для встроенных передач стандарт является рекомендуемым
Межосевые расстояния
| 1 ряд | 40 | 50 | 63 | 80 | 100 | 125 | — | 160 | — | 200 | — | 250 | — | 315 | — | 400 |
| 2 ряд | — | — | — | — | — | — | 140 | — | 180 | — | 225 | — | 280 | — | 355 | — |
| 1 ряд | — | 500 | — | 630 | — | 800 | — | 1000 | — | 1250 | — | 1600 | — | 2000 | — | 2500 |
| 2 ряд | 450 | — | 560 | — | 710 | — | 900 | — | 1120 | — | 1400 | — | 1800 | — | 2240 | — |
1-й ряд следует предпочитать 2-му
Межосевые расстояния для двухступенчатых несоосных редукторов общего назначения
| Быстроходная ступень | 40 | 50 | 63 | 80 | 100 | 125 | 140 | 160 | 180 | 200 | 225 | 250 | 280 | 315 |
| Тихоходная ступень | 63 | 80 | 100 | 125 | 160 | 200 | 225 | 250 | 280 | 315 | 355 | 400 | 450 | 500 |
| Быстроходная ступень | 355 | 400 | 450 | 500 | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 |
| Тихоходная ступень | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 | 1800 | 2000 | 2240 | 2500 |
Коэффициент запаса прочности при работе зуба двумя сторонами
Например: зубья реверсивных передач или зубья сателлитов в планетарных передачах
| Материал колес и термо- обработка | Отливки стальные и чугунные без термо- обработки | Отливки стальные и чугунные с термо- обработкой | Поковки стальные нормали- зованные или улучшенные | Поковки и отливки стальные с поверх- ностной закалкой (сердцевина вязкая) | Стальные, нормали- зованные или улучшенные, а также с поверх- ностной закалкой | Стальные с объемной закалкой | Стальные, подверг- нутые цементации, азоти- рованию, циани- рованию и др. | Чугунные и пласт- массовые колеса |
| Коэфф. | 1,9 | 1,7 | 1,5 | 2,2 | 1,4 — 1,6 | 1,8 | 1,2 | 1 — 1,2 |
Межосевые расстояния для трехступенчатых несоосных редукторов общего назначения
| Быстроходная ступень | 40 | 50 | 63 | 80 | 100 | 125 | 140 | 160 | 180 | 200 |
| Промежуточная ступень | 63 | 80 | 100 | 125 | 160 | 200 | 225 | 250 | 280 | 315 |
| Тихоходная ступень | 100 | 125 | 160 | 200 | 250 | 315 | 355 | 400 | 450 | 500 |
| Быстроходная ступень | 225 | 250 | 280 | 315 | 355 | 400 | 450 | 500 | 560 | 630 |
| Промежуточная ступень | 355 | 400 | 450 | 500 | 560 | 630 | 710 | 800 | 900 | 1000 |
| Тихоходная ступень | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 |
Номинальные передаточные числа
| 1 ряд | 1,0 | — | 1,25 | — | 1,6 | — | 2,0 | — | 2,5 | — | 3,15 | |
| 2 ряд | — | 1,12 | — | 1,4 | — | 1,8 | — | 2,24 | — | 2,8 | — | |
| 1 ряд | — | 4,0 | — | 5,0 | — | 6,3 | — | 8,0 | — | 10 | — | 12,5 |
| 2 ряд | 3,55 | — | 4,5 | — | 5,6 | — | 7,1 | — | 9,0 | — | 11,2 | — |
1-й ряд следует предпочитать 2-му Фактические значения передаточных чисел не должны отличаться от номинальных более чем на 2,5% при номинальном меньше 4,5 и на 4% при номинальном больше 4,5
Коэффициент ширины зубчатых колес (отношение ширины зубчатого колеса к межосевому расстоянию) должен соответствовать: 0,100; 0,125; 0,160; 0,200; 0,315; 0,400; 0,500; 0,630; 0,800; 1,0; 1,25
Численные значения ширины зубчатых колес округляются до ближайшего числа из ряда Ra20 по ГОСТу 6636.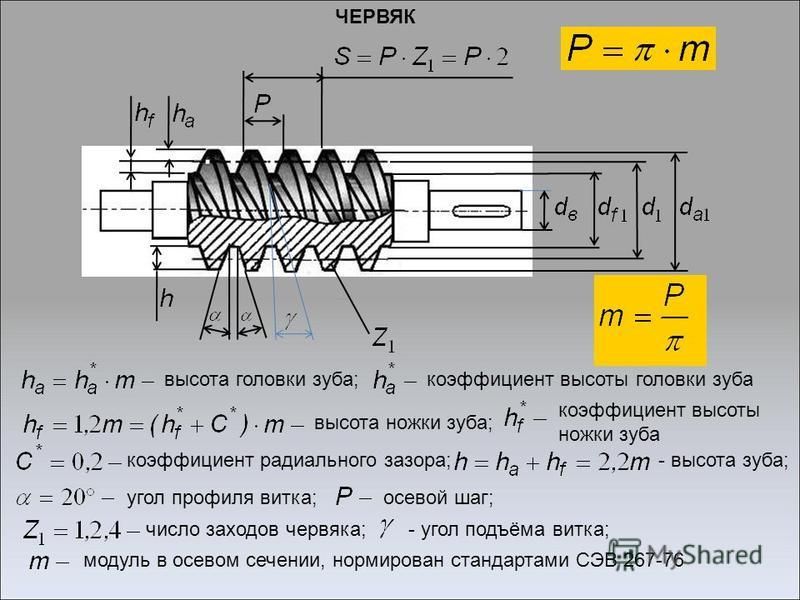
При различной ширине сопряженных зубчатых колес значение коэффициента ширины зубчатых колес относится к более узкому из них.
Почему шестерни часто выполняют заодно с валом?
Несмотря на это, в редукторах шестерню часто выполняют заодно с валом и даже при толщине, значительно превышающей указанные нормы. Это объясняется большей жесткостью и прочностью, а также технологичностью вала-шестерни, что в конечном итоге оправдывает ее стоимость.
Источники
- https://ru.wikipedia.org/wiki/%D0%97%D1%83%D0%B1%D1%87%D0%B0%D1%82%D0%BE%D0%B5_%D0%BA%D0%BE%D0%BB%D0%B5%D1%81%D0%BE
- https://doctordent.su/pulpit/kak-opredelit-modul-zuba-shesterni-po-diametru.html
- https://novoe-info.ru/chto-takoe-modul-zubchatogo-kolesa/
- https://novoe-info.ru/kak-nayti-modul-zubchatogo-kolesa/
- https://morflot.su/kak-vychislit-modul-zubchatogo-kolesa/
- https://wiki2.org/ru/%D0%97%D1%83%D0%B1%D1%87%D0%B0%D1%82%D0%BE%D0%B5_%D0%BA%D0%BE%D0%BB%D0%B5%D1%81%D0%BE
- https://nzmetallspb.
 ru/prochee/modul-zubev-zubchatogo-kolesa-raschet-standartnye-opredelenie.html
ru/prochee/modul-zubev-zubchatogo-kolesa-raschet-standartnye-opredelenie.html - https://armatool.ru/modul-zubev-zubcatogo-kolesa-rascet-standartnye-opredelenie/
Базовая терминология и расчет передач
ТОП
Знание передач
Азбука передач — B
Базовая терминология и расчет передач
>
>
>
Размер шестерни, угол давления, количество зубьев… мы вводим основную терминологию, измерения и относительные выражения, необходимые для понимания основных технологий зубчатых передач.
Сравнительный размер зубьев шестерни
В соответствии с рекомендациями ISO (Международной организации по стандартизации) размер модуля обозначается как единица, представляющая размеры зубьев шестерни.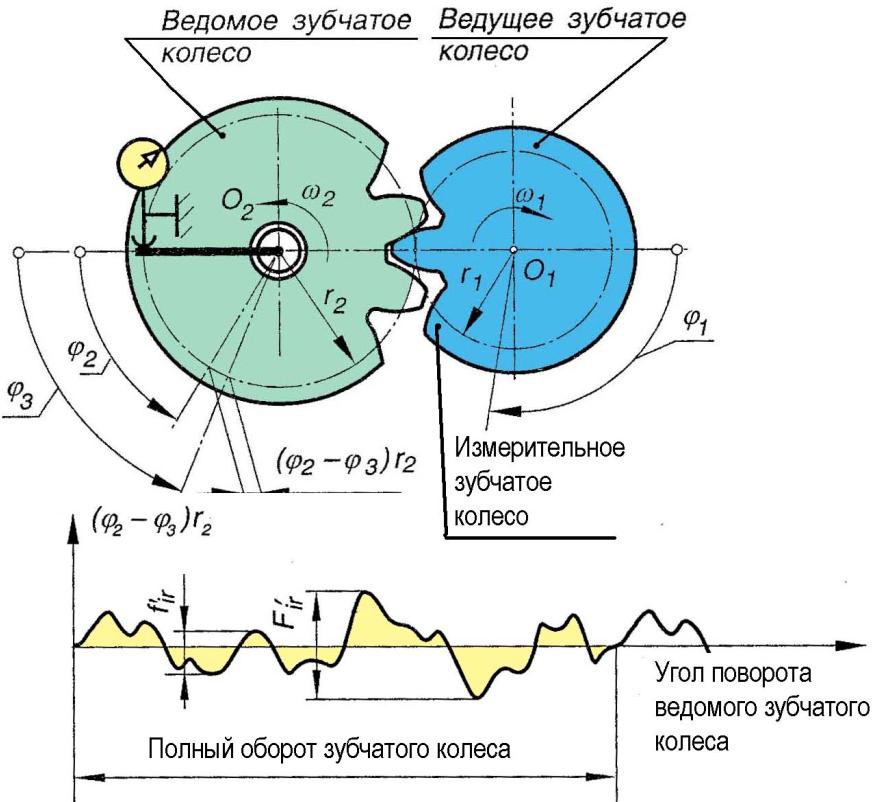 Однако используются и другие методы.
Однако используются и другие методы.
Модуль (м)
м = 1 (p = 3,1416)
м = 2 (p = 6,2832)
м = 4 (p = 12,566)
Пи, вы можете получить Шаг (p). Шаг – это расстояние между соответствующими точками на соседних зубах.
p = Pi x Module = πm (2.1)
Пример расчета
Каков размер шага (p) шестерни с модулем m = 3?
p = πm = 9,4248
CP (круговой шаг)
Круговой шаг (CP) обозначает эталонный шаг (p).
Например, вы можете производить шестерни с точным интегральным значением, например CP5/CP10/CP15/CP20.
Преобразование CP в модуль
m = CP / π (2.2)
Пример расчета
CP10 преобразуется в модуль следующим образом ;
м = 10 / 3,1416 = 3,1831
DP (диаметральный шаг)
DP означает диаметральный шаг.
По стандартам ISO единица миллиметр (мм) предназначена для выражения длины, однако в США, Великобритании и других странах используется единица измерения дюйм; Диаметральный шаг также используется в этих странах.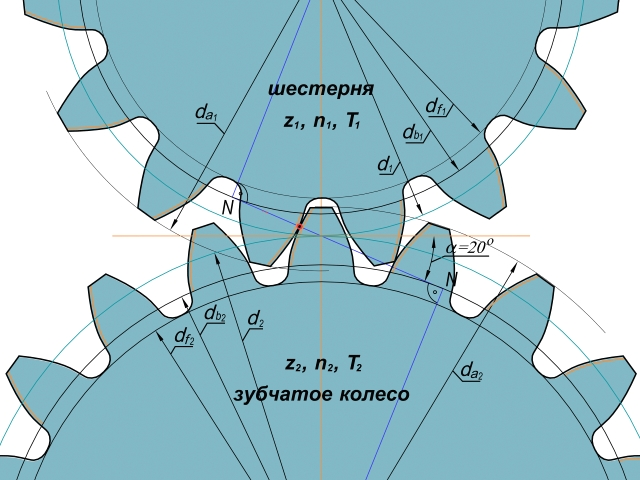
Преобразование DP в модуль
m = 25,4 / DP (2.3)
Пример расчета
DP 8 преобразуется в модуль следующим образом ;
м = 25,4 / 8 = 3,175
Угол давления (α)
Угол давления — это угол наклона зуба шестерни, элемент, определяющий профиль зуба.
В последнее время угол давления (α) обычно устанавливается равным 20°, однако преобладали шестерни 14,5°.
Рис. 2.2 Нормализованный профиль зуба по эталону
(Важная терминология и номенклатура зубчатых колес на рис. 2.2)
- Базовая линия
- Угол давления
- Нормальная опорная линия
- Шаг
- Поверхность зуба
- Корневая поверхность
- Верхняя земля
Количество зубьев
Количество зубьев обозначает количество зубьев шестерни.
Они подсчитываются, как показано на рисунке 2.3. Число зубьев этой шестерни равно 10.
Рис. 2.3 Число зубьев
Модуль (m), Угол давления (α) и Число зубьев, введенные здесь, являются тремя основными элементами в составе зубчатого колеса. механизм. На основе этих элементов рассчитываются размеры зубчатых колес.
механизм. На основе этих элементов рассчитываются размеры зубчатых колес.
Глубина и толщина зуба
Глубина зуба определяется размером модуля (м). Здесь представлены профили зубьев (полная глубина), указанные в стандартах ISO и JIS (японские промышленные стандарты).
Пожалуйста, см. рисунок 2.4 ниже для пояснений для Глубина зуба (h) / Дополнение (ha) / Dedendum (hf).
Глубина зуба (h) — это расстояние между вершиной зуба и корнем зуба.
h = 2,25 м
(= Дополнение + Вывод) (2.4)
Рис. 2.4 Глубина и толщина зуба
(Важная терминология и номенклатура зубчатых колес на рис. 2.4)
- Базовая линия
- Шаг
- Толщина зуба
- Приложение
- Дедендум
- Глубина зуба
- Наконечник зуба
- Корень зуба
Дополнение (га) — расстояние между базовой линией и вершиной зуба.
га = 1,00 м (2,5)
Дедендум (hf) — расстояние между базовой линией и корнем зуба.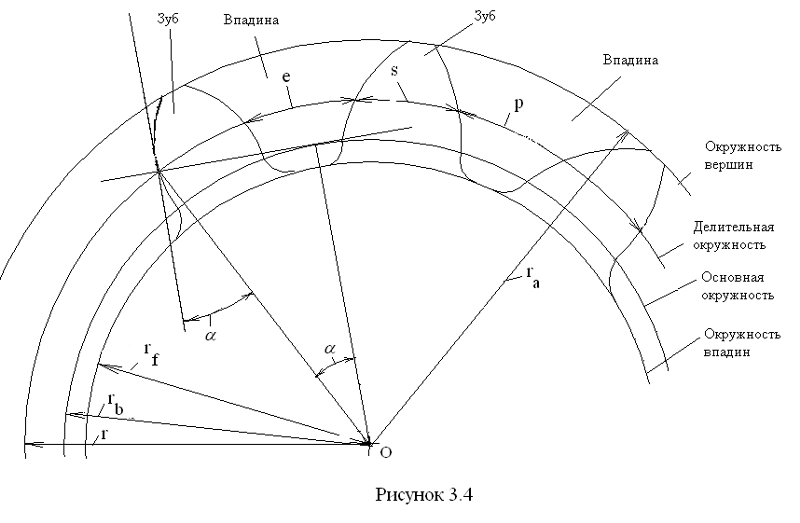
hf = 1,25 м (2,6)
Толщина зуба (s) в основном составляет половину значения шага (p). * Шаг (p) = πm
s = πm / 2 (2.7)
Примеры расчетов
Ниже приведены расчеты глубины зуба (h)/добавления (ha)/дедендума (hf) для зубчатого колеса с модулем 2.
h = 2,25 м = 2,25 × 2 = 4,50
га = 1,00 м = 1,00 × 2 = 2,00
hf = 1,25 м = 1,25 × 2 = 2,50 Модуль», «Угол давления», «Количество зубьев» и «Глубина и толщина зуба». В этом разделе мы познакомим вас с основными частями цилиндрических зубчатых колес (цилиндрическими зубчатыми колесами) и расчетами размеров.
Диаметр шестерен (размер)
Размер шестерен определяется в соответствии с эталонным диаметром (d) и определяется этими другими факторами; базовый круг, Шаг, Толщина зуба, Глубина зуба, Дополнение и Дедендум.
Базовый диаметр (d)
d = zm(2,8)
Диаметр наконечника (da)
da = d + 2 м(2,9)
Диаметр основания (df)
df 5 м2 (1,0 d2 — 2,0 )
Рис.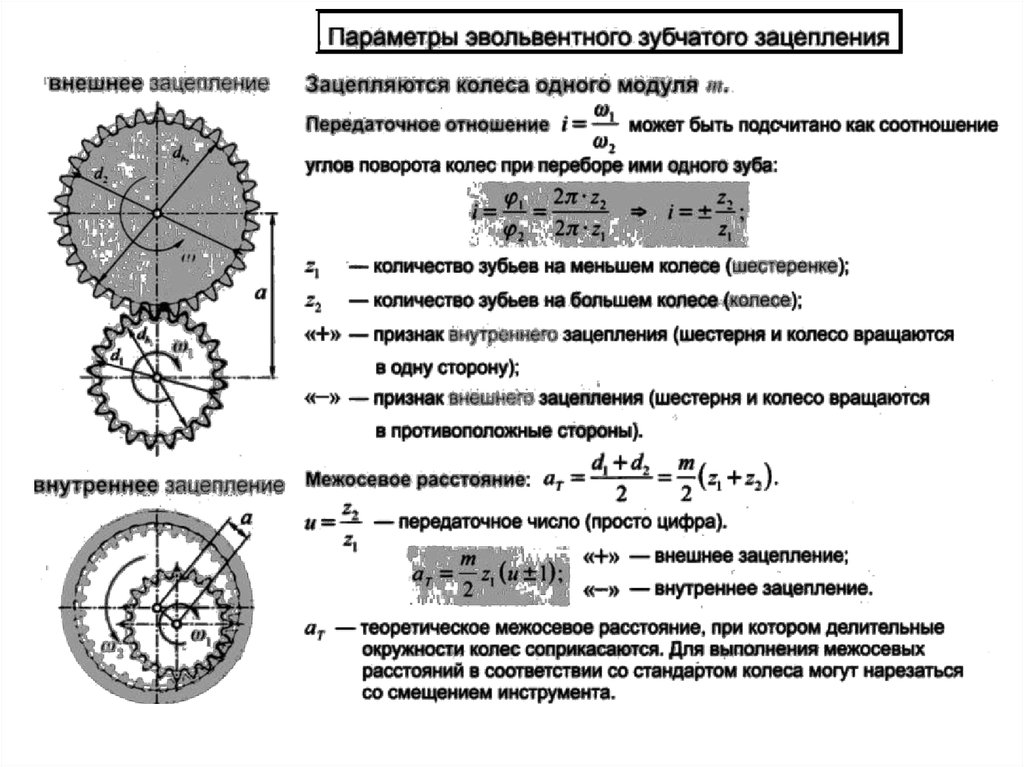 2.5 Диаметр шестерен
2.5 Диаметр шестерен
(Важная терминология и номенклатура шестерен на рис. 2.5)
- Приложение
- Дедендум
- Диаметр корня
- Базовый диаметр
- Диаметр наконечника
Добавление и окружность дедендума, представленные здесь, являются эталонной окружностью, которую нельзя увидеть на шестерне, так как это виртуальная окружность, определяемая размером шестерни.
Примеры расчетов
Ниже приведены расчеты исходного диаметра / диаметра вершины / диаметра основания для цилиндрического зубчатого колеса с модулем (m) 2 и 20 зубьями (z).
d = zm = 20 x 2 = 40
da = d + 2 m = 40 + 4 = 44
df = d – 2,5 m = 40 – 5 = 35 m) = 4
Количество зубьев (z) = 40 (угол зацепления α = 20°)
| Базовый диаметр | д = | |
| Диаметр наконечника | да = | |
| Диаметр основания | дф = |
Рис.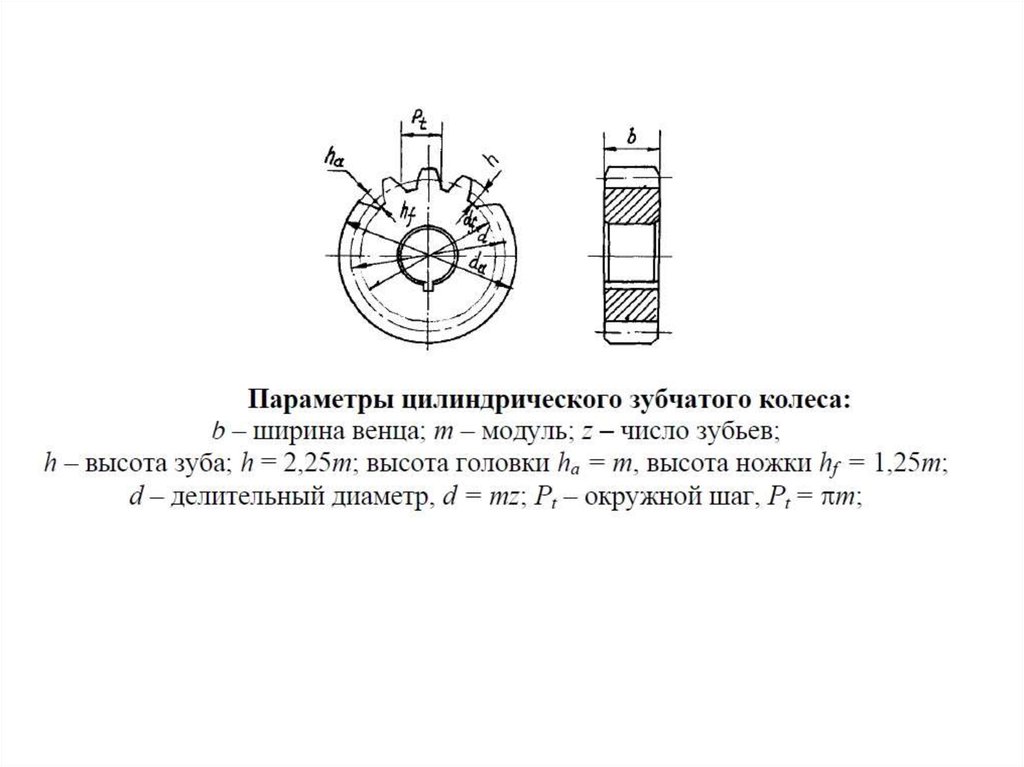 2.6 Номенклатура рабочих шестерен
2.6 Номенклатура рабочих шестерен
(Важная терминология и номенклатура шестерен на рис. 2.6)
- Диаметр наконечника
- Базовый диаметр
- Диаметр основания
- Диаметр корня
- Ширина лица
- Толщина зуба
- Базовый шаг
- Осевая линия
- Угол давления
- Люфт
- Глубина зуба
- Приложение
- Дедендум
- Межосевое расстояние
- Наконечник и корневой зазор
Таблица 2.1 Символы и номенклатура шестерен
| Термины | Символы | Условия | Символы |
|---|---|---|---|
| Модуль | м | Толщина зуба | с |
| Угол давления | α | Базовый диаметр | д |
| Номер зуба | с | Диаметр наконечника | да |
| Шаг | р | Диаметр корня | дф |
| Глубина зуба | ч | Расстояние до центра | и |
| Приложение | га | Люфт | и |
| Дедендум | хф | Наконечник и зазор корня | в |
Расстояние между центрами и люфт
Когда пара шестерен находится в зацеплении так, что их опорные окружности соприкасаются, межосевое расстояние (a) составляет половину суммы их опорных диаметров.
Расстояние до центра (а)
a = ( d1 + d2 ) / 2(2.11)
Рис. 2.7 Расстояние между центрами
Зубчатые колеса могут зацепляться, как показано на рис. может работать бесперебойно. Люфт – это люфт между поверхностями зубьев парных шестерен в зацеплении.
Сопрягаемые шестерни также имеют зазор (люфт) по вертикали глубины зуба. Это называется зазором между вершиной и корнем (c), расстоянием между основанием зуба и вершиной зуба сопрягаемых шестерен.
Зазор кончика и корня (c)
c = 1,25 м — 1,00 м
= 0,25 м (2,12)
Рис. 2.8 Зазор между вершиной и основанием
(Важная терминология и номенклатура зубчатых колес на рис. 2.8)
- Дополнение 04 круг
- Круг Дедендума
- Наконечник и корневой зазор
Примеры расчетов
Ниже приведены расчеты межцентрового расстояния (a) и зазора между вершинами и впадинами (c), когда модуль m = 2, шестерня z1 = 20, шестерня z2 = 40
Базовый диаметр шестерни d1 = 20 × 2 = 40
Базовый диаметр зубчатого колеса d2 = 40 × 2 = 80
Расстояние между центрами a = (40 + 80) / 2 = 60
c = 0,25 × 2 = 0,5
Примеры расчета
Практика расчета размеров шестерни.
| Термины | Символы | Формула | Шестерня | Шестерня |
|---|---|---|---|---|
| Модуль | м | — | 2,5 | |
| Угол давления | α | 20° | ||
| Кол-во зубьев | с | 15 | 30 | |
| Базовый диаметр | д | с м | 37,5 | 75 |
| Приложение | га | 1,00 м | 2,5 | 2,5 |
| Дедендум | вч | 1,25 м | 3,125 | 3,125 |
| Глубина зуба | ч | 2,25 м | 5,625 | 5,625 |
| Диаметр наконечника | да | д + 2 м | 42,5 | 80 |
| Диаметр основания | дф | г — 2,5 м | 31,25 | 68,75 |
| Межцентровое расстояние | и | д1 + д2/2 | 56,25 | |
Практический тест:
Расчеты размеров зубчатых колес.
| Условия | Символы | Формула | Шестерня | Шестерня |
|---|---|---|---|---|
| Модуль | м | — | 4 | |
| Угол давления | α | 20° | ||
| Кол-во зубьев | с | 12 | 60 | |
| Базовый диаметр | д | с м | ||
| Приложение | га | 1,00 м | ||
| Дедендум | вч | 1,25 м | ||
| Глубина зуба | ч | 2,25 м | ||
| Диаметр наконечника | да | г + 2 м | ||
| Диаметр основания | дф | г — 2,5 м | ||
| Расстояние между центрами | и | д1 + д2/2 | ||
Косозубая шестерня
Цилиндрические шестерни с геликоидными зубьями называются косозубыми шестернями.
Большинство расчетов для цилиндрических зубчатых колес можно применить и к косозубым. Этот тип зубчатого колеса поставляется с двумя видами профилей зубьев в соответствии с базовой поверхностью. (Рисунок 2.9)
Рис. 2.9 Правосторонняя косозубая шестерня
(Важная терминология и номенклатура шестерен на рис. 2.9)
- Обычный модуль
- Поперечный модуль
- Угол подъема спирали β
(a) Поперечная система (поперечный модуль / угол давления) * Поперечная ось обозначает центральную линию шестерни.
(b) Стандартная система (стандартный модуль/угол давления)
Реляционное выражение: поперечный модуль ( mt ) и нормальный модуль ( mn )
mt = mn / cos β(2.13)
Обе системы используются в стандартных редукторах KHK.
Поперечная система:KHG Заземляющие косозубые шестерни
Нормальная система:SH Косозубые шестерни
Базовый диаметр (d) косозубой шестерни с поперечной системой можно рассчитать по уравнению (2. 8).
8).
Базовый диаметр (d) косозубого колеса с нормальной системой можно рассчитать по уравнению (2.14).
d = zmn / cos β(2.14)
Примеры расчетов
Ниже приведен расчет эталонного диаметра косозубого колеса с: 15° (П)
Базовый диаметр d = zmt = 30 × 2 = 60
Ниже приведен расчет эталонного диаметра косозубой шестерни с:
Нормальным модулем mn = 2, числом зубьев z = 30, углом подъема винтовой линии β = 15° (R)
эталонным диаметром d = zmn / cos β = 30 × 2 / cos 15° = 62,117
Практический тест:
Технические характеристики косозубого колеса
Нормальный модуль (mn) = 4 Угол подъема винтовой линии (β) = 15°
Поперечный модуль mt =
Поиск и устранение неисправностей шестерен: объяснение терминологии
Точечная коррозия
Когда поверхность зубчатого колеса постоянно подвергается нагрузке, а усилие вблизи точки контакта превышает предел усталости материала, возникают мелкие трещины, которые в конечном итоге перерастают в разделение мелких частей, образуя ямки (кратеры).
Начальная стадия Точечная коррозия
Первоначальная причина связана с небольшими выпуклыми участками поверхностей зубчатого колеса, контактирующими друг с другом, и локальной нагрузкой, превышающей предел усталости. По мере приведения в движение шестерен и износа поверхностей локальные выпуклости исчезают, нагрузка выравнивается, питтинг прекращается.
Прогрессирующая точечная коррозия
Даже после износа поверхностей зубчатых колес и выравнивания нагрузки со временем начинает появляться больше точечной коррозии, и ямки увеличиваются.
(1) Когда существует состояние перегрузки и нагрузка на поверхность зубчатого колеса превышает предел усталости материала.
(2) Во время движения распределение нагрузки по поверхности зубчатого колеса может стать неравномерным из-за прогиба различных частей, что приведет к превышению предела усталости.
Вот некоторые из возможных причин прогрессирующей точечной коррозии.
Задиры
Это состояние, при котором смазочное покрытие разрушается из-за перегрева локальных контактных площадок, что приводит к износу поверхности зубчатого колеса от контакта металла к металлу. Это состояние может прогрессировать от умеренного до критического.
Это состояние может прогрессировать от умеренного до критического.
Проточка
В направлении скольжения шестерни появляются канавки. Это часть абразивного износа, и возможны следующие причины.
(1) Износ из-за попадания твердого постороннего предмета, превышающего толщину масляной пленки, в зацепление шестерни.
(2) Износ из-за твердого постороннего предмета, по какой-то причине застрявшего в зубе противоположной шестерни.
(3) Износ от твердой выпуклой части зуба противоположной шестерни, врезающейся в зацепляющую шестерню.
Абразивный износ
Износ, который выглядит как травма от истирания или имеет вид притирки. Ниже приведены некоторые из причин.
(1) Возможен износ из-за попадания в смазку твердых посторонних предметов (таких как металлические частицы износа, заусенцы, окалина, песок и т. д.).
(2) Износ из-за разницы в твердости двух зацепляющихся шестерен, в которых твердая выпуклая часть впивается в более мягкую поверхность шестерни.
Адгезионный износ
Износ, обычно возникающий между металлами при скользящем контакте. Снижение износа зависит от типа, давления, скорости, расстояния и смазки.
Незначительная часть материала в контактных сварных швах (прилипаниях) и механизм износа возникает в результате их отслоения под действием силы сдвига.
Выкрашивание
Относится к симптому отпадания относительно крупной металлической стружки с поверхности зубчатого колеса из-за усталости материала под поверхностью при высокой нагрузке. Вогнутая часть поверхности зубчатого колеса большая, а форма и глубина неправильные. Поскольку приложенная сила сдвига превышает предел выносливости материала, появляются и растут усталостные трещины, что может привести к поломке зуба.
Чрезмерный износ
Износ от поверхности зубчатого колеса, подвергающегося интенсивному повторяющемуся контакту металла с металлом, который возникает, когда масляная пленка тонкая и смазка недостаточна по сравнению с нагрузкой и шероховатостью поверхности зубчатого колеса. Это состояние имеет тенденцию возникать при работе на очень низкой скорости и высокой нагрузке.
Это состояние имеет тенденцию возникать при работе на очень низкой скорости и высокой нагрузке.
Поломка из-за перегрузки
Поломка из-за неожиданно большой нагрузки в течение одного или нескольких рабочих циклов (Обычно сюда не включаются ошибки проектирования или изготовления). Поверхность излома волокнисто распространяется от начальной точки и указывает на внезапное расщепление. Причина в том, что нагрузка превышает предел прочности на растяжение материала шестерни. Это может произойти из-за первичного двигателя, ведомого механизма или поломки подшипников или других шестерен, что может вызвать заедание зубьев, внезапную остановку или концентрацию нагрузки из-за неравномерного контакта зубьев.
Усталостная поломка
Это случай, когда корневая часть зубчатого колеса подвергается многократной нагрузке, превышающей предел усталости материала. Трещина, которая начинается в углу корня шестерни, распространяется до тех пор, пока зуб не сломается. Поверхность излома относительно гладкая, и начальную точку часто можно распознать по береговой отметине (рисунку раковины) вокруг нее.
Поломка при сдвиге
Описывает случай, когда зуб отделяется от тела в результате сдвига из-за однократной экстремальной перегрузки. Поломка прямая в окружном направлении и выглядит плоской, как если бы она была обработана механической обработкой. В близлежащей области наблюдается пластическая деформация. Это происходит, когда приложенная сила превышает прочность материала на сдвиг. Это происходит, когда зубчатое колесо высокой жесткости и прочности входит в зацепление с зубчатым колесом, имеющим относительно низкий модуль упругости и непрочный материал.
Ссылки по теме :
Шестерни для робототехники
Бесплатный калькулятор шестерен
Терминология шестерен
Типы шестерен и терминология
Расчет размеров шестерен
齿轮的基本用语和尺寸计算 — 中文鵗
Редукторный модуль | KHK Производитель зубчатых колес
ТОП
>
org/ListItem»>Модуль шестерни
Модуль (м) — это единица размера зуба шестерни, определяемая ISO.
Шестерни будут зацепляться друг с другом только в том случае, если они имеют зубья одного и того же модуля.
Изображение 1 — значение модуля правильно зацепленной пары шестерен такое же, как
(изображение показывает пару шестерен с модулем 2)
Шаг (p) представляет собой расстояние между зубьями, и поскольку больший шаг означает больший размер зуба, а меньший шаг означает меньший размер зуба, шаг можно использовать для представления размера зуба.
Делительная окружность шестерни соответствует внешней окружности фрикционного колеса (шестерни можно рассматривать как фрикционные колеса с прикрепленными зубьями) и является эталонной окружностью для определения шага зубьев шестерни.
Длина окружности делительной окружности (πd) равна ее диаметру (диаметр делительной окружности = d), умноженному на число пи π. Шаг получается путем деления окружности делительной окружности на количество зубьев (z).
р = πd / z
Однако этот шаг включает в себя пи, π (3,1415 ….), что усложняет расчет.
Таким образом, шаг делится на π (без π), чтобы получить d/z, который называется модулем и используется в качестве единицы для выражения размера зуба.
м = д / г
Поскольку единицей диаметра делительной окружности является мм, единица модуля, полученная путем деления диаметра делительной окружности на количество зубьев, также равна мм, но на практике модули часто используются только с номером после символа m, например как m1, m2 или m4 вместо добавления мм к модулю.
Как и в случае с шагом, чем больше значение модуля, тем больше размер зуба.
Изображение 2. Сравнение размеров зубов модуля 0,8 (слева) и зубов модуля 2 (справа)
Стандарт JIS определяет стандартные значения модуля (таблица 1) для прямозубых и косозубых зубчатых колес общего и тяжелого машиностроения и рекомендует максимально использовать ряд I и максимально избегать модуля 6. 5.
5.
Таблица 1 — Стандартные значения модуля (ед. мм)
Как упоминалось выше, ISO определяет модуль как единицу для выражения размера зубьев шестерни, но на практике DP (диаметральный шаг) часто используется в Соединенных Штатах и других странах, которые используют дюйм в качестве единицы длины, и иногда также используется круговой шаг (CP).
(сделав этот круговой шаг целым числом, легко сделать расстояние подачи в механизме подачи целым числом)
В таблице 2 сравниваются эквивалентные значения модуля (м), кругового шага (CP) и диаметрального шага (DP).
| Модуль м | Шаг CP | Диаметральный шаг DP |
|---|---|---|
| 0,39688 | 1.24682 | 64 |
| 0,5 | 1.57080 | 50,8 |
| 0,52917 | 1,66243 | 48 |
| 0,6 | 1.88496 | 42.33333 |
| 0,79375 | 2.49364 | 32 |
| 0,79577 | 2,5 | 31. 91858 91858 |
| 0,8 | 2,51327 | 31,75 |
| 1 | 3.14159 | 25,4 |
| 1.05833 | 3.32485 | 24 |
| 1,25 | 3,92699 | 20,32 |
| 1.27000 | 3,98982 | 20 |
| 1,5 | 4.71239 | 16.93333 |
| 1,59155 | 5 | 15.95929 |
| 1.58750 | 4,98728 | 16 |
| 2 | 6.28319 | 12,70 |
| 2.11667 | 6.64970 | 12 |
| 2,5 | 7,85398 | 10.16 |
| 2,54000 | 7,97965 | 10 |
| 3 | 9.42478 | 8.46667 |
| 3.17500 | 9,97456 | 8 |
| 3.18310 | 10 | 7,97965 |
| 4 | 12,56637 | 6,35 |
4. |

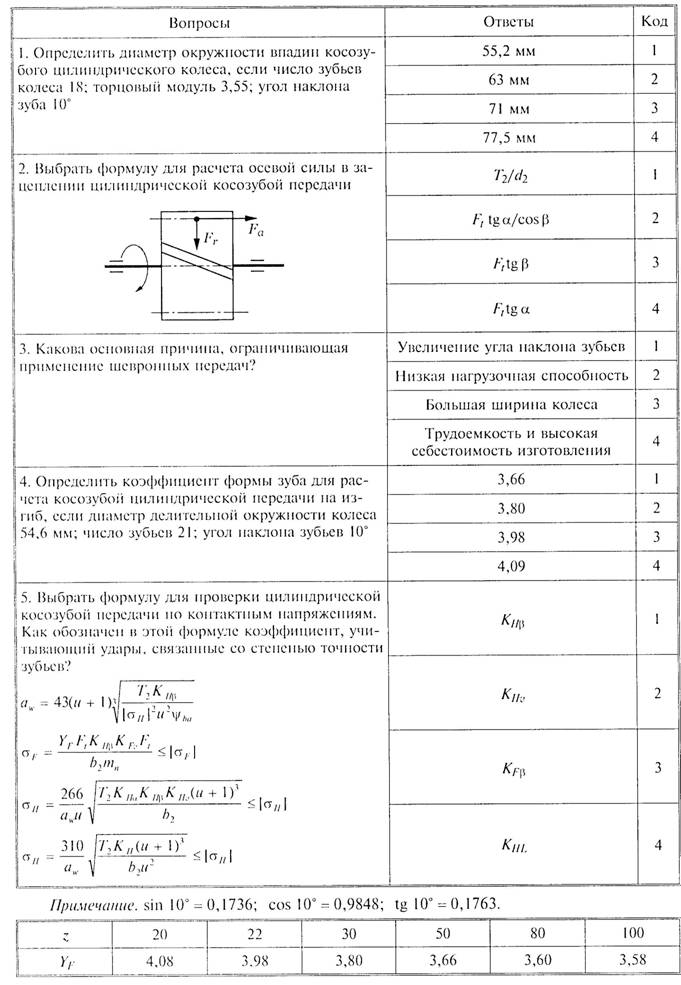
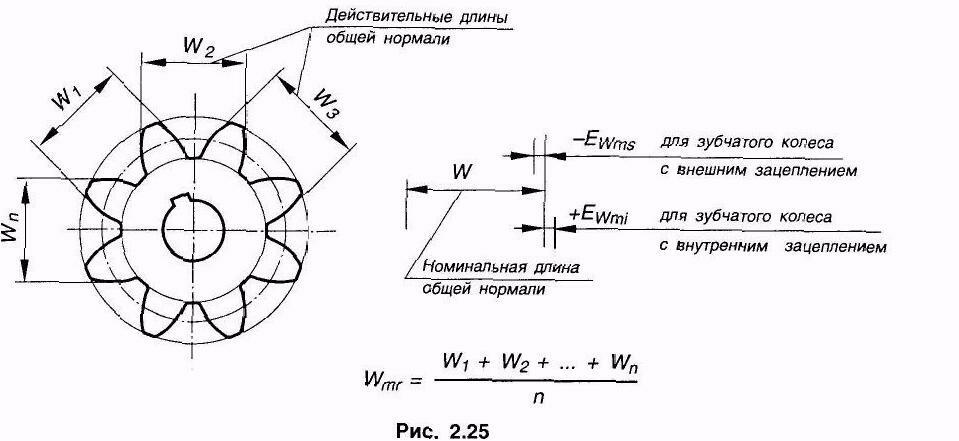

 Тёмное и светлое колёсо имеют одинаковый модуль. Самый главный параметр, стандартизирован, определяется из прочностного расчёта зубчатых передач. Чем больше нагружена передача, тем выше значение модуля. Через него выражаются все остальные параметры. Модуль измеряется в миллиметрах, вычисляется по формуле:
Тёмное и светлое колёсо имеют одинаковый модуль. Самый главный параметр, стандартизирован, определяется из прочностного расчёта зубчатых передач. Чем больше нагружена передача, тем выше значение модуля. Через него выражаются все остальные параметры. Модуль измеряется в миллиметрах, вычисляется по формуле: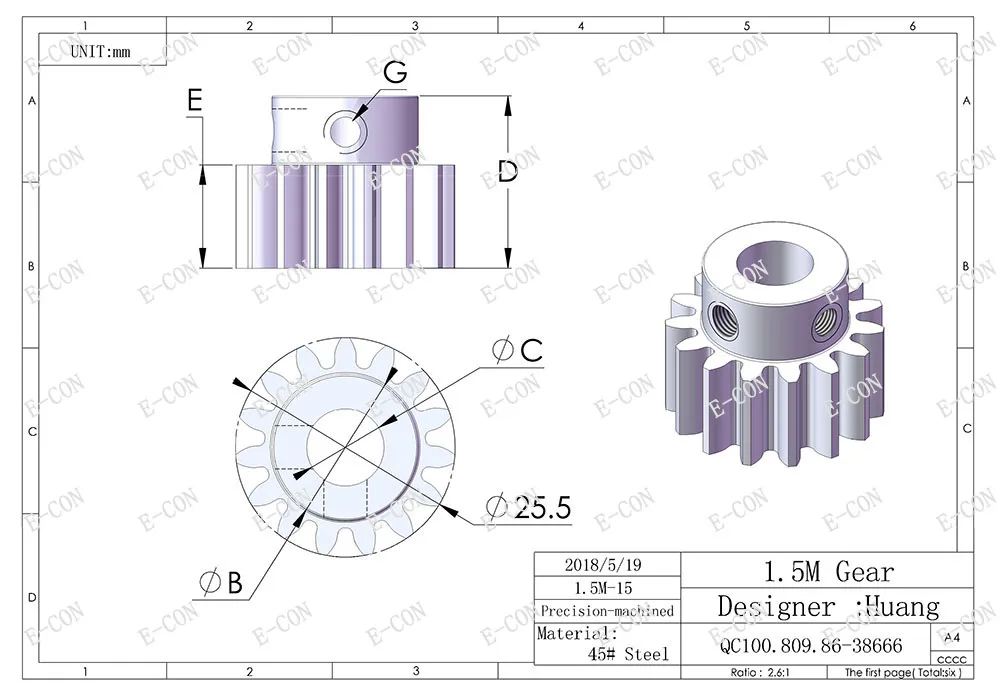
 ru/prochee/modul-zubev-zubchatogo-kolesa-raschet-standartnye-opredelenie.html
ru/prochee/modul-zubev-zubchatogo-kolesa-raschet-standartnye-opredelenie.html