Магнитный поток – формула, определение, правило
3.9
Средняя оценка: 3.9
Всего получено оценок: 106.
3.9
Средняя оценка: 3.9
Всего получено оценок: 106.
Для количественного описания явления электромагнитной индукции необходимо введение понятия магнитного потока. Рассмотрим эту тему подробнее.
Проводящая рамка в магнитном поле
Явление электромагнитной индукции состоит в том, что при изменении поля, пронизывающего проводящую рамку или катушку, в ней возникает электродвижущая сила (ЭДС):
Рис. 1. Электромагнитная индукция, опыт Фарадея.
Энергия используемого в этом опыте магнитного поля характеризуется магнитной индукцией. Однако, при попытке описать наблюдаемое явление выяснилось, что одной этой величины мало.
Если выписать в таблицу значения ЭДС, наводимые магнитным полем, имеющим одну и ту же плотность магнитных линий, в разных условиях, то окажется, что ЭДС, возникающая в квадратной рамке, имеет гораздо большее значение, чем ЭДС в длинной узкой рамке (при одном периметре).
А наибольшая ЭДС возникает в круглом витке.
Причиной этого оказался разный «охват поля» рамкой. Площадь длинной узкой рамки невелика, она «охватывает» малое «количество поля», и ЭДС в ней также мала. У квадратной рамки площадь при одинаковом периметре больше, а у круглого витка – она наибольшая, в результате рамка «охватывает» большее «количество поля», и ЭДС в такой рамке тоже получается больше.
Не менее важной оказалась ориентация рамки по отношению к направлению магнитного поля. Наибольшая ЭДС возникает, если проводящая рамка перпендикулярна линиям магнитной индукции. Если плоскость рамки параллельна этим линиям – то независимо от ее площади и силы магнитного поля ЭДС в рамке не возникнет.
Понятие магнитного потока
Таким образом, для описания явления электромагнитной индукции было введено понятие «магнитный поток», характеризующее «охват поля» рамкой. В этом понятии объединяются все величины, от которых зависит наведенная в рамке ЭДС – индукция поля, площадь и ориентация рамки. 2×cos\alpha$$,
2×cos\alpha$$,
то есть, магнитный поток 1 Вебер – это магнитный поток, проходящий через рамку площадью 1 квадратный метр, которая ориентирована перпендикулярно линиям однородного магнитного поля с индукцией 1Тесла.
Рис. 3. Магнитный поток зависит от…
Для понимания термина «магнитный поток» можно представить аналогию с обычным водяным потоком. Водяной поток, как правило, зависит от напора воды (аналог индукции) и площади сечения трубы (аналог площади рамки), а поскольку вода, в отличие от магнитного поля, всегда заключена внутрь трубы, то водяной поток всегда ориентирован поперек сечения трубы, и значение косинуса в формуле всегда равно единице.
Что мы узнали?
Для описания явления электромагнитной индукции в проводящем контуре необходимо учесть индукцию магнитного поля, «охват» поля контуром и ориентацию контура. Все эти факторы объединяются в понятии «магнитный поток». Изменение магнитного потока приводит к возникновению ЭДС в контуре. Постоянный магнитный поток ЭДС не вызывает.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
3.9
Средняя оценка: 3.9
Всего получено оценок: 106.
А какая ваша оценка?
что это такое, формулы, единица измерения, обозначение
Вероятно, термин «поток» ассоциируется у вас с потоком воды. Если бы вы хотели описать этот поток количественно, то имели бы в виду определенное количество воды, протекающей через поперечное сечение в определенной точке. Такой поток может нести большое или малое количество воды в зависимости от скорости воды и площади этого поперечного сечения.
Магнитный поток — это физическая величина, тесно связанная с явлением электромагнитной индукции. Это сложная величина, довольно абстрактная. Но, как вы правильно догадались, его название берет свое начало в гидродинамике. Здесь, однако, нет потока материи через поверхность, есть только векторы магнитной индукции B, «пронзающие» поверхность и иногда «скользящие» по ней.
Представьте себе однородное магнитное поле, описываемое вектором магнитной индукции B. Мы помещаем плоскую поверхность с полем S в это поле совершенно произвольным образом, то есть под любым углом по отношению к вектору B (рис. 1). Теперь определим вектор B, перпендикулярный плоскости поверхности. Пусть длина этого вектора равна величине поверхности.
Рис. 1. Плоская поверхность в магнитном поле. Красным цветом обозначен вектор S, представляющий эту поверхность.
Потоком вектора магнитной индукции ФB через поверхность S называется скалярное произведение векторов B и S.
Итак можно дать следующее определение термину «магнитный поток»:
Магнитный поток — это поток вектора магнитной индукции B через некоторую поверхность. Для бесконечно малого участка равен произведению модуля | B | на площадь участка dS и косинус угла α между B и нормалью n к плоскости участка. Для поверхности конечных размеров находится как сумма (интеграл) по её малым фрагментам.
Википедия
Зависимости магнитного потока
Используя формулу, можно увидеть, что магнитный поток зависит от трех переменных: магнитного поля B, площади S и угла α.
Магнитный поток линейно зависит от B и S. Например, если увеличить площадь S, но оставить магнитное поле B и угол α прежними, то магнитный поток будет больше. Поэтому большая площадь означает большой поток, а маленькая площадь — маленький магнитный поток.
Если, с другой стороны, увеличить магнитное поле B, то магнитный поток также увеличится. Сильное магнитное поле приводит к большому потоку, слабое поле — к малому магнитному потоку.
В целом, чем больше магнитное поле B или площадь S, тем больше магнитный поток.
Ситуация с углом α немного сложнее. Представьте, что ваша поверхность перпендикулярна магнитному полю, тогда ваш угол α = 0° . Здесь у вас самый большой магнитный поток. Если теперь шаг за шагом увеличивать угол, магнитный поток уменьшается.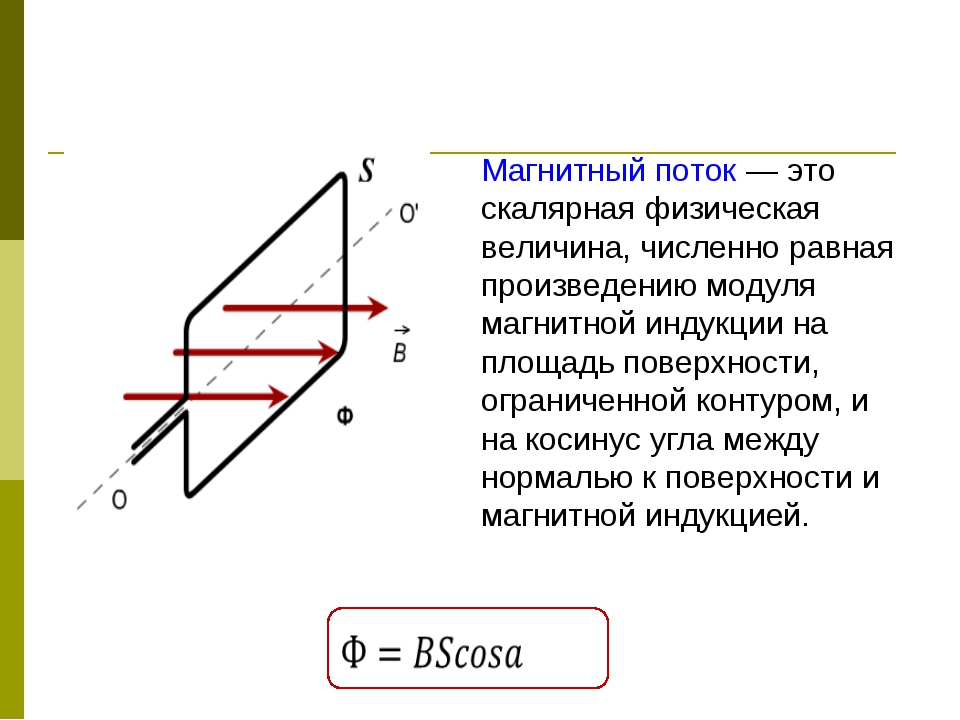 Когда вы достигаете α = 90°, магнитный поток равен нулю, потому что магнитное поле параллельно поверхности. После этого он снова начинает увеличиваться.
Когда вы достигаете α = 90°, магнитный поток равен нулю, потому что магнитное поле параллельно поверхности. После этого он снова начинает увеличиваться.
Единица измерения и обозначение магнитного потока
Магнитное поле B имеет единицу Тесла (T), а площадь — единицу квадратный метр м2 .
Поток является скалярной величиной и его единицей измерения является вебер (Вб): 1 Вб = 1 Т * м2 , то есть [Ф] = Т * м2 . Обозначается магнитный поток как Ф (символ формулы — греческая фи).
Примеры
Приведенные ниже примеры дадут вам лучшее понимание того, что представляет собой новая концепция и аналогия с потоком воды.
- В случае, показанном на рис. 2, поток магнитного поля с магнитной индукцией B через поверхность S составляет: ФB = B * S и при этом его значение максимально, так как:
Рис. 2. Поверхность перпендикулярна силовым линиям магнитного поля. Векторы B и S параллельны
Векторы B и S параллельны
2. А в каком случае при ненулевой магнитной индукции ФB = 0 ?
Рис. 3. Поверхность параллельна силовым линиям магнитного поля. Векторы B и S перпендикулярны
Определение магнитного потока показывает, что это тот случай, когда:
потому что cos 90° = 0.
На рис. 3 мы видим, как в этой ситуации располагается плоская поверхность относительно векторов магнитной индукции.
Обратите внимание, что ФB можно представить как произведение В и S⟂, где S⟂ = S * cos α. Аналогично, вы всегда можете рассчитать величину потока магнитного поля, умножив составляющую магнитной индукции, перпендикулярную поверхности, на величину площади поверхности (см. рис. 4а. и 4б.).
Рис. 4а. Поверхность S⊥ — это проекция поверхности S в направлении, параллельном линиям магнитного поляРис. 4б. Вектор B⟂ — это проекция вектора B на направление вектора S
Как можно рассчитать поток магнитного поля, если поле неоднородно и/или поверхность искривлена? Мы делим поверхность, через которую мы должны вычислить поток, на такие маленькие участки, что можно считать, что они плоские и поле однородное.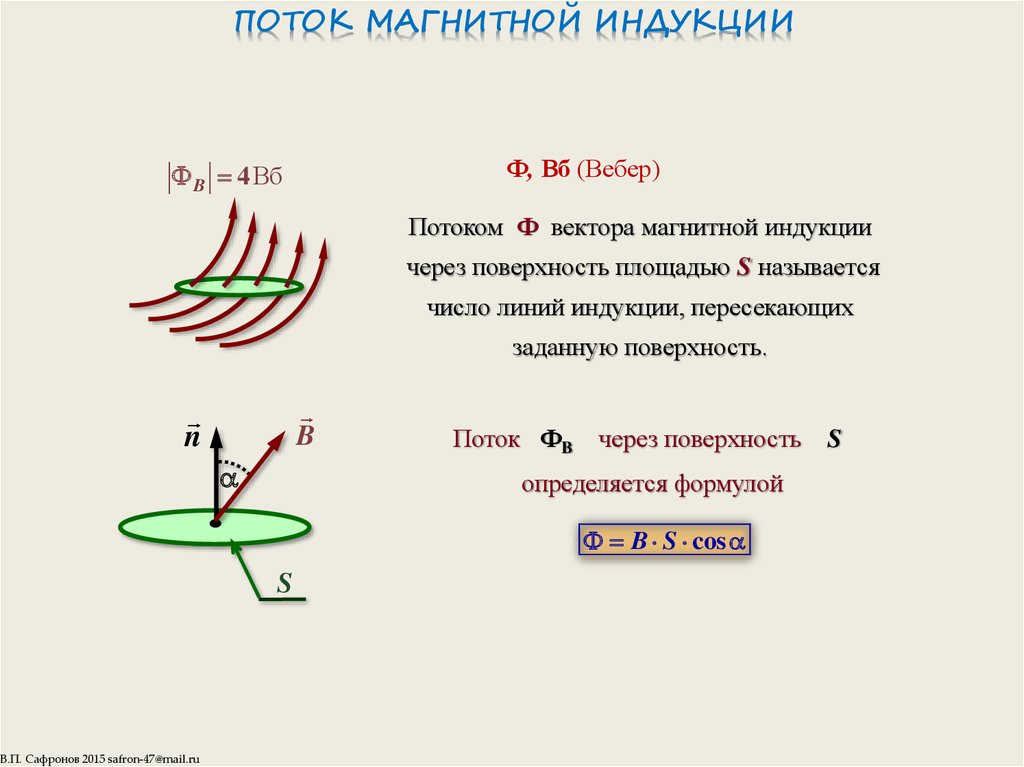 Все это для того, чтобы можно было применить определение потока. Поэтому мы вычисляем небольшие «потоки» и суммируем их. Описанная процедура называется вычислением поверхностного интеграла, который записывается в виде:
Все это для того, чтобы можно было применить определение потока. Поэтому мы вычисляем небольшие «потоки» и суммируем их. Описанная процедура называется вычислением поверхностного интеграла, который записывается в виде:
Вычислять такие интегралы совсем не обязательно, но полезно понимать смысл такой процедуры.
Закон Фарадея
Закон Фарадея
Давайте сначала внимательно рассмотрим уравнение 2 уравнений Максвелла. это
называется законом индукции Фарадея .
∫ A B ·d A = Φ B является потоком B через площадь, ограниченную кривой Γ.
∂/∂t∫ A B ·d A = ∂Φ B /∂t
частная производная этого потока по времени.
Взятие частной производной означает взятие производной потока
по времени, сохраняя при этом площадь фиксированной.
∮ Γ E ∙d r – работа, совершаемая на единицу заряда при перемещении пробного заряда один раз вокруг
кривая Г.
Закон Фарадея гласит, что абсолютная величина или величина циркуляции
электрическое поле E вокруг замкнутого контура равно скорости изменения из
магнитный поток через площадь, ограниченную петлей. Приведенное ниже уравнение выражает закон Фарадея в математической форме.
dΦ B /dt (через фиксированную площадь) = -∫ вокруг петли E ·d r (на
фиксированное время)
Знак минус в этом уравнении говорит нам о направлении
тираж. (См. ниже.)
Когда магнитный поток через закрытую область
заменами петель, ∫ вокруг цикла E ·d r не равно нулю,
циркулирует электрическое поле E .
E ∙d r проделанная работа
на единицу заряда электрическим полем при перемещении заряда на расстояние d r .
Если
петля является реальной проволочной петлей, тогда есть реальная работа, выполненная индуцированным
поле на бесплатных сборах.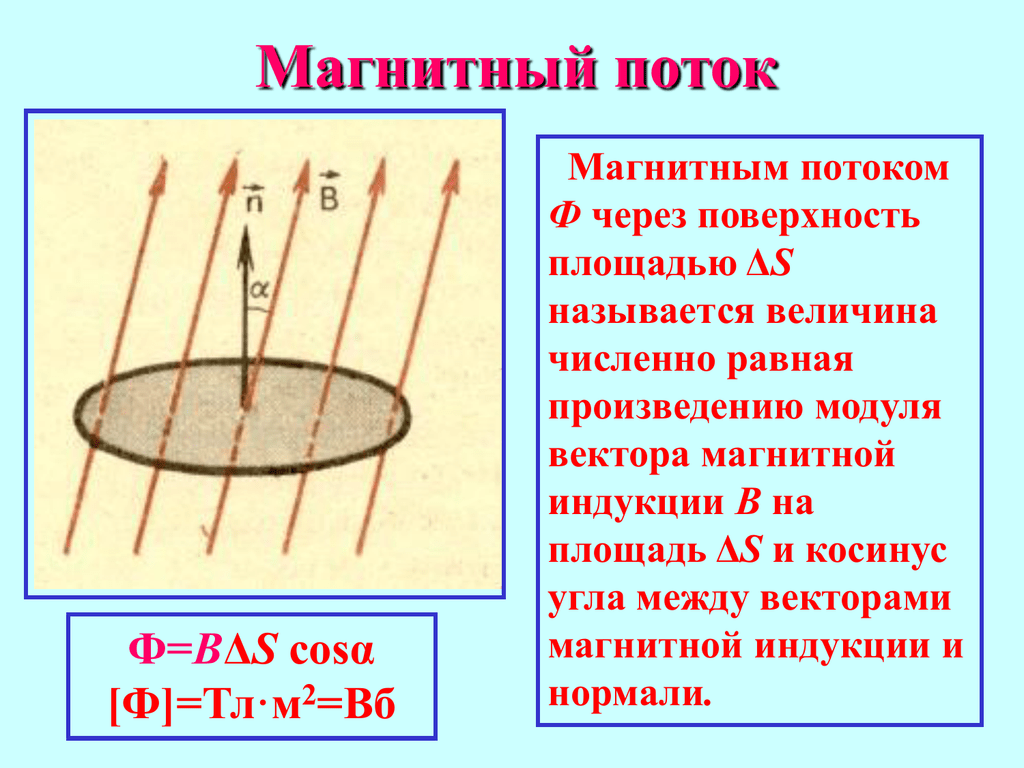
∫ вокруг петли E ·d r работа
на единицу заряда полем при однократном перемещении заряда по контуру.
Это
ЭДС индукции равна , и измеряется в вольтах.
dΦ B /dt (через фиксированную площадь) = ЭДС индукции
Если кривая Γ представляет собой кривую, описываемую проволочной петлей с сопротивлением R, то
по проводу будет течь ток I = ЭДС/R.
ЭДС индукции вызывает протекание тока без
разность потенциалов из-за разделенных зарядов.
Индуцированное электрическое поле НЕ
консервативное поле. Когда вы перемещаете заряд против индуцированного
поле один раз вокруг цикла, вы должны сделать работу. Но твоя работа
НЕ хранится как потенциальная энергия. Вы не можете позволить электрическому полю выполнять работу по восстановлению
энергия, затраченная вами на перемещение заряда. Наведенное электрическое поле исчезает, когда
как только магнитный поток перестанет изменяться. Работа, которую вы делаете
Работа, которую вы делаете
на заряд против индуцированного поля локально не сохраняется. Энергия может переноситься в виде
электромагнитная волна. Электромагнитные волны переносят энергию через свободное пространство.
Каково направление динамического (индуцированного) поля?
Знак минус в уравнении, выражающем закон Фарадея, говорит нам о
направление индуцированного поля.
Есть простой способ запомнить это направление.
Циркуляция индуцированного поля равна ЭДС.
Любой ток, протекающий в результате этой ЭДС, создает магнитное поле, противодействующее
изменения потока, которые его производят.
Это называется
Закон Ленца.
ЭДС индукции противостоит ИЗМЕНЕНИЮ потока, который ее вызывает.
Пример:
Магнит быстро движется к проволочной петле, как показано на рисунке.
Поток через проволочную петлю
увеличивается в нисходящем направлении.
В контуре начинает течь ток в направлении, указанном стрелкой.
Магнитная сила из-за петли на магните замедляет
приближающийся магнит.
Прелесть закона Ленца в том, что вам не нужно вглядываться в детали. Если
магнитный поток через проводник изменится, токи будут течь в противоположном направлении.
все, что вызвало изменение. Если какое-то относительное движение вызывает изменение потока,
ток попытается остановить это относительное движение. Если изменение тока в
цепь отвечает за изменение потока, то ЭДС индукции будет стремиться
предотвратить изменение тока в этой цепи.
Смотрите: Электромагнитная индукция
и Закон Фарадея (Youtube)
Проблема:
Рассмотрим плоскую квадратную катушку с N = 5 витками.
Катушка по 20 см с каждой стороны, имеет магнитное поле
через него проходит 0,3 Тл.
Плоскость катушки перпендикулярна
магнитное поле: поле направлено за пределы страницы.
(a) Если ничего не изменить, какова ЭДС индукции?
(б) Магнитное поле равномерно увеличивается от 0,3 Тл до 0,8 Тл за 1 с.
Чему равна ЭДС индукции в катушке, пока происходит изменение?
(c) При изменении магнитного поля ЭДС, наводимая в катушке, вызывает
ток течь. Течет ток по часовой или против часовой стрелки
вокруг катушки?
Решение:
- Рассуждение:
Если величина магнитного поля B меняется, то поток Φ = BA
изменяется, и возникает ЭДС. - Детали расчета:
(a) ЭДС индуцируется изменяющимся магнитным потоком. Если ничего
изменяется, ЭДС индукции равна нулю.
(b) Катушка имеет 5 витков. Каждый виток имеет площадь A = (0,2 м) 2 . Начальный магнитный поток через
каждый виток катушки Φ 0 = B 0 A = 0,3*(0,2) 2
Тм 2 = 0,012 Тм 2 .
Конечный магнитный поток через каждый виток катушки равен Φ f
= B f A = 0,8*(0,2) 2 Tm 2 = 0,032 Tm 2 .
Суммарное изменение потока через катушку N(Φ ф
— Φ 0 ),
при N = 5. ЭДС индукции равна
ЭДС индукции равна
ЭДС = -N∆Φ/∆t = -N(Φ f
— Φ 0 )/∆t = [-5*(0,032 -0,012)/1,0] В = -0,1 В.
(c) При изменении магнитного поля магнитный поток увеличился
вне страницы. По закону Ленца ЭДС индукции в контуре
благодаря этому изменяющемуся потоку создается ток, который создает поле, противодействующее
изменение. Поле, создаваемое током в катушке, направлено в
стр., противоположном направлению увеличения потока. Для производства
поле на страницу, ток должен течь по часовой стрелке вокруг петли
по правилу правой руки.
Встроенный вопрос 1
Стержневой магнит расположен перед горизонтальной проволочной петлей так, чтобы его
северный полюс указывает на петлю. Затем магнит оттягивается от
петля. Наведенный ток в петле течет по часовой стрелке или против часовой стрелки?
Обсудите это со своими однокурсниками на форуме!
Визуализируйте магнитное поле стержневого магнита. Как поток этого
поле через проволочную петлю изменить?
Самоиндукция
Если длинная катушка провода площадью поперечного сечения A и длиной ℓ с N витками
подключен или отключен от батареи, изменение магнитного потока через
катушка создает ЭДС индукции. Индуцированный ток создает магнитное
Индуцированный ток создает магнитное
поле, противодействующее изменению магнитного потока. Величина
ЭДС индукции можно рассчитать по закону Фарадея.
- Магнитное поле внутри длинной катушки B = μ 0 (Н/л)И.
- Поток через катушку равен NBA = μ 0 (N 2 /л)IA.
- Изменение потока в единицу времени составляет мк 0 (N 2 /л)A
∆I/∆t = L*∆I/∆t, так как I — единственная величина, изменяющаяся со временем.
L = μ 0 (N 2 /л)А называется
собственная индуктивность катушки. Единицы индуктивности: Генри (Гн). 1 Гн = 1 Вс/А. - ЭДС индукции равна ЭДС = -L*dI/dt, где знак минус является следствием закона Ленца.
ЭДС индукции пропорциональна скорости изменения тока в
катушка. Оно может в несколько раз превышать напряжение питания. Когда
выключатель в цепи с большим током размыкается, уменьшая ток до
ноль за очень короткий промежуток времени, это может привести к искре. Все
Все
цепи имеют собственную индуктивность, и у нас всегда есть ЭДС
= -L*∆I/∆t. Собственная индуктивность L зависит только
по геометрии цепи.
Проблема:
Катушка имеет собственную индуктивность 3 мГн, а ток через нее изменяется от 0,2 А
до 1,5 А за время 0,2 с. Найдите модуль средней ЭДС индукции
в катушке за это время.
Решение:
- Рассуждение:
ЭДС самоиндукции равна ЭДС = -L*∆I/∆t. - Детали расчета:
L = 3 мГн, ∆I/∆t = (1,5–0,2 А)/0,2 с = 6,5 А/с.
ЭДС = -L*∆I/∆t = -(0,003 Вс/А)(6,5 А/с) = -0,0195 В.
Знак минус указывает на то, что ЭДС индукции противодействует изменениям потока, которые
произвел его.
Проблема:
Круглая катушка из 25 витков диаметром 1 м. Он размещен со своим
ось вдоль направления магнитного поля Земли (величина 50 микроТл),
а затем за 0,2 с переворачивается на 180 o . Какова средняя ЭДС
сгенерировано
Решение:
- Рассуждение:
Ф B = B ∙ A является потоком B через площадь A.
Первоначально B и A выровнены, в конце концов они анти-выровнены. Точка
знак изменения продукта. - Детали расчета:
ЭДС = -∆Φ B /∆t.
Φ B (исходный) = NAB = 25*π*(0,5 м) 2 50*10 -6
Т = 9,82*10 -4 Тм 2 .
Φ B (конечный) = -Φ B (начальный), поскольку
катушка перевернута.
|∆Φ B | = 2Φ B (исходное).
|∆Φ B /∆t| знак равно
2*(9,82*10 -4 Тм 2 )/(0,2 с) = 9,82*10 -3 В.
Проблема:
Катушка радиусом 0,5 м, состоящая из 500 витков, поворачивается на четверть оборота за 4,17 с.
мс, первоначально имея плоскость, перпендикулярную однородному магнитному полю.
Найти напряженность магнитного поля, необходимую для индукции средней ЭДС 10 000 В.
Решение:
- Обоснование:
ЭДС = -∆Φ B /∆t. Φ B = NABcosθ
изменяется от NAB до 0 за 4,17 мс, так как θ изменяется от 0 до 90 o
за 4,17 мс.
- Детали расчета:
|∆Φ В | = NAB = 500*π*(0,5 м) 2 *B =
(393 м 2 ) * Б.
Хотим
|ЭДС| = |∆Φ B /∆t| = (393 м 2 )/(4,17*10 -3
с) * B = (94174 м 2 /с)*B = 10000 В.
В = 0,1 Вс/м 2 = 0,1 Тл.
Магнитный поток: значение и выражение
Магнитный поток — это количество линий магнитного поля или магнитных силовых линий, проходящих через поверхность. Таким образом, упрощенно говоря, магнитный поток через некоторую поверхность пропорционален числу силовых линий, проходящих через эту поверхность. Магнитный поток через поверхность определяется как поток электрического поля, используемый с законом Гаусса.
Определение
Физическое описание магнитного потока через поверхность представляет собой поверхностный интеграл скалярного произведения (точечного произведения) вектора магнитного поля (B) и вектора элементарной площади (dA). Он обозначается символом Φ или ΦB (B в суффиксе означает магнитный). Единицей магнитного потока в системе СИ является квадрат Вебера (Вб) или Тесла-метр (Тл·м2).
Он обозначается символом Φ или ΦB (B в суффиксе означает магнитный). Единицей магнитного потока в системе СИ является квадрат Вебера (Вб) или Тесла-метр (Тл·м2).
Математическое выражение
Рассмотрим поверхность, разделенную на площадь элемента dA. Для каждого элемента мы получаем компоненты нормали B и касательной к поверхности в положении этого элемента площади. Эти компоненты обычно изменяются от точки к точке на поверхности.
Нормальная составляющая магнитного поля равна B⟂ = B cosϴ.
Элементарный магнитный поток через эту площадь определяется как
d Φ= B⟂dA=B cosϴ dA = B.dA
Следовательно, полный магнитный поток через поверхность представляет собой сумму вкладов от отдельных элементов площади и определяется как
Φ=BdAcos =B.dA
Магнитный поток через замкнутую поверхность
Для магнитного потока через замкнутую поверхность поверхностный интеграл, используемый в определении магнитного потока, берется по замкнутому контуру.
т. е.
Φ=B.dA = 0
Магнитный поток через замкнутый контур равен нулю. Это называется законом Гаусса в магнетизме. Результаты этого закона показывают, что магнитные монополи никогда не встречались в природе, т. е. магнитные монополи не существуют.
Как мы измеряем магнитный поток?
Единицей магнитного потока в системе СИ является Вебер, названный в честь немецкого физика. Единица Вебера имеет символ Wb. Поскольку магнитный поток — это просто способ выражения магнитного поля в данной области, его можно измерить с помощью магнитометра так же, как магнитное поле.
Родственный термин, с которым вы можете столкнуться, — плотность магнитного потока. Измеряется в Вт/м2. Поскольку мы делим поток на площадь, мы могли бы также напрямую указать единицы измерения плотности потока в Теслах.
Магнитный поток и закон Фарадея
С помощью серии экспериментов Фарадей обнаружил, что изменяющийся магнитный поток индуцирует электрический ток через катушку, находящуюся в поле.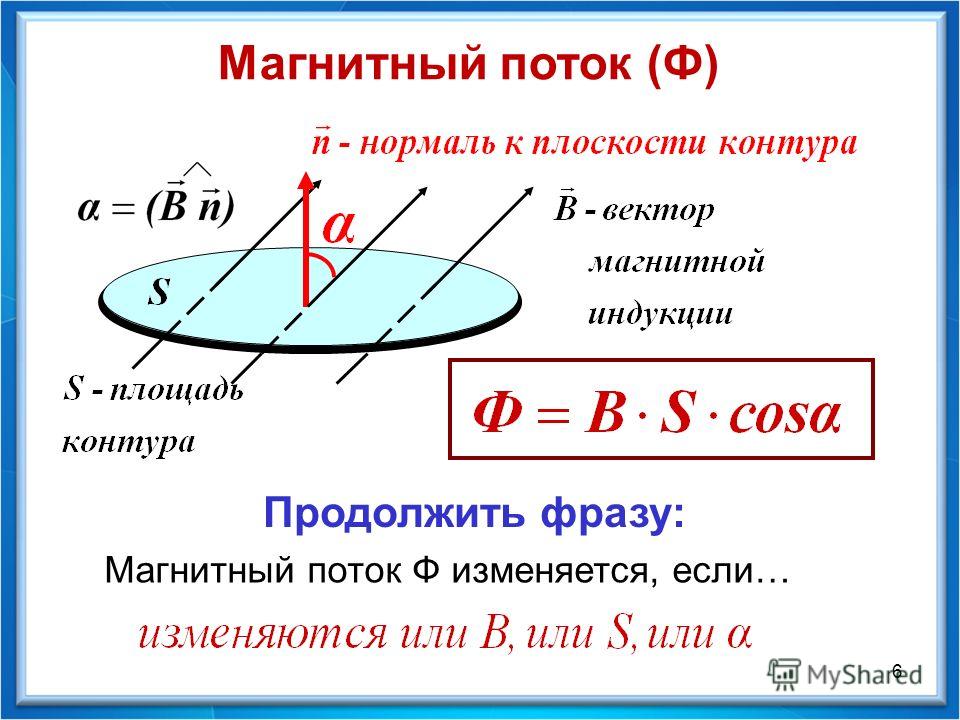 Таким образом, закон Фарадея объясняет принцип электромагнитной индукции.
Таким образом, закон Фарадея объясняет принцип электромагнитной индукции.
Таким образом, закон Фарадея формулируется как ЭДС/напряжение, возникающее в цепи всякий раз, когда существует относительное движение между проводником и магнитным полем. ЭДС индукции, в свою очередь, создает индукционный ток в цепи. Также величина ЭДС индукции/напряжения индукции пропорциональна скорости изменения магнитного потока.
Математическое выражение закона Фарадея
Скорость изменения магнитного потока = dΦ / dt
ЭДС индукции (e) α время скорость изменения магнитного потока (dΦ / dt)
«ЭДС индукции (напряжение индукции) ) пропорциональна скорости изменения магнитного потока во времени».
Φ = B.A = BA cosϴ (если B однородно)
Таким образом, чтобы производная магнитного потока по времени была отличной от нуля, должно выполняться следующее условие.
- Б(т)
Магнитное поле меняется во времени. Магнитное поле зависит от времени.
- A(t)
Изменение площади во времени. Предположим, что площадь цепи или витка катушки, находящегося в магнитном поле, изменяется.
- ϴ(t)
Theta изменяется со временем. Если петля катушки вращается, угол между вектором площади и магнитным полем изменяется.
Применение
Магнитный поток представляет собой скалярное произведение (точечное произведение) вектора магнитного поля (B) и вектора элементарной площади (dA). Таким образом, это скалярная величина. Замечено, что магнитный поток является значимой величиной в формулировке закона Фарадея. Кроме того, он имеет применение при обсуждении таких объектов, как трансформаторы и соленоиды. Аналогичное применение можно найти в электродвигателях и генераторах, в которых закон Фарадея применяется к катушкам, вращающимся в магнитном поле. Этот изменяющийся магнитный поток индуцирует электрический ток.
Заключение
Магнитный поток, являющийся скалярной величиной, может быть определен как число силовых линий магнитного поля, проходящих через данную поверхность.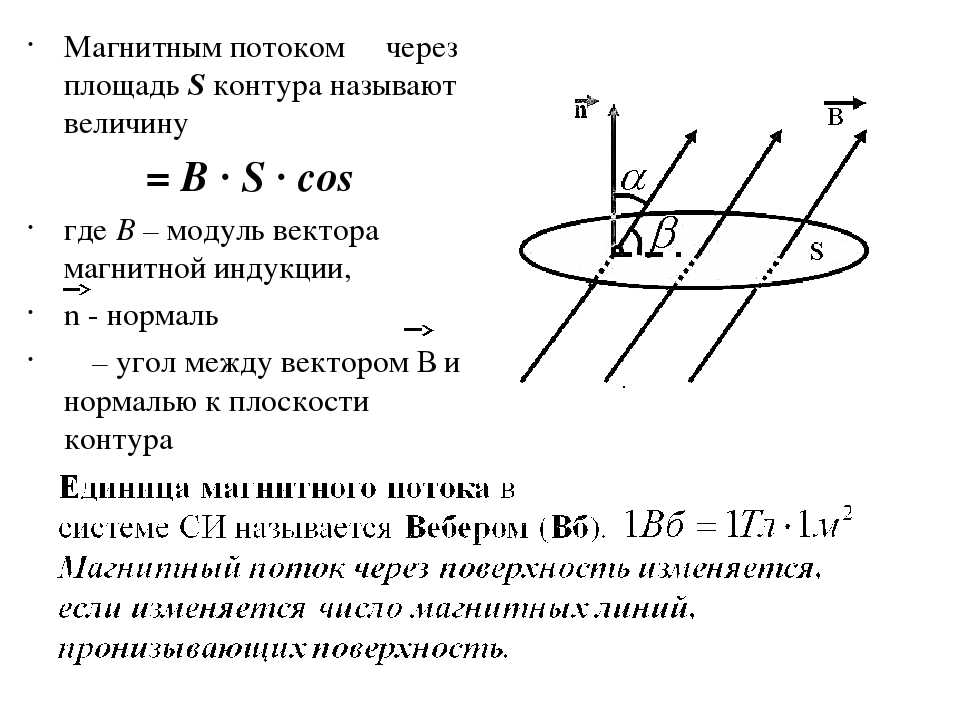


 ЭДС индукции равна
ЭДС индукции равна