Коэффициент абсорбции, коэффициент поляризации
Содержание
Как измерить абсорбцию
Для определения сопротивления требуются определенные условия. Температура среды должна быть от +10 до +35°С. Если показатель ниже, цифровое значение увеличивается, при повышении снижается.
Любой изоляционный материал имеет электрическую емкость. При подключении к напряжению в изоляционном материале образуются токи, насыщающие ее. Эти токи называются абсорбционными токами, время проникновения в материал зависит от качества и размеров.
Формула для расчета коэффициента абсорбции
Коэффициентом абсорбции называется показатель, определяющий уровень влажности изоляционного материала.
Формула для расчета простая:
где R60 – электросопротивление через 60 с после начала испытания;
R15 – электросопротивление через 15 с после начала испытания.
Допустимые значения при рабочей температуре можно узнать из специальных таблиц.
Измерение мегомметром
Для измерений используются мегомметры, на экране которых отображается коэффициент абсорбции через определенные интервалы времени. По умолчанию в этих приборах 3 интервала – через 15, 60 и 600 секунд. В большинстве современных мегомметров встроена функция установки других временных диапазонов.
Торговая сеть предлагает различные мегомметры (на 250, 500, 1000, 2500 В). Через их щупы проходит напряжение, фиксируются значения коэффициента через определенные интервалы времени. В стандартной ситуации сопротивление измеряется через 15 и 60 секунд после начала тестирования. Перед началом испытания преобразователь заземляется, с обмоток снимается напряжение.
Если необходимо измерить сопротивление между обмотками и корпусом или обмотками нескольких трансформаторов между собой, значение определяется для каждой независимой цепи (остальные соединяются между собой и с корпусом).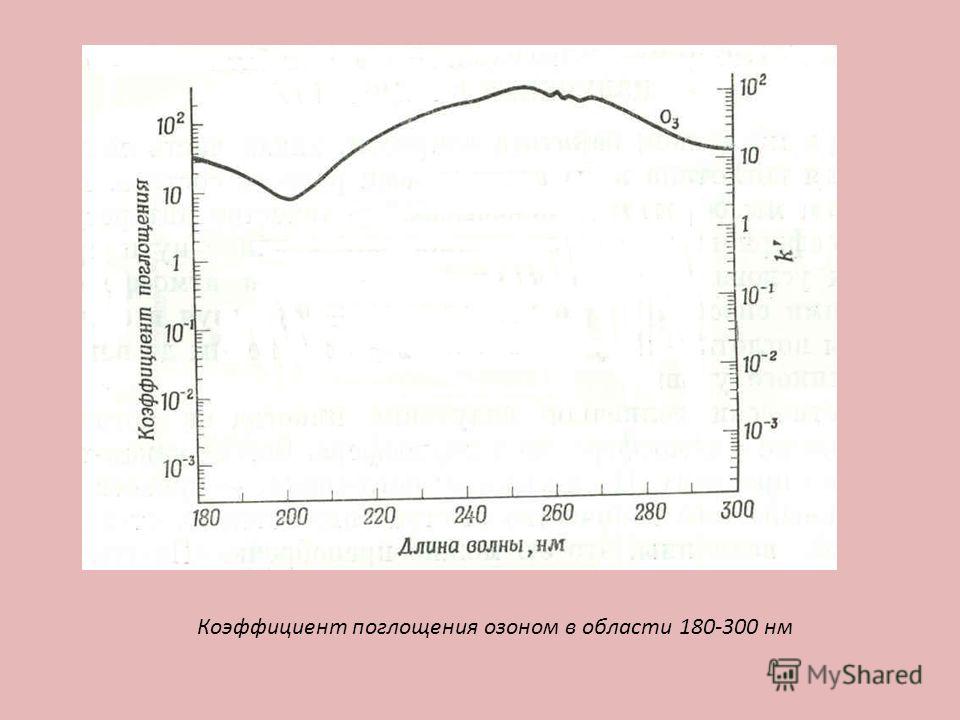
Коэффициент — абсорбция
Коэффициенты абсорбции определяли на опытном абсорбере диаметром 100 мм ; хотя влияние всех параметров не было полностью изучено, удалось выявить некоторые закономерности. Концентрация раствора и газа, температура и отношение жидкость: газ в этих опытах поддерживались в обычных для промышленных абсорберов пределах и полученные данные представляют практическую ценность.
Коэффициент абсорбции характеризует объем газа, растворяющегося при стандартных условиях в единице объема раствора, его значения приводятся в справочной литературе.
Коэффициент абсорбции измеряется при температуре не ниже 10 С.
| Кинетика абсорбции кислорода из воздуха 1 н. водным раствором сульфита натрия при 30 С в аппаратах с мешалкой в зависимости от удельных затрат энергии N / V. |
Коэффициенты абсорбции, полученные на системе воздух — раствор сульфита, по-видимому, применимы и для других систем кислород — вода при условии, если сопротивление массопередаче сосредоточено в жидкой фазе.
Коэффициенты абсорбции могут быть определены или непосредственно из опыта или вычислены путем применения обобщенных уравнений, установленных на основе применения теории подобия.
Коэффициент абсорбции дает возможность судить о состоянии изоляции обмоток. Увлажненные обмотки имеют коэффициент абсорбции, близкий к единице.
Коэффициенты абсорбции определены раздельно для процессов хемосорбции брома, абсорбции бромистого аммония ( продукта реакции) и для суммарного процесса абсорбции.
Коэффициент абсорбции характеризует скорость растворения газового компонента в жидкости и определяется общим сопротивлением диффузии этого компонента через газовую и жидкостную пленки.
Коэффициент абсорбции учитывает количество вещества, диффундирующее через пленки при движущей силе абсорбции 1 мм рт. ст. Естественно, что чем эта величина больше, тем интенсивнее идет процесс абсорбции. Для абсорбции бензола маслом, как и для всех систем, в которых жидкость поглощает хорошо растворяющийся газ, основным сопротивлением является сопротивление газовой пленки. Уменьшение сопротивления газовой пленки достигается увеличением турбулентности газового потока.
Для абсорбции бензола маслом, как и для всех систем, в которых жидкость поглощает хорошо растворяющийся газ, основным сопротивлением является сопротивление газовой пленки. Уменьшение сопротивления газовой пленки достигается увеличением турбулентности газового потока.
Коэффициент абсорбции в меньшей степени, чем сопротивление изоляции, зависит от размеров изоляции и ее температуры, что повышает надежность измерений.
Коэффициент абсорбции практически не зависит от размеров и мощности объекта, что дает возможность его нормировать.
| Зависимость вязкости глицерина и некоторых масел от температуры. |
Коэффициент абсорбции зависит от физических свойств перекачиваемой жидкости.
| Схема мегомметра. |
Значение — коэффициент — абсорбция
Возможность включения электрических машин без сушки решается на основании данных табл.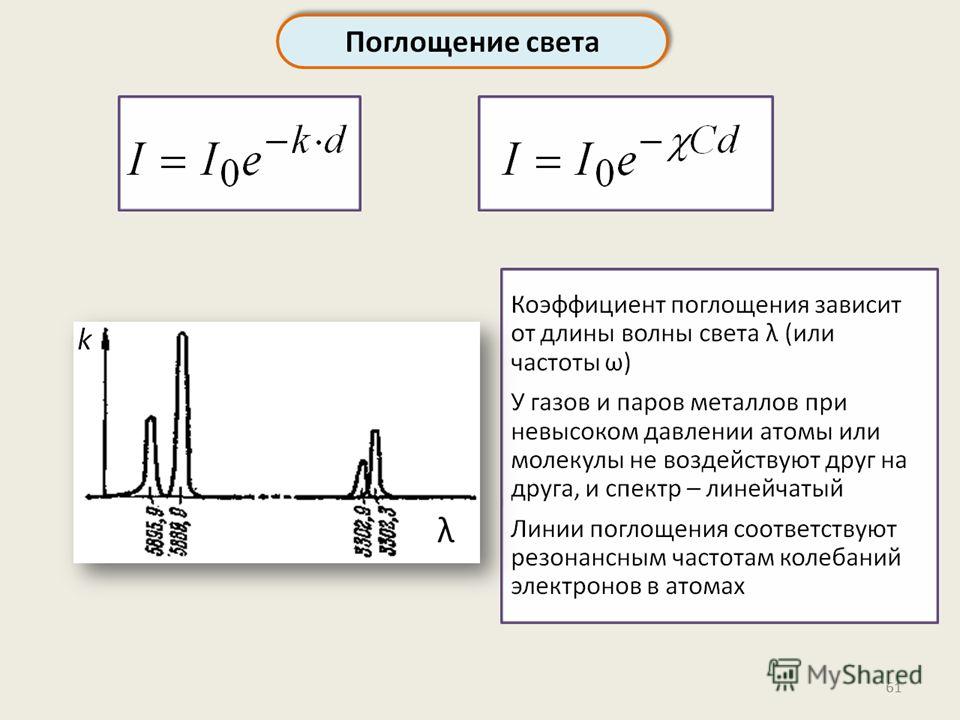 13 — 46, 13 — 47: измерения сопротивления изоляции; значения коэффициентов абсорбции; характеристики зависимости токов утечки через изоляцию обмотки от величины испытательного напряжения выпрямленного тока.
13 — 46, 13 — 47: измерения сопротивления изоляции; значения коэффициентов абсорбции; характеристики зависимости токов утечки через изоляцию обмотки от величины испытательного напряжения выпрямленного тока.
Коэффициент абсорбции Reo / Ris служит хорошим показателем степени увлажнения изоляции при температурах не выше 35 — 40 С, так как с повышением температуры значения коэффициентов абсорбции вне зависимости от их начальных значений приближаются к единице.
Коэффициент абсорбции изоляции Кл, представляющий отношение сопротивлений, измеренных через 60 и 15 с после приложения испытательного напряжения / Са бо / 15, применяют для определения влажности изоляции. При значении коэффициента абсорбции Ка1 2 изоляцию следует считать сухой, при значении 7Cal 2 — влажной.
| Предельная кривая режима захлебывания в насадочных колоннах, построенная на основании опытных значений A / F. |
Другим предельным случаем является весьма быстрое протекание химических реакций ( например, взаимодействие аммиака с сильными кислотами), когда растворенные молекулы до протекания реакции успевают продиффундировать лишь на очень небольшое расстояние.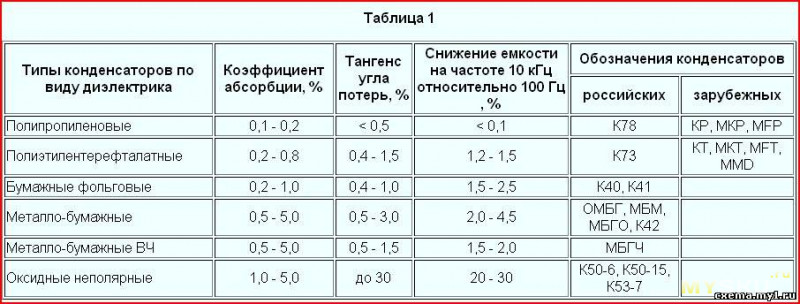 Положение реакционной зоны ( и значение коэффициента абсорбции) зависит в основном от скорости диффузии реагирующих веществ и продуктов реакции в реакционную зону и из нее, от концентрации абсорбируемого компонента на поверхности раздела фаз и от концентрации реагирующих веществ в основном ядре жидкости. Поскольку, однако, расстояние, которое должен пройти абсорбируемый компонент при диффузии его в жидкость, исключительно мало по сравнению с тем путем, который он мог бы пройти при простой физической абсорбции, коэффициент абсорбции, отнесенный к жидкостной пленке, оказывается довольно высоким, и во многих случаях определяющим фактором становится сопротивление газовой пленки.
Положение реакционной зоны ( и значение коэффициента абсорбции) зависит в основном от скорости диффузии реагирующих веществ и продуктов реакции в реакционную зону и из нее, от концентрации абсорбируемого компонента на поверхности раздела фаз и от концентрации реагирующих веществ в основном ядре жидкости. Поскольку, однако, расстояние, которое должен пройти абсорбируемый компонент при диффузии его в жидкость, исключительно мало по сравнению с тем путем, который он мог бы пройти при простой физической абсорбции, коэффициент абсорбции, отнесенный к жидкостной пленке, оказывается довольно высоким, и во многих случаях определяющим фактором становится сопротивление газовой пленки.
| Зависимость коэффициента абсорбции для конденсаторов из разных синтетических пленок от времени. |
Все приведенные выше данные относятся к непропитанным конденсаторам. Как указано выше, пропитка резко увеличивает значения коэффициента абсорбции.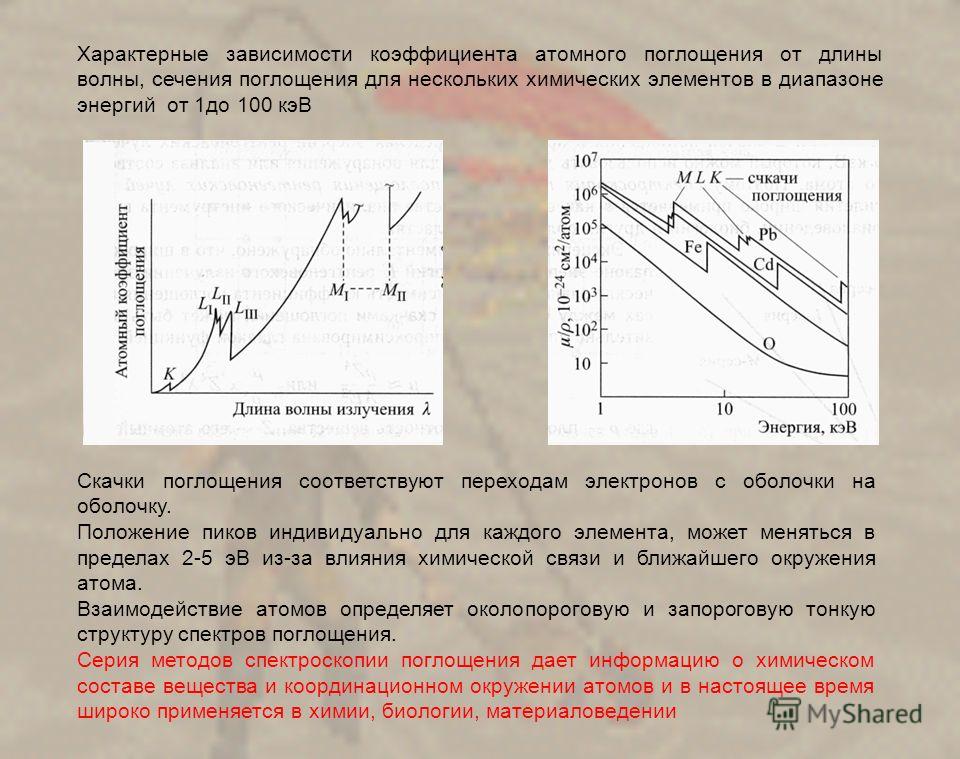
| Зависимость tg б полистирольных конденсаторов от частоты.| Зависимость tg б конденсаторов с неполярными диэлектриками от температуры. |
Конденсаторы из неполярных пленок обладают весьма малым коэффициентом диэлектрической абсорбции. Эти данные соответствуют непропитанным конденсаторам; пропитка может заметно повышать значения коэффициента абсорбции.
| Влияние способа орошения периферийных зон торца насадки на коэффициент абсорбции. |
Как видно из рис. 17 и табл. 4, с увеличением точечного расхода жидкости эффективность насадки возрастает. При постоянном расходе разбрызгивание жидкости ( кривые / и 2) приводит к увеличению значений коэффициентов абсорбции, причем в случае более интенсивного разбрызгивания ( розетками) значения К.
Как видно из рис. 12 и табл. 3, с увеличением точечного расхода жидкости эффективность насадки аппарата возрастает.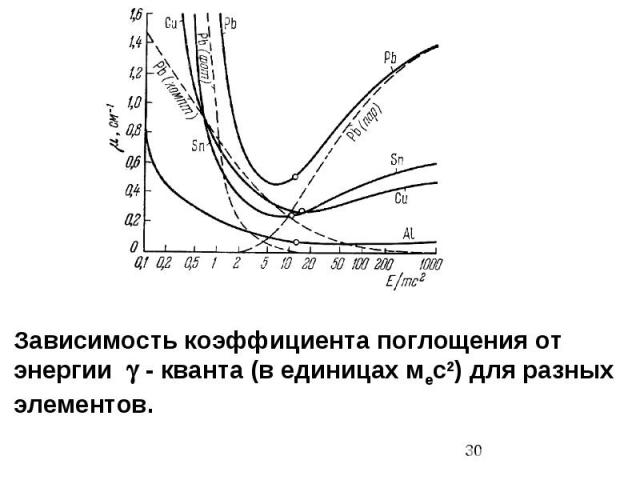 При постоянном расходе Q разбрызгивание жидкости ( кривые / и 2) приводит к увеличению значений коэффициентов абсорбции, причем в случае более интенсивного разбрызгивания ( розетками) значения Кг несколько выше.
При постоянном расходе Q разбрызгивание жидкости ( кривые / и 2) приводит к увеличению значений коэффициентов абсорбции, причем в случае более интенсивного разбрызгивания ( розетками) значения Кг несколько выше.
Условием включения без сушки для этих генераторов является значение сопротивления изоляции всех трех фаз не ниже допустимого либо значение коэффициента абсорбции не ниже 1 3 при сопротивлении изоляции всех трех фаз не ниже половины допустимого.
| Сопротивление изоляции обмоток электрических машин при различной температуре. |
Увлажнение изоляции обмоток существенно влияет на зависимость токов утечки через изоляцию от величины испытательного выпрямленного напряжения. Таким образом, чтобы узнать увлажнение обмотки, необходимо знать: 1) абсолютную величину сопротивления изоляции Ябг; 2) значение коэффициента абсорбции и 3) зависимость токов утечки от приложенного напряжения. {-a’l}.}
{-a’l}.}
Его вид в дифференциальной форме таков:
- dΦ=−a′Φ(l)dl.{\displaystyle d\Phi =-a’\Phi (l)dl.}
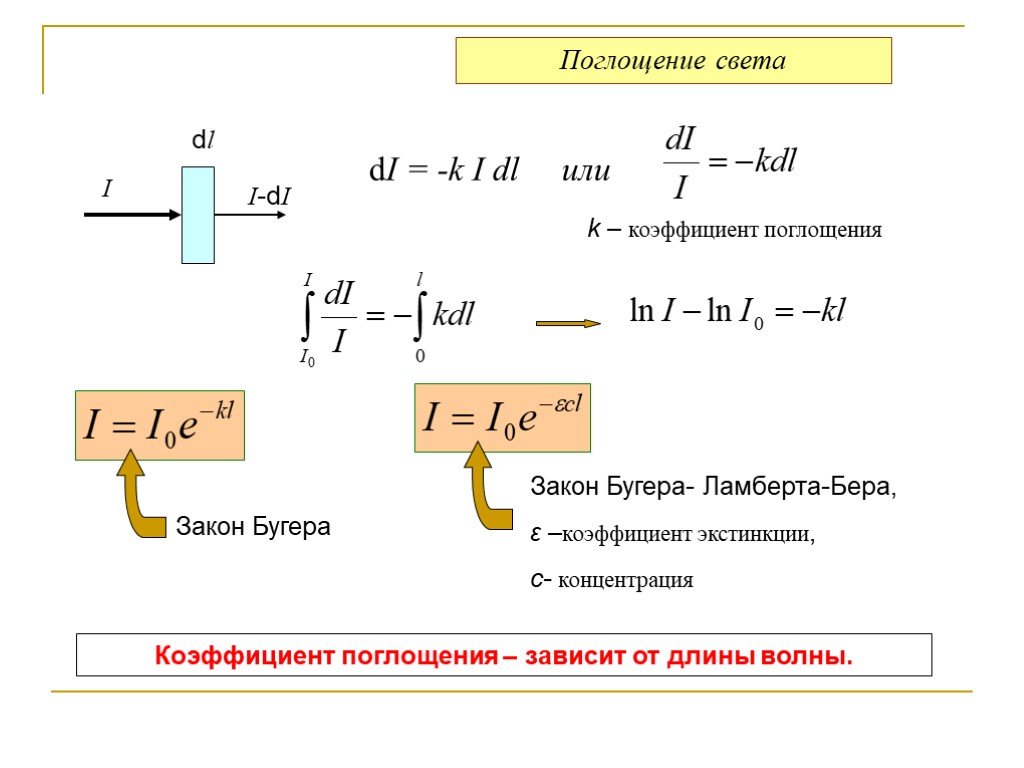
Всю энергию пучка, теряемую за счёт поглощения, получает среда. Поэтому для получаемой средой мощности P{\displaystyle P} справедливо:
- dP=a′Φ(l)dl,{\displaystyle dP=a’\Phi (l)dl,}
откуда для a′{\displaystyle a’} получается:
- a′=dPΦdl.{\displaystyle a’={\frac {dP}{{\Phi }dl}}.}
Из последнего равенства следует важное свойство натурального показателя поглощения, которое можно воспринимать и как его альтернативное определение: натуральный показатель поглощения равен относительному значению мощности, поглощаемой слоем вещества малой единичной толщины при падении на него излучения.
Уравнения с участием натурального показателя поглощения имеют более компактный вид, чем в случае использования десятичного показателя поглощения, и не содержат имеющего искусственное происхождение множителя ln(10). Поэтому в научных исследованиях фундаментального характера, в особенности, касающихся взаимодействия излучения с веществом, преимущественно используется натуральный показатель поглощения.
Норматив для изоляции
Значение коэффициента является показателем ресурса изоляционного материала. Это испытание занимает сравнительно много времени, позволяет определить характеристики тока, замедленного поляризацией. Различие показателей для сухой и влажной изоляции обусловлено различной продолжительностью заряда емкости материала.
Нормальная изоляция
Среднее нормативное значение абсорбционного коэффициента 1,3.
На практике:
- К
- К = 1,25-1,6 – изоляция хорошая;
- К>1,6 – изоляция очень хорошая
Если трансформатор новый, рассчитанный или измеренный показатель не должен быть ниже определенного производителем более чем на 20%. Если это условие не выполнено, оборудование требует сушки.
Сухая
Норма для неувлажненной обмотки K = 1,3-2,0. Ток в начале испытания резко повышается, потом снижается. Значение через 60 секунд отличается от показателя через 15 секунд примерно на 30% в сторону повышения.
Влажная
Если изоляция влажная, коэффициент имеет показатель, близкий к единице. Ток быстро устанавливается, в течение 45-и секунд меняется мало.
Значения электросопротивления для всех видов трансформаторов определены в ПУЭ (правилах устройства электроустановок):
- Для трансформаторов с мощностью до 35 кВ – 450-40 МОм (в зависимости от температуры).
- Для сухих преобразователей от:
- 100Мом при напряжении обмоток 1 кВ;
- 300 Мом при напряжении обмоток 1-6 кВ;
- от 500 МОм – от 6 кВ.
Помогла ли вам статья?
Задать вопрос
Пишите ваши рекомендации и задавайте вопросы в комментариях
Значение — коэффициент — абсорбция
Cтраница 2
Возможность включения электрических машин без сушки решается на основании данных табл. 13 — 46, 13 — 47: измерения сопротивления изоляции; значения коэффициентов абсорбции; характеристики зависимости токов утечки через изоляцию обмотки от величины испытательного напряжения выпрямленного тока.
[16]
Коэффициент абсорбции Reo / Ris служит хорошим показателем степени увлажнения изоляции при температурах не выше 35 — 40 С, так как с повышением температуры значения коэффициентов абсорбции вне зависимости от их начальных значений приближаются к единице.
[17]
Коэффициент абсорбции изоляции Кл, представляющий отношение сопротивлений, измеренных через 60 и 15 с после приложения испытательного напряжения / Са бо / 15, применяют для определения влажности изоляции. При значении коэффициента абсорбции Ка1 2 изоляцию следует считать сухой, при значении 7Cal 2 — влажной.
[18]
| Предельная кривая режима захлебывания в насадочных колоннах, построенная на основании опытных значений A / F.
[19] |
Другим предельным случаем является весьма быстрое протекание химических реакций ( например, взаимодействие аммиака с сильными кислотами), когда растворенные молекулы до протекания реакции успевают продиффундировать лишь на очень небольшое расстояние. Положение реакционной зоны ( и значение коэффициента абсорбции) зависит в основном от скорости диффузии реагирующих веществ и продуктов реакции в реакционную зону и из нее, от концентрации абсорбируемого компонента на поверхности раздела фаз и от концентрации реагирующих веществ в основном ядре жидкости. Поскольку, однако, расстояние, которое должен пройти абсорбируемый компонент при диффузии его в жидкость, исключительно мало по сравнению с тем путем, который он мог бы пройти при простой физической абсорбции, коэффициент абсорбции, отнесенный к жидкостной пленке, оказывается довольно высоким, и во многих случаях определяющим фактором становится сопротивление газовой пленки.
Положение реакционной зоны ( и значение коэффициента абсорбции) зависит в основном от скорости диффузии реагирующих веществ и продуктов реакции в реакционную зону и из нее, от концентрации абсорбируемого компонента на поверхности раздела фаз и от концентрации реагирующих веществ в основном ядре жидкости. Поскольку, однако, расстояние, которое должен пройти абсорбируемый компонент при диффузии его в жидкость, исключительно мало по сравнению с тем путем, который он мог бы пройти при простой физической абсорбции, коэффициент абсорбции, отнесенный к жидкостной пленке, оказывается довольно высоким, и во многих случаях определяющим фактором становится сопротивление газовой пленки.
[20]
| Зависимость коэффициента абсорбции для конденсаторов из разных синтетических пленок от времени.
[21] |
Все приведенные выше данные относятся к непропитанным конденсаторам. Как указано выше, пропитка резко увеличивает значения коэффициента абсорбции.
[22]
| Зависимость tg б полистирольных конденсаторов от частоты.| Зависимость tg б конденсаторов с неполярными диэлектриками от температуры.
[23] |
Конденсаторы из неполярных пленок обладают весьма малым коэффициентом диэлектрической абсорбции. Эти данные соответствуют непропитанным конденсаторам; пропитка может заметно повышать значения коэффициента абсорбции.
[24]
| Влияние способа орошения периферийных зон торца насадки на коэффициент абсорбции.
[25] |
Как видно из рис. 17 и табл. 4, с увеличением точечного расхода жидкости эффективность насадки возрастает. При постоянном расходе разбрызгивание жидкости ( кривые / и 2) приводит к увеличению значений коэффициентов абсорбции, причем в случае более интенсивного разбрызгивания ( розетками) значения К.
[26]
Как видно из рис. 12 и табл. 3, с увеличением точечного расхода жидкости эффективность насадки аппарата возрастает. При постоянном расходе Q разбрызгивание жидкости ( кривые / и 2) приводит к увеличению значений коэффициентов абсорбции, причем в случае более интенсивного разбрызгивания ( розетками) значения Кг несколько выше.
12 и табл. 3, с увеличением точечного расхода жидкости эффективность насадки аппарата возрастает. При постоянном расходе Q разбрызгивание жидкости ( кривые / и 2) приводит к увеличению значений коэффициентов абсорбции, причем в случае более интенсивного разбрызгивания ( розетками) значения Кг несколько выше.
[27]
Условием включения без сушки для этих генераторов является значение сопротивления изоляции всех трех фаз не ниже допустимого либо значение коэффициента абсорбции не ниже 1 3 при сопротивлении изоляции всех трех фаз не ниже половины допустимого.
[28]
| Сопротивление изоляции обмоток электрических машин при различной температуре.
[29] |
Увлажнение изоляции обмоток существенно влияет на зависимость токов утечки через изоляцию от величины испытательного выпрямленного напряжения. Таким образом, чтобы узнать увлажнение обмотки, необходимо знать: 1) абсолютную величину сопротивления изоляции Ябг; 2) значение коэффициента абсорбции и 3) зависимость токов утечки от приложенного напряжения.
[30]
Страницы:
1
2
3
Коэффициент звукопоглощения помещения
Коэффициент звукопоглощения представляет собой отношение интенсивности поглощенного звука в реальном материале к интенсивности падающего звука и может быть выражен как
α = I a / I I (1)
, где
α = Коэффициент поглощения звука
I A = Поглощенная интенсивность звука (W/M 2 )
I I = Инцидент Интенсивность звука (W/M 2 ) (W/M 2 ) 7000 70007777777777777 7.
Коэффициент поглощения — α — Для некоторых распространенных материалов можно найти в таблице ниже:
9 9074 9 9074 0,3 — 0,40070 Concrete block, painted
цемент 2 на цементе
Акустический пояс, 12 мм 0,5 Acoustic Tiles 0071 0. 4 — 0.8
Asbestos, sprayed 25 mm 0.6 — 0.7 Brickwork, painted 0.01 — 0.02 Brickwork, unpainted 0.02 — 0.05 Carpet, heavy на бетоне 0,3 — 0,6 Ковровое покрытие, тяжелое на поролоне 0,5 — 0,7 Бетонный блок, крупнозернистый 9 0.05 — 0.07 Cork sheet, 6 mm 0.1 — 0.2 Fiberboard on battens, 12 mm 0.3 — 0.4 Floor, concrete or terrazzo 0.02 Floor, linoleum, asphalt, rubber or cork tiles on concrete 0.03 Floor, wood 0.06 — 0.1 Hardwood 0.3 Glass, large panes heavy plate 0. 03 — 0.05
Glass, ordinary windows 0.1 — 0.2 Gypsum board, 12 mm 0.04 — 0.07 Mineral wool, 100 ММ 0,65 человек, каждая 0,2 — 0,5 Стены на гипсе0071 Полистирол, расширен на 50 мм Battens 0,35 Полистирол, расширенный жесткая поддержка 0,15 Polyurethan. 0,2 Шлаковая вата или стекловолокно, 50 мм 0,8 — 0,9 Снег 0,75 0071 0,6 — 0,07 1) Примечание! — коэффициент звукопоглощения зависит от частоты.
Скачать и распечатать таблицу коэффициентов звукопоглощения помещения
Общее звукопоглощение помещения
Общее звукопоглощение помещения можно выразить как
A = S 1 2 0 1 + 1 α 2 + .
. + S n α n
= ∑ S i α i (2)
where
A = the absorption of the room (m 2 Sabine)
S i = площадь фактической поверхности (м 2 )
α i = коэффициент поглощения фактической поверхности
Средний коэффициент поглощения0257
The mean absorption coefficient for the room can be expressed as:
α m = A / S (3)
where
α m = средний коэффициент звукопоглощения
S = общая площадь помещения (м 2 )
Акустические характеристики помещения можно рассчитать по приведенным выше формулам или оценить для типичных помещений.
- Постоянная комната
Пример — Акустический поглощение комнаты
Общая поглощение звука в комнате с
- 10 M 2 . бетонная крыша с коэффициентом поглощения 0,02
- 40 м 2 стены из ДВП с коэффициентом поглощения 0,3
можно рассчитать как
a = (10 M 2 ) (0,02) + (10 M 2 ) (0,02) + (40 M 2 ) (0,3)
= 12,2 M 2 Sabine
= 12,2 M 2 Sabine
Средний коэффициент поглощения можно рассчитать как
α м = (12,2 м 2 Сабина) / ((10 м 2 ) + (10 м 2 2
3 ) ))
= 0,2
Теория коэффициентов поглощения и экстинкции
Скорость распространения электромагнитной волны через твердое тело определяется частотно-зависимым комплексным показателем преломления N = n — ik , где действительная часть n связана со скоростью, а k , коэффициент ослабления связан с затуханием или затуханием амплитуды колебаний падающего электрического поля.
Таким образом, оптические свойства твердого тела определяются взаимодействием между твердым телом и электрическим полем электромагнитной волны.
Если плоская волна с частотой ( f ) распространяется через твердое тело со скоростью ( v ) в направлении, определяемом ( x ), электрическое поле ( E ) описывается следующей прогрессивной волной уравнение:
Где, ( E 0 ) — вектор падающего электрического поля, а
— смещение в момент времени t после возмущения, созданного электрическим полем в точке, расположенной на расстоянии x вдоль линия распространения.
Из уравнений Максвелла по электромагнитной теории скорость света в вакууме c связана с диэлектрической проницаемостью свободного пространства ε 0 , (степень, в которой среда может сопротивляться потоку заряда, определяемому формулой отношение электрического смещения к напряженности электрического поля, которое его производит), и магнитной проницаемости свободного пространства µ 0 (отношение плотности магнитного потока в твердом теле к напряженности внешнего магнитного поля, индуцирующего его, µ = B/H.
) по уравнению c= 1/(µ 0ε0 )½.
Скорость распространения через твердое тело с комплексным показателем преломления N = n — ik связана со скоростью света в вакууме, c , соотношением V = C / N , тогда:
Таким образом, подстановка 1/ V в приведенное выше уравнение дает:
, где последний член
является мерой коэффициента демпфирования или коэффициента ослабления ( k ).
Поскольку мощность ( P ) или интенсивность падающей волны через твердое тело представляет собой проводимость (σ) твердого тела, умноженную на квадрат вектора электрического поля ( P=σE 2 ), то используя коэффициент демпфирования, доля падающей мощности, которая распространилась из положения ( o ) на расстояние ( x ) через материал с проводимостью (σ), определяется как:
, из которого коэффициент поглощения (α ) можно выразить через коэффициент экстинкции ( k ) как:
Как скорость света в вакууме, c = fλ , тогда α = 4πk/λ , а мощность или интенсивность равна P = P o exp -αx .
Это уравнение известно как закон Бугера или закон поглощения Ламберта, согласно которому излучение поглощается в степени, зависящей от длины волны излучения, толщины и природы среды. Поэтому коэффициент поглощения описывается как величина, обратная глубине проникновения излучения в объемное твердое тело, т. е. равна глубине, на которой энергия излучения уменьшилась в 9 раз.0017 e -αx , или, альтернативно, интенсивность падающего излучения ослабляется твердым телом до 1/e от его начального значения на расстоянии от границы поверхности, определяемом λ /4πk .
При переходе электромагнитного излучения из одной среды в другую значения относительной диэлектрической проницаемости ε r и относительной проницаемости µ r должны изменяться в зависимости от характеристик материалов. В дополнение к этому необходимо определить граничные условия, чтобы обеспечить совпадение волн в двух средах на границе раздела. Это требует, чтобы тангенциальные компоненты E (вектор электрического поля) и H (вектор магнитного поля) были непрерывны поперек границы, а нормальные компоненты D (вектор электрического смещения) и B (вектор плотности магнитного потока) также были непрерывны поперек границы.
граница. Следовательно, ε 0ε1 E 1 = ε 0ε2 E 2 and µ 0µ1 H 1 = µ 0µ2 H 2 .
Оптический импеданс материала является еще одним полезным параметром при рассмотрении отражения и прохождения электромагнитных волн через поверхность раздела.0012 / H x = (µ 0µr /ε 0εr )½ . путем замены значений для ε 0 (8,854×10 -12 FM -1 ) и µ 0 (1,257×10 -6 HM -1 ), невыполнение -6 HM -1 ). Z 0 = (µ 0 /ε 0 )½ = 377 Ом. Оптическая проводимость свободного пространства Y определяется выражением Y = 1/Z 0 = (ε 0 / мк 0 )½ = 2,654×10 -3 Ом-1 .

 4 — 0.8
4 — 0.8 03 — 0.05
03 — 0.05 . + S n α n
. + S n α n 
 Таким образом, оптические свойства твердого тела определяются взаимодействием между твердым телом и электрическим полем электромагнитной волны.
Таким образом, оптические свойства твердого тела определяются взаимодействием между твердым телом и электрическим полем электромагнитной волны. ) по уравнению c= 1/(µ 0ε0 )½.
) по уравнению c= 1/(µ 0ε0 )½. Это уравнение известно как закон Бугера или закон поглощения Ламберта, согласно которому излучение поглощается в степени, зависящей от длины волны излучения, толщины и природы среды. Поэтому коэффициент поглощения описывается как величина, обратная глубине проникновения излучения в объемное твердое тело, т. е. равна глубине, на которой энергия излучения уменьшилась в 9 раз.0017 e -αx , или, альтернативно, интенсивность падающего излучения ослабляется твердым телом до 1/e от его начального значения на расстоянии от границы поверхности, определяемом λ /4πk .
Это уравнение известно как закон Бугера или закон поглощения Ламберта, согласно которому излучение поглощается в степени, зависящей от длины волны излучения, толщины и природы среды. Поэтому коэффициент поглощения описывается как величина, обратная глубине проникновения излучения в объемное твердое тело, т. е. равна глубине, на которой энергия излучения уменьшилась в 9 раз.0017 e -αx , или, альтернативно, интенсивность падающего излучения ослабляется твердым телом до 1/e от его начального значения на расстоянии от границы поверхности, определяемом λ /4πk . граница. Следовательно, ε 0ε1 E 1 = ε 0ε2 E 2 and µ 0µ1 H 1 = µ 0µ2 H 2 .
граница. Следовательно, ε 0ε1 E 1 = ε 0ε2 E 2 and µ 0µ1 H 1 = µ 0µ2 H 2 .