Что такое развертка конуса и как ее построить? Формулы и пример решения задачи
Круглый конус в геометрии
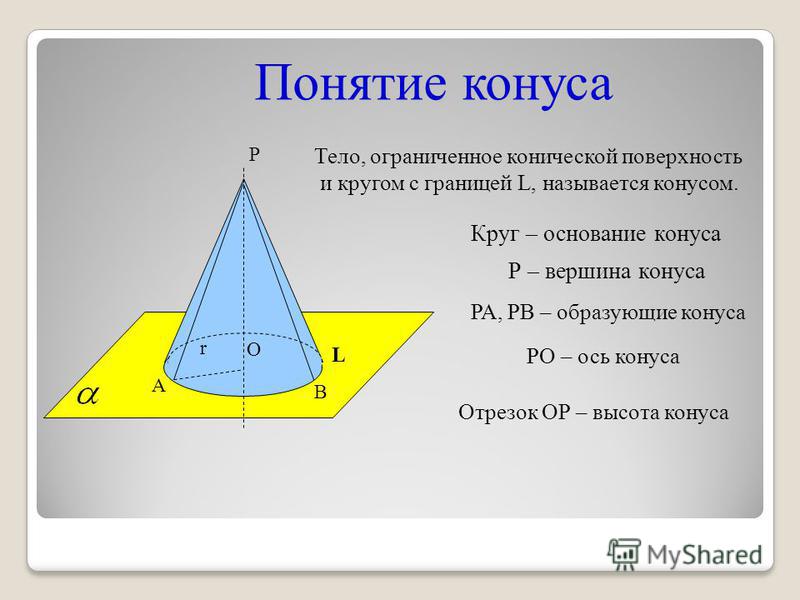
Приведем геометрическое определение этой фигуры. Круглым конусом называется поверхность, которая образована прямыми отрезками, соединяющими все точки некоторой окружности с одной-единственной точкой пространства. Эта единственная точка не должна принадлежать плоскости, в которой лежит окружность. Если вместо окружности взять круг, то указанный способ также приводит к получению конуса.
Вам будет интересно:Юридический колледж в Иваново: специальности, приемная комиссия, отзывы
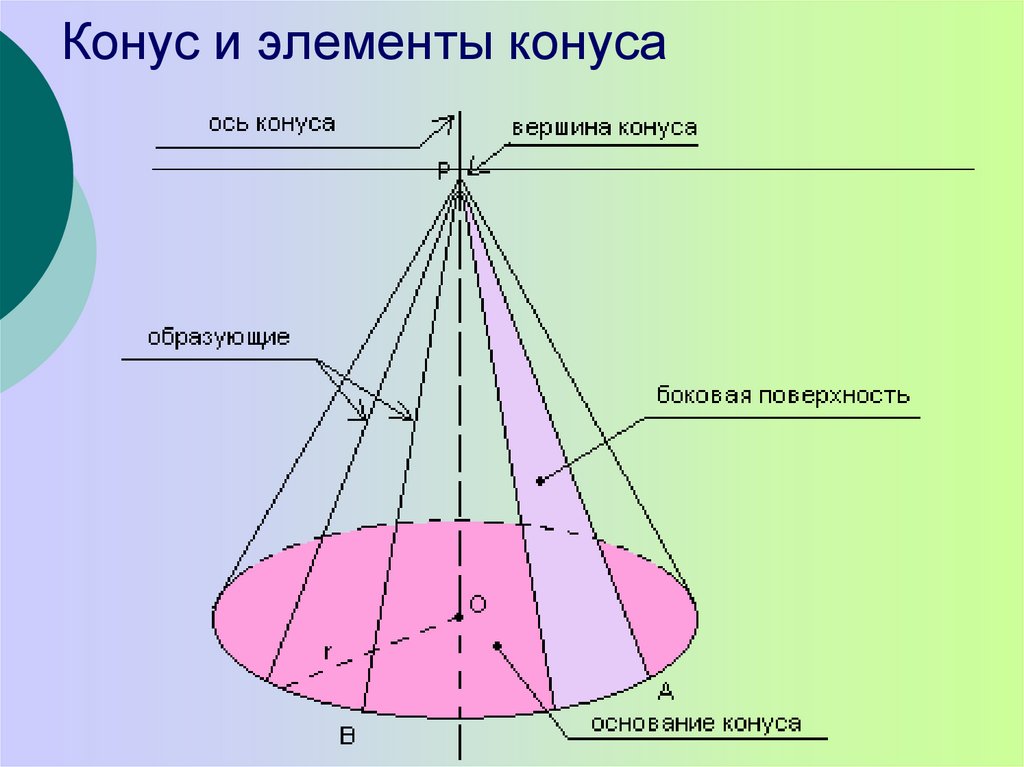
Круг называется основанием фигуры, его окружность — это директриса. Отрезки, соединяющие точку с директрисой, называются генератрисами или образующими, а точка, где они пересекаются — это вершина конуса.
Круглый конус может быть прямым и наклонным. Обе фигуры показаны ниже на рисунке.
Вам будет интересно:Термофильные бактерии: польза и вред для человека
Разница между ними заключается в следующем: если перпендикуляр из вершины конуса падает точно в центр окружности, то конус будет прямым. Для него перпендикуляр, который называется высотой фигуры, является частью его оси. В случае конуса наклонного высота и ось образуют некоторый острый угол.
Для него перпендикуляр, который называется высотой фигуры, является частью его оси. В случае конуса наклонного высота и ось образуют некоторый острый угол.
Ввиду простоты и симметричности фигуры далее будем рассматривать свойства только прямого конуса с круглым основанием.
Дед Мороз из конуса бумаги своими руками
Стоит отметить, что множество разнообразных поделок можно изготовить с использованием бумажного конуса. Они более привлекательны, индивидуальны, неординарны, всегда восхищают и поднимают настроение. Это не только поможет в Новый год сделать атмосферу сказочной, но и подарит множество неизгладимых впечатлений маленьким деткам.
Для начала работ нужно иметь в наличии такие приспособления:
- бумагу белую и красную;
- клей ПВА или канцелярский хорошего качества;
- вату;
- карандаши;
- циркуль;
- ножницы;
- линейку.
Этапы создания Деда Мороза следующие:
- Берем красную бумагу и вычерчиваем на ней круг с диаметром в 20 сантиметров.

- Вырезаем круг и складываем пополам.
- По сгибу разрезаем.
- Из полученного полукруга формируем конус.
- Тщательно склеиваем края.
- Берем белую бумагу и вычерчиваем на ней круг диаметром в 4 сантиметра.
- Маленький круг вырезается и наклеивается к основному конусу чуть ниже острия. Он будет служить лицом Деда Мороза. На нем рисуются глазки, носик и ротик.
- Из бумаги красного цвета вырезаем детали для рук Деда Мороза. Они приклеиваются по бокам большого конуса.
- На острие конуса прикрепить кусок ваты – это будет помпон на шапке. Можно таким же образом сделать и волосы из-под шапки.
- На маленьком круге из ваты (можно использовать и просто бумагу) изобразить усы и бороду.
Получение фигуры с помощью вращения
Перед тем как перейти к рассмотрению развертки поверхности конуса, полезно узнать, как с помощью вращения можно получить эту пространственную фигуру.
Предположим, что у нас имеется прямоугольный треугольник со сторонами a, b, c. Первые две из них являются катетами, c — это гипотенуза. Поставим треугольник на катет a и начнем его вращать вокруг катета b. Гипотенуза c при этом опишет коническую поверхность. Эта простая методика получения конуса изображена ниже на схеме.
Первые две из них являются катетами, c — это гипотенуза. Поставим треугольник на катет a и начнем его вращать вокруг катета b. Гипотенуза c при этом опишет коническую поверхность. Эта простая методика получения конуса изображена ниже на схеме.
Очевидно, что катет a будет радиусом основания фигуры, катет b — его высотой, а гипотенуза c соответствует образующей круглого прямого конуса.
Бумажный петушок из конуса
Прекрасное создание из цветной бумаги порадует не только малышей, но и взрослых. При изготовлении такой поделки могут участвовать и самые маленькие умельцы, им необходимо немного подсказать и помочь. Сделать петушка достаточно просто. Для этого необходимо иметь в доме:
| 1 | цветную бумагу |
| 2 | картон |
| 3 | карандаш |
| 4 | циркуль |
| 5 | клей |
| 6 | линейку |
| 7 | фломастеры |
| 8 | ножницы |
Изготавливается сказочный петушок таким образом:
- Берется картон, укладывается на горизонтальную поверхность, на нем вычерчивается циркулем круг, который впоследствии вырезается ножницами.

- Заготовка складывается строго пополам и разрезается.
- Полученный полукруг сворачивается в виде конуса.
- Шов склеивается и хорошо просушивается.
- Из цветной бумаги вырезается небольшая деталь и из нее делается клювик.
- Клюв приклеивается к основанию фигуры.
- К верхушке заготовки приклеивается вырезанная тонкая полоска.
- Если эту же полосочку приклеить в нескольких местах, то получится интересный гребешок.
- Из цветной бумаги вырезать фигурки в виде капелек и приклеить их к основанию конуса пониже клюва. Это будет бородка петушка.
- Нарезать полоски разных цветов в количестве 5 штук.
- Так же, как и гребешок, приклеить их к конусу по бокам. Получатся крылья птички.
- Из таких же полосок изготовить хвостик, который можно немножко закрутить при помощи ножниц.
Сказочный петушок готов!
Таким же образом можно создать и других сказочных животных, например ослика, коровку, кролика, собачку, бегемотика и многих других сказочных персонажей, насколько хватит фантазии и усидчивости.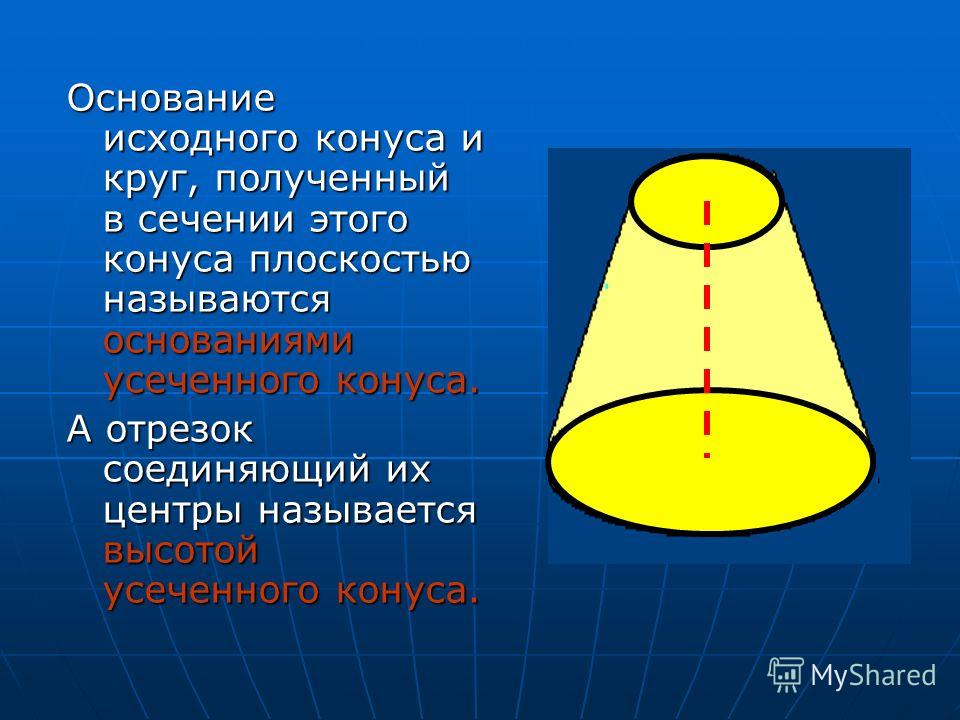
Вид развертки конуса
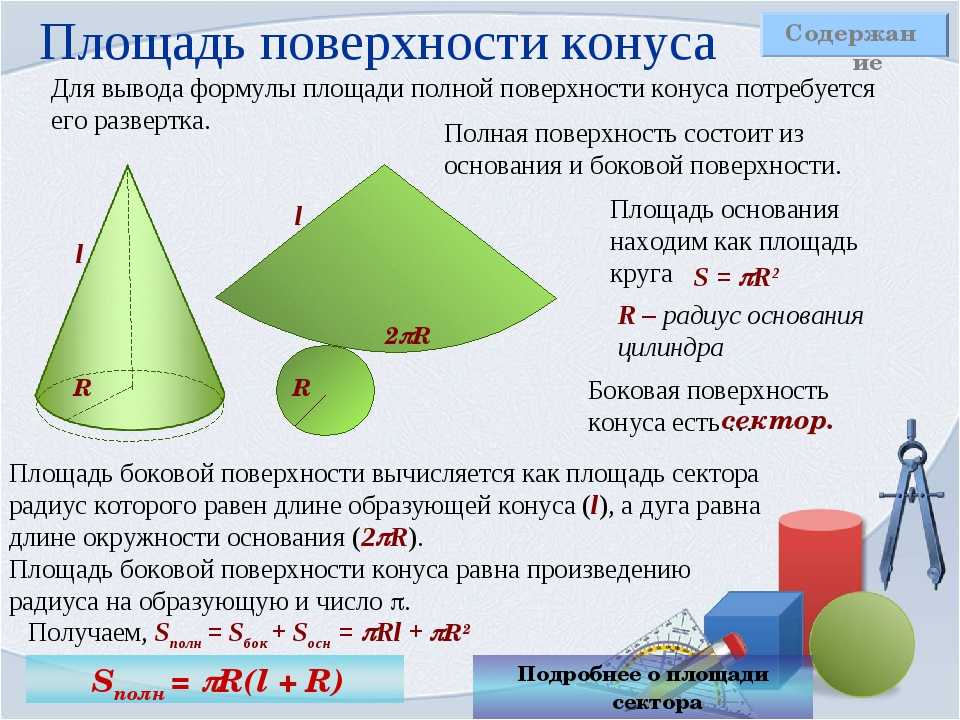
Как можно догадаться, конус образован двумя типами поверхностей. Одна из них — это плоский круг основания. Предположим, что он имеет радиус r. Вторая поверхность является боковой и называется конической. Пусть ее образующая будет равна g.
Если у нас имеется бумажный конус, то можно взять ножницы и отрезать от него основание. Затем, коническую поверхность следует разрезать вдоль любой образующей и развернуть ее на плоскости. Таким способом мы получили развертку боковой поверхности конуса. Две поверхности вместе с исходным конусом показаны на схеме ниже.
Внизу справа изображен круг основания. По центру показана развернутая коническая поверхность. Оказывается, что она соответствует некоторому круговому сектору круга, радиус которого равен длине образующей g.
Схемы разных конусов
Белым цветом на схемах выделена часть, которую нужно отрезать. Ну а из розовой части нужно скрутить конус. Соответственно, каждая представленная схема показывает, какой конус по ширине получится в итоге.
Схемы разных конусов.
Ну вот, теперь вы знаете, как сделать конус из бумаги. Нужно лишь выбрать один из представленных выше вариантов и смело воплотить его в жизнь. Все способы рабочие и неоднократно проверенные временем. Рекомендуем также посмотреть, как сделать маску для сна и комнатные тапочки. Удачных самоделок, и до новых встреч в следующих обзорах!
Угол и площадь развертки
Теперь получим формулы, которые по известным параметрам g и r позволяют рассчитать площадь и угол развертки конуса.
Очевидно, что дуга кругового сектора, показанного выше на рисунке, имеет длину, равную длине окружности основания, то есть:
l = 2*pi*r.
Если бы весь круг радиусом g был построен, то его бы длина составила:
L = 2*pi*g.
Поскольку длина L соответствует 2*pi радианам, тогда угол, на который опирается дуга l, можно определить из соответствующей пропорции:
L ==> 2*pi;
l ==> φ.
Тогда неизвестный угол φ будет равен:
φ = 2*pi*l/L.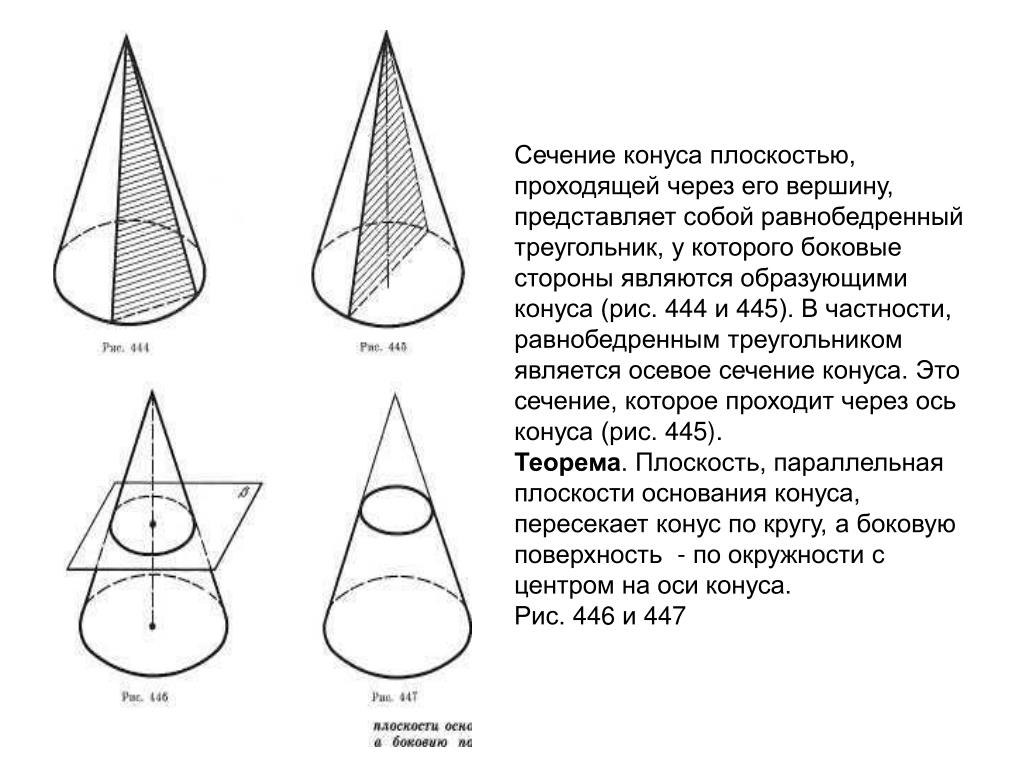
Подставляя выражения для длин l и L, приходим к формуле для угла развертки боковой поверхности конуса:
φ = 2*pi*r/g.
Угол φ здесь выражен в радианах.
Для определения площади Sb кругового сектора воспользуемся найденным значением φ. Составляем еще одну пропорцию, только уже для площадей. Имеем:
2*pi ==> pi*g2;
φ ==> Sb.
Откуда следует выразить Sb, а затем, подставить значение угла φ. Получаем:
Sb = φ*g2*pi/(2*pi) = 2*pi*r/g*g2/2 = pi*r*g.
Для площади конической поверхности мы получили достаточно компактную формулу. Величина Sb равна произведению трех множителей: числа пи, радиуса фигуры и ее образующей.
Тогда площадь всей поверхности фигуры будет равна сумме Sb и So (площадь круглого основания). Получаем формулу:
S = Sb + So = pi*r*(g + r).
Усеченный геометрический объект
Усеченная фигура представляет собой объект в пространстве, который состоит из двух оснований разной площади и конической боковой поверхности. В отличие от исходного конуса, его усеченный вариант не имеет вершины. Остальные линейные элементы для него такие же, как для конуса с вершиной. У усеченной фигуры также имеется две директрисы, ограничивающие каждое из оснований, и одна генератриса, которая опирается на линии направляющих кривых.
В отличие от исходного конуса, его усеченный вариант не имеет вершины. Остальные линейные элементы для него такие же, как для конуса с вершиной. У усеченной фигуры также имеется две директрисы, ограничивающие каждое из оснований, и одна генератриса, которая опирается на линии направляющих кривых.
Рассматриваемый геометрический объект также бывает нескольких видов (эллиптический, наклонный). Чаще всего в задачах по геометрии встречается именно круглый прямой усеченный конус, который ограничен двумя круглыми основаниями.
Способы построения
Можно выделить два основных способа построения усеченного круглого геометрического объекта:
- из круглого прямого конуса;
- с помощью трапеции.
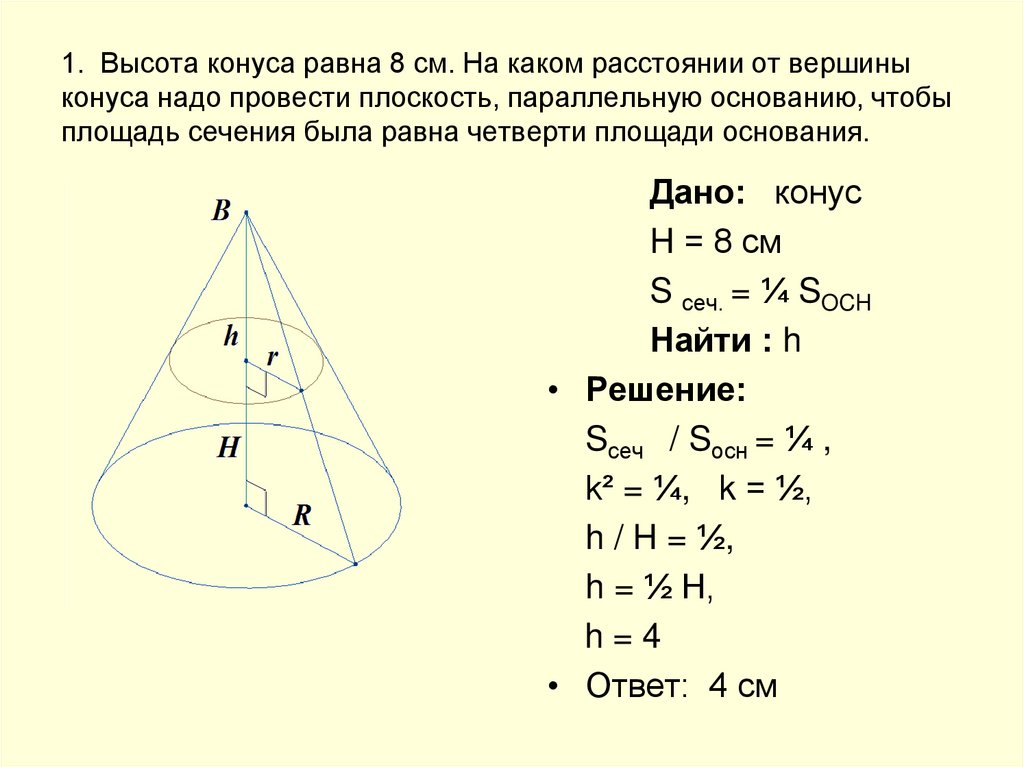
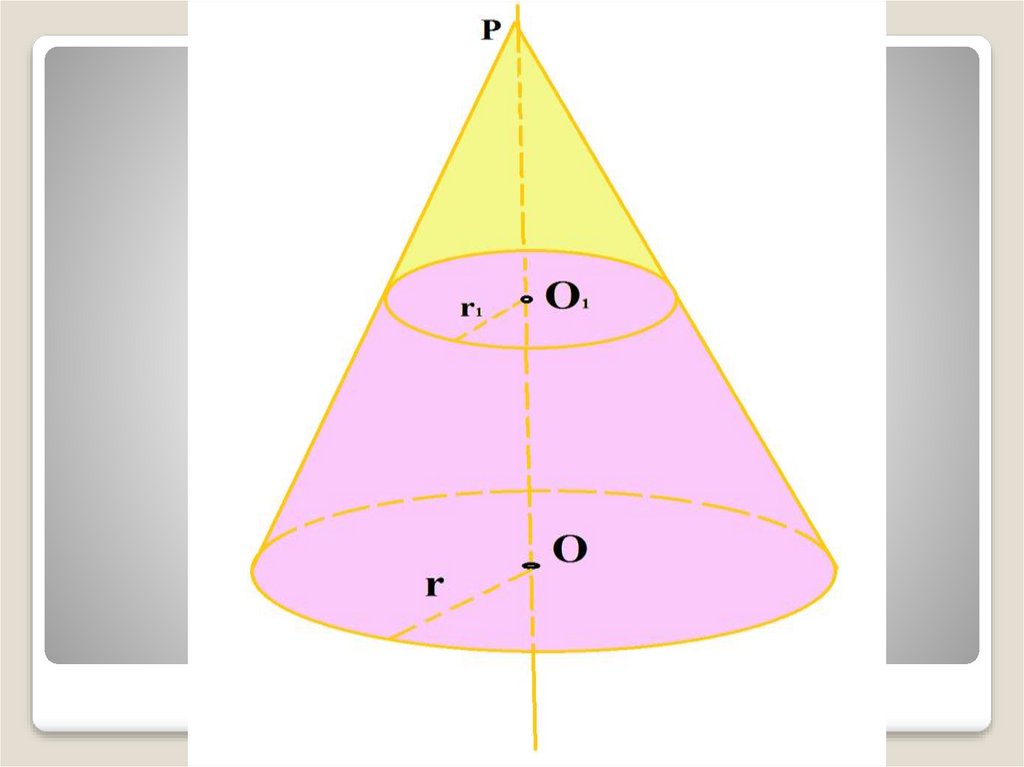
В первом случае необходимо взять коническую фигуру и режущую плоскость, которая будет параллельна основанию. После этого с помощью плоскости следует отсечь верхнюю часть конуса. Оставшаяся под плоскостью фигура будет усеченной. Следует отметить, что совершенно неважно, какая часть конуса с вершиной будет отсечена. Чем больше она будет, тем ближе окажутся друг к другу значения верхнего и нижнего радиусов в усеченной фигуре, то есть тем ближе она по форме будет походить на прямой цилиндр.
Чем больше она будет, тем ближе окажутся друг к другу значения верхнего и нижнего радиусов в усеченной фигуре, то есть тем ближе она по форме будет походить на прямой цилиндр.
Второй способ получения усеченного конического объекта связан с использованием фигуры трапеции прямоугольного типа. Такая трапеция представляет собой два параллельных отрезка, которые имеют длины a и b. Они соединены одним перпендикуляром h и косым отрезком g.
Если прямоугольную трапецию поставить на большее основание и вращать ее вокруг перпендикуляра h, то получится усеченный конус. В нем отрезки a и b будут радиусами оснований объемной фигуры, перпендикуляр h станет высотой, а наклонный отрезок g будет представлять собой длину образующей. Эти четыре линейных характеристики определяют рассматриваемую объемную фигуру. Следует заметить, что для однозначного построения фигуры достаточно лишь трех любых из них, например, высоты и двух радиусов.
Площадь поверхности
Поверхность усеченной фигуры, в отличие от полного конуса, образована тремя частями: два круглых основания и боковая поверхность.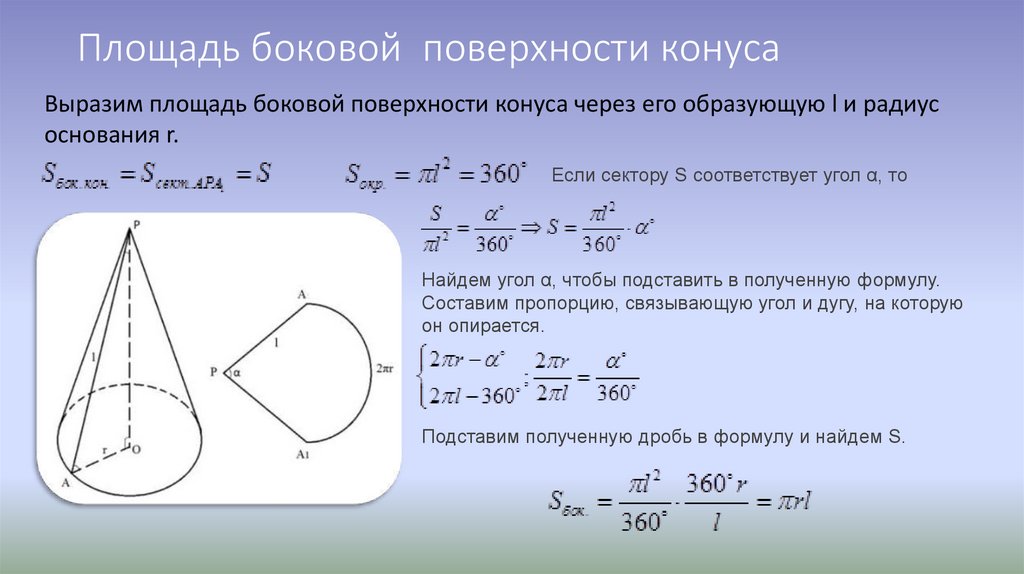 Площади круглых оснований вычисляются по известной формуле для круга: pi*r2. Для боковой поверхности следует выполнить следующие действия:
Площади круглых оснований вычисляются по известной формуле для круга: pi*r2. Для боковой поверхности следует выполнить следующие действия:
- Разрезать ее вдоль образующей и развернуть на плоскости.
- Обратить внимание, что полученная фигура представляет собой сектор круга, у которого в верхней его части вырезан другой маленький сектор.
- Достроить мысленно усеченную фигуру до полного конуса и определить его высоту H и директрису G. Через соответствующие параметры усеченного конуса они будут выражаться следующим образом: G = r1*g/(r1-r2), H = h*r1/(r1-r2), здесь радиусы оснований r1 и r2 такие, что r1>r2.
- Рассчитать площади большого и маленького круговых секторов, а затем вычесть из первой вторую. В итоге получится следующая простая формула: Sb = pi*g*(r1 + r2).
Площадь всей поверхности рассматриваемой фигуры вычисляется как сумма трех величин S1, S2 и Sb:
S = S1 + S2 + Sb = pi*r12 + pi*r22 + pi*g*(r1 + r2).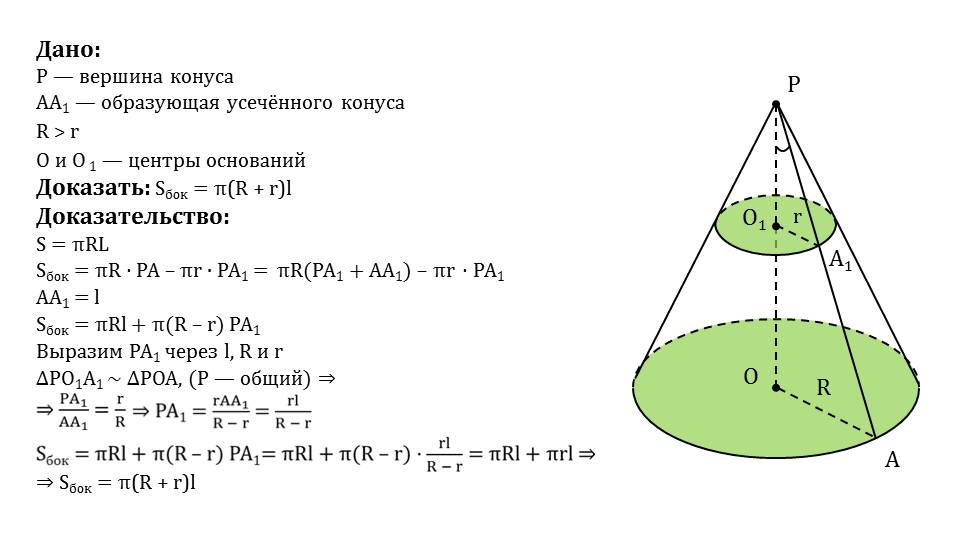 0,5).
0,5).
Записанная формула объема может быть получена универсальным способом без привлечения известного выражения для полного конуса. Для этого необходимо использовать интегральное исчисление, разбивая при этом усеченный геометрический объект на бесконечное количество тонких круглых дисков. Их радиусы будут постепенно уменьшаться от r1 до r2. Этот метод вывода формулы для объема не отличается от аналогичного для полного круглого конуса, изменяются лишь пределы интегрирования.
Построение развертки конуса на бумаге
Для выполнения этой задачи понадобится лист бумаги, карандаш, транспортир, линейка и циркуль.
В первую очередь начертим прямоугольный треугольник со сторонами 3 см, 4 см и 5 см. Его вращение вокруг катета в 3 см даст искомый конус. У фигуры r = 3 см, h = 4 см, g = 5 см.
Построение развертки начнем с рисования циркулем окружности радиусом r. Ее длина будет равна 6*pi см. Теперь рядом с ней нарисуем еще одну окружность, но уже радиусом g. Ее длина будет соответствовать 10*pi см.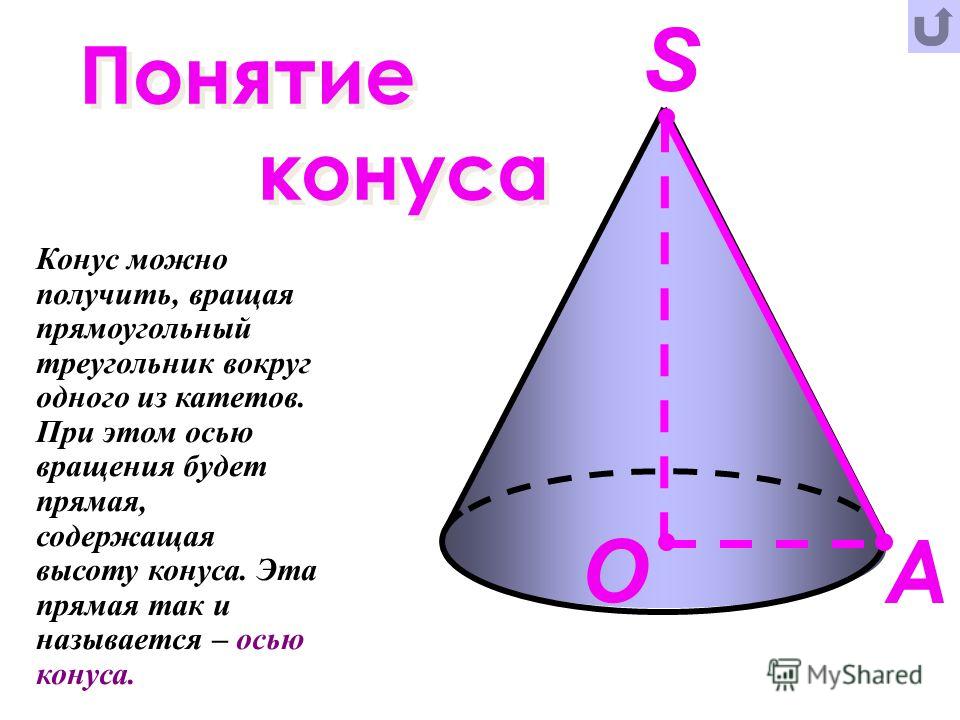 Теперь нам нужно от большой окружности отрезать круговой сектор. Его угол φ равен:
Теперь нам нужно от большой окружности отрезать круговой сектор. Его угол φ равен:
φ = 2*pi*r/g = 2*pi*3/5 = 216o.
Теперь откладываем транспортиром этот угол на окружности с радиусом g и проводим два радиуса, которые будут ограничивать круговой сектор.
Таким образом, мы построили развертку конуса с указанными параметрами радиуса, высоты и образующей.
Как сделать конус из полукруга
- Берем лист бумаги и кладем его на ровную горизонтальную поверхность. В середине края любой стороны листа ставим циркуль и рисуем полукруг на весь лист.
- Ножницами вырезаем полученный полукруг из бумаги.
- Далее нужно соединить два угла полученного полукруга. Для этого промазываем клеем ровную сторону полукруга от центра до угла. Затем несмазанный клеем угол нужно будет немного завести за другой, чтобы конус «закрылся» и наклеить его сторону на смазанную сторону.
Формула площади поверхности усеченного кругового конуса
Для усеченного кругового конуса площадь боковой поверхности можно найти по формуле:
S бок = π ⋅ l ⋅ ( r + r ′ ) S_{\text{бок}}=\pi\cdot l\cdot (r+r’) Sбок=π⋅l⋅(r+r′)
l l l — длина образующей конуса; r r r — радиус основания; r ′ r’ r′ — радиус круга, получаемый при усечении кругового конуса. 2\approx12.56 Sосн r’=π⋅r′2=π⋅22≈12.56 (см. кв.)
2\approx12.56 Sосн r’=π⋅r′2=π⋅22≈12.56 (см. кв.)
Площадь боковой поверхности:
S бок = π ⋅ l ⋅ ( r + r ′ ) = π ⋅ 5 ⋅ ( 3 + 2 ) ≈ 78.50 S_{\text{бок}}=\pi\cdot l\cdot (r+r’)=\pi\cdot 5\cdot (3+2)\approx78.50 Sбок=π⋅l⋅(r+r′)=π⋅5⋅(3+2)≈78.50 (см. кв.)
Полная площадь:
S = S осн + S бок = S осн r + S осн r’ + S бок ≈ 28.26 + 12.56 + 78.50 = 119 , 32 S=S_{\text{осн}}+S_{\text{бок}}=S_{\text{осн r}}+S_{\text{осн r’}}+S_{\text{бок}}\approx28.26+12.56+78.50=119,32 S=Sосн+Sбок=Sосн r+Sосн r’+Sбок≈28.26+12.56+78.50=119,32 (см. кв.)
Ответ: 119,32 см. кв.
Не знаете, как решить задачу по геометрии? Наши эксперты оперативно помогут вам с решением!
Конусы для слалома. Виды и назначение
29 августа 2019
Привет начинающий роллер! В этой статье мы разберемся для чего нужны конусы слалома, где они используются и каких типов бывают.
Авторы этой статьи — Александр Салогуб и Кузьмин Алексей, на двоих у нас 15 лет опыта в слаломе. Еще лет 5 назад мы проводили по 5 часов 3 раза в неделю, тренируя слалом на таких конусах и сейчас с радостью поделимся плюсами и минусами разных типов конусов для слалома.
Еще лет 5 назад мы проводили по 5 часов 3 раза в неделю, тренируя слалом на таких конусах и сейчас с радостью поделимся плюсами и минусами разных типов конусов для слалома.
Прежде чем рассказать какие виды слаломных конусов существуют, давайте разберемся,
Для чего используют фишки для слалома.
Основное предназначение конусов – разметка для катания слалома на роликах. Слалом делится на несколько категорий: слалом баттл (freestyle battle), классика (freestyle classic) и скоростной слалом (speed slalom)
Слалом баттл – соревнования между роллерами на трех дорожках из конусов – по 20 конусов с шагом 50 см, 80 см и 120 см. Все участники соревнований делятся на группы по 3-4 человека и соревнуются между собой в группах. У каждого участника есть 3 заезда по 30 секунд, чтобы показать свои самые сложные трюки и набрать максимальное количество баллов за их сложность. Из группы выходят только самые сильные роллеры, которые соревнуются с победителями в соседних группах. Обычно баттлы проходят в несколько этапов, включающие квалификацию, 1-2 тура и финал, а программа выступлений является экспромтом и состоит из заранее заученых связок или импровизации из трюков различной сложности.
Из группы выходят только самые сильные роллеры, которые соревнуются с победителями в соседних группах. Обычно баттлы проходят в несколько этапов, включающие квалификацию, 1-2 тура и финал, а программа выступлений является экспромтом и состоит из заранее заученых связок или импровизации из трюков различной сложности.
Freestyle Classic – набирающий популярность тип соревнований, кардинально отличающийся от баттла. В Классике соревнующиеся выступают по очереди, без деления на группы. У каждого роллера есть 1 минута на заранее приготовленное выступление. Судьи оценивают не только сложность исполненных трюков, но и их красоту и образ выступающего. После выступления всех участников судьи сравнивают поставленные балы и определяют победителей. Также как и Баттл, Классик слалом проходит на трех дорожках из 20 конусов, с расстоянием между фишками 50 см, 80 см и 120 см.
Speed Slalom – скоростное прохождение дорожки из 20 конусов с расстоянием 80 см между фишками. Проводится с использованием системы старт-финиш для определения точного времени прохождения дистанции. Задача стоит в максимально быстром прохождении дорожки на одной ноге. В 99% случаев соревнующиеся используют слаломный элемент One Foot, как самый стабильный и удобный для этого вида соревнования трюк. Но в нашей практике бывали случаи когда в этом виде слалома соревновались и на одноколесном элементе One Wheel, хотя скорость прохождения дистанции в этом случае заметно увеличивалась.
Проводится с использованием системы старт-финиш для определения точного времени прохождения дистанции. Задача стоит в максимально быстром прохождении дорожки на одной ноге. В 99% случаев соревнующиеся используют слаломный элемент One Foot, как самый стабильный и удобный для этого вида соревнования трюк. Но в нашей практике бывали случаи когда в этом виде слалома соревновались и на одноколесном элементе One Wheel, хотя скорость прохождения дистанции в этом случае заметно увеличивалась.
Помимо слалома, конусы используются детскими инструкторами для занятий с детьми, а на соревнованиях по слайдам конусами ограничивают зону торможения и отмечают дальность торможения.
Возможно, прочитав статью до этого места Вам стало понятнее чем занимается Ваш знакомый, друг или ребенок. В таком случае, конусы для слалома могут стать отличным подарком слаломисту на день рождения.
Теперь давайте разберемся, какие виды конусов для слалома существуют.
Конуса для слалома бывают из пластика, из резины, двухкомпонентные пластиковые конуса с прорезиненым верхом, а некоторые спортсмены еще помнят, как сами делали конуса для слалома из линолеума своими руками.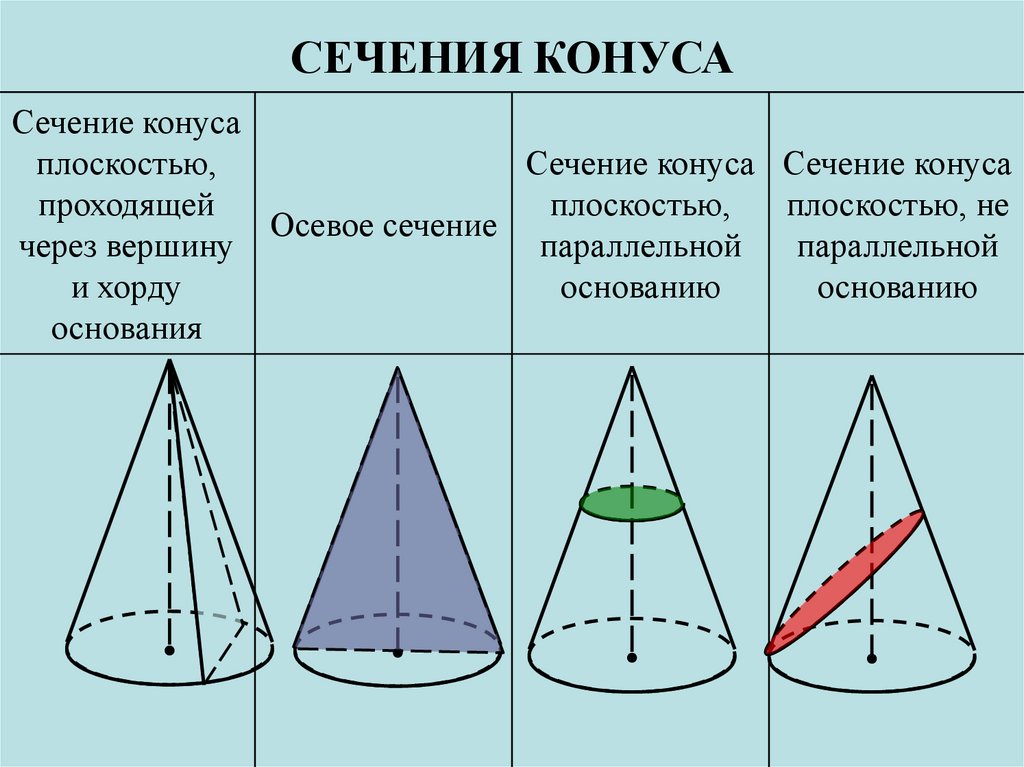
Резиновые конусы для слалома
Такие конуса заводского изготовления появились первыми в Украине и если роллер не делал сам себе конуса из подручных средств, то у него были именно такие фишки для тренировок по слалому.
Плюсы резиновых конусов:
+ При падении на фишку она сминается.
+ Не сдувается ветром
+ Не ломается и не трескается при наезде машиной или при падении
Минусы резиновых конусов:
— При наезде на фишку она сминается и попадает между колес. Категорически не рекомендуем использовать для изучения сложных трюков в слаломе, особенно одноколесных.
Пластиковые конуса для слалома
Такие конуса может сдувать ветер. потому что пластиковые конуса достаточно легкие и скользкие. Падать прямо на них весом своего тела не приятно, но чаще всего они отскакивают всторону при малейшем ударе или задевании. Живучесть таких конусов чуть хуже чем у резиновых. Если на резиновые можно наезжать даже машиной сколько угодно раз, то пластиковые трескаются проще. Но из нашего опыта — за год катания ломается не больше 1 конуса, они чаще случайно теряются чем трескаются от падений на них.
Но из нашего опыта — за год катания ломается не больше 1 конуса, они чаще случайно теряются чем трескаются от падений на них.
При выборе пластиковых конусов, проверяйте чтобы ободок у основания конуса был не очень широкий. Конуса с широким ободком в основании отлетают из под колес как только его задеваешь. что очень раздражает на тренировках — ты не задел конус, только проехал очень близко рядом с ним, а он отлетел в сторону. У наших конусов Flying Eagle есть маленький ободок у основания, он не большой, а стандартного размера, который не мешает катанию, но и не позволяет фишке уезжать при легком ветерке.
Также, кроме пластиковых конусов изображенных на фото ниже, бывают и другие варианты пластиковых конусов. Например с дополнительными отверстиями в конусах, которые еще легче сдуваются ветром или без ободка у основания — такие фишки делает Powerslide.
Плюсы пластиковых конусов:
+ При наезде на фишку она отскакивает в сторону.
+/- Выдерживает падения и наезды машины, но при этом может деформироваться.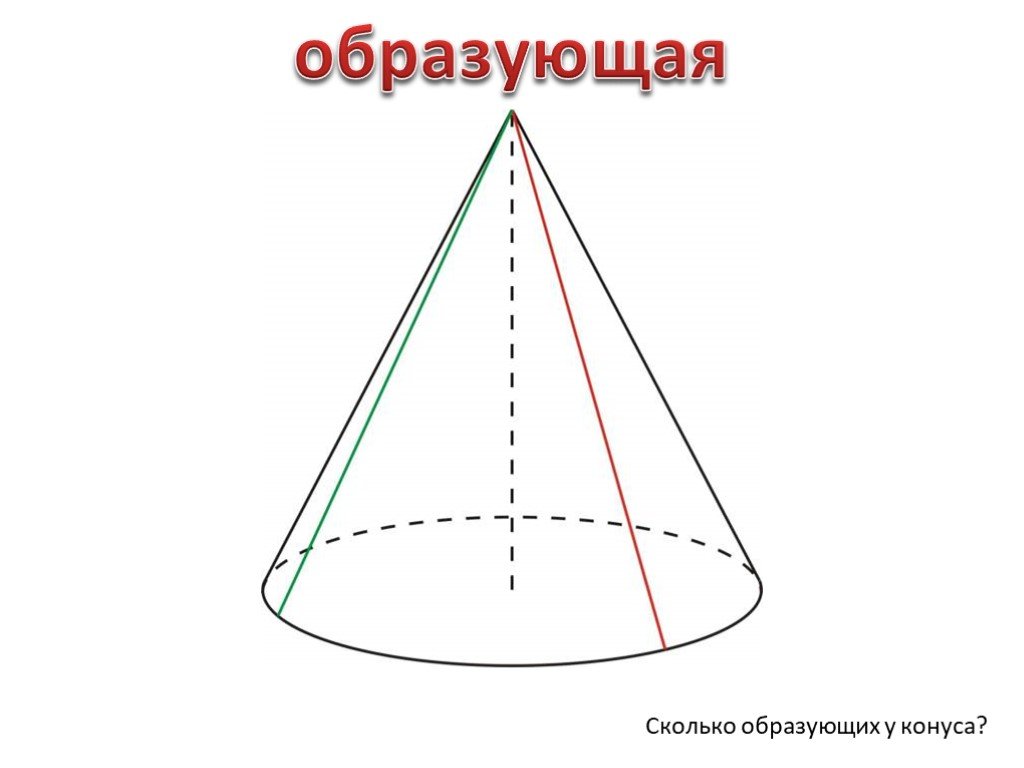
Минусы пластиковых конусов:
— Сдувается порывами ветра
Фишки из пластика и резины
Верхняя часть конуса выполнена из мягкой резины (на нее не больно падать), а нижняя — с пластика (фишки хорошо отлетают при ударах). Такое технологичное чудо выпускает компания Seba и комплект фишек стоит как маленький самолёт. В Украине данное новшество не стало очень популярным (лучше немного подкопить и за эти же деньги купить колес).
Плюсы двухкомпонентных фишек:
+ На такую фишку не больно падать сверху, благодаря резиновому верху. При этом она отскакивает от колес как пластиковая фишка, поскольку имеет низ как у конуса из пластика.
Минусы двухкомпонентных фишек:
— Недоработанная технология, в результате чего пластиковое основание часто трескается от падения и наездов на конус, а резиновый верх отрывается от пластика или рвется.
— Стоимость таких фишек значительно выше остальных вариантов.
Конусы из линолеума
Да, было время когда фишки для слалома делались из подручных средств. Хотите знать, как сделать конуса для слалома своими руками? Для этого достаточно хоть немного разбираться в геометрии. Рисуем развертку усеченного конуса, вырезаем, склеиваем или сшиваем по линии стыка и…..готово. Осталось повторить еще 19 раз чтобы сделать хоть одну дорожку для занятий. К счастью с появлением китайских товаров на рынке, необходимость так сильно мучаться осталась в прошлом!
Плюсы конусов из линолеума и прочих подручных средств:
+ Условная бесплатность (при наличии дома старого линолеума и необходимых инструментов)
+ Скорее всего такие фишки не будут сдуваться ветром.
Минусы конусов из линолеума и прочих подручных средств:
— Сложный процесс изготовления, в сравнении с процессом заказа в нашем магазине.
— Фишки отличаются друг от друга, поскольку делаются своими руками а не на производстве
— Отскочит фишка или попадет между колес и застопорит их – чистая лотерея, зависящая от формы фишки и типа линолеума.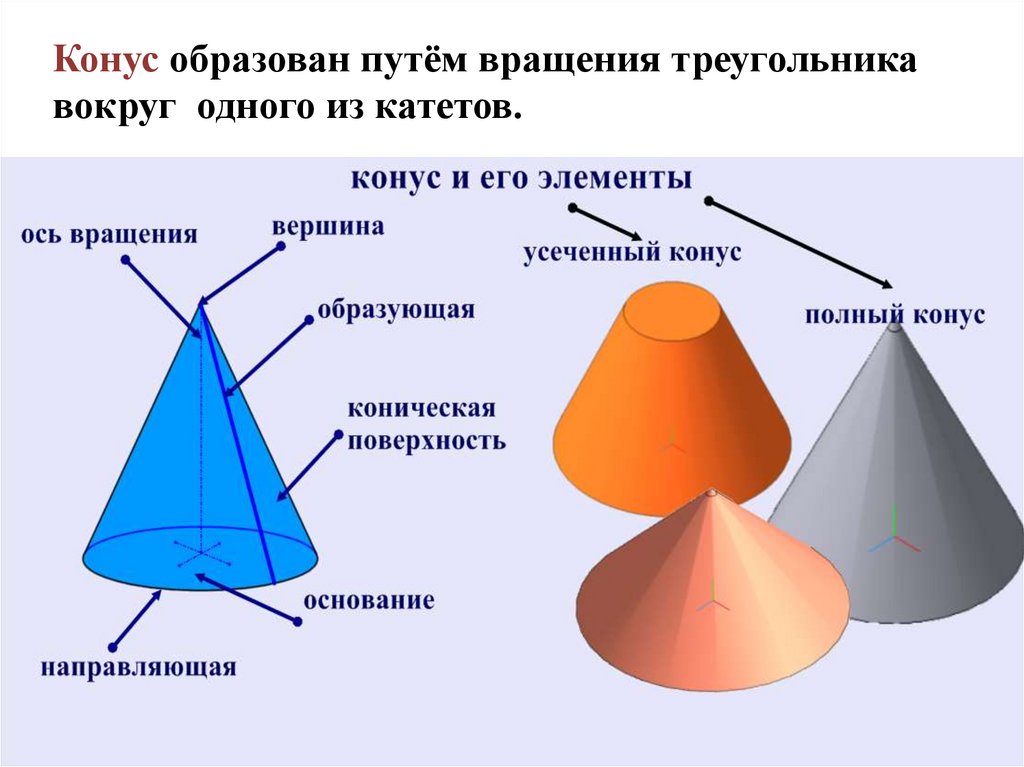
— Не выдерживает наезды машины
Мы осознанно не делали обзор на еще пару видов устаревши конусов, чтобы статья была полезной для современных слаломистов, а не была местом сбора неработающих конструкций конуса. Сегодня пластиковые фишки считаются самыми удобными и распространенными для изучения слалома, именно такие мы продаем в нашем магазине. Купить конусы для слалома с логотипом Flying Eagle можно на нашем сайте, с доставкой новой почтой или самовывозом с нашего магазина. Продаем фишки для слалома от 1 штуки.
Статья написана для сайта uroll.com.ua
Авторы статьи — Салогуб Александр и Кузьмин Алексей.
Рассказать
Поделиться
Поделиться
Поделится
Поделится
Новый комментарий
Войти с помощью
Отправить
Конус — формула, свойства, типы, примеры
Конус — это трехмерная форма, имеющая круглое основание и сужающаяся к острой точке, называемой вершиной. Один из самых простых примеров из жизни, который можно привести, — это шапка на день рождения в форме конуса. Что касается конуса, у нас есть два типа областей. Один из них — это общая площадь поверхности, а другой — площадь криволинейной поверхности. Полная площадь поверхности конуса определяется как площадь, покрытая его основанием и криволинейной частью конуса, тогда как площадь криволинейной поверхности определяется только как площадь криволинейных поверхностей конуса.
Один из самых простых примеров из жизни, который можно привести, — это шапка на день рождения в форме конуса. Что касается конуса, у нас есть два типа областей. Один из них — это общая площадь поверхности, а другой — площадь криволинейной поверхности. Полная площадь поверхности конуса определяется как площадь, покрытая его основанием и криволинейной частью конуса, тогда как площадь криволинейной поверхности определяется только как площадь криволинейных поверхностей конуса.
| 1. | Определение конуса |
| 2. | Свойства конуса |
| 3. | Формула конуса |
| 4. | Типы конусов |
| 5. | Часто задаваемые вопросы о конусе |
Определение конуса
Конус представляет собой трехмерную твердую геометрическую форму, имеющую круглое основание и заостренный край наверху, называемый вершиной. Конус имеет одну грань и вершину. У конуса нет ребер.
Конус имеет одну грань и вершину. У конуса нет ребер.
Тремя элементами конуса являются его радиус, высота и наклонная высота. Радиус «r» определяется как расстояние между центром круглого основания и любой точкой на окружности основания. Высота «h» конуса определяется как расстояние от вершины конуса до центра круглого основания. Наклонная высота l определяется как расстояние от вершины конуса до любой точки на окружности конуса. На приведенном ниже рисунке показано, как будут выглядеть радиус, высота и высота наклона конуса. Некоторые из реальных примеров конуса включают кепку на день рождения, палатку и разделитель дорог.
Свойства конуса
Конус представляет собой форму с изогнутой поверхностью и круглым основанием. Следующие свойства конуса помогают нам легко его идентифицировать. Они следующие.
- Основание конуса круглое.
- У конуса одна грань, одна вершина и нет ребер.
- Наклонная высота конуса — это длина отрезка, соединяющего вершину конуса с любой точкой окружности основания конуса.

- Конус, вершина которого находится прямо над круглым основанием на перпендикулярном расстоянии, называется прямым круглым конусом.
- Конус, у которого вершина не находится непосредственно над круглым основанием, называется наклонным конусом.
Формула конуса
Есть три важные формулы, связанные с конусом. Это наклонная высота конуса, объем конуса и площадь его поверхности. Наклонная высота конуса получается путем нахождения суммы квадратов радиуса и высоты цилиндра, которая определяется по формуле, приведенной ниже. наклонная высота 92}\)
Площадь криволинейной поверхности конуса
Площадь криволинейной поверхности конуса – это площадь, ограниченная криволинейной частью конуса. Для конуса с радиусом «r», высотой «h» и наклонной высотой «l» площадь криволинейной поверхности будет следующей:
Площадь криволинейной поверхности = πrl квадратных единиц.
Общая площадь поверхности конуса
Общая площадь поверхности представляет собой сумму площади круглого основания и площади изогнутой части конуса. Другими словами, это сумма площади криволинейной поверхности конуса и площади круглого основания, что математически можно записать как:
Другими словами, это сумма площади криволинейной поверхности конуса и площади круглого основания, что математически можно записать как:
Общая площадь поверхности (TSA) = площадь основания (окружности) + площадь криволинейной поверхности конуса (CSA).
TSA = (πr 2 + πrl) квадратных единиц.
Общая площадь поверхности иногда упоминается как только площадь поверхности. Итак, всякий раз, когда нас просят вычислить площадь поверхности конуса, это означает, что мы должны найти общую площадь поверхности.
Объем конуса
Объем конуса — это пространство, занимаемое конусом. Формула для нахождения объема конуса, радиус которого равен «r», а высота равна «h», задается следующим образом: Объем = (1/3) πr 2 ч куб.ед. Пусть A = площадь основания конуса и h = высота конуса. Следовательно, объем конуса = (1/3) × A × h. Поскольку основание конуса круглое, мы заменяем площадь на πr 2 . Объем конуса = (1/3) × π × r 2 × h кубических единиц. Кроме того, объем конуса составляет одну треть объема цилиндра.
Кроме того, объем конуса составляет одну треть объема цилиндра.
Объем конуса = (1/3) × объем цилиндра.
Типы конусов
Обычно конусы бывают двух типов. Один из них представляет собой правильный круговой конус, а другой — наклонный конус. В таблице ниже перечислены некоторые отличия этих двух типов конусов.
| Правый круглый конус | Косой конус |
|---|---|
| Вершина прямого кругового конуса противоположна круговому основанию. | Наклонный конус не имеет вершины, прямо противоположной круглому основанию. |
| Линия, представляющая высоту конуса, проходит через центр базовой окружности и перпендикулярна радиусу. | Линия, представляющая высоту конуса, не проходит через центр базовой окружности. |
☛Темы, связанные с конусом
Ознакомьтесь с некоторыми интересными статьями, связанными с конусом.
- Формула высоты конуса
- Калькулятор наклонной высоты конуса
- Площадь основания конуса
- Боковая часть конуса
Примеры конусов
Пример 1: Сэм должен найти отношение объема конуса к объему цилиндра. Как вы можете помочь Сэму найти требуемое соотношение?
Решение:
Чтобы найти отношение, Сэм сначала должен найти объемы конуса и цилиндра. Используя формулу конуса и формулу цилиндра, имеем:
Объем конуса = (1/3)πr 2 h
Объем цилиндра = πr 2 h
Отношение объема конуса и объем цилиндра = (1/3)πr 2 h: πr 2 h
Объем конуса: Объем цилиндра = 1/3: 1
= 1:3
Следовательно, отношение объема конуса к объему цилиндра равно 1:3.Пример 2: Мэри использует толстый лист бумаги и готовит праздничную шапку в форме конуса. Радиус шапки равен 3 единицам, а высота — 4 единицам.
 Как Мэри может найти наклонную высоту шапочки на день рождения?
Как Мэри может найти наклонную высоту шапочки на день рождения?Решение:
Дан радиус (r) = 3 единицы и высота (h) = 4 единицы.
Используя формулу высоты наклона конуса, т. е. высота наклона 2 = радиус 2 + высота 2
л 2 = р 2 + ч 2
3 2 + 4 2 = 9 + 16
л 2 = 25
л = √25
л = 5
Следовательно, наклонная высота конуса = 5 ед.Пример 3: Джейн была в походе на выходных. Там она наблюдает коническую палатку и аппроксимирует, что высота палатки в три раза больше радиуса (r) палатки. Вам нужно помочь Джейн, найти примерный объем палатки, исходя из ее радиуса.
Решение:
Учитывая, что высота в три раза больше радиуса. Таким образом, мы можем сказать, что h = 3r. Следовательно, объем конуса равенОбъем конуса = (1/3) πr 2 ч.
 Подставив значение h = 3r, получим
Подставив значение h = 3r, получим
Объем конуса = (1/3) πr 2 × 3r
= (1/3) 3πr 3
= πr 3
Следовательно, объем палатки равен πr 3 кубических единиц.
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с сертифицированными экспертами ourCuemath.
Записаться на бесплатный пробный урок
Практические вопросы на конусе
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о конусе
Что такое конус?
Конус представляет собой трехмерную фигуру с круглым основанием и криволинейной поверхностью. Заостренный кончик наверху конуса называется «Вершина». Конус имеет одну грань (круглую) без ребер и одну вершину, являющуюся вершиной конуса.
Сколько граней, ребер и вершин у конуса?
Конус имеет одну грань без ребер и одну вершину. Конус имеет круглое основание и криволинейную поверхность. Поскольку конус имеет только одну вершину, у него нет ребра. Также в конусе есть только одна плоская поверхность, образующая основание.
Конус имеет круглое основание и криволинейную поверхность. Поскольку конус имеет только одну вершину, у него нет ребра. Также в конусе есть только одна плоская поверхность, образующая основание.
Что такое наклонная высота конуса?
Расстояние от вершины или вершины конуса до точки на окружности основания называется наклонной высотой. Наклонная высота получается квадратным корнем из суммы квадратов радиуса и высоты конуса.
Какова площадь поверхности конуса?
Площадь поверхности конуса может быть получена путем сложения площади его основания и криволинейной поверхности. Основание конуса круглое. Формула для нахождения площади поверхности конуса: (πr 2 + πrl) квадратных единиц. Здесь «r» — радиус конуса, а «l» — наклонная высота конуса. Здесь πr 2 — площадь его основания, а площадь криволинейной поверхности — πrl.
Каков объем конуса?
Объем конуса — это количество пространства, занимаемого конусом. Конус радиуса r и высоты h имеет объем (1/3)πr 2 ч.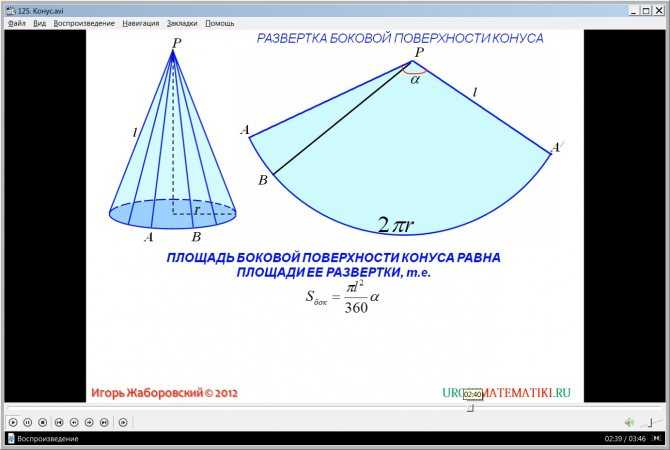
Что такое площадь основания конуса?
Основание конуса — это величина, показывающая площадь, покрытую круглым основанием конуса. Формула площади основания конуса: A = πr 2 , где r — радиус основания конуса.
Какие бывают два типа конуса?
Два типа конусов: прямой круговой конус и наклонный конус. У прямого круглого конуса линия оси проходит через центр круглого основания, тогда как в наклонном конусе линия оси не проходит через центр круглого основания.
Для чего нужен калькулятор конуса?
В геометрии конус определяется как объемная объемная геометрическая фигура, имеющая круглое основание на одном конце и заостренный край на другом конце. Попробуйте онлайн-инструмент Cuemath’s Cone Calculator, который поможет вам за несколько секунд рассчитать такие параметры, как площадь поверхности, объем и наклонная высота конуса.
Скачать БЕСПЛАТНЫЕ учебные материалы
Конусные листы
Что такое конус? Определение, формула, свойства, примеры
Конусы можно найти во многих предметах, которые мы видим каждый день.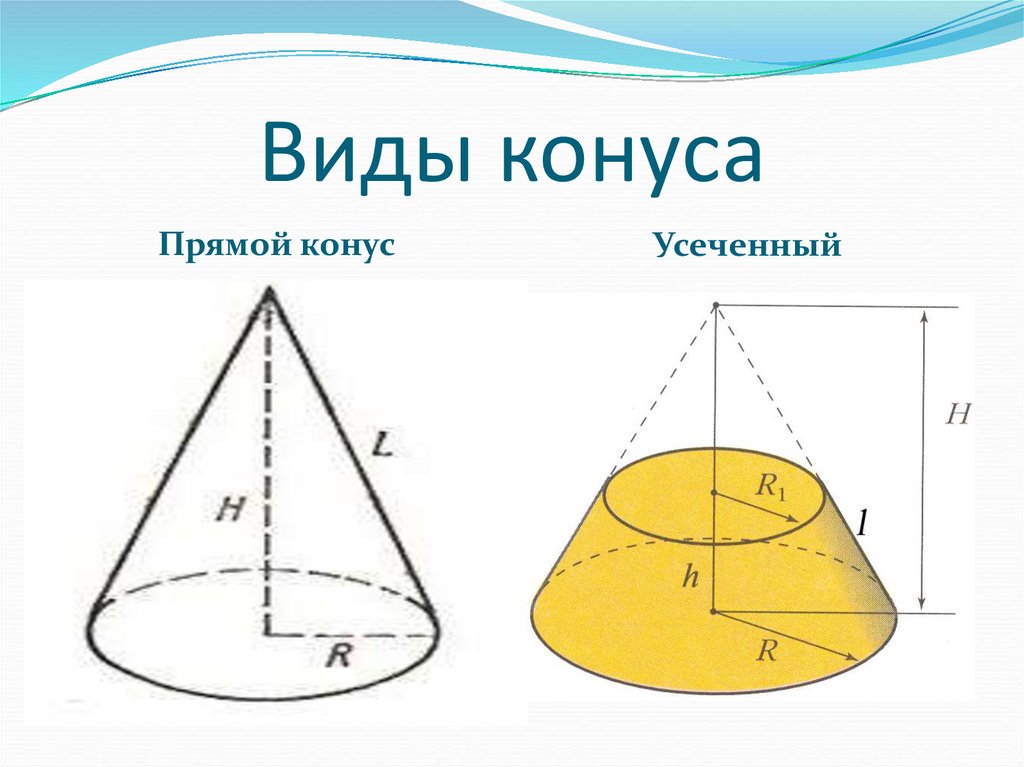 Рожок для мороженого, дорожный конус и кепка на день рождения — это лишь некоторые распространенные примеры формы конуса.
Рожок для мороженого, дорожный конус и кепка на день рождения — это лишь некоторые распространенные примеры формы конуса.
Несмотря на то, что конусы в изобилии присутствуют в нашей повседневной жизни, мы все еще не можем понять основы конусов в геометрии.
Чтобы помочь вам понять чудо шишек, мы подготовили руководство, которое познакомит вас со всеми основами. Давайте начнем!
Что такое конус в математике?
В математике конус определяется как отличительная трехмерная геометрическая фигура с плоской изогнутой поверхностью, направленной вверх. Термин «конус» происходит от греческого слова «конос», что означает клин или пик. Заостренный конец называется вершиной, а плоская поверхность называется основанием.
Три основных свойства конуса:
- Он имеет одну круглую грань.
- Не имеет ребер.
- Имеет одну вершину (угол).
Какие элементы конуса?
Тремя основными элементами конуса являются его радиус, высота и наклонная высота.
Радиус конуса
Радиус определяется как расстояние между центром круглого основания и любой точкой на окружности основания.
Высота конуса
Высота представляет собой расстояние от вершины конуса до центра круглого основания.
Наклонная высота конуса
Наклонная высота конуса — это расстояние от вершины конуса до точки на внешнем крае круглого основания. Формула для наклонной высоты получена с использованием теоремы Пифагора.
Здесь l — наклонная высота конуса, r — радиус, h — высота конуса.
Типы конусов
При изучении конусов в геометрии мы обычно рассматриваем правильный круг. Но конус может быть двух категорий, в зависимости от положения вершины на основании:
- Прямой круговой конус — это конус, вершина которого перпендикулярна основанию. Здесь ось образует прямой угол.
- Если положение вершины находится где-то за пределами центра основания, это наклонный конус. Здесь ось неперпендикулярна.

Несколько интересных фактов о конусах
1. Конус и пирамида связаны между собой. Формулы их площади поверхности также схожи!
2. Наши глаза имеют 6–7 миллионов колбочек, которые помогают им приспосабливаться к цветовой чувствительности.
Конус образован набором линий, которые соединяются с одной точкой, называемой вершиной.
Давайте изучим различные формулы, связанные с конусом, которые помогут вам решить некоторые интересные задачи в будущем.
Изогнутая поверхность конуса
Конус имеет как плоскую, так и изогнутую поверхность. Когда мы говорим о площади криволинейной поверхности конуса, это относится только к площади изогнутой части конуса, а не к круглому основанию.
Площадь криволинейной поверхности конуса определяется по формуле:
Площадь криволинейной поверхности = π ✕ r ✕ l квадратных единиц,
, где r = радиус основания конуса, l = наклонная высота конуса, и π = 3,14
Общая площадь поверхности конуса
Общая площадь поверхности конуса равна сумме площадей его круглого основания и криволинейной поверхности.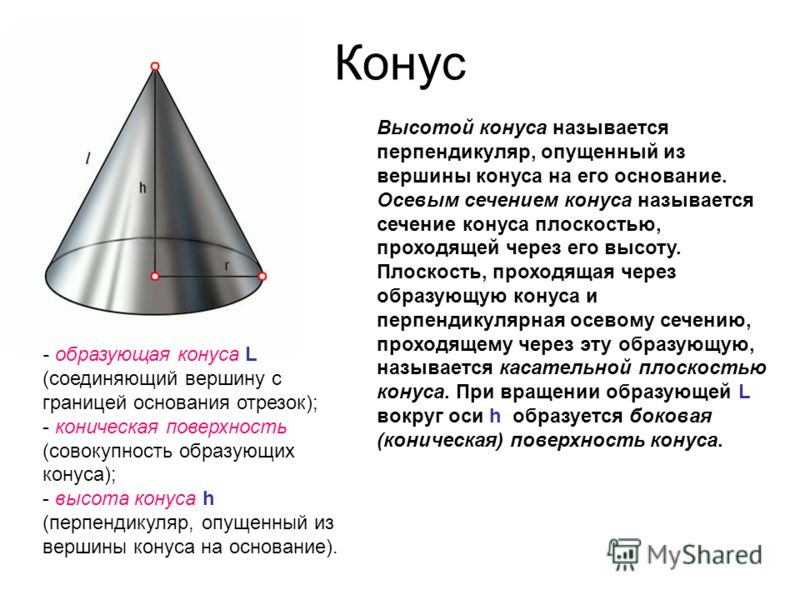
Площадь криволинейной поверхности конуса определяется по формуле:
Общая площадь поверхности = площадь криволинейной поверхности + площадь круглого основания
TSA = π ✕ r ✕ l + π ✕ r²
или TSA = π ✕ r ✕ (l + r) квадратных единиц.
Объем конуса
Объем конуса в геометрии — это количество пространства, которое занимает конус. Объем конуса также можно определить как вместимость жидкости, которую может удержать конус, если бы он был полым изнутри. Поскольку конус имеет круглое основание, мы можем легко рассчитать объем конуса, измерив радиус «r» и высоту «h».
V = $\frac{1}{3}$ ✕ (π ✕ r² ✕ h) кубическая единица.
Решенные примеры
Пример 1: Найдите объем конуса, где r = 5 см и h = 7 см.
Решение : Используя формулу объема конуса, получаем:
V = (1/3)πr² h
Здесь r = 5 см, h = 7 см
V= $ \frac{1}{3}$ ✕ 3,14 ✕ 5 ✕ 5 ✕ 7
= $\frac{1}{3}$ ✕ 549,5 = 183,16 см³
Пример 2. Рассчитайте площадь криволинейной поверхности конуса, где радиус основания 8 см, высота наклона 24 см.
Рассчитайте площадь криволинейной поверхности конуса, где радиус основания 8 см, высота наклона 24 см.
Решение . Площадь криволинейной поверхности конуса можно найти по формуле
Площадь криволинейной поверхности данного конуса = 3,14 ✕ 8 ✕ 24 = 602,88 см².
Пример 3. Если высота наклона конуса 25 см, а его радиус 7,5 см, найдите общую площадь поверхности конуса.
Решение :
Общая площадь поверхности конуса равна,
Общая площадь поверхности = π ✕ r ✕ (l + r)
Здесь r = 7,5 см, а l = 25 см.
Следовательно,
Общая площадь поверхности заданного конуса = 3,14 ✕ 7,5 ✕ (7,5 + 25)
= 23,55 ✕ (32,5)
= 765,37 см²
Практические задачи
1
Найдите объем. где радиус 8 см, а высота 13 см.
870,82 смА
335,54 смЧ нетерпением
840,54 смА
820,53 CM³
Правильный ответ: 870,82 CM³
, используя формулу для объема Cone, мы получаем:
V = (1/3) πr n).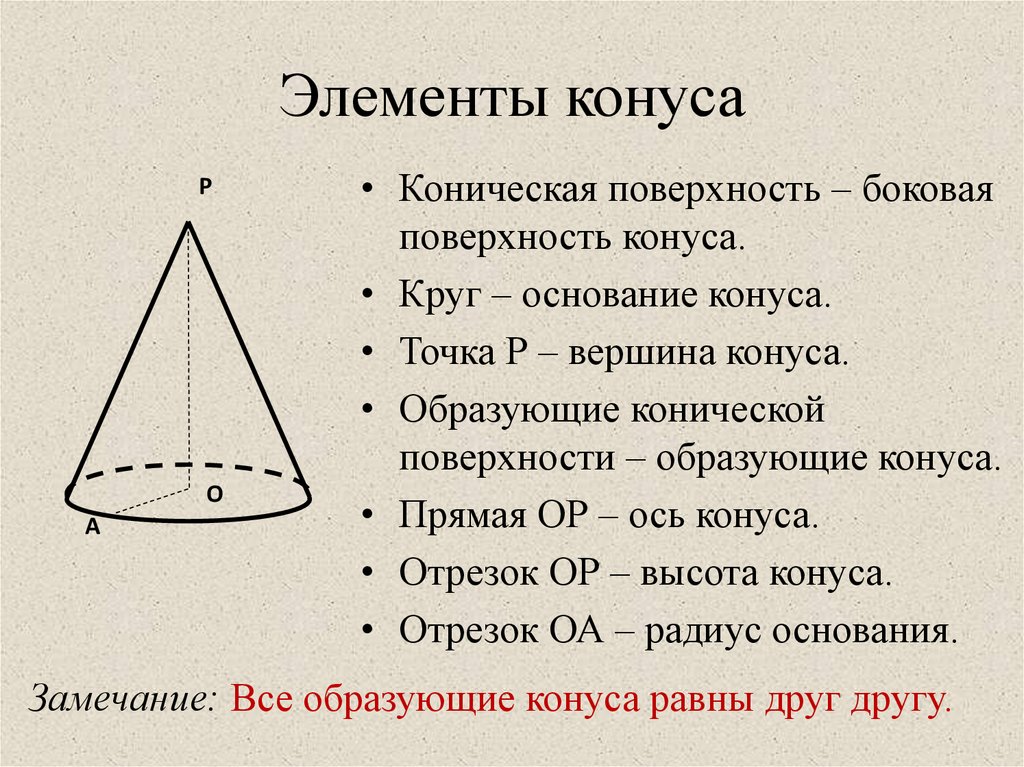 , r = 8 см, h = 13 см
, r = 8 см, h = 13 см
V= $\frac{1}{3}$ ✕ 3,14 ✕ 8 ✕ 8 ✕ 13
= $\frac{1}{3}$ ✕ 2612,48 = 870,82 см³
2
Наклонная высота конуса 21 см, радиус 12 см. Найдите полную площадь поверхности конуса.
1298,67 см²
13490,50 см²
1243,44 см²
1344,67 см²
Правильный ответ: 1243,44 см²
Общая площадь поверхности конуса определяется выражением
Общая площадь поверхности = π ✕ r = ✕ (l + r) 9004 12 см, а l = 21 см.
Следовательно,
Полная площадь поверхности данного конуса = 3,14 ✕ 12 ✕ (12 + 21)
= 37,68 ✕ 33
= 1243,44 см²
3
Найдите площадь криволинейной поверхности конуса, где r = 10 см высота 21см.
659,4 см²
782,4 см²
689 см²
679,6 см²
Правильный ответ: 659,4 см²
Площадь криволинейной поверхности конуса можно найти по формуле
Площадь криволинейной поверхности = π ✕ r ✕ l
l = 21 см
Следовательно,
площадь криволинейной поверхности данного конуса = 3,14 ✕ 10 ✕ 21 = 659,4 см².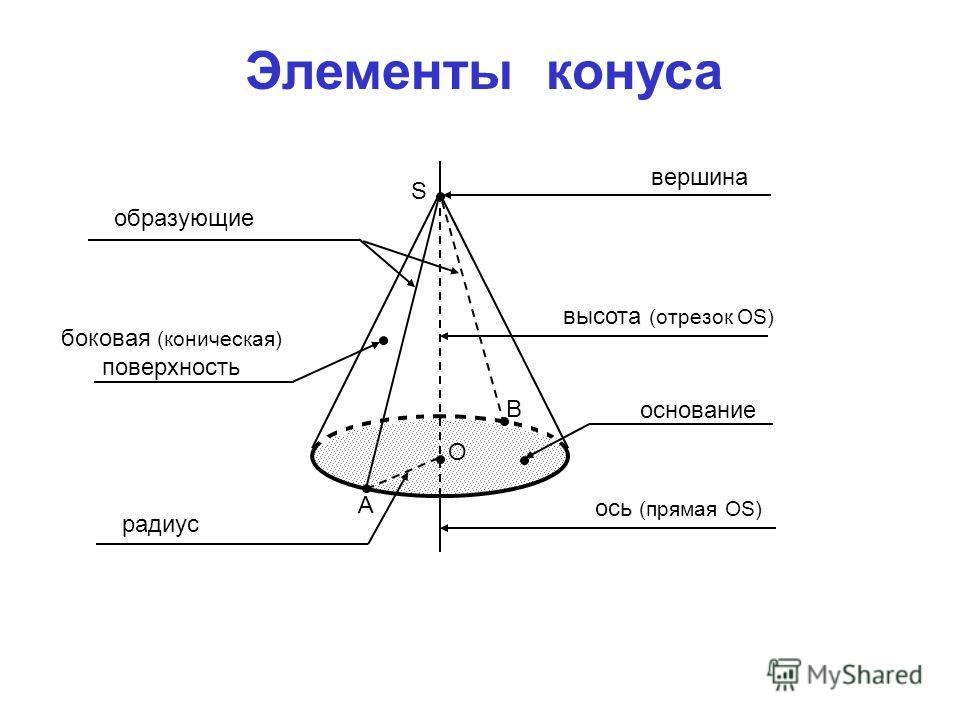

 Как Мэри может найти наклонную высоту шапочки на день рождения?
Как Мэри может найти наклонную высоту шапочки на день рождения? Подставив значение h = 3r, получим
Подставив значение h = 3r, получим