Задачи для самостоятельного решения

Задача
1. Идеальная
тепловая машина, работающая по циклу
Карно, получает за каждый цикл от
нагревателя 2500 Дж. Температура нагревателя
400 К, температура холодильника 300 К. Найти
работу, совершаемую машиной за один
цикл, и количество тепла, отданное
холодильнику за один цикл.

Ответ:
А
= 

= 630 Дж;
=
1880 Дж.

Задача
2. Идеальная
тепловая машина работает по циклу Карно.
Определить КПД цикла, если известно,
что за один цикл была произведена работа
3000 Дж и холодильнику передано 13,3 кДж
тепла.

Ответ:

= 18 %.

Задача
3. Идеальная
тепловая машина работающая по циклу
Карно, совершает за один цикл работу
7,35^.Дж.
Температура нагревателя 100⁰С,
температура холодильника 0 ⁰С.
Найти: 1) КПД машины; 2) количество тепла,
получаемое машиной за один цикл от
нагревателя; 3) количество тепла, отданное
за один цикл холодильнику.

Ответ:
1) 
= 26,8 %; 2)
=
2,74^. Дж;
3)=
2^.Дж.

Задача
4. Идеальная
тепловая машина, работающая по циклу
Карно, 80 % тепла, полученного от нагревателя,
передает холодильнику. Количество
тепла, полученное от нагревателя, равно
6,3 кДж. Найти: 1) КПД цикла; 2) работу,
совершенную при полном цикле.

Ответ:
1) 
= 20 %; 2) А
= 1,26 ^.Дж.

Задача
5. Цикл состоит
из двух изотерм и двух изобар,
= 600 К,= 300 К,.
Определить КПД цикла, если рабочим телом
служит один моль идеального газа, число
степеней свободы молекул которого равно
5.

Ответ:

= 0,221.

Задача
6. Холодильная
машина работает по обратному циклу
Карно в интервале температур
⁰С
и
=
3 ⁰С.
Рабочее тело — азот, масса которого т
= 0,2 кг. Найти количество тепла, отбираемого
от охлаждаемого тела, и работу внешних
сил за цикл, если степень сжатия
.

Ответ:
= 21,6 кДж;А
= 
2,4 кДж.

Задача
7. Определить
изменение энтропии одного моля идеального
газа в изобарном, изохорном и изотермическом
процессах.

Ответ:

Задача
8*. Какую
максимальную работу может произвести
тепловая машина, если в качестве
нагревателя используется кусок железа
массой 100 кг с начальной температурой
= 1500 К, а в качестве холодильника – вода
океана с температурой= 285 К? (С = 500).

Ответ:
А
= 4,5 ^.Дж.

Задача
9*. Идеальный
газ совершает цикл Карно. Температура
холодильника 290 К. Во сколько раз
увеличится КПД цикла, если температура
нагревателя повысится от 400 до 600 К?

Ответ:
в 1,88 раза.

Задача
10*. Идеальный
газ, расширяясь изотермически при
температуре Т
= 400 К, совершает работу А
= 800 Дж. Как изменится энтропия газа?

Ответ:
S
= 2
.

Задача
11. Во сколько
раз следует изотермически увеличить
объем газа в количестве 
= 4 моль, чтобы его энтропия изменилась
на S
= 23
?

Ответ:
в 2 раза.

Задача
12*. Один грамм
водорода первоначально имеет объем
V₁
= 200 л и давление р₁
= 500 Па.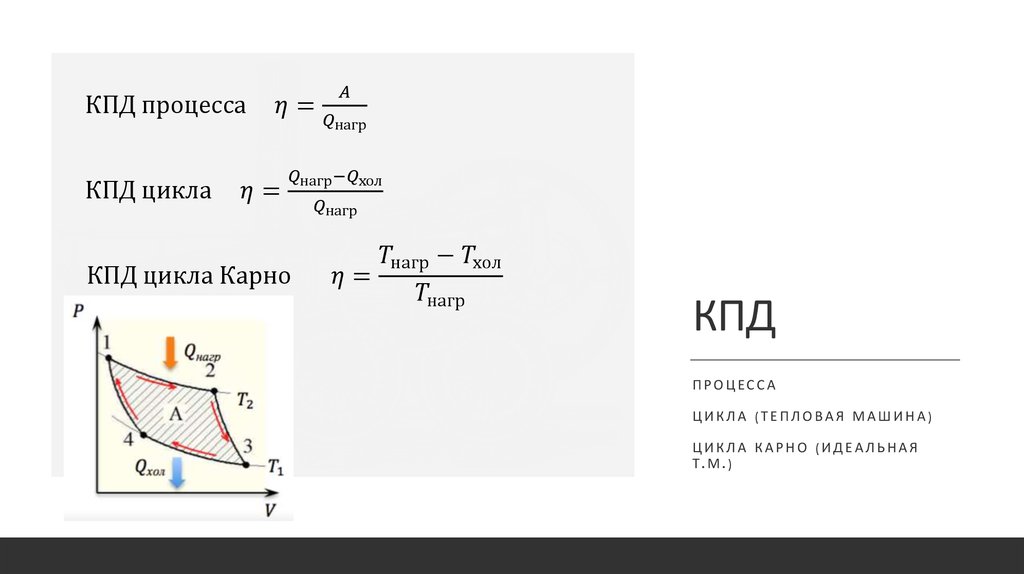 После расширения объем газа стал
V₂
= 500 л, а давление р₂
= 200 Па. Считая газ идеальным, определить:
а) приращение внутренней энергии
;
б) приращение энтропииS.

Ответ:
S
=3,8
;U
= 0.

Задача
13. Найти
изменение энтропии при переходе 6 г
водорода от объема V₁
= 20 л под давлением 1,5
Па к объемуV₂
= 40 л при температуре 300 ⁰С
при неизменном давлении.

Ответ:
S
=60,5
.

Задача
14. Найти
изменение энтропии при изобарическом
расширении 8 г гелия от объема V₁
= 10 л до объема V₂
= 25 л.

Ответ:
S
= 38,1
.

Задача
15. 10,5 г азота
изотермически расширяются от объема
V₁
= 2 л до объема V₂
= 5 л. Найти прирост энтропии в этом
процессе.

Ответ:
S
= 2,9
.

Задача
16. При
нагревании одного киломоля двухатомного
газа его абсолютная температура
увеличивается в 1,5 раза. Найти изменение
энтропии, если нагревание происходит:
1) изохорически; 2) изобарически.

Ответ:
1) S
= 8,5
;
2) S
= 11,8
.

Задача
17*. В результате
нагревания 22 г азота его абсолютная
температура увеличилась в 1,2 раза, а
энтропия увеличилась на 4,19
.
При каких условиях производилось
нагревание (при постоянном объеме или
при постоянном давлении)?

Ответ:
нагревание проводилось при постоянном
давлении.

Задача
18. Совершая
замкнутый цикл, газ получил от нагревателя
теплоту Q
= 4,19 кДж. Какую работу совершил газ в
результате всего цикла, если термический
КПД цикла 
= 0,1?

Ответ:
А
= 
= 419 Дж.

Задача
19. Один моль
идеального двухатомного газа совершает
цикл, состоящий из двух изохор и двух
изобар. Наименьший объем V_min
= 10 л, наибольший объем V_max=
20 л, наименьшее давление p_min
= 2,46 атм, наибольшее давление p_max
= 4,1 атм.
Начертить график цикла, в координатах
р,
V
определить температуру газа для
характерных точек цикла и его термический
КПД.

Ответ:
300 К; 500 К; 1000 К; 605 К; 
= 8,55 %.

Задача
20. Один
киломоль двухатомного идеального газа
совершает замкнутый цикл, график которого
изображен на рис. 22.18. Определить: 1)
теплоту, полученную от нагревателя; 2)
теплоту, переданную холодильнику; 3)
работу, совершаемую газом за цикл; 4)
термический КПД цикла.

Ответ:
1)
= 7,61Дж; 2)= 7,21 ·Дж; 3)А
= 0,4
Дж; 4)
= 5,3 %.

Задача
21. Один моль
идеального двухатомного газа, находящийся
под давлением р₁
= 1 атм при температуре
= 27⁰С,
нагревают при постоянном объеме до
давления р₂
= 2 атм. После этого газ расширился
изотермически до начального давления
и затем был изобарически сжат до
начального объема V₁.
Начертить график процесса в координатах
р,
V;
р,
т;
V,
Т. Определить температуру газа для
характерных точек цикла и его термический
КПД.

Ответ:
600
К,
= 9,9 %.

Задача
22. Одноатомный
газ 0,1 кмоль, имевший при давлении
р₁
= 10⁵
Па объем V₁
= 5 м³,
сжимался изобарически до объема V₂
= 1 м³,
затем сжимался адиабатически и, наконец,
расширялся при постоянной температуре
до начального объема и давления. Построить
график процесса в координатах р,
V.
Найти: 1) температуру, объем и давление
для характерных точек цикла; 2) теплоту,
полученную газом от нагревателя; 3)
теплоту, переданную газом холодильнику;
4) работу, совершенную за весь цикл; 5)
термический КПД цикла.

Ответ:
= 600 К;= 120 К;V₃
= 0,09 м³;
Па;= 600 К;Дж;Дж;А
=
Дж;
= 50 %.

Задача
23. Идеальный
многоатомный газ совершает цикл,
состоящий из двух изохор и двух изобар,
причем наибольшее давление газа в два
раза больше наименьшего, а наибольший
объем в 4 раза больше наименьшего.
Определить термодинамический КПД цикла.

Ответ:

= 0,11.

Задача
24. Газ,
совершающий цикл Карно,
теплоты,
полученной от нагревателя, отдает
холодильнику. Температура холодильника
0⁰С.
Определить температуру нагревателя.

Ответ:
= 409 К.

Задача
25. Газ
совершает цикл Карно. Температура
холодильника
= 17⁰С.
Во сколько раз увеличится КПД цикла,
если температура нагревателя повысится
от
= 127⁰С
до
= 347⁰С?

Ответ:
1,93 раза.

Задача
26. Газ
совершает цикл Карно. Абсолютная
температура нагревателя в три раза
выше, чем температура холодильника.
Нагреватель передал газу теплоту
=
10 ккал. Какую работу совершил газ?

Ответ:
А
= 2,81
Дж.

Задача
27. Газ
совершает цикл Карно. Абсолютная
температура
нагревателя в 4 раза выше абсолютной
температурыхолодильника. Какую долю теплоты,
получаемой за один цикл от нагревателя,
газ отдает холодильнику.

Ответ:

Задача
28. Газ,
совершающий цикл Карно, за счет каждой
килокалории теплоты, полученной от
нагревателя, совершает работу А
= 598 Дж. Каков КПД этого цикла? Во сколько
раз абсолютная температура
нагревателя больше абсолютной температурыхолодильника?

Ответ:

= 14,3 %;
.

Задача
29. Газ
совершает цикл Карно. Работа изотермического
расширения
= 5 Дж. Определить работу изотермического
сжатия, если термический КПД цикла
= 0,2.

Ответ:
А =
4 Дж.

Задача
30. Наименьший
объем газа, совершающего цикл Карно,
V₁=
153 л. Определить наибольший объем V₃,
если объем газа в конце изотермического
расширения V₂
= 189 л, а в конце изотермического сжатия
V₄
= 600 л.

Ответ:
V₃
= 0,74 м³.

Задача
31. Смешано
= 5 кг воды при температуре= 10⁰С
с
= 8 кг воды при температуре= 80⁰С.
Найти: 1) температуру смеси; 2) изменение
энтропии, происходящее при смешивании.

Ответ:
t
= 53 ⁰С;
S
=296
.

Задача
32. В результате
изохорического нагревания водорода
массой т
= 1 г давление газа увеличилось в два
раза. Определить изменение энтропии
газа.

Ответ:
S
= 7,2
.

Задача
33. Найти
изменение энтропии при изобарическом
расширении азота массой т
= 4 г от объема V₁
= 5 л до объема V₂
= 9 л.

Ответ:
S
= 2,43
.

Задача
34. Кусок льда
массой т
= 200 г, взятый при температуре
=
10 ⁰С,
был нагрет до
= 0⁰С
и расплавлен, после чего образовавшаяся
вода была нагрета до температуры
=
10⁰С.
Определить изменение энтропии льда.

Ответ:
S
= 291
.

Задача
35. Кислород
массой т
= 2 кг увеличил свой объем в 5 раз, один
раз – изотермически при температуре
= 10⁰С,
другой раз – изотермически при температуре
= 100⁰С,
третий раз – адиабатически. Каково
будет изменение энтропии в этих трех
случаях?

Ответ:
;S
= 0.

Задача
36. Водород
массой т
= 100 г был изобарически нагрет так, что
его объем увеличился в 3 раза, а затем
водород был изохорически охлажден так,
что давление его уменьшилось в три раза.
Найти изменение энтропии.

Ответ:
= 457.

Задача
37. Идеальный
двухатомный газ, занимающий объем V₁
= 2 л, подвергли адиабатному расширению.
При этом его объем возрос в 5 раз. Затем
газ подвергли изобарному сжатию до
начального объема. В результате изохорного
нагревания он был возвращен в первоначальное
состояние. Постройте график цикла и
определите термический КПД цикла.

Ответ:

= 34,1%.

Задача
38. Идеальный
двухатомный газ (
= 3 моль), занимающий объем V₁
= 5 л и находящийся под давлением р₁
= 1 МПа, подвергли изохорному нагреванию
до Т₂
= 500 К. После этого газ подвергли
изотермическому расширению до начального
давления, а затем он в результате
изобарного сжатия возвращен в
первоначальное состояние. Постройте
график цикла и определите термический
КПД цикла.

Ответ:

= 13,3%.

Задача
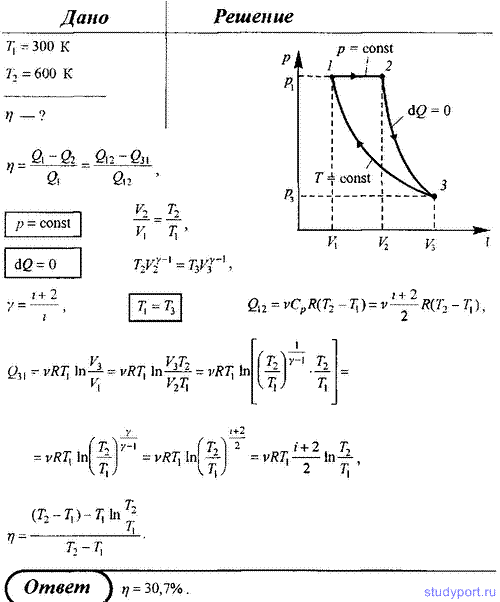
39. Рабочее
тело – идеальный газ – теплового
двигателя совершает цикл, состоящий из
последовательных процессов: изобарного,
адиабатного и изотермического. В
результате изобарного процесса газ
нагревается от Т₁
= 300 К до Т₂
= 600 К. Определите термический КПД
теплового двигателя.

Ответ:

= 30,7%.

Задача
40. Азот массой
500 г находящийся под давлением р₁
= 1 МПа при температуре t₁
= 127 С,
подвергли изотермическому расширению,
в результате которого давление газа
уменьшилось в п
= 3 раза. После этого газ подвергли
адиабатному сжатию до начального
давления, а затем он был изобарно сжат
до начального объема. Постройте график
цикла и определите работу, совершенную
газом за цикл.

Ответ:
А
= -11,5 кДж.

Задача
41. Идеальный
газ, совершающий цикл Карно, 70% количества
теплоты, полученного от нагревателя,
отдает холодильнику. Количество теплоты,
получаемое от нагревателя, равно 5 кДж.
Определите: 1) термический КПД цикла; 2)
работу, совершенную при полном цикле.

Ответ:
1) 
= 30%; 2) А
= 1,5 кДж.

Задача
42. Идеальный
газ совершает цикл Карно. Температура
нагревателя
Т₁
= 500 К, холодильника Т₂
= 300 К. Работа изотермического расширения
газа составляет 2 кДж. Определите: 1)
термический КПД цикла; 2) количество
теплоты, отданное газом при изотермическом
сжатии холодильнику.

Ответ:
1)
= 40%, 2) Q₂
= 1,2 кДж.

Задача
43. Многоатомный
идеальный газ совершает цикл Карно, при
этом в процессе адиабатного расширения
объем газа увеличивается в п
= 4 раза. Определите термический КПД
цикла.

Ответ:

= 37 %.

Задача
44. Во сколько
раз необходимо увеличить объем (
= 5 моль) идеального газа при изотермическом
расширении, если его энтропия увеличилась
на S
= 57,6
?

Ответ:

Задача
45. При
нагревании двухатомного идеального
газа (
= 2 моль) его термодинамическая температура
увеличилась в п
= 2 раза. Определите изменение энтропии,
если нагревание происходит: 1) изохорно;
2) изобарно.

Ответ:
1) S₁
= 28,8
;
2)S₂
= 40,3
.

Задача
46. Идеальный
газ (
= 2 моль) сначала изобарно нагрели, так
что объем газа увеличился в
п₁
= 2 раза, а затем изохорно охладили, так
что давление его уменьшилось в п₂
= 2 раза. Определите приращение энтропии
в ходе указанных процессов.

Ответ:
S
= 11,5
.

Задача
47. Азот массой
28 г адиабатно расширили в п
= 2 раза, а затем изобарно сжали до
начального объема. Определите изменение
энтропии газа в ходе указанных процессов.

Ответ:
S
= -20,2
.

газ совершает цикл карно

Второй закон термодинамики (обновлено 05.07.2014)

Глава 5: Второй закон термодинамики (обновлено 05.07.2014)

В этой главе мы рассмотрим более абстрактный подход
нагревать циклы двигателя, холодильника и теплового насоса, пытаясь
определить, выполнимы ли они, и получить предельный максимум
производительность, доступная для этих циклов. Понятие механического и
термообратимость занимает центральное место в анализе, что приводит к
идеальные циклы Карно. (См. Википедию: Сади
Карно французский физик, математик
и инженер, который первым успешно описал тепловые двигатели,
цикл Карно и заложил основы второго закона
термодинамика). Для получения дополнительной информации об этом
тему, см. документ: A
Встреча Роберта Стирлинга и Сади Карно в 1824 году
представлен на выставке 2014
МЭК .

Мы представляем тепловой двигатель и цикл теплового насоса в
минималистский абстрактный формат, как на следующих диаграммах. В обоих
корпусов два температурных резервуара Т _Н и
Т _Л , с Т _Х >
Т _Л .

В случае теплового двигателя тепло Q _H извлекается из высокотемпературного источника T _H ,
часть этого тепла превращается в работу W, совершаемую над окружающей средой,
а остальное отбрасывается в низкотемпературную мойку T _L .
Обратное происходит с тепловым насосом, в котором работа W совершается на
система для извлечения тепла Q _L из
низкотемпературный источник Т _Л и
«закачать» его в высокотемпературную раковину T _H .
Обратите внимание, что толщина линии представляет собой количество тепла.
или переданная рабочая энергия.

Теперь мы представляем два утверждения второго закона
Термодинамика, первая о тепловой машине, а вторая
по поводу теплового насоса. Ни одно из этих утверждений не может быть доказано,
однако никогда не наблюдалось нарушений.

Заявление Кельвина-Планка: Оно
невозможно построить устройство, работающее по циклу и
не производит никакого другого эффекта, кроме передачи тепла от одного тела
для того, чтобы произвести работу.

Мы предпочитаем менее формальное описание этого оператора
с точки зрения лодки, извлекающей тепло из океана для производства
его требуемая двигательная работа:

Заявление Клаузиуса: Оно
невозможно построить устройство, работающее по циклу и
не производит никакого другого эффекта, кроме передачи тепла от более холодного тела
к более горячему телу.

Эквивалентность Клаузиуса и Кельвина-Планка
Выписки

Примечательно, что два вышеуказанных утверждения
Второй закон фактически эквивалентен. Для демонстрации своих
эквивалентности рассмотрим следующую диаграмму. Слева мы видим тепло
насос, который нарушает утверждение Клаузиуса, перекачивая теплоту Q _L из низкотемпературного резервуара в высокотемпературный
температурный резервуар без каких-либо затрат труда. Справа мы видим
тепловой двигатель, отводящий тепло Q _L в
низкотемпературный резервуар.

Если мы теперь соединим два устройства, как показано ниже, то
что теплота, отводимая тепловой машиной Q _L , равна
просто закачивается обратно в высокотемпературный резервуар, тогда
отсутствие необходимости в низкотемпературном резервуаре, что приводит к
двигатель, который нарушает утверждение Кельвина-Планка, отбирая тепло
от одного источника тепла и преобразования его непосредственно в работу.

Механическая и термическая обратимость

Обратите внимание, что утверждения о втором законе
отрицательные утверждения в том, что они описывают только то, что невозможно
достигать. Чтобы определить максимальную производительность, доступную от
тепловая машина или тепловой насос нам необходимо ввести понятие
Реверсивность ,
включая механическую и термическую обратимость. мы попробуем
пояснить эти понятия на следующем примере
реверсивный поршневой цилиндр, находящийся в тепловом равновесии с
окружающей среды при температуре T ₀ и
подвергается циклическому процессу сжатия/расширения.

Для механической обратимости мы предполагаем, что
процесс без трения, однако мы также требуем, чтобы процесс
квазиравновесный. На диаграмме мы видим, что во время
при сжатии частицы газа, находящиеся ближе всего к поршню, будут
более высокое давление, чем те, которые находятся дальше, поэтому поршень будет
делать больше работы по сжатию, чем если бы мы ждали
условия равновесия, возникающие после каждого дополнительного шага.
Точно так же термическая обратимость требует, чтобы вся теплопередача
изотермический. Таким образом, если происходит постепенное повышение температуры из-за
к сжатию, то нужно дождаться установления теплового равновесия
учредил. При расширении постепенное падение температуры
приведет к передаче тепла из окрестности по
систему до тех пор, пока не установится равновесие.

Итак, есть три условия, необходимые для
реверсивный режим:

• Все механические
  процессы без трения.

• При каждом приращении
  шаг в процессе условия теплового и барического равновесия
  учредил.

• Все процессы теплопередачи являются изотермическими.

Теорема Карно

Теорема Карно, также известная как правило Карно, или
Принцип Карно можно сформулировать следующим образом:

Тепловая машина не работает между двумя
резервуары могут быть более эффективными, чем обратимая тепловая машина
работающий между одними и теми же двумя резервуарами.

Самый простой способ доказать эту теорему — рассмотреть
сценарий, показанный ниже, в котором у нас есть необратимый двигатель как
а также реверсивный двигатель, работающий между резервуарами Т _Н и Т _L , однако
необратимая тепловая машина имеет более высокий КПД, чем обратимая
один. Оба они получают одинаковое количество тепла Q _H от
высокотемпературный резервуар, однако необратимый двигатель
производит больше работы W _I , чем
реверсивный двигатель W _R .

Обратите внимание, что реверсивный двигатель по своей природе может
работать в обратном порядке, т. е. если мы используем часть выхода работы (W _R )
от нереверсивного двигателя для привода реверсивного двигателя
то он будет работать как тепловой насос, передавая тепло Q _H в высокотемпературный резервуар, как показано на
следующая диаграмма:

Обратите внимание, что высокотемпературный резервуар становится
избыточны, и в итоге мы получаем чистое количество тепла (Q _LR — Q _LI ) из
температурный резервуар для производства чистого количества работы (W _I — W _R ) — метод Кельвина-Планка
нарушитель — тем самым доказывая теорему Карно.

Следствие 1 теоремы Карно:

Можно сформулировать первое следствие теоремы Карно
следующим образом:

Все реверсивные тепловые двигатели действующие
между теми же двумя тепловыми резервуарами должны иметь одинаковую эффективность.

Таким образом, независимо от типа тепловой машины,
рабочее тело или любой другой фактор, если тепловая машина обратима,
то он должен иметь такой же максимальный КПД. Если это не тот
случае, то мы можем управлять реверсивным двигателем с нижней
КПД как тепловой насос, а нарушитель Кельвина-Планка как
выше.

Следствие 2 теоремы Карно:

Второе следствие теоремы Карно может быть
заявлено следующим образом:

Эффективность реверсивного теплогенератора
двигатель является функцией только соответствующих температур горячего
и холодные резервуары. Его можно оценить, заменив отношение
Трансферные передачи тепла Q _L и Q _H по отношению к температурам T _L и T _H 9003 of _H 9003 of _H и T _H
соответствующие тепловые резервуары.

Таким образом, используя это следствие, мы можем оценить тепловую
КПД обратимой тепловой машины:

Обратите внимание, что мы всегда переходим в «режим медитации».
до замены отношения теплоты отношением абсолютных
температуры, что справедливо только для реверсивных машин.
Простейшим концептуальным примером обратимой тепловой машины является машина Карно.
цикла двигателя, как показано на следующей диаграмме:

Совершенно непрактичный двигатель, который не может
реализоваться на практике, поскольку для каждого из четырех процессов в
цикл окружающей среды должен быть изменен с изотермического
к адиабатическому. Более практический пример — идеальный цикл Стирлинга.
двигатель, как показано на следующей схеме:

Этот двигатель имеет поршень для сжатия и
работы по расширению, а также вытеснитель для перемещения рабочей
газа между горячим и холодным пространством, и было описано ранее в
Глава 3b .
Отметим, что при одинаковых условиях температуры и сжатия
отношение идеальный двигатель Карно имеет такой же КПД, однако
значительно меньшая полезная производительность за цикл, чем у Ideal Stirling
цикла двигателя, как легко увидеть на следующей диаграмме:

Когда реверсивный двигатель работает в обратном направлении,
становится тепловым насосом или холодильником. Коэффициент производительности
из этих машин разработано следующее:

__________________________________________________________________________

Решено
Задача 5.1 — Реверсивный домашний воздух
Кондиционер и горячая вода
Подогреватель
_____________________________________________________________

Проблема 5.2 — Тепловой насос
используется для удовлетворения потребностей в отоплении дома и поддержания его
при 20°С. В день, когда температура наружного воздуха опускается до -10°C
подсчитано, что дом теряет тепло в размере 10 кВт.
В этих условиях фактический коэффициент полезного действия (COP _HP )
теплового насоса 2,5.

• а) Нарисуйте схему
  представляющая систему теплового насоса, показывающую поток энергии и
  температуры и определить:

• б) фактическая мощность
  потребляется тепловым насосом [4
  кВт]

• в) сила, которая
  будет потребляться обратимым
  тепловой насос в этих условиях [1,02
  кВт]

• г) сила, которая
  будет потребляться электрическим нагревателем сопротивления при этих
  условия [10 кВт]

• e) Сравнение реального теплового насоса с
  обратимый тепловой насос определить, если производительность фактического тепла
  насос возможен,

Вывести все используемые уравнения, начиная с основного
значение
КС _лс .
__________________________________________________________________________

Проблема 5.3 — Во время
эксперимент, проведенный в старшей лаборатории при 25 ° C, студент измерил, что
холодильник с циклом Стирлинга, который потребляет 250 Вт энергии, удален
1000кДж тепла от охлаждаемого помещения, поддерживаемого при -30°С.
время работы холодильника во время эксперимента составляло 20 мин.
Нарисуйте схему, представляющую холодильную систему, показывающую поток
энергии и температуры, и определить, являются ли эти измерения
разумны [COPR
= 3,33, COPR, об.
= 4,42, соотношение COPR/COPR, об.
= 75% > 60% — нет
достижимый]. Укажите причины вашего
выводы. Получить все
уравнения, используемые, начиная с основного определения коэффициента
производительности холодильника
(КС _Р ).
__________________________________________________________________________

К главе 6:
Энтропия — новое свойство

__________________________________________________________________________________________

Инженерная термодинамика Израиля
Уриэли находится под лицензией Creative
Commons Attribution-Noncommercial-Share Alike 3.0 США
Лицензия

Применение термодинамики: тепловые насосы и холодильники

Цели обучения

К концу этого раздела вы сможете:

• Описывать использование тепловых двигателей в тепловых насосах и холодильниках.
• Продемонстрируйте, как работает тепловой насос для обогрева внутренних помещений.
• Объясните разницу между тепловыми насосами и холодильниками.
• Рассчитайте коэффициент полезного действия теплового насоса.

Рисунок 1. Почти в каждом доме есть холодильник. Большинство людей не осознают, что они также делят свои дома с тепловым насосом. (кредит: Id1337x, Викисклад)

Тепловые насосы, кондиционеры и холодильники используют передачу тепла от холодного к горячему. Это тепловые двигатели, работающие в обратном направлении. Мы говорим «назад», а не «назад», потому что, за исключением двигателей Карно, все тепловые машины, хотя и могут работать в обратном направлении, на самом деле не могут быть реверсированы. Теплопередача происходит из холодного резервуара Q _c в горячий. Для этого требуется затрата работы Вт , которая также преобразуется в теплопередачу. Таким образом, теплоотдача к горячему резервуару равна Q _h  =  Q _c  +  W . (Обратите внимание, что Q _h , Q _c и W положительны, и их направления указаны на схемах, а не знаком.) Тепловой насос предназначен для передачи тепла Q _h происходить в теплой среде, например, в доме зимой. Q _c Задача кондиционеров и холодильников заключается в передаче тепла из прохладной среды, например, при охлаждении помещения или хранении продуктов при более низких температурах, чем окружающая среда. (На самом деле тепловой насос можно использовать как для обогрева, так и для охлаждения помещения. По сути, это кондиционер и обогреватель в одном лице. В этом разделе мы сосредоточимся на его режиме обогрева.)

Рисунок 2. Тепловые насосы, кондиционеры и холодильники — это тепловые двигатели, работающие в обратном направлении. Показанный здесь основан на двигателе Карно (реверсивном). (а) Схематическая диаграмма, показывающая передачу тепла от холодного резервуара к теплому резервуару с тепловым насосом. Направления W , Q _h и Q _c противоположны тому, что было бы в тепловой машине. (b) диаграмма для цикла Карно, аналогичная диаграмме на рисунке 3, но перевернутая, по пути ADCBA. Площадь внутри цикла отрицательна, что означает наличие сетевого входа. Есть теплопередача Q _c в систему из холодного резервуара по пути DC, а теплообмен Q _h из системы в горячий резервуар по пути BA.

Тепловые насосы

Большим преимуществом использования теплового насоса для обогрева дома, а не просто сжигания топлива, является то, что тепловой насос обеспечивает Q _ч  =  Q _c  +  Вт . Теплопередача происходит от наружного воздуха, даже при минусовой температуре, во внутреннее пространство. Вы платите только за W , и вы получаете дополнительную теплоотдачу Q _c снаружи без затрат; во многих случаях в отапливаемое помещение передается как минимум в два раза больше энергии, чем используется для работы теплового насоса.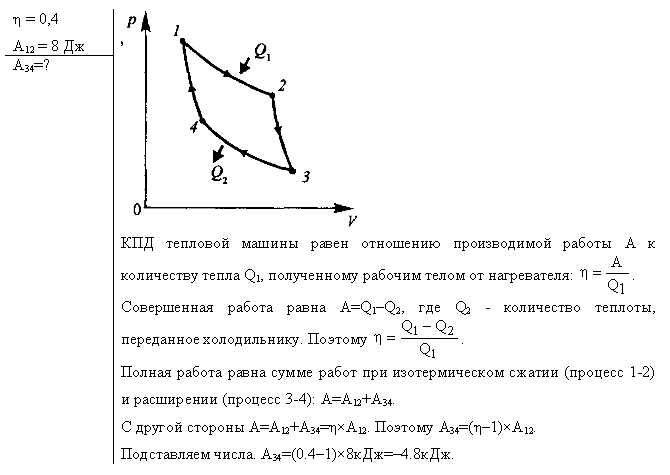 Когда вы сжигаете топливо, чтобы согреться, вы платите за все это. Недостатком является то, что ввод работы (требуемый вторым законом термодинамики) иногда дороже, чем простое сжигание топлива, особенно если работа выполняется за счет электроэнергии.

Основные компоненты теплового насоса в режиме обогрева показаны на рис. 3. В качестве рабочей жидкости используется хладагент, не содержащий хлорфторуглеродов. В наружных змеевиках (испарителях) теплообмен Q _c поступает в рабочую жидкость из холодного наружного воздуха, превращая ее в газ.

Рис. 3. Простой тепловой насос состоит из четырех основных компонентов: (1) конденсатор, (2) расширительный клапан, (3) испаритель и (4) компрессор. В режиме обогрева теплообмен Q _c происходит к рабочему телу в испарителе (3) от более холодного наружного воздуха, превращая его в газ. Компрессор с электрическим приводом (4) повышает температуру и давление газа и нагнетает его в змеевики конденсатора (1) внутри отапливаемого помещения. Поскольку температура газа выше температуры в помещении, теплопередача от газа в помещение происходит по мере того, как газ конденсируется в жидкость. Затем рабочая жидкость охлаждается, возвращаясь через расширительный клапан (2) к змеевикам наружного испарителя.

Компрессор с электрическим приводом (рабочая мощность Вт ) повышает температуру и давление газа и нагнетает его в змеевики конденсатора, находящиеся внутри отапливаемого помещения. Поскольку температура газа выше температуры внутри помещения, происходит передача тепла в помещение, и газ конденсируется в жидкость. Затем жидкость возвращается через редукционный клапан к наружным змеевикам испарителя, охлаждаясь за счет расширения. (В цикле охлаждения змеевики испарителя и конденсатора меняются ролями, и направление потока жидкости меняется на противоположное.)

О качестве теплового насоса судят по тому, сколько тепла Q _ч передается в теплое помещение по сравнению с тем, сколько работы требуется Вт .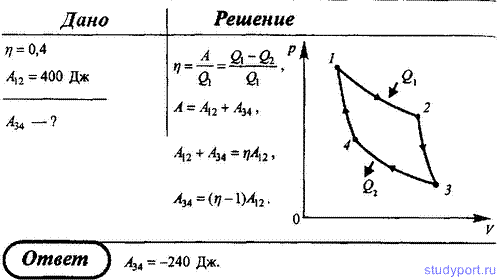 В соответствии с отношением того, что вы получаете, к тому, что вы тратите, мы определяем коэффициент полезного действия теплового насоса ( COP _л.с. ) как [latex]COP _ {\ text {hp}} = \ frac {Q_{\text{h}}}{W}\\[/латекс].

Поскольку КПД тепловой машины равен [латекс]Eff=\frac{W}{Q_{\text{h}}}\\[/latex], мы видим, что [latex]COP_{\text{hp} }=\frac{1}{Eff}\\[/latex], важный и интересный факт. Во-первых, поскольку КПД любой тепловой машины меньше 1, это означает, что COP _л.с.  всегда больше 1, то есть теплопередача теплового насоса Q _ч всегда больше, чем затраченная на него работа. Во-вторых, это означает, что тепловые насосы лучше всего работают при небольшой разнице температур. Эффективность идеальной машины Карно равна [латекс]Eff_{\text{C}}=1-\left(\frac{T_{\text{c}}}{T_{\text{h}}} \справа)\\[/латекс]; таким образом, чем меньше разница температур, тем меньше КПД и больше КПД _л.с.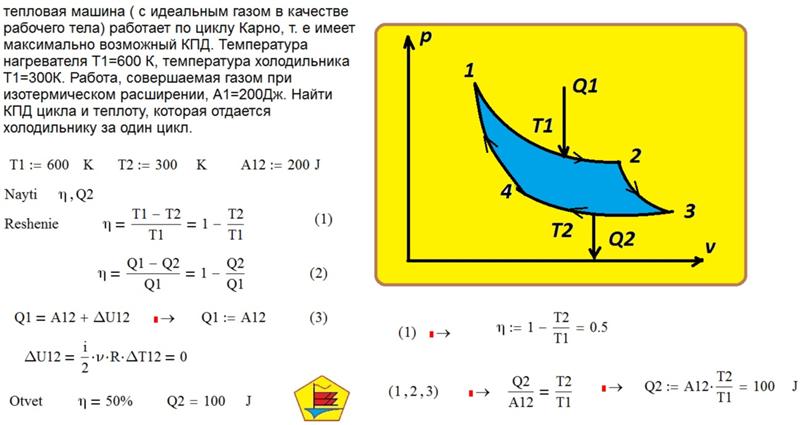  (поскольку [латекс]КПД _{\текст{л.с.}}=\frac{1}{Эфф}\\[/латекс] ). Другими словами, тепловые насосы не так хорошо работают в очень холодном климате, как в более умеренном климате.

Трение и другие необратимые процессы снижают КПД теплового двигателя, но они , а не приносят пользу работе теплового насоса — вместо этого они уменьшают подводимую работу, преобразовывая часть ее в теплопередачу обратно в холодный резервуар до того, как она попадет в тепловой насос.

Рис. 4. Когда реальная тепловая машина работает в обратном направлении, часть предполагаемой подводимой работы ( Вт ) уходит на теплопередачу до того, как она попадет в тепловую машину, тем самым снижая ее коэффициент полезного действия. На этом рисунке W ′ представляет собой часть W , которая поступает в тепловой насос, а оставшаяся часть W теряется в виде теплоты трения ( Q _f ) в холодный резервуар. Если бы все Вт пошли в тепловой насос, то Q _ч было бы больше. В лучшем тепловом насосе используются адиабатические и изотермические процессы, так как в теории не было бы диссипативных процессов, снижающих теплоотдачу к горячему резервуару.

Пример 1. Лучший [латекс]COP_{\text{hp}}\\[/latex] теплового насоса для домашнего использования

Тепловой насос, используемый для обогрева дома, должен использовать цикл, который производит рабочую жидкость при температурах выше, чем типичная температура в помещении, чтобы могла происходить теплопередача внутрь. Точно так же он должен производить рабочую жидкость при температурах ниже температуры наружного воздуха, чтобы теплопередача происходила извне. Следовательно, температура его горячего и холодного пласта не может быть слишком близкой, что ограничивает его КС _лс . (См. рис. 5.) Каков наилучший возможный коэффициент полезного действия для такого теплового насоса, если он имеет температуру горячего резервуара 45,0ºC и температуру холодного резервуара −15,0ºC?

Стратегия

Перевернутый двигатель Карно обеспечивает наилучшую возможную производительность теплового насоса. Как отмечалось выше, [latex]COP_{\text{hp}}=\frac{1}{Eff}\\[/latex], поэтому для решения этой задачи нам нужно сначала вычислить эффективность Карно.

Раствор

Эффективность Карно по абсолютной температуре определяется как:

[латекс]Eff _{\text{C}}=1-\frac{T_{\text{c}}}{T_{\text{h}}} \\[/латекс].

Температуры в кельвинах равны T _h  = 318 K и T _c  = 258 K, так что

[латекс]Eff_{\text{C}}=1-\frac{258 text{K}}{318\text{K}}=0,1887\\[/latex].

Таким образом, из обсуждения выше,

[латекс]COP_{\text{hp}}=\frac{1}{Eff}=\frac{1}{0,1887}=5,30\\[/latex], или [латекс]COP_{\text{hp}}=\frac{Q_{\text{h}}}{W}=\frac{1}{0,1887}=5,30\\[/latex] , так что Q _ч = 5,30 Вт.

Обсуждение

Этот результат означает, что теплопередача тепловым насосом в 5,30 раз больше затраченной на него работы. Такая же теплопередача электрическим комнатным обогревателем обошлась бы в 5,30 раза дороже, чем теплопередача, производимая этим тепловым насосом. Это не нарушение закона сохранения энергии. Холодный окружающий воздух обеспечивает 4,3 Дж на 1 Дж работы от электрической розетки.

Рис. 5. В тепловом насосе из приведенного выше примера происходит передача тепла снаружи внутрь вместе с работой, необходимой для запуска насоса. Обратите внимание, что температура холода, создаваемая тепловым насосом, ниже температуры наружного воздуха, поэтому происходит передача тепла в рабочую жидкость. Компрессор насоса создает температуру выше температуры в помещении, чтобы происходила передача тепла в дом.

Рисунок 6. В жаркую погоду происходит передача тепла от воздуха внутри помещения к воздуху снаружи, охлаждая помещение. В прохладную погоду происходит передача тепла от воздуха снаружи к воздуху внутри, нагревая помещение. Это переключение достигается реверсированием направления потока рабочей жидкости.

Реальные тепловые насосы работают не так хорошо, как идеальный насос в предыдущем примере; их значения КПД _{л. с.}  колеблются примерно от 2 до 4. Этот диапазон означает, что теплопередача Q _h от тепловых насосов в 2-4 раза больше, чем затраченная на них работа W . Однако их экономическая целесообразность по-прежнему ограничена, поскольку Вт обычно снабжаются электрической энергией, которая стоит больше в пересчете на джоуль, чем теплопередача при сжигании топлива, такого как природный газ. Кроме того, первоначальная стоимость теплового насоса выше, чем у многих печей, поэтому тепловой насос должен прослужить дольше, чтобы его стоимость окупилась. Тепловые насосы, скорее всего, будут экономически выгоднее там, где зимние температуры мягкие, электричество относительно дешевое, а другие виды топлива относительно дорогие. Кроме того, поскольку они могут как охлаждать, так и обогревать помещение, они имеют преимущества там, где желательно охлаждение в летние месяцы. Таким образом, одними из лучших мест для тепловых насосов являются районы с теплым летним климатом и прохладной зимой. На рис. 6 показан тепловой насос, называемый « обратный цикл» или « охладитель сплит-системы» в некоторых странах.

Кондиционеры и холодильники

Кондиционеры и холодильники предназначены для охлаждения чего-либо в теплой среде. Как и в случае с тепловыми насосами, для передачи тепла от холодного к горячему требуется затрата труда, а это дорого. О качестве кондиционеров и холодильников судят по тому, сколько тепла Q _c происходит от холодной среды по сравнению с тем, сколько работы W требуется. То, что считается преимуществом в тепловом насосе, считается отходящим теплом в холодильнике. Таким образом, мы определяем коэффициент полезного действия ( COP _ref ) кондиционера или холодильника как

[латекс] {COP} _ {\ text {ref}} = \ frac {Q _ {\ text { c}}}{W}\\[/латекс].

Еще раз отметив, что Q _h = Q _c + W , мы можем увидеть, что кондиционер будет иметь более низкий коэффициент полезного действия, чем тепловой насос, потому что [латекс]{COP}_ {\text{hp}}=\frac{Q_{\text{h}}}{W}\\[/latex] и Q _h больше Q _c . В задачах и упражнениях этого модуля вы покажете, что COP _ref = COP _л.с.  − 1 для теплового двигателя, используемого либо в качестве кондиционера, либо в качестве теплового насоса, работающего между двумя одинаковыми температурами. Настоящие кондиционеры и холодильники, как правило, работают на удивление хорошо, имея значения COP _ref в диапазоне от 2 до 6. Эти числа лучше, чем 9.0293 COP _л.с.  значения для тепловых насосов, упомянутых выше, потому что разница температур меньше, но они меньше, чем у двигателей Карно, работающих между теми же двумя температурами.

Разработан тип рейтинговой системы COP , называемый «рейтинг энергоэффективности» ( EER ). Этот рейтинг является примером того, как единицы, не входящие в систему СИ, все еще используются и актуальны для потребителей. Чтобы облегчить задачу потребителю, Австралия, Канада, Новая Зеландия и США используют рейтинг Energy Star Rating из 5 звезд — чем больше звезд, тем более энергоэффективно устройство. EER s выражаются в смешанных единицах британских тепловых единиц (БТЕ) ​​в час нагрева или охлаждения, разделенных на потребляемую мощность в ваттах. Комнатные кондиционеры легко доступны с EER в диапазоне от 6 до 12. Хотя это не то же самое, что только что описанные COP , эти EER хороши для целей сравнения — чем больше EER , тем дешевле кондиционер должен работать (но тем выше, вероятно, будет его закупочная цена).

EER кондиционера или холодильника можно представить как

[латекс]\displaystyle{EER}=\frac{\frac{Q _{\text{c}}}{t_1}}{\frac{W}{ t_2}}\\[/latex],

где Q _c — количество теплоотдачи от холодной среды в британских тепловых единицах, t ₁ — время в часах, W — вложенная работа в джоулях, а t ₂ — время в секундах.

Стратегии решения задач по термодинамике

1. Изучите ситуацию, чтобы определить, что происходит: теплота, работа или внутренняя энергия . Найдите любую систему, в которой основными способами передачи энергии являются тепло и работа. Примерами таких систем являются тепловые двигатели, тепловые насосы, холодильники и кондиционеры.
2. Определите интересующую вас систему и начертите диаграмму системы, показывающую поток энергии.
3. Точно определить, что необходимо определить в задаче (определить неизвестные) . Письменный список полезен. Максимальная эффективность означает, что задействован двигатель Карно. Эффективность не то же самое, что коэффициент полезного действия.
4. Составьте список того, что дано или может быть выведено из поставленной задачи (укажите известное). Обязательно отличайте теплопередачу в систему от теплопередачи из системы, а также работу, вводимую от работы. Во многих ситуациях полезно определить тип процесса, например изотермический или адиабатический.
5. Решите соответствующее уравнение для определяемой величины (неизвестной).
6. Подставьте известные величины вместе с их единицами измерения в соответствующее уравнение и получите численное решение с единицами измерения.
7. Проверьте ответ, чтобы убедиться, что он разумен: Имеет ли он смысл? Например, эффективность всегда меньше 1, тогда как коэффициенты полезного действия больше 1.

Резюме раздела

• Артефакт второго закона термодинамики — способность нагревать внутреннее пространство с помощью теплового насоса. Тепловые насосы сжимают холодный окружающий воздух и при этом нагревают его до комнатной температуры без нарушения принципов сохранения.
• Для расчета коэффициента полезного действия теплового насоса используйте уравнение [латекс]{\текст{COP}}_{\text{hp}}=\frac{{Q}_{\text{h}}}{W} \\[/латекс].
• Холодильник — это тепловой насос; он берет теплый окружающий воздух и расширяет его, чтобы охладить.

Концептуальные вопросы

1. Объясните, почему тепловые насосы не так хорошо работают в очень холодном климате, как в более мягком. То же самое относится и к холодильникам?
2. В некоторых странах Северной Европы дома строятся без каких-либо систем отопления. Они очень хорошо изолированы и согреваются теплом тел жильцов. Однако, когда жильцов нет дома, в этих домах все равно тепло. Каково возможное объяснение?
3. Почему холодильники, кондиционеры и тепловые насосы работают наиболее рентабельно для циклов с небольшой разницей между T _h и T _c ? (Обратите внимание, что температура используемого цикла имеет решающее значение для его COP .)
4. Менеджеры продовольственных магазинов утверждают, что общее потребление энергии летом меньше, если в магазине поддерживается низкая температура. Приведите аргументы в поддержку или опровержение этого утверждения, принимая во внимание, что в магазине имеется множество холодильников и морозильников.
5. Можно ли охладить кухню, оставив дверцу холодильника открытой?

Задачи и упражнения

1. Каков коэффициент полезного действия идеального теплового насоса, передающего тепло от холодной температуры -25,0ºC до горячей температуры 40,0ºC?
2. Предположим, у вас есть идеальный холодильник, который охлаждает окружающую среду при температуре -20,0ºC и передает тепло в другую среду при температуре 50,0ºC. Каков его коэффициент полезного действия?
3. Каков наилучший возможный коэффициент полезного действия для гипотетического холодильника, который может производить жидкий азот при температуре -200ºC и передавать тепло в окружающую среду при температуре 35,0ºC?
4. В условиях очень мягкого зимнего климата тепловой насос передает тепло от окружающей среды с температурой 5,00°C к окружающей среде с температурой 35,0°C. Каков наилучший возможный коэффициент полезного действия для этих температур? Подробно покажите, как вы выполняете шаги, описанные в разделе «Стратегии решения проблем в термодинамике».
5. (a) Каков наилучший коэффициент полезного действия для теплового насоса с температурой горячего резервуара 50,0ºC и температурой холодного резервуара −20,0ºC? (b) Сколько тепла передается в теплую среду, если 3,60 × 10 ⁷ Дж работы (10,0 кВт·ч) вложено в него? (c) Если стоимость этой подводимой работы составляет 10,0 центов/кВт · ч, как ее стоимость соотносится с прямой передачей тепла, достигаемой путем сжигания природного газа при стоимости 85,0 центов за тепло. (Терм — это обычная единица энергии природного газа, равная 1,055 × 10 ⁸ Дж.)
6. (a) Каков наилучший коэффициент полезного действия для холодильника, который охлаждает окружающую среду при температуре −30,0 ºC и передает тепло в другую среду при температуре 45,0 ºC? (b) Какую работу в джоулях необходимо совершить для передачи тепла 4186 кДж из холодной среды? (c) Какова стоимость выполнения этого, если работа стоит 10,0 центов за 3,60 × 10 ⁶ Дж (киловатт-час)? (d) Сколько кДж тепла передается в теплую среду? (e) Обсудите, какой тип холодильника может работать при этих температурах.
7. Предположим, вы хотите, чтобы в идеальном холодильнике работала холодная температура −10,0ºC, и вы хотели бы, чтобы его коэффициент полезного действия был равен 7,00. Какова температура горячего резервуара для такого холодильника?
8. Рассматривается идеальный тепловой насос для обогрева помещений с температурой 22,0ºC. Какова температура холодного резервуара, если насос должен иметь коэффициент полезного действия 12,0?
9. 4-тонный кондиционер удаляет 5,06 × 10 ⁷ Дж (48 000 британских тепловых единиц) из холодной среды за 1,00 ч. (a) Какая энергия в джоулях необходима для этого, если кондиционер имеет рейтинг энергоэффективности ( EER ) 12,0? (b) Какова стоимость выполнения этого, если работа стоит 10,0 центов за 3,60 × 10 ⁶ Дж (один киловатт-час)? (c) Обсудите, кажутся ли эти затраты реалистичными. Обратите внимание, что рейтинг энергоэффективности ( EER ) кондиционера или холодильника определяется как количество британских тепловых единиц теплопередачи из холодной среды в час, деленное на потребляемую мощность в ваттах.
10. Покажите, что коэффициенты полезного действия холодильников и тепловых насосов связаны соотношением COP _ref = COP _{л.с. ч , Q c и W .}

Глоссарий

тепловой насос:  машина, обеспечивающая передачу тепла от холодного к горячему

КПД:  для теплового насоса – это отношение теплопередачи на выходе (горячий резервуар) к подводимой работе; для холодильника или кондиционера это отношение теплопередачи от резервуара холода к произведенной работе

Избранные решения задач и упражнений

1.