Емкость конденсаторов: определение, формулы, примеры.

Определение 1

Конденсатор – это совокупность двух любых проводников, заряды которых одинаковы по значению и противоположны по знаку.

Его конфигурация говорит о том, что поле, созданное зарядами, локализовано между обкладками. Тогда можно записать формулу электроемкости конденсатора:

C=qφ1-φ2=qU.

Значением φ1-φ2=U обозначают разность потенциалов, называемую напряжением, то есть U. По определению емкость положительна. Она зависит только от размерностей обкладок конденсатора их взаиморасположения и диэлектрика. Ее форма и место должны минимизировать воздействие внешнего поля на внутреннее. Силовые линии конденсатора начинаются на проводнике с положительным зарядом, а заканчиваются с отрицательным. Конденсатор может являться проводником, помещенным в полость, окруженным замкнутой оболочкой.

Выделяют три большие группы: плоские, сферические, цилиндрические. Чтобы найти емкость, необходимо обратиться к определению напряжения конденсатора с известными значениями зарядов на обкладках.

Плоский конденсатор

Определение 2

Плоский конденсатор – это две противоположно заряженные пластины, которые разделены тонким слоем диэлектрика, как показано на рисунке 1.

Формула для расчета электроемкости записывается как

C=εε0Sd, где S является площадью обкладки, d – расстоянием между ними, ε — диэлектрической проницаемостью вещества. Меньшее значение d способствует большему совпадению расчетной емкости конденсатора с реальной.

Рисунок 1

При известной электроемкости конденсатора, заполненного N слоями диэлектрика, толщина слоя с номером i равняется di, вычисление диэлектрической проницаемости этого слоя εi выполняется, исходя из формулы:

C=ε0Sd1ε1+d2ε2+…+dNεN.

Сферический конденсатор

Определение 3

Когда проводник имеет форму шара или сферы, тогда внешняя замкнутая оболочка является концентрической сферой, это означает, что конденсатор сферический.

Он состоит из двух концентрических проводящих сферических поверхностей с пространством между обкладками, заполненным диэлектриком, как показано на рисунке 2. Емкость рассчитывается по формуле:

C=4πεε0R1R2R2-R1, где R1 и R2 являются радиусами обкладок.

Рисунок 2

Цилиндрический конденсатор

Емкость цилиндрического конденсатора равняется:

C=2πεε0llnR2R1, где l — высота цилиндров, R1 и R2 — радиусы обкладок. Данный вид конденсатора имеет две соосные поверхности проводящих цилиндрических поверхности, как показано на рисунке 3.

Рисунок 3

Определение 4

Важной характеристикой конденсаторов считается пробивное напряжение — напряжение, при котором происходит электрический разряд через слой диэлектрика.

Umax находится от зависимости от толщины слоя и свойств диэлектрика, конфигурации конденсатора.

Электроемкость плоского конденсатора. Формулы

Кроме отдельных конденсаторов используются их соединения. Наличие параллельного соединения конденсаторов применяют для увеличения его емкости. Тогда поиск результирующей емкости соединения сводится к записи суммы Ci, где Ci- это емкость конденсатора с номером i:

C=∑i=1NCi.

При последовательном соединении конденсаторов суммарная емкость соединения всегда будет по значению меньше, чем минимальная любого конденсатора, входящего в систему. Для расчета результирующей емкости следует сложить величины, обратные к емкостям отдельных конденсаторов:

Пример 1

Произвести вычисление емкости плоского конденсатора при известной площади обкладок
1 см2 с расстоянием между ними 1 мм. Пространство между обкладками находится в вакууме.

Решение

Чтобы рассчитать электроемкость конденсатора, применяется формула:

C=εε0Sd.

Значения:

ε=1, ε0=8,85·10-12 Фм;S=1 см2=10-4 м2;d=1 мм=10-3 м.

Подставим числовые выражения и вычислим:

C=8,85·10-12·10-410-3=8,85·10-13 (Ф).

Ответ: C≈0,9 пФ.

Пример 2

Найти напряженность электростатического поля у сферического конденсатора на расстоянии x=1 см=10-2 м от поверхности внутренней обкладки при внутреннем радиусе обкладки, равном R1=1 см=10-2 м, внешнем – R2=3 см=3·10-2 м. Значение напряжения — 103 В.

Решение

Производящая заряженная сфера создает напряженность поля. Его значение вычисляется по формуле:

E=14πεε0qr2, где q обозначают заряд внутренней сферы, r=R1+x — расстояние от центра сферы.

Нахождение заряда предполагает применение определения емкости конденсатора С:

q=CU.

Для сферического конденсатора предусмотрена формула вида

C=4πεε0R1R2R2-R1 с радиусами обкладок R1 и R2.

Производим подстановку выражений для получения искомой напряженности:

E=14πεε0U(x+R1)24πεε0R1R2R2-R1=U(x+R1)2R1R2R2-R1.

Данные представлены в системе СИ, поэтому достаточно заменить буквы числовыми выражениями:

E=103(1+1)2·10-4·10-2·3·10-23·10-2-10-2=3·10-18·10-6=3,45·104 Вм.

Ответ: E=3,45·104 Вм.

Решение задач

от 1 дня / от 150 р.

Курсовая работа

от 5 дней / от 1800 р.

Реферат

от 1 дня / от 700 р.

Автор:
Роман Адамчук

Преподаватель физики

По какой формуле найти ёмкость (объем) конденсаторов

Содержание

• 1 Расчёт конденсаторов
  • 1. 1 Расчет плоской конструкции
  • 1.2 Расчет конструкции цилиндрической формы
  • 1.3 Расчёт сферической конструкции
  • 1.4 Ёмкость одиночного проводника
• 2 Способы соединения элементов
  • 2.1 Параллельное соединение
  • 2.2 Последовательное соединение
  • 2.3 Смешанное соединение
• 3 Видео

Во всех электронных устройствах используются конденсаторы. При их конструировании или изготовлении своими руками параметры устройств рассчитываются по специальным формулам.

Конденсаторы

Расчёт конденсаторов

Один из главных параметров таких устройств – ёмкость. Рассчитать её можно по следующей формуле:

C=q/U, где:

• C – ёмкость,
• q – заряд одной из обкладок элемента,
• U – разность потенциалов между обкладками.

В электротехнике вместо понятия «разность потенциалов между обкладками» используется «напряжение на конденсаторе».

Ёмкость элемента не зависит от конструкции и размеров устройства, а только от напряжения на нём и заряда обкладок. Но эти параметры могут изменяться в зависимости от расстояния между ними и материала диэлектрика. Это учитывается в формуле:

С=Co*ε, где:

• С – реальная ёмкость,
• Со – идеальная, при условии, что между пластинами вакуум или воздух,
• ε – диэлектрическая проницаемость материала между ними.

Например, если в качестве диэлектрика используется слюда, «ε» которой 6, то ёмкость такого устройства в 6 раз больше, чем воздушного, а при изменении количества диэлектрика меняются параметры конструкции. На этом принципе основана работа ёмкостного датчика положения.

Устройство конденсатора

Единицей ёмкости в системе СИ является 1 фарад (F). Это большая величина, поэтому чаще применяются микрофарады (1000000mkF=1F) и пикофарады (1000000pF=1mkF).

Расчет плоской конструкции

Если нужно рассчитать плоский конденсатор, то необходимо учесть площадь обкладок и расстояние между ними. Это отражено в формуле, по которой рассчитывается ёмкость плоского конденсатора:

C=ε/d, где:

• ε – диэлектрическая проницаемость изолирующего материала,
• d – расстояние между пластинами.

Расчет конструкции цилиндрической формы

Цилиндрический конденсатор – это две соосные трубки различного диаметра, вставленные друг в друга. Между ними находится диэлектрик. При радиусе цилиндров, близком друг к другу и намного большем, чем расстояние между ними, цилиндрической формой можно пренебречь и свести расчёт к формуле, аналогичной той, по которой рассчитывается плоский конденсатор.

Вычисляются параметры такого устройства по формуле:

C=(2π*l*R*ε)/d, где:

• l – длина устройства,
• R – радиус цилиндра,
• ε – диэлектрическая проницаемость изолятора,
• d – его толщина.

Расчёт сферической конструкции

Есть устройства, обкладки которых представляют собой два шара, вложенные друг в друга. Формула ёмкости такого прибора:

C=(4π*l*R1*R2*ε)/(R2-R1), где:

• R1 – радиус внутренней сферы,
• R2 – радиус внешней сферы,
• ε – диэлектрическая проницаемость.

Формулы ёмкости конденсаторов различной формы

Ёмкость одиночного проводника

Кроме конденсаторов, способностью накапливать заряд обладают отдельные проводники. Одиночным проводником считается такой проводник, который бесконечно далёк от других проводников. Параметры заряженного элемента рассчитывается по формуле:

C=Q/φ, где:

• Q – заряд,
• φ – потенциал проводника.

Объём заряда определяется размером и формой устройства, а также окружающей средой. Материал прибора значения не имеет.

Способы соединения элементов

Что измеряется в фарадах

Не всегда есть в наличии элементы с необходимыми параметрами. Приходится соединять их различными способами.

Соединение конденсаторов

Параллельное соединение

Это такое соединение деталей, при котором к одной клемме или контакту присоединяются первые обкладки каждого конденсатора. При этом вторые обкладки присоединяются к другой клемме.

При таком соединении напряжение на контактах всех элементов будет одинаковым. Заряд каждого из них происходит независимо от остальных, поэтому общая ёмкость равна сумме всех величин. Её находят по формуле:

C=C1+C2+…Cn,

где C1-Cn – параметры деталей, участвующих в параллельном соединении.

Важно! Конденсаторы имеют предельное допустимое напряжение, превышение которого приведёт к выходу элемента из строя. При параллельном соединении устройств с различным допустимым напряжением этот параметр получившейся сборки равен элементу с наименьшим значением.

Последовательное соединение

Это такое соединение, при котором к клемме присоединяется только одна пластина первого элемента. Вторая пластина присоединяется к первой пластине второго элемента, вторая пластина второго – к первой пластине третьего и так далее. Ко второй клемме присоединяется только вторая обкладка последнего элемента.

При таком соединении заряд на обкладках конденсатора в каждом приборе будет равен остальным, однако напряжение на них будет разным: для зарядки устройств большей ёмкости тем же зарядом требуется меньшая разность потенциалов. Поэтому вся цепочка представляет собой одну конструкцию, разность потенциалов которой равна сумме напряжений на всех элементах, а заряд конденсатора равен сумме зарядов.

Последовательное соединение увеличивает допустимое напряжение и уменьшает общую ёмкость, которая меньше самого меньшего элемента.

Рассчитываются эти параметры следующим образом:

• Допустимое напряжение:

Uобщ=U1+U2+U3+…Un, где U1-Un – напряжение на конденсаторе;

• Общая ёмкость:

1/Собщ=1/С1+1/С2+1/С3+…1/Сn, где С1-Сn – параметры каждого устройства.

Интересно. Если в цепи только два элемента, то можно воспользоваться упрощённой формулой: Собщ=(С1*С2)/(С1+С2).

Смешанное соединение

Это такое соединение, в котором есть детали, соединённые последовательно, и есть соединённые параллельно. Параметры всей цепи рассчитывается в следующей последовательности:

1. определяются группы элементов, соединённые параллельно;
2. для каждой группы в отдельности рассчитывается эквивалентные значения;
3. рядом с каждой группой параллельно соединённых деталей пишутся получившиеся величины;
4. получившаяся схема эквивалентна последовательной схеме и рассчитывается по соответствующим формулам.

Знание формул, по которым можно найти емкость при изготовлении конденсаторов или их соединении необходимо при конструировании электронных схем.

Видео

Оцените статью:

8.1 Конденсаторы и емкость — Университетская физика, том 2

Цели обучения

К концу этого раздела вы сможете:

• Объяснить понятия конденсатора и его емкости
• Опишите, как оценить емкость системы проводников

Конденсатор — это устройство, используемое для хранения электрического заряда и электрической энергии. Конденсаторы обычно имеют два электрических проводника, разделенных расстоянием. (Обратите внимание, что такие электрические проводники иногда называют «электродами», но правильнее было бы назвать их «пластинами конденсатора».) Пространство между конденсаторами может быть просто вакуумом, и в этом случае конденсатор называется «вакуумный конденсатор». Однако это пространство обычно заполнено изоляционным материалом, известным как диэлектрик. (Вы узнаете больше о диэлектриках в разделах, посвященных диэлектрикам, далее в этой главе.) Объем памяти в конденсаторе определяется свойством, называемым емкость , о которой вы узнаете подробнее чуть позже в этом разделе.

Применение конденсаторов варьируется от фильтрации статического электричества от радиоприема до накопления энергии в сердечных дефибрилляторах. Как правило, коммерческие конденсаторы имеют две проводящие части, расположенные близко друг к другу, но не соприкасающиеся, как показано на рис. 8.2. В большинстве случаев между двумя пластинами используется диэлектрик. Когда клеммы батареи подключены к изначально незаряженному конденсатору, потенциал батареи перемещает небольшое количество заряда величиной 9.0013 Q от положительной пластины к отрицательной. Конденсатор в целом остается нейтральным, но с зарядами +Q+Q и -Q-Q, расположенными на противоположных пластинах.

Рисунок
8.2

Оба конденсатора, показанные здесь, были изначально разряжены перед подключением к батарее. Теперь у них на пластинах есть заряды +Q+Q и −Q−Q (соответственно). (a) Конденсатор с плоскими пластинами состоит из двух пластин противоположного заряда площадью A , разделенных расстоянием d . (b) Скрученный конденсатор имеет диэлектрический материал между двумя проводящими листами (пластинами).

Система, состоящая из двух одинаковых пластин с параллельными проводниками, разделенных расстоянием, называется конденсатором с параллельными пластинами (рис. 8.3). Величина электрического поля в пространстве между параллельными пластинами равна E=σ/ε0E=σ/ε0, где σσ — поверхностная плотность заряда на одной пластине (напомним, что σσ — заряд Ом , приходящийся на площадь поверхности А). ). Таким образом, величина поля прямо пропорциональна Q .

Рисунок
8.3

Разделение зарядов в конденсаторе показывает, что заряды остаются на поверхности пластин конденсатора.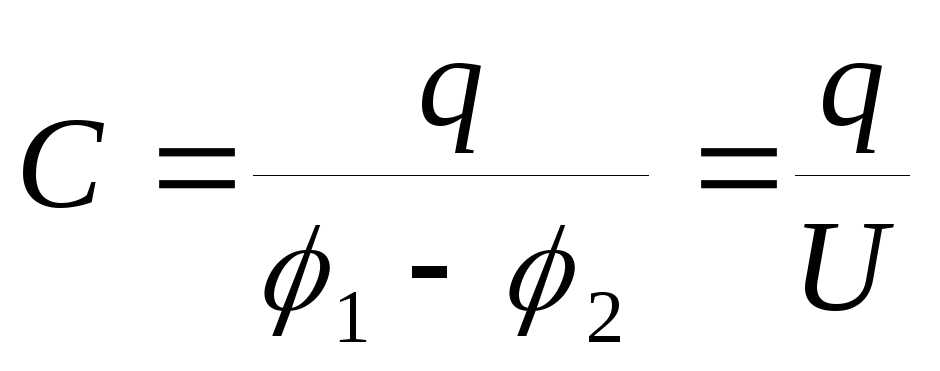 Линии электрического поля в конденсаторе с плоскими пластинами начинаются с положительных зарядов и заканчиваются отрицательными зарядами. Величина электрического поля в пространстве между пластинами прямо пропорциональна количеству заряда на конденсаторе.

Конденсаторы с разными физическими характеристиками (такими как форма и размер их пластин) сохраняют разное количество заряда при одном и том же приложенном на их пластинах напряжении В . Емкость C конденсатора определяется как отношение максимального заряда Q , который может храниться в конденсаторе, к приложенному напряжению В на его обкладках. Другими словами, емкость — это наибольшее количество заряда на вольт, которое может храниться на устройстве:

C=QV.C=QV.

8.1

Единицей измерения емкости в системе СИ является фарад (Ф), названный в честь Майкла Фарадея (1791–1867). Поскольку емкость — это заряд на единицу напряжения, один фарад равен одному кулону на один вольт, или

1F=1C1V.1F=1C1V.

По определению, конденсатор емкостью 1,0 Ф способен накапливать 1,0 Кл заряда (очень большой заряд), когда разность потенциалов между его пластинами составляет всего 1,0 В. Таким образом, один фарад — это очень большая емкость. Типичные значения емкости находятся в диапазоне от пикофарад (1 пФ = 10–12 Ф) (1 пФ = 10–12 Ф) до миллифарад (1 мФ = 10–3 Ф) (1 мФ = 10–3 Ф), включая микрофарад (1 мкФ = 10–6 Ф1 мкФ = 10–10–3). 6Ф). Конденсаторы могут изготавливаться различных форм и размеров (рис. 8.4).

Рисунок
8.4

Это некоторые типичные конденсаторы, используемые в электронных устройствах. Размер конденсатора не обязательно связан со значением его емкости. (кредит: Windell Oskay)

Расчет емкости

Мы можем рассчитать емкость пары проводников с помощью следующего стандартного подхода.

Стратегия решения проблем

Расчет емкости

1. Предположим, что конденсатор имеет заряд Q .
2. Определите электрическое поле E→E→ между проводниками. Если в расположении проводников присутствует симметрия, вы можете использовать закон Гаусса для этого расчета.
3. Найдите разность потенциалов между проводниками из

   VB-VA=-∫ABE→·dl→, VB-VA=-∫ABE→·dl→,

   8,2

   где путь интегрирования ведет от одного проводника к другому. Тогда величина разности потенциалов равна V=|VB-VA|V=|VB-VA|.

4. С В известно, получите емкость непосредственно из уравнения 8.1.

Чтобы показать, как работает эта процедура, мы рассчитаем емкости пластинчатых, сферических и цилиндрических конденсаторов. Во всех случаях мы предполагаем вакуумные конденсаторы (пустые конденсаторы) без диэлектрического вещества в пространстве между проводниками.

Конденсатор с параллельными пластинами

Конденсатор с плоскими пластинами (рис. 8.5) имеет две одинаковые проводящие пластины, каждая из которых имеет площадь поверхности А , разделенные расстоянием d . Когда к конденсатору прикладывается напряжение В , он накапливает заряд Q , как показано на рисунке. Мы можем видеть, как его емкость может зависеть от A и d , рассматривая характеристики кулоновской силы. Мы знаем, что сила между зарядами увеличивается с увеличением заряда и уменьшается с расстоянием между ними. Следует ожидать, что чем больше пластины, тем больше заряда они могут хранить. Таким образом, C должно быть больше для большего значения А . Точно так же, чем ближе пластины друг к другу, тем сильнее притяжение к ним противоположных зарядов. Следовательно, C должно быть больше для меньшего d .

Рисунок
8,5

В конденсаторе с плоскими пластинами, пластины которого расположены на расстоянии d , каждая пластина имеет одинаковую площадь поверхности A .

Определим поверхностную плотность заряда σσ на пластинах как

σ=QA.σ=QA.

Мы знаем из предыдущих глав, что когда d мало, электрическое поле между пластинами довольно однородно (без учета краевых эффектов) и его величина определяется выражением

E=σε0,E=σε0,

, где константа ε0ε0 — диэлектрическая проницаемость свободного пространства, ε0=8,85×10−12F/м.ε0=8,85×10−12F/м. Единица СИ Ф/м эквивалентна C2/N·m2.C2/N·m2. Поскольку электрическое поле E→E→ между пластинами однородно, разность потенциалов между пластинами равна

V=Ed=σdε0=Qdε0A.V=Ed=σdε0=Qdε0A.

Следовательно, уравнение 8.1 дает емкость плоского конденсатора как

C=QV=QQd/ε0A=ε0Ad.C=QV=QQd/ε0A=ε0Ad.

8,3

Обратите внимание, что из этого уравнения емкость является функцией только геометрии и того, какой материал заполняет пространство между пластинами (в данном случае вакуум) этого конденсатора. На самом деле это верно не только для плоского конденсатора, но и для всех конденсаторов: Емкость не зависит от Q или V . Если заряд меняется, соответственно изменяется и потенциал, так что Q / В остается постоянным.

Пример
8.1

Емкость и заряд, хранящиеся в конденсаторе с параллельными пластинами

а) Какова емкость пустого плоского конденсатора с металлическими пластинами площадью 1,00 м21,00 м2, разделенными расстоянием 1,00 мм? б) Сколько заряда накопится в этом конденсаторе, если к нему приложить напряжение 3,00×103 В3,00×103 В?

Стратегия

Нахождение емкости C является прямым применением уравнения 8.3. Как только мы найдем C , мы можем найти накопленный заряд, используя уравнение 8. 1.

Решение

1. Ввод данных значений в уравнение 8.3 дает

   C=ε0Ad=(8,85×10−12Fm)1,00m21,00×10−3m=8,85×10−9F=8,85nF.C=ε0Ad=(8,85×10−12Fm)1,00m21,00×10−3m= 8,85×10-9Ф=8,85нФ.

   Это маленькое значение емкости указывает на то, насколько сложно сделать устройство с большой емкостью.

2. Инвертирование уравнения 8.1 и ввод известных значений в это уравнение дает

   Q=CV=(8,85×10−9F)(3,00×103 В)=26,6 мкКл. Q=CV=(8,85×10-9F)(3,00×103 В)=26,6 мкКл.

Значение

Этот заряд лишь немного больше, чем в типичных приложениях статического электричества. Поскольку воздух разрушается (становится проводящим) при напряженности электрического поля около 3,0 МВ/м, на этом конденсаторе больше не может накапливаться заряд при увеличении напряжения.

Пример
8.2

A 1-F Конденсатор с параллельными пластинами

Предположим, вы хотите построить конденсатор с плоскими пластинами емкостью 1,0 Ф.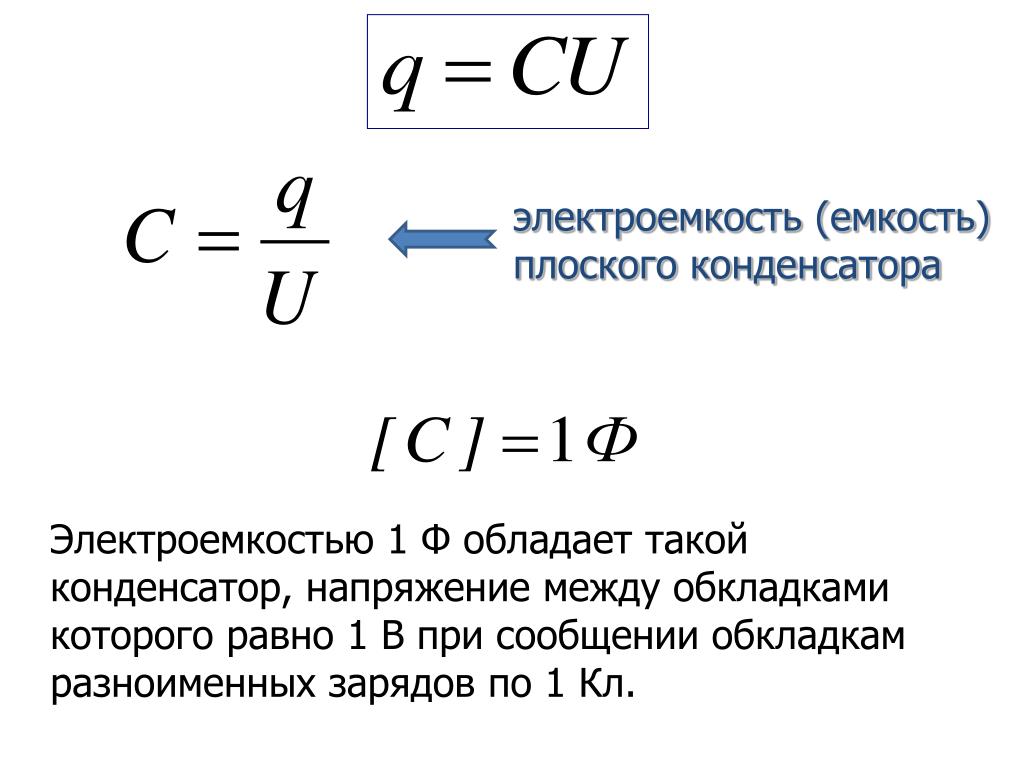 Какую площадь вы должны использовать для каждой пластины, если расстояние между пластинами составляет 1,0 мм?

Решение

Преобразуя уравнение 8.3, мы получаем

A=Cdε0=(1,0F)(1,0×10-3м)8,85×10-12F/м=1,1×108м2.A=Cdε0=(1,0F)(1,0×10-3м)8,85×10-12F/ м=1,1×108м2.

Каждая квадратная пластина должна иметь диаметр 10 км. Раньше было обычной шуткой просить студента пойти на склад лаборатории и попросить конденсатор с плоскими пластинами 1-Ф, пока обслуживающему персоналу не надоела эта шутка.

Проверьте свое понимание
8.1

Проверьте свое понимание Емкость плоского конденсатора равна 2,0 пФ. Если площадь каждой пластины 2,4 см22,4 см2, каково расстояние между пластинами?

Проверьте свое понимание
8.2

Проверьте свое понимание Убедитесь, что σ/Vσ/V и ε0/dε0/d имеют одинаковые физические единицы.

Сферический конденсатор

Сферический конденсатор представляет собой еще один набор проводников, емкость которых можно легко определить (рис. 8.6). Он состоит из двух концентрических проводящих сферических оболочек радиусами R1R1 (внутренняя оболочка) и R2R2 (внешняя оболочка). Оболочки получают равные и противоположные заряды +Q+Q и −Q−Q соответственно. Из-за симметрии электрическое поле между оболочками направлено радиально наружу. Мы можем получить величину поля, применив закон Гаусса к сферической поверхности Гаусса радиусом 9dr)=Q4πε0∫R1R2drr2=Q4πε0(1R1−1R2).

В этом уравнении разность потенциалов между пластинами равна V=-(V2-V1)=V1-V2V=-(V2-V1)=V1-V2. Подставим этот результат в уравнение 8.1, чтобы найти емкость сферического конденсатора:

C=QV=4πε0R1R2R2−R1.C=QV=4πε0R1R2R2−R1.

8,4

Рисунок
8,6

Сферический конденсатор состоит из двух концентрических проводящих сфер. Обратите внимание, что заряды проводника находятся на его поверхности.

Пример
8.3

Емкость изолированной сферы

Рассчитайте емкость одиночной изолированной проводящей сферы радиусом R1R1 и сравните ее с уравнением 8. 4 в пределе, когда R2→∞R2→∞.

Стратегия

Мы предполагаем, что заряд на сфере равен Q , и поэтому мы следуем четырем шагам, описанным ранее. Мы также предполагаем, что другой проводник представляет собой концентрическую полую сферу бесконечного радиуса.

Раствор

Снаружи изолированной проводящей сферы электрическое поле определяется уравнением 8.2. Величина разности потенциалов между поверхностью изолированной сферы и бесконечностью равна
9dr)=Q4πε0∫R1+∞drr2=14πε0QR1.

Следовательно, емкость изолированной сферы равна

C=QV=Q4πε0R1Q=4πε0R1.C=QV=Q4πε0R1Q=4πε0R1.

Значение

Тот же результат можно получить, взяв предел уравнения 8.4 при R2→∞R2→∞. Таким образом, отдельная изолированная сфера эквивалентна сферическому конденсатору, внешняя оболочка которого имеет бесконечно большой радиус.

Проверьте свое понимание
8.3

Проверьте свое понимание Радиус внешней сферы сферического конденсатора в пять раз больше радиуса его внутренней оболочки. Каковы размеры этого конденсатора, если его емкость 5,00 пФ?

Цилиндрический конденсатор

Цилиндрический конденсатор состоит из двух концентрических проводящих цилиндров (рис. 8.7). Внутренний цилиндр радиусом R1R1 может быть как оболочкой, так и сплошным телом. Внешний цилиндр представляет собой оболочку с внутренним радиусом R2R2. Предположим, что длина каждого цилиндра равна l и что избыточные заряды +Q+Q и −Q−Q располагаются на внутреннем и внешнем цилиндрах соответственно.

Рисунок
8,7

Цилиндрический конденсатор состоит из двух концентрических проводящих цилиндров. Здесь заряд на внешней поверхности внутреннего цилиндра положителен (обозначен ++), а заряд на внутренней поверхности внешнего цилиндра отрицателен (обозначен —). 9dr)=Q2πε0l∫R1R2drr=Q2πε0llnr|R1R2=Q2πε0llnR2R1.

Таким образом, емкость цилиндрического конденсатора равна

C=QV=2πε0lln(R2/R1).C=QV=2πε0lln(R2/R1).

8,6

Как и в других случаях, эта емкость зависит только от геометрии расположения проводников. Важным применением уравнения 8.6 является определение емкости на единицу длины коаксиального кабеля , который обычно используется для передачи изменяющихся во времени электрических сигналов. Коаксиальный кабель состоит из двух концентрических цилиндрических проводников, разделенных изоляционным материалом. (Здесь мы предполагаем вакуум между проводниками, но физика качественно почти такая же, когда пространство между проводниками заполнено диэлектриком.) Такая конфигурация экранирует электрический сигнал, распространяющийся по внутреннему проводнику, от паразитных электрических полей, внешних по отношению к проводнику. кабель. Ток течет в противоположных направлениях во внутреннем и внешнем проводниках, при этом внешний проводник обычно заземлен. Теперь из уравнения 8.6 емкость на единицу длины коаксиального кабеля равна

Cl=2πε0ln(R2/R1).Cl=2πε0ln(R2/R1).

В практических приложениях важно выбрать конкретные значения C / l . Этого можно добиться соответствующим выбором радиусов проводников и изоляционного материала между ними.

Проверьте свое понимание
8.4

Проверьте свои знания Когда цилиндрический конденсатор получает заряд 0,500 нКл, между цилиндрами измеряется разность потенциалов 20,0 В. а) Чему равна емкость этой системы? б) Чему равно отношение их радиусов, если длина цилиндров 1,0 м?

На рис. 8.4 показано несколько типов практических конденсаторов. Обычные конденсаторы часто изготавливают из двух небольших кусочков металлической фольги, разделенных двумя небольшими кусочками изоляции (см. рис. 8.2(b)). Металлическая фольга и изоляция покрыты защитным покрытием, а два металлических вывода используются для подключения фольги к внешней цепи. Некоторыми распространенными изоляционными материалами являются слюда, керамика, бумага и антипригарное покрытие Teflon™.

Другим популярным типом конденсатора является электролитический конденсатор. Он состоит из окисленного металла в токопроводящей пасте. Основным преимуществом электролитического конденсатора является его высокая емкость по сравнению с другими распространенными типами конденсаторов. Например, емкость алюминиевого электролитического конденсатора одного типа может достигать 1,0 Ф. Однако вы должны быть осторожны при использовании электролитического конденсатора в цепи, потому что он работает правильно только тогда, когда металлическая фольга находится под более высоким потенциалом, чем проводящая паста. Когда возникает обратная поляризация, электролитическое воздействие разрушает оксидную пленку. Конденсатор этого типа нельзя подключать к источнику переменного тока, потому что в половине случаев переменное напряжение будет иметь неправильную полярность, поскольку переменный ток меняет полярность (см. Цепи переменного тока в цепях переменного тока).

Переменный воздушный конденсатор (рис. 8.8) имеет два набора параллельных пластин. Один набор пластин закреплен (обозначен как «статор»), а другой набор пластин прикреплен к валу, который может вращаться (обозначен как «ротор»). Поворачивая вал, можно изменить площадь поперечного сечения в области нахлеста пластин; следовательно, емкость этой системы может быть настроена на желаемое значение. Конденсаторная настройка находит применение в любом типе радиопередачи и при приеме радиосигналов от электронных устройств. Каждый раз, когда вы настраиваете автомобильный радиоприемник на любимую станцию, подумайте о емкости.

Рисунок
8,8

В переменном воздушном конденсаторе емкость можно регулировать, изменяя эффективную площадь пластин. (кредит: модификация работы Робби Спроула)

Символы, показанные на рис. 8.9, представляют собой схемы различных типов конденсаторов. Обычно мы используем символ, показанный на рис. 8.9(а). Символ на рис. 8.9(c) обозначает конденсатор переменной емкости. Обратите внимание на сходство этих символов с симметрией плоского конденсатора. Электролитический конденсатор представлен символом в части рисунка 8.9.(б), где изогнутая пластина указывает на отрицательную клемму.

Рисунок
8,9

Это показывает три различных представления схемы конденсаторов. Символ в (а) является наиболее часто используемым. Символ в (b) представляет собой электролитический конденсатор. Символ в (c) представляет собой конденсатор переменной емкости.

Интересный прикладной пример модели конденсатора взят из клеточной биологии и касается электрического потенциала плазматической мембраны живой клетки (рис. 8.10). Клеточные мембраны отделяют клетки от их окружения, но позволяют некоторым избранным ионам проходить внутрь или наружу клетки. Разность потенциалов на мембране составляет около 70 мВ. Клеточная мембрана может иметь толщину от 7 до 10 нм. Рассматривая клеточную мембрану как наноразмерный конденсатор, оценка наименьшей напряженности электрического поля на ее «пластинах» дает значение E=Vd=70×10−3V10×10−9. m=7×106В/м>3МВ/мE=Vd=70×10−3В10×10−9m=7×106В/м>3МВ/м.

Эта величина электрического поля достаточно велика, чтобы создать электрическую искру в воздухе.

Рисунок
8.10

Полупроницаемая мембрана биологической клетки имеет разные концентрации ионов на внутренней поверхности, чем на внешней. Диффузия перемещает ионы K+K+ (калий) и Cl–Cl– (хлорид) в указанных направлениях до тех пор, пока кулоновская сила не остановит дальнейший перенос. Таким образом, внешняя поверхность мембраны приобретает положительный заряд, а ее внутренняя поверхность приобретает отрицательный заряд, создавая на мембране разность потенциалов. Мембрана в норме непроницаема для Na+ (ионов натрия).

Интерактивный

Посетите PhET Explorations: Capacitor Lab, чтобы узнать, как работает конденсатор. Измените размер пластин и добавьте диэлектрик, чтобы увидеть влияние на емкость. Измените напряжение и увидите заряды на пластинах. Наблюдайте за электрическим полем в конденсаторе. Измерьте напряжение и электрическое поле.

Емкость конденсатора Формула

Электричество и магнетизмЭлектроника

Емкость конденсатора

Емкость конденсатора – это способность конденсатора накапливать электрический заряд на единицу напряжение на его обкладках конденсатора. Емкость находится путем деления электрического заряда на напряжение по формуле C=Q/V. Его единицей является Фарада.

Формула

Его формула выглядит следующим образом:

C=Q/V

Где C — емкость, Q — напряжение, а V — напряжение. Мы также можем найти заряд Q и напряжение V, переформулировав приведенную выше формулу следующим образом:

Q=CV

V=Q/C

  Фарад — единица измерения емкости. Один фарад — это величина емкости, когда один кулон заряда хранится с одним вольтом на его пластинах.

Большинство конденсаторов, используемых в электронике, имеют емкость, указанную в микрофарадах (мкФ) и пикофарадах (пФ). Микрофарад — это одна миллионная часть фарада, а пикофарад — одна триллионная часть фарада.

Какие факторы влияют на емкость конденсатора?

Зависит от следующих факторов:

Площадь пластин

Емкость прямо пропорциональна физическому размеру пластин, определяемому площадью пластин, A. Большая площадь пластины дает большую емкость и меньшую емкость. На рис. (а) показано, что площадь пластины конденсатора с параллельными пластинами равна площади одной из пластин. Если пластины перемещаются относительно друг друга, как показано на рис. (b), площадь перекрытия определяет эффективную площадь пластины. Это изменение эффективной площади пластины является основным для определенного типа переменного конденсатора.

Разделение пластин

`Емкость обратно пропорциональна расстоянию между пластинами. Разделение пластин обозначено буквой d, как показано на рис. (а). Чем больше расстояние между пластинами, тем меньше емкость, как показано на рис. (b). Как обсуждалось ранее, напряжение пробоя прямо пропорционально расстоянию между пластинами. Чем дальше разнесены пластины, тем больше напряжение пробоя .

Диэлектрическая проницаемость материала

Как известно, изоляционный материал между обкладками конденсатора называется диэлектриком. Диэлектрические материалы имеют тенденцию уменьшать напряжение между пластинами для данного заряда и, таким образом, увеличивать емкость. Если напряжение фиксировано, из-за присутствия диэлектрика может быть сохранено больше заряда, чем без диэлектрика. Мера способности материала создавать электрическое поле называется диэлектрической проницаемостью или относительной диэлектрической проницаемостью, обозначаемой символом ∈ 9.0373 р .

Емкость прямо пропорциональна диэлектрической проницаемости. Диэлектрическая проницаемость вакуума определяется как 1, а диэлектрическая проницаемость воздуха очень близка к 1. Эти значения используются в качестве справочных, и все другие материалы имеют значения εr, указанные по отношению к вакууму или воздуху. Например, материал с εr=8 может иметь емкость, в восемь раз превышающую емкость воздуха, при прочих равных условиях.

Диэлектрическая проницаемость ∈r безразмерна, поскольку является относительной мерой. Это отношение абсолютной диэлектрической проницаемости материала,∈r, к абсолютной диэлектрической проницаемости вакуума,∈ ₀ , что выражается следующей формулой:

∈ _r =∈/∈ ₀

Ниже приведены некоторые распространенные диэлектрические материалы и типичные диэлектрические постоянные для каждого из них. Значения могут варьироваться, поскольку зависят от конкретного состава материала.

Материал Типичные значения ∈R

• воздух 1.0
• Тефлон 2,0
• Бумага 2.5
• Масло 4.0
• Mica 5.0
• Стекло 7,5
• Ceramic 1200

Диэлектрическая проницаемость ∈R безразличия, поскольку это относительная мера. Это отношение абсолютной диэлектрической проницаемости материала,∈r, к абсолютной диэлектрической проницаемости вакуума,∈0, выражаемое следующей формулой:

∈r=∈/∈0

8,85×10-12 Ф/м.

Формула емкости в пересчете на физические параметры

Вы видели, что емкость напрямую связана с площадью пластины, A, и диэлектрической проницаемостью,εr, и обратно пропорциональна расстоянию между пластинами, d. Точная формула для расчета емкости через эти три величины: m)

Производная емкость плоского конденсатора

Рассмотрим конденсатор с плоскими пластинами. Размер пластины большой, а расстояние между пластинами очень маленькое, поэтому электрическое поле между пластинами однородно.

Электрическое поле ‘E’ между пластинчатым конденсатором составляет:

отношение плоскопараллельного конденсатора

Емкость цилиндрических конденсаторов физика

Рассмотрим цилиндрический конденсатор длиной L, образованный двумя коаксиальными цилиндрами радиусов ‘a’ и ‘b ‘.Предположим, что L >> b такое, что на концах цилиндров нет окантовывающего поля.

Пусть «q» — заряд конденсатора, а «V» — разность потенциалов между пластинами. Внутренний цилиндр заряжен положительно, а внешний цилиндр заряжен отрицательно.