Физика. Период и частота | Частная школа. 9 класс

Конспект по физике для 9 класса «Период и частота». Что такое период обращения. Что такое частота обращения. Как вычислить скорость и ускорение тела, движущегося по окружности, если известны его период и частота обращения.

Конспекты по физике    Учебник физики    Тесты по физике

Измерить скорость тела, движущегося по окружности, не всегда просто. Однако её можно вычислить, используя такие понятия, как период и частота обращения.

ПЕРИОД

Когда тело движется по окружности с постоянной по модулю скоростью, через определённые промежутки времени движение повторяется снова и снова. Примером этому может служить движение на обычной детской карусели.

Время, в течение которого тело совершает один полный оборот, называют периодом обращения. Период обращения принято обозначать буквой Т. Единица этой физической величины в СИ — секунда.

С понятием периода обращения вы уже знакомились при изучении географии. Например, период обращения Земли вокруг своей оси составляет 23 ч 56 мин 4 с, а период обращения Земли вокруг Солнца — 1,00004 земных года. Самый короткий период обращения вокруг Солнца в нашей Солнечной системе имеет планета Меркурий. Её период обращения составляет 0,24085 земных лет. Интересно, что самая большая планета Солнечной системы — Юпитер — имеет самый короткий период обращения вокруг своей оси — всего 9 ч 50 мин. В 226 000 000 лет оценивается период обращения Солнечной системы вокруг ядра Галактики.

ЧАСТОТА

Число оборотов в единицу времени, которое совершает тело при движении по окружности, называют частотой обращения. Частоту обращения обозначают греческой буквой ν.

Если, катаясь на карусели в парке, мы совершаем один оборот за 20 с, то период обращения в этом случае Т = 20 с. Как определить частоту обращения при этом движении? Сколько оборотов совершает карусель за 1 с?

Очевидно, ν = 1/Т = 1/20 ¹/с, т. е. за 1 с карусель совершает одну двадцатую часть своего полного оборота.

Таким образом, частота обращения является величиной, обратной периоду обращения:

Именно поэтому единица этой физической величины обратна секунде, т. е. ¹/с, или с^-1.

СВЯЗЬ МОДУЛЯ СКОРОСТИ С ПЕРИОДОМ И ЧАСТОТОЙ ОБРАЩЕНИЯ

Чтобы определить модуль скорости тела, движущегося по окружности, достаточно знать радиус окружности R и период или частоту обращения. Действительно, один полный оборот тело совершает за время, равное периоду обращения Т. Путь, пройденный телом, в этом случае равен длине окружности: l = 2πR. Тогда можно записать:

или с учётом формулы (1):

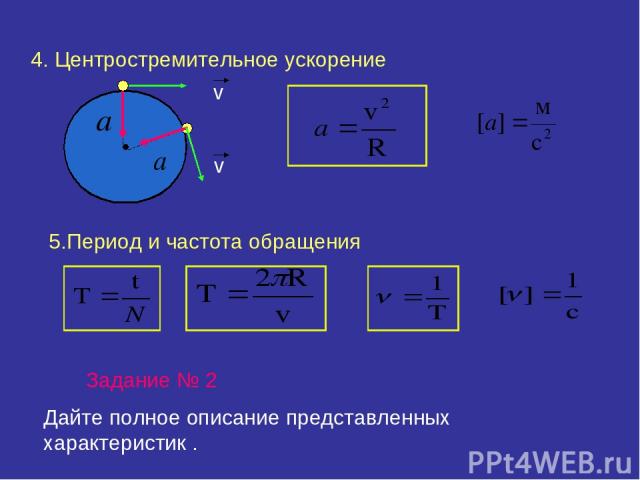
С учётом формул (2) и (3) можно найти центростремительное ускорение тела, выразив скорость через период или частоту обращения:

Часто мгновенную скорость движения по окружности называют линейной скоростью.

Модуль скорости движения тела по окружности рассчитывается по формуле:

Умение описывать движение тела по окружности чрезвычайно важно, так как движение по криволинейной траектории можно приближённо представить как движение по дугам окружностей различных радиусов.

РЕШЕНИЕ ЗАДАЧ

Задача 1. Найдём модуль скорости вращения ребёнка на карусели, если радиус окружности, по которой происходит движение, равен 2,3 м, а время, за которое карусель совершает один полный оборот, равно 20 с.

Ответ: υ = 0,722 м/с.

Задача 2.  Земля делает один оборот вокруг Солнца за 365 дней. Расстояние от Солнца до Земли составляет 149,6 • 10⁶ км. Определим линейную скорость движения Земли вокруг Солнца, считая орбиту окружностью.

Ответ: υ ≈ 30 км/с.

Вы смотрели Конспект по физике для 9 класса «Период и частота».

Вернуться к Списку конспектов по физике (Оглавление).

Формула частоты в физике

Формула частоты в физике

Определение

Частота — это физический параметр, которые используют для характеристики периодических процессов.
Частота равна количеству повторений или свершения событий в единицу времени.

Чаще всего в физике частоту обозначают буквой $\nu ,$ иногда встречаются другие обозначения частоты, например $f$ или $F$.

Частота (наряду со временем) является самой точно измеряемой величиной.

Формула частоты колебаний

При помощи частоты характеризуют колебания. В этом случае частота является физической величиной обратной периоду колебаний $(T).$

\[\nu =\frac{1}{T}\left(1\right). {-1}=Гц.\]

Герц — это единица измерения частоты периодического процесса, при которой за время равное одной секунде происходит один цикл процесса. Единица измерения частоты периодического процесса получила свое наименование в честь немецкого ученого Г. Герца.

Частота биений, которые возникают при сложении двух колебаний, происходящих по одной прямой с разными, но близкими по величине частотами (${\nu }_1\ и\ {\nu }_2$) равна:

\[{\nu =\nu }_1-\ {\nu }_2\left(3\right).\]

Еще одно величиной характеризующей колебательный процесс является циклическая частота (${\omega }_0$), связанная с частотой как:

\[{\omega }_0=2\pi \nu \left(4\right).\]

Циклическая частота измеряется в радианах, деленных на секунду:

\[\left[{\omega }_0\right]=\frac{рад}{с}.\]

Частота колебаний тела, имеющего массу$\ m,$ подвешенного на пружине с коэффициентом упругости $k$ равна:

\[\nu =\frac{1}{2\pi \sqrt{{m}/{k}}}\left(5\right). \]

Формула (4) верна для упругих, малых колебаний. Кроме того масса пружины должна быть малой по сравнению с массой тела, прикрепленного к этой пружине.

Для математического маятника частоту колебаний вычисляют как: длина нити:

\[\nu =\frac{1}{2\pi \sqrt{{l}/{g}}}\left(6\right),\]

где $g$ — ускорение свободного падения; $\ l$ — длина нити (длина подвеса) маятника.

Физический маятник совершает колебания с частотой:

\[\nu =\frac{1}{2\pi \sqrt{{J}/{mgd}}}\left(7\right),\]

где $J$ — момент инерции тела, совершающего колебания относительно оси; $d$ — расстояние от центра масс маятника до оси колебаний.

Формулы (4) — (6) приближенные. Чем меньше амплитуда колебаний, тем точнее значение частоты колебаний, вычисляемых с их помощью.

Формулы для вычисления частоты дискретных событий, частота вращения

дискретных колебаний ($n$) — называют физическую величину, равную числу действий (событий) в единицу времени. Если время, которое занимает одно событие обозначить как $\tau $, то частота дискретных событий равна:

\[n=\frac{1}{\tau }\left(8\right).\]

Единицей измерения частоты дискретных событий является обратная секунда:

\[\left[n\right]=\frac{1}{с}.\]

Секунда в минус первой степени равна частоте дискретных событий, если за время, равное одной секунде происходит одно событие.

Частотой вращения ($n$) — называют величину, равную количеству полных оборотов, которое совершает тело в единицу времени. Если $\tau $ — время, затрачиваемое на один полный оборот, то:

\[n=\frac{1}{\tau }\left(9\right).\]

Примеры задач с решением

Пример 1

Задание. Колебательная система совершила за время равное одной минуте ($\Delta t=1\ мин$) 600 колебаний. Какова частота этих колебаний?

Решение. Для решения задачи воспользуемся определением частоты колебаний: Частота, в этом случае — это число полных колебаний, совершающихся за единицу времени.

\[\nu =\frac{N}{\Delta t}\left(1.1\right).\]

Прежде чем переходить к вычислениям, переведем время в единицы системы СИ: $\Delta t=1\ мин=60\ с$. Вычислим частоту:

\[\nu =\frac{600}{60}=10\ \left(Гц\right).\]

Ответ. $\nu =10Гц$

Пример 2

Задание. На рис.1 изображен график колебаний некоторого параметра $\xi \ (t)$, Какова амплитуда и частота колебаний этой величины?

Решение. Из рис.1 видно, что амплитуда величины $\xi \ \left(t\right)={\xi }_{max}=5\ (м)$. Из графика получаем, что одно полное колебание происходит за время, равное 2 с, следовательно, период колебаний равен:

\[T=2\ \left(c\right).\]

Частота — величина обратная периоду колебаний, значит:

\[\nu =\frac{1}{T}=0,5\ \left(Гц\right).\]

Ответ. 1) ${\xi }_{max}=5\ (м)$. 2) $\nu =0,5$ Гц

Читать дальше: формулы математического маятника.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Низкая скорость циркуляции

Автор: DrillingFormulas.Com | 28 июня 2011 г. — 9:37 | 9 августа 2011 г. Знание нефтяных месторождений, управление скважиной

Просмотры сообщений:
17 719

Медленная скорость циркуляции — скорость циркуляции, которая будет использоваться при операции глушения скважины. Как правило, давление медленной скорости циркуляции (SCR) записывается для каждой конкретной скорости потока, а давление представляет собой потерю давления в системе во время циркуляции. Поскольку на буровой установке так много манометров, вы можете запутаться в цифрах. Чтобы быть на одной странице для каждого персонала на буровой, SCR должен регистрироваться манометром, который мы будем использовать для глушения скважины.

Существует множество причин, по которым следует глушить скважину с низкой скоростью, а не со скоростью бурения:

• Чтобы минимизировать давление трения использовать метод ожидания и взвешивания

• Чтобы уменьшить давление на наземное оборудование

• Чтобы позволить дегазатору отделить газ от бурового раствора

• Чтобы уменьшить потребность в быстрой работе штуцера

• Чтобы позволить персоналу подумать, если что-то пойдет не так

Давайте разберемся, как получить предварительно записанный SCR.

1. Включите насос на малой скорости 10, 20, 30 и 40 ходов в минуту

2. Запишите давление без вращения или перемещения бурильной колонны

3. Каждое давление, зарегистрированное при определенной скорости насоса, является SCR.

Пожалуйста, всегда помните, что SCR, который вы принимаете для каждого времени, представляет собой потерю давления в это время. Не рекомендую использовать для оценки начального циркуляционного давления.

Поясню почему. В предварительно записанном SCR есть ошибки, из-за которых у вас могут возникнуть проблемы.

• Предварительно записанный SCR может не отражать текущее давление из-за изменения свойств бурового раствора.

• Глубина предварительно записанного SCR не совпадает с текущей глубиной сверления.

• SCR может быть изменен из-за неизвестного состояния в скважине, такого как механизм КНБК, забитые форсунки и т. д.

Как мы можем получить ICP без использования предварительно записанного SCR?

Чтобы получить начальное давление циркуляции, вы просто увеличиваете скорость насоса, поддерживая постоянное давление в обсадной трубе, пока не достигнете скорости глушения. Кроме того, вы сможете рассчитать фактический SCR расчетным путем.

Давайте посмотрим на приведенное ниже уравнение.

ICP = SIDPP + SCR

Где; ICP – начальное циркуляционное давление.

SIDPP перекрыта давлением в бурильной трубе.

SCR — давление медленной скорости циркуляции.

Следовательно, SCR = ICP – SIDPP

Если вы хотите проверить SCR, вам следует проверить SCR в следующий раз.

• Проверка перед разбуриванием башмака обсадной колонны

• Проверка после спуска на забой

• Проверка при изменении свойств бурового раствора

• Проверка не менее двух раз в смену на глубине бурения в это время

Справочник: Книги контроля скважины

Разделите радость

Собственные частоты артериальной системы и их связь с частотой сердечных сокращений

. 2004 г., январь; 51 (1): 193-5.

doi: 10.1109/TBME.2003.820378.

Ю-Ин Линь Ван
¹
, Мин-Йе Ян, Чинг-Шоу Шью, Чи-Анг Чианг, Вэй-Кунг Ван

принадлежность

• ¹ Факультет физики Тайваньского национального педагогического университета, № 88, сек. 4, Ting-Chou Rd., Тайбэй 116, Тайвань. [email protected]

• PMID:

  14723511

• DOI:

  10.1109/ТБМЭ.2003.820378

Юй-Ин Линь Ван и соавт.

IEEE Trans Biomed Eng.

2004 Январь

. 2004 г., январь; 51 (1): 193-5.

doi: 10.1109/TBME.2003.820378.

Авторы

Ю-Ин Линь Ван
¹
, Мин-Йи Джан, Чинг-Шоу Шью, Чи-Анг Чианг, Вэй-Кунг Ван

принадлежность

• ¹ Факультет физики, Тайваньский национальный педагогический университет, №. 88, сек. 4, Ting-Chou Rd., Тайбэй 116, Тайвань. [email protected]

• PMID:

  14723511

• DOI:

  10.1109/ТБМЭ.2003.820378

Абстрактный

Мы предполагаем, что основной функцией артериальной системы является транспортировка энергии через ее поперечную вибрацию, чтобы облегчить движение крови по всему пути до микроциркуляторного русла. Высокоэффективная система связана с поддержанием большого импульса давления вдоль артерии при заданной мощности желудочка. Артериальная система описывается как композиция множества бесконечно малых Виндкесселей. Сильная связь в продольном направлении соединяет все виндкессели вместе и заставляет их вибрировать в сопряженных модах. Предполагалось, что в состоянии покоя артериальная система находится в устойчивом распределенном колебательном состоянии, представляющем собой суперпозицию многих гармонических мод поперечных колебаний артериальной стенки и прилипшей к ней крови. Каждая мода вибрации имеет свою собственную характеристическую частоту, которая зависит от геометрии, плотности массы, эластичности и фиксации артериальной системы. Если частота сердечных сокращений близка к основной собственной частоте, система находится в хорошем состоянии резонанса, мы называем это «согласованием частот». В этом состоянии пульсирующая волна давления максимальна. Выведенное ранее уравнение волны давления использовалось для предсказания этой основной частоты. Теоретический результат показал, что частота сердечных сокращений пропорциональна средней высокочастотной фазовой скорости волны давления и обратно пропорциональна длине тела животного. Упоминается также соответствие площади, связанное с эффективностью системы кровообращения.

Похожие статьи

• Трубки, струны и резонанс в артериальной системе — что заставляет ритм продолжаться?

  Аволио А.П., Керхофская пл.
  Аволио А.П. и др.
  IEEE Trans Biomed Eng. 2004 г., январь; 51 (1): 196-7. doi: 10.1109/TBME.2003.820607.
  IEEE Trans Biomed Eng. 2004.

  PMID: 14723513

  Аннотация недоступна.

• Связь артериального ветра с периферической вазомоторной функцией: моделирование воздействия на низкочастотные колебания.

  Базелли Г., Порта А., Пагани М.
  Базелли Г. и соавт.
  IEEE Trans Biomed Eng. 2006 г., январь; 53 (1): 53–64. doi: 10.1109/TBME.2005.859787.
  IEEE Trans Biomed Eng. 2006.

  PMID: 16402603

• Влияние длины на основную резонансную частоту моделей артерий с радиальным расширением.

  Ван Ю.Ю., Лия В.К., Хсиу Х., Ян М.Ю., Ван В.К.
  Ван Ю.Ю. и др.
  IEEE Trans Biomed Eng. 2000 март; 47(3):313-8. дои: 10.1109/10.827291.
  IEEE Trans Biomed Eng. 2000.

  PMID: 10743772

• Пульсирующее диастолическое повышение и систолическое снижение артериального давления: механизм их возникновения и физиологическая роль.

  Мандоки Дж.Дж., Каса-Тирао Б., Молина-Гуарнерос Х.А., Хименес-Ороско Ф.А., Гарсия-Мондрагон М. Дж., Мальдонадо-Эспиноза А.
  Мандоки Дж.Дж. и соавт.
  Прог Биофиз Мол Биол. 2013 авг.; 112(3):55-7. doi: 10.1016/j.pbiomolbio.2013.05.002. Epub 2013 28 мая.
  Прог Биофиз Мол Биол. 2013.

  PMID: 23727290

  Обзор.

• Жесткость крупных артерий, артериальная гипертензия и сердечно-сосудистый риск у пожилых пациентов.

  Блахер Дж., Сафар М.Э.
  Блахер Дж. и соавт.
  Nat Clin Pract Cardiovasc Med. 2005 г., сен; 2 (9): 450-5. DOI: 10.1038/ncpcardio0307.
  Nat Clin Pract Cardiovasc Med. 2005.

  PMID: 16265585

  Обзор.

Посмотреть все похожие статьи

Цитируется

• Использование радиальной пульсовой волны в качестве гемодинамических измерений для количественной оценки эффектов терапии иглоукалыванием у пациентов с черепно-мозговой травмой и ишемическим инсультом.

  Чен Дж.К., Цай В.Т., Линь С.З., Ван С.Х., Ван Г.К., Ван Т.К., Чен Х.П., Хо Т.Дж.
  Чен Дж. К. и соавт.
  J Tradit Комплемент Мед. 2022 1 сентября; 12 (6): 594-598. doi: 10.1016/j.jtcme.2022.08.005. электронная коллекция 2022 нояб.
  J Tradit Комплемент Мед. 2022.

  PMID: 36325244
  Бесплатная статья ЧВК.

• Влияние частоты пульсации вспомогательного устройства для левого желудочка (LVAD) на коронарную перфузию: исследование численного моделирования.

  Чжу И, Ян М, Чжан И, Мэн Ф, Ян Т, Фанг З.
  Чжу Ю и др.
  Медицинский научный монит. 2020 17 сентября; 26:e925367. doi: 10.12659/MSM.925367.
  Медицинский научный монит. 2020.

  PMID: 32940255
  Бесплатная статья ЧВК.

• Оценка риска макрососудистых и микрососудистых событий у больных сахарным диабетом 2 типа путем анализа амплитуды вариации четвертой гармоники радиальной пульсовой волны.

  Ляо К.М., Чанг К.В., Ван С.Х., Чанг Ю.Т., Чен Ю.К., Ван Г.К.
  Ляо К.М. и др.
  Physiol Rep. 7 октября 2019 г. (19): e14252. дои: 10.14814/phy2.14252.
  Физиол Респ. 2019.

  PMID: 31591828
  Бесплатная статья ЧВК.

• Применение анализа спектра пульса для облегчения диагностики ишемической болезни сердца.

  Хуан Ю.С., Чанг Ю.Х., Ченг С.М., Лин С.Дж., Лин С.Дж., Су Ю.С.
  Хуан Ю.С. и др.
  Комплемент на основе Evid Alternat Med. 2019 3 июня; 2019: 2709486. дои: 10.1155/2019/2709486. Электронная коллекция 2019.
  Комплемент на основе Evid Alternat Med. 2019.

  PMID: 31275406
  Бесплатная статья ЧВК.

• Различные гармонические характеристики были обнаружены в каждом месте при диагностике радиального импульса TCM с помощью спектрального анализа.