Активная и реактивная мощность. За что платим и работа
Активная и реактивная мощность — потребители электрической энергии на то и потребители, чтобы эту энергию потреблять. Потребителя интересует та энергия, потребление которой идет ему на пользу, эту энергию можно назвать полезной, но в электротехнике ее принято называть активной. Это энергия, которая идет на нагрев помещений, готовку пищи, выработку холода, и превращаемая в механическую энергию (работа электродрелей, перфораторов, электронасосов и пр.).
Кроме активной электроэнергии существует еще и реактивная. Это та часть полной энергии, которая не расходуется на полезную работу. Как понятно из вышесказанного, полная мощность – это активная и реактивная мощность в целом.
В понятиях активная и реактивная мощность сталкиваются противоречивые интересы потребителей электрической энергии и ее поставщиков. Потребителю выгодно платить только за потребленную им полезную электроэнергию, поставщику выгодно получать оплату за сумму активной и реактивной электроэнергии.
 Можно ли совместить эти кажущиеся противоречивыми требования? Да, если свести количество реактивной электроэнергии к нулю.
Можно ли совместить эти кажущиеся противоречивыми требования? Да, если свести количество реактивной электроэнергии к нулю.
Активная мощность
Существуют потребители электроэнергии, у которых полная и активная мощности совпадают. Это потребители, у которых нагрузка представлена активными сопротивлениями (резисторами). Среди бытовых электроприборов примерами подобной нагрузки являются лампы накаливания, электроплиты, жарочные шкафы и духовки, обогреватели, утюги, паяльники и пр.
Указанная у этих приборов в паспорте, одновременно является активная и реактивная мощность . Это тот случай, когда мощность нагрузки можно определить по известной из школьного курса физики формуле, перемножив ток нагрузки на напряжение в сети. Ток измеряется в амперах (А), напряжение в вольтах (В), мощность в ваттах (Вт). Конфорка электрической плиты в сети с напряжением 220 В при токе в 4,5 А потребляет мощность 4,5 х 220 = 990 (Вт).
Реактивная мощность
Иногда, проходя по улице, можно увидеть, что стекла балконов покрыты изнутри блестящей тонкой пленкой.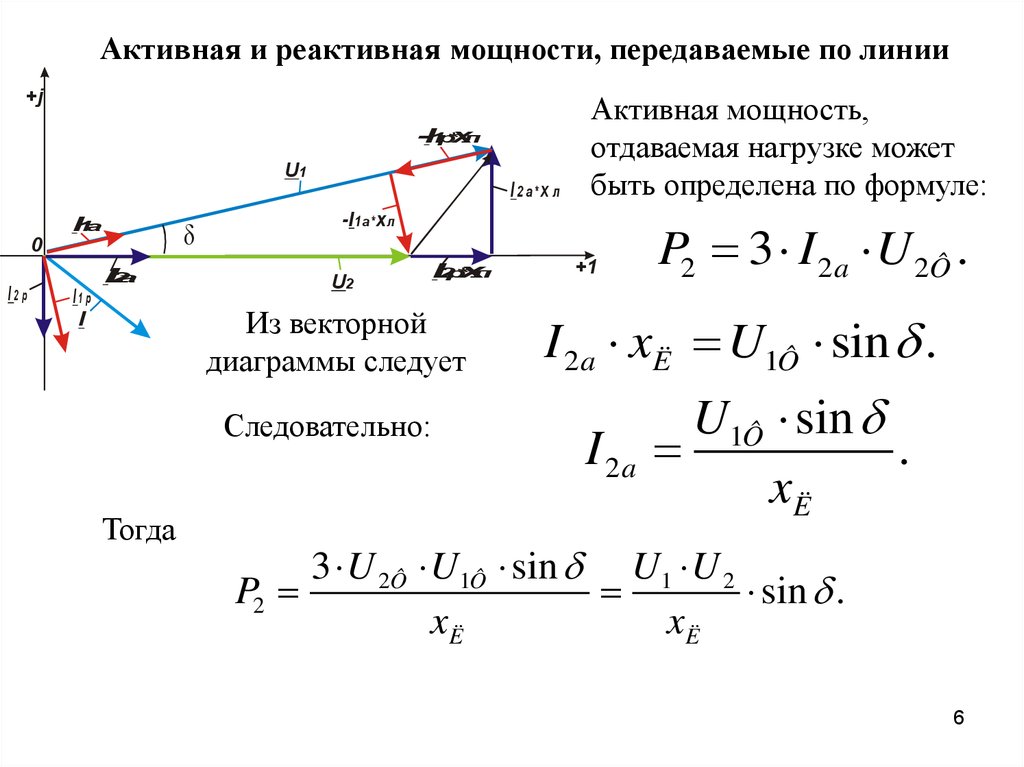 Эта пленка изъята из бракованных электрических конденсаторов, устанавливаемых с определенными целями на питающих мощных потребителей электрической энергии распределительных подстанциях. Конденсатор – типичный потребитель реактивной мощности. В отличие от потребителей активной мощности, где главным элементом конструкции является некий проводящий электричество материал (вольфрамовый проводник в лампах накаливания, нихромовая спираль в электроплитке и т.п.). В конденсаторе главный элемент – не проводящий электрический ток диэлектрик (тонкая полимерная пленка или пропитанная маслом бумага).
Эта пленка изъята из бракованных электрических конденсаторов, устанавливаемых с определенными целями на питающих мощных потребителей электрической энергии распределительных подстанциях. Конденсатор – типичный потребитель реактивной мощности. В отличие от потребителей активной мощности, где главным элементом конструкции является некий проводящий электричество материал (вольфрамовый проводник в лампах накаливания, нихромовая спираль в электроплитке и т.п.). В конденсаторе главный элемент – не проводящий электрический ток диэлектрик (тонкая полимерная пленка или пропитанная маслом бумага).
Реактивная емкостная мощность
Красивые блестящие пленки, что вы видели на балконе – это обкладки конденсатора из токопроводящего тонкого материала. Конденсатор замечателен тем, что он может накапливать электрическую энергию, а затем отдавать ее – своеобразный такой аккумулятор. Если включить конденсатор в сеть постоянного тока, он зарядится кратковременным импульсом тока, а затем ток через него протекать не будет. Вернуть конденсатор в исходное состояние можно, отключив его от источника напряжения и подключив к его обкладкам нагрузку. Некоторое время через нагрузку будет течь электрический ток, и идеальный конденсатор отдает в нагрузку ровно столько электрической энергии, сколько он получил при зарядке. Подключенная к выводам конденсатора лампочка может на короткое время вспыхнуть, электрический резистор нагреется, а неосторожного человека может «тряхнуть» или даже убить при достаточном напряжении на выводах и запасенном количестве электричества.
Вернуть конденсатор в исходное состояние можно, отключив его от источника напряжения и подключив к его обкладкам нагрузку. Некоторое время через нагрузку будет течь электрический ток, и идеальный конденсатор отдает в нагрузку ровно столько электрической энергии, сколько он получил при зарядке. Подключенная к выводам конденсатора лампочка может на короткое время вспыхнуть, электрический резистор нагреется, а неосторожного человека может «тряхнуть» или даже убить при достаточном напряжении на выводах и запасенном количестве электричества.
Интересная картина получается при подключении конденсатора к источнику переменного электрического напряжения. Поскольку у источника переменного напряжения постоянно меняются полярность и мгновенное значение напряжения (в домашней электросети по закону, близкому к синусоидальному). Конденсатор будет непрерывно заряжаться и разряжаться, через него будет непрерывно протекать переменный ток. Но этот ток не будет совпадать по фазе с напряжением источника переменного напряжения, а будет опережать его на 90°, т. е. на четверть периода.
е. на четверть периода.
Это приведет к тому, что суммарно половину периода переменного напряжения конденсатор потребляет энергию из сети, а половину периода отдает, при этом суммарная потребляемая активная электрическая мощность равна нулю. Но, поскольку через конденсатор течет значительный ток, который может быть измерен амперметром, принято говорить, что конденсатор – потребитель реактивной электрической мощности.
Вычисляется реактивная мощность как произведение тока на напряжение, но единица измерения уже не ватт, а вольт-ампер реактивный (ВАр). Так, через подключенный к сети 220 В частотой 50 Гц электрический конденсатор емкостью 4 мкФ течет ток порядка 0,3 А. Это означает, что конденсатор потребляет 0,3 х 220 = 66 (ВАр) реактивной мощности – сравнимо с мощностью средней лампы накаливания, но конденсатор, в отличие от лампы, при этом не светится и не нагревается.
Реактивная индуктивная мощность
Если в конденсаторе ток опережает напряжение, то существуют ли потребители, где ток отстает от напряжения? Да, и такие потребители, в отличие от емкостных потребителей, называются индуктивными, оставаясь при этом потребителями реактивной энергии. Типичная индуктивная электрическая нагрузка – катушка с определенным количеством витков хорошо проводящего провода, намотанного на замкнутый сердечник из специального магнитного материала.
Типичная индуктивная электрическая нагрузка – катушка с определенным количеством витков хорошо проводящего провода, намотанного на замкнутый сердечник из специального магнитного материала.
На практике хорошим приближением чисто индуктивной нагрузки является работающий без нагрузки трансформатор (или стабилизатор напряжения с автотрансформатором). Хорошо сконструированный трансформатор на холостом ходу потребляет очень мало активной мощности, потребляя мощность в основном реактивную.
Реальные потребители электрической энергии и полная электрическая мощность
Из рассмотрения особенностей емкостной и индуктивной нагрузки возникает интересный вопрос – что произойдет, если емкостную и индуктивную нагрузку включить одновременно и параллельно. Ввиду их противоположной реакции на приложенное напряжение, эти две реакции начнут компенсировать друг друга. Суммарная нагрузка окажется только емкостной или индуктивной, и в некотором идеальном случае удастся добиться полной компенсации. Выглядеть это будет парадоксально – подключенные амперметры зафиксируют значительные (и равные!) токи через конденсатор и катушку индуктивности, и полное отсутствие тока в объединяющих их общей цепи. Описанная картина несколько нарушается лишь тем, что не существует идеальных конденсаторов и катушек индуктивности, но подобная идеализация помогает понять суть происходящих процессов.
Выглядеть это будет парадоксально – подключенные амперметры зафиксируют значительные (и равные!) токи через конденсатор и катушку индуктивности, и полное отсутствие тока в объединяющих их общей цепи. Описанная картина несколько нарушается лишь тем, что не существует идеальных конденсаторов и катушек индуктивности, но подобная идеализация помогает понять суть происходящих процессов.
Вернемся к реальным потребителям электрической энергии. В быту мы пользуемся в основном потребителями чисто активной мощности (примеры приведены выше), и смешанной активно-индуктивной. Это электродрели, перфораторы, электродвигатели холодильников, стиральных машин и прочей бытовой техники. Также к ним относятся электрические трансформаторы источников питания бытовой радиоэлектронной аппаратуры и стабилизаторов напряжения. В случае подобной смешанной нагрузки, помимо активной (полезной) мощности, нагрузка потребляет еще и реактивную мощность, в итоге полная мощность отказывается больше активной мощности. Полная мощность измеряется в вольт-амперах (ВА), и всегда представляет собой произведение тока в нагрузке на напряжение на нагрузке.
Полная мощность измеряется в вольт-амперах (ВА), и всегда представляет собой произведение тока в нагрузке на напряжение на нагрузке.
Таинственный «косинус фи»
Отношение активной мощности к полной называется в электротехнике «косинусом фи». Обозначается cos φ. Это отношение называется также и коэффициентом мощности. Нетрудно видеть, что для случая чисто активной нагрузки, где полная мощность совпадает с активной, cos φ = 1. Для случаев чисто емкостной или индуктивной нагрузок, где нулю равна активная мощность, cos φ = 0.
В случае смешанной нагрузки значение коэффициента мощности заключается в пределах от 0 до 1. Для бытовой техники обычно в диапазоне 0,5-0,9. В среднем можно считать его равным 0,7, более точное значение указывается в паспорте электроприбора.
За что платим?
И, наконец, самый интересный вопрос – за какой вид энергии платит потребитель. Исходя из того, что реактивная составляющая суммарной энергии не приносит потребителю никакой пользы, при этом долю периода реактивная энергия потребляется, а долю отдается, платить за реактивную мощность незачем. Но бес, как известно, кроется в деталях. Поскольку смешанная нагрузка увеличивает ток в сети, возникают проблемы на электростанциях, где электроэнергия вырабатывается синхронными генераторами, а именно: индуктивная нагрузка «развозбуждает» генератор, и приведение его в прежнее состояние обходится в затраты уже реальной активной мощности на его «довозбуждение».
Но бес, как известно, кроется в деталях. Поскольку смешанная нагрузка увеличивает ток в сети, возникают проблемы на электростанциях, где электроэнергия вырабатывается синхронными генераторами, а именно: индуктивная нагрузка «развозбуждает» генератор, и приведение его в прежнее состояние обходится в затраты уже реальной активной мощности на его «довозбуждение».
Таким образом, заставить потребителя платить за потребляемую реактивную индуктивную мощность вполне справедливо. Это побуждает потребителя компенсировать реактивную составляющую своей нагрузки, а, поскольку эта составляющая в основном индуктивная, компенсация заключается в подключении конденсаторов наперед рассчитанной емкости.
Потребитель находит возможность платить меньше
Если потребителем оплачивается отдельно потребляемая активная и реактивная мощность. Он готов идти на дополнительные затраты и устанавливать на своем предприятии батареи конденсаторов, включаемые строго по графику в зависимости от средней статистики потребления электроэнергии по часам суток.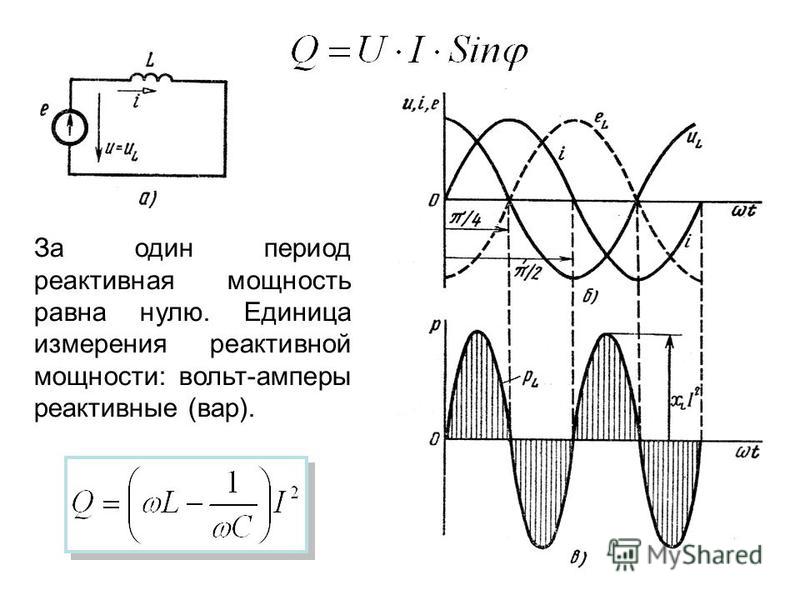
Существует также возможность установки на предприятии специальных устройств (компенсаторов реактивной мощности), подключающих конденсаторы автоматически в зависимости от величины и характера потребляемой в данный момент мощности. Эти компенсаторы позволяют поднять значение коэффициента мощности с 0,6 до 0,97, т.е. практически до единицы.
Принято также, что если соотношение потребленной реактивной энергии и общей не превышает 0,15, то корпоративный потребитель от оплаты за реактивную энергию освобождается.
Что же касается индивидуальных потребителей, то, ввиду сравнительно невысокой потребляемой ими мощности, разделять счета на оплату потребляемой электроэнергии на активную и реактивную не принято. Бытовые однофазные счетчики электрической энергии учитывают лишь активную мощность электрической нагрузки, за нее и выставляется счет на оплату. Т.е. в настоящее время даже не существует технической возможности выставить индивидуальному потребителю счет за потребленную реактивную мощность.
Особых стимулов компенсировать индуктивную составляющую нагрузки у потребителя нет, да это и сложно осуществить технически. Постоянно подключенные конденсаторы при отключении индуктивной нагрузки будут бесполезно нагружать подводящую электропроводку. За электросчетчиком (перед счетчиком тоже, но за то потребитель не платит), что вызовет потребление активной мощности с соответствующим увеличением счета на оплату, а автоматические компенсаторы дороги и вряд ли оправдают затраты на их приобретение.
Другое дело, что производитель иногда устанавливает компенсационные конденсаторы на входе потребителей с индуктивной составляющей нагрузки. Эти конденсаторы, при правильном их подборе, несколько снизят потери энергии в подводящих проводах, при этом несколько повысив напряжение на подключенном электроприборе за счет уменьшения падения напряжения на подводящих проводах.
Но, что самое главное, компенсация реактивной энергии у каждого потребителя, от квартиры до огромного предприятия, снизит токи во всех линиях электропитания, от электростанции до квартирного щитка. За счет реактивной составляющей полного тока, что уменьшит потери энергии в линиях и повысит коэффициент полезного действия электросистем.
За счет реактивной составляющей полного тока, что уменьшит потери энергии в линиях и повысит коэффициент полезного действия электросистем.
Похожие темы:
- Приборы для экономии электроэнергии. работа и альтернатива
- Компенсация реактивной мощности. Виды и нагрузки. Применение
- Перекос фаз. Причины возникновения и устранение. Защита
- Качество электроэнергии. Показатели и характеристики. Факторы
- Трехфазные и однофазные сети. Отличия. Преимущества и недостатки
- Глухозаземленная нейтраль
- Изолированная нейтраль. Устройство и принцип действия
активная, реактивная, полная (P, Q, S), коэффициент мощности (PF)
Из письма клиента:
Подскажите, ради Бога, почему мощность ИБП указывается в Вольт-Амперах, а не в привычных для всех киловаттах. Это сильно напрягает. Ведь все уже давно привыкли к киловаттам. Да и мощность всех приборов в основном указана в кВт.
Алексей. 21 июнь 2007
В технических характеристиках любого ИБП указаны полная мощность [кВА] и активная мощность [кВт] – они характеризуют нагрузочную способность ИБП. Пример, см. фотографии ниже:
Пример, см. фотографии ниже:
Мощность не всех приборов указана в Вт, например:
- Мощность трансформаторов указывается в ВА:
http://www.mstator.ru/products/sonstige/powertransf (трансформаторы ТП: см приложение)
http://metz.by/download_files/catalog/transform/tsgl__tszgl__tszglf.pdf (трансформаторы ТСГЛ: см приложение) - Мощность конденсаторов указывается в Варах:
http://www.elcod.spb.ru/catalog/k78-39.pdf (конденсаторы K78-39: см приложение)
http://www.kvar.su/produkciya/25-nizkogo-napraygeniya-vbi (конденсаторы УК: см приложение) - Примеры других нагрузок — см. приложения ниже.
Мощностные характеристики нагрузки можно точно задать одним единственным параметром (активная мощность в Вт) только для случая постоянного тока, так как в цепи постоянного тока существует единственный тип сопротивления – активное сопротивление.
Мощностные характеристики нагрузки для случая переменного тока невозможно точно задать одним единственным параметром, так как в цепи переменного тока существует два разных типа сопротивления – активное и реактивное. Поэтому только два параметра: активная мощность и реактивная мощность точно характеризуют нагрузку.
Принцип действия активного и реактивного сопротивлений совершенно различный. Активное сопротивление – необратимо преобразует электрическую энергию в другие виды энергии (тепловую, световую и т.д.) – примеры: лампа накаливания, электронагреватель (параграф 39, Физика 11 класс В.А. Касьянов М.: Дрофа, 2007).
Реактивное сопротивление – попеременно накапливает энергию затем выдаёт её обратно в сеть – примеры: конденсатор, катушка индуктивности (параграф 40,41, Физика 11 класс В.А. Касьянов М.: Дрофа, 2007).
Дальше в любом учебнике по электротехнике Вы можете прочитать, что активная мощность (рассеиваемая на активном сопротивлении) измеряется в ваттах, а реактивная мощность (циркулирующая через реактивное сопротивление) измеряется в варах; так же для характеристики мощности нагрузки используют ещё два параметра: полную мощность и коэффициент мощности. Все эти 4 параметра:
Все эти 4 параметра:
- Активная мощность: обозначение P, единица измерения: Ватт
- Реактивная мощность: обозначение Q, единица измерения: ВАр (Вольт Ампер реактивный)
- Полная мощность: обозначение S, единица измерения: ВА (Вольт Ампер)
- Коэффициент мощности: обозначение k или cosФ, единица измерения: безразмерная величина
Эти параметры связаны соотношениями: S*S=P*P+Q*Q, cosФ=k=P/S
Также cosФ называется коэффициентом мощности (Power Factor – PF)
Поэтому в электротехнике для характеристики мощности задаются любые два из этих параметров так как остальные могут быть найдены из этих двух.
Например, электромоторы, лампы (разрядные) — в тех. данных указаны P[кВт] и cosФ:
http://www.mez.by/dvigatel/air_table2.shtml (двигатели АИР: см. приложение)
приложение)
http://www.mscom.ru/katalog.php?num=38 (лампы ДРЛ: см. приложение)
(примеры технических данных разных нагрузок см. приложение ниже)
То же самое и с источниками питания. Их мощность (нагрузочная способность) характеризуется одним параметром для источников питания постоянного тока – активная мощность (Вт), и двумя параметрами для ист. питания переменного тока. Обычно этими двумя параметрами являются полная мощность (ВА) и активная (Вт). См. например параметры ДГУ и ИБП.
Большинство офисной и бытовой техники, активные (реактивное сопротивление отсутствует или мало), поэтому их мощность указывается в Ваттах. В этом случае при расчёте нагрузки используется значение мощности ИБП в Ваттах. Если нагрузкой являются компьютеры с блоками питания (БП) без коррекции входного коэффициента мощности (APFC), лазерный принтер, холодильник, кондиционер, электромотор (например погружной насос или мотор в составе станка), люминисцентные балластные лампы и др. – при расчёте используются все вых. данные ибп: кВА, кВт, перегрузочные характеристики и др.
– при расчёте используются все вых. данные ибп: кВА, кВт, перегрузочные характеристики и др.
См. учебники по электротехнике, например:
1. Евдокимов Ф. Е. Теоретические основы электротехники. — М.: Издательский центр «Академия», 2004.
2. Немцов М. В. Электротехника и электроника. — М.: Издательский центр «Академия», 2007.
3. Частоедов Л. А. Электротехника. — М.: Высшая школа, 1989.
Так же см. AC power, Power factor, Electrical resistance, Reactance http://en.wikipedia.org
(перевод: http://electron287.narod.ru/pages/page1.html)
Приложение
Пример 1: мощность трансформаторов и автотрансформаторов указывается в ВА (Вольт·Амперах)
Трансформаторы питания номинальной выходной мощностью 25-60 ВА
http://www.mstator.ru/products/sonstige/powertransf (трансформаторы ТП)
|
|
http://metz. by/download_files/catalog/transform/tsgl__tszgl__tszglf.pdf (трансформаторы ТСГЛ)
by/download_files/catalog/transform/tsgl__tszgl__tszglf.pdf (трансформаторы ТСГЛ)
|
| |
| АОСН-2-220-82 | |
| Латр 1.25 | АОСН-4-220-82 |
| Латр 2.5 | АОСН-8-220-82 |
| АОСН-20-220 | |
| АОМН-40-220 | |
http://www.gstransformers.com/products/voltage-regulators.html (ЛАТР / лабораторные автотрансформаторы TDGC2)
Пример 2: мощность конденсаторов указывается в Варах (Вольт·Амперах реактивных)
http://www. elcod.spb.ru/catalog/k78-39.pdf (конденсаторы K78-39)
elcod.spb.ru/catalog/k78-39.pdf (конденсаторы K78-39)
http://www.kvar.su/produkciya/25-nizkogo-napraygeniya-vbi (конденсаторы УК)
Пример 3: технические данные электромоторов содержат активную мощность (кВт) и cosФ
Для таких нагрузок как электромоторы, лампы (разрядные), компьютерные блоки питания, комбинированные нагрузки и др. — в технических данных указаны P [кВт] и cosФ (активная мощность и коэффициент мощности) или S [кВА] и cosФ (полная мощность и коэффициент мощности).
http://www.mez.by/dvigatel/air_table2.shtml (двигатели АИР)
http://www.weiku.com/products/10359463/Stainless_Steel_cutting_machine.html
(комбинированная нагрузка – станок плазменной резки стали / Inverter Plasma cutter LGK160 (IGBT)
Технические данные разрядных ламп содержат активную мощность (кВт) и cosФ
http://www. mscom.ru/katalog.php?num=38 (лампы ДРЛ)
mscom.ru/katalog.php?num=38 (лампы ДРЛ)
http://www.silverstonetek.com.tw/product.php?pid=365&area=en (блок питания ПК)
Дополнение 1
Если нагрузка имеет высокий коэффициент мощности (0.8 … 1.0), то её свойства приближаются к активной нагрузке. Такая нагрузка является идеальной как для сетевой линии, так и для источников электроэнергии, т.к. не порождает реактивных токов и мощностей в системе.
Если нагрузка имеет низкий коэффициент мощности (менее 0.8 … 1.0), то в линии питания циркулируют большие реактивные токи (и мощности). Это паразитное явление приводит к повышению потерь в проводах линии (нагрев и др.), нарушению режима работы источников (генераторов) и трансформаторов сети, а также др. проблемам.
Поэтому во многих странах приняты стандарты нормирующие коэффициент мощности оборудования.
Дополнение 2
Оборудование однонагрузочное (например, БП ПК) и многосоставное комбинированное (например, фрезерный промышленный станок, имеющий в составе несколько моторов, ПК, освещение и др. ) имеют низкие коэффициенты мощности (менее 0.8) внутренних агрегатов (например, выпрямитель БП ПК или электромотор имеют коэффициент мощности 0.6 .. 0.8). Поэтому в настоящее время большинство оборудования имеет входной блок корректора коэффициента мощности. В этом случае входной коэффициент мощности равен 0.9 … 1.0, что соответствует нормативным стандартам.
) имеют низкие коэффициенты мощности (менее 0.8) внутренних агрегатов (например, выпрямитель БП ПК или электромотор имеют коэффициент мощности 0.6 .. 0.8). Поэтому в настоящее время большинство оборудования имеет входной блок корректора коэффициента мощности. В этом случае входной коэффициент мощности равен 0.9 … 1.0, что соответствует нормативным стандартам.
Дополнение 3. Важное замечание относительно коэффициента мощности ИБП и стабилизаторов напряжения
Нагрузочная способность ИБП и ДГУ нормирована на стандартную промышленную нагрузку (коэффициент мощности 0.8 с индуктивным характером). Например, ИБП 100 кВА / 80 кВт. Это означает, что устройство может питать активную нагрузку максимальной мощности 80 кВт, или смешанную (активно-реактивную) нагрузку максимальной мощности 100 кВА с индуктивным коэффициентом мощности 0.8.
В стабилизаторах напряжения дело обстоит иначе. Для стабилизатора коэффициент мощности нагрузки безразличен. Например, стабилизатор напряжения 100 кВА. Это означает, что устройство может питать активную нагрузку максимальной мощности 100 кВт, или любую другую (чисто активную, чисто реактивную, смешанную) мощностью 100 кВА или 100 кВАр с любым коэффициентом мощности емкостного или индуктивного характера. Обратите внимание, что это справедливо для линейной нагрузки (без высших гармоник тока). При больших гармонических искажениях тока нагрузки (высокий КНИ) выходная мощность стабилизатора снижается.
Это означает, что устройство может питать активную нагрузку максимальной мощности 100 кВт, или любую другую (чисто активную, чисто реактивную, смешанную) мощностью 100 кВА или 100 кВАр с любым коэффициентом мощности емкостного или индуктивного характера. Обратите внимание, что это справедливо для линейной нагрузки (без высших гармоник тока). При больших гармонических искажениях тока нагрузки (высокий КНИ) выходная мощность стабилизатора снижается.
Дополнение 4
Наглядные примеры чистой активной и чистой реактивных нагрузок:
- К сети переменного тока 220 VAC подключена лампа накаливания 100 Вт – везде в цепи есть ток проводимости (через проводники проводов и вольфрамовый волосок лампы). Характеристики нагрузки (лампы): мощность S=P~=100 ВА=100 Вт, PF=1 => вся электрическая мощность активная, а значит она целиком поглащается в лампе и превращается в мощность тепла и света.
- К сети переменного тока 220 VAC подключен неполярный конденсатор 7 мкФ – в цепи проводов есть ток проводимости, внутри конденсатора идёт ток смещения (через диэлектрик).
 Характеристики нагрузки (конденсатора): мощность S=Q~=100 ВА=100 ВАр, PF=0 => вся электрическая мощность реактивная, а значит она постоянно циркулирует от источника к нагрузке и обратно, опять к нагрузке и т.д.
Характеристики нагрузки (конденсатора): мощность S=Q~=100 ВА=100 ВАр, PF=0 => вся электрическая мощность реактивная, а значит она постоянно циркулирует от источника к нагрузке и обратно, опять к нагрузке и т.д.
Дополнение 5
Для обозначения преобладающего реактивного сопротивления (индуктивного либо ёмкостного) коэффициенту мощности приписывается знак:
+ (плюс) – если суммарное реактивное сопротивление является индуктивным (пример: PF=+0.5). Фаза тока отстаёт от фазы напряжения на угол Ф.
— (минус) – если суммарное реактивное сопротивление является ёмкостным (пример: PF=-0,5). Фаза тока опережает фазу напряжения на угол Ф.
Дополнение 6
В различных областях техники мощность может быть либо полезной, либо паразитной НЕЗАВИСИМО от того активная она или реактивная. Например, необходимо различать активную полезную мощность рассеиваемую на рабочей нагрузке и активную паразитную мощность рассеиваемую в линии электропередачи. Так, например, в электротехнике при расчете активной и реактивной мощностей наиболее часто активная мощность является полезной мощностью, передаваемой в нагрузку и является реальной (не мнимой) величиной. А в электронике при расчёте конденсаторов или расчёте самих линий передач активная мощность является паразитной мощностью, теряемой на разогрев конденсатора (или линии) и является мнимой величиной. Причём, деление на мнимые и немнимые величины производится только для удобства рассчётов. На самом деле, все физические величины конечно реальные.
Так, например, в электротехнике при расчете активной и реактивной мощностей наиболее часто активная мощность является полезной мощностью, передаваемой в нагрузку и является реальной (не мнимой) величиной. А в электронике при расчёте конденсаторов или расчёте самих линий передач активная мощность является паразитной мощностью, теряемой на разогрев конденсатора (или линии) и является мнимой величиной. Причём, деление на мнимые и немнимые величины производится только для удобства рассчётов. На самом деле, все физические величины конечно реальные.
Дополнительные вопросы
Вопрос 1:
Почему во всех учебниках электротехники при расчете цепей переменного тока используют мнимые числа / величины (например, реактивная мощность, реактивное сопротивление и др.), которые не существуют в реальности?
Ответ:
Да, все отдельные величины в окружающем мире – действительные. В том числе температура, реактивное сопротивление, и т.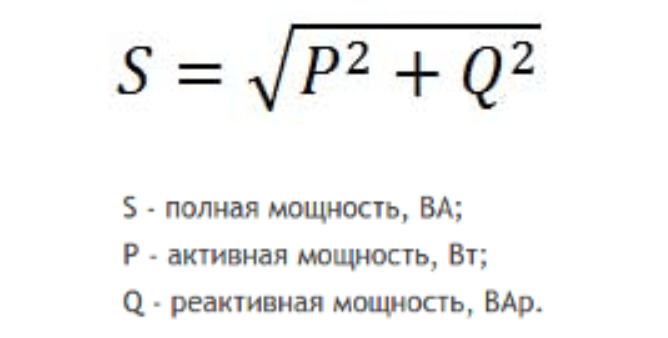 д. Использование мнимых (комплексных) чисел – это только математический приём, облегчающий вычисления. В результате вычисления получается обязательно действительное число. Пример: реактивная мощность нагрузки (конденсатора) 20кВАр – это реальный поток энергии, то есть реальные Ватты, циркулирующие в цепи источник–нагрузка. Но что бы отличить эти Ватты от Ваттов, безвозвратно поглащаемых нагрузкой, эти «циркулирующие Ватты» решили называть Вольт·Амперами реактивными [6].
д. Использование мнимых (комплексных) чисел – это только математический приём, облегчающий вычисления. В результате вычисления получается обязательно действительное число. Пример: реактивная мощность нагрузки (конденсатора) 20кВАр – это реальный поток энергии, то есть реальные Ватты, циркулирующие в цепи источник–нагрузка. Но что бы отличить эти Ватты от Ваттов, безвозвратно поглащаемых нагрузкой, эти «циркулирующие Ватты» решили называть Вольт·Амперами реактивными [6].
Замечание:
Раньше в физике использовались только одиночные величины и при расчете все математические величины соответствовали реальным величинам окружающего мира. Например, расстояние равно скорость умножить на время (S=v*t). Затем с развитием физики, то есть по мере изучения более сложных объектов (свет, волны, переменный электрический ток, атом, космос и др.) появилось такое большое количество физических величин, что рассчитывать каждую в отдельности стало невозможно. Это проблема не только ручного вычисления, но и проблема составления программ для ЭВМ. Для решения данное задачи близкие одиночные величины стали объединять в более сложные (включающие 2 и более одиночных величин), подчиняющиеся известным в математике законам преобразования. Так появились скалярные (одиночные) величины (температура и др.), векторные и комплексные сдвоенные (импеданс и др.), векторные строенные (вектор магнитного поля и др.), и более сложные величины – матрицы и тензоры (тензор диэлектрической проницаемости, тензор Риччи и др.). Для упрощения рассчетов в электротехнике используются следующие мнимые (комплексные) сдвоенные величины:
Для решения данное задачи близкие одиночные величины стали объединять в более сложные (включающие 2 и более одиночных величин), подчиняющиеся известным в математике законам преобразования. Так появились скалярные (одиночные) величины (температура и др.), векторные и комплексные сдвоенные (импеданс и др.), векторные строенные (вектор магнитного поля и др.), и более сложные величины – матрицы и тензоры (тензор диэлектрической проницаемости, тензор Риччи и др.). Для упрощения рассчетов в электротехнике используются следующие мнимые (комплексные) сдвоенные величины:
- Полное сопротивление (импеданс) Z=R+iX
- Полная мощность S=P+iQ
- Диэлектрическая проницаемость e=e’+ie»
- Магнитная проницаемость m=m’+im»
- и др.
Вопрос 2:
На странице http://en.wikipedia.org/wiki/Ac_power показаны S P Q Ф на комплексной, то есть мнимой / несуществующей плоскости. Какое отношение это все имеет к реальности?
Ответ:
Проводить расчеты с реальными синусоидами сложно, поэтому для упрощения вычислений используют векторное (комплексное) представление как на рис. выше. Но это не значит, что показанные на рисунке S P Q не имеют отношения к реальности. Реальные величины S P Q могут быть представлены в обычном виде, на основе измерений синусоидальных сигналов осциллографом. Величины S P Q Ф I U в цепи переменного тока «источник-нагрузка» зависят от нагрузки. Ниже показан пример [5] реальных синусоидальных сигналов S P Q и Ф для случая нагрузки состоящей из последовательно соединённых активного и реактивного (индуктивного) сопротивлений.
выше. Но это не значит, что показанные на рисунке S P Q не имеют отношения к реальности. Реальные величины S P Q могут быть представлены в обычном виде, на основе измерений синусоидальных сигналов осциллографом. Величины S P Q Ф I U в цепи переменного тока «источник-нагрузка» зависят от нагрузки. Ниже показан пример [5] реальных синусоидальных сигналов S P Q и Ф для случая нагрузки состоящей из последовательно соединённых активного и реактивного (индуктивного) сопротивлений.
Вопрос 3:
Обычными токовыми клещами и мультиметром измерен ток нагрузки 10 A, и напряжение на нагрузке 225 В. Перемножаем и получаем мощность нагрузки в Вт: 10 A · 225В = 2250 Вт.
Ответ:
Вы получили (рассчитали) полную мощность нагрузки 2250 ВА. Поэтому ваш ответ будет справедлив только, если ваша нагрузка чисто активная, тогда действительно Вольт·Ампер равен Ватту. Для всех других типов нагрузок (например электромотор) – нет.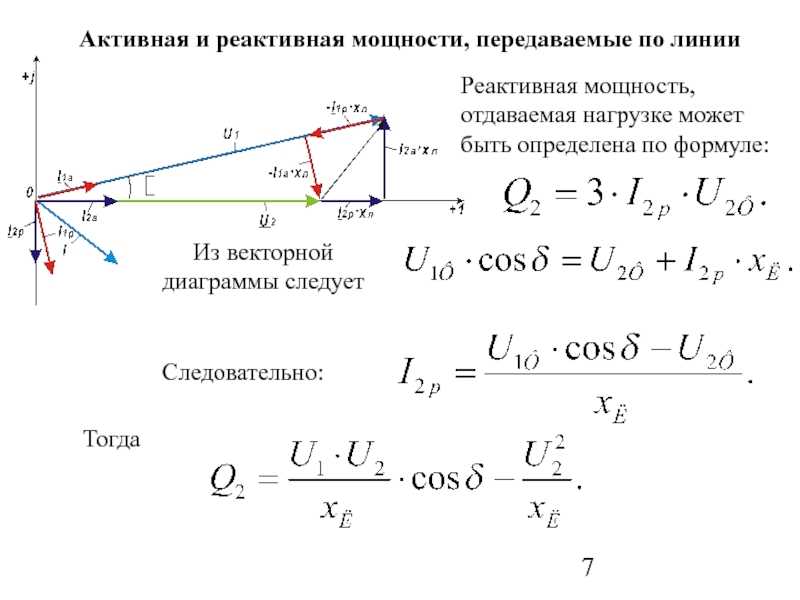 Для измерения всех характеристик любой произвольной нагрузки необходимо использовать анализатор сети, например APPA137:
Для измерения всех характеристик любой произвольной нагрузки необходимо использовать анализатор сети, например APPA137:
См. дополнительную литературу, например:
[1]. Евдокимов Ф. Е. Теоретические основы электротехники. — М.: Издательский центр «Академия», 2004.
[2]. Немцов М. В. Электротехника и электроника. — М.: Издательский центр «Академия», 2007.
[3]. Частоедов Л. А. Электротехника. — М.: Высшая школа, 1989.
[4]. AC power, Power factor, Electrical resistance, Reactance
http://en.wikipedia.org (перевод: http://electron287.narod.ru/pages/page1.html)
[5]. Теория и расчёт трансформаторов малой мощности Ю.Н.Стародубцев / РадиоСофт Москва 2005 г. / rev d25d5r4feb2013
[6]. Международная система единиц, СИ, см напр. ГОСТ 8.417-2002. ЕДИНИЦЫ ВЕЛИЧИН
Реальная, реактивная и активная мощность — интеллектуальные сети
Цепь постоянного тока
В цепи постоянного тока могут использоваться все производные формулы мощности в сочетании с законом Ома, такие как мощность = V * I, мощность = I 2 R, и мощность = V 2 /R . Единицами мощности постоянного тока являются ватты [названы в честь Джеймса Ватта (1736-1819)]. Мощность постоянного тока можно рассматривать как мощность, потребляемую резистором.
Единицами мощности постоянного тока являются ватты [названы в честь Джеймса Ватта (1736-1819)]. Мощность постоянного тока можно рассматривать как мощность, потребляемую резистором.
Цепь переменного тока
В цепи переменного тока питание становится намного сложнее. В США мощность переменного тока вырабатывается по стандарту 60 Гц, 120 вольт. Гц означает количество циклов в секунду. Следовательно, 60 раз в секунду генерируется синусоидальная волна с пиковой амплитудой приблизительно 170 вольт. Эта циклическая синусоида переменного тока может создавать три типа мощности: 1) активная мощность, 2) реактивная мощность и 3) полная мощность.
- Реальная, активная или средняя мощность — это мощность, потребляемая резистором. Обозначается буквой «П». Как и в цепях постоянного тока, реальная мощность измеряется в ваттах. Для расчета активной мощности можно использовать только две формулы мощности:
P = I 2 R или P = V 2 /R.
Примеры
#1 Рассчитайте мощность, потребляемую резистором 1 кОм, через который протекает ток 5 мА.
P = I 2 R = (5 мА) 2 *1 кОм = 25 мВт
#2 Рассчитайте мощность, потребляемую резистором 1 кОм при падении напряжения на нем 15 В.
P = V 2 /R = (15 В) 2 /1 кОм = 225 мВт
Примерами электрических устройств, потребляющих только реальную мощность, являются электрические плиты, фены, электрические водонагреватели и тостеры. - Реактивная мощность — это мощность, потребляемая катушками индуктивности и конденсаторами. Обозначается буквой «Q». Реактивная мощность измеряется в варах (реактивных вольтамперах). Следовательно, в катушках индуктивности и конденсаторах сохраняется и высвобождается в 60 раз больше энергии, чем в секунду. Индуктивное сопротивление чистых катушек индуктивности +jX л . Это означает, что индуктор на +90 градусов не совпадает по фазе с резистором (который находится на 0 градусов).
 Емкостное сопротивление чистого конденсатора -jX C . Это означает, что конденсатор на -90 градусов не совпадает по фазе с резистором (который находится на 0 градусов). Чистое реактивное сопротивление в цепи равно X = +jX L -jX C . Следовательно, реактивное сопротивление всегда будет либо чистым емкостным, либо чистым индуктивным. Для расчета реактивной мощности можно использовать только две формулы мощности:
Емкостное сопротивление чистого конденсатора -jX C . Это означает, что конденсатор на -90 градусов не совпадает по фазе с резистором (который находится на 0 градусов). Чистое реактивное сопротивление в цепи равно X = +jX L -jX C . Следовательно, реактивное сопротивление всегда будет либо чистым емкостным, либо чистым индуктивным. Для расчета реактивной мощности можно использовать только две формулы мощности:
Q = I 2 X или Q = V 2 /X. Если чистое реактивное сопротивление индуктивное, Q положительное, а если чистое реактивное сопротивление емкостное, Q отрицательное.
Примеры
#1 Рассчитайте мощность, потребляемую индуктивным сопротивлением 2 кОм при протекании через него тока 4 мА.
Q = I 2 R = (4 мА) 2 *2 кОм = 32 мВАР
#2 Рассчитайте мощность, потребляемую катушкой индуктивности 1 кОм при падении напряжения на ней 15 В.
P = V 2 /XL = (15v) 2 /1 кОм = 225 мВАР
Примерами электрических устройств, генерирующих некоторую реактивную мощность, являются микроволновые печи, стиральные машины, вентиляторы и кондиционеры. - Полная мощность представляет собой гипотенузу активной и реактивной мощности (см. рисунок ниже). Обозначается буквой «С». Полная мощность измеряется в ВА (Вольт-Ампер). Полная мощность полезна, поскольку она показывает общий ток, используемый комбинацией резистивных, индуктивных и емкостных компонентов. Полная мощность = V*I. S = sqrt(R 2 + Q 2 ).
изображение автора - Коэффициент мощности
Коэффициент мощности определяется как Fp = cos Θ. Где Θ — угол в треугольнике мощности, показанном выше (угол между кажущейся мощностью и реальной мощностью). Если Fp = 1 (единица), то реальная и кажущаяся мощности совпадают; следовательно, реактивная мощность будет равна нулю. В идеале коммунальные предприятия хотели бы, чтобы все потребители электроэнергии просто использовали только реальную мощность, чтобы коэффициент мощности оставался равным единице. Дома в среднем имеют коэффициент мощности 0,9.5, рестораны 0,88 и промышленное производство 0,77 (Кутитас 15).
Дома в среднем имеют коэффициент мощности 0,9.5, рестораны 0,88 и промышленное производство 0,77 (Кутитас 15).
ПРИМЕРЫ
Вот несколько примеров. В таблице ниже предполагается источник переменного тока 120 В и R L = 5 Ом для всех катушек индуктивности.Значение Общее сопротивление = RL + R Импеданс прямоугольный Текущий Реальная мощность Реактивная мощность Полная мощность Коэффициент мощности 1 мкФ + 47 мГн f = 100 Гц
5 Ом 5 + j29 -j 1592 Ом = 5 -j1562 Ом 76,8 мА 29,5 мВт -9,2 ВАР 9,2 ВА приблизительно 0 1 мкФ + 47 мГн f = 1 кГц
5 Ом 5 + j295 -j 159 Ом = 5 +j139 Ом 863 мА 3,74 Вт +104 ВАР 104 ВА приблизительно 0 1 мкФ + 47 мГн f = 10 кГц
5 Ом 5 + j2953 -j 16 Ом = 5 +j2938 Ом 40,8 мА 8,3 мВт +4,9 ВАР 4,9 ВА приблизительно 0 300 Ом + 47 мГн + 1 мкФ f = 100 Гц
305 Ом 305 + j29 -j 1592 Ом = 305 -j1562 Ом 75,4 мА 1,73 Вт -8,88 ВАР 9,04 ВА 0,191 300 Ом + 47 мГн + 1 мкФ f = 1 кГц
305 Ом 305 + j295 -j 159 Ом = 305 + j139 Ом 358 мА 39,1 Вт +17,8 ВАР 43 ВА 0,909 300 Ом + 47 мГн + 1 мкФ f = 10 кГц
305 Ом 305 + j2953 -j 16 Ом = 305 +j2938 Ом 40,63 мА 503 мВт +4,84 ВАР 4,87 ВА 0,1 3,3 кОм + 22 нФ + 470 мГн f = 100 Гц 3305 Ом 3305 + j29 -j 1592 Ом = 3305 -j1562 Ом 32,83 мА 3,56 Вт -1,68 ВАР 3,94 ВА 0,904 3,3 кОм + 22 нФ + 470 мГн f = 1 кГц 3305 Ом 3305 + j295 -j 159 Ом = 3305 +j139 Ом 36,3 мА 4,34 Вт +183 мВАр 4,34 ВА примерно 1 3,3 кОм + 22 нФ + 470 мГн f = 10 кГц 3305 Ом 3305 + j2953 -j 16 Ом = 3305 +j2938 Ом 27,13 мА 2,43 Вт +2,16 ВАР 3,256 ВА 0,746 Выполните прилагаемый рабочий лист https://kirkwood.
 pressbooks.pub/app/uploads/sites/13/2022/01/Real-Reactive-and-Apparent-Power-2.docx
pressbooks.pub/app/uploads/sites/13/2022/01/Real-Reactive-and-Apparent-Power-2.docxПроцитированные работы
Кутитас, Джордж и Стэн Макклеллан. Smart Grid как платформа для разработки приложений . Дом Артех, 2017.
Активная, реактивная и полная мощность
Многие практические схемы содержат комбинацию резистивных, индуктивных и емкостных элементов. Эти элементы вызывают фазовый сдвиг между параметрами электропитания, такими как напряжение и ток.
[адсенс1]
Из-за поведения напряжения и тока, особенно при воздействии этих компонентов, величина мощности принимает различные формы.
В цепях переменного тока амплитуды напряжения и тока постоянно изменяются с течением времени. Поскольку мощность представляет собой произведение напряжения на ток, она будет максимальной, когда токи и напряжения совпадают друг с другом.
Это означает, что нулевая и максимальная точки на кривых тока и напряжения возникают одновременно. Это можно назвать полезной мощностью.
Это можно назвать полезной мощностью.
В случае элементов катушки индуктивности или конденсатора существует 90 0 фазовый сдвиг между напряжением и током. Таким образом, мощность будет иметь нулевое значение каждый раз, когда либо напряжение, либо ток имеют нулевое значение.
Это нежелательное состояние, поскольку на нагрузке не выполняется работа, даже если источник вырабатывает энергию. Эта мощность называется реактивной мощностью. Кратко обсудим эти формы мощности в электрических цепях переменного тока.
Краткое описание
Питание в цепях переменного тока
Мощность в любой электрической цепи можно получить путем умножения значений напряжения и тока в этой цепи. Это применимо как для цепей постоянного, так и переменного тока.
т. е. мощность = (значение тока) x (значение напряжения)
P = V x I
Мощность измеряется в ваттах. В цепях постоянного тока и чистых цепях переменного тока без каких-либо нелинейных компонентов формы сигналов тока и напряжения находятся «в фазе».
[adsense2]
Таким образом, мощность в любой момент времени в этой цепи получается путем умножения напряжения и тока. Однако в случае цепей переменного тока это будет не так (выше упоминалось о наличии фазового сдвига).
Рассмотрим описанную выше цепь, в которой переменный ток подается на нагрузку. Напряжения и токи в цепи задаются как = √2 I sin (ωt ± ϕ)
Где V (= Vm/√2) и I (= Im/√2) – среднеквадратичные значения приложенного напряжения и тока, протекающего по цепи соответственно. Φ — разность фаз между напряжением и током, где знак + указывает на опережающий фазовый угол, а отрицательный указывает на отстающий фазовый угол.
Тогда мгновенная мощность, отдаваемая источником в нагрузку, определяется как cos ϕ (1 – cos 2wt) ± VI sin ϕ sin2wt
Приведенное выше уравнение мощности состоит из двух членов, а именно
- Член, пропорциональный VI cos ϕ, который пульсирует вокруг среднего значения VI cos ϕ
- Член, пропорциональный VI sin ϕ, пульсирующий с удвоенной частотой питания, дающий в среднем нулевое значение за цикл.

Итак, в цепях переменного тока есть 3 формы мощности. Это
- Активная мощность или Истинная мощность или Реальная мощность
- Реактивная мощность
- Полная мощность
Активная мощность
Фактическое количество мощности, рассеиваемой или выполняющей полезную работу в цепи, называется активной, истинной или реальной мощностью. Измеряется в ваттах, практически измеряется в кВ (киловаттах) и МВт (мегаваттах) в энергосистемах.
Обозначается буквой P (заглавная) и равен среднему значению p = VI cos ϕ. Это желаемый результат электрической системы, которая управляет цепью или нагрузкой.
P = VI cos ϕ
Реактивная мощность
Среднее значение второго члена в полученном выше выражении равно нулю, поэтому мощность, вносимая этим членом, равна нулю. Составляющая, пропорциональная VI sin ϕ, называется реактивной мощностью и обозначается буквой Q.
Хотя это и мощность, но не измеряемая в ваттах, так как это неактивная мощность и, следовательно, она измеряется в Вольт-ампер-реактивная (ВАР). Значение этой реактивной мощности может быть отрицательным или положительным в зависимости от коэффициента мощности нагрузки.
Значение этой реактивной мощности может быть отрицательным или положительным в зависимости от коэффициента мощности нагрузки.
Это связано с тем, что индуктивная нагрузка потребляет реактивную мощность, а емкостная нагрузка генерирует реактивную мощность.
Q = VI sin ϕ
Значение реактивной мощности
Реактивная мощность является одной из составляющих общей мощности, которые перемещаются туда и обратно в цепи или линии. Его можно назвать скоростью изменения энергии во времени, которое продолжает течь от источника к реактивным компонентам в течение положительного полупериода и обратно к компонентам от источника во время отрицательного цикла. Поэтому он никогда не потребляется нагрузкой.
В обычном смысле эта фиктивная мощность вовсе не мощность, а лишь степенная мера реактивной составляющей тока. При наличии избыточной реактивной мощности коэффициент мощности значительно снижается. Такой низкий коэффициент мощности нежелателен с точки зрения эффективности работы и эксплуатационных расходов.
А также эта мощность вызывает дополнительный ток от источника питания, что приводит к дополнительным потерям и увеличению мощности оборудования. Вот почему эту мощность в шутку называют холестерином линий электропередач.
Чтобы свести к минимуму потери и увеличить мощность имеющегося оборудования, коммунальные предприятия используют методы компенсации VAR или оборудование для коррекции коэффициента мощности. Как правило, эти методы реактивной компенсации реализуются на стороне нагрузки.
Однако эта реактивная мощность полезна для создания необходимых магнитных полей для работы индуктивных устройств, таких как трансформаторы, двигатели переменного тока и т. д. Она также помогает регулировать напряжение в мощных механизмах электропитания.
Полная мощность
Комплексная комбинация истинной или активной мощности и реактивной мощности называется полной мощностью. Без привязки к какому-либо фазовому углу произведение напряжения и тока дает полную мощность. Полная мощность полезна для оценки силового оборудования.
Полная мощность полезна для оценки силового оборудования.
Его также можно выразить как квадрат тока, умноженный на импеданс цепи. Обозначается буквой S и измеряется в вольт-амперах (ВА), практические единицы включают кВА (киловольт-ампер) и МВА (мегавольт-ампер).
Полная мощность = среднеквадратичное напряжение × среднеквадратичное значение тока
Полная мощность, S = V × I
В комплексной форме, S = V I*
S = V ∠0 0 I ∠ ϕ (для тока отстающей нагрузки)
S = V I ∠ ϕ
S = V I cos ϕ + jV I sin ϕ
S = P + jQ
Или S = I 2 Z
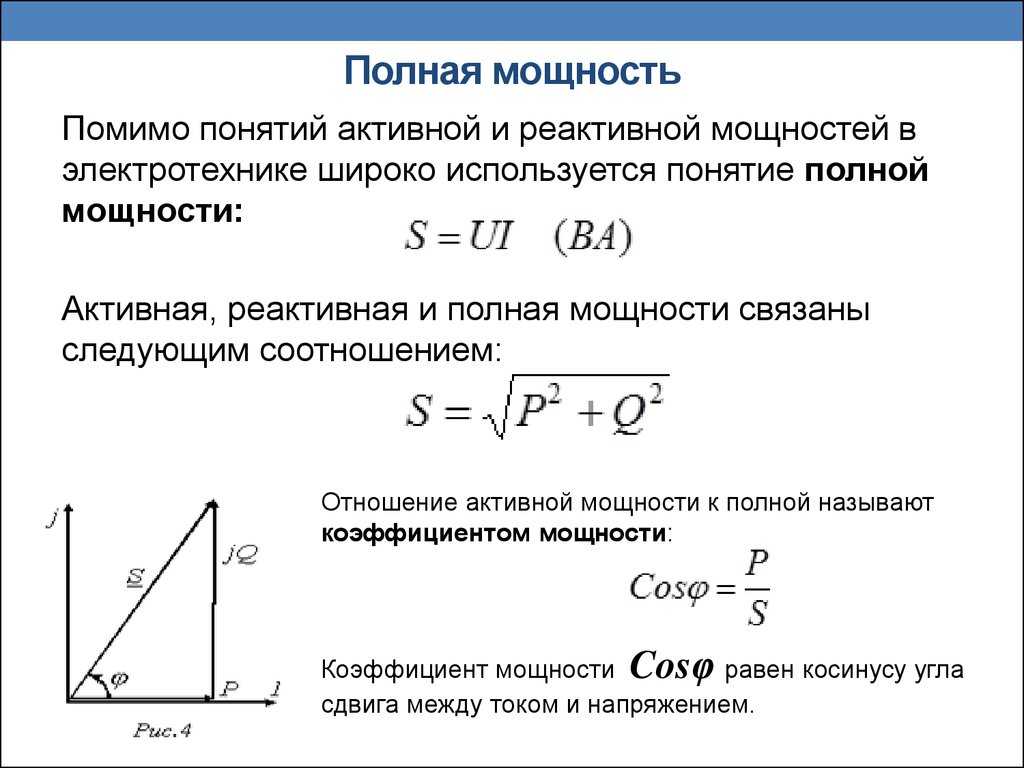
Мощный треугольник
Соотношение между активной и реактивной мощностью может быть выражен путем представления величин в виде векторов, что также называется методом треугольника мощности, как показано ниже. На этой векторной диаграмме напряжение рассматривается как опорный вектор. Диаграмма векторов напряжения и тока является основой для формирования треугольника мощности.
На рисунке (a) ток отстает от приложенного напряжения на угол ϕ. Горизонтальная составляющая тока равна I cos ϕ, а вертикальная составляющая тока равна I sin ϕ. Если каждый вектор тока умножить на напряжение V, получится треугольник мощности, как показано на рисунке (b).
В активную мощность входит составляющая I cos ϕ, совпадающая по фазе с напряжением, в то время как реактивная мощность создается квадратурной составляющей.
Таким образом, полная мощность или гипотенуза треугольника получается путем векторного объединения активной и реактивной мощностей.
По теореме Пифагора сумма квадратов двух соседних сторон (активная мощность и реактивная мощность) равна квадрату диагонали (полной мощности). т.е.,
(видимая мощность) 2 = (реальная мощность) 2
S 2 = P 2 + Q 2
S = √ ((Q 2 + P 2 2 ))
Где
S = полная мощность, измеренная в киловольт-амперах, кВА
Q = реактивная мощность, измеренная в киловольт-амперах реактивная, кВАр
P = активная мощность, измеренная в киловаттах, кВт
С точки зрения резистивных, индуктивных и импедансных элементов формы мощности могут быть выражены как
Активная мощность = P = I 2 R
Реактивная мощность = Q = I 2 X
Полная мощность = S = I 2 Z
Где
X — индуктивность,
Z — импеданс.

 Характеристики нагрузки (конденсатора): мощность S=Q~=100 ВА=100 ВАр, PF=0 => вся электрическая мощность реактивная, а значит она постоянно циркулирует от источника к нагрузке и обратно, опять к нагрузке и т.д.
Характеристики нагрузки (конденсатора): мощность S=Q~=100 ВА=100 ВАр, PF=0 => вся электрическая мощность реактивная, а значит она постоянно циркулирует от источника к нагрузке и обратно, опять к нагрузке и т.д.
 Емкостное сопротивление чистого конденсатора -jX C . Это означает, что конденсатор на -90 градусов не совпадает по фазе с резистором (который находится на 0 градусов). Чистое реактивное сопротивление в цепи равно X = +jX L -jX C . Следовательно, реактивное сопротивление всегда будет либо чистым емкостным, либо чистым индуктивным. Для расчета реактивной мощности можно использовать только две формулы мощности:
Емкостное сопротивление чистого конденсатора -jX C . Это означает, что конденсатор на -90 градусов не совпадает по фазе с резистором (который находится на 0 градусов). Чистое реактивное сопротивление в цепи равно X = +jX L -jX C . Следовательно, реактивное сопротивление всегда будет либо чистым емкостным, либо чистым индуктивным. Для расчета реактивной мощности можно использовать только две формулы мощности: 
 Дома в среднем имеют коэффициент мощности 0,9.5, рестораны 0,88 и промышленное производство 0,77 (Кутитас 15).
Дома в среднем имеют коэффициент мощности 0,9.5, рестораны 0,88 и промышленное производство 0,77 (Кутитас 15).  pressbooks.pub/app/uploads/sites/13/2022/01/Real-Reactive-and-Apparent-Power-2.docx
pressbooks.pub/app/uploads/sites/13/2022/01/Real-Reactive-and-Apparent-Power-2.docx