Сдвиг фаз переменного тока и напряжения
Мощность постоянного тока, как мы уже знаем, равна произведению напряжения на силу тока. Но при постоянном токе направления тока и напряжения всегда совпадают. При переменном же токе совпадение направлений тока и напряжения имеет место только в случае отсутствия в цепи тока конденсаторов и катушек индуктивности.
Для этого случая формула мощности
остается справедливой.
На рисунке 1 представлена кривая изменения мгновенных значений мощности для этого случая (направление тока и напряжения совпадают). Обратим внимание на то обстоятельство, что направления векторов напряжения и тока в этом случае совпадают, то есть фазы тока и напряжения всегда одинаковы.
Рисунок 1. Сдвиг фаз тока и напряжения. Сдвига фаз нет, мощность все время положительная.
При наличии в цепи переменного тока конденсатора или катушки индуктивности, фазы тока и напряжения совпадать не будут.
О причинах этого несовпадения читайте в моем учебники для емкостной цепи и для индуктивной цепи, а сейчас установим, как будет оно влиять на величину мощности переменного тока.
Представим себе, что при начале вращения радиусы-векторы тока и напряжения имеют различные направления. Так как оба вектора вращаются с одинаковой скоростью, то угол между ними будет оставаться неизменным во все время их вращения. На рисунке 2 изображен случай отставания вектора тока Im от вектора напряжения Um на угол в 45°.
Рисунок 2. Сдвиг фаз тока и напряжения. Фазы тока и напряжения сдвинуты на 45, мощность в некоторые периоды времени становиться отрицательной.
Рассмотрим, как будут изменяйся при этом ток и напряжение. Из построенных синусоид тока и напряжения видно, что когда напряжение проходит через ноль, ток имеет отрицательное значение.
Затем напряжение достигает своей наибольшей величины и начинает уже убывать, а ток хотя и становится положительным, но еще не достигает наибольшей величины и продолжает возрастать.
Напряжение изменило свое направление, а ток все еще течет в прежнем направлении и т. д. Фаза тока все время запаздывает по сравнению с фазой напряжения. Между фазами напряжения и тока существует постоянный сдвиг, называемый сдвигом фаз.
Действительно, если мы посмотрим на рисунок 2, то заметим, что синусоида тока сдвинута вправо относительно синусоиды напряжения. Так как по горизонтальной оси мы откладываем градусы поворота, то и сдвиг фаз можно измерять в градусах. Нетрудно заметить, что сдвиг фаз в точности равен углу между радиусами-векторами тока и напряжения.
Вследствие отставания фазы тока от фазы напряжения его направление в некоторые моменты не будет совпадать с направлением напряжения. В эти моменты мощность тока будет отрицательной, так как произведение положительной величины на отрицательную величину всегда будет отрицательным. Эта значит, что внешняя электрическая цепь в эти моменты становится не потребителем электрической энергии, а источником ее.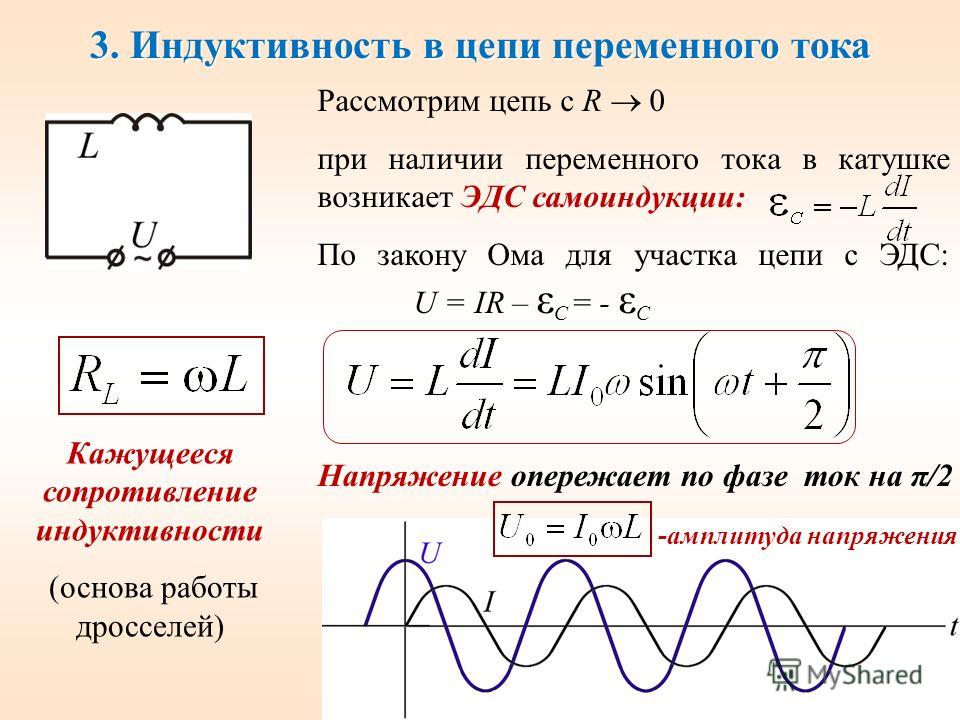
Некоторое количество энергии, поступившей в цепь во время части периода, когда мощность была положительной, возвращается источнику энергии в ту часть периода, когда мощность отрицательна.
Чем больше сдвиг фаз, тем продолжительнее становятся части периода, в течение которых мощность делается отрицательной, тем, следовательно, меньше будет средняя мощность тока.
При сдвиге фаз в 90° мощность в течение одной четверти периода будет положительной, а в течение другой четверти периода — отрицательной. Следовательно, средняя мощность тока будет равна нулю, и ток не будет производить никакой работы (рисунок 3).
Рисунок 3. Сдвиг фаз тока и напряжения. Фазы тока и напряжения сдвинуты на 90, мощность в течении одной четвери периода положительна, а в течении другой отрицательна. В среднем мощьноть равна нулю.
Теперь ясно, что мощность переменного тока при наличии сдвига фаз будет меньше произведения эффективных значений тока и напряжения, т.
е. формулы
в этом случае будут неверны
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Угол сдвига фаз между током и напряжением. Измерение и вычисление | ENARGYS.RU
Начальные фазы электромагнитных синусоидальных колебаний первичного и вторичного напряжения, с частотой одинаковой величины, могут существенно различаться на некоторый угол сдвига фаз (угол φ). Переменные величины могут неоднократно в течение определенного периода некоторого времени изменяются с определенной частотой. Если электрические процессы имеют неизменный характер, а сдвиг фаз равен нулю, это свидетельствует о синхронизме источников величин переменного напряжения, например, трансформаторов. Сдвиг фазы служит определяющим фактором коэффициента мощности в электрических сетях переменного тока.
Угол сдвига фаз находится при необходимости, тогда, если один из сигналов является опорным, а второй сигнал с фазой в самом начале совпадает с углом сдвига фаз.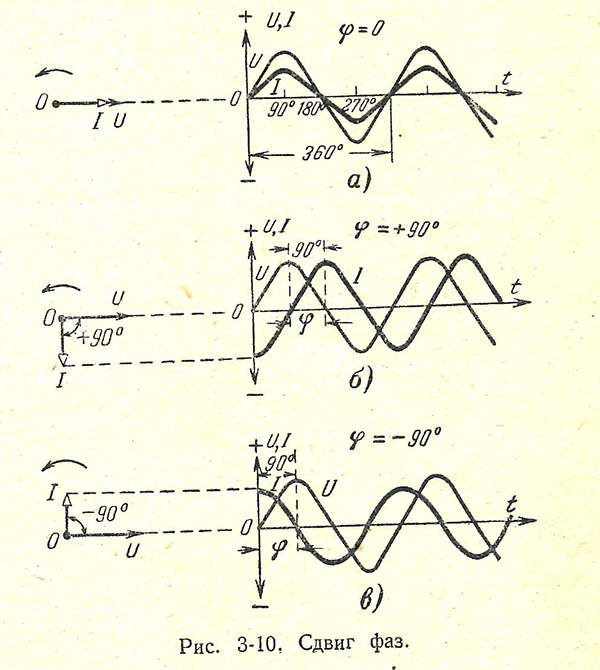
Измерение угла сдвига фаз производится прибором, в котором присутствует нормированная погрешность.
Фазометр может производить измерение угла сдвига в границах от 0о до 360о в некоторых случаях от -180оС до +180оС, а диапазон измеряемых частот сигналов может колебаться от 20Гц до 20 ГГц. Измерение гарантируется в том случае если напряжение входного сигнала равно от 1 мВ до 100 В, если же напряжение входного сигнала превышает эти границы точность измерения не гарантируется.
Методы измерения угла сдвига фаз
Существует несколько способов измерения угла сдвига фаз, это:
- Использование двухлучевого или двухканального осциллографа.
- Компенсационный метод основан на сравнении измеряемого фазового сдвига, с фазовым сдвигом, который предоставляется образцовым фазовращателем.
- Суммарно-разностный метод, он заключается в использовании гармонических или сформированных прямоугольных сигналов.
- Преобразование сдвига фаз во временном интервале.
Как измеряется угол сдвига фаз осциллографом
Осциллографический способ можно отнести к самому простейшему с погрешностью в районе 5о. Определение сдвига осуществляется при помощи осциллограмм. Существует четыре осциллографических метода:
- Применение линейной развертки.
- Метод эллипса.
- Метод круговой развертки.
- Использование яркостных меток.
Определение угла сдвига фаз зависит от характера нагрузки. При определении фазного сдвига в первичной и вторичной цепях трансформатора, углы могут считаться равными и практически не отличаются друг от друга.
Угол сдвига фаз напряжений, измеряемый по эталонному источнику частоты и при использовании измерительного органа лает возможность обеспечить точность всех последующих измерений. Фазные напряжения и угол сдвига фаз зависят от нагрузки, так симметричная нагрузка обуславливает равенство фазного напряжения , токов нагрузки и угол фазного сдвига, также будет равна нагрузка по потребляемой мощности на всех фазах электроустановки.
Угол сдвига фаз между током и напряжением в несимметричных трехфазных цепях не равны друг другу. Для того чтобы вычислить угол сдвига фаз (угол φ) в цепь включают последовательно присоединенные сопротивления (резисторы), индуктивности и конденсаторы (емкости).
Рис. №1. Последовательное соединение сопротивления, индуктивности и емкости для вычисления угла сдвига фаз. В этом контуре протекает переменный ток, который способствует возникновению ЭДС.
Рис. №2. Схема проведения опыта по определению сдвига фаз между током и напряжением. Слева показаны схемы подключения конденсаторов, катушек индуктивности и резисторов, справа показаны результаты опыта.
Из результатов опыта можно определить, что сдвиг фаз между напряжением и током служит при определении нагрузки и не может зависеть от переменных величины тока и напряжения в электрической сети.
Как вывод, можно сказать, что:
- Составляющие элементы комплексного сопротивления, такие как резистор и емкость, а также проводимость не будут взаимообратными величинами.
- Отсутствие одного из элементов делает резистивные и реактивные значения, которые входят в состав комплексного сопротивления и проводимости и делают их величинами взаимообратными.
- Реактивные величины в комплексном сопротивлении и проводимости используются с противоположным знаком.
Угол сдвига фаз между напряжением и током всегда выражается, как главный аргументированный фактор комплексного сопротивления φ.
Фазовый сдвиг
- Изучив этот раздел, вы сможете описать:
- • Фазовый сдвиг в общих компонентах переменного тока.
Рис. 5.1.1 Сопротивление в цепях переменного тока
Сопротивление в цепях переменного тока
В чисто резистивных цепях ток и напряжение изменяются одинаково и одновременно, как описано в Модуле 4.1. Это соотношение верно независимо от того, является ли приложенное напряжение постоянным или переменным. Основное отличие цепей переменного тока состоит в том, что напряжение продолжает изменяться в зависимости от формы входной волны.
Когда к чисто резистивной цепи прикладывается синусоидальное напряжение, возникает синусоидальный (синусоидальный) ток. Обе формы волны достигают своих пиковых значений в одно и то же время и проходят через ноль в одно и то же время. Поэтому говорят, что напряжение и ток в чисто резистивной цепи находятся «В ФАЗЕ» друг с другом.
Рис. 5.1.2 Индуктивность в цепях переменного тока
Индуктивность в цепях переменного тока
В чисто индуктивной цепи кривые напряжения и тока не совпадают по фазе. Индуктивность противодействует изменению тока из-за эффекта обратной ЭДС. Это приводит к тому, что ток достигает своего пикового значения через некоторое время после напряжения. Так что в индуктивной цепи ток «ОТСТАЕТ» от напряжения.
В цепях постоянного тока ток в конечном итоге устанавливается на установившееся значение, и период изменения до установившегося состояния зависит от постоянной времени (т. е. значений компонентов) цепи. Однако в цепи переменного тока, поскольку напряжение постоянно меняется, ток также продолжает изменяться, а в чисто индуктивной цепи пиковые значения тока приходятся на четверть периода (90°) после значений напряжения.
В цепи, содержащей как индуктивность, так и сопротивление, что обычно имеет место, поскольку катушка индуктивности (катушка провода) будет иметь некоторое внутреннее сопротивление, ток будет отставать от напряжения на величину между практически 0° (почти чистое сопротивление) и почти -90 ° (почти чистая индуктивность). Поскольку напряжение и ток больше не растут и не падают одновременно, в цепи происходит «ФАЗОВЫЙ СДВИГ».
Рис. 5.1.3 Емкость в цепях переменного тока
Емкость в цепях переменного тока
Емкость имеет свойство задерживать изменения напряжения, как описано в Модуле 4.3. То есть приложенное напряжение достигает устойчивого состояния только по истечении времени, определяемого постоянной времени. В цепях переменного тока напряжение и ток изменяются непрерывно, а в чисто емкостной цепи переменного тока пиковое значение осциллограммы напряжения возникает через четверть периода после пикового значения тока. Следовательно, в конденсаторе происходит фазовый сдвиг, величина фазового сдвига между напряжением и током составляет +90° для чисто емкостной цепи, где ток опережает напряжение.
Противоположный фазовый сдвиг в индуктивной цепи.
Очень ГРАЖДАНСКОЕ отношение
Один из способов запомнить эти соотношения ток/напряжение (I/V) в конденсаторах (C) и катушках индуктивности (L) состоит в том, чтобы рассмотреть положения букв в слове CIVIL. Первые три буквы CIV указывают, что в конденсаторе (C) V отстает (идет после) I, а последние три буквы VIL указывают, что I отстает (идет после) от V в катушке индуктивности (L).
Использование формулы фазового сдвига в анализе цепи переменного тока
Ключевые выводы
● Узнайте о формуле фазового сдвига.
● Получите более полное представление о важности расчета фазового сдвига для анализа цепи переменного тока.
● Узнайте, как рассчитать фазовый сдвиг.
Различные фазы синусоиды.
В любой отрасли, включая область электроники, смещение является синонимом той или иной формы изменения.
В некоторых случаях этот сдвиг вызван внешними силами и может быть даже непреднамеренным. В других случаях сдвиг является внутренним и, возможно, преднамеренным, частично из-за функциональных требований.
Когда мы изучаем природу смещения в отношении частоты, эти изменения обычно могут отрицательно или положительно влиять на функциональность.
Когда мы смотрим на понимание фазового сдвига в электронном дизайне, обнаруживаем, что различное фазное напряжение и амплитуда коррелируют с такими вещами, как периодическая функция, угловая частота, а затем соответствуют эффективности изменения фазы. Катушки индуктивности и низкочастотные устройства часто используют этот метод.
Что такое фаза и что такое фазовый сдвиг?
Мы определяем «фазу» как сигнал, имеющий ту же длину волны, тот же цикл и ту же частоту, что и другой, но при этом они представляют собой две (или более) формы волны, которые не точно выровнены. Фаза не является свойством отдельного радиочастотного сигнала; скорее, это касается отношения между этими двумя или более сигналами, которые также имеют одну и ту же частоту.
«Фазовый сдвиг» — это незначительное изменение между двумя формами волны. Как в электронике, так и в математике фазовый сдвиг — это задержка, присутствующая между этими двумя формами сигналов, имеющими одну и ту же частоту или период.
Таким образом, мы выражаем фазовые сдвиги в терминах угла, который мы измеряем в радианах или градусах, которые могут быть положительными или отрицательными.
Например, положительный фазовый сдвиг на 90° составляет четверть полного цикла. В этом случае наша вторая волна опережает первую на 90°. Мы можем рассчитать фазовый сдвиг, используя временную задержку между ними и частоту сигналов.
Что такое формула фазового сдвига?
Во-первых, существует корреляция между синусоидальной волновой функцией и фазой. В области математики, а точнее, в тригонометрии, тригонометрическая синусоидальная функция генерирует гладкий волнообразный график. На этом графике чередуются минимальное и максимальное значения, и он повторяется каждые 360° (2 * пи радиан).
Note:
Pi radians = 180o
or
3.14159265359 * 57.295779513o = 180o
π rad = 180o
π = 3.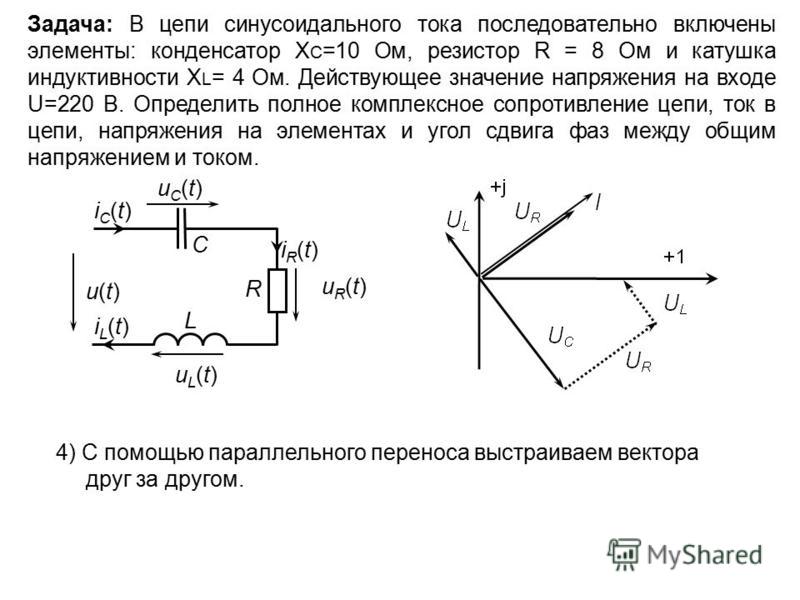
14159265359
A radian = 57.295779513o
1 рад = 180°/3,14159265359 = 57,295779513°
При 0° функция будет иметь нулевое значение, а при 90° она достигает максимального положительного значения. При 180° она стремится к нулю, а при 270° функция достигает максимального отрицательного значения. Однако на 360° он вернется к нулю, таким образом завершив полный цикл.
Любой угол больше 360° будет просто повторять предыдущий цикл. Кроме того, синусоида со сдвигом фазы будет начинаться и заканчиваться со значением, отличным от нуля, даже если во всех других аспектах она выглядит как стандартная синусоида. Это означает, что это s-образный сигнал, который является гладким и колеблется снизу, вверх или из стороны в сторону относительно нуля.
Вычисление фазового сдвига
Вычисление фазового сдвига включает сравнение двух сигналов, что также означает определение того, какая из этих двух волн является первой, а какая второй.
В области электроники вторая волна обычно является выходом чего-то вроде усилителя, а вход мы обозначаем как первую волну.
В области математики первая волна может быть исходной функцией, а вторичная функция, конечно же, будет второй волной. Чтобы дополнительно проиллюстрировать это, мы можем использовать следующий пример: здесь ваша первая функция y = sin(x), а ваша вторая функция y = cos(x). Хотя порядок двух волн не влияет на абсолютное значение фазового сдвига, он определяет, является фазовый сдвиг отрицательным или положительным.
Когда мы сравниваем осциллограммы, мы организуем их так, чтобы они читались слева направо с использованием одних и тех же единиц времени или угла оси X. Например, график для обоих может начинаться с 0 секунд; здесь мы найдем пик на второй волне и найдем эквивалентный пик на первой. Всякий раз, когда мы ищем соответствующий пик, мы остаемся в пределах одного полного цикла, чтобы избежать неточностей разности фаз.
Примечание.
Чтобы найти разницу, найдите значения по оси X для обоих пиков и вычтите их. Например, если пик первой волны приходится на 0,005 секунды, а пик второй волны приходится на 0,003 секунды, тогда разница составляет 0,005 — 0,003 = 0,002 секунды.
Вычисление фазового сдвига Продолжение
Таким образом, при вычислении фазового сдвига вам понадобятся период и частота волн. Например, осциллятор может генерировать синусоиду частотой 100 Гц. Мы определяем период или продолжительность цикла, разделив частоту на 1. Таким образом, в этом случае 1 ÷ 100 = 0,01 секунды для периода или продолжительности цикла.
Формула фазового сдвига выглядит следующим образом:
пс = 360 × (td ÷ p)
пс = фазовый сдвиг в градусах
td = разница во времени между сигналами 90445
5 900 период
При использовании вышеприведенных примеров формула будет иметь следующий результат:
360 × (0,002 ÷ 0,01) = фазовый сдвиг (пс) в 72 градуса
Поскольку результатом является положительное число, фазовый сдвиг тоже положителен.
С учетом этого вторая волна отстает от первой на 72 градуса. Чтобы вычислить разность фаз в радианах, мы используем следующее:
2 × pi × (td ÷ p)
Using the example results in the following solution:
2 × 3.14159265359 × (0.002 ÷ 0.01)
or
6.28 × 0.2 = 1.256 радианы
Мы используем формулу фазового сдвига, чтобы определить взаимосвязь между двумя сигналами и их результирующий фазовый угол. Это дает возможность проводить измерения в любом месте вдоль горизонтальной нулевой оси, в которой каждая волна проходит с одним и тем же направлением наклона, как отрицательным, так и положительным. Это важно, поскольку дает возможность описать взаимосвязь между напряжением и синусоидой тока в одной и той же цепи. Это жизненно важный инструмент в силовых цепях переменного тока, который служит основой для анализа цепей переменного тока.
Части синусоиды.
Прежде чем беспокоиться об измерении фазового сдвига в цепях переменного тока, вы должны убедиться, что используете правильный набор программного обеспечения для проектирования, компоновки и анализа печатных плат. Allegro PCB Designer и полный набор инструментов проектирования Cadence помогут вам создавать проекты на основе проверенных моделей компонентов и анализировать все аспекты их функциональности. У вас также будет доступ к набору инструментов для проектирования MCAD и подготовки к производству. Наличие правильных инструментов может гарантировать, что ваш дизайн будет выполнен правильно с первого раза.
Если вы хотите узнать больше о том, какое решение может предложить Cadence, обратитесь к нам и нашей команде экспертов.
Решения Cadence PCB — это комплексный инструмент для проектирования от начала до конца, позволяющий быстро и эффективно создавать продукты.