Механическая работа | это… Что такое Механическая работа?
Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины, направления силы (сил) и от перемещения точки (точек) тела или системы[1].
Содержание
|
Определение
В механике можно ввести понятие работы, исходя из довольно простых представлений[2]
Работа силы (сил) над одной точкой
- Работа нескольких сил определяется естественным образом как работа их равнодействующей (их векторной суммы).
 Поэтому дальше будем говорить об одной силе.
Поэтому дальше будем говорить об одной силе.
При прямолинейном движении одной материальной точки и постоянном значении приложенной к ней силы работа (этой силы) равна произведению величины проекции вектора силы на направление движения и величины совершённого перемещения[3]:
Здесь точкой обозначено скалярное произведение[4], — вектор перемещения; подразумевается, что действующая сила постоянна в течение всего того времени, за которое вычисляется работа.
Если сила не постоянна, то в этом случае она вычисляется как интеграл[5]:
(подразумевается суммирование по кривой, которая является пределом ломаной, составленной из последовательных перемещений если вначале считать их конечными, а потом устремить длину каждого к нулю).
Если существует зависимость силы от координат[6], интеграл определяется[7] следующим образом:
- ,
где и — радиус-векторы начального и конечного положения тела соответственно.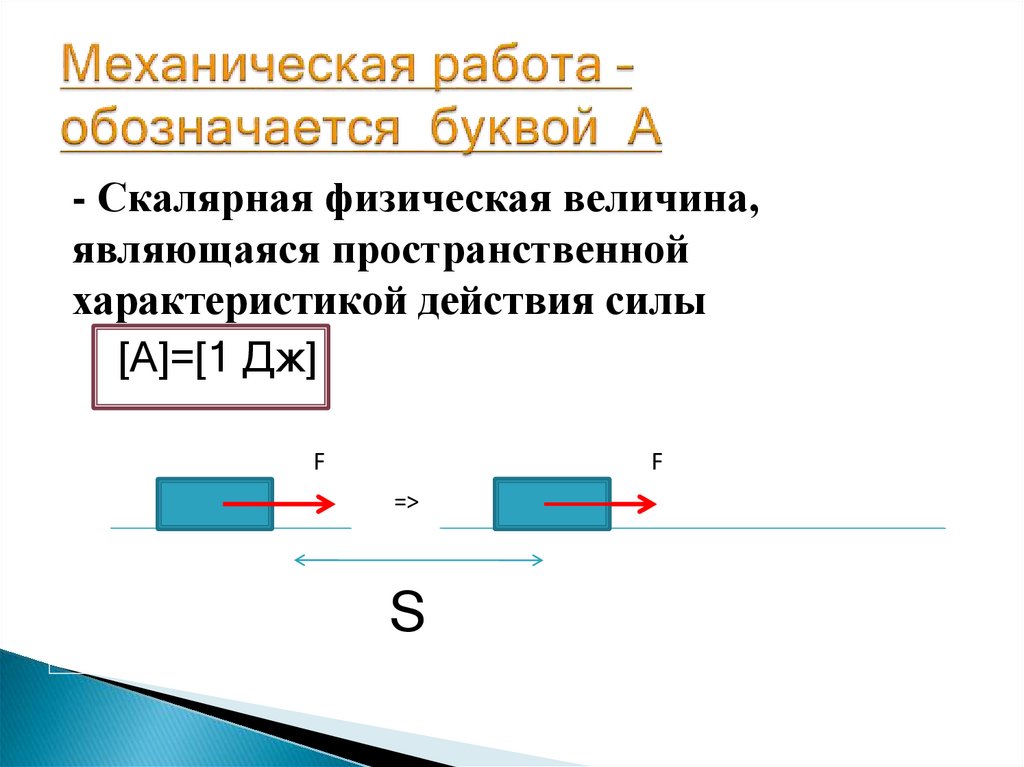
- Cледствие: если направление движения тела ортогонально силе, работа (этой силы) равна нулю.
Работа силы (сил) над системой или неточечным телом
Работа сил над системой материальных точек определяется как сумма работ этих сил над каждой точкой (работы, совершённые над каждой точкой системы, суммируются в суммарную работу этих сил над системой).
Даже если изначально тело не является системой дискретных точек, можно разбить его (мысленно) на множество бесконечно малых элементов (кусочков), каждый из которых считать материальной точкой, вычисляя работу в соответствии с определением выше. В этом случае дискретная сумма заменяется на интеграл.
- Эти определения могут быть использованы как для какой-то конкретной силы или класса сил — для вычисления именно их работы отдельно, так и для вычисления полной работы, совершаемой всеми силами, действующими на систему.
Кинетическая энергия
Кинетическая энергия вводится в механике в прямой связи с понятием работы.
Схема рассуждений такова: 1) попробуем записать работу, совершаемую всеми силами, действующими на материальную точку и, пользуясь вторым законом Ньютона (позволяющим выразить силу через ускорение), попытаться выразить ответ только через кинематические величины, 2) убедившись, что это удалось, и что этот ответ зависит только от начального и конечного состояния движения, введём новую физическую величину, через которую эта работа будет просто выражаться (это и будет кинетическая энергия).
Если — полная работа, совершённая над частицей, определяемая как сумма работ совершенных приложенными к частице силами, то она выражается как:
где называется кинетической энергией. Для материальной точки, кинетическая энергия определяется как работа силы, ускорившей точку от нулевой скорости до величины скорости и выражается как:
Для сложных объектов, состоящих из множества частиц, кинетическая энергия тела равна сумме кинетических энергий частиц.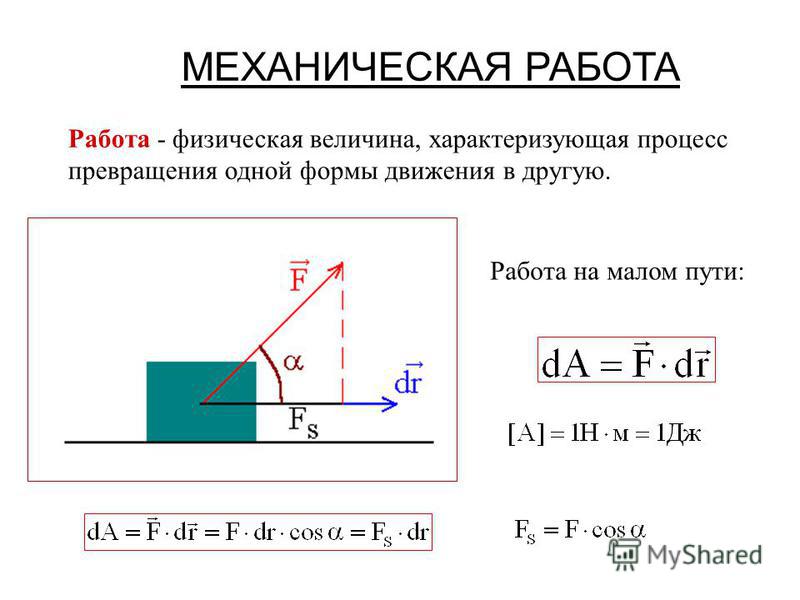
Потенциальная энергия
Сила называется потенциальной, если существует скалярная функция координат, известная как потенциальная энергия и обозначаемая , такая что
Если все силы, действующие на частицу консервативны, и является полной потенциальной энергией, полученной суммированием потенциальных энергий соответствующих каждой силе, тогда:
| . |
Этот результат известен как сохранение механической энергии и утверждает, что полная механическая энергия в замкнутой системе, в которой действуют консервативные силы
является постоянной относительно времени. Этот закон широко используется при решении задач классической механики.
Работа в термодинамике
Основная статья: Термодинамическая работа
В термодинамике работа, совершенная газом при расширении[8], рассчитывается как интеграл давления по объёму:
Работа, совершенная над газом, совпадает с этим выражением по абсолютной величине, но противоположна по знаку.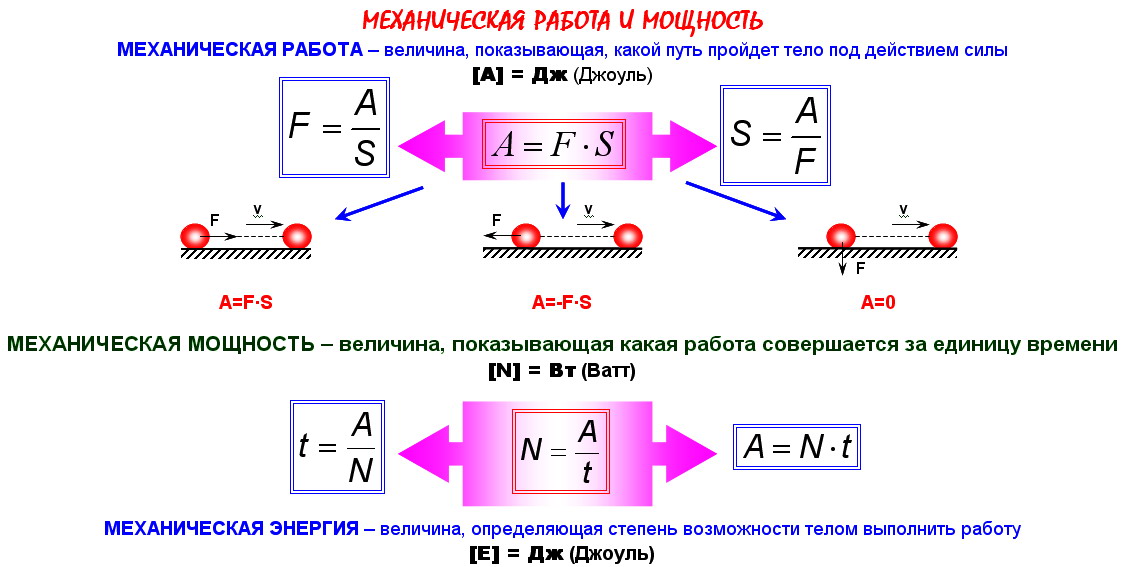
- Естественное обобщение этой формулы применимо не только к процессам, где давление есть однозначная функция объема, но и к любому процессу (изображаемому любой кривой в плоскости PV), в частности, к циклическим процессам.
- В принципе, формула применима не только к газу, но и к чему угодно, способному оказывать давление (надо только чтобы давление в сосуде было всюду одинаковым, что неявно подразумевается в формуле).
Эта формула прямо связана с механической работой. Действительно, попробуем написать механическую работу при расширении сосуда, учитывая, что сила давления газа будет направлена перпендикулярно каждой элементарной площадке, равна произведению давления P на площадь dS площадки, и тогда работа, совершаемая газом для смещения h одной такой элементарной площадки будет
Видно, что это и есть произведение давления на приращение объема вблизи данной элементарной площадкой. А просуммировав по всем dS получим конечный результат, где будет уже полное приращение объема, как и в главной формуле параграфа.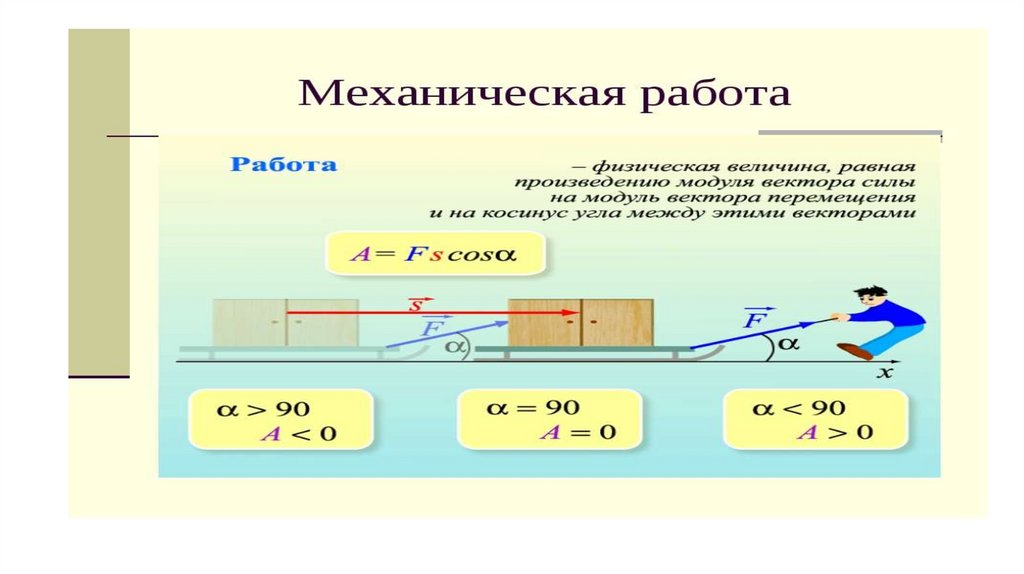
Рассмотрим несколько детальнее, чем это было сделано выше, построение определения энергии как риманова интеграла.
Пусть материальная точка движется по непрерывно дифференцируемой кривой , где s — переменная длина дуги, и на неё действует сила , направленная по касательной к траектории в направлении движения (если сила не направлена по касательной, то будем понимать под проекцию силы на положительную касательную кривой, таким образом сведя и этот случай к рассматриваемому далее). Величина , называется элементарной работой силы на участке и принимается за приближенное значение работы, которую производит сила , воздействующая на материальную точку, когда последняя проходит кривую . Сумма всех элементарных работ является интегральной суммой Римана функции .
В соответствии с определением интеграла Римана, можем дать определение работе:
Предел, к которому стремится сумма всех элементарных работ, когда мелкость разбиения стремится к нулю, называется работой силы вдоль кривой .
Таким образом, если обозначить эту работу буквой , то, в силу данного определения,
- ,
следовательно,
- (1).
Если положение точки на траектории её движения описывается с помощью какого-либо другого параметра (например, времени) и если величина пройденного пути , является непрерывно дифференцируемой функцией, то из формулы (1) получим
Единицей измерения работы в СИ является Джоуль, в СГС — эрг
- 1 Дж = 1 кг·м²/с² = 1 Н·м
- 1 эрг = 1 г·см²/с² = 1 дин·см
- 1 эрг = 10−7Дж
Ссылки
- ↑ Концепции современного естествознания
- ↑ Такие представления можно конкретизировать как систему постулатов, приводящую достаточно однозначно к определению, описанному в основной статье:
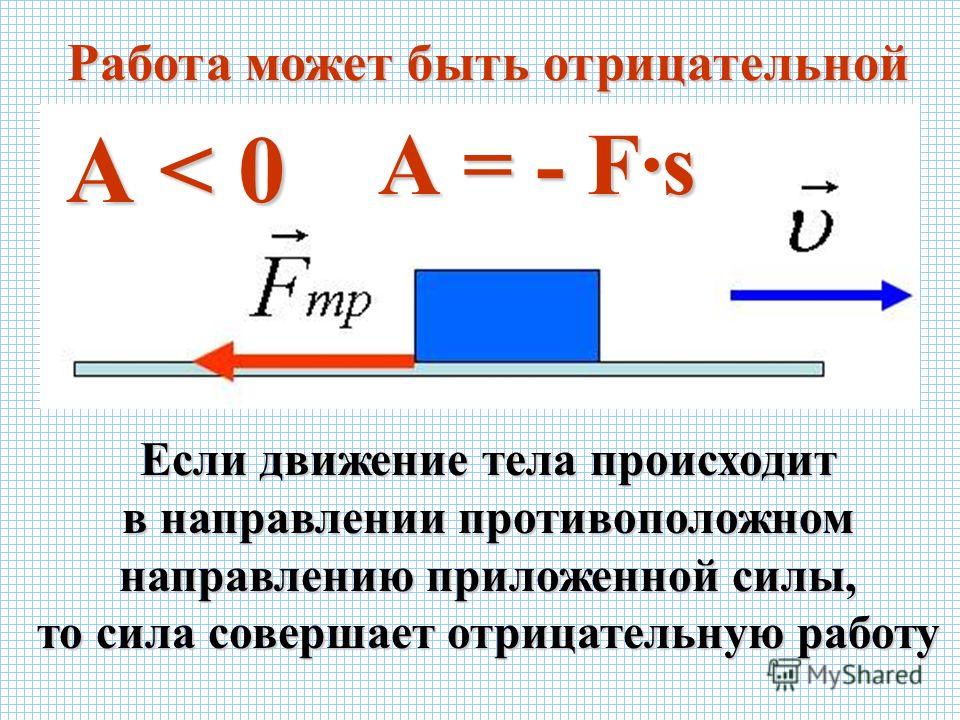
- работу совершает только компонента силы, совпадающая с направлением перемещения точки, к которой она приложена, или противоположная направлению перемещения точки (в последнем случае работа считается отрицательной),
- работа постоянной силы пропорциональна компоненте такой силы, описанной в пункте 1, и длине вектора перемещения,
- работа по перемещению точки за несколько последовательных промежутков времени суммируется (работа за всё это время равна сумме работ, совершенных за каждый промежуток),
- работа суммы (векторной суммы) сил, приложенных к точке равна сумме работ, совершенных каждой силой в отдельности,
- работа, совершенная над системой (телом) равна сумме работ, совершенных над каждой ее частью (в частности — равна сумме работ, совершенных над каждой точкой системы).

- ↑ Механическая работа. Мощность
- ↑ Можно считать, что механическая работа может служить в области физики одной из главных иллюстраций для скалярного произведения.
- ↑ Это делается исходя из того, что можно разбить суммарное конечное перемещение на маленькие последовательные перемещения , на каждом из которых сила будет почти постоянной, а значит можно будет воспользоваться определением для постоянной силы, введенным выше. Затем работы на всех этих перемещениях суммируется, что и дает в результате интеграл.
- ↑ Как это очень часто бывает. Например, в случае кулоновского поля, растягивающейся пружины, силы тяготения планеты итд итд.
- ↑ По сути через предыдущий, поскольку здесь ; вектор же малого перемещения совпадает с .
- ↑ Работа, совершаемая газом при его сжатии, очевидно отрицательна, но вычисляется по той же формуле. Работа, совершаемая газом (или над газом) без его расширения или сжатия (например, в процессе перемешивания мешалкой), в принципе может быть выражена подобной формулой, но всё же не прямо этой, так как она требует обобщения: дело в том, что в формуле давление подразумевается одинаковым по всему объему (что часто выполняется в термодинамике, поскольку речь там часто идет о процессах, близких к равновесным), что и приводит к наиболее простой формуле (в случае же вращающейся мешалки, например, давление будет разным на передней и задней стороне лопасти, что приведет к необходимому усложнению формулы, если мы захотим применить ее к такому случаю; эти соображения относятся и ко всем другим неравновесным случаям, когда давление неодинаково в разных частях системы).

Литература
- Кудрявцев Л. Д. Курс математического анализа. — 5-е, переработанное и дополненное. — М.: Дрофа, 2003. — Т. 1. — С. 640—641. — 703 с.
См. также
- Закон сохранения энергии
- Механические приложения криволинейных интегралов
Механическая работа | это… Что такое Механическая работа?
Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины, направления силы (сил) и от перемещения точки (точек) тела или системы[1].
Содержание
|
Определение
В механике можно ввести понятие работы, исходя из довольно простых представлений[2]
Работа силы (сил) над одной точкой
- Работа нескольких сил определяется естественным образом как работа их равнодействующей (их векторной суммы). Поэтому дальше будем говорить об одной силе.
При прямолинейном движении одной материальной точки и постоянном значении приложенной к ней силы работа (этой силы) равна произведению величины проекции вектора силы на направление движения и величины совершённого перемещения[3]:
Здесь точкой обозначено скалярное произведение[4], — вектор перемещения; подразумевается, что действующая сила постоянна в течение всего того времени, за которое вычисляется работа.
Если сила не постоянна, то в этом случае она вычисляется как интеграл[5]:
(подразумевается суммирование по кривой, которая является пределом ломаной, составленной из последовательных перемещений если вначале считать их конечными, а потом устремить длину каждого к нулю).
Если существует зависимость силы от координат[6], интеграл определяется[7] следующим образом:
- ,
где и — радиус-векторы начального и конечного положения тела соответственно.
- Cледствие: если направление движения тела ортогонально силе, работа (этой силы) равна нулю.
Работа силы (сил) над системой или неточечным телом
Работа сил над системой материальных точек определяется как сумма работ этих сил над каждой точкой (работы, совершённые над каждой точкой системы, суммируются в суммарную работу этих сил над системой).
Даже если изначально тело не является системой дискретных точек, можно разбить его (мысленно) на множество бесконечно малых элементов (кусочков), каждый из которых считать материальной точкой, вычисляя работу в соответствии с определением выше. В этом случае дискретная сумма заменяется на интеграл.
- Эти определения могут быть использованы как для какой-то конкретной силы или класса сил — для вычисления именно их работы отдельно, так и для вычисления полной работы, совершаемой всеми силами, действующими на систему.

Кинетическая энергия
Кинетическая энергия вводится в механике в прямой связи с понятием работы.
Схема рассуждений такова: 1) попробуем записать работу, совершаемую всеми силами, действующими на материальную точку и, пользуясь вторым законом Ньютона (позволяющим выразить силу через ускорение), попытаться выразить ответ только через кинематические величины, 2) убедившись, что это удалось, и что этот ответ зависит только от начального и конечного состояния движения, введём новую физическую величину, через которую эта работа будет просто выражаться (это и будет кинетическая энергия).
Если — полная работа, совершённая над частицей, определяемая как сумма работ совершенных приложенными к частице силами, то она выражается как:
где называется кинетической энергией. Для материальной точки, кинетическая энергия определяется как работа силы, ускорившей точку от нулевой скорости до величины скорости и выражается как:
Для сложных объектов, состоящих из множества частиц, кинетическая энергия тела равна сумме кинетических энергий частиц.
Потенциальная энергия
Сила называется потенциальной, если существует скалярная функция координат, известная как потенциальная энергия и обозначаемая , такая что
Если все силы, действующие на частицу консервативны, и является полной потенциальной энергией, полученной суммированием потенциальных энергий соответствующих каждой силе, тогда:
| . |
Этот результат известен как сохранение механической энергии и утверждает, что полная механическая энергия в замкнутой системе, в которой действуют консервативные силы
является постоянной относительно времени. Этот закон широко используется при решении задач классической механики.
Работа в термодинамике
Основная статья: Термодинамическая работа
В термодинамике работа, совершенная газом при расширении[8], рассчитывается как интеграл давления по объёму:
Работа, совершенная над газом, совпадает с этим выражением по абсолютной величине, но противоположна по знаку.
- Естественное обобщение этой формулы применимо не только к процессам, где давление есть однозначная функция объема, но и к любому процессу (изображаемому любой кривой в плоскости PV), в частности, к циклическим процессам.
- В принципе, формула применима не только к газу, но и к чему угодно, способному оказывать давление (надо только чтобы давление в сосуде было всюду одинаковым, что неявно подразумевается в формуле).
Эта формула прямо связана с механической работой. Действительно, попробуем написать механическую работу при расширении сосуда, учитывая, что сила давления газа будет направлена перпендикулярно каждой элементарной площадке, равна произведению давления P на площадь dS площадки, и тогда работа, совершаемая газом для смещения h одной такой элементарной площадки будет
Видно, что это и есть произведение давления на приращение объема вблизи данной элементарной площадкой. А просуммировав по всем dS получим конечный результат, где будет уже полное приращение объема, как и в главной формуле параграфа.
Рассмотрим несколько детальнее, чем это было сделано выше, построение определения энергии как риманова интеграла.
Пусть материальная точка движется по непрерывно дифференцируемой кривой , где s — переменная длина дуги, и на неё действует сила , направленная по касательной к траектории в направлении движения (если сила не направлена по касательной, то будем понимать под проекцию силы на положительную касательную кривой, таким образом сведя и этот случай к рассматриваемому далее). Величина , называется элементарной работой силы на участке и принимается за приближенное значение работы, которую производит сила , воздействующая на материальную точку, когда последняя проходит кривую . Сумма всех элементарных работ является интегральной суммой Римана функции .
В соответствии с определением интеграла Римана, можем дать определение работе:
Предел, к которому стремится сумма всех элементарных работ, когда мелкость разбиения стремится к нулю, называется работой силы вдоль кривой .
Таким образом, если обозначить эту работу буквой , то, в силу данного определения,
- ,
следовательно,
- (1).
Если положение точки на траектории её движения описывается с помощью какого-либо другого параметра (например, времени) и если величина пройденного пути , является непрерывно дифференцируемой функцией, то из формулы (1) получим
Единицей измерения работы в СИ является Джоуль, в СГС — эрг
- 1 Дж = 1 кг·м²/с² = 1 Н·м
- 1 эрг = 1 г·см²/с² = 1 дин·см
- 1 эрг = 10−7Дж
Ссылки
- ↑ Концепции современного естествознания
- ↑ Такие представления можно конкретизировать как систему постулатов, приводящую достаточно однозначно к определению, описанному в основной статье:
- работу совершает только компонента силы, совпадающая с направлением перемещения точки, к которой она приложена, или противоположная направлению перемещения точки (в последнем случае работа считается отрицательной),
- работа постоянной силы пропорциональна компоненте такой силы, описанной в пункте 1, и длине вектора перемещения,
- работа по перемещению точки за несколько последовательных промежутков времени суммируется (работа за всё это время равна сумме работ, совершенных за каждый промежуток),
- работа суммы (векторной суммы) сил, приложенных к точке равна сумме работ, совершенных каждой силой в отдельности,
- работа, совершенная над системой (телом) равна сумме работ, совершенных над каждой ее частью (в частности — равна сумме работ, совершенных над каждой точкой системы).

- ↑ Механическая работа. Мощность
- ↑ Можно считать, что механическая работа может служить в области физики одной из главных иллюстраций для скалярного произведения.
- ↑ Это делается исходя из того, что можно разбить суммарное конечное перемещение на маленькие последовательные перемещения , на каждом из которых сила будет почти постоянной, а значит можно будет воспользоваться определением для постоянной силы, введенным выше. Затем работы на всех этих перемещениях суммируется, что и дает в результате интеграл.
- ↑ Как это очень часто бывает. Например, в случае кулоновского поля, растягивающейся пружины, силы тяготения планеты итд итд.
- ↑ По сути через предыдущий, поскольку здесь ; вектор же малого перемещения совпадает с .
- ↑ Работа, совершаемая газом при его сжатии, очевидно отрицательна, но вычисляется по той же формуле. Работа, совершаемая газом (или над газом) без его расширения или сжатия (например, в процессе перемешивания мешалкой), в принципе может быть выражена подобной формулой, но всё же не прямо этой, так как она требует обобщения: дело в том, что в формуле давление подразумевается одинаковым по всему объему (что часто выполняется в термодинамике, поскольку речь там часто идет о процессах, близких к равновесным), что и приводит к наиболее простой формуле (в случае же вращающейся мешалки, например, давление будет разным на передней и задней стороне лопасти, что приведет к необходимому усложнению формулы, если мы захотим применить ее к такому случаю; эти соображения относятся и ко всем другим неравновесным случаям, когда давление неодинаково в разных частях системы).

Литература
- Кудрявцев Л. Д. Курс математического анализа. — 5-е, переработанное и дополненное. — М.: Дрофа, 2003. — Т. 1. — С. 640—641. — 703 с.
См. также
- Закон сохранения энергии
- Механические приложения криволинейных интегралов
Механическая работа — Энциклопедия Нового Света
Бейсбольный питчер работает с мячом, передавая ему энергию.
В физике механическая работа — это количество энергии, переданной силой. Как и энергия, это скалярная величина с единицами СИ в джоулях. Теплопроводность не считается формой работы, поскольку нет макроскопически измеримой силы, а есть только микроскопические силы, возникающие при атомных столкновениях. В 1830-х годах французский математик Гаспар-Гюстав Кориолис ввел термин 9.0007 произведение силы на расстояние . [1]
Содержание
- 1 Расчет
- 2 шт.
- 3 Виды работ
- 3.
 1 Работа в связи с изменением объема
1 Работа в связи с изменением объема
- 3.
- 4 Механическая энергия
- 4.1 Связь между работой и кинетической энергией
- 4.2 Сохранение механической энергии
- 5 См. также
- 6 Примечания
- 7 Каталожные номера
- 8 Внешние ссылки
- 9 кредитов
Положительные и отрицательные знаки работы указывают на то, передает ли объект, прилагающий силу, энергию другому объекту или получает ее. Например, бейсбольный питчер совершает над мячом положительную работу, а кэтчер — отрицательную. Работа может быть равна нулю даже при наличии силы. Например, центростремительная сила при равномерном круговом движении совершает нулевую работу, потому что кинетическая энергия движущегося объекта не меняется. Точно так же, когда книга лежит на столе, стол не воздействует на книгу, потому что энергия не передается ни внутрь книги, ни из нее.
Расчет
Когда сила постоянна и движется по той же линии, что и движение, работа может быть рассчитана путем умножения силы на расстояние W=Fd{\displaystyle W=Fd} (пусть и F, и d имеют положительные или отрицательные знаки, в зависимости от выбранной системы координат). Когда сила не лежит на той же линии, что и движение, это можно обобщить до скалярного произведения векторов силы и смещения.
Когда сила не лежит на той же линии, что и движение, это можно обобщить до скалярного произведения векторов силы и смещения.
В простейшем случае, когда тело движется в постоянном направлении и на него действует постоянная сила, параллельная этому направлению, работа определяется следующими формулами:
9{2}} (получено просто из приведенного выше уравнения)
, где
- F часть силы, действующей в том же направлении, что и движение, а
- D — расстояние, пройденное объектом. Обратите внимание, что расстояние является скалярной величиной, как и работа.
- м масса объекта
- v 2 это конечная скорость
- v 1 начальная скорость
Работа считается отрицательной, когда сила противодействует движению. В более общем случае сила и расстояние считаются векторными величинами и объединяются с помощью скалярного произведения:
- W = F→⋅D→=|F→||D→|cosϕ{\ displaystyle W = {\ vec {F}} \ cdot {\ vec {D}} = | {\ vec {F }}||{\vec {D}}|\cos \phi } (2)
где ϕ {\ displaystyle \ phi \,} — угол между силой и вектором смещения. Эта формула верна даже тогда, когда объект меняет направление своего движения на протяжении всего движения.
Эта формула верна даже тогда, когда объект меняет направление своего движения на протяжении всего движения.
В ситуациях, когда сила изменяется с течением времени и/или направление движения изменяется с течением времени, уравнение (1) неприменимо напрямую. Однако при умеренных ограничениях можно разделить движение на небольшие шаги, чтобы сила и движение были хорошо аппроксимированы как постоянные для каждого шага, а затем выразить общую работу как сумму этих шагов. Это формализуется следующим линейным интегралом, который можно рассматривать как довольно общее определение работы:
- WC:=∫CF→⋅ds→{\displaystyle W_{C}:=\int _{C}{\vec {F}}\cdot \mathrm {d} {\vec {s}}} (3)
, где:
- C — это путь или кривая, пройденная объектом
- F→{\displaystyle {\vec {F}}} — вектор силы
- s→{\displaystyle {\vec {s}}} — вектор положения
Следует подчеркнуть, что WC{\displaystyle W_{C}\,} явно является функцией пути C{\displaystyle C\ !}. В общем случае работа зависит от полного смещения пути C {\ displaystyle C \!} (чем длиннее путь, пройденный объектом, тем больше работы будет выполнено).
В общем случае работа зависит от полного смещения пути C {\ displaystyle C \!} (чем длиннее путь, пройденный объектом, тем больше работы будет выполнено).
Используя векторную запись, уравнение (3) легко объясняет, как ненулевая сила может выполнять нулевую работу. В простейшем случае сила всегда перпендикулярна направлению движения, поэтому подынтегральная функция всегда равна нулю (как в случае кругового движения).
Возможность того, что ненулевая сила совершает нулевую работу, иллюстрирует различие между работой и соответствующей величиной, импульсом, который является интегралом силы по времени. Импульс измеряет изменение количества движения тела, векторной величины, чувствительной к направлению, тогда как работа учитывает только величину скорости. Например, когда объект в равномерном круговом движении проходит половину оборота, его центростремительная сила не действует, но он передает ненулевой импульс.
Единицы
Единицей работы в системе СИ является джоуль (Дж), который определяется как работа, совершаемая силой в один ньютон, действующей на расстоянии одного метра. Это определение основано на определении работы Сади Карно 1824 года как «вес , поднятый на высоту », что основано на том факте, что ранние паровые машины в основном использовались для подъема ведер с водой, хотя и на гравитационную высоту, из затопленной руды. шахты. Вместо этого иногда используется размерно-эквивалентный ньютон-метр (Н•м); однако иногда он также используется для крутящего момента, чтобы отличать его единицы от работы или энергии.
Это определение основано на определении работы Сади Карно 1824 года как «вес , поднятый на высоту », что основано на том факте, что ранние паровые машины в основном использовались для подъема ведер с водой, хотя и на гравитационную высоту, из затопленной руды. шахты. Вместо этого иногда используется размерно-эквивалентный ньютон-метр (Н•м); однако иногда он также используется для крутящего момента, чтобы отличать его единицы от работы или энергии.
Единицы работы, не входящие в систему СИ, включают эрг, фут-фунт, фут-фунтал и литр-атмосферу.
Виды работы
Виды работы, которые не являются явно механическими, фактически представляют собой частные случаи этого принципа. Например, в случае «электрической работы» электрическое поле совершает работу над заряженными частицами, когда они движутся через среду.
Одним из механизмов теплопроводности являются столкновения быстродвижущихся атомов в теплом теле с медленно движущимися атомами в холодном теле. Хотя сталкивающиеся атомы действуют друг на друга, в массе сила в среднем почти равна нулю, поэтому проводимость не считается механической работой.
Хотя сталкивающиеся атомы действуют друг на друга, в массе сила в среднем почти равна нулю, поэтому проводимость не считается механической работой.
Работа при изменении объема
Работа выполняется при изменении объема жидкости. Работа в таких условиях представлена следующим уравнением:
- WC = -∫CPdV {\ displaystyle W_ {C} = — \ int _ {C} P \, \ mathrm {d} V} (4)
, где:
- W = работа, выполненная в системе
- P = внешнее давление
- V = объем
Как и все рабочие функции, работа PV зависит от пути C{\displaystyle C\!}.
Работа PV часто измеряется в (не СИ) единицах литр-атмосфер, где 1 л•атм = 101,3 Дж.
Механическая энергия
механическая энергия тела — это та часть его полной энергии, которая может быть изменена посредством механической работы. Она включает в себя кинетическую энергию и потенциальную энергию. Некоторые известные формы энергии, которые он не включает, — это тепловая энергия (которая может быть увеличена за счет работы трения, но ее нелегко уменьшить) и энергия покоя (которая постоянна, пока масса покоя остается неизменной).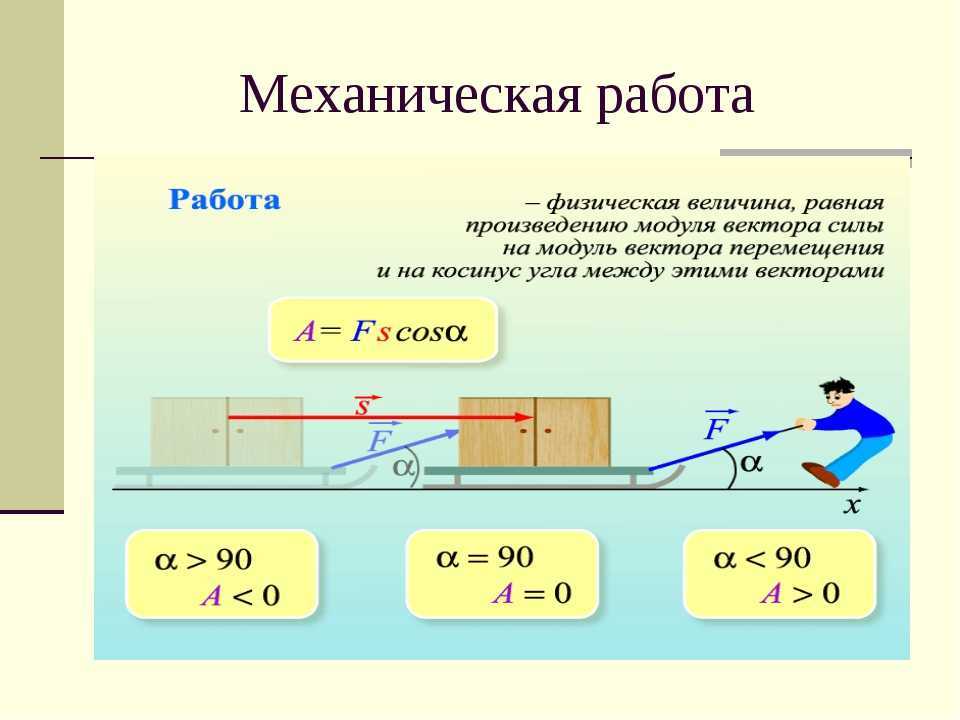
Связь между работой и кинетической энергией
9{2}} [2]
Сохранение механической энергии
Принцип сохранения механической энергии гласит, что если на систему действуют только консервативные силы (такие как гравитационная сила), ее полная механическая энергия остается постоянной.
Например, если объект с постоянной массой находится в свободном падении, полная энергия положения 1 будет равна энергии положения 2.
- (KE + PE) 1 = (KE + PE) 2 {\ displaystyle (K_ {E} + P_ {E}) _ {1} = (K_ {E} + P_ {E}) _ {2} \,\!}
где
- KE{\displaystyle K_{E}} — кинетическая энергия, а
- PE{\displaystyle P_{E}} — потенциальная энергия.
Внешняя работа обычно выполняется силой трения между системой при движении или внутренней, неконсервативной силой в системе, или потерей энергии из-за тепла.
См. также
- Сила
- Электричество
- Энергия
- Тепло
Примечания
- ↑ Подавитель, макс.
 Концепции Силы . Кембридж, Массачусетс: Издательство Гарвардского университета, 1957. ISBN 0-486-40689-X.
Концепции Силы . Кембридж, Массачусетс: Издательство Гарвардского университета, 1957. ISBN 0-486-40689-X. - ↑ Zitzewitz, Paul et al. Физика: основы и задачи . Нью-Йорк: Glencoe/McGraw-Hill, 2005. ISBN 0-07-845813-7.
Ссылки
Ссылки ISBN поддерживают NWE за счет реферальных сборов
- Янг, Хью Д. и Фридман, Роджер А. Физика для ученых и инженеров . 11-е изд. Сан-Франциско, Калифорния: Пирсон, 2003. ISBN 080538684X
- Паркер, Сибил П. Энциклопедия физики McGraw-Hill. Нью-Йорк: McGraw-Hill, 1983. ISBN 0070452539
- Serway, Raymond A. Физика для ученых и инженеров с современной физикой. Форт-Уэрт, Техас: Колледж Сондерс, 2004. ISBN 0534409490
- Типлер, Пол Аллен. Физика для ученых и инженеров. Нью-Йорк: WH Freeman/Worth Publishers, 1999. ISBN 9781572598140
Внешние ссылки
Все ссылки получены 8 ноября 2022 г.
- Работа гиперфизика.
 Университет штата Джорджия.
Университет штата Джорджия.
Авторы
Энциклопедия Нового Света писатели и редакторы переписали и дополнили статью Википедии
в соответствии со стандартами New World Encyclopedia . Эта статья соответствует условиям лицензии Creative Commons CC-by-sa 3.0 (CC-by-sa), которая может использоваться и распространяться с надлежащим указанием авторства. Кредит должен соответствовать условиям этой лицензии, которая может ссылаться как на Энциклопедия Нового Света участников и самоотверженных добровольных участников Фонда Викимедиа. Чтобы процитировать эту статью, щелкните здесь, чтобы просмотреть список допустимых форматов цитирования. История более ранних вкладов википедистов доступна исследователям здесь:
- Механическая работа история
История этой статьи с момента ее импорта в New World Encyclopedia :
- История «Механические работы»
Примечание. На использование отдельных изображений, которые лицензируются отдельно, могут распространяться некоторые ограничения.
Примеры механической работы В физике О
Механика
В физике это называется механической работой , которая развивает силу на объекте и может влиять на его положение или величину его движения. Другими словами, механическая работа — это количество энергии, необходимое для приведения объекта в движение , изменения характеристик указанного перемещения или даже его остановки.
Как и другие физические формы работы, она обычно обозначается буквой Вт ( Работа ) и измеряется в джоулях, единице измерения энергии. Июль эквивалентен работе, которую сила в 1 Ньютон совершает над телом , которое перемещается на 1 метр в точном направлении и направлении первоначальной силы .
Хотя сила и перемещение являются векторными величинами , требующими направления и смысла, работа считается скалярной величиной , так как он не вносит изменений в направление и направление силы, которая его производит.
В случае, если объект уже находится в движении, работа будет выполняться в направлении, противоположном траектории перемещения , успевая отменить или отклонить траекторию. В некоторых случаях для этого могут потребоваться векторные представления.
Первая модель считается положительной или двигательной работой , вторая резистентной или отрицательной работой .
Так, в простейшем варианте механическая работа может быть рассчитана по формуле :
Вт (работа в джоулях) = F (сила в ньютонах). d (расстояние в метрах).
Примеры механической работы
- Передвинуть стол из одного конца комнаты в другой.
- Тянет плуг как волы на традиционном поле.
- Откройте раздвижное окно с постоянным усилием до упора.
- Толкание автомобиля , у которого закончился бензин.

- Переносить велосипед вручную не взбираясь на него к педали.
- Потянув за дверь чтобы войти в комнату.
- Буксировка автомобиля другим или краном, который тянет и перемещает его.
- Волочение кого-либо за руки или за ноги.
- Поднимите пианино с системой струн и шкивов.
- Поднимите ведро , полное воды, со дна колодца.
- Поднимите коробку с книгами с пола .
- Вытяните груз из поезда локомотивом, который тянет вперед.
- Снесите стену, потянув за нее мощным пикапом или грузовиком.
- Потяните за веревку , за другой конец которой тянут другие люди (затянут).
- Поддержите рушащуюся стену, приложив собственный вес.
- Держите гелиевый шар на уровне земли имеет тенденцию к росту.


 Поэтому дальше будем говорить об одной силе.
Поэтому дальше будем говорить об одной силе.

 также
также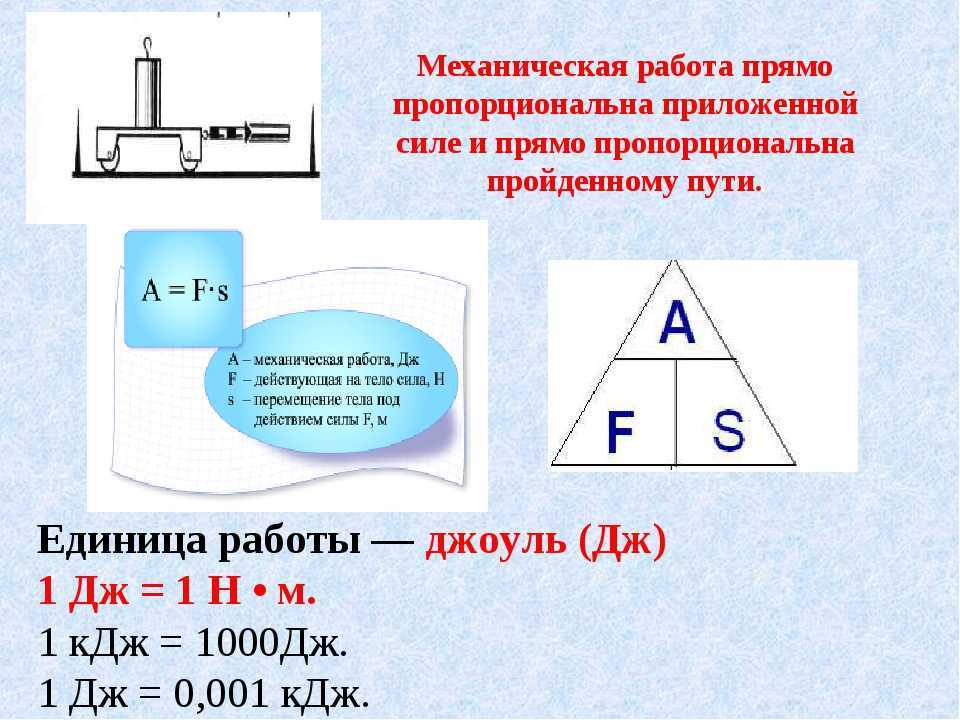

 1 Работа в связи с изменением объема
1 Работа в связи с изменением объема Концепции Силы . Кембридж, Массачусетс: Издательство Гарвардского университета, 1957. ISBN 0-486-40689-X.
Концепции Силы . Кембридж, Массачусетс: Издательство Гарвардского университета, 1957. ISBN 0-486-40689-X. Университет штата Джорджия.
Университет штата Джорджия.