Вопросы»Угловая скорость вращения вала автомобильного двигателя и угловая скорость вращения колес автомобиля измеряются в оборотах в минуту|Поступи в ВУЗ

Вопросы »
Задачи 10 ЕГЭ (мат.методы в физике, химии,биол) » Угловая скорость вращения вала автомобильного двигателя и угловая скорость вращения колес автомобиля измеряются в оборотах в минуту

Угловая скорость вращения вала автомобильного двигателя и угловая скорость вращения колес автомобиля измеряются в оборотах в минуту

создана: 20.03.2020 в 10:01
…………………………………………

liliana :

Угловая скорость вращения вала автомобильного двигателя ω_двиг  

и угловая скорость вращения колёс автомобиля ω_кол 

измеряются в оборотах в минуту.   Эти величины связаны соотношением

           ω_кол = ω_двиг / (kb)

где k — передаточное число дифференциала автомобиля, а b — передаточное число

коробки передач при выбранной передаче.

В таблице указаны передаточные числа для автомобиля «Лада-Калина».

Водитель разгонялся на 5-й передаче, пока число оборотов двигателя не достигло 2000 об/мин.

В этот момент водитель, не меняя скорости, включил 2-ю передачу.

Найдите угловую скорость вращения вала двигателя после переключения.

Результат округлите до целого числа оборотов.

Ответ: 4974

404 Cтраница не найдена

Размер:

AAA

Изображения

Вкл.
Выкл.

Обычная версия сайта

К сожалению запрашиваемая страница не найдена.

Но вы можете воспользоваться поиском или картой сайта ниже

11.

3 Сохранение углового момента

Цели обучения

К концу этого раздела вы сможете:

• Применять закон сохранения углового момента для определения угловой скорости вращающейся системы, в которой момент инерции изменяется
• Объясните, как изменяется кинетическая энергия вращения, когда в системе изменяются как момент инерции, так и угловая скорость

До сих пор мы рассматривали угловой момент систем, состоящих из точечных частиц и твердых тел. Мы также проанализировали задействованные крутящие моменты, используя выражение, которое связывает внешний чистый крутящий момент с изменением углового момента (рисунок). Примеры систем, которые подчиняются этому уравнению, включают свободно вращающуюся велосипедную шину, которая со временем замедляется из-за крутящего момента, возникающего в результате трения, или замедление вращения Земли в течение миллионов лет из-за сил трения, действующих на приливные деформации.

Однако предположим, что в системе нет чистого внешнего крутящего момента, [латекс] \sum \overset{\to }{\tau }=0. [/latex] В этом случае (Рисунок) становится законом сохранения углового момента .

Закон сохранения углового момента

Угловой момент системы частиц вокруг точки в фиксированной инерциальной системе отсчета сохраняется, если вокруг этой точки нет чистого внешнего крутящего момента:

[латекс] \frac{d\ overset{\to}}{L}}{dt}=0 [/latex]

или

[латекс] \ overset {\ to {L} = {\ overset {\ to {l}} _ {1} + {\ overset {\ to {l}} _ {2} \ ,\text{+}\,\text{⋯}\,\text{+}\,{\overset{\to }{l}}_{N}=\text{constant}\text{.} [/ латекс]

Обратите внимание, что общий угловой момент [латекс] \overset{\to }{L} [/латекс] сохраняется. Любой из отдельных угловых моментов может изменяться до тех пор, пока их сумма остается постоянной. Этот закон аналогичен сохранению импульса, когда внешняя сила, действующая на систему, равна нулю.

В качестве примера сохранения углового момента (Рисунок) показан фигурист, выполняющий вращение. Чистый крутящий момент на ней очень близок к нулю, потому что между ее коньками и льдом относительно небольшое трение. Кроме того, трение возникает очень близко к точке поворота. Оба [латекс] |\overset{\to }{F}|\,\text{and}\,|\overset{\to }{r}| [/латекс] маленькие, поэтому [латекс] |\overset{\to }{\tau}| [/латекс] ничтожно мало. Следовательно, она может крутиться довольно долго. Она также может увеличить скорость вращения, стягивая руки и ноги. Почему стягивание рук и ног увеличивает скорость ее вращения? Ответ состоит в том, что ее угловой момент постоянен, так что 9{\prime} [/latex] должен увеличиваться, чтобы сохранить постоянный угловой момент.

Рис. 11.14 (a) Фигуристка крутится на кончике конька с вытянутыми руками. Ее угловой момент сохраняется, потому что чистый крутящий момент на ней пренебрежимо мал. (b) Скорость ее вращения сильно увеличивается, когда она вытягивает руки, уменьшая момент инерции. Работа, которую она выполняет, чтобы подтянуть руки, приводит к увеличению кинетической энергии вращения.

Интересно посмотреть, как изменяется кинетическая энергия вращения фигуристки, когда она сводит руки. Ее начальная энергия вращения равна 9{\prime }

Солнечная система — еще один пример того, как работает закон сохранения углового момента в нашей Вселенной. Наша Солнечная система родилась из огромного облака газа и пыли, изначально обладавшего вращательной энергией. Гравитационные силы заставили облако сжаться, а скорость вращения увеличилась в результате сохранения углового момента ((Рисунок)).

Рисунок 11.15 Солнечная система образовалась из облака газа и пыли, которое первоначально вращалось. Орбитальные движения и вращения планет имеют то же направление, что и исходное вращение, и сохраняют угловой момент родительского облака. (кредит: модификация работы НАСА)

Мы продолжим наше обсуждение на примере, имеющем приложения к технике.

Пример

Спаренные маховики

Маховик вращается без трения с угловой скоростью [латекс] {\omega }_{0}=600\,\text{об}\текст{/}\текст{мин} [/ латекс] на вертикальном валу без трения с незначительной инерцией вращения. На него опущен второй маховик, который находится в состоянии покоя и имеет момент инерции, в три раза превышающий момент инерции вращающегося маховика (рисунок). Поскольку между поверхностями существует трение, маховики очень быстро достигают одинаковой скорости вращения, после чего вращаются вместе. (a) Используйте закон сохранения углового момента, чтобы определить угловую скорость [латекс] \ омега [/латекс] комбинации. б) Какая часть начальной кинетической энергии теряется при соединении маховиков?

Рисунок 11.16 Два маховика соединены и вращаются вместе.

Стратегия

Часть (a) легко решить для угловой скорости связанной системы. Мы используем результат (а) для сравнения начальной и конечной кинетической энергии системы в части (б).

Раствор

а. На систему не действуют внешние моменты. Сила трения создает внутренний крутящий момент, который не влияет на угловой момент системы. Следовательно, сохранение углового момента дает 9{2}}=\фракция{1}{4}. [/latex]

Таким образом, 3/4 начальной кинетической энергии теряется на сцепление двух маховиков.

Значение

Поскольку инерция вращения системы увеличилась, угловая скорость уменьшилась, как и следовало ожидать из закона сохранения углового момента. В этом примере мы видим, что конечная кинетическая энергия системы уменьшилась, так как энергия теряется на сцепление маховиков. Сравните это с фигуристкой на (рис.), выполняющей работу, сводя руки внутрь и добавляя кинетическую энергию вращения.

Проверьте свое понимание

Карусель на детской площадке вращается со скоростью 4,0 об/мин. Трое детей запрыгивают и увеличивают момент инерции карусели/детской вращающейся системы на [латекс] 25% [/латекс]. Какова новая скорость вращения?

Показать решение

Пример

Соскок с перекладины

Гимнастка весом 80,0 кг спрыгивает с перекладины. Он начинает соскок с полного выпрямления, затем делает несколько оборотов перед приземлением. Его момент инерции в полностью вытянутом состоянии может быть аппроксимирован стержнем длиной 1,8 м, а в сложенном виде — стержнем вдвое меньшей длины. Если его скорость вращения при полном выпрямлении составляет 1,0 об/с, и он входит в группировку, когда его центр масс находится на высоте 3,0 м, двигаясь горизонтально к полу, сколько оборотов он может сделать, если выйдет из группировки на высоте 1,8 м. ? См. (Рисунок).

Рисунок 11.17 Гимнастка спрыгивает с высокой перекладины и выполняет несколько оборотов в группировке перед приземлением в вертикальном положении.

Стратегия

Используя закон сохранения углового момента, мы можем найти скорость его вращения в группировке. Используя уравнения кинематики, можно найти интервал времени от высоты 3,0 м до 1,8 м. Поскольку он движется горизонтально по отношению к земле, уравнения свободного падения упрощаются. Это позволит рассчитать количество оборотов, которое может быть выполнено. Поскольку мы используем соотношение, мы можем сохранить единицы измерения как обороты в секунду и не нужно преобразовывать их в радианы в секунду. 9{2}}=4.0\,\text{rev}\text{/}\text{s} [/latex].

Интервал времени в сборке: [латекс] t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2(3.0-1.8)\text{m}}{9.8\,\text {m}\text{/}\text{s}}}=0,5\,\text{s} [/latex].

За 0,5 с он сможет совершить два оборота со скоростью 4,0 об/с.

Значение

Обратите внимание, что количество оборотов, которое он может совершить, будет зависеть от того, как долго он находится в воздухе. В задаче он выходит из перекладины горизонтально на землю. Он также мог выходить под углом к ​​земле, что давало ему больше или меньше времени в воздухе в зависимости от угла, положительного или отрицательного, по отношению к земле. Гимнасты должны учитывать это при выполнении соскоков.

Пример

Сохранение углового момента при столкновении

Пуля массой [латекс] m=2.0\,\text{g} [/латекс] движется горизонтально со скоростью [латекс] 500.0\,\текст {м}\текст{/}\текст{с}. [/latex] Пуля попадает и застревает в краю твердого диска массой [латекс] M=3,2\,\text{кг} [/latex] и радиусом [латекс] R=0,5\,\text{м }\text{.} [/latex] Цилиндр может свободно вращаться вокруг своей оси и изначально находится в состоянии покоя ((Рисунок)). Какова угловая скорость диска сразу после попадания пули?

Рисунок 11. 18 Пуля выпущена горизонтально и застревает в краю диска, который может свободно вращаться вокруг своей вертикальной оси.

Стратегия

Для системы пуля-цилиндр внешний крутящий момент не действует вдоль вертикальной оси, проходящей через центр диска. Таким образом, угловой момент вдоль этой оси сохраняется. Начальный угловой момент пули равен [латекс] mvR [/латекс], который берется относительно оси вращения диска за момент до столкновения. Начальный момент импульса цилиндра равен нулю. Таким образом, суммарный угловой момент системы равен [латекс] mvR [/латекс]. Поскольку момент импульса сохраняется, начальный момент импульса системы равен моменту импульса пули, застрявшей в диске сразу после удара. 9{-3}\,\text{кг}\,+\,1,6\,\text{кг})(0,50\,\text{м})}=1,2\,\text{рад}\text{/} \текст{ы}. [/latex]

Значение

Система состоит из точечной частицы и твердого тела. Следует соблюдать осторожность при формулировании углового момента до и после столкновения. Непосредственно перед ударом угловой момент пули измеряется относительно оси вращения диска.

Резюме

• В отсутствие внешних крутящих моментов полный угловой момент системы сохраняется. Это вращательный аналог сохранения линейного количества движения, когда внешняя сила, действующая на систему, равна нулю.
• Для твердого тела, которое изменяет свой угловой момент в отсутствие чистого внешнего крутящего момента, сохранение углового момента дает [латекс] {I}_{f}{\omega }_{f}={I}_{i} {\omega}_{i} [/латекс]. Это уравнение говорит о том, что угловая скорость обратно пропорциональна моменту инерции. Таким образом, если момент инерции уменьшается, угловая скорость должна увеличиваться, чтобы сохранить угловой момент.
• Системы, содержащие как точечные частицы, так и твердые тела, можно анализировать с использованием закона сохранения углового момента. Момент количества движения всех тел в системе должен быть взят относительно общей оси.

Концептуальные вопросы

Для чего предназначен маленький пропеллер в задней части вертолета, который вращается в плоскости, перпендикулярной большому пропеллеру?

Показать решение

Предположим, ребенок идет от внешнего края вращающейся карусели внутрь. Угловая скорость карусели увеличивается, уменьшается или остается неизменной? Поясните свой ответ. Предположим, что карусель крутится без трения.

Когда веревка привязанного мяча обвивается вокруг шеста, что происходит с угловой скоростью мяча?

Показать решение

Предположим, что полярные ледяные щиты откололись и поплыли к экватору Земли, не тая. Что произойдет с угловой скоростью Земли?

Объясните, почему звезды вращаются быстрее, когда коллапсируют.

Показать ответ

Соревнующиеся дайверы втягивают конечности и сгибают тело, когда делают сальто. Непосредственно перед входом в воду они полностью вытягивают конечности, чтобы войти прямо вниз (см. ниже). Объясните влияние обоих воздействий на их угловые скорости. Также объясните влияние на их угловой момент. 9{2} [/latex] вращается против часовой стрелки вокруг той же оси с угловой скоростью [latex] {\omega }_{2}=8.0\,\text{rad}\text{/}\text{s} [/latex] .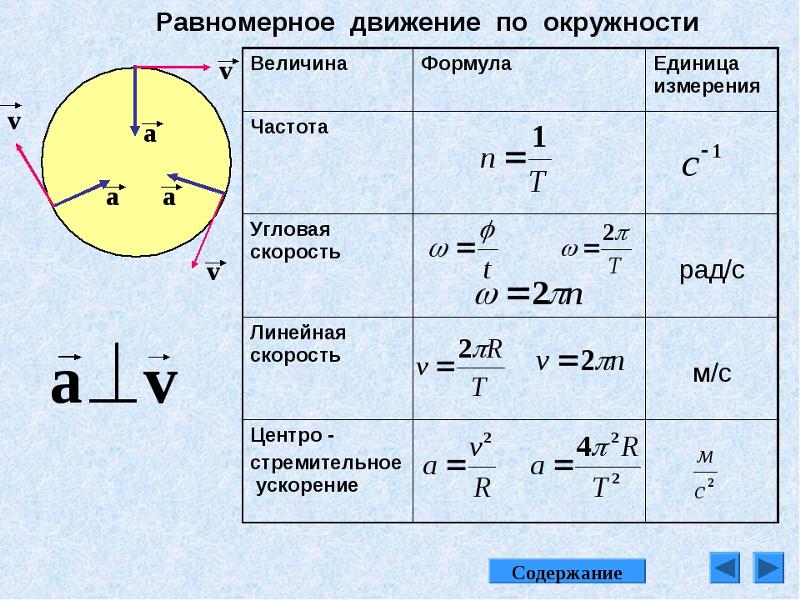 Если цилиндры соединены так, что они имеют одну и ту же ось вращения, какова угловая скорость комбинации? Какой процент первоначальной кинетической энергии теряется на трение?

Прыгун с хайборда выполняет начальное вращение с полностью вытянутым телом, затем входит в группировку и выполняет три сальто назад перед тем, как удариться о воду. Если его момент инерции перед группировкой [латекс] 16,9{2} [/latex], какую скорость вращения он должен сообщить своему телу непосредственно от доски и перед группировкой, если ему требуется 1,4 с, чтобы выполнить сальто до удара о воду?

Показать решение

Спутник Земли имеет апогей на высоте 2500 км над поверхностью Земли и перигей на высоте 500 км над поверхностью Земли. В апогее его скорость 730 м/с. Какова его скорость в перигее? Радиус Земли составляет 6370 км (см. ниже).

Орбита «Молния» — орбита спутника связи с большим эксцентриситетом, обеспечивающая непрерывное покрытие связью Скандинавских стран и соседней России. Орбита расположена таким образом, что эти страны имеют спутник в поле зрения в течение длительных периодов времени (см. ниже). Если спутник на такой орбите имеет апогей на высоте 40 000,0 км от центра Земли и скорость 3,0 км/с, какова будет его скорость в перигее, измеренная на высоте 200,0 км?

Показать ответ

Ниже показана маленькая частица массой 20 г, движущаяся со скоростью 10,0 м/с, когда она сталкивается и прилипает к краю однородного твердого цилиндра. Цилиндр может свободно вращаться вокруг своей оси, проходящей через его центр, и перпендикулярен странице. Цилиндр имеет массу 0,5 кг и радиус 10 см и изначально покоится. а) Какова угловая скорость системы после столкновения? б) Сколько кинетической энергии теряется при столкновении?

Жук массой 0,020 кг покоится на краю сплошного цилиндрического диска [латекс] (M=0,10\,\text{кг,}\,R=0,10\,\text{м}) [ /латекс] вращается в горизонтальной плоскости вокруг вертикальной оси, проходящей через ее центр. Диск вращается со скоростью 10,0 рад/с. Жучка ползет к центру диска. а) Чему равна новая угловая скорость диска? б) Как изменится кинетическая энергия системы? в) Если жук подползет к внешнему краю диска, какова тогда будет угловая скорость диска? г) Чему равна новая кинетическая энергия системы? д) В чем причина увеличения и уменьшения кинетической энергии?

Показать решение

Однородный стержень массой 200 г и длиной 100 см может свободно вращаться в горизонтальной плоскости вокруг неподвижной вертикальной оси, проходящей через его центр, перпендикулярно его длине. В канавки вдоль стержня вставлены две маленькие бусины массой 20 г каждая. Первоначально две бусинки удерживаются защелками с противоположных сторон от центра стержня, на расстоянии 10 см от оси вращения. При таком положении бусинок стержень вращается с угловой скоростью 10,0 рад/с. Когда защелки отпущены, бусины выскальзывают наружу вдоль стержня. а) Какова угловая скорость стержня, когда бусины достигают концов стержня? б) Какова будет угловая скорость стержня, если бусины слетят со стержня? 9{2}. [/latex] Мальчик массой 50 кг бежит по касательной к ободу со скоростью 4,0 м/с и прыгает дальше. Если карусель изначально покоится, какова угловая скорость после того, как мальчик запрыгнет на нее?

Показать решение

Игровая карусель имеет массу 120 кг, радиус 1,80 м и вращается с угловой скоростью 0,500 об/с. Какова его угловая скорость после того, как ребенок массой 22,0 кг заберется на него, схватившись за внешний край? Сначала ребенок находится в состоянии покоя.

Трое детей катаются на краю карусели весом 100 кг, радиусом 1,60 м и скоростью вращения 20,0 об/мин. Дети имеют массу 22,0, 28,0 и 33,0 кг. Если ребенок массой 28,0 кг переместится в центр карусели, какова новая угловая скорость в об/мин? 9{2} [/латекс]. (b) Он уменьшает скорость вращения (свою угловую скорость), вытягивая руки и увеличивая момент инерции. Найдите значение его момента инерции, если его угловая скорость уменьшится до 1,25 об/с. (c) Предположим вместо этого, что он держит руки и позволяет трению льда замедлить его до 3,00 об/с. Какой средний крутящий момент был приложен, если это заняло 15,0 с?

Фигуристы-близнецы подходят друг к другу, как показано ниже, и берутся за руки. (a) Рассчитайте их конечную угловую скорость, учитывая, что начальная скорость каждого из них относительно льда равна 2,50 м/с. Каждый имеет массу 70,0 кг, и каждый имеет центр масс, расположенный на расстоянии 0,800 м от их сцепленных рук. Вы можете приблизить их моменты инерции к моменту инерции точечных масс на этом радиусе. (b) Сравните начальную кинетическую энергию и конечную кинетическую энергию.

Показать ответ

Бейсболист вытягивает руку вверх, чтобы поймать быстрый мяч со скоростью 40 м/с. Вес бейсбольного мяча 0,145 кг, длина руки ловца 0,5 м, масса 4,0 кг. а) Какова угловая скорость руки сразу после ловли мяча, измеренная от сустава руки? б) Какой крутящий момент будет приложен, если кэтчер прекратит вращение руки через 0,3 с после ловли мяча?

В 2015 году в Варшаве, Польша, Оливия Оливер из Новой Шотландии побила мировой рекорд, став самой быстрой спиннингисткой на коньках. Она достигла рекорда в 342 об/мин, побив существующий мировой рекорд Гиннеса на 34 оборота. Если фигуристка вытянет руки с такой скоростью вращения, какой будет ее новая скорость вращения? Предположим, что она может быть аппроксимирована 45-килограммовым стержнем высотой 1,7 м и радиусом 15 см при рекордном вращении. С ее вытянутыми руками примите приближение к стержню длиной 130 см с [латексом] 10% [/латекса] массы ее тела, выровненными перпендикулярно оси вращения. Силами трения пренебречь.

Показать решение

Спутник на геосинхронной круговой орбите находится на расстоянии 42 164,0 км от центра Земли. Небольшой астероид сталкивается со спутником, отправляя его на эллиптическую орбиту с апогеем 45 000,0 км. Какова скорость спутника в апогее? Предположим, что его угловой момент сохраняется.

Гимнастка делает кувырки по полу, а затем подбрасывает себя в воздух и выполняет несколько сальто в группировке, находясь в воздухе. Если ее момент инерции при выполнении колес составляет [латекс] 13,5\,\text{кг}·{\текст{м}}^{2} [/латекс] и ее скорость вращения составляет 0,5 об/с, сколько оборотов сделает ли она в воздухе, если ее момент инерции в группировке [латекс] 3,4\,\text{кг}·{\text{м}}^{2} [/латекс] и у нее есть 2,0 с, чтобы выполнить кувыркается в воздухе?

Показать решение

Центрифуга в Исследовательском центре Эймса НАСА имеет радиус действия 8,8 м и может создавать силы на своем полезном грузе в 20 г с, что в 20 раз превышает силу гравитации на Земле. а) Каков угловой момент полезного груза массой 20 кг, который испытывает 10 г с в центрифуге? (b) Если приводной двигатель был выключен в (a) и полезная нагрузка потеряла 10 кг, какова будет его новая скорость вращения, принимая во внимание отсутствие сил трения?

Карнавальный аттракцион состоит из четырех спиц, к которым прикреплены капсулы, способные вместить двух человек. Спицы имеют длину 15 м каждая и прикреплены к центральной оси. Каждая спица имеет массу 200,0 кг, а гондолы имеют массу 100,0 кг. Если аттракцион вращается со скоростью 0,2 об/с, а в каждой капсуле находятся двое детей весом 50,0 кг, какова будет новая скорость вращения, если все дети спрыгнут с аттракциона? 9{11}[/latex] км и если вещество, составившее эти планетезимали, ставшие впоследствии Нептуном, было равномерно распределено по его краям, то каков был период обращения внешних краев первичного диска?

Глоссарий

закон сохранения углового момента

угловой момент сохраняется, то есть начальный угловой момент равен конечному угловому моменту, когда к системе не приложен внешний крутящий момент

10.

1 Угловое ускорение – Колледж физики главы 1-17

10 Вращательное движение и угловой момент

Резюме

• Описать равномерное круговое движение.
• Объясните неравномерное круговое движение.
• Рассчитать угловое ускорение объекта.
• Соблюдайте связь между линейным и угловым ускорением.

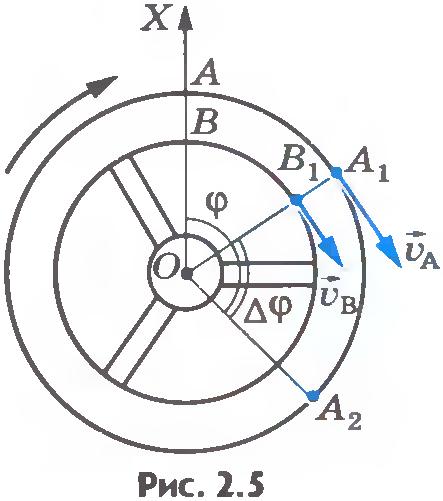
Глава 6 Равномерное круговое движение и гравитация обсуждали только равномерное круговое движение, то есть движение по окружности с постоянной скоростью и, следовательно, с постоянной угловой скоростью. Напомним, что угловая скорость[латекс]\boldsymbol{\omega}[/латекс] определялась как скорость изменения угла[латекс]\жирныйсимвол{\тета}:[/латекс]

[латекс]\boldsymbol{\omega\:=}[/латекс][латекс]\boldsymbol{\frac{\Delta\theta}{\Delta{t}}},[/latex]

, где[латекс]\жирныйсимвол{\тета}[/латекс] — угол поворота, как показано на рисунке 1. Связь между угловой скоростью[латекс]\жирныйсимвол{\омега}[/латекс] и линейной скоростью[латекс] \boldsymbol{v}[/latex] также был определен в главе 6. 1 «Угол вращения и угловая скорость» как

.

[латекс]\boldsymbol{v=r\omega}[/латекс]

или

[латекс]\boldsymbol{\omega\:=}[/латекс][латекс]\boldsymbol{\frac{v}{r}},[/латекс]

, где[latex]\boldsymbol{r}[/latex] — радиус кривизны, также показанный на рисунке 1. Согласно соглашению о знаках, направление против часовой стрелки считается положительным направлением, а направление по часовой стрелке — отрицательным

Рисунок 1. На этом рисунке показано равномерное круговое движение и некоторые его определяемые величины.

Угловая скорость непостоянна, когда фигурист тянет руки, когда ребенок запускает карусель из состояния покоя или когда жесткий диск компьютера останавливается при выключении. Во всех этих случаях есть угловое ускорение , в котором[латекс]\жирныйсимвол{\омега}[/латекс]изменяется. Чем быстрее происходит изменение, тем больше угловое ускорение. Угловое ускорение[латекс]\boldsymbol{\alpha}[/латекс] определяется как скорость изменения угловой скорости. 2}.[/латекс]Если[латекс ]\boldsymbol{\omega}[/latex] увеличивается, тогда [латекс]\boldsymbol{\alpha}[/latex] положителен. Если [латекс]\boldsymbol{\omega}[/latex]убывает, то [латекс]\boldsymbol{\alpha}[/латекс]отрицательно. 92},[/latex]сколько времени нужно колесу, чтобы остановиться?

Стратегия для (a)

Угловое ускорение можно найти непосредственно из его определения в [latex]\boldsymbol{\alpha=\frac{\Delta\omega}{\Delta{t}}}[/latex ]потому что заданы конечная угловая скорость и время. Мы видим, что [латекс]\boldsymbol{\Delta\omega}[/латекс]составляет 250 об/мин, а [латекс]\boldsymbol{\Delta{t}}[/латекс]составляет 5,00 с.

Решение для (а)

Вводя известные сведения в определение углового ускорения, получаем 92}[/latex]для углового ускорения нам нужно преобразовать[latex]\boldsymbol{\Delta\omega}[/latex]из об/мин в рад/с:

[latex]\begin{array}{lcl} \ boldsymbol{\Delta\omega} & \boldsymbol{=} & \boldsymbol{250\frac{\textbf{rev}}{\textbf{min}}\cdotp\frac{2\pi\textbf{rad}}{\ textbf{rev}}\cdotp\frac{1\textbf{ мин}}{60\textbf{ сек}}} \\ {} & \boldsymbol{=} & \boldsymbol{26,2\textbf{ рад. 2}.[/ латекс] Таким образом, 92}} \\ {} & \boldsymbol{=} & \boldsymbol{0.300\textbf{ с.}} \end{array}[/latex]

Обсуждение

Обратите внимание, что угловое ускорение при вращении девушки колесо маленькое и положительное; для получения заметной угловой скорости требуется 5 с. Когда она нажимает на тормоз, угловое ускорение большое и отрицательное. Угловая скорость быстро стремится к нулю. В обоих случаях отношения аналогичны тому, что происходит с линейным движением. Например, когда вы врезаетесь в кирпичную стену, происходит большое замедление — изменение скорости сильно за короткий промежуток времени.

Если бы велосипед в предыдущем примере стоял на колесах, а не в перевернутом положении, он сначала разогнался бы по земле, а затем остановился бы. Эту связь между круговым движением и линейным движением необходимо исследовать. Например, было бы полезно знать, как связаны линейное и угловое ускорения. При круговом движении линейное ускорение составляет по касательной к окружности в интересующей точке, как показано на рисунке 2. Таким образом, линейное ускорение называется тангенциальным ускорением[латекс]\жирныйсимвол{a_{\textbf{t}}}.[ /латекс]

Рисунок 2. При движении по окружности линейное ускорение a возникает при изменении величины скорости: a касается движения. В контексте кругового движения линейное ускорение также называется тангенциальным ускорением a _t .

Линейное или тангенциальное ускорение относится к изменениям величины скорости, но не ее направления. Из главы 6 «Равномерное круговое движение и гравитация» мы знаем, что при круговом движении центростремительное ускорение,[latex]\boldsymbol{a_{\textbf{c}}},[/latex]относится к изменениям направления скорости, но не ее величины. . Объект, совершающий круговое движение, испытывает центростремительное ускорение, как показано на рис. 3. Таким образом, }}[/latex] перпендикулярны и независимы друг от друга. Тангенциальное ускорение[латекс]\boldsymbol{a_{\textbf{t}}}[/латекс]прямо связано с угловым ускорением[латекс]\жирныйсимвол{\альфа}[/латекс]и связано с увеличением или уменьшением скорость, но не ее направление.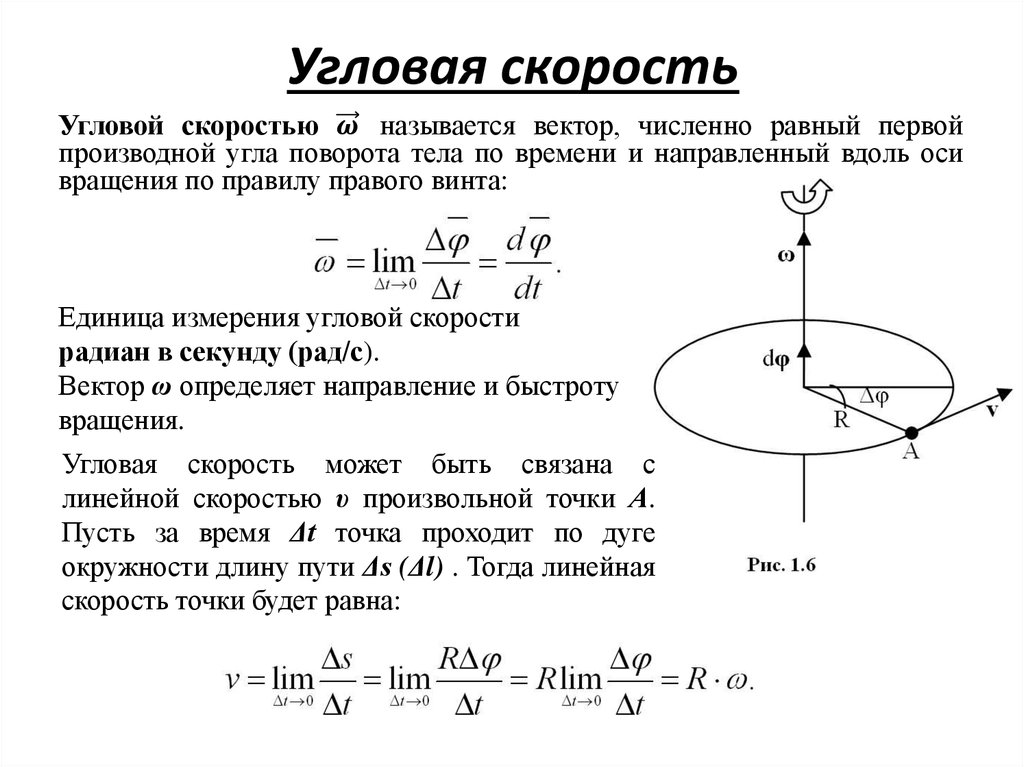

Рис. 3. Центростремительное ускорение a _c возникает при изменении направления скорости; оно перпендикулярно круговому движению. Таким образом, центростремительное и тангенциальное ускорения перпендикулярны друг другу.

Теперь мы можем найти точное соотношение между линейным ускорением[latex]\boldsymbol{a_{\textbf{t}}}[/latex]и угловым ускорением[latex]\boldsymbol{\alpha}.[/latex]Потому что линейное ускорение пропорциональна изменению модуля скорости, она определяется (как это было в главе 2 «Одномерная кинематика») равной

[латекс]\boldsymbol{a_{\textbf{t}}\:=}[/latex][латекс]\boldsymbol{\frac{\Delta{v}}{\Delta{t}}.}[/latex ]

Для кругового движения обратите внимание, что[latex]\boldsymbol{v=r\omega},[/latex], так что

[латекс]\boldsymbol{a _{\textbf{t}}\:=}[/latex][латекс]\boldsymbol{\frac{\Delta(r\omega)}{\Delta{t}}.}[ /латекс]

Радиус[латекс]\boldsymbol{r}[/latex]постоянен для кругового движения, поэтому [латекс]\boldsymbol{\Delta(r\omega)=r(\Delta\omega)}. [/latex] Таким образом,

[латекс]\boldsymbol{a_{\textbf{t}}=r}[/latex][латекс]\boldsymbol{\frac{\Delta\omega}{\Delta{t}}.}[/latex]

По определению,[латекс]\жирныйсимвол{\альфа=\фракция{\Delta\omega}{\Delta{t}}}.[/latex] Таким образом,

[латекс]\boldsymbol{a_{\textbf{t}}=r\alpha},[/латекс]

или

[латекс]\boldsymbol{\alpha\:=}[/латекс][латекс]\boldsymbol{\frac{a _{\textbf{t}}}{r}.}[/latex]

Эти уравнения означают, что линейное ускорение и угловое ускорение прямо пропорциональны. Чем больше угловое ускорение, тем больше линейное (тангенциальное) ускорение, и наоборот. Например, чем больше угловое ускорение ведущих колес автомобиля, тем больше ускорение автомобиля. Радиус тоже имеет значение. Например, чем меньше колесо, тем меньше его линейное ускорение при заданном угловом ускорении[latex]\boldsymbol{\alpha}.[/latex]

Пример 2: Расчет углового ускорения колеса мотоцикла

Мощный мотоцикл может разгоняться от 0 до 30,0 м/с (около 108 км/ч) за 4,20 с. 2.} \end{массив}[/latex]

Обсуждение

Радианы безразмерны и появляются в любом соотношении между угловыми и линейными величинами.

На данный момент мы определили три величины вращения — [латекс]\boldsymbol{\theta,\:\omega},[/latex]и [латекс]\boldsymbol{\alpha}.[/latex]Эти величины аналогичны поступательные величины[latex]\boldsymbol{x},\:\boldsymbol{v},[/latex]и[latex]\boldsymbol{a}.[/latex]В таблице 1 показаны вращательные величины, аналогичные поступательные величины и отношения между ними.

Поворотный	Трансляционное	Отношения
[латекс]\boldsymbol{\theta}[/латекс]	[латекс]\boldsymbol{x}[/латекс]	[латекс] \boldsymbol{\theta=\frac{x}{r}}[/латекс]
[латекс]\boldsymbol{\omega}[/латекс]	[латекс]\boldsymbol{v}[/латекс]	[латекс] \boldsymbol{\omega=\frac{v}{r}}[/латекс]
[латекс]\boldsymbol{\alpha}[/латекс]	[латекс]\boldsymbol{a}[/латекс]	[латекс] \boldsymbol{\alpha=\frac{a_{\textbf{t}}}{r}}[/latex]
Таблица 1. Вращательные и поступательные величины.

СОЗДАНИЕ СОЕДИНЕНИЙ: ЭКСПЕРИМЕНТ ДЛЯ ДОМАШНИХ УСЛОВИЙ

Сядьте, поставив ноги на землю, на вращающийся стул. Поднимите одну ногу так, чтобы она была разогнута (выпрямлена). Используя другую ногу, начните вращать себя, отталкиваясь от земли. Прекратите использовать ногу, чтобы отталкиваться от земли, но позвольте стулу вращаться. Из исходной точки, с которой вы начали, зарисуйте угол, угловую скорость и угловое ускорение вашей ноги как функцию времени в виде трех отдельных графиков. Оцените величины этих величин.

ИССЛЕДОВАНИЯ PHET: РЕВОЛЮЦИЯ БОЖЬЕЙ КОРОВКИ

Присоединяйтесь к божьей коровке в исследовании вращательного движения. Вращайте карусель, чтобы изменить ее угол, или выберите постоянную угловую скорость или угловое ускорение. Изучите, как круговое движение связано с положением жука по осям x, y, скоростью и ускорением, используя векторы или графики.

Рисунок 5. Революция божьей коровки

• Равномерное круговое движение – это движение с постоянной угловой скоростью[latex]\boldsymbol{\omega=\frac{\Delta\theta}{\Delta{t}}}.[/latex]
• При неравномерном круговом движении скорость изменяется со временем, а скорость изменения угловой скорости (т.е. углового ускорения) равна [латекс]\boldsymbol{\alpha=\frac{\Delta\omega}{\Delta{t} }}.[/латекс]
• Линейное или тангенциальное ускорение относится к изменениям величины скорости, но не ее направления, задается как [латекс]\жирныйсимвол{а_{\textbf{t}}=\frac{\Delta{v}}{\Delta{t} }}.[/латекс]
• Для кругового движения обратите внимание, что[latex]\boldsymbol{v=r\omega},[/latex], так что

  [латекс]\boldsymbol{a _{\textbf{t}}\:=}[/latex][латекс]\boldsymbol{\frac{\Delta(r\omega)}{\Delta{t}}}.[ /латекс]

• Радиус r постоянен для кругового движения, поэтому[латекс]\boldsymbol{\Delta(r\omega)=r\Delta\omega}.[/latex] Таким образом,

  [латекс]\boldsymbol{a_{\textbf{t}}=r}[/latex][латекс]\boldsymbol{\frac{\Delta\omega}{\Delta{t}}}.