Температура нагревателя идеального теплового двигателя,работающего по циклу Карно, равна T1, а температурахолодильника равна T2. Физика 18295
Задание 18295
Температура нагревателя идеального теплового двигателя,
работающего по циклу Карно, равна T1, а температура
холодильника равна T2. За цикл двигатель получает от
нагревателя количество теплоты Q1.
Установите соответствие между физическими величинами и формулами, по которым их
можно рассчитать.
К каждой позиции первого столбца подберите соответствующую
позицию второго и запишите в таблицу выбранные цифры под
соответствующими буквами.
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ФОРМУЛЫ | ||
| А) | КПД двигателя | 1) | 1−T2T1 |
| Б) | работа, совершаемая двигателем за цикл | 2) | Q1(T1−T2)T1 |
| 3) | T1−T2T2 | ||
| 4) | Q1T2T1 |
12
Задание 17648
Задание 18193
Задание 18295
Задание 18325
Задание 18354
Задание 18381
Задание 18464
Задание 18529
Задание 18556
Задание 18587
Задачи для самостоятельного решения
Задача
1. Идеальная
Идеальная
тепловая машина, работающая по циклу
Карно, получает за каждый цикл от
нагревателя 2500 Дж. Температура нагревателя
400 К, температура холодильника 300 К. Найти
работу, совершаемую машиной за один
цикл, и количество тепла, отданное
холодильнику за один цикл.
Ответ:
А
=
= 630 Дж;
=
1880 Дж.
Задача
2. Идеальная
тепловая машина работает по циклу Карно.
Определить КПД цикла, если известно,
что за один цикл была произведена работа
3000 Дж и холодильнику передано 13,3 кДж
тепла.
Ответ:
= 18 %.
Задача
3. Идеальная
тепловая машина работающая по циклу
Карно, совершает за один цикл работу
7,35.Дж.
Температура нагревателя 1000С,
температура холодильника 0 0С.
Найти: 1) КПД машины; 2) количество тепла,
получаемое машиной за один цикл от
нагревателя; 3) количество тепла, отданное
за один цикл холодильнику.
Ответ:
1)
= 26,8 %; 2)
=
2,74.Дж;
3)=
2. Дж.
Дж.
Задача
4. Идеальная
тепловая машина, работающая по циклу
Карно, 80 % тепла, полученного от нагревателя,
передает холодильнику. Количество
тепла, полученное от нагревателя, равно
6,3 кДж. Найти: 1) КПД цикла; 2) работу,
совершенную при полном цикле.
Ответ:
1)
= 20 %; 2) А
= 1,26 .Дж.
Задача
5. Цикл состоит
из двух изотерм и двух изобар,
= 600 К,= 300 К,.
Определить КПД цикла, если рабочим телом
служит один моль идеального газа, число
степеней свободы молекул которого равно
5.
Ответ:
= 0,221.
Задача
6. Холодильная
машина работает по обратному циклу
Карно в интервале температур
0С
и
=
3 0С.
Рабочее тело — азот, масса которого т
= 0,2 кг. Найти количество тепла, отбираемого
от охлаждаемого тела, и работу внешних
сил за цикл, если степень сжатия
.
Ответ:
= 21,6 кДж;А
=
2,4 кДж.
Задача
7. Определить
изменение энтропии одного моля идеального
газа в изобарном, изохорном и изотермическом
процессах.
Ответ:
Задача
8*. Какую
максимальную работу может произвести
тепловая машина, если в качестве
нагревателя используется кусок железа
массой 100 кг с начальной температурой
= 1500 К, а в качестве холодильника – вода
океана с температурой= 285 К? (С = 500).
Ответ:
А
= 4,5 .Дж.
Задача
9*. Идеальный
газ совершает цикл Карно. Температура
холодильника 290 К. Во сколько раз
увеличится КПД цикла, если температура
нагревателя повысится от 400 до 600 К?
Ответ:
в 1,88 раза.
Задача
10*. Идеальный
газ, расширяясь изотермически при
температуре Т
= 400 К, совершает работу А
= 800 Дж. Как изменится энтропия газа?
Ответ:
S
= 2
.
Задача
11. Во сколько
раз следует изотермически увеличить
объем газа в количестве
= 4 моль, чтобы его энтропия изменилась
на S
= 23
?
Ответ:
в 2 раза.
Задача
12*. Один грамм
водорода первоначально имеет объем
V1
= 200 л и давление р1
= 500 Па. После расширения объем газа стал
После расширения объем газа стал
V2
= 500 л, а давление р2
= 200 Па. Считая газ идеальным, определить:
а) приращение внутренней энергии
;
б) приращение энтропииS.
Ответ:
S
=3,8
;U
= 0.
Задача
13. Найти
изменение энтропии при переходе 6 г
водорода от объема V1
= 20 л под давлением 1,5
Па к объемуV2
= 40 л при температуре 300 0С
при неизменном давлении.
Ответ:
S
=60,5
.
Задача
14. Найти
изменение энтропии при изобарическом
расширении 8 г гелия от объема V1
= 10 л до объема V2
= 25 л.
Ответ:
S
= 38,1
.
Задача
15. 10,5 г азота
изотермически расширяются от объема
V1
= 2 л до объема V2
= 5 л. Найти прирост энтропии в этом
процессе.
Ответ:
S
= 2,9
.
Задача
16. При
нагревании одного киломоля двухатомного
газа его абсолютная температура
увеличивается в 1,5 раза. Найти изменение
Найти изменение
энтропии, если нагревание происходит:
1) изохорически; 2) изобарически.
Ответ:
1) S
= 8,5
;
2) S
= 11,8
.
Задача
17*. В результате
нагревания 22 г азота его абсолютная
температура увеличилась в 1,2 раза, а
энтропия увеличилась на 4,19
.
При каких условиях производилось
нагревание (при постоянном объеме или
при постоянном давлении)?
Ответ:
нагревание проводилось при постоянном
давлении.
Задача
18. Совершая
замкнутый цикл, газ получил от нагревателя
теплоту Q
= 4,19 кДж. Какую работу совершил газ в
результате всего цикла, если термический
КПД цикла
= 0,1?
Ответ:
А
=
= 419 Дж.
Задача
19. Один моль
идеального двухатомного газа совершает
цикл, состоящий из двух изохор и двух
изобар. Наименьший объем Vmin
= 10 л, наибольший объем Vmax=
20 л, наименьшее давление pmin
= 2,46 атм, наибольшее давление pmax
= 4,1 атм.
Начертить график цикла, в координатах
р,
V
определить температуру газа для
характерных точек цикла и его термический
КПД.
Ответ:
300 К; 500 К; 1000 К; 605 К;
= 8,55 %.
Задача
20. Один
киломоль двухатомного идеального газа
совершает замкнутый цикл, график которого
изображен на рис. 22.18. Определить: 1)
теплоту, полученную от нагревателя; 2)
теплоту, переданную холодильнику; 3)
работу, совершаемую газом за цикл; 4)
термический КПД цикла.
Ответ:
1)
= 7,61Дж; 2)= 7,21 ·Дж; 3)А
= 0,4
Дж; 4)
= 5,3 %.
Задача
21. Один моль
идеального двухатомного газа, находящийся
под давлением р1
= 1 атм при температуре
= 270С,
нагревают при постоянном объеме до
давления р2
= 2 атм. После этого газ расширился
изотермически до начального давления
и затем был изобарически сжат до
начального объема V1.
Начертить график процесса в координатах
р,
V;
р,
т;
V,
Т. Определить температуру газа для
Определить температуру газа для
характерных точек цикла и его термический
КПД.
Ответ:
600
К,
= 9,9 %.
Задача
22. Одноатомный
газ 0,1 кмоль, имевший при давлении
р1
= 105
Па объем V1
= 5 м3,
сжимался изобарически до объема V2
= 1 м3,
затем сжимался адиабатически и, наконец,
расширялся при постоянной температуре
до начального объема и давления. Построить
график процесса в координатах р,
V.
Найти: 1) температуру, объем и давление
для характерных точек цикла; 2) теплоту,
полученную газом от нагревателя; 3)
теплоту, переданную газом холодильнику;
4) работу, совершенную за весь цикл; 5)
термический КПД цикла.
Ответ:
= 600 К;= 120 К;V3
= 0,09 м3;
Па;= 600 К;Дж;Дж;А
=
Дж;
= 50 %.
Задача
23. Идеальный
многоатомный газ совершает цикл,
состоящий из двух изохор и двух изобар,
причем наибольшее давление газа в два
раза больше наименьшего, а наибольший
объем в 4 раза больше наименьшего.
Определить термодинамический КПД цикла.
Ответ:
= 0,11.
Задача
24. Газ,
совершающий цикл Карно,
теплоты,
полученной от нагревателя, отдает
холодильнику. Температура холодильника
00С.
Определить температуру нагревателя.
Ответ:
= 409 К.
Задача
25. Газ
совершает цикл Карно. Температура
холодильника
= 170С.
Во сколько раз увеличится КПД цикла,
если температура нагревателя повысится
от
= 1270С
до
= 3470С?
Ответ:
1,93 раза.
Задача
26. Газ
совершает цикл Карно. Абсолютная
температура нагревателя в три раза
выше, чем температура холодильника.
Нагреватель передал газу теплоту
=
10 ккал. Какую работу совершил газ?
Ответ:
А
= 2,81
Дж.
Задача
27. Газ
совершает цикл Карно. Абсолютная
температура
нагревателя в 4 раза выше абсолютной
температурыхолодильника. Какую долю теплоты,
получаемой за один цикл от нагревателя,
газ отдает холодильнику.
Ответ:
Задача
28. Газ,
Газ,
совершающий цикл Карно, за счет каждой
килокалории теплоты, полученной от
нагревателя, совершает работу А
= 598 Дж. Каков КПД этого цикла? Во сколько
раз абсолютная температура
нагревателя больше абсолютной температурыхолодильника?
Ответ:
= 14,3 %;
.
Задача
29. Газ
совершает цикл Карно. Работа изотермического
расширения
= 5 Дж. Определить работу изотермического
сжатия, если термический КПД цикла
= 0,2.
Ответ:
А =
4 Дж.
Задача
30. Наименьший
объем газа, совершающего цикл Карно,
V1=
153 л. Определить наибольший объем V3,
если объем газа в конце изотермического
расширения V2
= 189 л, а в конце изотермического сжатия
V4
= 600 л.
Ответ:
V3
= 0,74 м3.
Задача
31. Смешано
= 5 кг воды при температуре= 100С
с
= 8 кг воды при температуре= 800С.
Найти: 1) температуру смеси; 2) изменение
энтропии, происходящее при смешивании.
Ответ:
t
= 53 0С;
S
=296
.
Задача
32. В результате
изохорического нагревания водорода
массой т
= 1 г давление газа увеличилось в два
раза. Определить изменение энтропии
газа.
Ответ:
S
= 7,2
.
Задача
33. Найти
изменение энтропии при изобарическом
расширении азота массой т
= 4 г от объема V1
= 5 л до объема V2
= 9 л.
Ответ:
S
= 2,43
.
Задача
34. Кусок льда
массой т
= 200 г, взятый при температуре
=
10 0С,
был нагрет до
= 00С
и расплавлен, после чего образовавшаяся
вода была нагрета до температуры
=
100С.
Определить изменение энтропии льда.
Ответ:
S
= 291
.
Задача
35. Кислород
массой т
= 2 кг увеличил свой объем в 5 раз, один
раз – изотермически при температуре
= 100С,
другой раз – изотермически при температуре
= 1000С,
третий раз – адиабатически. Каково
будет изменение энтропии в этих трех
случаях?
Ответ:
;S
= 0.
Задача
36. Водород
массой т
= 100 г был изобарически нагрет так, что
его объем увеличился в 3 раза, а затем
водород был изохорически охлажден так,
что давление его уменьшилось в три раза.
Найти изменение энтропии.
Ответ:
= 457.
Задача
37. Идеальный
двухатомный газ, занимающий объем V1
= 2 л, подвергли адиабатному расширению.
При этом его объем возрос в 5 раз. Затем
газ подвергли изобарному сжатию до
начального объема. В результате изохорного
нагревания он был возвращен в первоначальное
состояние. Постройте график цикла и
определите термический КПД цикла.
Ответ:
= 34,1%.
Задача
38. Идеальный
двухатомный газ (
= 3 моль), занимающий объем V1
= 5 л и находящийся под давлением р1
= 1 МПа, подвергли изохорному нагреванию
до Т2
= 500 К. После этого газ подвергли
изотермическому расширению до начального
давления, а затем он в результате
изобарного сжатия возвращен в
первоначальное состояние. Постройте
Постройте
график цикла и определите термический
КПД цикла.
Ответ:
= 13,3%.
Задача
39. Рабочее
тело – идеальный газ – теплового
двигателя совершает цикл, состоящий из
последовательных процессов: изобарного,
адиабатного и изотермического. В
результате изобарного процесса газ
нагревается от Т1
= 300 К до Т2
= 600 К. Определите термический КПД
теплового двигателя.
Ответ:
= 30,7%.
Задача
40. Азот массой
500 г находящийся под давлением р1
= 1 МПа при температуре t1
= 127 С,
подвергли изотермическому расширению,
в результате которого давление газа
уменьшилось в п
= 3 раза. После этого газ подвергли
адиабатному сжатию до начального
давления, а затем он был изобарно сжат
до начального объема. Постройте график
цикла и определите работу, совершенную
газом за цикл.
Ответ:
А
= -11,5 кДж.
Задача
41. Идеальный
газ, совершающий цикл Карно, 70% количества
теплоты, полученного от нагревателя,
отдает холодильнику. Количество теплоты,
Количество теплоты,
получаемое от нагревателя, равно 5 кДж.
Определите: 1) термический КПД цикла; 2)
работу, совершенную при полном цикле.
Ответ:
1)
= 30%; 2) А
= 1,5 кДж.
Задача
42. Идеальный
газ совершает цикл Карно. Температура
нагревателя
Т1
= 500 К, холодильника Т2
= 300 К. Работа изотермического расширения
газа составляет 2 кДж. Определите: 1)
термический КПД цикла; 2) количество
теплоты, отданное газом при изотермическом
сжатии холодильнику.
Ответ:
1)
= 40%, 2) Q2
= 1,2 кДж.
Задача
43. Многоатомный
идеальный газ совершает цикл Карно, при
этом в процессе адиабатного расширения
объем газа увеличивается в п
= 4 раза. Определите термический КПД
цикла.
Ответ:
= 37 %.
Задача
44. Во сколько
раз необходимо увеличить объем (
= 5 моль) идеального газа при изотермическом
расширении, если его энтропия увеличилась
на S
= 57,6
?
Ответ:
Задача
45. При
При
нагревании двухатомного идеального
газа (
= 2 моль) его термодинамическая температура
увеличилась в п
= 2 раза. Определите изменение энтропии,
если нагревание происходит: 1) изохорно;
2) изобарно.
Ответ:
1) S1
= 28,8
;
2)S2
= 40,3
.
Задача
46. Идеальный
газ (
= 2 моль) сначала изобарно нагрели, так
что объем газа увеличился в
п1
= 2 раза, а затем изохорно охладили, так
что давление его уменьшилось в п2
= 2 раза. Определите приращение энтропии
в ходе указанных процессов.
Ответ:
S
= 11,5
.
Задача
47. Азот массой
28 г адиабатно расширили в п
= 2 раза, а затем изобарно сжали до
начального объема. Определите изменение
энтропии газа в ходе указанных процессов.
Ответ:
S
= -20,2
.
Идеальная тепловая машина Карно: второй закон термодинамики в новой редакции | Физика |
Цели обучения
К концу этого раздела вы сможете:
- Идентифицировать цикл Карно.

- Рассчитайте максимальный теоретический КПД ядерного реактора.
- Объясните, как диссипативные процессы влияют на идеальную машину Карно.
Рисунок 1. Пьющая птица (фото: Arabesk.nl, Wikimedia Commons)
Новая игрушка, известная как пьющая птица (на рисунке 1), является примером двигателя Карно. Он содержит хлористый метилен (смешанный с красителем) в брюшной полости, который кипит при очень низкой температуре — около 100ºF. Для работы нужно намочить голову птицы. Когда вода испаряется, жидкость поднимается в голову, заставляя птицу утяжеляться и нырять вперед обратно в воду. Это охлаждает хлористый метилен в голове, и он перемещается обратно в брюшную полость, в результате чего низ птицы становится тяжелым, и она опрокидывается вверх. Если не считать очень небольшого вклада энергии — первоначального смачивания головы — птица становится своего рода вечным двигателем.
Из второго закона термодинамики мы знаем, что тепловая машина не может быть КПД на 100 %, так как всегда должна быть некоторая теплопередача Q c в окружающую среду, которую часто называют отработанным теплом. Насколько эффективной может быть тепловая машина? На этот вопрос на теоретическом уровне ответил молодой французский инженер Сади Карно (1796–1832) в 1824 г., изучая появлявшуюся тогда технологию теплового двигателя, решающую для промышленной революции. Он разработал теоретический цикл, который сейчас называется 9-м циклом.0019 Цикл Карно , который является наиболее эффективным из возможных циклических процессов. Второй закон термодинамики можно переформулировать в терминах цикла Карно, и, таким образом, Карно на самом деле открыл этот фундаментальный закон. Любая тепловая машина, использующая цикл Карно, называется двигателем Карно .
Насколько эффективной может быть тепловая машина? На этот вопрос на теоретическом уровне ответил молодой французский инженер Сади Карно (1796–1832) в 1824 г., изучая появлявшуюся тогда технологию теплового двигателя, решающую для промышленной революции. Он разработал теоретический цикл, который сейчас называется 9-м циклом.0019 Цикл Карно , который является наиболее эффективным из возможных циклических процессов. Второй закон термодинамики можно переформулировать в терминах цикла Карно, и, таким образом, Карно на самом деле открыл этот фундаментальный закон. Любая тепловая машина, использующая цикл Карно, называется двигателем Карно .
Важнейшее значение цикла Карно — и, по сути, его определение — заключается в том, что используются только обратимые процессы. Необратимые процессы связаны с диссипативными факторами, такими как трение и турбулентность. Это увеличивает теплоотдачу Q c к окружающей среде и снижает КПД двигателя. Очевидно, что обратимые процессы предпочтительнее.
Двигатель Карно
Сформулированный в терминах обратимых процессов, второй закон термодинамики имеет третью форму:
Двигатель Карно, работающий между двумя заданными температурами, имеет максимально возможный КПД любой тепловой машины, работающей между этими двумя температурами. Кроме того, все двигатели, использующие только обратимые процессы, имеют одинаковую максимальную эффективность при работе в пределах одних и тех же заданных температур.
На рисунке 2 показана диаграмма PV для цикла Карно. Цикл включает два изотермических и два адиабатических процесса. Напомним, что и изотермические, и адиабатические процессы в принципе обратимы.
Карно также определил КПД идеальной тепловой машины, то есть двигателя Карно. Всегда верно, что эффективность циклической тепловой машины определяется выражением:
Eff=Qh−QcQh=1−QcQh\displaystyle{Eff}=\frac{Q_{\text{h}}-Q_{\text{ c}}}{Q_{\text{h}}}=1-\frac{Q_{\text{c}}}{Q_{\text{h}}}\\Eff=QhQh−Qc =1−QhQc
Карно обнаружил, что для идеальной тепловой машины отношение
QcQh\frac{Q_{\text{c}}}{Q_{\text{h}}}\\QhQc
равно отношению абсолютных температур теплоносителей. То есть
То есть
QcQh=TcTh\frac{Q_{\text{c}}}{Q_{\text{h}}}=\frac{T_{\text{c}}}{T_{\text{h }}}\\QhQc=ThTc
для двигателя Карно, так что максимальный или КПД Карно Eff C задается как
EffC=1−TcTh\displaystyle {Eff}_{\text{C}}=1-\frac{T_{\text{c}}}{T_{\text{h}}}\\EffC=1−ThTc
где T h и T c в градусах Кельвина (или в любой другой абсолютной шкале температур). Ни одна настоящая тепловая машина не может работать так же хорошо, как КПД Карно — фактический КПД около 0,7 от этого максимума обычно является лучшим, чего можно достичь. Но идеальный двигатель Карно, как и пьющая птица выше, хотя и является увлекательной новинкой, но имеет нулевую мощность. Это делает его нереальным для любых приложений.
Интересный результат Карно означает, что 100% эффективность возможна только при T c = 0 K, то есть только в том случае, если бы холодный резервуар был при абсолютном нуле, что практически и теоретически невозможно. Но физический смысл таков: единственный способ заставить всю теплопередачу пойти на работу — это убрать всю тепловую энергию, а для этого требуется холодный резервуар при абсолютном нуле.
Но физический смысл таков: единственный способ заставить всю теплопередачу пойти на работу — это убрать всю тепловую энергию, а для этого требуется холодный резервуар при абсолютном нуле.
Также очевидно, что наибольшая эффективность достигается, когда отношение
TcTh\frac{T_{\text{c}}}{T_{\text{h}}}\\ThTc как можно меньше. Как обсуждалось для цикла Отто в предыдущем разделе, это означает, что эффективность максимальна при максимально возможной температуре горячего резервуара и минимально возможной температуре холодного резервуара. (Эта установка увеличивает площадь внутри замкнутого контура на PV диаграмма; Кроме того, кажется разумным, что чем больше разница температур, тем легче направить теплопередачу на работу.) Фактические температуры резервуара тепловой машины обычно связаны с типом источника тепла и температурой окружающей среды, в которую происходит теплообмен. Рассмотрим следующий пример.
Рисунок 2. PV диаграмма для цикла Карно, использующего только обратимые изотермические и адиабатические процессы. Теплопередача Q h поступает в рабочее тело при изотермическом пути AB, который протекает при постоянной температуре T h . Теплообмен Q c происходит вне рабочего тела по изотермическому пути CD, который протекает при постоянной температуре T c . Чистый выход W равен площади внутри пути ABCDA. Также показана схема двигателя Карно, работающего между горячим и холодным резервуарами при температуре T h и T c . Любая тепловая машина, использующая обратимые процессы и работающая между этими двумя температурами, будет иметь такой же максимальный КПД, как и машина Карно.
PV диаграмма для цикла Карно, использующего только обратимые изотермические и адиабатические процессы. Теплопередача Q h поступает в рабочее тело при изотермическом пути AB, который протекает при постоянной температуре T h . Теплообмен Q c происходит вне рабочего тела по изотермическому пути CD, который протекает при постоянной температуре T c . Чистый выход W равен площади внутри пути ABCDA. Также показана схема двигателя Карно, работающего между горячим и холодным резервуарами при температуре T h и T c . Любая тепловая машина, использующая обратимые процессы и работающая между этими двумя температурами, будет иметь такой же максимальный КПД, как и машина Карно.
Пример 1. Максимальная теоретическая эффективность ядерного реактора
В ядерном энергетическом реакторе вода под давлением находится при температуре 300ºC.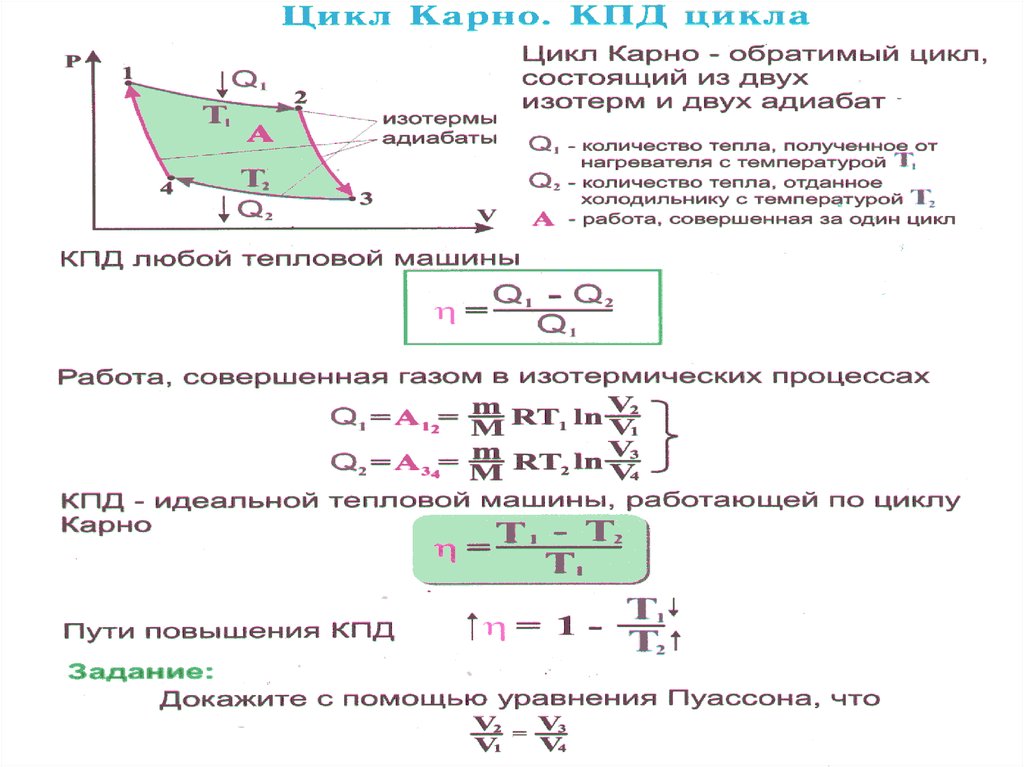 (Более высокие температуры теоретически возможны, но практически невозможны из-за ограничений материалов, используемых в реакторе.) Теплопередача этой воды представляет собой сложный процесс (см. рис. 3). Пар, вырабатываемый в парогенераторе, используется для привода турбогенераторов. В конце концов пар конденсируется в воду при температуре 27ºC, а затем снова нагревается, чтобы начать цикл заново. Рассчитайте максимальный теоретический КПД тепловой машины, работающей между этими двумя температурами.
(Более высокие температуры теоретически возможны, но практически невозможны из-за ограничений материалов, используемых в реакторе.) Теплопередача этой воды представляет собой сложный процесс (см. рис. 3). Пар, вырабатываемый в парогенераторе, используется для привода турбогенераторов. В конце концов пар конденсируется в воду при температуре 27ºC, а затем снова нагревается, чтобы начать цикл заново. Рассчитайте максимальный теоретический КПД тепловой машины, работающей между этими двумя температурами.
Рис. 3. Принципиальная схема ядерного реактора с водой под давлением и паровых турбин, преобразующих работу в электрическую энергию. Теплообмен используется для производства пара, отчасти для того, чтобы избежать загрязнения генераторов радиоактивностью. Две турбины используются, потому что это дешевле, чем работа одного генератора, который производит такое же количество электроэнергии. Пар конденсируется в жидкость перед возвратом в теплообменник, чтобы поддерживать низкое давление пара на выходе и способствовать прохождению пара через турбины (эквивалентно использованию холодного резервуара с более низкой температурой).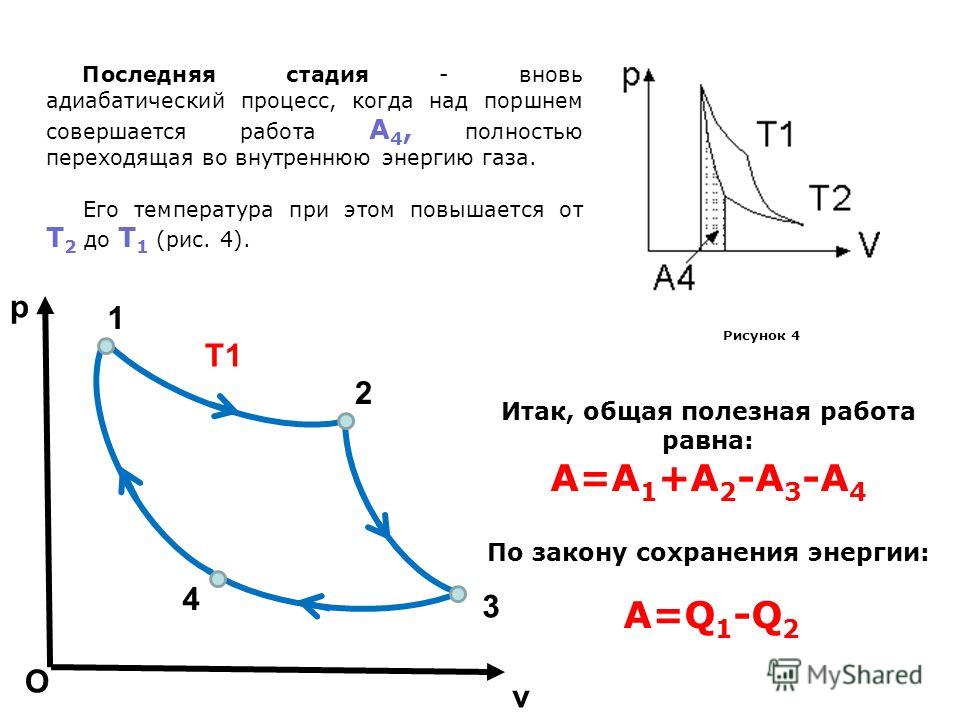 Значительная энергия, связанная с конденсацией, должна рассеиваться в окружающей среде; в этом примере используется градирня, поэтому прямая передача тепла в водную среду отсутствует. (Обратите внимание, что вода, поступающая в градирню, не контактирует с паром, проходящим через турбины.)
Значительная энергия, связанная с конденсацией, должна рассеиваться в окружающей среде; в этом примере используется градирня, поэтому прямая передача тепла в водную среду отсутствует. (Обратите внимание, что вода, поступающая в градирню, не контактирует с паром, проходящим через турбины.)
Стратегия
Так как температуры даны для горячего и холодного резервуаров этой тепловой машины,
EffC=1−TcTh{Eff}_{\text{C}}=1-\frac{T_{\text{c}}}{T_ {\text{h}}}\\EffC=1−ThTc
можно использовать для расчета эффективности Карно (максимальной теоретической). Эти температуры должны быть сначала преобразованы в кельвины.
Раствор
Температура горячего и холодного пласта составляет 300ºC и 27,0ºC соответственно. Тогда в кельвинах T h = 573 K и T c = 300 K, так что максимальная эффективность
EffC=1−TcTh\displaystyle{Eff}_{\text{C}}=1-\frac{T_ {\text{c}}}{T_{\text{h}}}\\EffC=1−ThTc
.
Таким образом,
EffC=1−300 K573 K =0,476, или 47,6%\begin{array}{lll}{Eff}_{\text{C}}&=&1-\frac{300\text{ K }}{573\text{ K}}\\\text{ }&=&0,476\text{ или }47,6\%\end{массив}\\EffC ==1−573 K300 K0,476 , или 47,6%
Обсуждение
Фактический КПД типичной атомной электростанции составляет около 35%, что немногим лучше, чем в 0,7 раза больше максимально возможного значения, что является данью превосходной инженерной мысли. Электростанции, работающие на угле, нефти и природном газе, имеют больший фактический КПД (около 42%), потому что их котлы могут достигать более высоких температур и давлений. Температура холодного резервуара на любой из этих электростанций ограничена местными условиями. На рисунке 4 показан внешний вид атомной электростанции (а) и внешний вид угольной электростанции (б). У обоих есть градирни, в которые вода из конденсатора поступает в градирню в верхней части и распыляется вниз, охлаждаясь за счет испарения.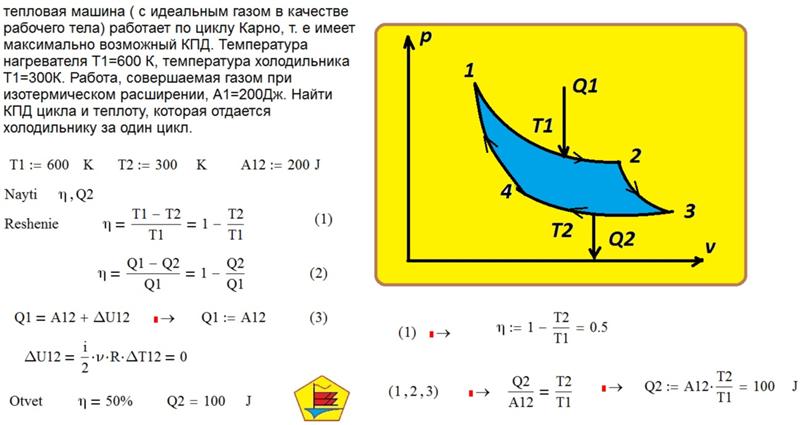
Рис. 4. (а) Атомная электростанция (фото: BlatantWorld.com) и (б) угольная электростанция. Оба имеют градирни, в которых вода испаряется в окружающую среду, что соответствует Q c . Ядерный реактор, поставляющий Q h , расположен внутри куполообразной защитной оболочки. (кредит: Роберт и Михаэла Викол, publicphoto.org)
Поскольку все реальные процессы необратимы, реальный КПД тепловой машины никогда не может быть таким же большим, как у машины Карно, как показано на рис. 5а. Даже при наличии наилучшей тепловой машины в периферийном оборудовании, таком как электрические трансформаторы или автомобильные трансмиссии, всегда присутствуют диссипативные процессы. Это еще больше снижает общую эффективность за счет преобразования части выходной мощности двигателя обратно в теплопередачу, как показано на рисунке 5b.
Рис. 5. Настоящие тепловые двигатели менее эффективны, чем двигатели Карно. (а) В реальных двигателях используются необратимые процессы, уменьшающие передачу тепла на работу. Сплошные линии представляют реальный процесс; пунктирные линии — это то, что двигатель Карно сделал бы между теми же двумя резервуарами. б) Трение и другие диссипативные процессы в выходных механизмах тепловой машины преобразуют часть ее работы в теплопередачу окружающей среде.
(а) В реальных двигателях используются необратимые процессы, уменьшающие передачу тепла на работу. Сплошные линии представляют реальный процесс; пунктирные линии — это то, что двигатель Карно сделал бы между теми же двумя резервуарами. б) Трение и другие диссипативные процессы в выходных механизмах тепловой машины преобразуют часть ее работы в теплопередачу окружающей среде.
Резюме раздела
- Цикл Карно — это теоретический цикл, который является наиболее эффективным из возможных циклических процессов. Любой двигатель, использующий цикл Карно, в котором используются только обратимые процессы (адиабатический и изотермический), известен как двигатель Карно.
- Любой двигатель, использующий цикл Карно, обладает максимальным теоретическим КПД.
- Хотя двигатели Карно являются идеальными двигателями, в действительности ни один двигатель не достигает теоретического максимального КПД Карно, поскольку определенную роль играют диссипативные процессы, такие как трение.
 Циклы Карно без потери тепла могут быть возможны при абсолютном нуле, но это никогда не наблюдалось в природе.
Циклы Карно без потери тепла могут быть возможны при абсолютном нуле, но это никогда не наблюдалось в природе.
Концептуальные вопросы
- Подумайте о пьющей птице в начале этого раздела (рис. 1). Хотя птица обладает теоретически максимально возможной эффективностью, если со временем ее предоставить самой себе, она перестанет «пить». Какие диссипативные процессы могут привести к прекращению движения птицы?
- Можно ли использовать усовершенствованные технологии и материалы в тепловых двигателях для уменьшения передачи тепла в окружающую среду? Могут ли они полностью устранить передачу тепла в окружающую среду?
- Изменяет ли второй закон термодинамики принцип сохранения энергии?
Задачи и упражнения
1. Определенный бензиновый двигатель имеет КПД 30,0%. Какой будет температура горячего резервуара для двигателя Карно с таким КПД, если он работает с температурой холодного резервуара 200ºC?
2. Ядерный реактор с газовым охлаждением работает в диапазоне температур горячего и холодного резервуаров от 700°C до 27,0°C. а) Каков максимальный КПД тепловой машины, работающей при этих температурах? б) Найдите отношение этого КПД к КПД Карно стандартного ядерного реактора (найденного в примере 1).
Ядерный реактор с газовым охлаждением работает в диапазоне температур горячего и холодного резервуаров от 700°C до 27,0°C. а) Каков максимальный КПД тепловой машины, работающей при этих температурах? б) Найдите отношение этого КПД к КПД Карно стандартного ядерного реактора (найденного в примере 1).
3. (a) Какова температура горячего резервуара двигателя Карно с КПД 42,0% и температуры холодного резервуара 27,0ºC? (б) Какой должна быть температура горячего резервуара для реальной тепловой машины, которая достигает 0,700 от максимального КПД, но при этом имеет КПД 42,0% (и холодный резервуар при 27,0ºC)? (c) Подразумевает ли ваш ответ практические пределы эффективности автомобильных бензиновых двигателей?
4. Паровозы имеют КПД 17,0% и работают с температурой горячего пара 425ºC. а) Какой была бы температура холодного резервуара, если бы это был двигатель Карно? б) Каков был бы максимальный КПД этой паровой машины, если бы температура ее холодного резервуара была 150°С?
5. Практические паровые двигатели используют пар с температурой 450ºC, который позже выбрасывается при температуре 270ºC. а) Каков максимальный КПД такой тепловой машины? (b) Поскольку пар с температурой 270ºC все еще довольно горячий, вторая паровая машина иногда приводится в действие с использованием выхлопных газов первой. Каков максимальный КПД второго двигателя, если его выхлоп имеет температуру 150°С? в) Каков общий КПД двух двигателей? (d) Покажите, что это такой же КПД, как у одной машины Карно, работающей при температуре от 450°C до 150°C.
Практические паровые двигатели используют пар с температурой 450ºC, который позже выбрасывается при температуре 270ºC. а) Каков максимальный КПД такой тепловой машины? (b) Поскольку пар с температурой 270ºC все еще довольно горячий, вторая паровая машина иногда приводится в действие с использованием выхлопных газов первой. Каков максимальный КПД второго двигателя, если его выхлоп имеет температуру 150°С? в) Каков общий КПД двух двигателей? (d) Покажите, что это такой же КПД, как у одной машины Карно, работающей при температуре от 450°C до 150°C.
6. Угольная электростанция имеет КПД 38%. Температура пара, выходящего из котла, составляет
550°C550\text{\textgrade }\text{C}550°C
. Какой процент от максимального КПД дает эта станция? (Предположим, что температура окружающей среды составляет
20°C20\text{\textgrade }\text{C}20°C
.)
7. Готовы ли вы оказать финансовую поддержку изобретателю, который продает устройство, которое она утверждает, что имеет 25 кДж теплопередачи при 600 К, имеет теплопередачу в окружающую среду при 300 К и выполняет работу 12 кДж? Поясните свой ответ.
8. Необоснованные результаты (a) Предположим, вы хотите спроектировать паровую машину, которая передает тепло в окружающую среду при 270ºC и имеет КПД Карно 0,800. Какой температуры горячего пара вы должны использовать? б) Что неразумного в температуре? в) Какая посылка неразумна?
9. Необоснованные результаты Рассчитайте температуру холодного резервуара паровой машины, использующей горячий пар при 450ºC и имеющей КПД Карно 0,700. б) Что неразумного в температуре? в) Какая посылка неразумна?
Глоссарий
Цикл Карно: циклический процесс, в котором используются только обратимые процессы, адиабатические и изотермические процессы
Двигатель Карно: тепловой двигатель, использующий цикл Карно для тепловой машины
Избранные решения задач и упражнений
1. 403ºC
3. (а) 244ºC; (б) 477°С; (c) Да, поскольку двигатели автомобилей не могут перегреться без перегрева, их эффективность ограничена.
5. (a)
Eff1=1−Tc,1Th,1=1−543 K723 K=0,249 или 24,9%{\matit{\text{Eff}}}_{\text{1}}=1 -\frac{{T}_{\text{c,1}}}{{T}_{\text{h,1}}}=1-\frac{\text{543 K}}{\text{ 723 K}}=0\text{.}\text{249}\text{ или }\text{24}\text{.}9\%\\Eff1=1−Th,1Tc,1 =1−723 K543 K=0,249 или 24,9 %
(b)
Eff2=1−423 K543 K=0,221 или 22,1 %{\matit{\text{Eff}}}_{2}=1-\ frac{\text{423 K}}{\text{543 K}}=0\text{.}\text{221}\text{ или }\text{22}\text{.}1\%\\Eff2 =1−543 K423 K=0,221 или 22,1%
(c)
Eff1=1−Tc,1Th,1⇒Tc,1=Th,1(1,−,eff1)аналогично, Tc,2=Th,2(1−Eff2){\mathit{\ text{Eff}}}_{1}=1-\frac{{T}_{\text{c,1}}}{{T}_{\text{h,1}}}\Rightarrow{T} _{\text{c,1}}={T}_{\text{h,1}}\left(1,-,{\mathit{\text{eff}}}_{1}\right)\ текст {аналогично, {T} _ {\ text {c, 2}} = {T} _ {\ text {h, 2}} \ left (1 — {\ mathit {\ text {Eff}}} _ { 2}\right)\\Eff1=1−Th,1Tc,1⇒Tc,1=Th,1(1,−,eff1) аналогично, Tc,2=Th,2 (1−Eff2)
с использованием T h,2 = T c,1 в приведенном выше уравнении дает
Tc,2=Th,1(1-Eff1)(1-Eff2)≡Th,1(1-Effoverall)∴(1-Effoverall)=(1-Eff1)(1-Eff2)Effoverall=1-( 1−0,249) (1−0,221) = 41,5% \ begin {array} {l} {T} _ {\ text {c, 2}} = {T} _ {\ text {h, 1}} \ left ( 1-{Eff}_{1}\right)\left(1-{Eff}_{2}\right)\equiv{T}_{\text{h,1}}\left(1-{Eff} _ {\ text {общий}} \ справа) \\\ поэтому \ влево (1- {Eff} _ {\ text {общий}} \ справа) = \ влево (1 — {\ mathit {\ text {Eff}} }_{1}\right)\left(1-{Eff}_{2}\right)\\{Eff}_{\text{общий}}=1-\left(1-0,249\right)\left (1-0,221\справа)=41,5\%\end{массив}\\Tc,2=Th,1(1−Eff1)(1−Eff2)≡Th,1(1−Effoverall) ∴(1-Effoverall)=(1-Eff1)(1-Eff2)Effoverall=1-(1-0,249)(1−0,221)=41,5%
(d)
Effoverall=1−423K723K=0,415 или 41,5{\text{Eff}}_{\text{общий}}=1-\frac{\text{423 K}}{\text{723 K }}=0\text{. }\text{415}\text{ или }\text{41}\text{.}5\\%\\Effoverall=1−723 K423 K=0,415 или 41,5
}\text{415}\text{ или }\text{41}\text{.}5\\%\\Effoverall=1−723 K423 K=0,415 или 41,5
7. Теплопередача в холодный резервуар составляет
Qc=Qh−W=25kJ−12kJ=13kJ{Q}_{\text{c}}={Q}_{\text{h}}-W=\ text{25}\text{kJ}-\text{12}\text{kJ}=\text{13}\text{kJ}\\Qc=Qh−W=25kJ−12kJ=13kJ
, поэтому эффективность
Eff=1−QcQh=1−13kJ25kJ=0,48\mathit{Eff}=1-\frac{{Q}_{\text{c}}}{{Q}_{\text{h}}}=1 -\frac{\text{13}\text{кДж}}{\text{25}\text{кДж}}=0\text{.}\text{48}\\Eff=1−QhQc =1−25кДж13кДж=0,48
. Эффективность Карно составляет
c}}}{{T}_{\text{h}}}=1-\frac{\text{300}\text{K}}{\text{600}\text{K}}=0\text {.}\text{50}\\EffC=1−ThTc=1−600K300K=0,50
. Фактическая эффективность составляет 96% от эффективности Карно, что намного выше, чем лучший из когда-либо достигнутых примерно 70%, поэтому ее схема, вероятно, мошенническая.
9. (a) -56,3ºC (b) Температура слишком низкая для работы паровой машины (местные условия). Это ниже точки замерзания воды. (c) Предполагаемая эффективность слишком высока.
Это ниже точки замерзания воды. (c) Предполагаемая эффективность слишком высока.
Лицензии и ссылки
Контент по лицензии CC, совместно используемый ранее
- College Physics. Автор : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/college-physics/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units. Лицензия : CC BY: Attribution . Условия лицензии : Находится в Лицензии
температура — Почему второй закон термодинамики препятствует 100% эффективности?
Тот факт, что тепловая машина не может быть на 100% эффективнее, является следствием формулировки второго закона Кельвина-Планка, которую можно резюмировать как
Формулировка второго закона Кельвина-Планка
«Никакая тепловая машина не может работать в цикле , передавая тепло с помощью одного теплового резервуара» (мой акцент на цикл )
СЛЕДСТВИЕ по Кельвину-Планку : Никакая тепловая машина не может иметь более высокий КПД, чем цикл Карно, работающий между одними и теми же резервуарами.
Вы, наверное, знаете, что при обратимом изотермическом расширении Карно тепло, выделяемое высокотемпературным резервуаром, равно работе, выполненной при расширении. Этот процесс преобразует тепло в работу со 100% эффективностью. Но процесс не является циклом . Для работы в цикле система должна вернуться в исходное состояние. После обратимого изотермического расширения нет возможности вернуться в исходное состояние и совершить чистую работу, не отдав часть тепла в более низкотемпературный резервуар.
Можно, например, сразу после обратимого изотермического расширения выполнить обратимое изотермическое сжатие и вернуться в исходное состояние. Но отрицательная работа сжатия была бы равна положительной работе расширения, если бы «цикл» не выполнял чистую работу.
Чтобы произвести чистую работу в цикле Карно, необходимо следовать изотермическому расширению с обратимым адиабатическим расширением. Это снижает температуру системы до температуры резервуара с более низкой температурой. Затем обратимое изотермическое сжатие, за которым следует обратимое адиабатическое сжатие, возвращает систему и окружающую среду в их исходное состояние, и сетевая работа выполняется. Но эта работа равна теплу, поступающему в систему, за вычетом отводимого тепла для эффективности менее 100 %.
Затем обратимое изотермическое сжатие, за которым следует обратимое адиабатическое сжатие, возвращает систему и окружающую среду в их исходное состояние, и сетевая работа выполняется. Но эта работа равна теплу, поступающему в систему, за вычетом отводимого тепла для эффективности менее 100 %.
Все циклы теплового двигателя должны отводить некоторое количество тепла для КПД менее 100 %. Наиболее эффективно это делает цикл Карно.
Я понимаю это, я думаю, что я не вижу, как
утверждение Δ𝑆≥0 эквивалентно утверждению планки Кельвина.
На самом деле мы можем показать, что единственный способ завершить цикл и получить $\Delta S_{system}=0$ — это отвести тепло в низкотемпературный резервуар. По определению, термодинамический цикл — это цикл, в котором все свойства системы (энтропия, внутренняя энергия, давление, температура и т. д.) возвращаются в исходное состояние.
Итак, передадим теплоту из окружающей среды в систему посредством обратимого изотермического расширения идеального газа.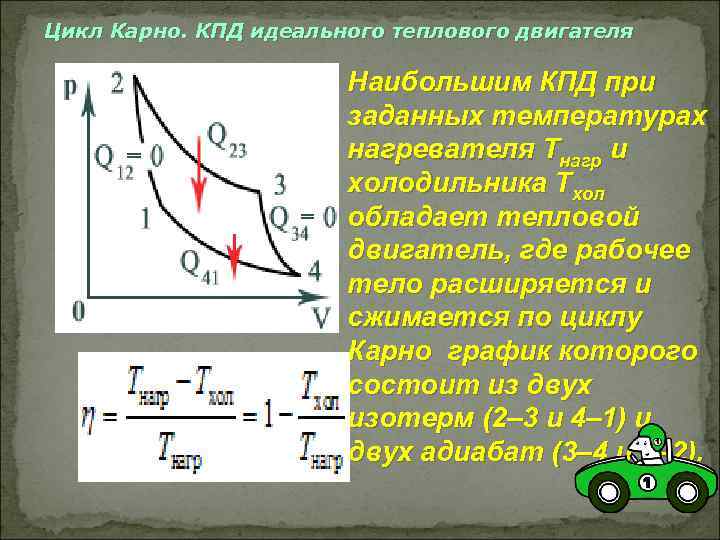 Так как для идеального газа $\Delta U$ зависит только от температуры, то из первого закона $\Delta U=0$ и $W=Q$, и теоретически мы имеем полное преобразование теплоты в работу при 100% КПД для процесс. Однако при изотермическом расширении энтропия системы увеличилась на $\Delta S_{sys}=+\frac{Q_H}{T_H}$, где $Q_H$ — теплоотдача от высокотемпературного резервуара $T_H$.
Так как для идеального газа $\Delta U$ зависит только от температуры, то из первого закона $\Delta U=0$ и $W=Q$, и теоретически мы имеем полное преобразование теплоты в работу при 100% КПД для процесс. Однако при изотермическом расширении энтропия системы увеличилась на $\Delta S_{sys}=+\frac{Q_H}{T_H}$, где $Q_H$ — теплоотдача от высокотемпературного резервуара $T_H$.
Чтобы завершить цикл, мы должны вернуть энтропию системы в исходное состояние, то есть избавиться от энтропии в размере $\frac{Q_H}{T_H}$. Теперь, вот ключевой момент. Единственный способ передачи энтропии — это передача тепла. Значит, чтобы вернуть систему в исходное состояние, надо передать тепло $Q_L$ низкотемпературному резервуару. Когда мы делаем это, чистая работа, выполненная в цикле, равна
$$W_{net}=Q_{H}-Q_{L}$$
Эффективность $ζ$ любого цикла равна чистой выполненной работе, деленной на общее добавленное тепло, или
$$ζ=\frac{W_{net}}{Q_H}=\frac{Q_{H}-Q_{L}}{Q_H}$$
Следовательно, для любого цикла
$$ζ< 1$$
Вышесказанное относится к любому циклу. Именно то, является ли цикл обратимым, определяет максимальную эффективность цикла. Максимальная эффективность достигается, когда цикл обратим. Для обратимого цикла и $\Delta S_{sys}$, и $\Delta S_{sur}$ равны нулю при $\Delta S_{tot}=0$. Для необратимого цикла в системе генерируется дополнительная энтропия, которая должна быть передана в окружающую среду в виде дополнительного тепла, что приводит к $\Delta S_{sur}>0$ и уменьшает количество работы, которую можно выполнить при том же подводимом тепле. .
Именно то, является ли цикл обратимым, определяет максимальную эффективность цикла. Максимальная эффективность достигается, когда цикл обратим. Для обратимого цикла и $\Delta S_{sys}$, и $\Delta S_{sur}$ равны нулю при $\Delta S_{tot}=0$. Для необратимого цикла в системе генерируется дополнительная энтропия, которая должна быть передана в окружающую среду в виде дополнительного тепла, что приводит к $\Delta S_{sur}>0$ и уменьшает количество работы, которую можно выполнить при том же подводимом тепле. .
Наконец, как сказано в Следствии Кельвина-Планка, «Никакая тепловая машина не может иметь более высокую эффективность, чем цикл Карно, работающий между одними и теми же резервуарами», что означает, что цикл Карно является наиболее эффективным из всех обратимых циклов.
Я искал более явный математический результат, показывающий, что вы можете
не экономить энергию и одновременно следовать Δ𝑆≥0.
Вы можете сохранять энергию и одновременно иметь $\Delta S_{tot}$ ≥0.


 Циклы Карно без потери тепла могут быть возможны при абсолютном нуле, но это никогда не наблюдалось в природе.
Циклы Карно без потери тепла могут быть возможны при абсолютном нуле, но это никогда не наблюдалось в природе.